Как найти эквивалентную ставку простых процентов

Эквивалентность процентных ставок

Краткая теория

---

Для процедур наращения и дисконтирования могут применяться
различные виды процентных ставок. Одну процентную ставку можно эквивалентным
образом выразить через другую ставку процентов. При этом замена одного вида
ставки на другой при соблюдении принципа эквивалентности не изменяет отношения
сторон в рамках одной операции. Для участвующих в сделке сторон безразлично,
какой вид ставки фигурирует в контракте.

Формулы эквивалентности
ставок во всех случаях получим, исходя из равества взятых попарно множителей
наращения. Приведем лишь пример. Определим соотношение
эквивалентности между

простой ставкой наращения
и

сложной ставкой наращения. 
Для этого приравняем друг к другу
соответствующие множители наращения:

 – ставка простых процентов

 – ставка
сложных процентов

Приведенное равенство
предполагает, что начальные и наращенные суммы при применении двух видов ставок
идентичны. Решение дает следующие отношения эквивалентности ставок:

Аналогичным образом определяются и другие соотношения
эквивалентности ставок. Например соотношение между годовой номинальной учетной ставкой и номинальной ставкой процента,
между

номинальной и эффективной ставкой процента

Примеры решения задач

---

Задача 1

На какую

годовую ставку простых процентов
можно заменить годовую

номинальную ставку процентов, равную 17%,
если начисление по ней производилось ежеквартально в течение четырех лет?

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Годовую ставку можно найти из
равенства:

 -номинальная
годовая ставка

 -число лет

 -число
начислений процентов в году (ежеквартальное)

 -искомая
годовая ставка простых процентов

Получаем:

Ответ: i=48.66%.

---

Задача 2

Предприятию
выдан кредит финансовой организацией на 2 года под 11,5% процентов годовых.

Определить
эквивалентную

простую учетную ставку, если кредит был выдан по ставке простых процентов.

Решение

Ответ

Кредит,
выданный под 11.5% простых процентов, эквивалентен кредиту под 9,3% по простой
учетной ставке на срок 2 года.

Эквивалентная
процентная ставка
– это ставка, которая для рассматриваемой
финансовой операции даст точно такой
же денежный результат (наращенную сумму
или современную стоимость), что и
применяемая в этой операции процентная
ставка.

Определение
эквивалентной ставки основывается на
приравнивании множителей наращения
или дисконтированием для различных
вариантов начисления процентов.

Пример
1.
Каковы будут эквивалентные номинальные
процентные ставки с полугодовым и
ежемесячным начислением процентов,
если соответствующая им эффективная
ставка должна быть равна 25 %?

Решение:

1.Находим
номинальную ставку из формулы (3.4):

j
= m*[(1
+ i)^{1
/ m}
– 1]

2.
Рассчитываем номинальную ставку для
полугодового начисления процентов:

j=2*[(1+0.25)^1/2-1]=0,2361

3.
Рассчитываем номинальную ставку для
ежемесячного начисления процентов:

j
= 12*[(1
+0,25i)^1
/12
– 1] = 0,2252.

Таким
образом, номинальные ставки 23,61 % с
полугодовым начислением процентов и
22,52 % с ежемесячным начислением процентов
являются эквивалентными.

Пример
2.
Найти оптимальный вариант для размещения
капитала на 4 года либо под сложную
процентную ставку 18 % годовых с полугодовым
начислением процентов, либо под простую
процентную ставку 22 % годовых.

Решение:

Составляем
уравнение эквивалентности в виде
равенства коэффициентов наращения по
простой и сложной процентным ставкам:

(1+i*n)=(1+j/m)^m*n

Находим
для сложной процентной ставки эквивалентную
простую ставку:

i
= [(1 + j
/ m)^m*
n
– 1] / n
= [(1 + 0,18 / 2)^{2
• 4}
– 1] / 4 = 0,2481.

Таким
образом, эквивалентная сложной ставке
по первому варианту простая процентная
ставка составляет 24,81 % годовых, что выше
предлагаемой простой ставки в 22 % годовых
по второму варианту, следовательно,
выгоднее разместить капитал по первому
варианту, т.е. под 18 % годовых с полугодовым
начислением процентов.

В
практической деятельности часто
возникает необходимость изменения
условий ранее заключенного контракта
– объединение нескольких платежей или
замене единовременного платежа рядом
последовательных платежей. Естественно,
что в таких условиях ни один из участников
финансовой операции не должен иметь
убыток, вызванный изменением финансовых
условий, поэтому изменение условий
контрактов базируется на принципе
финансовой эквивалентности платежей.
Эквивалентными считаются такие платежи,
которые будучи приведенными к одному
моменту времени, оказываются равными.
Приведение осуществляется путем
дисконтирования (приведение к более
ранней дате) или наращения суммы платежа
(если эта дата относится к будущему).
Решение подобных задач сводится к
построению уравнения
эквивалентности,
в котором сумма заменяемых платежей,
приведенная к какому-то одному моменту
времени, приравнена к сумме платежей
по новому обязательству, приведенному
к тому же моменту времени.

На
принципе эквивалентности платежей
основывается сравнение разновременных
платежей, рассмотренное в примерах 3 и
4 данного раздела.

Пример
3.
Можно ли считать равноценными два
обязательства со следующими условиями:
первое – выплатить 15000 грн. через 4
месяца, второе – выплатить 18000 грн через
6 месяцев. Для сравнения использовать
простую процентную ставку 20 % годовых.

Решение:

Для
сравнения обязательств, рассчитаем
современную стоимость каждого на начало
операции по формуле (4.1).

PV₁=15000*(1+0.2)^-4/12
=
14115.54 грн.

PV₂=18000*(1+0.2)^-6/12
=
16431.68 грн.

Таким
образом, сравниваемые обязательства
не являются эквивалентными при заданной
ставке.

Пример
4.
Клиент положил в банк на текущий счет
1000 грн, Банк выплачивает проценты
ежемесячно по ставке 2 % годовых. Через
месяц клиент положил на счет 500 грн.,
через 2 месяца снял 400 грн., а через 6
месяцев после этого закрыл счет. Какую
сумму клиент получил при закрытии счета?

Решение:

В
соответствии с принципом эквивалентности
платежей, суммарная современная стоимость
снятых со счета денег равна современной
стоимости вложенных денег, т.е.

1000+500*(1+0,02/12)^-12*1/12=400*(1+0,02/12)^-12*2/12+X*(1+0.02/12)^-2*8/12,

где
X
– сумма при закрытии счета.

Из
этого уравнения находим X=
1115,26 грн.

Таким
образом, при закрытии счета клиент
получил 1115,26 грн.

Консолидация
(объединение) платежей предполагает
замену платежей S₁,
S₂,
S₃,….
S_k

со сроками n₁
n₂,n₃,…..n
_k

одним в сумме S₀
и сроком n₀
.
Для решения этой задачи составляется
уравнение эквивалентности в виде
равенства суммы объединенного платежа
(S₀)
сумме наращенных и дисконтированных
платежей по первоначальным условиям.
Размер консолидированного платежа
определяется по следующим формулам:

а)
простые проценты

(5.1)

б)
сложные проценты

(5.2)

где
S_j
–
размеры объединяемых платежей со сроками
n_j
< n₀,

S_k
–
размеры объединяемых платежей со сроками
n_k
> n₀,

Пример
5.
Решено консолидировать два платежа со
сроками 20.04 и 10.05 и суммами платежа 20000
грн и 30000 грн. соответственно. Срок
консолидации платежей 31.05. Определить
сумму консолидированного платежа при
условии, что ставка равна 15 % простых
годовых и временная база 360 дней.

Решение:

Определим
временной интервал между сроками

1.
первого платежа и консолидированного
платежа:

t₁=
11(апрель) + 31(май) – 1 = 41 день;

2.
второго платежа и консолидированного
платежа:

t₂
= 22(май) – 1 = 21 день.

3.
Сумму консолидированного платежа
определим по формуле (5.1):

S_0.=
20000 * (1 + 0,15*41/360 )+30000 * (1 + 0,15*21/360) = =50604,17 грн.

Таким
образом, консолидированный платеж со
сроком 31.05 составит 50604,17 грн.

Срок
объединенного платежа определяется по
следующим формулам:

а)
простые проценты

(5.3)

б)
сложные проценты

(5.4)

где
PV
– современная стоимость объединяемых
платежей.

Пример
6.
Платежи
в
сумме 5000 грн. и 7000 грн. и сроками уплаты
через 6 месяцев и один год объединяются
в один суммой 13000 грн. Определить срок
консолидированного платежа, если при
консолидации используется сложная
процентная ставка 17 % годовых.

Решение:

1.
Определим современную стоимость
объединяемых платежей:

PV=
5000* (1+0,17)^-6/12
+
7000*(1+0,17)^-1=
10605,41

2.
Срок консолидированного платежа
определяем по формуле (5.4):

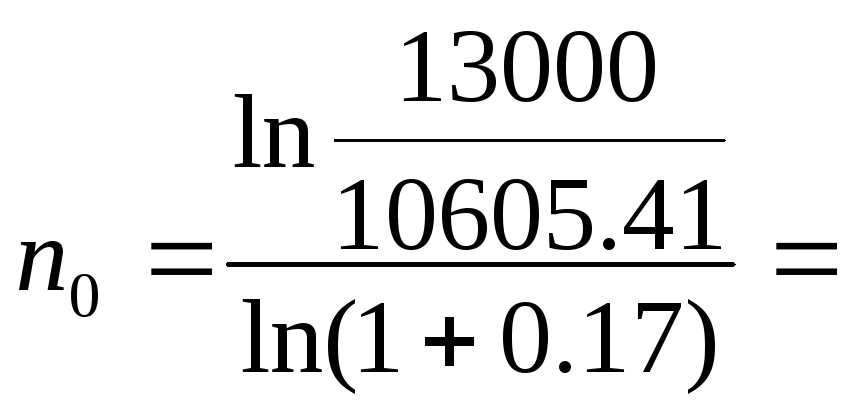1,3
года

Таким
образом, платежи можно объединить в
один с уплатой через 1,3 года.

Существуют
различные варианты изменения условий
финансового соглашения, и, в соответствии
с этим. и многообразие уравнений
эквивалентности. В общем виде уравнения
эквивалентности при использовании
сложной процентной ставки имеют следующий
вид:

(5.5)

где
S_q
и p_q
–
платежи и сроки, в которые должны быть
произведены эти платежи, по новым
условиям договора;

R_k
и t_k

– платежи и сроки, в которые должны быть
произведены эти платежи, по старым
условиям договора;

v=1+i
– если соответствующие платежи
производятся ранее момента, к которому
приводятся платежи;

v=(1+i)^-1
если
соответствующие платежи производятся
позднее момента, к которому приводятся
платежи.

Пример
7.
Две
суммы 6000 грн. и 8000 грн.
должны
бать выплачены 1 ноября текущего года
и 1 февраля следующего не високосного
года. Обе стороны договора согласились
пересмотреть порядок выплат следующим
образом: 1 декабря выплачивают 7000 грн,
остаток долга гасится 1 марта. Найти
сумму погашающего остатка, если расчет
осуществляется при ставке простых
процентов, равной 18 % и временной базе
K=365.

Решение:

За
современный момент (дата операции, к
которой будут приводится все платежи)
возьмем момент выплаты 8000 грн. 1 февраля
следующего года. Уравнение эквивалентности
будет следующего вида:
6000*(1+0,18*94/365)+8000=7000*(1+0,18*61/365)+S*(1+0,18*28/365)^-1

Отсюда
S=
7165,15 грн.

Таким
образом, сумма погашающего платежа
составит 7165,15 грн.

Вопросы
для самостоятельного изучения

1.
Эквивалентность простых процентных и
учетных ставок.

2.
Эквивалентность сложных процентных и
учетных ставок.

3.
Составление уравнения эквивалентности
процентных и учетных ставок.

4.
Определение суммы и срока консолидированного
платежа.

5.
Общая задача изменения условий контракта.

Задачи

1.
Банк начисляет на вложенные в него
деньги проценты по ставке j₄
= 16 % и собирается перейти к непрерывному
начислению процентов. Какую силу роста
должен установить банк, чтобы доходы
клиентов не изменились?

2.
Определить при какой номинальной ставке
j₄
деньги удваиваются через 12 лет?

3.
Сумма денег инвестируется при j₄
= 18 % на один год. Определить, какая ставка
j₁₂
накопила бы такую же сумму в конце года?

4.
Коммерческий банк предлагает по
депозитному вкладу следующие простые
процентные ставки:

а)
15 % при сроке вклада 1 месяц;

б)
16 % при сроке вклада 3 месяца;

в)
17 % при сроке вклада 6 месяцев.

Рассчитать
эквивалентные данным простым ставкам
ставки сложных процентов при ежегодной
капитализации.

5.
Банк учитывает вексель за 60 дней до
срока его оплаты по простой учётной
ставке d = 22 %. Определить сложную учётную
ставку, которую должен установить банк,
чтобы доход банка не изме­нился при
временной базе 365 дней и начисление
процентов один раз в год.

6.
Банк учитывает вексель по учётной ставке
f₄
= 16 % и желает перейти к сложной учётной
ставке d. Определить величину сложной
учетной ставки, чтобы доход банка не
изменился.

7.
Определить ставку сложных процентов,
эквивалентную ставке: а) j₂=
16 %, б) j₆=
18 %, в) j₁₂
=
20 %, г) σ = 15 %.

8.
«Дельтабанк» предлагает частным лицам
денежный вклад на год, доход по которому
составляет за первые 2 месяца 15 % годовых,
за следующие 2 месяца – 15,5 %, за следующие
5 месяцев – 16 %, за последние 3 месяца –
17 % годовых. Определите эффективную
процентную ставку при размещении денег
на год под указанные простые и сложные
проценты. В последнем случае начисление
процентов ежемесячное.

9.
Реклама одного коммерческого банка
предлагает 18 % годовых при ежемесячном
начислении процентов. Другой коммерческий
банк предлагает 19 % годовых при
ежеквартальном начислении процентов.
Срок хранения вклада – 12 месяцев. Какому
банку отдать предпочтение?

10.
Сопоставьте условия четырех банков при
сроке депозита 1 год: а) проценты простые
и процентная ставка 18,5 %; б) номинальная
процентная ставка – 17 % годовых, начисление
процентов происходит по полугодиям; в)
номинальная процентная ставка – 17,5 %,
начисление процентов поквартальное;
г) номинальная процентная ставка – 18
%, начисление процентов ежемесячное.

11.
Предприятие получило кредит на год под
номинальную процентную ставку 21 % простых
годовых. Комиссионные составляют 3 % от
суммы кредита. Определите эффективную
процентную ставку при начислении сложных
процентов: а) один раз в год, б) ежеквартально,
в) ежемесячно.

12.
Определить реальную процентную ставку,
если номинальная процентная ставка
составляет 19 %, а темп инфляции определен
в 9 % в год.

13.
Мебельная фабрика продает товары по
одной из следующих схем:

1.
25 % скидка цены при покупке наличными;

2.
20 % стоимости наличными и остальное в
виде 12 одинаковых ежемесячных платежей.
Определить, какая эффективная процентная
ставка делает эти схемы эквивалентными.

14.
Определить, какова современная ценность
10000 грн., если: а) эта сумма будет
получена через 3 года 6 месяцев, б) эта
сумма была получена
2 года 9 месяцев тому назад, в) эта сумма
получена в
настоящий момент времени. Стоимость
денег – 18 % сложных годовых.

15.
Сравниваются два платежа: 20000 грн. с
выплатой через 2 года, и 30000 грн. с
выплатой через 4 года. Можно ли
считать их равноценными? При расчете
применить ставку сложных процентов
20 % годовых.

16.
Клиент положил в банк, выплачивающий
проценты по годовой
ставке 15% сложных сумму 12000 грн. Через 1
год 6 месяцев он снял со счёта 4500 грн., а
ещё через 2 года положил
на свой счёт 2 000 грн. После этого, через
3 года 6
месяцев, он закрыл счёт. Определить,
какую сумму получил клиент при закрытии
счета.

17.
Фермер приобрёл трактор, который стоит
120000 грн.
под 19 % сложных годовых. Через 1 год 6
месяцев он уплатил
70000 грн., а ещё через 6 месяцев полностью
пога­сил
долг и проценты. Определить, какую сумму
фермер выплатил при погашении долга.

18.
Строительный комбинат продаёт коттеджи
стоимостью 180000 грн.,
предоставляя покупателям кредит под
22 % годовых (слож­ных).
Фирма приобрела коттедж, выплатив
20000
грн. через 3 месяца после покупки,
30000 грн. – ещё через
6 месяцев, 10000 грн. – в конце первого года
с момента покупки
и погасила весь долг через 1.5 года с
момента покупки. Определить, какую
сумму составил последний платёж.

19.
Покупатель обязался уплатить фермеру
за купленное у него зерно
35000 грн. через 2 месяца после покупки,
30000 грн. ещё
через 2 месяца и 52000 грн. ещё через 3
месяца. Стороны договорились
объединить эти платежи в один и выплатить
его через
5 месяцев после покупки. Определить
сумму объединенного платежа, если на
деньги начисляется 18 % простых годовых.

20.
Покупатель обязался уплатить фермеру
за купленное у него зерно
55000 грн. через 2 месяца после покупки,
10000 грн. ещё
через 2 месяца и 20000 грн. ещё через 3
месяца. Стороны договорились
объединить эти платежи в один и выплатить
его одним платежом, равным 100000 грн., при
условии начисления процентов по сложной
ставке 21 % годовых.
Определить срок
объединенного платежа, считая с момента
покупки.

21.
Покупатель обязался уплатить фермеру
за купленное у него зерно 55000 грн. через
2 месяца после покупки, 10000 грн. ещё через
2 месяца и 20000 грн. ещё через 3 месяца.
Стороны договорились изменить условия
следующим образом: покупатель выплатит
долг двумя равными уплатами через 3 и
через 6 месяцев после покупки, при условии
начисления процентов по ставке 20 %
сложных годовых. Определить, какова
должна быть величина этих уплат?

22.
Три векселя номинальной стоимостью
3000 грн., 5000 грн. и 8000 грн. со сроками
погашения через 210, 240 и 270 дней объединяются
в один номинальной стоимостью 18000 грн.
Объединение происходит по годовой
ставке сложных процентов – 19 %. Найдите
срок погашения объединенного векселя
при временной базе 365 дней.

23.
Четыре векселя номинальной стоимостью
2000 грн., 3000 грн., 3800 грн и 5000 грн. со сроками
погашения через 38. 60, 80 и 140 дней требуется
объединить в один со сроком погашения
100 дней. Объединение происходит: а) по
ставке простых про­центов – 18 %, б) по
ставке сложных процентов – 18 % годо­вых.
Определить стоимость объединенного
векселя при временной базе 360 дней.

24.
Существует обязательство уплатить
10000 грн через один год. Стороны согласились
изменить условия погашения обязательства
следующим образом: через 2 месяца
выплачивается 3000 грн, еще через 2 месяца
4000 грн., а оставшийся долг спустя год
после последней выплаты. Определить
сумму последнего платежа при условии,
что перерасчет осуществляется по ставке
сложных процентов равной 20 % годовых.

25.
Должник обратился к своему кредитору
(владельцу векселя) с просьбой об
объединении двух векселей в один с
одновременным продлением срока оплаты.
Первый вексель выдан на сумму 15000
грн. со сроком 20.07, второй на сумму
20000 грн. со сроком уплаты 01.09 текущего
года. Владелец векселя согласился на
пролонгацию до 01.10 текущего года,
применив сложную процентную ставку
20 % годовых. Найти сумму консолидированного
векселя при временной базе 360 дней.

Тесты

Возможно
несколько вариантов ответов

1.
Эквивалентная процентная ставка – это:

a)
ставка, которая для рассматриваемой
финансовой операции даст такой же
денежный результат, что и применяемая
в этой операции ставка;

b)
ставка, используемая в банковском
учете;

c)
ставка, при применении которой проценты
начисляются на проценты;

d)
ставка, с помощью которой разрабатывается
уравнение эквивалентности финансовых
обязательств.

2.
Для определения эквивалентных процентных
ставок составляется уравнение
эквивалентности в виде:

a)
равенства коэффициентов наращения;

b)
равенства коэффициентов дисконтирования;

c)
равенства сроков операций.

3.
Эквивалентность ставки сложных процентов
при начислении процентов один раз в год
(i)
и номинальной ставки (j)
не зависят от:

a)
срока операции;

b)
частоты начисления процентов в году;

c)
временной базы

4.
Формула эквивалентности простых и
сложных ставок:

a)

;

b)

;

c).

5.
Сравнить
результаты начисления в зависимости
от срочности вклада, если годовые ставки
начисления простого и сложного процента
одинаковы:

a)
сложный процент всегда выгоднее для
вкладчика независимо от периода
начисления;

b)
для долгосрочных депозитов (больше
года) сложный процент выгоднее простого;

c)
для краткосрочных депозитов (меньше
года) простой процент отстает от
начисления сложного процента;

d)
в пределах года простой процент выгоднее
сложного.

6.
Если при изменении условий контракта
не соблюдается принцип эквивалентности,
то:

a)
ни одна из участвующих сторон не терпит
убытка;

b)
одна из участвующих сторон терпит
убыток.

7.
Уравнение финансовой эквивалентности
обязательств связывает величины
следующих типов:

a)
суммы погашения и нормы процента;

b)
суммы погашения и даты выплат;

c)
суммы погашения, нормы процента и даты
выплат.

8.
Результат сравнения платежей при
изменении условий контракта зависит
от:

a)
выбора размера процентной ставки;

b)
выбора современного момента времени;

c)
выбора метода начисления процентов.

9.
Платежи считаются эквивалентными, если

a)
они равны по абсолютной величине;

b)
равны их современные величины;

c)
платежи, будучи приведенными по одной
и той же процентной ставке на один момент
времени, оказываются равными;

d)
они производятся в начале срока финансовой
операции;

е)
на них начисляются проценты по одной и
той же процентной ставке.

Эквивалентная процентная ставка

это ставка, которая для рассматриваемой финансовой операции даст точно такой же денежный результат (наращенную сумму), что и применяемая в этой операции ставка.

Повышай знания с онлайн-тренажером от Автор24!

1. Напиши термин
2. Выбери определение из предложенных или загрузи свое
3. Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
   карточек

Лекция № 3 1 Эффективные и эквивалентные ставки процентов Учебные вопросы 1. Эквивалентные ставки простых и сложных процентов 2. Эффективные и номинальные ставки процентов. Финансовые функции MS Excel ЭФФЕКТ, НОМИНАЛ 3. Эквивалентность простых учетных и простых процентных ставок 4. Эквивалентные ставки простых и сложных процентов с учетом инфляции

Литература 1. Кочетыков А. А. Финансовая математика. Серия «Учебники, учебные пособия» . – Ростов н/Д: Феникс» , 2004. – 480 с. 2. Кутуков В. Б. Основы финансовой и страховой математики: методы расчета кредитных, инвестиционных, пенсионных и страховых схем. – М. : Дело, 1998. – 304 с. 3. Овчаренко Е. К. , Ильина О. П. , Балыбердин Е. В. Финансово-экономические расчеты в Excel. Издание 3 -е, перераб. и доп. – М. : «Филин» , 1999. – 328 с. 4. Четыркин Е. М. Методы финансовых и коммерческих расчетов. – 2 -е изд. , испр. и доп. – М. : Дело Лтд. , 1995. – 320 с. 2

3 1. Эквивалентные ставки простых и сложных процентов

4 Определим эквивалентную процентную ставку, при которой наращенная сумма по простым и сложным процентам одинакова.

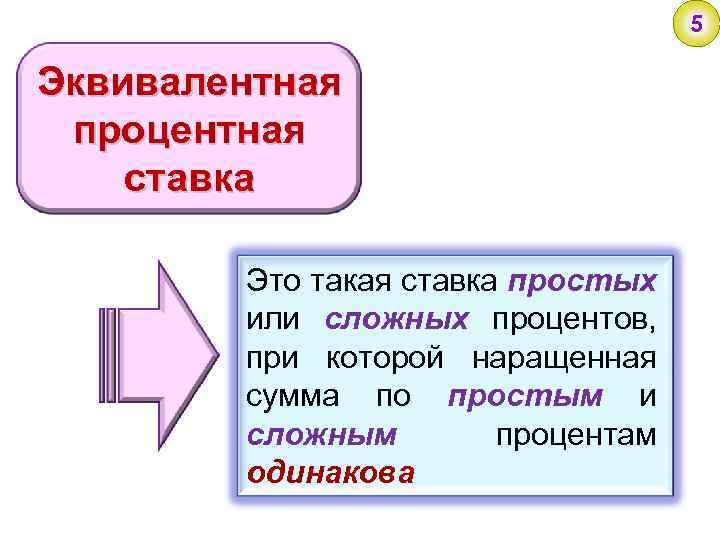
5 Эквивалентная процентная ставка Это такая ставка простых или сложных процентов, при которой наращенная сумма по простым и сложным процентам одинакова

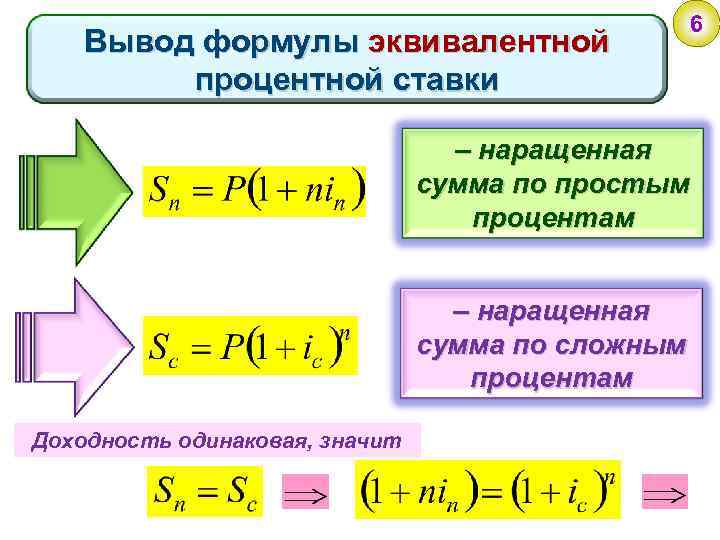
Вывод формулы эквивалентной процентной ставки 6 – наращенная сумма по простым процентам – наращенная сумма по сложным процентам Доходность одинаковая, значит

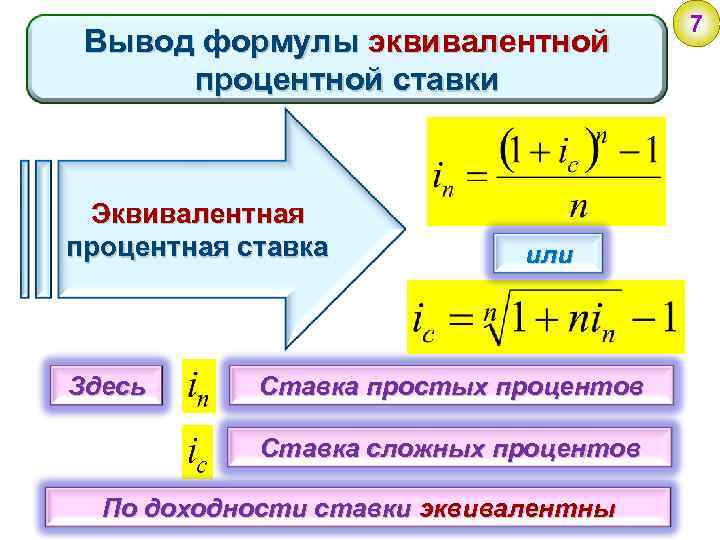
Вывод формулы эквивалентной процентной ставки Эквивалентная процентная ставка Здесь или Ставка простых процентов Ставка сложных процентов По доходности ставки эквивалентны 7

8 Пример 1 Определить эквивалентную ставку сложных процентов iс, если ставка простых процентов составляет iп=50%, а срок кредита n=2 года. Ответ: iс=40%

9 2. Эффективные и номинальные ставки процентов. Финансовые функции MS Excel ЭФФЕКТ, НОМИНАЛ

10 Определим эффективную процентную ставку i, при которой наращенная сумма по сложным процентам и начислении процентов один раз в году такая же, что и при m – разовом наращении в год по ставке j m

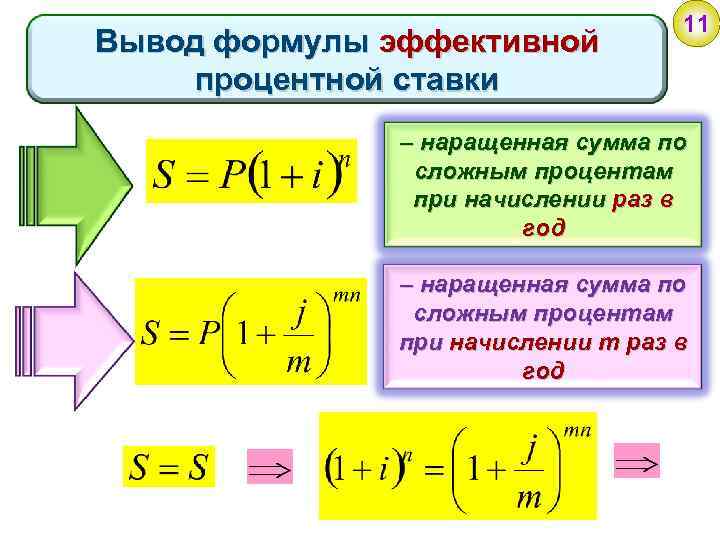
Вывод формулы эффективной процентной ставки 11 – наращенная сумма по сложным процентам при начислении раз в год – наращенная сумма по сложным процентам при начислении m раз в год

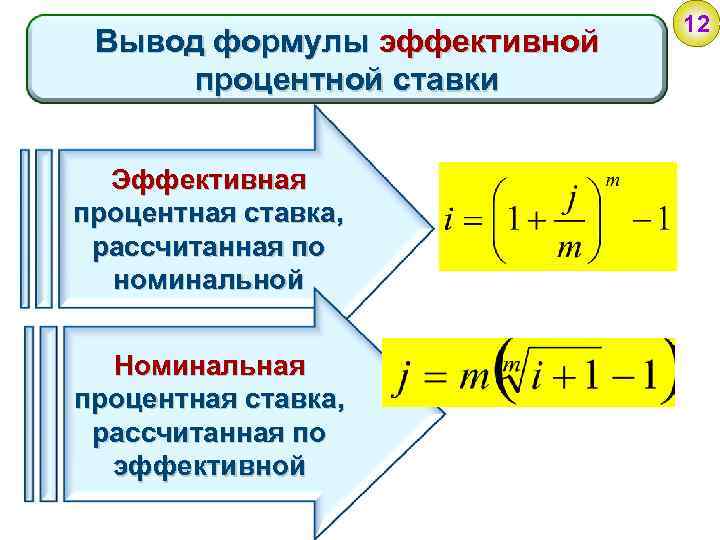
Вывод формулы эффективной процентной ставки Эффективная процентная ставка, рассчитанная по номинальной Номинальная процентная ставка, рассчитанная по эффективной 12

13 1. При m>1 эффективная (годовая) ставка больше номинальной i>j 2. При m=1 эффективная ставка равна номинальной, то есть i=j В принципе в договоре заемщика и кредитора номинальную ставку можно заменить на эффективную, так как никто от этой замены не проигрывает в финансовом отношении.

14 Пример 2 Определить эффективную ставку i, если номинальная ставка равна j=25%, при помесячном начислении, то есть при m=12, n=1 Вывод: для сторон безразлично, применять ли ставку j=25% при помесячном начислении или годовую ставку i=28%.

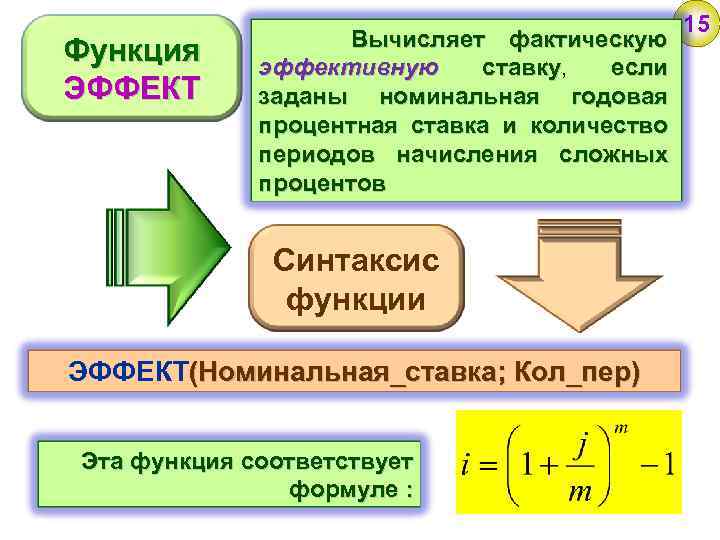
Функция ЭФФЕКТ Вычисляет фактическую эффективную ставку, если ставку заданы номинальная годовая процентная ставка и количество периодов начисления сложных процентов Синтаксис функции ЭФФЕКТ(Номинальная_ставка; Кол_пер) Эта функция соответствует формуле : 15

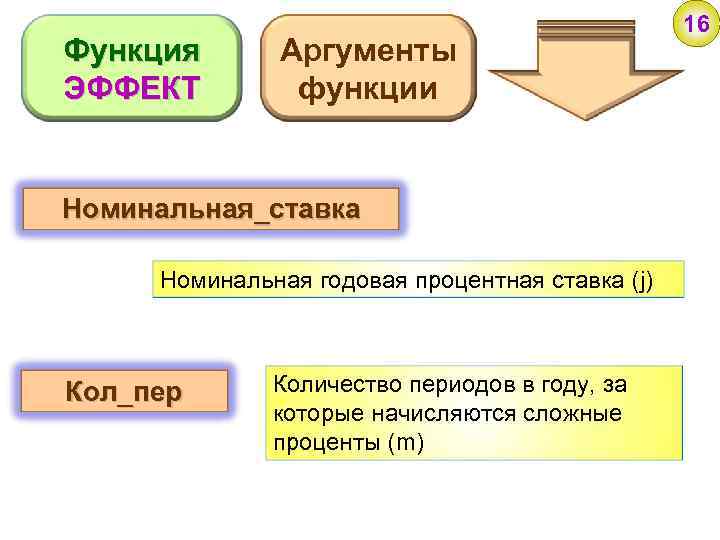
Функция ЭФФЕКТ Аргументы функции Номинальная_ставка Номинальная годовая процентная ставка (j) Кол_пер Количество периодов в году, за которые начисляются сложные проценты (m) 16

17 Пример 3 Имеется заем P=5 000 руб. с номинальной годовой процентной ставкой 19% и сроком уплаты 4 года. Рассчитать эффективные процентные ставки, если начисление процентов: а) полугодовое, т. е. m=2; б) квартальное, т. е. m=4; в) ежемесячное, т. е. m=12; г) ежедневное, т. е. m=365. Определить также сумму, которая будет выплачена (S).

18 Пример 3 а) ЭФФЕКТ(19%; 2) = 0, 1990; б) ЭФФЕКТ(19%; 4) = 0, 2040; в) ЭФФЕКТ(19%; 12) = 0, 2075; г) ЭФФЕКТ(19%; 365) = 0, 2092. Проверить в Excel по формуле: Самостоятельно а) БС (19%/2; 2*4; ; -5000000) = 10 334 345, 04 руб. ; б) БС (19%/4; 4*4; ; -5000000) = 10 505 930, 18 руб. ; в) БС (19%/12; 12*4; ; -5000000) = 10 627 914, 79 руб. ; г) БС (19%/365; 365 * 4; ; -5000000) = 10 689 267, 20 руб.

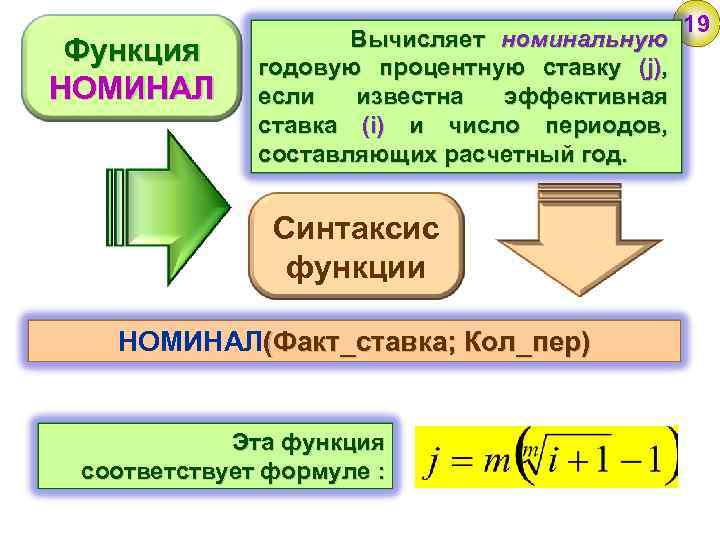
Функция НОМИНАЛ Вычисляет номинальную годовую процентную ставку (j), если известна эффективная ставка (i) и число периодов, составляющих расчетный год. Синтаксис функции НОМИНАЛ(Факт_ставка; Кол_пер) Эта функция соответствует формуле : 19

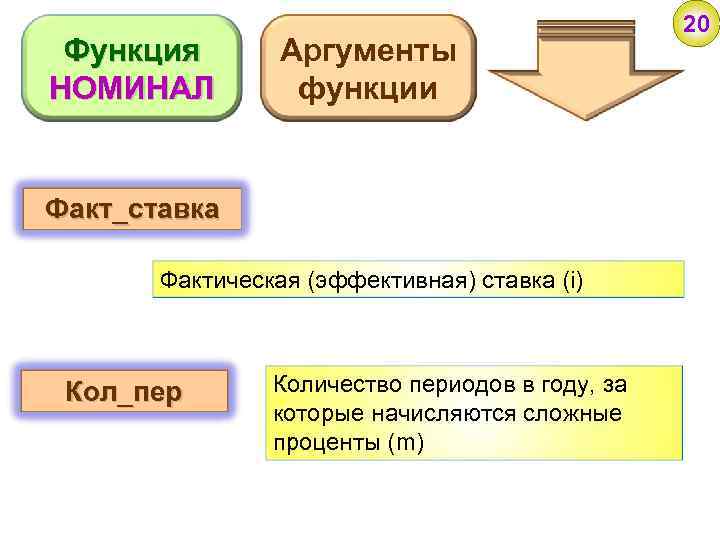
Функция НОМИНАЛ Аргументы функции Факт_ставка Фактическая (эффективная) ставка (i) Кол_пер Количество периодов в году, за которые начисляются сложные проценты (m) 20

21 Пример 4 Допустим, эффективная ставка составляет i=25 %, а начисление процентов производится ежемесячно, то есть m=12. Рассчитать номинальную процентную ставку (j). НОМИНАЛ(25%; 12) = 0, 2252 или j=22, 52 %.

22 3. Эквивалентность простых учетных и простых процентных ставок

23 Определим простую учетную ставку (d), эквивалентную простой процентной ставке (i)

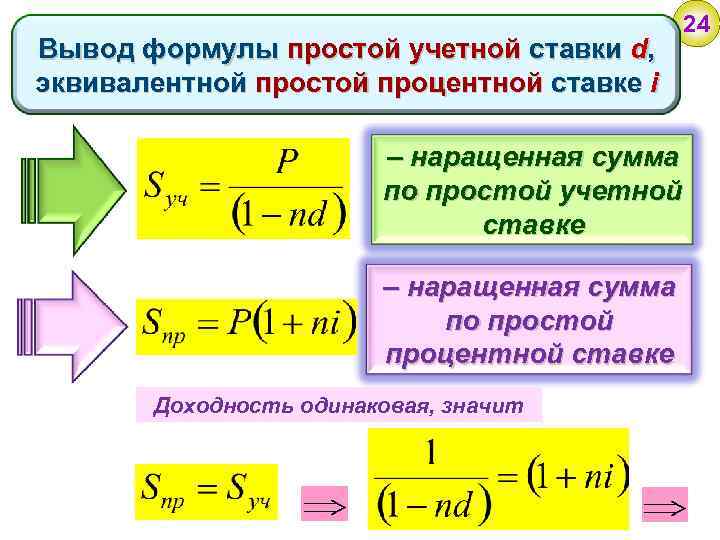
Вывод формулы простой учетной ставки d, эквивалентной простой процентной ставке i 24 – наращенная сумма по простой учетной ставке – наращенная сумма по простой процентной ставке Доходность одинаковая, значит

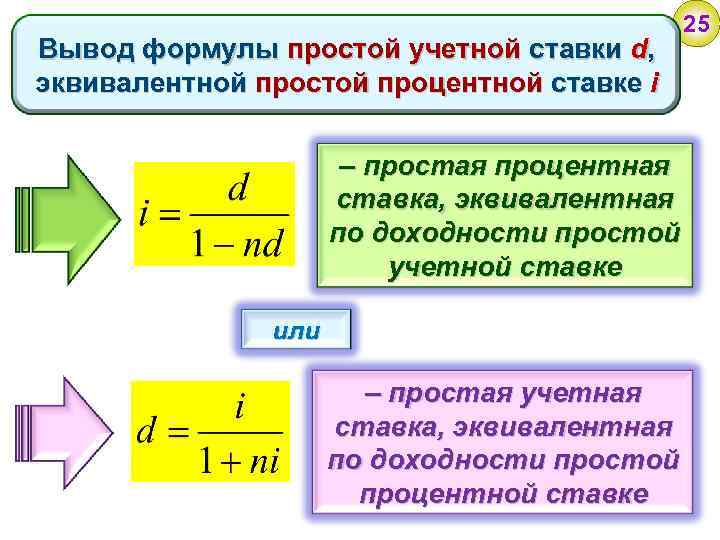
Вывод формулы простой учетной ставки d, эквивалентной простой процентной ставке i – простая процентная ставка, эквивалентная по доходности простой учетной ставке или – простая учетная ставка, эквивалентная по доходности простой процентной ставке 25

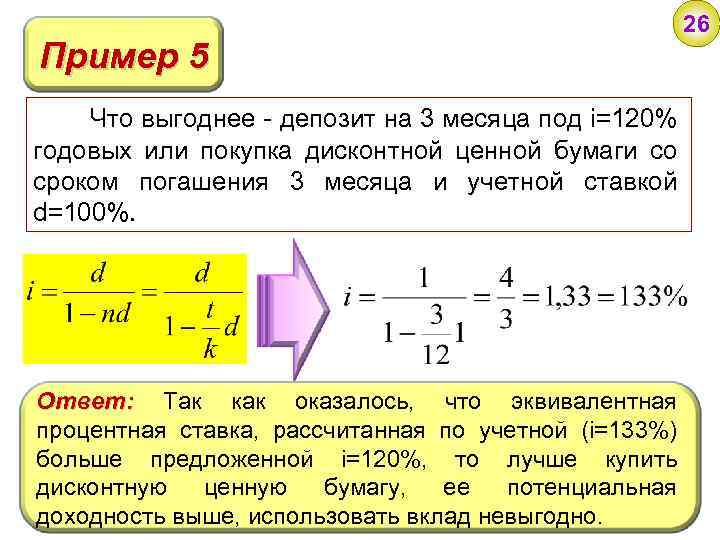
Пример 5 Что выгоднее – депозит на 3 месяца под i=120% годовых или покупка дисконтной ценной бумаги со сроком погашения 3 месяца и учетной ставкой d=100%. Ответ: Так как оказалось, что эквивалентная процентная ставка, рассчитанная по учетной (i=133%) больше предложенной i=120%, то лучше купить дисконтную ценную бумагу, ее потенциальная доходность выше, использовать вклад невыгодно. 26

27 4. Эквивалентные ставки простых и сложных процентов с учетом инфляции

28 Виды инфляции: Ползучая (умеренная) Iinf=3… 10% в год Галопирующая Iinf=10… 100% в год Гиперинфляция Iinf свыше 30% в год

29 Определим эквивалентную ставку простых процентов с учетом инфляции, то есть найдем такую ставку iэкв, которая компенсировала бы рост цен

30 Обозначим: S – номинальная наращенная сумма С – реальная наращенная сумма Iinf – индекс (уровень) инфляции Ip – индекс цен (показывает во сколько раз за период выросли цены) Так как , то

31 Определим эквивалентную ставку сложных процентов с учетом инфляции, то есть найдем такую ставку iэкв, которая компенсировала бы рост цен

32 Если в каждом из n периодов начисления процентов индивидуальный индекс цен одинаковый, то или