Как найти эквивалентные дроби

Была ли эта статья полезной?

Equivalent Fractions are the fractions that represent the same value and by simplifying the fraction in simplest form we always get the same fraction. We define the fraction as a way of representing a part of some quantity. Suppose we have one pizza with six equal sizes and Shiv takes two slices from it then the remaining pizza is represented as, 4/6 which is equivalent fraction to 2/3. The various other examples of equivalent fractions are 1/3, 2/6, 3/9, and others.

The simplest form of all the equivalent fractions is the same, i.e. if all the equivalent fraction is reduced to the simplest term then they all are the same. For example, the simplest form of 1/3, 2/6, and 3/9 is 1/3. Let’s learn more about equivalent fractions, its example, and others in detail in this article.

What are Equivalent Fractions?

Equivalent fractions are defined as fractions that have the same value but have different numerators and denominators. For instance, 3/9, 4/12, 5/15, and 6/18 are equivalent fractions as their values in the simplest form is 1/3. Equivalent fractions indicate the same portion of the whole value. We can find an equivalent fraction for every fraction by multiplying or dividing both the numerator and the denominator with the same number.

Equivalent Fractions Definition

We define an equivalent fraction as the fraction that denotes the same value of any quantity. Suppose we write 1/2 or 5/10 they both denote half of any value and are thus called an equivalent fraction. We can easily find the equivalent fractions of any fraction by simply multiplying or dividing the numerator and denominator with the same number. For example, 3.9, 6/18, and 2/6 all are equivalent fractions and they all result in 1/3 as their simplest form.

Equivalent Fractions Examples

We represent the equivalent fraction as the fraction which results in the same value but it is interesting to note that they represent the same value when represented graphically.

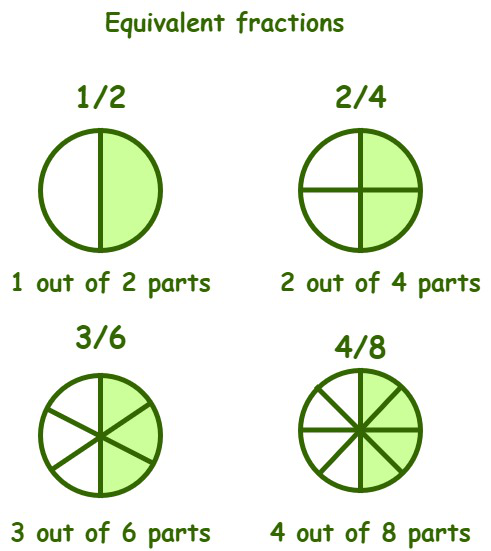
We can understand with the help of the following example. Suppose we have to distribute a chapatti in two equal parts then each part is represented using a 1/2 fraction. Now, we distribute the similar chapatti into four parts a take two out of them which is represented as 2/4, similarly if the chapati is broken into six parts and out of which three parts are taken which is represented as 3/6 and lastly if it is broken into eight parts and out of which four parts are taken then we represent this fraction as 4/8. Here in the above example, we see that all the fraction represents half of all the values, and thus all are equivalent fractions. The image added below represent the equivalent fraction of 1/2

Here, 1/2 = 2/4 = 3/6 = 4/8 all are equivalent fractions and their simplest form is 1/2.

How to Find Equivalent Fractions?

For every fraction, we can determine an equivalent fraction either by multiplying or dividing both the numerator and the denominator with the same number. That’s why when all equivalent fractions are simplified, they are reduced to the same fraction. We have two ways of finding the equivalent fraction of any number,

• Multiplying Numerator and Denominator by Same Number
• Dividing Numerator and Denominator by Same Number

Now, let’s study these two cases in detail.

Case 1: Multiplying Numerator and Denominator by Same Number

For every fraction, we can determine an equivalent fraction by multiplying both the numerator and the denominator with the same number. For instance, to determine the equivalent fraction of 2/3, multiply both the numerator and the denominator with the same number, i.e., 2. Thus, the equivalent fraction of 2/3 is 4/6. Similarly, we can find some other equivalent fractions by repeating the same process.

Equivalent fractions of 2/3

• Multiplying Numerator and Denominator by 3, we get 2/3 × 3/3 = 6/9
• Multiplying Numerator and Denominator by 4, we get 2/3 × 4/4 = 8/12
• Multiplying Numerator and Denominator by 5, we get 2/3 × 5/5 = 10/15

Hence, we can conclude that equivalent fractions of 2/3 are 4/6, 8/12, and 10/15

Case 2: Dividing Numerator and Denominator by Same Number

For every fraction, we can determine an equivalent fraction by dividing both the numerator and the denominator by the same number. For instance, to find the equivalent fraction of 45/300, first, we have to find their common factors. Here, 3 is a common factor of both 45 and 300. So, the equivalent fraction of 45/300 can be found by dividing its numerator and denominator by 3. Thus, the equivalent fraction of  45/300 is 15/100. 

Let us simplify the fraction further.

5 is a common factor of 15 and 100. So, 15/100 = (15÷5)/(100÷5) = 3/20

Hence, the equivalent fractions of 45/300 are 15/100 and 3/20. As there are no common factors for 3 and 20 other than 1, 3/20 is the simplified form of 45/300.

Equivalent Fractions Chart

The chart that represents the equivalent fraction of any quantity is called the equivalent fraction chart. The chart added below represents the equivalent fraction of 1, 1/3, 1/6, etc.

From the given chart, we can observe that the equivalent fractions of 1/3 are 2/6, 4/12, 8/24,… Now, let us see the equivalent fractions of some unit fractions.

Fraction	Equivalent Fractions
1/2	2/4, 3/6, 4/8, 5/10,…
1/3	2/6, 3/9, 4/12, 5/15,…
1/4	2/8, 3/12, 4/16, 5/20,…
1/5	2/10, 3/15, 4/20, 5/25,…
1/6	2/12, 3/18, 4/24,5/30,…
1/7	2/14, 3/21, 4/28, 5/35,…
1/8	2/16, 3/24, 4/32, 5/40,…
1/9	2/18, 3/27, 4/36, 5/45,..
1/10	2/20, 3/30, 4/40, 5,50,…

How to check if Two Fractions are Equivalent?

We can check whether two fractions are equivalent or not by using the three methods that include,

• Make Denominators of both fraction Equal
• Determining decimal form of both Fractions
• Cross Multiplication Method

Now let’s learn about each method in detail.

Making Denominators Equal

We can check whether the given fractions are equivalent by just making their denominator equal. And if they have an equal denominator along with an equal numerator they are equivalent fractions.

Example: Find if 4/10 and 6/15 are equivalent fractions or not.

Solution:

LCM of 10 and 15 is 30.

Multiply 4/10 by 3/3 and 6/15 by 2/2 to make their denominators equal to 30.

4/10 × 3/3 = 12/30

6/15 × 2/2 = 12/30

Now comparing two fractions we get that the denominator and the numerator of both the fractions are equal and hence, they are equivalent fratcion.

Note: If the fractions are NOT equivalent, we can check the greater or smaller fraction by looking at the numerator of both the resultant fractions in which denominators are equal. Hence, this method can also be used for comparing fractions.

Determining Decimal form of both Fractions

By finding the decimals of the given fractions, we can check whether they are equivalent or not. If the decimal form of both fractions is equal they are equivalent fractions and if the decimal form of both the fraction is not equal they are not equivalent fractions.

Example: Find if 3/4, 6/8, and 12/16 are equivalent fractions or not.

Solution:

Decimal form of all the fractions is,

3/4 = 0.25

6/8 = 0.25

12/16 = 0.25

As the decimal values of the given fractions are the same, the given fractions are equivalent.

Cross Multiplication method

To identify whether two fractions are equivalent or not, cross-multiplication is also used. The fractions are equivalent if both the products of the cross multiplication are the same.

Example: Find if 3/6 and 4/8 are equivalent fractions or not.

Solution:

The given fractions are equivalent as both the products of cross multiplication are 24.

Visual Method

Using the visual method we can easily find whether two fractions are equivalent or not as equivalent fractions represent the same shaded value in their visual structure. Such as 1/2 and 2/4 as shown in the image below both represent half of the value of any disc and thus they are equivalent fractions.

We simply observe the shaded portion of the given fractions and if they are equal our fraction is equivalent.

Read More,

• Fractions
• Percentage

Solved Example based on Equivalent Fractions

Example 1: Find “a” if 10/21 and a/16 are equivalent fractions.

Solution:

Given,

 10/21 = a/16

Using Cross Multiplication

a×21 = 10×42

a = 10×42 / 21

a = 20

Hence, the required value of “a” is 20

Example 2: Find the value of “x” if 5/36 and x/9 are equivalent fractions.

Solution: 

Given,

5/36 and x/9 are equivalent fraction

Using Cross Multiplication Method

5/36 = x/9

x = (5 × 9)/36

x = 5/4

Hence, the required value of “x” is 5/4

Example 3: Find if 5/9 and 11/15 are equivalent fractions or not.

Solution:

Let us use Cross Multiplication Method to check whether 5/9 and 11/15 are equivalent fractions or not.

Now, by Cross Multiplication of the given fractions we get,

5 × 15 = 75

9 × 11 = 99. 

Here, both products are not equal, i.e., 75 ≠ 99. 

Hence, 5/9 and 11/15 are not equivalent fractions.

Example 4: What are the equivalent fractions of 7/8?

Solution: 

To find equivalent fractions of 7/8, multiply the numerator and denominator by the same numbers.

7/8 × (2/2) = 14/16

7/8 × (3/3) = 21/24

7/8 × (4/4) = 28/32

7/8 × (5/5) = 35/40

7/8 × (6/6) = 42/48

Hence, the equivalent fractions of 7/8 are 14/16, 21/24, 28/32, 35/40, 42/48, and so on.

Example 5: What is its denominator, if the numerator of a fraction equivalent to 6/24 is 14?

Solution:

Let the unknown denominator be “x”.

Given, 

6/24 = 14/x

We know that, if two fractions are equivalent their products when they are cross-multiplied are equal, i.e.

6 × x = 24 × 14

x = (24 × 14)/6 = 56.

Hence, the value of x is 56.

FAQs on Equivalent Fractions

Q1: What are equivalent fractions?

Answer:

Two or more fractions containing different numerators and denominators but their simplest form is the same then they are called equivalent fractions. e.g. 2/10, 3/15 etc, are equivalent fractions as their simplest form is 1/5

Q2: What are examples of Equivalent Fractions?

Answer:

Some examples of Equivalent Fractions are:

• 1/3, 3/9 and 4/12 are Equivalent Fractions
• 1/2 6/12 and 4/8 are Equivalent Fractions

Q3: How to Find Equivalent Fractions?

Answer:

Equivalent Fractions of any given fraction can easily be found by multiplying or dividing the numerator and the denominator of the fraction by the same number.

Q4: How to determine whether fractions are equivalent?

Answer:

We simplify the given fractions and if their simplest form is the same then the fractions are equivalent fractions. For example, check if 4/6, 6/9 and 8/12 are equivalent fractions, or not.

Finding the simplest form of each fraction.

• 4/6 = 2/3
• 6/9 = 2/3
• 8/12 = 2/3

As the simplest form of all the fractions is the same they are equivalent fractions.

Q5: How to check if the given fractions are Equivalent Fractions or not?

Answer:

There are various methods which tell us whether the fractions are equivalent or not that are,

• Making Denominators the Same.
• By finding the Decimal Form of both fractions.
• Cross Multiplication Method.
• Visual Method.

Q6: What are the equivalent fractions of 1/7?

Answer:

Equivalent fraction of 1/7 are calculated by multiplying, the numerator and denominator of 1/7 by the same number.

• 1/7 = 1/7 × 2/2 = 2/14
• 1/7 = 1/7 × 3/3 = 3/21
• 1/7 = 1/7 × 4/4 = 4/28

Как родители, мы обычно хотим поддержать наших детей в их обучении.

Но многие из нас беспокоятся, когда дело доходит до помощи по определенным темам, и математика, в частности, часто является проблемой для родителей. Это может даже вернуть нас к нашей собственной борьбе с математикой в ​​школьные годы: вдвое больше длинное деление, кто угодно?

К счастью, многие концепции, которым обучают в начальной школе, не так сложны, как может показаться на первый взгляд. Это означает, что вы, вероятно, лучше подготовлены, чем можете себе представить, в обучении математика.

Итак, если ваш ребенок 4-го класса узнает все об эквивалентных дробях, и вы нарисовали большой мысленный пробел, вот что вам нужно знать, чтобы научить их правильно.

Что такое эквивалентные дроби?

Название – большая подсказка. Эквивалентные дроби – это просто дроби, которые имеют одинаковые значения, но выглядят по-разному.

Дроби состоят из двух частей: число вверху называется числителем, а число внизу – знаменателем, и они делятся этой контрольной короткой линией посередине.

Дроби вводятся в KS1, где дети изучают простые идеи, такие как половинки и четверти. Затем обучение переходит к более сложным дробям (третьи и пятые) по мере того, как дети переходят в 3 класс. Эквивалентные дроби затем преподаются в рамках учебной программы 4-го класса.

Некоторые примеры эквивалентных дробей:

1/2 эквивалентно 2/4, 3/6, 4/8 и 5/10.

1/3 эквивалентно 2/6, 3/9 и 4/12.

1/5 эквивалентно 2/10, 3/15 и 4/20.

3/4 эквивалентно 6/8, 9/12 и 15/20.

На первый взгляд все они могут выглядеть по-разному, но на самом деле каждая линия представляет одни и те же значения или пропорции целого (1).

Когда вы умножаете или делите верхнее и нижнее число дроби на одно и то же число, оно будет иметь одинаковое значение.

Так: 1/2 х 2 = 2/4. И 2/4 х 2 = 4/8.

Вы также можете разделить дроби на одно и то же число, чтобы получить дроби, эквивалентные друг другу.

Например: 4/8 ÷ 2 = 2/4. И 2/4 ÷ 2 = 1/2.

Такое деление называется «упрощением». Когда вы не можете пойти дальше с делением, вы достигли самой простой формы дроби; в этом примере 1/2. (Помните, что при делении вам нужно оставить целые числа внутри дроби.)

Ожидается, что к 5-му классу дети научатся понимать эквивалентные дроби, включая 1/10 и 1/100.

Как распознать эквивалентные дроби?

Обучая ребенка, имейте в виду, что его могут попросить определить эквивалентные дроби, которые выражаются в наглядной форме.

Это может быть изображение или диаграмма, и их могут попросить заштриховать или раскрасить их: например, на круговой диаграмме или на гистограмме. Обдумывание дробей визуально может быть простым способом помочь детям полностью понять их.

Детей также можно попросить заполнить пропуски в числовых вопросах:

Например: 4/5 = ?/10.

Или 5/15 =? / 3.

Использование числовой прямой может быть особенно полезным инструментом для обучения детей пониманию дробей. Здесь на горизонтальной линии будут нанесены отметки, показывающие, как целое (1) можно разбить на пятые, восьмерки и так далее.

Некоторые игры с эквивалентными дробями

Обучение часто бывает более эффективным, если вы можете привнести в него элемент веселья. Игры могут стать отличным способом помочь вашим детям разобраться в дробях, в каком бы году они ни находились. В частности, включение визуального элемента действительно может помочь упасть центу.

Идеи, которые стоит попробовать, включают:

Вырежьте из картона или цветной бумаги несколько больших квадратов или кружков. Держите по два каждой формы в качестве своего «мастера». Затем разрежьте оставшиеся формы на половинки, четвертинки и восьмые; или трети и шестые и так далее. Затем попробуйте попросить ребенка создать эквивалентные дроби, используя эти вырезы, размещенные на вершине мастера. Так, например, 1/4 и 2/8. Попросите их создать одинаковые эквивалентные дроби, используя две разные одинаковые формы. Держите под рукой запас наград на тот момент, когда они все сделают правильно.

Используйте подручные хозяйственные материалы. Попробуйте разрезать яблоко на половинки и четвертинки или плитку шоколада на восьмые и шестнадцатые части. Или приготовьте два морковных торта или банановые буханки и нарежьте их.

Предложите ребенку подумать, можно ли проще выразить дробь. Обычно мы не говорим о 2/6 чего-либо, но мы говорим о 1/3.

Используйте числовые линии: нарисуйте свои собственные или распечатайте их из Интернета.

Ищите онлайн-игры по математике, в которых используются герои мультфильмов и испытания на время; это может быть отличным способом научить детей практиковать новые математические концепции.

Использовать свое воображение. Напишите вместе песню или рэп об эквивалентных дробях или даже попросите своих детей написать стихотворение!

Обучение эквивалентным дробям и десятичным знакам

Дети также начинают изучать десятичные дроби в KS2, что является еще одним способом выражения пропорций.

Они также узнают, как они могут быть эквивалентны дробям. Например: 0,5 = 1/2 и 0,3 = 3/10. Это то, к чему можно перейти, когда они поняли концепцию дробей. Не начинайте обучать их слишком рано, так как это может их сбить с толку; вы можете подождать, пока эти идеи не будут представлены в школе.

Как работать с эквивалентными дробями

5 методика:Получение эквивалентных дробейИспользование операции умножения для определения эквивалентностиИспользование операции деления для определения эквивалентностиИспользование умножения крест-накрест для нахождения переменнойИспользование формулы для нахождения корней квадратного уравнения

Две дроби эквивалентны, если они имеют одинаковое значение. Дроби 1/2 и 2/4 эквивалентны, поскольку значение 1 делить на 2 равно значению 2 делить на 4 или 0,5 в виде десятичной дроби. Преобразование дробей в эквивалентные дроби полезно при проведении обычных и сложных вычислений. Эта статья расскажет вам, как получать эквивалентные дроби через деление и умножение, а также о том, как решать уравнения с эквивалентными дробями.

Шаги

Метод 1 из 5: Получение эквивалентных дробей

1. 1
   Умножьте числитель и знаменатель на одно и то же число. У двух эквивалентных дробей числители делятся друг на друга нацело, и знаменатели делятся друг на друга нацело (при этом вы должны получить одно число). Другими словами, умножив числитель и знаменатель какой-либо дроби на одно и то же число, вы получите эквивалентную дробь (значения исходной и полученной дробей будут одинаковыми).
2. Например, дана дробь 4/8. Умножьте числитель и знаменатель на 2 и получите: (4 × 2) / (8 × 2) = 8/16. Эти две дроби эквивалентны.
3. (4 × 2) / (8 × 2) = 4/8 × 2/2. Помните, что при умножении двух дробей нужно перемножить их числители, а затем перемножить их знаменатели.
4. Обратите внимание, что 2/2 = 1. Таким образом, 4/8 и 8/16 – это эквивалентные дроби, так как умножая 4/8 на 1 (2/2 = 1), значение дроби не меняется. Поэтому 4/8 = 8/16.
5. Любая дробь имеет бесконечное число эквивалентных дробей. Вы можете умножить числитель и знаменатель на любое целое число, чтобы получить эквивалентную дробь.
6. 2
   Разделите числитель и знаменатель на одно и то же число. Аналогично умножению, операция деления также может быть использована для того, чтобы получить новую дробь, которая будет эквивалентна исходной дроби. Для этого разделите числитель и знаменатель на одно и то же число (числитель и знаменатель должны делиться на это число без остатка, и в числителе и знаменателе должны быть целые числа).
7. Например, дана дробь 4/8. Если вместо умножения вы разделите числитель и знаменатель на 2, то получите: (4 ÷ 2) / (8 ÷ 2) = 2/4. 2 и 4 – целые числа, поэтому дробь 2/4 эквивалентна дроби 4/8.

Метод 2 из 5: Использование операции умножения для определения эквивалентности

1. 1
   Если вам дана задача на определение эквивалентности двух дробей, то найдите число, на которое нужно умножить меньший знаменатель, чтобы получить больший знаменатель. Так вы приведете дроби к общему знаменателю.
2. Например, даны дроби 4/8 и 8/16. Меньший знаменатель 8 вы умножаете на 2 и получаете больший знаменатель 16. Таким образом, искомое число в данном примере – это число 2.
3. Для облегчения нахождения нужного числа просто разделите больший знаменатель на меньший знаменатель. В этом случае 16/8 = 2.
4. Число не обязательно будет целым. Например, если знаменатели равны 2 и 7, то число равно 3,5.
5. 
   2
   Умножьте числитель и знаменатель меньшей дроби (с меньшим знаменателем) на найденное число. Если в результате вы получите большую дробь (с большим знаменателем), то данные дроби эквивалентны.[1]
6. В нашем примере умножьте меньшую дробь 4/8 на найденное число 2: (4 х 2)/(8 х 2) = 8/16. Вы получили большую дробь, поэтому данные дроби 4/8 и 8/16 являются эквивалентными.

Метод 3 из 5: Использование операции деления для определения эквивалентности

1. 1
   Выразите каждую дробь в виде десятичной дроби, чтобы определить их эквивалентность. Для этого просто разделите числитель дроби на ее знаменатель.
2. Например, даны дроби 4/8 и 8/16. 4/8= 0,5; 8/16 = 0,5. Так как две десятичные дроби равны, то исходные дроби эквивалентны.
3. Помните, что в десятичной дроби после десятичной запятой может стоять бесконечной число цифр. Это надо учитывать при определении эквивалентности. Например, 1/3 = 0,333, а 3/10 = 0,3. Таким образом, дроби 1/3 и 3/10 не являются эквивалентными.
4. 2
   Разделите числитель и знаменатель дроби на одно и то же число, чтобы получить эквивалентную дробь. При этом и в числителе, и в знаменателе должны находиться целые числа.
5. Например, дана дробь 4/8. Если вместо умножения вы разделите числитель и знаменатель на 2, то получите (4 ÷ 2)/(8 ÷ 2) = 2/4. 2 и 4 являются целыми числами, поэтому дробь 2/4 эквивалентна дроби 4/8.
6. 3
   Упростите дробь, разделив числитель и знаменатель на наибольший общий делитель (НОД). Это самое большое число, на которое можно разделить и числитель и знаменатель. Этот шаг должен привести две дроби к наименьшему общему знаменателю (только если дроби эквивалентны).
7. При упрощении дроби вы получите дробь с наименьшими возможными числителем и знаменателем. Числитель и знаменатель не могут быть разделены на любое целое число; их необходимо делить на их НОД.
   
8. В нашем примере (дробь 4/8) НОД = 4, так как 4 – это наибольшее число, которое делит 4 и 8 без остатка. Чтобы упростить дробь, разделите числитель и знаменатель на 4: (4 ÷ 4)/(8 ÷ 4) = 1/2. Аналогично, в случае дроби 8/16 НОД = 8 и: (8 ÷ 8)/(16 ÷ 8) = 1/2.

Метод 4 из 5: Использование умножения крест-накрест для нахождения переменной

1. 
   1
   Умножение крест-накрест используется в задачах с двумя эквивалентными дробями, одно из чисел в которых заменено на переменную (обычно «х»); эту переменную необходимо найти. Так как дроби эквивалентны, то их можно приравнять (поставить между ними знак равенства) и найти переменную при помощи умножения крест-накрест.[2]
2. 2
   При умножении крест-накрест нужно умножить числитель первой дроби на знаменатель второй дроби, а затем умножить числитель второй дроби на знаменатель первой дроби; между результатами перемножения поставьте знак равенства.[3]
3. Например, даны две дроби 4/8 и 8/16. Они не содержат переменную, но используем умножение крест-накрест, чтобы проверить их эквивалентность: 4 х 16 = 8 х 8 или 64 = 64. Таким образом, эти дроби эквивалентны (если равенство не сохраняется, то дроби не являются эквивалентными).
4. 3
   Введите переменную в одну из эквивалентных дробей, чтобы при помощи умножения крест-накрест найти ее.
5. Например, рассмотрим уравнение 2/х = 10/13. Умножьте 2 на 13 и 10 на «х», а затем приравняйте результаты друг другу:
6. 2 × 13 = 26
7. 10 × x = 10x
8. 10x = 26. Разделите обе части уравнения на 10 и получите х = 26/10 = 2,6.
9. 
   4
   Умножение крест-накрест работает с любыми дробями, включая дроби со сложными выражениями. Например, если обе дроби содержат переменные, в процессе вычислений их необходимо сократить; если же числитель или знаменатель данных дробей содержат выражения (например, х + 1), то при умножении крест-накрест необходимо раскрыть скобки (перемножив число за скобками и каждый член выражения в скобках) и решить полученное уравнение стандартным способом.[4]
10. Например, рассмотрим уравнение ((х + 3)/2) = ((х + 1)/4).
11. (x + 3) × 4 = 4x + 12
12. (x + 1) × 2 = 2x + 2
13. 2x + 2 = 4x + 12. Перенесите 2х на правую сторону уравнения.
14. 2 = 2x + 12. Теперь перенесите 12 на левую сторону уравнения.
15. -10 = 2x. Разделите на 2 обе стороны уравнения.
16. -5 = х

Метод 5 из 5: Использование формулы для нахождения корней квадратного уравнения

1. 1
   Этот метод также начинается с умножения крест-накрест, которое может привести к тому, что вы получите переменную во второй степени (в квадрате). В таких случаях, возможно, потребуется использовать такие методы, как разложение квадратного уравнения на множители или решение квадратного уравнения при помощи формулы.[5]
2. Например, рассмотрим уравнение ((x +1)/3) = (4/(2x – 2)). Умножьте крест-накрест:
3. (x + 1) × (2x – 2) = 2×2 + 2x -2x – 2 = 2×2 – 2
4. 4 × 3 = 12
5. 2×2 – 2 = 12.
6. 2
   Выразите полученное уравнение в виде квадратного уравнения (ax2 + bx + c = 0), приравняв уравнение к нулю. В нашем примере перенесите 12 на левую сторону уравнения и получите 2×2 – 14 = 0.
7. Некоторые члены могут равняться 0. Хотя 2×2 – 14 = 0 является простейшей формой квадратного уравнения, его можно записать в виде 2×2 + 0х + (-14) = 0. Это, вероятно, поможет на ранней стадии, чтобы записать уравнение в стандартной форме квадратного уравнения, даже если некоторые члены 0.
8. 3
   Решите уравнение, подставив числа из квадратного уравнения в формулу для вычисления корней квадратного уравнения. Формула: x = (-b +/- √(b2 – 4ac))/2a) поможет найти значения «х».[6] В эту формулу подставьте соответствующие числа из уравнения, полученного в шаге 2.
9. x = (-b +/- √(b2 – 4ac))/2a. В нашем примере 2×2 – 14 = 0, a = 2, b = 0, c = -14.
10. x = (-0 +/- √(02 – 4(2)(-14)))/2(2)
11. x = (+/- √( 0 – -112))/2(2)
12. x = (+/- √(112))/2(2)
13. x = (+/- 10,58/4)
14. x = +/- 2,64
15. 4
    Проверьте ответ, подставив найденные значения «х» в исходное квадратное уравнение.[7] В нашем примере подставьте 2,64 и -2,64 в исходное квадратное уравнение.

Советы

• Преобразование дробей в эквивалентные дроби на самом деле является их умножением на 1. При преобразовании 1/2 в 2/4, умножение числителя и знаменателя на 2 на самом деле есть умножение 1/2 на 2/2, где 2/2=1.
• Если необходимо проверить эквивалентность смешанных чисел (например, 1 3/4, 2 5/8, 5 2/3 и так далее), то сначала их необходимо преобразовать в неправильные дроби. Если вам нужно найти эквивалентную дробь смешанного числа, то это можете сделать двумя способами: преобразуйте смешанное число в неправильную дробь и воспользуйтесь методами, описанными в данной статье; или примените методы, описанные в данной статье, непосредственно к смешанному числу.

• Для преобразования смешанного числа в неправильную дробь умножьте целую часть смешанного числа на знаменатель дробной части, а затем сложите полученный результат с числителем дробной части. Знаменатель оставьте без изменений. Например, 1 2/3 = ((1 × 3) + 2)/3 = 5/3. Затем найдите эквивалентную дробь: 5/3 × 2/2 = 10/6; полученная дробь эквивалентна смешанному числу 1 2/3.
• Если вы не хотите конвертировать смешанное число в неправильную дробь, просто игнорируйте целую часть смешанного числа и работайте с его дробной частью. Например, в смешанном числе 3 4/16 работайте только с 4/16. 4/16 ÷ 4/4 = 1/4. Затем к полученному результату припишите целую часть исходного смешанного числа и получите эквивалентную дробь: 3 1/4.

Предупреждения

• Несмотря на то, что при перемножении дробей и числители, и знаменатели соответственно перемножаются, при сложении и вычитании дробей знаменатель остается прежним.

• Например, 4/8 ÷ 4/4 = 1/2 . Но 4/8 + 4/4 = 4/8 + 8/8 = 12/8 = 1 1/2 или 3/2, то есть при сложении вы получите совершенно другой результат.

Для получения эквивалентных дробей вы умножаете или делите числитель и знаменатель на одно и то же число; это верно, так как в этом случае вы умножаете или делите всю дробь на 1 (2/2, 3/3 и так далее), что не меняет значения исходной дроби. Этого нельзя достичь при сложении или вычитании дробей.