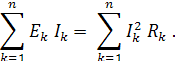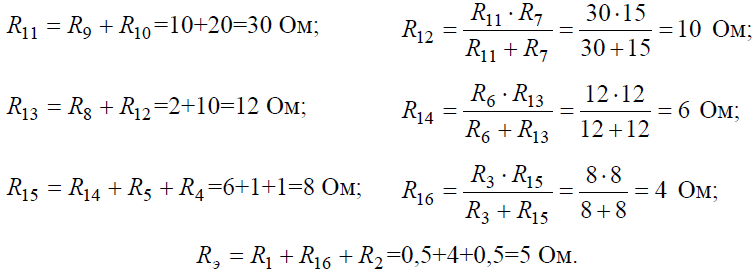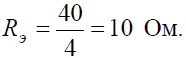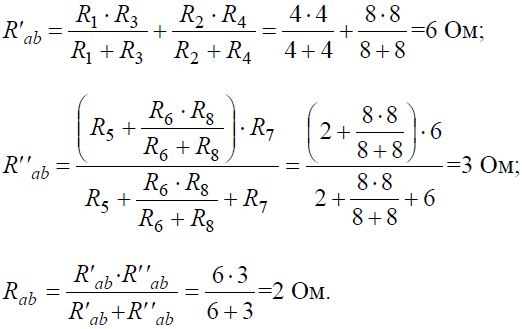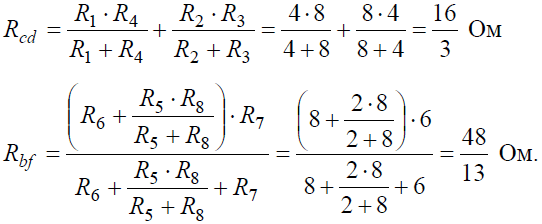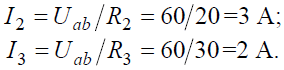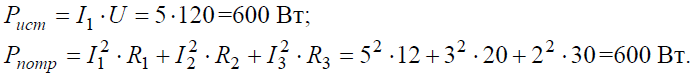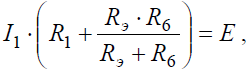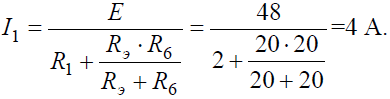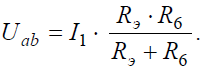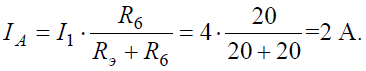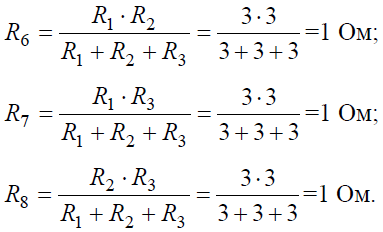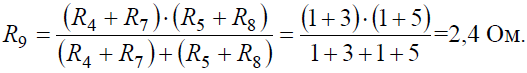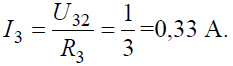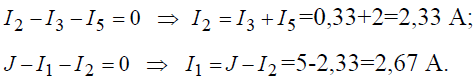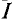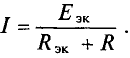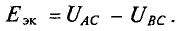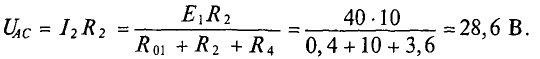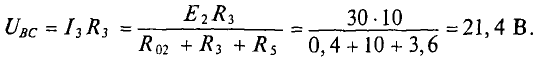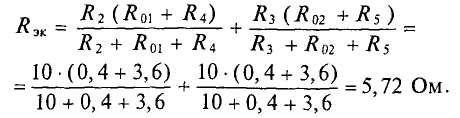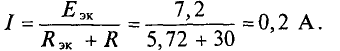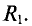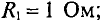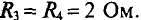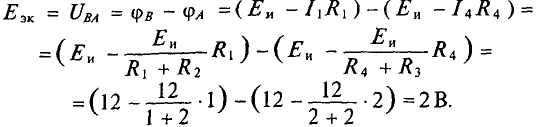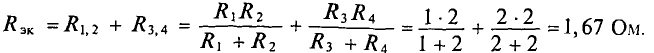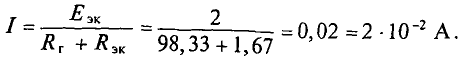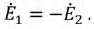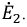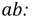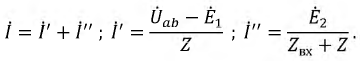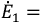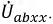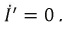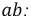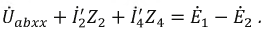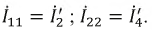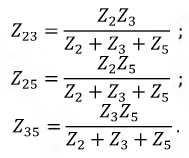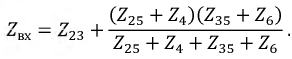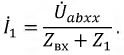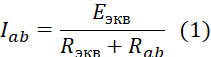Неразветвлённая
электрическая цепь характеризуется
тем, что на всех её участках протекает
один и тот же ток, а разветвлённая
содержит одну или несколько узловых
точек, при этом на участках цепи протекают
разные токи.
При
расчётах неразветвлённых и разветвлённых
линейных электрических
цепей постоянного тока могут быть
использованы различные
методы, выбор которых зависит от вида
электрической цепи.
П
расчётах сложных электрических цепей
во многих случаях
целесообразно производить их упрощение
путём свертывания, заменяя
отдельные участки цепи с последовательным,
параллельным
и смешанным соединениями сопротивлений
одним эквивалентным сопротивлением с
помощью метода эквивалентных
преобразований
электрических
цепей.
Рис. 1.1 Рис.1.2
Электрическая
цепь с последовательным соединением
сопротивлений
(рис. 1.1) заменяется
при этом цепью с одним эквивалентным
сопротивлением Rэк
(рис. 1.2), равным сумме всех сопротивлений
цепи:
где R1,
R2,
R3,…,
Rn
– сопротивления отдельных участков
цепи. При этом ток I
электрической
цепи сохраняет неизменным своё значение,
все сопротивления обтекаются одним и
тем же током. Напряжения
(падения напряжения) на сопротивлениях
при их последовательном соединении
распределяются пропорционально
сопротивлениям отдельных участков:
Рис. 1.3 Рис. 1.4
При
параллельном соединении сопротивлений
все сопротивления
находятся под одним и тем же напряжением
U
(рис. 1.3).
Электрическую цепь, состоящую из
параллельно соединённых
сопротивлений, целесообразно заменить
цепью с эквивалентным
сопротивлением Rэк
(рис. 1.2), которое определяется из
выражения:
обратных
сопротивлениям участков параллельных
ветвей электрической цепи (сумма
проводимостей ветвей цепи);
Rк
− сопротивление параллельного участка
цепи; qэк
−
эквивалентная
проводимость параллельного участка
цепи,
n
– число параллельных ветвей цепи.
Эквивалентное сопротивление участка
цепи, состоящего из одинаковых параллельно
соединённых сопротивлений,
При параллельном соединении двух
сопротивлений
R1
и
R2
эквивалентное coпротивление
а токи распределяются
обратно пропорционально их сопротивлениям,
при этом U
= R1
I1
= R2
I2
= R3
I3
=…= Rn
In.
При смешанном
соединении сопротивлений (рис.
1.4), т. е. при наличии участков электрической
цепи с последовательным
и параллельным
соединением
сопротивлений, эквивалентное
сопротивление (рис. 1.2) цепи
определяется в
соответствии с выражением:
Литература.
ГОСТ Р 52002 – 2003; [2]
с. 15 – 18, 22 − 26;
[3]
с. 14 – 17; [4] с. 18 – 23, 25 – 29.
П
решения
Рис. 1.5
Определить
общее
эквивалентное сопротивление Rэк
и распределение токов в электрической
цепи постоянного тока (рис. 1.5). Сопротивления
резисторов R1=R2=1
Oм;
R3=6
Oм;
R5=R6=1
Oм;
R4=R7=6
Oм;
R8=10
Oм;
R9=5
Oм;
R10=10
Oм.
Напряжение питающей сети U=120
В.
Решение.
Сопротивление участка цепи между узлами
1
и 4:
Сопротивление
участка между узлами 1′
и 3
цепи:
Сопротивление
участка между узлами 1”
и 2
цепи:
Эквивалентное
сопротивление всей электрической цепи:
Ток в неразветвлённой
электрической части цепи:
Напряжение между
узлами 1
и 2
цепи в соответствии со II
законом Кирхгофа:
Напряжение между
узлами 1′
и 3
цепи:
По I
закону Кирхгофа
ток в ветви резистора R3:
Токи в ветвях
резисторов R5
, R6:
Напряжение между
узлами 1
и 4
цепи:
Токи в ветвях
резисторов
Проверка:
По I
закону Кирхгофа
для узла 1”:
24 A
= 12 + 8 +2,4 + 1,6 = 24 A,
т. е. 24 А = 24 А – тождество.
Составим уравнение
баланса мощностей:
Значит, задача
решена верно.
Контрольное задание
Задача № 1
Определить
эквивалентное сопротивление Rэк
электрической
цепи постоянного
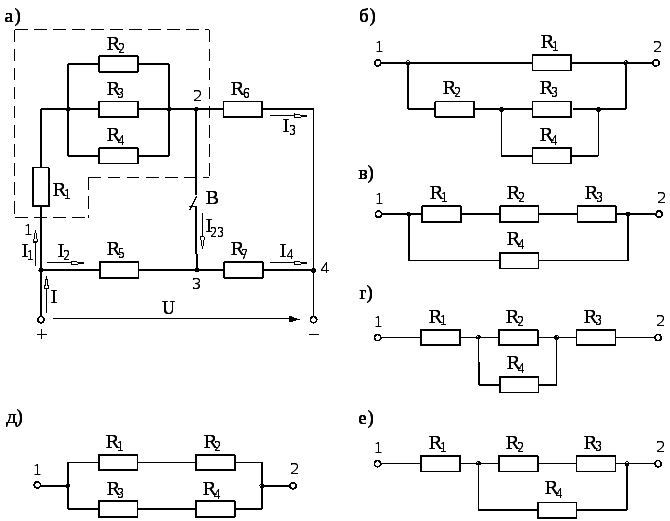
тока (рис. 1.6 с. 14)
и распределение
токов по ветвям. Вариант электрической
цепи (включая её участок 1—
2,
рис.
1.6, б
– з,
ограниченный на схеме рис.
1.6, а пунктиром), положение выключателей
B1
и В2
в схемах, величины сопротивлений
резисторов R1
− R12
и питающего напряжения U
для
каждого из вариантов
задания представлены в
таблице
1.1 (с.
15).
Примечание. Для
расширения числа вариантов задания в
вариантах 31—60
сопротивления
резисторов:
R6
= ∞, R12
= 0.
Сделать проверку решения, используя I
закон Кирхгофа
и уравнение баланса мощностей.
Задача №2
Для электрической
цепи постоянного тока (рис. 1.7 с. 16)
определить общий ток I,
токи I1,
I2,
I3,
I4
в ветвях резисторов и ток I23
в перемычке 2
– 3 цепи при
разомкнутом и замкнутом выключателе
В,
а также напряжение U23
между узлами 2
и 3
при разомкнутом выключателе. Напряжение
U,
подводимое к электрической цепи,
сопротивления резисторов R1
– R7,
положение выключателя В
и участок электрической цепи между
узлами 1
и 2
цепи, показанный на рис. 1.7 пунктиром
для соответствующего варианта рис. 1.7
б – е,
приведены в таблице 1.2(с. 17).
Примечание.
В вариантах 31 – 60 сопротивление резистора
R2=0.
Сделать проверку решения, используя I
закон Кирхгофа
и уравнение баланса мощностей.
Р
1.6
Таблица 1.1
|
Величины |
Варианты |
|||||||||||||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
|
R1, |
2 |
2 |
1 |
1 |
2 |
1 |
3 |
3 |
2 |
1 |
2 |
2 |
4 |
2 |
3 |
2 |
6 |
2 |
1 |
2 |
1 |
3 |
2 |
3 |
4 |
4 |
3 |
1 |
2 |
2 |
|
R2, |
4 |
1 |
1 |
1 |
2 |
1 |
3 |
2 |
1 |
2 |
1 |
2 |
3 |
2 |
2 |
4 |
6 |
4 |
6 |
4 |
2 |
3 |
2 |
2 |
3 |
3 |
4 |
2 |
2 |
1 |
|
R3, |
6 |
6 |
8 |
6 |
3 |
6 |
2 |
8 |
2 |
1 |
4 |
1 |
2 |
4 |
5 |
1 |
4 |
3 |
1 |
2 |
1 |
4 |
5 |
5 |
4 |
2 |
2 |
8 |
1 |
2 |
|
R4, |
6 |
7 |
7 |
6 |
3 |
6 |
4 |
12 |
3 |
1 |
4 |
1 |
1 |
2 |
6 |
1 |
2 |
1 |
2 |
2 |
2 |
2 |
3 |
4 |
2 |
1 |
5 |
6 |
6 |
4 |
|
R5, |
1 |
1 |
3 |
1 |
2 |
2 |
4 |
1 |
2 |
2 |
2 |
3 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
2 |
3 |
3 |
2 |
4 |
4 |
2 |
1 |
2 |
2 |
3 |
|
R6, |
2 |
2 |
6 |
1 |
2 |
2 |
1 |
1 |
4 |
2 |
1 |
1 |
2 |
2 |
1 |
3 |
3 |
6 |
3 |
3 |
2 |
2 |
1 |
2 |
1 |
2 |
4 |
2 |
6 |
4 |
|
R7, |
5 |
3 |
3 |
6 |
3 |
3 |
4 |
2 |
3 |
4 |
5 |
4 |
3 |
3 |
2 |
4 |
4 |
6 |
4 |
3 |
2 |
2 |
2 |
4 |
6 |
1 |
3 |
4 |
4 |
2 |
|
R8, |
10 |
5 |
5 |
10 |
10 |
10 |
5 |
15 |
5 |
5 |
5 |
5 |
5 |
10 |
10 |
10 |
5 |
10 |
4 |
2 |
3 |
1 |
5 |
10 |
15 |
5 |
10 |
5 |
5 |
5 |
|
R9, |
5 |
15 |
15 |
5 |
10 |
5 |
10 |
10 |
10 |
10 |
6 |
8 |
10 |
8 |
15 |
5 |
15 |
10 |
6 |
8 |
10 |
10 |
10 |
5 |
5 |
5 |
5 |
15 |
15 |
15 |
|
R10, |
5 |
10 |
10 |
10 |
5 |
10 |
5 |
20 |
5 |
10 |
15 |
20 |
10 |
5 |
10 |
5 |
10 |
5 |
5 |
10 |
15 |
5 |
10 |
10 |
10 |
10 |
5 |
10 |
10 |
10 |
|
R11, |
5 |
2 |
4 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
2 |
4 |
6 |
1 |
5 |
4 |
2 |
3 |
4 |
6 |
7 |
8 |
8 |
10 |
6 |
8 |
10 |
|
R12, |
8 |
8 |
7 |
2 |
4 |
6 |
8 |
10 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
2 |
4 |
3 |
5 |
8 |
10 |
1 |
2 |
3 |
4 |
6 |
6 |
2 |
4 |
|
U, |
110 или 220 |
|||||||||||||||||||||||||||||
|
Положение |
1 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
2 |
1 |
2 |
1 |
|
В2 |
– |
– |
– |
– |
– |
– |
– |
– |
– |
– |
4 |
4 |
5 |
5 |
– |
– |
– |
– |
– |
– |
– |
– |
– |
– |
– |
– |
– |
– |
– |
– |
|
Схема |
См. рис. 1.6, |
См. рис. 1.6, |
См. рис. 1.6, |
См. рис. 1.6, |
См. рис. 1.6, |
См. рис. 1.6, |
См. рис. 1.6, |
См. рис. 1.6, |
Рис. 1.7
Таблица 1.2
|
Величины |
Варианты |
|||||||||||||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
|
U, |
110 или 220 |
|||||||||||||||||||||||||||||
|
R1, |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
20 |
30 |
40 |
10 |
30 |
20 |
30 |
40 |
30 |
10 |
10 |
40 |
20 |
10 |
20 |
20 |
30 |
40 |
10 |
10 |
20 |
30 |
40 |
|
R2, |
10 |
10 |
20 |
30 |
40 |
10 |
10 |
20 |
30 |
40 |
10 |
20 |
20 |
30 |
40 |
30 |
10 |
10 |
40 |
20 |
10 |
10 |
20 |
30 |
40 |
10 |
10 |
20 |
30 |
40 |
|
R3, |
10 |
20 |
20 |
30 |
40 |
10 |
20 |
20 |
30 |
40 |
10 |
10 |
20 |
30 |
40 |
30 |
10 |
20 |
40 |
20 |
10 |
10 |
10 |
10 |
10 |
10 |
20 |
20 |
30 |
40 |
|
R4, |
10 |
30 |
20 |
30 |
40 |
10 |
30 |
20 |
30 |
40 |
10 |
10 |
20 |
30 |
40 |
30 |
10 |
30 |
40 |
20 |
20 |
20 |
30 |
30 |
30 |
10 |
30 |
20 |
30 |
40 |
|
R5, |
10 |
10 |
5 |
20 |
10 |
10 |
10 |
5 |
20 |
10 |
5 |
10 |
10 |
20 |
20 |
20 |
10 |
10 |
10 |
5 |
10 |
10 |
10 |
5 |
20 |
10 |
20 |
5 |
20 |
10 |
|
R6, |
10 |
20 |
10 |
5 |
5 |
10 |
20 |
10 |
5 |
5 |
5 |
10 |
20 |
10 |
10 |
5 |
10 |
20 |
5 |
10 |
5 |
10 |
20 |
10 |
5 |
10 |
20 |
10 |
5 |
5 |
|
R7, |
5 |
10 |
20 |
30 |
40 |
5 |
10 |
20 |
30 |
40 |
40 |
30 |
20 |
10 |
5 |
30 |
5 |
10 |
40 |
20 |
10 |
20 |
30 |
40 |
5 |
5 |
10 |
20 |
40 |
40 |
|
Схема |
рис. 1.34, а |
рис. 1.34, б |
рис. 1.34, в |
рис. 1.34, г |
рис. 1.34, д |
рис. 1.34, е |
||||||||||||||||||||||||
|
Положение |
разомкнут |
замкнут |
разомкнут |
замкнут |
разомкнут |
замкнут |
||||||||||||||||||||||||
|
замкнут |
разомкнут |
замкнут |
разомкнут |
замкнут |
разомкнут |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Главная
→
Примеры решения задач ТОЭ
→
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Основными законами, определяющими расчет электрической цепи, являются законы Кирхгофа.
На основе законов Кирхгофа разработан ряд практических методов расчета электрических цепей постоянного тока, позволяющих сократить вычисления при расчете сложных схем.
Существенно упростить вычисления, а в некоторых случаях и снизить трудоемкость расчета, возможно с помощью эквивалентных преобразований схемы.
Преобразуют параллельные и последовательные соединения элементов, соединение «звезда» в эквивалентный «треугольник» и наоборот. Осуществляют замену источника тока эквивалентным источником ЭДС. Методом эквивалентных преобразований теоретически можно рассчитать любую цепь, и при этом использовать простые вычислительные средства. Или же определить ток в какой-либо одной ветви, без расчета токов других участков цепи.
В данной статье по теоретическим основам электротехники рассмотрены примеры расчета линейных электрических цепей постоянного тока с использованием метода эквивалентных преобразований типовых схем соединения источников и потребителей энергии, приведены расчетные формулы.
Решение задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований
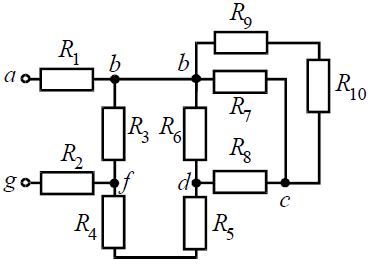
Задача 1. Для цепи (рис. 1), определить эквивалентное сопротивление относительно входных зажимов a−g, если известно: R1 = R2 = 0,5 Ом, R3 = 8 Ом, R4 = R5 = 1 Ом, R6 = 12 Ом, R7 = 15 Ом, R8 = 2 Ом, R9 = 10 Ом, R10= 20 Ом.
Рис. 1
Решение
Начнем эквивалентные преобразования схемы с ветви наиболее удаленной от источника, т.е. от зажимов a−g:
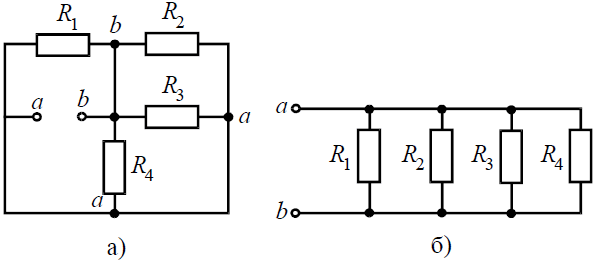
Задача 2. Для цепи (рис. 2, а), определить входное сопротивление если известно: R1 = R2 = R3 = R4= 40 Ом.
Решение
Исходную схему можно перечертить относительно входных зажимов (рис. 2, б), из чего видно, что все сопротивления включены параллельно. Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивленияможно воспользоваться формулой:
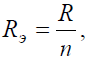
n — количество параллельно соединенных сопротивлений.
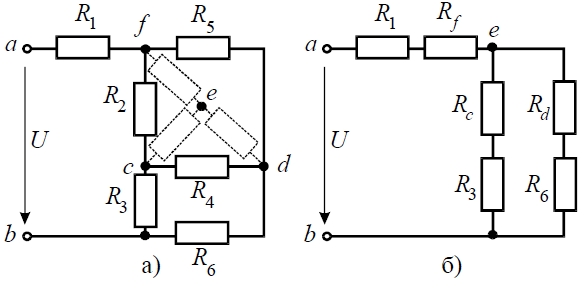
Задача 3. Определить эквивалентное сопротивление относительно зажимов a–b, если R1 = R2 = R3 = R4 = R5 = R6 = 10 Ом (рис. 3, а).
Рис. 3
Решение
Преобразуем соединение «треугольник» f−d−c в эквивалентную «звезду». Определяем величины преобразованных сопротивлений (рис. 3, б):
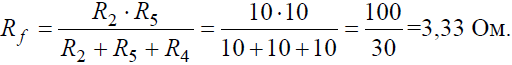
На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно:
И тогда эквивалентное сопротивление исходной схемы представляет последовательное соединение сопротивлений:
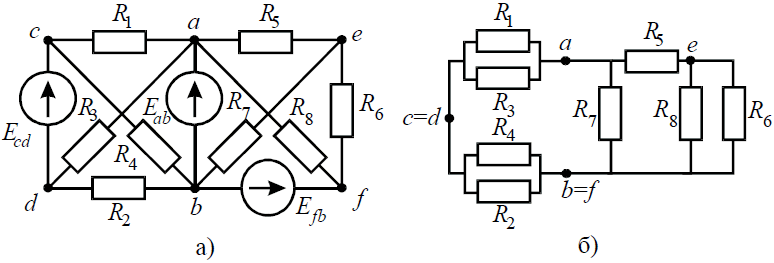
Задача 4. В заданной цепи (рис. 4, а) определить методом эквивалентных преобразований входные сопротивления ветвей a−b, c–d и f−b, если известно, что: R1 = 4 Ом, R2 = 8 Ом, R3 =4 Ом, R4 = 8 Ом, R5 = 2 Ом, R6 = 8 Ом, R7 = 6 Ом, R8 =8 Ом.
Решение
Для определения входного сопротивления ветвей исключают из схемы все источники ЭДС. При этом точки c и d, а также b и f соединяются накоротко, т.к. внутренние сопротивления идеальных источников напряжения равны нулю.
Рис. 4
Ветвь a−b разрывают, и т.к. сопротивление Ra–b = 0, то входное сопротивление ветви равно эквивалентному сопротивлению схемы относительно точек a и b (рис. 4, б):
Аналогично методом эквивалентных преобразований определяются входные сопротивления ветвей Rcd и Rbf. Причем, при вычислении сопротивлений учтено, что соединение накоротко точек a и b исключает ( «закорачивает») из схемы сопротивления R1, R2, R3, R4 в первом случае, и R5, R6, R7, R8 во втором случае.
Задача 5. В цепи (рис. 5) определить методом эквивалентных преобразований токи I1, I2, I3 и составить баланс мощностей, если известно: R1 = 12 Ом, R2 = 20 Ом, R3 = 30 Ом, U = 120 В.
Рис. 5
Решение
Эквивалентное сопротивлениедля параллельно включенных сопротивлений:
Эквивалентное сопротивление всей цепи:
американские сигареты парламент.
Ток в неразветвленной части схемы:
Напряжение на параллельных сопротивлениях:
Токи в параллельных ветвях:
Баланс мощностей:
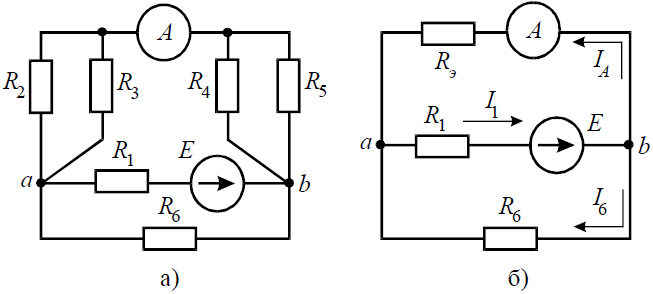
Задача 6. В цепи (рис. 6, а), определить методом эквивалентных преобразований показания амперметра, если известно: R1 = 2 Ом, R2 = 20 Ом, R3 = 30 Ом, R4 = 40 Ом, R5 = 10 Ом, R6 = 20 Ом, E = 48 В. Сопротивление амперметра можно считать равным нулю.
Рис. 6
Решение
Если сопротивления R2, R3, R4, R5 заменить одним эквивалентным сопротивлением RЭ, то исходную схему можно представить в упрощенном виде (рис. 6, б).
Величина эквивалентного сопротивления:
проститутки академическая. Смотри здесь строительство и ремонт деревянного дома.
Преобразовав параллельное соединение сопротивлений RЭ и R6 схемы (рис. 6, б), получим замкнутый контур, для которого по второму закону Кирхгофа можно записать уравнение:
откуда ток I1:
Напряжение на зажимах параллельных ветвей Uab выразим из уравнения по закону Ома для пассивной ветви, полученной преобразованием RЭ и R6:
Тогда амперметр покажет ток:
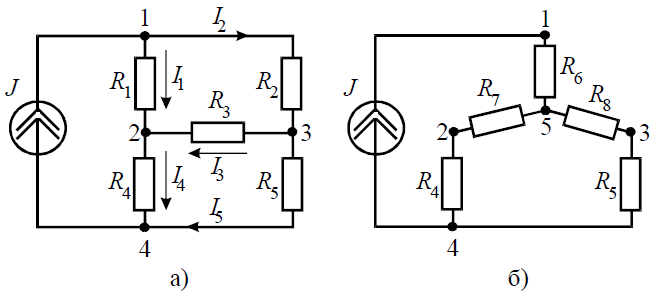
Задача 7. Определить токи ветвей схемы методом эквивалентных преобразований (рис. 7, а), если R1 = R2 = R3 = R4 = 3 Ом, J = 5 А, R5 = 5 Ом.
Рис. 7
Решение
Преобразуем «треугольник» сопротивлений R1, R2, R3 в эквивалентную «звезду» R6, R7, R8 (рис. 7, б) и определим величины полученных сопротивлений:
Преобразуем параллельное соединение ветвей между узлами 4 и 5
Ток в контуре, полученном в результате преобразований, считаем равным току источника тока J, и тогда напряжение:
И теперь можно определить токи I4 и I5:
Возвращаясь к исходной схеме, определим напряжение U32 из уравнения по второму закону Кирхгофа:
Тогда ток в ветви с сопротивлением R3 определится:
Величины оставшихся неизвестными токов можно определить из уравнений по первому закону Кирхгофа для узлов 3 и 1:
Электронная версия статьи Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Примеры решения задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Метод эквивалентного генератора:
Метод эквивалентного генератора рационально применять в случае необходимости определения тока (напряжения, мощностн и др.) только одной ветви сложной электрической цепи.
Для этой цели разбивают сложную электрическую цепь на две части — на сопротивление R, ток которого
Активным этот двухполюсник называют потому, что в нем имеется источник ЭДС. Этот активный двухполюсник обладает определенной ЭДС
Ток в резисторе с сопротивлением R определяют по закону Ома
Таким образом, определение тока 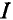
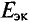
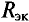
Величина ЭДС 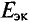
Внутреннее сопротивление эквивалентного генератора 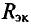
Практически для определения внутреннего сопротивления эквивалентного генератора измеряют амперметром ток между точки А и В работающего двухполюсника при коротком замыкании так как сопротивление амперметра настолько мало, что им можно пренебречь. Тогда
где 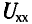
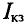
Такой метод практического определения внутреннего сопротивления эквивалентного генератора 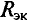
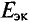
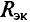
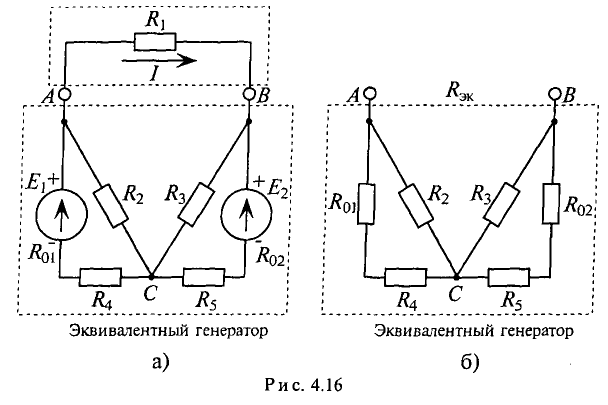
Пример 4.12
Определить ток в сопротивлении 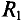
Решение
Для определения тока 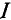
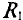
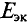
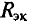
Знак «минус» обусловлен тем, что источники в схеме включены встречно и потенциал в точке А больше потенциала в точке В, так как 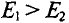
Напряжение
Напряжение
Следовательно, 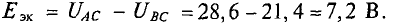
Искомый ток
Такой же ток получен в примере 4.6 на сопротивлении
Пример 4.13
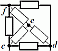
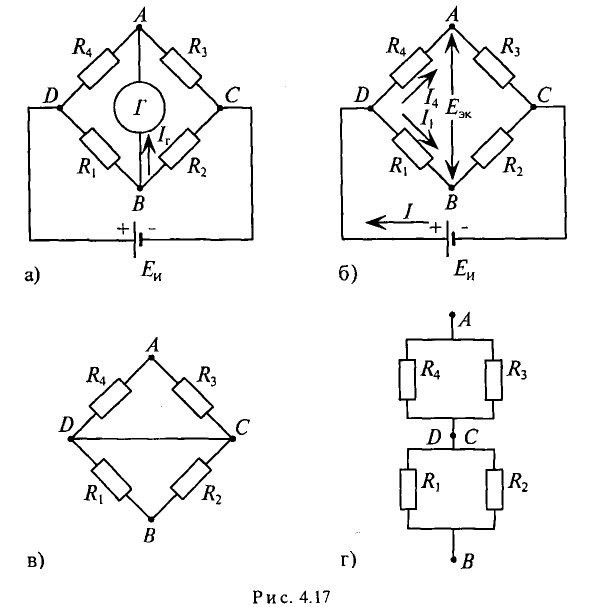
В схеме рис. 4.17а сопротивления плеч моста равны
Сопротивление гальванометра Rr = 98,33 Ом, ЭДС источника 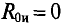
Решение
Для определения тока в цепи гальванометра 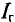
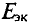
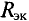
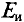
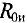
Для определения ЭДС эквивалентного генератора 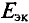
Тогда
При замене источника ЭДС 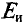
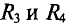
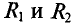
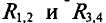
Тогда ток в ветви с гальванометром, который направлен из точки В в точку А, т. е. из точки с большим потенциалом в точку с наименьшим потенциалом (рис. 4.17а), будет равен
Метод эквивалентного генератора (активного двухполюсника)
Все методы, рассмотренные ранее, предполагали расчет токов одновременно во всех ветвях цепи. Однако в ряде случаев бывает необходимым контролировать ток в одной отдельно взятой ветви. В этом случае применяют для расчета метод эквивалентного генератора.
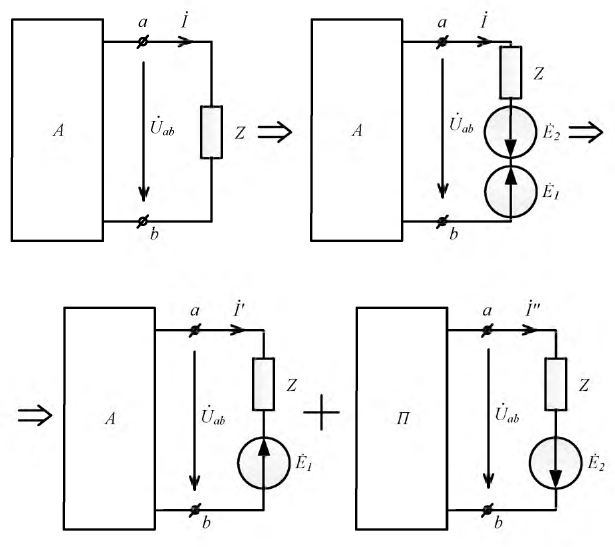
Пусть дана некоторая электрическая цепь, которую заменим активным двухполюсником (рис. 3.10), оставив только ветвь 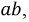
Сначала, введем в ветвь 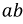
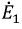
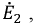
Затем, используя принцип наложения, данную цепь представим суммой двух цепей. В первой оставим все источники активного двухполюсника и источник ЭДС 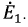
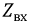
Рис. 3.10. Преобразование исходного двухполюсника в сумму двух цепей
На основании принципа наложения ток ветви
Поскольку 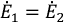
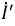
Напряжение на зажимах источника в режиме холостого хода численно равно его ЭДС. Тогда активный двухполюсник с источником 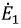
Рис. 3.11. Схема замещения активного двухполюсника
В этой схеме ЭДС 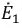
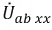
Таким образом, ток в ветви
Пусть дана цепь (рис. 3.12), в которой необходимо рассчитать ток 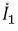
Рис. 3.12. Исходная цепь
Последовательность расчета:
1. Разомкнем ветвь с сопротивлением 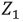
2. Зададим положительное направление 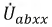
3. Токи 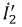
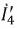
Тогда
4. Определим эквивалентное сопротивление пассивного двухполюсника. Для этого мысленно закоротим все источники ЭДС исходной цепи, оставляя в схеме для реальных источников их внутренние сопротивления.
В образовавшейся схеме пассивного двухполюсника невозможно определить эквивалентное сопротивление относительно зажимов 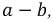
Преобразуем, например, «треугольник» сопротивлений 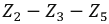
Рис. 3.14. Схема пассивного двухполюсника
Сопротивления этой схемы будут:
Входное сопротивление цепи 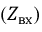
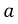
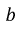
Окончательно имеем:
- Теоремы теории цепей
- Теорема обратимости (или взаимности)
- Теорема компенсации
- Теорема об изменении токов в электрической цепи при изменении сопротивления в одной ветви
- Метод свертывания электрической цепи
- Метод преобразования схем электрических цепей
- Параллельное соединение генераторов
- Метод узловых и контурных уравнений
Демьян Бондарь
Эксперт по предмету «Электроника, электротехника, радиотехника»
преподавательский стаж — 5 лет
Задать вопрос автору статьи
Методы расчета электрических цепей
Определение 1
Электрическая цепь – это соединение различных электронных и электрических деталей в одно целое.
Основными методами расчета электрических цепей являются:
- Метод наложения.
- Расчет электрических цепей с использованием законов Кирхгофа и Ома.
- Метод эквивалентного генератора.
- Метод эквивалентных преобразований.
- Метод узловых потенциалов.
- Метод контурных токов.
Большинство методов расчета электрических цепей основано на упрощении процедуры нахождения тока в ее ветвях. Некоторые из них основаны на упрощении систем уравнений, по которым осуществляется расчет, а в других случаях упрощается сама схема. Упрощение схемы применяется тогда, когда есть необходимость в определении электрического тока только в одной ветви.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Метод эквивалентных преобразований. Примеры расчета
Определение 2
Метод эквивалентных преобразований – это метод расчета электрической цепи, который основан на ее свертывании.
Преобразование электрической цепи считается эквивалентным, в том случае, если при замене участка рассматриваемой электрической цепи более простыми электрические токи и напряжения участка, который не был преобразован, остаются неизменными. На практике, при расчетах электрических цепей используется преобразование со смешанным соединением элементов, представляющее собой сочетание простых параллельных и последовательных соединений. При помощи метода эквивалентных преобразований можно рассчитать практически любую цепь, при этом используются простые вычислительные средства и операции. Данный метод также позволяет рассчитать ток в ветви цепи, без расчета других участков.
Рассмотри схему, которая представлена на рисунке ниже.
«Метод эквивалентных преобразований» 👇
Рисунок 1. Схема. Автор24 — интернет-биржа студенческих работ
Так как в представленной схеме всего один источник, то можно определить истинные направления токов, как и показано на рисунке. Таким образом мы можем рассчитать эквивалентное сопротивление всей схемы:
$Rэк = ((((R3*R4)/(R3+R4)+R5))/R2) / ((R3*R4)/(R3+R4)+R5+R2))+R1$
Поэтому эквивалентная схема будет иметь следующий вид
Рисунок 2. Схема. Автор24 — интернет-биржа студенческих работ
Так как при эквивалентности замены участка схемы необходима неизменность токов и напряжений остальной цепи, то электрический ток будет везде одинаков. Таким образом электрический ток источника можно рассчитать следующим образом:
$I1 = E/Rэкв$
Так как нам известно сопротивление на первом участке, то мы можем рассчитать напряжение на элементе R1:
$U1 = I1*R1$
Согласно второму закону Кирхгофа запишем уравнение для контура R1-E-R2:
$E = U1+U2 = I*=I1*R1+I2*R2$
Откуда
$U2 = E-U1$
Теперь согласно закону Ома можно рассчитать ток на втором участке:
$I2 = U2/R2$
Применяя закон на третьем участке рассчитываем электрический ток на третьем участке:
$I3 = I1-I2$
Напряжение на резисторе 3 рассчитывается по второму закону Кирхгофа, действительного для контура R2-R5-R3:
$U4 = U2-U3$
Так как в рассматриваемой схеме сопротивления 3 и 4 соединены параллельно, то напряжение на них будет одинаково, поэтому можно рассчитать токи I4 и I5 по следующим формулам:
$I4 = U4/R3$
$I5 = U4/R4$
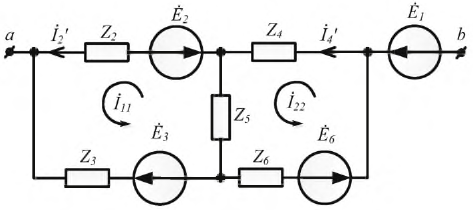
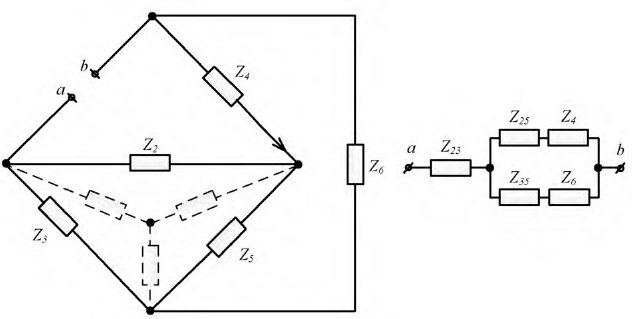
Рассмотрим схему, которая представлена на рисунке ниже.
Рисунок 3. Схема. Автор24 — интернет-биржа студенческих работ
Предположим, что нам известны следующие величины R1, R2, R3, R4, R5, R6, E1, E2, J. На рисунках ниже изображено поэтапное преобразование исходной схемы, задачей которого является расчет I3.
Рисунок 4. Схема. Автор24 — интернет-биржа студенческих работ
Рисунок 5. Схема. Автор24 — интернет-биржа студенческих работ
Рисунок 6. Схема. Автор24 — интернет-биржа студенческих работ
Рисунок 7. Схема. Автор24 — интернет-биржа студенческих работ
Рисунок 8. Схема. Автор24 — интернет-биржа студенческих работ
На схеме б резисторы 4 и 6 соединены последовательно и могут быть заменены на один резистор R46, который рассчитывается следующим образом:
$R46 = R4+R6$
В схеме в источник электродвижущей силы 1 пересчитывается в эквивалентный источник тока следующим образом:
$Jэ = Е1/R3$
Затем сопротивление R2 и R3 могут быть заменены эквивалентны R23, которое рассчитывается по формуле:
$R23 = (R2*R3) / (R2+R3)$
Затем производится (рисунок д) обратный расчет эквивалентного источника электрического тока в эквивалентный источник электродвижущей силы:
$Eэ = Jэ*R23$
Рассмотрим рисунок е, на котором изображен пересчет электродвижущей силы Е2 в эквивалентный источник тока:
$Jэ1 = Е2/R46$
Теперь Jэ1 с источником J объединяется в один эквивалентный источник тока, суммарный ток которого можно рассчитать по следующей формуле:
$Jэ2 = J + Jэ1$
В данном случае сопротивление (рисунок з) R5 не будет учитываться, потому что сопротивление источника тока бесконечно. В последнем рисунке производится обратный переход к источнику электродвижущей силы:
$Еэ1 = Jэ2*R46$
В итоге получается одноконтурная схема, по которой можно рассчитать I3
$I3 = (Eэ+Еэ1) / (R1+R23+R46)$
Из схемы д можно рассчитать электрический ток I4, для чего используется первый закон Кирхгофа:
$I4+J-I3=0$
Отсюда
$I4 = I3-J$
Так как теперь известны токи I3 и I4, то по рисунку б можно рассчитать электрический ток I1, для чего составляется уравнение по второму закону Кирхгофа для внешнего контура схемы:
$I1*R3+I4*R46+I3*R1 = E1+E2$
Из вышепредставленного уравнения находится I1, а затем по второму закону рассчитывается электрический ток I2:
$I2+I3-I1 = 0$
Отсюда
$I2 = I1-I3$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме

Метод эквивалентного генератора применяется для определения тока одной из ветвей электрической цепи в том случае, когда расчет всей схемы не требуется. В основу метода положена теорема об активном двухполюснике (теорема Гельмгольца-Тевенена). Основная идея метода заключается в том, что часть цепи, параметры которой определять нет необходимости, заменяется эквивалентным генератором с известной эдс и сопротивлением. Метод часто применяется для расчета режима электрической цепи.
Алгоритм состоит из следующих шагов:
- Выбранная для расчета ветвь удаляется из схемы, а места образовавшегося разрыва обозначаются буквами. Оставшаяся часть схемы будет представлять собой эквивалентный генератор.
- Рассчитывается эквивалентная эдс генератора.
- Определяется эквивалентное сопротивление генератора.
- По найденным в пунктах 2 и 3 параметрам генератора определяется ток через исключенную в пункте 1 ветвь.
Метод эквивалентного генератора: примеры решения
Рассмотрим пример расчета электрической схемы методом эквивалентного генератора (рисунок 1).
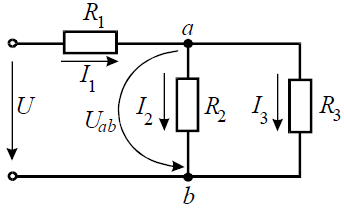
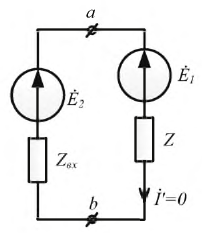
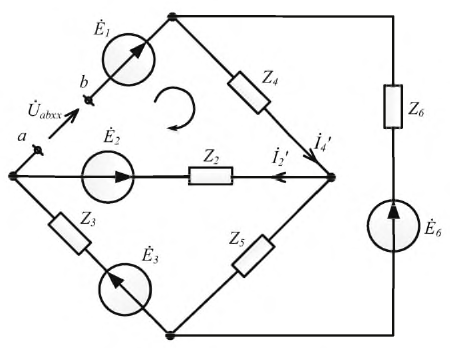
Допустим, что необходимо рассчитать ток Iab через резистор R4. Тогда преобразования схема будет иметь вид, представленный на рисунке 2.
После преобразования ток через резистор Rab (R4) определяется по формуле
Для того, чтобы рассчитать значения Еэкв и Rэкв необходимо рассмотреть режим холостого хода генератора. Для этого необходимо обеспечить его работу без нагрузки, то есть условно отсоединить от цепи исследуемую ветвь ab (рисунок 3).
Для представленной схемы напряжение Еэкв будет равно
Далее требуется определить эквивалентное сопротивление. Для этого воспользуемся методом пассивного двухполюсника. В этом случае необходимо исключить из схемы источник эдс и найти общее сопротивление цепи (рисунок 4).
Эквивалентное сопротивление полученной схемы определяется по формуле
Теперь можно определить ток, проходящий через резистор ab согласно выражению (1).
Поставленная задача решена.