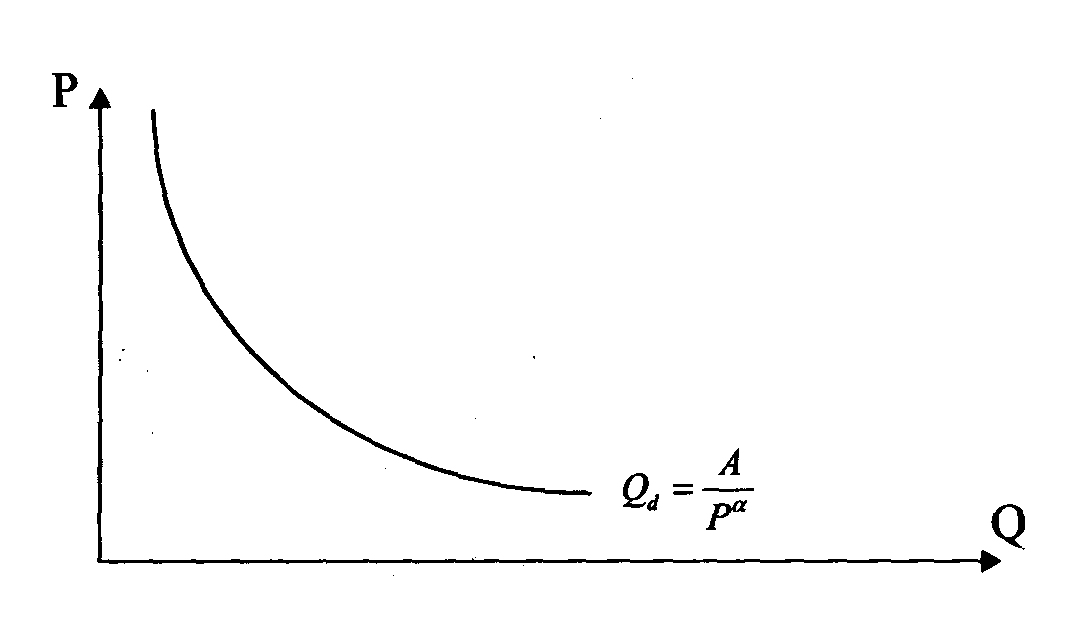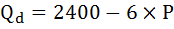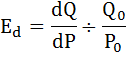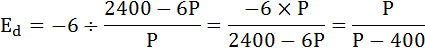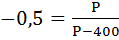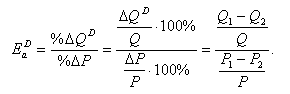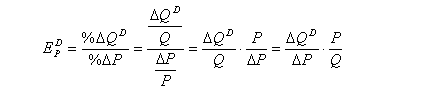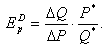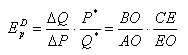Как найти эластичность функции по цене - Сайт, где вы сможете решить свои вопросы

ПРИЛОЖЕНИЯ ПРОИЗВОДНЫХ К ЭКОНОМИЧЕСКИМ
ЗАДАЧАМ

Ни одно
человеческое исследование не может называться наукой, если оно не прошло через
математические
доказательства.

Леонардо
да Винчи

ПЛАН

1.
Экономический смысл производной.

2.
Эластичность. Задача о спросе и
предложении

3.
Применение производной для
функции, заданной таблично.

15.1.
Экономический смысл производной

Рассмотрим задачу, иллюстрирующую экономический смысл
производной. Издержки производства y будем рассматривать как функцию количества выпускаемой
продукции x. Пусть Dx – прирост продукции, тогда Dy – приращение
издержек производства. Воспользуемся формулой (11.12)

Если ,
то получим

Таким
образом, производная характеризует приближенно
дополнительные затраты на производство единицы дополнительной продукции
и выражает предельные издержки производства.

Аналогичным образом, могут быть определены предельные
выручка, предельный продукт и другие предельные показатели. Предельные величины
характеризуют не состояние (как суммарная или средняя величина), а процесс,
изменение экономического объекта.

Пример
15.1. Функция издержек производства продукции некоторой фирмы имеет вид

Найти средние и предельные
издержки и вычислить их значение при .

Решение.
Найдем производную и ее значение – предельные издержки
производства:

, .

Средние издержки:

, .

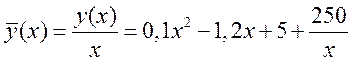
Это означает,
что при данном уровне производства (количестве выпускаемой продукции) средние
затраты на производство одной единицы продукции составляют 28 ден. ед., а
увеличение объема производства на одну единицу продукции обойдутся фирме
приближенно в 11 ден. ед.

15.2.
Эластичность. Задача спроса и предложения

Для исследования экономических процессов и решения
других прикладных задач часто используется понятие эластичности.

Определение 15.1. Эластичностью функции называется предел
отношения относительного приращения функции y(x)
к относительному приращению переменной xпри :

. (15.1)

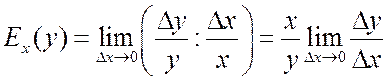
Вспоминая
определение производной, получим

.
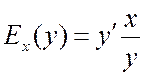
(15.2)

Эластичность функции показывает приближенно, на
сколько процентов изменится функция при увеличении
независимой переменной на 1%.

Отметим,
что эластичность можно представить в виде

.
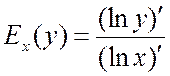
(15.3)

В связи с этим становятся
понятными следующие свойства эластичности:

, .

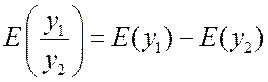
Пример
15.2. Найти эластичность функций: а) ,
б) .

Решение.
а) Поскольку , то по формуле (15.2)
получаем

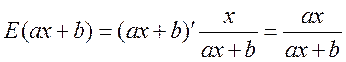
б) Для степенной функции

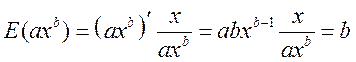
Как мы видим, эластичность степенной функции есть
величина постоянная, равная показателю степени. Это характерное свойство только
степенных функций. Поэтому степенные функции довольно часто используются в экономической
теории, т.к. все ее параметры имеют четкий экономический смысл.

В случае табличного задания функции определение
эластичности не однозначно. Это связано с тем, что в отношении не ясно, что брать в качестве x:
первоначальное значение x₁, конечное
значение x₂ или
среднее значение . В зависимости от этого
различают:

конечную
эластичность

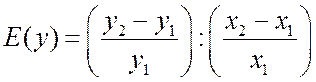
среднюю
эластичность

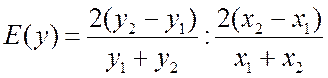
а
также логарифмическую эластичность

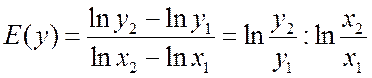
Все эти выражения мало отличаются друг от друга при
небольших относительных изменениях величин x
и y.

Эластичность функций часто применяется при анализе
спроса и потребления. Например, эластичность спроса y
относительно цены x
(или дохода x) показывает, на сколько процентов изменится спрос (объем
потребления) при увеличении цены (или дохода) на 1%. Спрос называется эластичным,
если , неэластичным, если , и нейтральным, если .

Пример
15.3. Зависимость между себестоимостью единицы продукции y (тыс. руб.) и выпуском продукции x
(млн. руб.) выражается функцией

Найти эластичность себестоимости
при выпуске продукции, равном 60 млн. руб.

Решение.
Воспользуемся решением предыдущей задачи

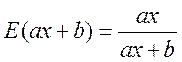
В нашем случае

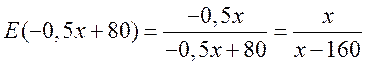
При

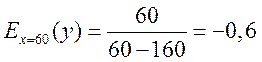
т.е. при выпуске продукции,
равном 60 млн. руб., увеличение его на 1% приведет к снижению себестоимости на
0,5%.

Пример
15.4. Функция спроса и предложения имеют соответственно вид:

, ,

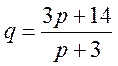
где q
и s – количество товара, соответственно
покупаемого и продаваемого в единицу времени, p
– цена единицы товара. Найти: а) равновесную цену, т.е. цену, при которой спрос
и предложения уравновешиваются; б) эластичности спроса и предложения при
равновесной цене; в) изменение дохода при увеличении цены на 10% от
равновесной.

Решение.
а) Равновесная цена определяется из условия ,
т.е.

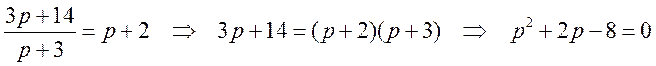
откуда
находим и .
Последний корень отбрасываем, т.к. цена не может быть отрицательной и
устанавливаем, что равновесная цена равна 2 ден. ед.

б) Найдем
эластичности спроса и предложения. Вычисляем соответствующие производные:

, ,

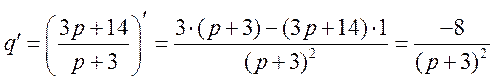
и подставляем их в формулу
(15.2):

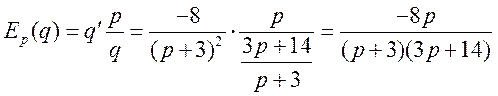
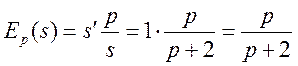
Для равновесной цены имеем

, .

Так как
полученные значения эластичностей меньше 1, то спрос и предложение данного
товара при равновесной (рыночной) цене неэластичны относительно цены.
Это означает, что изменение цен не приведет к резкому изменению спроса и
предложения.

в) При
увеличении цены p на 10% от равновесной цены
спрос уменьшится на , следовательно, доход от проданной продукции (цена p умноженная на количество q
проданного товара) возрастет в целом на .
Несмотря на то, что цена на товар увеличилась и спрос на нее упал, предприятие
все равно получает прибыль.

Пример
15.5. Зависимость между спросом и ценой q и
ценой p за единицу продукции, выпускаемой
некоторым предприятием, дается соотношением:

Найти эластичность спроса.
Выяснить, при каких значениях цен спрос является эластичным, нейтральным и
неэластичным. Какие рекомендации о цене за единицу продукции можно дать
руководителям предприятия при и при ден. ед.?

Решение.
Найдем эластичность по формуле (15.2):

Для нахождения
p воспользуемся тем, что при нейтральном спросе , т.е.

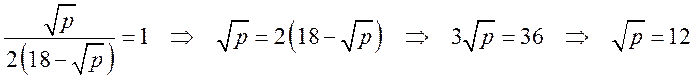
Тогда .

Далее,
принимая во внимание, что цена и спрос , получим еще одно ограничение на p:

Таким образом, область изменения
цены p интервал (0; 324). Причем он точкой p = 144 делится на две части. Посмотрим модуль
эластичности на каждой из них.

Источник

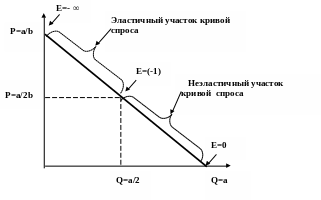
Рассмотрим
линейную кривую спроса Q=a-bP. Наклон этой
кривой спроса есть константа(-b).
–b=
.Подставив
значение –b в формулу (3), получим

.
Для линейной кривой спроса наклон –
постоянная величина, он не зависит от
цены и величины спроса. Напротив, с
изменением цены отношение P/Q меняется
при движении вдоль кривой спроса
(рис.
7).

Следовательно,
для линейной кривой спроса эластичность
спроса по цене – переменная величина.

При
Р=0 эластичность спроса равна нулю. При
Q=0 коэффициент эластичности спроса
равен минус бесконечности. Если Q=a/2,
P=a/2b,
то эластичность спроса по цене E=
-1. Таким образом, точка единичной
эластичности спроса по цене находится
в середине линии спроса.

Спрос
является

неэластичным
при

;
эластичным
при

.

Рис.
7

Пример
3.

Дана
функция спроса на товар Qd = 9 – 0,5Р.
Определить коэффициент эластичности
спроса по цене составит при цене 6 ден.
ед.

Решение:

По
формуле точечной эластичности

,
откуда

.

Ответ:
-0,5.

Пример
4.

Функция
спроса имеет следующий вид: Qd = 2100 – 3P.
При какой цене ценовая эластичность
спроса (Е_Р)
составит (-0,75)?

Решение:

,
откуда

.
Получаем, что Р=300.

Ответ:
300.

1.4 Функция спроса с постоянной эластичностью

Рассмотрим
эластичность функции спроса: вида:

(Рис.8)

где
А и а – некоторые константы. Выведем
формулу эластичности для этой функции:

Таким
образом, мы выяснили, что значение
эластичности для подобной гиперболической
функции спроса не зависит от координаты
точки и при любом уровне цены равно -а.
Обратите внимание, что свойством
постоянной эластичности обладает не
всякая гиперболическая функция спроса,
а только удовлетворяющая указанному
выше общему уравнению.

Рис.
8

1.5. Эластичность и общий доход

Общий
доход (выручка) определяется как
произведение цены на проданное количество
товара. ТR=P∙Q.Выясним,
как общая выручка зависит от эластичности
спроса при линейной
функции спроса:
Q=a-bP.
Выручка – прямая функция от объема
продаж: TR=
F(Q).
Чтобы ее определить, надо выразить цену
товара через Q: Р=

(обратная функция спроса) и подставить
это выражение в ТR: ТR=P∙Q=(
)∙Q.
Графическое представление функции –
это парабола, ветви которой опущены
вниз. Вершина параболы (максимум выручки)
достигается при Q=a/2; P=a/2b,
то есть при единичной эластичности
спроса. При снижении цены товара (синяя
стрелка на графике) общая выручка
продавцов возрастает от нуля до максимума
на эластичном участке кривой спроса, а
затем она снижается от максимального
значения до нуля на неэластичном участке
кривой спроса.

При
снижении цены товара (красная стрелка
на графике) общая выручка продавцов
возрастает от нуля до максимума на
неэластичном участке кривой спроса, а
затем она снижается от максимального
значения до нуля на эластичном участке
кривой спроса.

Если
спрос на товар эластичен по цене, то
цена и общая выручки изменяются в
противоположных направлениях: P↓-
TR↑;
P↑- TR↓.

Если
спрос на товар неэластичен по цене, то
цена и общая выручка изменяются в одном
направлении:

P↓-
TR↓;
P↑- TR↑.

Рассчитаем
выручку для нелинейной функции спроса
вида

TR=
.
Таким образом, выручка постоянна и не
зависит от Р и Q

Рис.9

Пример
5.

По
исходным данным, приведенным в таблице,
определите общую выручку, коэффициент
эластичности спроса по цене, тип
эластичности спроса по цене для товаров
A, B, С.

Таблица 1
	Товар А	Товар В	Товар С
Показатель	В начале периода	В конце периода	В начале периода	В конце периода	В начале периода	В конце периода
Цена, тыс. р.	4	3	10000	5000	500	250
Количество шт.	100	120	10	30	20	40
Выручка, тыс. р.
Коэффициент эластичности
Тип эластичности

Решение:
Общую выручку можно найти по формуле
TR
= Q∙P,
где Q
– объем продаж, а Р
– цена товара. Для нахождения коэффициента
эластичности необходимо воспользоваться
формулой:

,
где Е_Р
– коэффициент ценовой эластичности
спроса.

	Товар А	Товар В	Товар С
Выручка, тыс. р.	400	360	100 000	150 000	10 000	10 000
Коэф. эласт.	– 7/11	– 1,5	– 1
Тип эластичности	Неэластичный спрос	Эластичный спрос	Единичная эластичность

Пример
6.

Цены
на товар снизились на 15%, а объем спроса
вырос с 200 ед. до 230 ед. Определите изменение
выручки и сделайте вывод об эластичности
спроса на товар.

Решение:
Общую выручку можно найти по формуле
TR
= Q∙P,
где Q
– количество, а Р – цена товара. до
изменения цены выручка составляла TR₁
= 200∙Р, а после изменения цены выручка
стала равна TR₂
= 230∙0,85Р = 195,5∙Р.

Поскольку,
при снижении цены выручка уменьшилась,
спрос является неэластичным.

Ответ:
неэластичный спрос.

Пример
7.

Цена
товара увеличилась на 1% при эластичности
спроса по цене, равной (-3). Как изменилась
выручка продавца?

Решение:
Общую выручку можно найти по формуле
TR
= Q∙P,
где Q
– количество, а Р – цена товара. Получаем,
что до изменения цены выручка составляла
TR₁
= Q∙Р,
а после ее изменения выручка стала равна
TR₂
= 0,97Q∙1,01Р
= 0,98Q∙Р.
Таким образом, выручка уменьшилась на
2%.

Ответ:
уменьшилась на 2%.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Функция задана уравнением

а) Выведите формулу эластичности этого спроса.

б) При какой цене эластичность спроса по цене составит – 0,5?

в) При какой цене в интервале цен от 200 до 300 эластичность будет максимальной по абсолютной величине?

Решение:

а) Так как в условии задачи нам дана непрерывная функция, для вывода формулы эластичности этого спроса воспользуемся коэффициентом точечной эластичности.

В точке (P₀,Q₀) точечная эластичность вычисляется как

Где

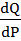
– производная функции спроса в этой точке.

б)

Отсюда:

Р = 133,33

в) Чем больше P, тем больше эластичность по абсолютной величине. Поэтому на интервале цен от 200 до 300 она достигает максимума в точке Р=300.

Источник

5.5. Эластичность спроса по цене: углубление анализа

Анализируя поведение потребителя, мы обосновали закон спроса. Если цена на товар растёт, то, ceteris paribus (при прочих равных условиях), величина спроса на этот товар на рынке уменьшается, и наоборот. Но вот на сколько? Это зависит от чувствительности спроса к изменению цены, то есть от ценовой эластичности спроса. Знание эластичности спроса по цене имеет большое практическое значение. В правильной оценке эластичности спроса заинтересованы и фирмы, и правительство.

Напомним, что для измерения эластичности
используется коэффициент эластичности
спроса (E^D), который
в самом общем виде представляет собой отношение процентного изменение величины
спроса к процентному изменению цены:

(1)

Коэффициент эластичности
показывает, на сколько процентов
изменится спрос, если цена изменится на 1 %. Поскольку цена и величина спроса
изменяются (по закону спроса) в противоположном друг другу направлении,
постольку коэффициент эластичности имеет знак «минус» , который, впрочем,
экономисты по молчаливому соглашению часто опускают. К примеру, | Е^d| для электроэнергии равняется 0,13 – это значит, что если тариф на электроэнергию
повысится на 1 % , то спрос на неё понизится на 0,13 %. Если тариф повысится на 10 %, то спрос
понизится на 1,3 % и т.д.

Напомним также, что в зависимости от
степени чувствительности спроса к изменению цены можно выделить пять видов
эластичности:

1. Эластичный
спрос. Покупатели чувствительны к изменению цены. Спрос в
процентном отношении изменяется больше, чем цена, то есть для эластичного спроса | Е^d| >
1,0;

2. Неэластичный
спрос. Покупатели нечувствительны к изменению цены. Спрос в
процентном отношении изменяется меньше, чем цена, то есть для эластичного спроса | Е^d| <
1,0;

3. Единичная
эластичность спроса. Спрос в процентном отношении
изменяется так же как цена, то есть для
этого вида спроса | Е^d| =
1,0;

4. Совершенно
эластичный спрос. Покупатели гиперчувствительны к
изменению цены. Например, при ничтожно малом повышении цены спрос стремится к
бесконечно малой величине. Для этого вида спроса| Е^d| =
∞. На графике кривая спроса представляет собой прямую линию параллельную
абсциссе;

5. Совершенно
неэластичный спрос. Покупатели абсолютно нечувствительны к
изменению цены. При любом процентном изменении цены величина спроса остаётся
неизменной. Для этого вида спроса | Е^d| = 0.
На графике кривая спроса представляет собой прямую линию параллельную
ординате.

Существуют два способа точного
измерения эластичности. Ценовую эластичность спроса можно определить: (1) в
некотором диапазоне изменения цены – на отрезке (дуге) кривой спроса. Этот
способ измерения называется дуговой
эластичностью; (2) для определённого уровня цены, то есть в некоторой точке
кривой спроса. Этот способ называется точечной
эластичностью.

Например, на рис. 5-12 дуговая эластичность
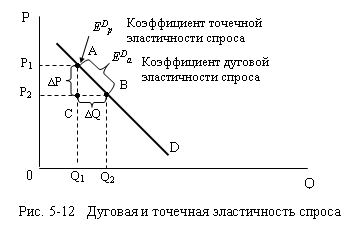
измеряется в ценовом диапазоне Р₁
– Р₂на отрезке АВ
кривой спроса, а точечная – для уровня цены Р₁ в точке А.

Выведем формулу для дуговой эластичности спроса.

Поскольку в приведенной выше формуле не ясно, какое
значение Q: Q₁ или Q₂, берётся
за базу, а это может сильно повлиять на результат измерения, экономисты
договорились брать среднее арифметическое значение. То есть, Q = (Q₁ + Q₂ /2. То же самое делается
по отношению к цене, выступающей в качестве базы: Р = (Р₁ + Р₂)/2. Тогда формула коэффициента
дуговой эластичности спроса по цене примет окончательный вид:

(2)

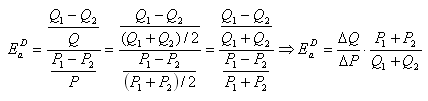
Дуговая эластичность спроса используется в случае
значительного изменения цены. Если же это изменение незначительно, то
целесообразно использовать точечную эластичность спроса. Коэффициент точечной
эластичности спроса легко выводится из формулы (2):

Посмотрим на рис. 5-12 и представим, что ∆P сжимается
так, что точка С приближается
вплотную к точке А. Тогда ∆Q также
сжимается и точка В стремится к точке
А как к своему пределу. Если мы
примем ∆P и, следовательно,
∆Q за
бесконечно малые величины, то получим измерение ценовой эластичности в точке А:

(3)

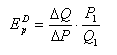
Математическое приложение 5-2

Можно выразить точечную эластичность спроса по цене
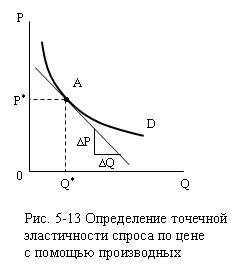
через производные. Предположим, требуется определить Е^D_p в точке А кривой спроса на рис. 5-13:

Тогда
при бесконечно малом изменении Р
«скорость» изменения Q
будет dQ/dP и формула примет
вид:

(4)

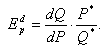
Коэффициент ценовой эластичности спроса
в точке можно определить по уравнению функции
спроса. Линейное уравнение имеет вид: Q^D= a – bP (например, Q^D= 10 – 2P). Коэффициент b показывает,
на сколько единиц изменяется величина спроса при изменении цены на 1 рубль (в
нашем примере b = – 2, что
означает, что каждый раз, когда цена изменяется на 1 рубль, величина спроса
изменяется в противоположном направлении на 2 единицы). То есть -b = -∆Q/∆Р = наклону
кривой спроса.

Тогда,
подставив b в уравнение (3) получим:

(5)

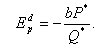
Пример.

Пусть функция спроса описывается
уравнением: Q^D= 10 – 2P.
Определить ценовую эластичность спроса при Р^* = 4.

Решение:

Подставим в уравнение (5) все данные, получим:

Измерение
точечной эластичности спроса геометрическим способом («правило РАРО»). Есть
простой способ измерения эластичности в любой точке кривой спроса с помощью
линейки. Этот способ известен как «правило РАРО» (PAPO rule).

Правило
РАРО гласит: чтобы
определить точечную эластичность нужно измерить расстояние от точки до
абсциссы, РА (point
– abscissa),
и
расстояние от точки до ординаты, РО (point – ordinate), а
затем отнести первое ко второму, то есть Е^D = РА/РО.

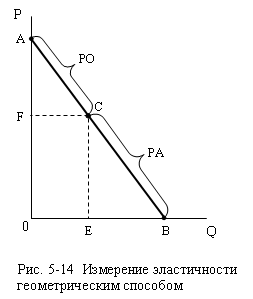
Выведем правило,
используя рис. 5-14. Определим эластичность в точке С.

Так как АОВ и СЕВ – подобные треугольники, то

Но (при пересечении сторон угла параллельными прямыми по
сторонам угла отсекаются пропорциональные отрезки).

И,
следовательно

СВ
– это расстояние от точки, в которой измеряется эластичность, до абсциссы (РА),
а СА – это расстояние от той же точки
до ординаты (РО).

На рис. 5-14 РА= 5,5
см., а РО = 4 см. Следовательно, Е^D=
5,5:4 = 1,375.

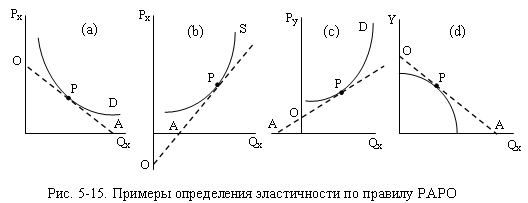
Правило РАРО универсально. Оно позволяет
определить эластичность спроса по цене, доходу, перекрёстную эластичность
спроса, эластичность предложения. Правило применимо и тогда, когда линии спроса
и предложения являются кривыми. В этом случае отрезки РА и РО находятся на
касательной, проведённой через интересующую нас точку на кривой спроса или
предложения (примеры приведены на рис. 5-15).

На рис. 5-15а спрос
в точке Р имеет единичную эластичность по цене (РА=РО). На рис. 5-15b ценовая
эластичность предложения в точке Р меньше единицы (PA<PO), то есть предложение
неэластично. На рис. 5-15с перекрёстная эластичность спроса на товар Х по цене
товара У больше единицы (PA>PO), то есть спрос эластичен. На
рис. 5-15d спрос на низший товар Х эластичен по доходу У (PA>PO).

Эластичность нельзя
отождествлять с наклоном кривой спроса (наклон линии представляет собой
отношение горизонтального изменения к вертикальному, то есть -∆Q/∆Р.

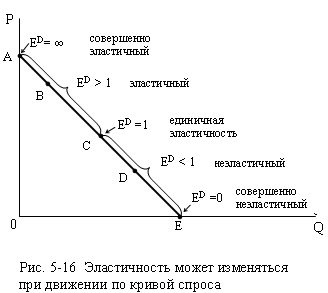
Рассмотрим рис. 5-16. В каждой точке кривой
спроса наклон одинаков. Поэтому в
формуле (5) – b является постоянной величиной. В то же время отношение P/Q при
движении по кривой спроса меняется. Поэтому эластичность в разных точках кривой
спроса будет разной. Применим «правило РАРО» для расчёта коэффициента
эластичности. В точке А эластичность
равна бесконечности (= АЕ/0). В точке В эластичность больше 1 ( = ВЕ/АВ).
В точке С, которая находится в середине кривой спроса эластичность равна единице (так как СЕ = СА, то СЕ/СА = 1). В точке D она меньше
единицы (= DE/DA). И
наконец, в Е эластичность равна 0 (= 0/AE).

Рис. 5-16 показывает, почему некорректно говорить об «эластичности кривой спроса», считая что пологая кривая спроса демонстрирует эластичный спрос, а крутая – неэластичный спрос. Исключением являются три случая:

1) горизонтальная кривая спроса (эластичность в каждой точке равна бесконечности);

2) вертикальная кривая спроса (в каждой точке эластичность равна нулю);

3) кривая спроса, имеющая форму равносторонней гиперболы;

В последнем случае кривая описывается уравнением обратной пропорциональности:

,
где
с – есть некоторая постоянная величина.

Применительно к функции спроса уравнение
выглядит:

Тогда, учитывая, что с – это коэффициент при цене, который мы раньше обозначали как b, получим:

Следовательно, кривая спроса, имеющая форму
равносторонней гиперболы, имеет единичную эластичность (в любой её точке
эластичность спроса по цене равна –1).

Почему эластичность спроса по цене для
разных товаров различна? Основные факторы, определяющие эластичность:

1. Наличие
доступных товаров-субститутов. Чем больше таких товаров, тем больше эффект
замещения при изменении цены данного товара и тем эластичнее спрос.

2. Доля
расходов на товар в бюджете потребителя. Чем она больше, тем больше эффект
дохода и тем эластичнее спрос. Это зависимость помогает понять, почему при
высоких ценах (в верхней части кривой спроса) спрос эластичен, а при низких
ценах (нижняя часть кривой спроса) неэластичен. Более высокая цена
означает большую долю в расходах
потребителя при фиксированном бюджете.

3. Направление
эффекта дохода. В случае нормальных товаров эффект дохода усиливает эффект замещения
и спрос становится эластичнее. Для низших товаров эффект дохода ослабляет
действие эффекта замещения и спрос поэтому менее эластичен.

4. Время,
прошедшее после изменения цены. Чем продолжительнее этот период, тем больше
возможности у потребителя найти замещающие товары и тем эластичнее спрос.

Эластичность и доходы продавцов (расходы покупателей). Очень важно в практическом отношении знать, как поведёт себя выручка (доход) с изменением рыночной цены. Если цена, к примеру, растёт, то выручка может увеличиться, а может и уменьшиться. Так,
повышение средней цены на зерно в России в 2003 году с 2,5 тыс. до 4,5 тыс.руб. за тонну улучшило положение сельхозпроизводителей, увеличив их доходы. В то же время повышение платы за проезд в муниципальном транспорте города Томска в 2003 г. с 3,5 до 4,5 рублей привело к тому, что выручка у Трамвайно-троллейбусного управления значительно упала.

Поскольку выручка определяется как произведение цены товара на количество проданного товара (ТR = P·Q), то результат зависит от того будет ли процентное изменение количества
больше или меньше процентного изменения цены, то есть от ценовой эластичности
спроса. Так, если цена повысится на 10 %, а физический объём продаж вследствие
этого сократится на 20 % (эластичность спроса по цене равна 2,0 – спрос эластичен), то выручка уменьшится.

Общее правило таково: при эластичном спросе доходы (расходы)
изменяются в направлении противоположном изменению цены. При неэластичном
спросе доходы (расходы) изменяются в том же направлении, что и цена. В случае единичной эластичности доход не
изменяется.

Все возможные случаи отражены в таблице 5-1.

Эластичность спроса по цене, │E^D│	Цена повышается	Цена понижается
Эластичный спрос (>1)	TR падает	TR растёт
Единичная эластичность (=1)	TR не меняется	TR не меняется
Неэластичный спрос (<1)	TR растёт	TR падает

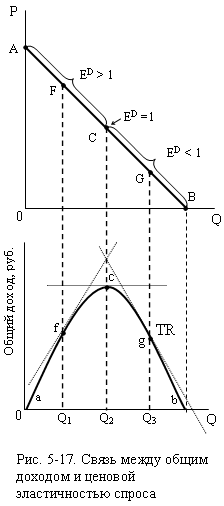
На рис.
5-17 показана связь между общим доходом (расходами) и ценовой эластичностью
спроса. Предположим, что цена товара всё время понижается, и мы движемся по
кривой спроса (на верхнем рисунке) вниз из точки А в точку В. На отрезке АС,
где спрос эластичен, снижение цены будет перекрываться ещё большим ростом (в
процентном отношении) величины спроса. Общий доход, следовательно, будет расти
(участок ас на нижнем рисунке). На
участке СА, где спрос неэластичен дальнейшее снижение цены вызывает уже меньший
рост (в процентном отношении) спроса, и доход падает (участок сb). В точке С, где
эластичный спрос переходит в неэластичный (эластичность равна единице) доход
перестаёт расти, достигая максимума при объёме Q_2.

Математическое приложение 5-3

Связь между ценовой эластичностью спроса и общим доходом можно определить с помощью методов предельного анализа.

Общий доход, TR = P∙Q. Следовательно,

(1)

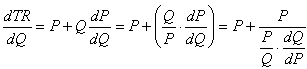
Так как ценовая эластичность спроса равна

(2)

то, подставив (2) в (1), получим:

(3)

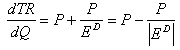
Таким образом, когда спрос эластичен, то есть │ED│ > 1, то

TR изменяется в том же направлении, что и Q, и в направлении противоположном Р (для нормальной, нисходящей кривой спроса).

Когда спрос имеет единичную эластичность, то есть │ED│ = 1, то

TR с изменением Q не меняется.

Когда спрос неэластичен, то есть │ED│ < 1, то

TR изменяется в направлении противоположном Q и в том же направлении что и Р (для нормальной кривой спроса).

Снова обратимся к рис. 5-17. Возьмём на кривой спроса точку F, в которой спрос эластичен. С понижением цены объём спроса будет расти. Изменение общего дохода, обусловленное бесконечно малым увеличением объёма продаж при уровне Q1, то есть dTR/dQ, показывается наклоном касательной к кривой общего дохода в точке f. Этот наклон положителен. Следовательно, общий доход будет увеличиваться.

При единичной эластичности спроса (точка С), наклон касательной к кривой общего дохода в точке с будет равен 0. Следовательно общий доход при объёме продаж Q2, не изменяется ни в сторону увеличения, ни в сторону уменьшения. Он достигает максимума.

Наконец, при неэластичном спросе, к примеру, в точке G, при снижении цены общий доход будет уменьшаться. Об этом говорит отрицательный наклон касательной к кривой общего дохода в точке g.

Источник

Лекция 4. Эластичность и ее свойства.

Эластичности элементарных функций

Изучение различных экономических вопросов, таких, как определение динамики спроса населения на данный товар при изменении его цены или при изменении доходов населения, исследование диапазона взаимозаменяемости ресурсов производства, определение эффективности тех или иных затрат, прогнозирование изменения прибыли предприятия или фирмы под воздействием различных факторов и решение многих других проблем, приводит к необходимости выяснения на сколько процентов изменится одна величина, если другая увеличилась на 1%.

Характеристика, дающая ответ на поставленный вопрос, называется эластичностью соответствующей функции.

Приступим к построению этого показателя. Пусть аргумент функции получил приращение . Тогда значение функции изменится на величину

Приращения называют абсолютными приращениями аргумента и функции соответственно. Составим относительные приращения переменных и выразим их в процентах.

Величина указывает, на сколько процентов изменилось значение аргумента, а дает соответствующее изменение значения функции.

Отношение показывает, на сколько процентов в среднем меняется (увеличивается или уменьшается) значение функции, когда значение аргумента возрастает на 1% (увеличивается от до ).

Рекомендуемые материалы

Это отношение будет характеризовать поведение функции в данной точке тем точнее, чем меньше . Пусть неограниченно убывает. Вычислим предел указанного отношения при условии .

(3)

Отношение не зависит от изменения . Оно играет роль постоянной и может быть вынесено за знак предела.

Определение. Предел отношения относительного приращения функции к соответствующему относительному приращению аргумента при условии, что абсолютное приращение аргумента стремится к нулю, называется эластичностью функции по переменной и обозначается символом

(4)

Если функция дифференцируема в точке , то

и формула (4) принимает вид

или

(5)

Из (3) следует, что эластичность показывает, на сколько процентов изменится значение функции при увеличении независимой переменной на 1% (с до ).

Формулу (5) можно переписать в виде

Это означает, что для функции выпуска эластичность равна отношению предельной производительности ресурса к его средней производительности.

Пример 17.

Эластичность данной функции вычисляется по формуле

При показатель эластичности равен 0.6. Это означает, что при увеличении с 2 до 2.02 значение функции возрастает примерно на 0.6%. Если , то . Следовательно, увеличение с 0 до 0.01 практически не меняет значения функции.

Пример 18. .

Здесь

При показатель эластичности равен нулю. При увеличении с 1 до 1.01 значении функции практически не меняется. Если , то . Увеличение значения с 2 до 2.02 приводит к уменьшению значения функции на 4 %.

Свойства эластичности

1. Эластичность – безразмерная величина, значение которой не зависит от того, в каких единицах измерены величины у и х. .

2. Эластичности взаимно обратных функций – взаимно обратные величины:

Например, эластичность величины спроса по цене обратна эластичности цены по величине спроса

3. Эластичность произведения двух функций u(x) и v(x), зависящих от одного и того же аргумента х, равна сумме эластичностей:

4. Эластичность частного двух функций u(x) и v(x), зависящих от одного и того же аргумента х, равна разности эластичностей

5. Эластичность суммы двух функций u(x) и v(x) может быть найдена по формуле:

Например, эластичность величины спроса по цене обратна эластичности цены по величине спроса

5. Эластичность суммы двух функций u(x) и v(x) может быть найдена по формуле:

Эластичности элементарных функций

1. Эластичность степенной функции у=х^a постоянна и равна показателю степени a: Е_х(х^a) = a.

2. Эластичность показательной функции у=а^х пропорциональна х:

3. Эластичность линейной функции

Если график линейной функции имеет отрицательный наклон (а<0), то эластичность функции меняется от нуля к точке y_m пересечения графиком оси у до минус бесконечности (-¥) в точке пересечения оси х, проходя через значение (-1) в средней точке.

Таким образом, хотя прямая имеет постоянный наклон, её эластичность зависит не только от наклона, но и от того, в какой точке х мы её находим (рис.10). Функция с бесконечной эластичностью во всех точках называется совершенно эластичной, с нулевой эластичностью во всех точках – совершенно неэластичной.

Задания для самостоятельной работы

1. Используя свойства эластичности, найдите , если:

а) , б) , в) ,

г) , д) , е) .

Лекция 5. Виды эластичностей в экономике

Рассмотрим основные виды эластичностей.

1.Эластичность спроса по цене (прямая)

показывающая относительное изменение (выраженное в процентах) величины спроса на какое-либо благо при изменении цены этого блага на один процент и характеризующая чувствительность потребителей к изменению цен на продукцию. Если ценовая эластичность спроса по абсолютной

величине больше единицы, то спрос называют эластичным (совершенно эластичным при бесконечно большой величине эластичного спроса). Если ценовая эластичность спроса по абсолютной величине меньше единицы, то спрос называют неэластичным (совершенно неэластичным при нулевой эластичности спроса).

И, наконец, если ценовая эластичность спроса по абсолютной величине равна единице, то говорят о спросе с единичной эластичностью.

2.Эластичность спроса по доходу

характеризующая относительное изменение (в процентах) величины спроса на какое-либо благо при изменении дохода потребителей этого блага на один процент. Положительная эластичность спроса по доходу характеризует нормальные (качественные) товары, а отрицательная величина – малоценные (некачественные) товары

Так, высокий положительный коэффициент спроса по доходу в отрасли указывает, что её вклад в экономический рост больше, чем доля в структуре экономики, и она имеет шансы на расширение и процветание в будущем. Наоборот, если коэффициент эластичности спроса на продукцию отрасли по доходу имеет небольшое положительное или отрицательное значение, то её может ожидать застой и перспектива сокращения производства.

3. Перекрестная эластичность спроса по цене

характеризующая относительное изменение (в процентах) величины спроса на одно благо при изменении цены на другое благо (замещающее или дополняющее его в потреблении) на один процент. Положительный знак перекрестной эластичности спроса по цене свидетельствует о замещаемости благ, а отрицательный – о дополняемости.

4.Ценовая эластичность ресурсов

характеризующая относительное изменение (в процентах) величины спроса на какой-нибудь ресурс (например, труд) при изменении цены этого ресурса (соответственно, заработной платы) на один процент.

5.Эластичность замещения одного ресурса другим

характеризующая необходимое изменение (в процентах) величины одного ресурса (например, капитала) при изменении количества другого ресурса (например, труда) на один процент с тем, чтобы выпуск при этом не изменился.

Рассмотрим подробнее эластичность спроса относительно цены. Изучается зависимость спроса на товар от цены на него.

Предположим, что цены на аналогичные товары, доходы потребителей и структура их потребностей – постоянные величины. Тогда зависимость спроса от цены можно описать с помощью функции

Во многих экономических исследованиях необходимо установить не величину спроса при каждом конкретном уровне цены, а характер изменения спроса при определенном изменении цены. В этом случае находят эластичность спроса относительно цены. В наших обозначениях

Эластичность спроса относительно цены определяет, на сколько процентов изменится спрос на товар, если цена на него увеличится на 1%. Так как в большинстве случаев спрос является убывающей функцией цены и

то, чтобы избежать отрицательных чисел, в этих случаях при изучении эластичности принимают

Знак «-» показывает, что спрос уменьшается при увеличении цены.

Пример 19. Если функция спроса линейная:

то

При имеем . Это означает, что увеличении цены на 1% спрос падает на %. При , показатель эластичности равен 1. Увеличение цены с 5 до 0.05 приводит к уменьшению спроса на 1%. При спрос уменьшается на 9%.

Пример 20. Для (– постоянная, ) показатель эластичности равен 1 при любом уровне цены.

Действительно,

Если спрос обратно пропорционален цене, то при любой цене увеличение ее на 1% влечет за собой уменьшение спроса также на 1 %.

Определение. Говорят, что спрос эластичен, если повышению цены на 1% соответствует снижение спроса более чем на 1%, т.е. ; спрос нейтрален, если ; спрос неэластичен, если .

В примере 19 спрос нейтрален при ; при – неэластичен и для – эластичен. Для функции спрос нейтрален при любой цене.

Другими словами, спрос на товар эластичен, если небольшое изменение цены товара вызывает значительные изменения величины спроса на него. В обратной ситуации, когда изменение цены ведет к сравнительно небольшому изменению величины спроса, последний является неэластичным. Примерами товаров с эластичным спросом могут служить, например, яблоки, помидоры, персики и т.п. При росте цен на них покупательский спрос может переключиться на другие виды овощей и фруктов. При определенном уровне цен покупатели могут полностью отказаться, например, от употребления фруктов или заменить их соками и другими консервами. В то же время спрос на товары первой необходимости (лекарства, обувь, электричество, газ, телефон), на вещи, цена которых малоощутима для семейного бюджета (карандаш, зубная паста, крем для обуви) и труднозаменяемые товары (электрические лампочки, хлеб, бензин) является неэластичным.

Исследуем динамику выручки при различных видах спроса.

Общие расходы населения на данный товар (выручка от его продажи) при цене составляют

Предельная выручка равна

или

а) Если спрос эластичен, т.е. , то

и с повышением цены выручка от продажи снижается.

б) При нейтральном спросе ()

и выручка практически не зависит от цены.

В этом случае (– постоянная) и

Следовательно, в случае нейтрального взноса его размер пропорционален цене (см. пример 20).

в) При неэластичном спросе () выручка увеличивается с ростом цены, так как в этом случае .

Из сказанного видно, что знание эластичности спроса на данный товар позволяет прогнозировать направление изменения суммы выручки под влиянием роста или снижения цены. Очевидно, каждой фирме выгодно, чтобы спрос на ее продукцию был как можно более эластичным, ибо в такой ситуации существует возможность назначать сравнительно высокие цены.

Значит, фирма должна прилагать все усилия к поддержанию спроса на ее товар на достаточно высоком уровне. Достижению этой цели способствуют хорошее качество продукции, четко организованное обслуживание потребителей, высокое качество рекламы

Пример 21. Известно, что эластичность спроса на товар составляет 0.4. Определим, как изменится доход от реализации товара, если цену на него увеличить на 5%.

При эластичности увеличение цены на 1% вызывает уменьшение спроса на 0.4%. Увеличение цены на 5% способствует уменьшению спроса на . Цена выросла на 5% и стала равной 1.05, где – старая цена. Если – спрос, соответствующий цене , то 0.98– величина спроса при цене 1.05.

Выручка от реализации товара по цене составляла денежных единиц. После увеличения цены выручка возросла приблизительно на 3%. При неэластичном спросе (0.4<1) увеличение цены приводит к возрастанию выручки.

Эластичность предложения определяется аналогично эластичности спроса:

(6)

Для дифференцируемой функции формула (5) принимает вид

(7)

или

. (8)

В отличии от формулы (5), выражающей эластичность спроса, в (7) и (8) отсутствует знак «-». Это связано с тем, что с ростом рыночной цены на товар предложение этого товара обычно растет. Каждому предпринимателю выгодно реализовать свою продукцию по более высокой цене. Поэтому – возрастающая функция и .

Равенство (8) означает, что эластичность предложения равна отношению предельного предложения к среднему.

Предложение также может быть эластичным и неэластичным.

Определение. Предложение называется эластичным, если , неэластичным, если , и нейтральным, если .

Например, фирма решила пригласить на работу дополнительное количество разнорабочих и квалифицированных наладчиков для скорейшего ввода в строй новой автоматической линии. Чтобы увеличить предложение услуг, руководство фирмы объявило об увеличении заработной платы на 1000 рублей в месяц. Если в городе много безработных, студентов, малооплачиваемых трудящихся, то такая надбавка к семейному бюджету может оказаться для них существенной, и предложение услуг в качестве разнорабочего будет эластичным по цене. Однако едва ли много квалифицированных, а следовательно и высокооплачиваемых наладчиков согласиться сменить место работы из-за такой прибавки к зарплате. Транспортные расходы, моральный ущерб, необходимость хотя бы частичной переквалификации для работы с новым для них оборудованием не окупятся дополнительной суммой в 1000 рублей. Здесь предложение услуг едва ли окажется эластичным по цене.

Пример 22. Пусть зависимость предложения от цены описывается формулой

а) , т.е. – возрастающая функция цены.

б) – функция вогнутая, темп изменения предложения постоянный.

в) Предложение эластично по цене.

Зависимость между спросом на товар и его ценой (а значит, и вид соответствующей кривой) в значительной степени определятся полезностью товара. На вид функции предложения в первую очередь оказывают влияние издержки производства.

Определение. Цена, при которой величина спроса равняется величине предложения, называется равновесной (или ценой равновесия).

В точке М величина спроса равна величине предложения, – цена равновесия (рис.1).

Пример 23. – функция спроса, – функция предложения. Из уравнения найдем цену равновесия

отсюда

или

и .

Следовательно, цена равновесия .

Задания для самостоятельной работы

1. Спрос и предложение изменяются по следующим законам:

2. Найдите цену, при которой спрос совпадает с предложением (цену равновесия). Рассчитайте эластичность спроса при этой цене. Постройте графики спроса и предложения.

3. Формула

выражает зависимость спроса от цены. Определите, при каких значениях спрос эластичен, нейтрален, неэластичен. Как зависит выручка от изменения цены? Сопоставьте с критериями эластичности.

4. Функция спроса имеет вид . Постройте график функции. Определите при каких значениях спрос эластичен, нейтрален, неэластичен.

5. Определите, на сколько процентов приблизительно изменится выручка от реализации товара. Если эластичность спроса равна , а цена на товар увеличена на %:

а) %;

б) %;

в) %.

Лекция 6. Многофакторные производственные функции, эластичности

Определение. Функция независимых переменных, устанавливающая зависимость между затратами производственных ресурсов и объемом выпускаемой продукции, называется -факторной производственной функцией – ПФ (функцией выпуска)

. (9)

Если (9) выражает зависимость объема выпускаемой данным предприятием продукции от затрат ресурсов , запасы которых ограничены, то, очевидно, допустимыми можно считать значения , удовлетворяющие следующей системе неравенств:

где – запасы i-го ресурса (в стоимостном или натуральном выражении).

Не нарушая общности рассуждений, в дальнейшем будем рассматривать лишь функции двух независимых переменных.

При моделировании экономики страны в качестве основных ресурсов используют затраты труда L и объём производственных фондов К. Национальный доход Y выступает в роли результата деятельности экономики:

Y=F(K,L).

В математических моделях функционирования отдельного предприятия, цеха, участка и т.д. Y обозначает объем выпускаемой данным экономическим объектом продукции.

Формальные свойства производственных функций

Производственная функция f(x₁, x₂) определена при х₁≥0, х₂≥0. ПФ должна удовлетворять ряду (для каждой конкретной ПФ – своему) свойств:

1. ;

;

2. ;

3. ;

;

4. .

Свойство 1 означает, что без ресурсов нет выпуска, что при отсутствии хотя бы одного из ресурсов нет выпуска.

Свойство 2 означает, что с ростом затрат хотя бы одного ресурса объем выпуска растет, и что с ростом затрат одного ресурса при неизменном количестве другого ресурса объем выпуска растет.

Свойство 3 означает что с ростом затрат одного (i-го) ресурса при неизменном количестве другого ресурса величина прироста выпуска на каждую дополнительную единицу i-го ресурса не растет (закон убывающей эффективности), при росте одного ресурса предельная эффективность другого ресурса возрастает. Если выполнены условия 3, то график Г ПФ есть поверхность, расположенная в неотрицательном ортанте трехмерного пространства Ох₁х₂у и выпуклая вверх. Вообще геометрический образ ПФ должен прежде всего ассоциироваться с выпуклой горкой, крутизна которой убывает, если точка (х₁, х₂) уходит в плоскости Ох₁х₂ на «северо-восток».

Свойство 4 означает, что ПФ является однородной функцией (ОФ) степени p>0. При p>1 с ростом масштаба производства в t раз (число t>1), т.е. с переходом от вектора х к вектору tx, объем выпуска возрастает в t^p (>t) раз, т.е. имеет рост эффективности производства от роста масштаба производства. При p<1 имеем падание эффективности производства от роста масштаба производства. При p=1 имеем постоянную эффективность производства при росте его масштаба (или имеем независимость удельного выпуска от масштаба производства – в английской терминологии constant returns to scale).

Для ПФКД свойства 1-4 выполняются.

Для ЛПФ свойства 1 (при ) и свойство 4 не выполняются.

Множество (линия) l_qуровня (0<q – действительное число) ПФ называется изоквантой ПФ. Иными словами, линия уровня q – это множество точек, в котором ПФ постоянна и равна q.

Различные наборы и затрачиваемых (используемых) ресурсов, принадлежащие одной и той же изокванте l_q (т.е. ), дают один и тот же объем выпуска q. Изокванта есть линия, расположенная в неотрицательном ортанте двумерной плоскости Ох₁х₂.

Функция Кобба-Дугласа, функция с постоянными пропорциями

Функция Кобба-Дугласа имеет вид:

При результат функционирования экономического объекта

К такому же выводу приходим и при , т.е. оба ресурса абсолютно необходимы.

Если K и L увеличить в λ раз, то в такое же количество раз возрастает и Y.

Действительно,

Эта функция находит широкое применение в моделях долгосрочного прогнозирования.

Функцию с постоянными пропорциями

выбирают тогда, когда один из ресурсов производства резко дефицитен, а второй избыточен.

Убедимся в том, что в этой функции реализуются предположения о свойствах производственных функций.

1. Если или ,

2. Предположим, что и . Тогда

К такому же результату придем, если . В процессе производства, описываемом функцией вида (9), следует использовать ресурсы в постоянной пропорции (16). Уровень выпуска возрастает в λ раз лишь при одновременном увеличении затрат обоих ресурсов в такое же число раз. Отношение задает рациональную пропорцию между K и L.

Предельные (маржинальные) и средние значения

производственной функции

Пусть – ПФ. Дробь

называется средней производительностью i-го ресурса (фактора производства) (СПФ) или средним выпуском по i-му ресурсу (фактору производства). Символика: .

Напомним, что в случае двухфакторной ПФКД для средних производительностей и основного капитала и труда были использованы соответственно термины капиталоотдача и производительность труда. Эти термины используют и применительно к любым двухфакторным ПФ, у которых и .

Пусть – ПФ. Ее первая частная производная

называется предельной (маржинальной) производительностью i-го ресурса (фактора производства) (ППФ) или предельным выпуском по i-му ресурсу (фактору производства). Символика: .

Обозначим символами и ;

соответственно, приращение переменной и соответствующее ей частное приращение ПФ f(x). При малых имеем приближенное равенство

Следовательно, ППФ (приближенно) показывает, на сколько единиц увеличится объем выпуска у, если объем затрат i-го ресурса вырастает на одну (достаточно малую) единицу при неизменных объемах другого затрачиваемого ресурса. Здесь предельную величину (т.е. ППФ) целесообразно интерпретировать, используя близкое к ней отношение малых конечных величин, т.е. и . Отмеченное обстоятельство является ключевым для понимания экономического смысла ППФ. С другими предельными величинами следует поступать аналогичным образом.

Пример 24. 1). Для ПФКД найти в явном виде , , и .

Решение задачи. Имеем:

; ;

; .

Для ПФ (не только для ПФКД) неравенства

(т.е. предельная производительность i-го ресурса не больше средней производительности этого ресурса) обычно выполняются.

2). Для ЛПФ найти в явном виде А₁, А₂, М₁ и М₂.

Решение задачи. Имеем:

; ,

, ,

; .

Пусть – ПФ, . Отношение предельной производительности i-го ресурса к его средней производительности называется (частной) эластичностью выпуска по i-му ресурсу (по фактору производства) (ЭФМ). Символика:

Сумма называется эластичностью производства.

Поскольку при малом приращении имеем приближенное равенство

(крайнее правое выражение есть отношение двух относительных величин и ), поскольку (приближенно) показывает, на сколько процентов увеличится выпуск у, если затраты i-го ресурса увеличатся на один процент при неизменных объемах другого ресурса. Пояснение выражения , содержащего предельную величину , с помощью выражения, содержащего конечное приближение этой предельной величины, является ключевым в понимании экономической сути частной эластичности выпуска по i-му ресурсу.

Пример 25. 1). Выписать в явном виде для ПФКД выражения для Е₁, Е₂ и Е_х.

Решение задачи. Имеем:

, ,

2). Для ЛПФ выписать в явном виде выражения для Е₁, Е₂ и Е_х.

Решение задачи. Имеем:

; ;

Пусть – ПФ, . Предельной нормой замены (замещения) i-го ресурса (фактора производства) j-м (аббревиатура: ПНЗФ и символика: R_ij) называется выражение

(10)

при постоянной у.

Обратим внимание на то, что i – номер заменяемого ресурса, j – номер замещающего ресурса. Используется также термин: предельная технологическая норма замены (замещения) i-ого ресурса (фактора производства) j-м ресурсом (фактором производства). Приведем более краткий (но не менее точный) термин: (предельная) норма замены (замещения) ресурсов.

Пусть выпуск у является постоянным (т.е. все наборы затрачиваемых ресурсов расположены на одной изокванте), тогда первый полный дифференциал dy ПФ тождественно равен нулю:

(здесь dx₁, dx₂ – дифференциалы переменных x₁, x₂), откуда, выражая первый дифференциал dx_j, получим ():

, (11)

откуда, поделив на dx_i, получим

. (12)

На основании (10), (11) и (12) имеем:

(13)

Отметим, что строгий вывод формулы (13) опирается в действительности на теорему о неявной функции, формулировка которой в настоящем пособии не приводится.

Непосредственно проверяется, что для двухфакторной ПФ справедливо равенство