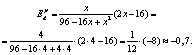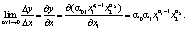Рассмотренные
в предыдущем подразделе экономические
понятия имеют размерность, что не вполне
удобно для анализа взаимосвязи
относительных изменений переменных.
Вводят понятия: эластичность
выпуска по труду EL
и эластичность выпуска по капиталу EK,
определяемые формулами
EL
=
;
(2.6)
EK
=
.
(2.7)
Безразмерные
показатели EL
и EK
показывают, на сколько процентов
произойдет относительное увеличение
выпуска при относительном увеличении
соответствующего ресурса на 1%.
Сумма
значений эластичности выпуска по всем
ресурсам называется эластичностью
производства:
E
= EK
+ EL.
(2.8)
Для
эластичности
KL
предельной
нормы замещения труда капиталом
справедливо соотношение:
KL
=
.
(2.9)
Эффективность
производственного процесса (эффект от
масштаба производства) можно оценить
математически, увеличив одновременно
все ресурсы в t
раз. Если
использовать более общую аппроксимирующую
формулу Кобба—Дугласа
Q
= AKL,
получаем: Q
(tK,
tL)
= AKtLt
= tt
Q
(K,
L)
= t+
Q
(K,
L).
Отсюда вытекает, что если
и
в сумме превышают единицу, то говорят,
что производственная функция имеет
возрастающий эффект от масштаба
производства (если ресурсы K
и L увеличиваются
в некоторой пропорции, то выпуск Q
растет в большей пропорции). Если их
сумма меньше, чем единица, то имеет место
убывающий эффект от масштаба производства.
В
своей первой статье Ч. Коббс и П. Дуглас
описывали производственную функцию в
виде (2.1), предполагающем постоянную
отдачу от масштаба:
и
в сумме точно составляют единицу.
Впоследствие они ослабили это допущение,
предпочитая оценивать степень отдачи
от масштаба производства. Как указывалось
нами ранее, при обработке исходных
данных, использованных Ч. Коббсом и П.
Дугласом, методом наименьших квадратов,
получаем значения
= 0,23 и
= 0,81. Сумма
и ,
равная 1,04, лишь несколько превышает
единицу, т.е. первоначальное предположение
Ч. Коббса и П. Дугласа о постоянной отдаче
от масштаба было вполне оправдано.
Пример
4. Рассчитать
эластичность выпуска по труду и капиталу
для производственной функции Q
= K1/4L3/4
в точке K
= 2, L
= 3. Оценить эффект от масштаба производства.
Решение.
Эластичность выпуска по труду определяется
формулой (2.6). Так как предельный продукт
труда
=
=3/4
,
получаем:
EL
=
=
=
(3/4
)
= (L /
K1/4L3/4)(3/4
)
= 3/4.
Эластичность
выпуска по капиталу определяется
формулой (2.7). Так как предельный продукт
капитала
=
=1/4
,
получаем:
EK
=
=
=
(1/4
)
= (K
/ K1/4L3/4)(1/4
)
= 1/4.
Таким
образом, эластичность выпуска по труду
и капиталу в случае производственной
функции Кобба—Дугласа
вида Q
= AKL
не зависит от точки производства и равна
показателям степени при соответствующих
переменных
= 0,75 и
= 0,25 соответственно.
Сумма
значений эластичности выпуска по всем
ресурсам (эластичность производства)
равна
+
= 1, т.е. в данном случае имеет место
постоянная отдача от масштаба производства.
Для
эластичности KL
предельной нормы замещения труда
капиталом в общем случае производственной
функции вида
Q = AKL
получаем:
KL
=
=
=
1,
т.е.
для функции Кобба—Дугласа
эластичность предельной нормы замещения
труда капиталом постоянна и равна
единице. Это важнейшее свойство функции
Кобба—Дугласа.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Эластичность выпуска по труду и рентабельность: тайные взаимосвязи
Совершенно конкурентная фирма, закупающая на конкурентном рынке единственный фактор производства – труд, столкнулась со следующими значениями эластичности выпуска по труду и рентабельности при различных количествах нанятых работников:
| $L$ | $L_1$ | $L_2$ | $L_3$ | $L_4$ | $L_5$ | $L_6$ | $L_7$ | $L_8$ | $L_9$ |
| $E_Q^L$ | 0,762 | 0,778 | 0,735 | 0,667 | 0,58 | 0,476 | 0,346 | 0,19 | 0 |
| Рентабельность | 250% | 200% | 170% | 150% | 130% | 110% | 93% | 75% | 57% |
Известно, что среди указанных в таблице объемов труда есть объем, оптимальный для фирмы. Определите его.
Решение и ответ
$E_Q^L = MP_L frac{L}{Q}$.
Рентабельность = $frac{pi}{TC}$.
В точке оптимума $ MP_L = frac{w} {p} Rightarrow E_Q^L = MP_L frac{L} {Q} = frac{w} {p}frac{L} {Q} = frac{{TC}} {{TR}} = frac{1} {{pi /TC + 1}} $
Таким образом, в точке оптимума существует явная функциональная связь между эластичностью выпуска по труду и рентабельностью. Осталось обнаружить эту связь для какого-то $L$ из таблицы.
По данным о рентабельности рассчитаем для каждого $L$ значение $TC/TR$.
| $L$ | $L_1$ | $L_2$ | $L_3$ | $L_4$ | $L_5$ | $L_6$ | $L_7$ | $L_8$ | $L_9$ |
| $E_Q^L$ | 0,762 | 0,778 | 0,735 | 0,667 | 0,58 | 0,476 | 0,346 | 0,19 | 0 |
| Рентабельность | 250% | 200% | 170% | 150% | 130% | 110% | 93% | 75% | 57% |
| $TC/TR$ | 0,286 | 0,333 | 0,37 | 0,4 | 0,434 | 0,476 | 0,518 | 0,571 | 0,637 |
Как видим, равенство $E_Q^L = frac{{TC}}{{TR}}$выполняется при $L = L_6$. Это и есть искомая точка оптимума.
Примечание:
Подумайте:
- как можно было бы по-другому решить эту задачу, если бы в условии были даны конкретные количества труда?
- имела бы задача решение, если бы в условии не было сказано, что одно из приведенных в таблице значений труда точно оптимально?
- Авторы
- Файлы
- Литература
Попова Е.С
1
Дырдасова А.С.
1
1 Самарский государственный экономический университет
1. Предельный анализ в экономике. Эластичность функции [Электронный ресурс]. – Режим доступа: http://www.mathelp.spb.ru/book1/lim_an_ec.htm. – (Дата обращения: 16.12.2015).
2. Яшина Ю.Е, Карнавская Н.В., Чехута В.А. и др. Эластичность функции и ее применение экономике [Электронный ресурс] / Ю.Е. Яшина, Н.В. Карнавская, В.А. Чехута и др./ Международный студенческий научный вестник: эл.науч.журн. – 2015. – №3. – Режим доступа: http://www.eduherald.ru/140–14166. – (Дата обращения:16.12.2015).
На современном этапе развития человечества одну из ведущих ролей в развитии общества играют экономические отношения, поскольку именно они являются той материальной основой, которая в свою очередь делает возможным формирование и развитие различных общественных институтов. Для наиболее полного изучения экономических явлений и процессов, происходящих в обществе, экономическая теория использует различные методы, прибегая к «помощи» других не менее важных наук. Одной из таких наук является математический анализ. Одними из базовых, ключевых понятий в экономической теории являются такие широко известные категории как спрос и предложение, которые, в свою очередь, обладают определенными признаками и свойствами, что и является главным предметом экономической теории. Спрос и предложение товаров обладают различной степенью чувствительности к изменению определяющих их факторов. Мерой такого изменения является эластичность спроса и эластичность предложения. В свою очередь, выделяется несколько основных видов эластичности: ценовая эластичность, эластичность по доходу и перекрестная эластичность.
Ценовая (прямая) эластичность спроса (предложения) показывает, какое процентное изменение спроса (предложения) последует за однопроцентным изменением цены товара.
Эластичность спроса по доходу показывает, какое процентное изменение спроса последует за однопроцентным изменением дохода потребителя.
Перекрестная эластичность спроса показывает, какое изменение спроса на товар A последует за однопроцентным изменением цены товара B, при условии, что товары A и B являются комплементарными (комплементами) или взаимозаменяемыми (субститутами). Количественным выражением эластичности спроса и предложения является коэффициент эластичности E, который рассчитывается в одной точке кривой спроса и предложения или на дуге этой кривой.
Эластичностью функции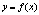 
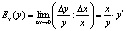
называется
.
Таким образом, эластичность функции можно вычислить по формуле
.
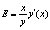
Эластичность функции также называется относительной производной. Эластичность функции по аргументу показывает, на сколько процентов изменится значение функции при изменении аргумента в точке x на 1 %. Пусть спрос задан функцией Q(d)=96–16P+P2, необходимо определить ценовую точечную эластичность спроса по цене при P=4.
Найдем первую производную функции
.
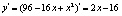
Подставим полученное выражение в формулу эластичности:
Таким образом, при изменении цены на 1 % величина спроса изменяется на 0,7 %. Спрос неэластичен.
Также в качестве примера можно рассмотреть производственную функцию Кобба-Дугласа. Данная функция устанавливает зависимость между величиной созданного общественного продукта и совокупными затратами живого труда, а также суммарным объемом применяемых производственных фондов.
Данная функция имеет следующий вид
,
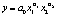
где a0 – коэффициент,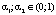 
. Несмотря на то, что каждый из данных коэффициентов меньше 1, их сумма может быть меньше, равна или больше 1. Она показывает эффект одновременного пропорционального увеличения объема трудовых ресурсов и производственных фондов.
Каждый из используемых ресурсов характеризуется средней и предельной величинами. средняя производительность труда показывает, сколько единиц продукции приходится на единицу труда. Предельная производительность труда показывает, сколько дополнительных единиц продукции приносит дополнительная единица труда.
Рассчитаем вторую частную производную:
.
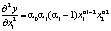
Вторая частная производная отрицательна, а значит, предельная производительность с увеличением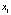 
снижается.
Для производственной функции Кобба-Дугласа предельная производительность всегда меньше средней.
Кроме того, можно определить показатель, характеризующий относительный прирост объема производства на единицу относительно увеличения труда
.
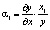
Полученный показатель называется эластичностью выпуска продукции по затратам труда. Он показывает, на сколько процентов увеличивается выпуск продукции при увеличении затрат труда на 1 %.
Подобные показатели можно рассчитать и для производственных фондов. Объем продукции в расчете на единицу производственных фондов называется фондоотдачей. Можно рассчитать среднюю и предельную фондоотдачу. Из функции Кобба_Дугласа имеем
.
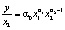
Предельная фондоотдача равна частной производной выпуска продукции по объему фондов:
.
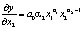
Предельная фондоотдача всегда ниже средней.
Относительная фондоотдача (эластичность выпуска продукции по объему производственных фондов) определяется как
.
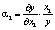
Если производственная функция задана формулой
,
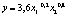
где y – объем продукции в стоимостном выражении, x1 – фонд заработной платы, x2 – стоимость основных производственных фондов.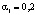 
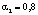
. Это означает, что при изменении затрат труда на 1 % выпуск продукции изменится на 0,2 % (увеличится или уменьшится). 
. Следовательно, при изменении объема основных производственных фондов на 1 %, выпуск продукции изменится на 0,8 % (увеличится или уменьшится).
Библиографическая ссылка
Попова Е.С, Дырдасова А.С. ЭЛАСТИЧНОСТЬ В ПРОИЗВОДСТВЕННЫХ ФУНКЦИЯХ // Международный студенческий научный вестник. – 2016. – № 4-4.
;
URL: https://eduherald.ru/ru/article/view?id=16408 (дата обращения: 19.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
эластичность выпуска по капиталу равна 0.4, эластичность выпуска по труду равна 0.5. Использование труда увеличилось на 5%, а использование труда снизилось на 6%. на сколько в процентном отношении и в каком направлении изменится величина выпуска?
Светило науки – 553134 ответа – 388270 раз оказано помощи
Решение:
Изменение количества производимой
продукции можно рассчитать как сумму произведений соответствующей эластичности
на процентное изменение количества используемого фактора:
0,4*5+0,5*(-6) = 2 – 3 = –
1;
Ответ: Объем выпуска снизился на 1%.
