В этой статье мы расскажем о самых важных вещах, связанных с диэлектрической проницаемостью. Среди прочего, вы узнаете о важных ролях, которые она играет, и о её типичных значениях.
Простое объяснение
В повседневной жизни вы сталкиваетесь с различными веществами, такими как металлы, вода или кислород. Каждое из этих веществ по-разному реагирует на электрические поля.
Диэлектрическая проницаемость (диэлектрическая постоянная или абсолютная диэлектрическая проницаемость) ε описывает способность материала к поляризации электрическими полями и определяется следующим образом: ε = εr * ε0 .
Здесь εr — относительная проницаемость, а ε0 — электрическая постоянная (или диэлектрическая проницаемость вакуума).
Если понимать значение термина «проницаемость» буквально, то это мера того, насколько сильно материя «пропускает» электрическое поле. Поэтому проницаемость можно рассматривать как меру того, насколько материя может быть поляризована.
Диэлектрическая проницаемость вакуума
Особую роль играет диэлектрическая проницаемость вакуума (также называемая проницаемостью вакуума). В этом разделе мы расскажем вам о значении и единицах измерения проницаемости вакуума, о том, как она связана с другими константами, и о ее значении в контексте других важных законов.
Числовое значение и единица измерения
Диэлектрическая проницаемость вакуума ε0 имеет значение 8,85418781762039 * 10-12 или 8.85 * 10-12, что более практично для расчетов. Единицей измерения константы является [ Ф·м−1 ] или если выражать через основные единицы СИ [ м−3·кг−1·с4·А2 ].
Взаимосвязь с другими константами
Существует замечательная связь между электрической постоянно ε0, магнитной постоянно μ0 и скоростью света в вакууме с0. То есть верно следующее соотношение: c02 = 1 / ε0 * μ0 .
До 2019 года это уравнение точно определяло значение постоянной электрического поля. Однако в ходе пересмотра ситуация изменилась, и с 20 мая 2019 года как электрическая постоянная, так и магнитная постоянная имеют определенную погрешность измерения.
Это уравнение было первым указанием на то, что свет может быть электромагнитной волной.
Закон Кулона и электрический потенциал
Помимо связи со скоростью света, электрическая постоянная фигурирует в других важных законах электродинамики. К ним относятся, например:
- Закон Кулона:

- Электрический потенциал заряженной частицы : φ ( r ) = q / 4 * π * ε0 * r .
В частности, закон Кулона является основой электростатики, поэтому константа электрического поля также имеет большое значение.
Диэлектрическая проницаемость: общий случай
В этом разделе мы рассмотрим общий случай. Мы объясним физический смысл абсолютной диэлектрической проницаемости с помощью электроизоляционных материалов и объясним, что такое относительная диэлектрическая проницаемость.
Диэлектрическая проницаемость диэлектриков
В электроизолирующих материалах (диэлектриках) электрические заряды связаны с атомами или молекулами. Поэтому они могут лишь немного перемещаться внутри атомов или молекул. Электрическое поле может изменить распределение заряда в диэлектрике двумя важными способами: деформацией и вращением. Даже если отдельные электрические заряды могут двигаться незначительно, совокупность всех движений определяет поведение электроизоляционного материала.
Поляризация
В зависимости от того, состоит ли материал из полярных или неполярных молекул, реакция на внешнее электрическое поле различна. С неполярной молекулой происходит растягивание (деформация), при котором поле индуцирует дипольный момент в каждой молекуле материала. Все эти дипольные моменты направлены в ту же сторону, что и электрическое поле.
В полярной молекуле, с другой стороны, происходит вращение, так что и здесь все дипольные моменты направлены в сторону электрического поля. В целом внешнее электрическое поле вызывает образование в материале большого количества диполей, все из которых ориентированы в том же направлении, что и внешнее поле. Таким образом, материал поляризуется. Поляризация P описывает, сколько дипольных моментов приходится на единицу объема материала.

Таким образом, поляризация диэлектрика вызывается электрическим полем. Возникающие направленные дипольные моменты, в свою очередь, создают электрическое поле, противодействующее внешнему полю. Таким образом, это противоположное поле ослабляет внешнее поле. В целом, связь между поляризацией и внешним электрическим полем сложная. Для многих веществ, так называемых линейных диэлектриков, поляризация пропорциональна полю. Применяется следующее соотношение:
P = ε0 * χ * E , где
Здесь ε0 — электрическая постоянная, а χ — электрическая поляризуемость. Электрическое поле E в этом уравнении является полным полем. Поэтому причиной этого могут быть частично свободные заряды и частично сама поляризация.. Свободные заряды — это все те носители заряда, которые не являются результатом поляризации. Таким образом, это полное электрическое поле очень трудно рассчитать, поскольку мы обычно не имеем информации о распределении поляризационных зарядов.
Для справки: χ — коэффициент, зависящий от химического состава, концентрации, структуры (в том числе от агрегатного состояния) среды, температуры, механических напряжений и т. д. (от одних факторов более сильно, от других слабее, конечно же и в зависимости от диапазона изменений каждого), и называемый (электрической) поляризуемостью (а чаще, по крайней мере для того случая, когда он выражается скаляром — диэлектрической восприимчивостью) данной среды.
Википедия
Электрическая индукция
Чтобы иметь возможность рассчитать электрическое поле даже в присутствии диэлектрика, вводится электрическая индукция D. В линейной среде: D = ε0 * E + P = ε0 * E + ε0 * χe * E = ε0 * ( 1 + χe ) * E и поэтому D также пропорциональна E.
Если вы объедините константы вместе ε = ε0 * ( 1 + χe ), то получится: D = ε * E .
Постоянная ε и называется диэлектрической проницаемостью.
Относительная диэлектрическая проницаемость
Величина: εr = 1 + χe = ε / ε0 называется относительной проницаемостью (также относительной диэлектрической проницаемостью). С его помощью полное электрическое поле в присутствии диэлектрика определяется следующим образом: E = D / ε = D / εr * ε0 .
При постоянной электрической индукции относительная проницаемость, таким образом, определяет, насколько сильно ослабляется электрическое поле. Чем больше относительная проницаемость, тем больше ослабляется электрическое поле и, следовательно, уменьшается общая напряженность электрического поля.
Термин относительная проницаемость может привести к неправильному пониманию того, что относительная проницаемость для данного материала является константой. На самом деле, относительная проницаемость зависит от многих факторов. Среди них:
- температура материала;
- частота внешнего электрического поля;
- напряженность внешнего электрического поля.
Для некоторых материалов относительная проницаемость дополнительно зависит от направления. Следовательно, в случае таких материалов это не просто число, а часто тензор второго порядка.
Особенно наглядную иллюстрацию влияния диэлектриков с разной относительной проницаемостью можно получить, поместив диэлектрик между двумя пластинами конденсатора. Если измерить электрическое напряжение на конденсаторе до и после введения диэлектрика, то можно обнаружить, что напряжение на конденсаторе уменьшается ровно на величину εr относительной диэлектрической проницаемости. Это следует непосредственно из уравнения: E = U / d для величины электрического поля между пластинами конденсатора, расположенными на расстоянии d друг от друга. Это также иллюстрирует, почему εr называется относительной проницаемостью. Напряжение на конденсаторе уменьшается на коэффициент εr за счет введения диэлектрика, по сравнению со случаем, когда между пластинами только вакуум.
Относительные диэлектрические проницаемости отдельных материалов
Наконец, мы приводим таблицу с типичными значениями относительной диэлектрической проницаемости (относительной диэлектрической проницаемости) различных материалов. Следует отметить, что в таких таблицах обычно указывается относительная проницаемость, а не сама абсолютная диэлектрическая проницаемость. Поэтому, если вы ищете таблицу для определения абсолютной диэлектрической проницаемости определенного материала, вы должны помнить, что приведенное там значение не является непосредственно той проницаемостью, которую вы ищете. Однако для заданного значения относительной проницаемости можно вычислить соответствующую абсолютную диэлектрическую проницаемость без особых дополнительных усилий. То есть нужно применять следующую уже известную нам формулу: ε = εr * ε0 .
| Вещество | εr |
| Вакуум | ровно 1 |
| Гелий | 1,000065 |
| Медь | 5,6 |
| Воздух (сухой) | 1,00059 |
| Метанол | 32,6 |
| Бумага | 1 – 4 |
| Вода ( 20°C, 0 — 3 ГГц ) | 80 |
| Вода ( 0°C, 0 — 1 ГГц ) | 88 |
(если не указано иное: при 18°C и 50 Гц)
В предыдущем разделе мы упоминали, что относительная проницаемость зависит, помимо прочего, от температуры и частоты. Поэтому важно знать и температуру, и частоту, если вы хотите получить значение из таблицы. Например, относительная проницаемость воды при температуре 20°C и частоте 0 ГГц равна 80. Если температура 0°C, а частота та же, относительная проницаемость воды равна 88. Медь, с другой стороны, имеет относительную проницаемость 5,6. Это означает, что вода как среда уменьшит напряжение на конденсаторе в 80 раз, в то время как медь уменьшит его только в 5,6 раз.
Список использованной литературы
- Курс физики для ФМШ при НГУ, раздел «Электромагнитное поле», гл. 2: «Диэлектрики».
- Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. — М.: Мир, 1965.
- Сивухин Д. В. Общий курс физики. — М.. — Т. III. Электричество.
- Гольдштейн Л. Д., Зернов Н. В. Электромагнитные поля и волны. М.: Сов. радио, 1971. С. 11.
Диэлектри́ческая проница́емость (




а также в уравнение связи вектора электрической индукции с напряжённостью электрического поля:
в рассматриваемой среде[1].
Вводятся абсолютная (

где 
Cам термин «диэлектрическая проницаемость» применяется и для 




Величина 


Проницаемость 

Отличие проницаемости от единицы обусловлено эффектом поляризации диэлектрика под действием внешнего электрического поля, в результате которой создаётся внутреннее противоположно направленное поле. В области низких частот 



Относительная диэлектрическая проницаемость 
Абсолютная диэлектрическая проницаемость вакуума[править | править код]
Электрическая постоянная, она же «абсолютная диэлектрическая проницаемость вакуума», в системе единиц СИ равна:
Ф/м
(имеет размерность L−3 M−1 T4 I2).
В системе СГС эта же постоянная составляет 

Электрическая постоянная связана с магнитной постоянной и скоростью света в вакууме:
Ниже все формулы приводятся для СИ, а символ 


Эффект поляризации диэлектрика и проницаемость[править | править код]

Схематическое изображение ориентации диполей в диэлектрической среде под воздействием электрического поля
Под воздействием электрического поля в диэлектрике происходит поляризация — явление, связанное с ограниченным смещением зарядов относительно положения равновесия без наложенного электрического поля или поворотом электрических диполей.
Это явление характеризует вектор электрической поляризации 


Помимо дипольно-ориентационного, имеются и другие механизмы поляризации. Поляризация не изменяет суммарного заряда в любом макроскопическом объёме, однако она сопровождается появлением связанных электрических зарядов на поверхности диэлектрика и в местах неоднородностей материала. Эти связанные заряды создают в диэлектрике дополнительное макроскопическое поле, как правило, направленное против внешнего наложенного поля. В итоге то, что 
Роль диэлектрической проницаемости среды в физике[править | править код]
Относительная диэлектрическая проницаемость 


Среду со значениями 


Относительная диэлектрическая проницаемость реальных диэлектриков (диэлектриков с потерями, диэлектриков с поглощением, для которых 
Относительная диэлектрическая проницаемость среды влияет на электрическую ёмкость расположенных в ней проводников: увеличение 






Таким образом, 
Диэлектрическая проницаемость непоглощающей среды[править | править код]
Проницаемость и связанные с ней величины[править | править код]
Применительно к диэлектрической среде без потерь справедливы соотношения:
В большинстве случаев 


Особая ситуация возникает для нелинейных сред, когда 


Распределение электрического поля в пространстве с различными диэлектриками находится из численного решения уравнения Максвелла:
или уравнения Пуассона для электрического потенциала 
- где
обозначает плотность свободных зарядов.
На незаряженной границе двух диэлектрических сред отношение нормальных компонент напряжённости поля 
В случае однородного диэлектрика его наличие приводит к снижению электрического поля 

Проницаемость в оптическом диапазоне частот[править | править код]
Диэлектрическая проницаемость, совместно с магнитной, определяют фазовую скорость распространения электромагнитной волны в рассматриваемой среде, а именно:
Показатель преломления диэлектрика без потерь можно выразить как квадратный корень из произведения его магнитной и диэлектрической проницаемостей:
Для немагнитных сред 


Однако, если рассматривать оптический диапазон частот сам по себе, то в нём с ростом 


Тензор проницаемости анизотропных сред[править | править код]
Диэлектрическая проницаемость связывает электрическую индукцию 

В электрически анизотропных средах компонента вектора напряжённости 


В общем случае проницаемость является тензором, определяемым из следующего соотношения (в записи использовано соглашение Эйнштейна):
или, иначе:
- где жирный шрифт использован для векторных и тензорных величин, а

— вектор электрической индукции,
— тензор абсолютной диэлектрической проницаемости.
В изотропном случае любая компонента вектора напряженности 




Статическая проницаемость некоторых диэлектриков[править | править код]
Значение 







Значение 

| Статическая диэлектрическая проницаемость материалов (таблица) | |||
|---|---|---|---|
| Вещество | Химическая формула | Условия измерения | Характерное значение εr |
| Вакуум | – | – | 1 |
| Воздух | – | Нормальные условия, 0,9 МГц | 1,00058986 ± 0,00000050 |
| Углекислый газ |  |
Нормальные условия | 1,0009 |
| Тефлон (политетрафторэтилен, фторопласт) | ![{displaystyle {ce {[{-CF2-CF2-}]_n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75baf7e9d77f3b4520e1594499bc780edd18dcad) |
– | 2,1 |
| Нейлон | – | – | 3,2 |
| Полиэтилен | ![{displaystyle {ce {[{-CH2-CH2-}]_n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2ba275fd929b5f06ef84f82d872e5a46a01aca1) |
– | 2,25 |
| Полистирол | ![{displaystyle {ce {[{-CH2-{(C6H5)}H-}]_{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c2b607aa9a5beb70b32ae4b51f835a98a24506f) |
– | 2,4-2,7 |
| Каучук | – | – | 2,4 |
| Битум | – | – | 2,5-3,0 |
| Сероуглерод |  |
– | 2,6 |
| Парафин |  |
– | 2,0-3,0 |
| Бумага | – | – | 2,0-3,5 |
| Электроактивные полимеры | − | − | 2-12 |
| Эбонит |  |
− | 2,5-3,0 |
| Плексиглас (оргстекло) | – | – | 3,5 |
| Кварц |  |
– | 3,5-4,5 |
| Диоксид кремния |  |
− | 3,9 |
| Бакелит | – | – | 4,5 |
| Бетон | − | − | 4,5 |
| Фарфор | − | − | 4,5-4,7 |
| Стекло | − | − | 4,7 (3,7-10) |
| Стеклотекстолит FR-4 | – | – | 4,5-5,2 |
| Гетинакс | – | – | 5-6 |
| Слюда | – | – | 7,5 |
| Резина | − | − | 7 |
| Поликор | 98 %  |
– | 9,7 |
| Алмаз |  |
Нормальные условия | 5,5-10 |
| Поваренная соль |  |
− | 3-15 |
| Графит |  |
− | 10-15 |
| Керамика | − | − | 10-20 |
| Кремний |  |
− | 11.68 |
| Бор |  |
− | 2.01 |
| Аммиак |  |
20 °C | 17 |
| 0 °C | 20 | ||
| −40 °C | 22 | ||
| −80 °C | 26 | ||
| Спирт этиловый |  или или  |
− | 27 |
| Метанол |  |
− | 30 |
| Этиленгликоль |  |
− | 37 |
| Фурфурол |  |
− | 42 |
| Глицерин |  или или  |
0 °C | 41,2 |
| 20 °C | 47 | ||
| 25 °C | 42,5 | ||
| Вода |  |
200 °C | 34,5 |
| 100 °C | 55,3 | ||
| 20 °C | 81 | ||
| 0 °C | 88 | ||
| Плавиковая кислота |  |
0 °C | 83,6 |
| Формамид |  |
20 °C | 84 |
| Серная кислота |  |
20-25 °C | 84-100 |
| Пероксид водорода |  |
−30 °C — +25 °C | 128 |
| Синильная кислота |  |
(0-21 °C) | 158 |
| Диоксид титана |  |
– | 86-173 |
| Титанат кальция |  |
– | 170 |
| Титанат стронция |  |
– | 310 |
| Титанат бария-стронция |  , ,  |
– | 500 |
| Титанат бария |  |
(20-120 °C) | 1250-10000 |
| Цирконат-титанат свинца | ![{displaystyle {ce {(Pb[Zr_xTi_{1-x}]O3)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4327fc6470b255bb0ac3e135939715b209b767eb) , ,  ) ) |
500-6000 | |
| Сополимеры | – | – | до 100000 |
| Сульфид кадмия |  |
9,3 |
Большой диэлектрической проницаемостью обладают некоторые сложные вещества: CCTO-керамика и LSNO-керамика (
Кроме того, исследуются и метаматериалы. Например диэлектрическая проницаемость порядка 107—108 была обнаружена у металлических наноостровковых структур на диэлектрических подложках[5][6].
В электронике диэлектрическая проницаемость изоляционных материалов является одним из основных параметров для электрических конденсаторов. Применение материала с высокой диэлектрической проницаемостью позволяет существенно сократить габаритные размеры конденсатора. Например, ёмкость плоского конденсатора:
- где
— относительная диэлектрическая проницаемость материала между обкладками,
— площадь обкладок конденсатора,
— расстояние между обкладками.
Таким образом, требуемая площадь 

Помимо обозначения 


Традиционно в таких приборах используется диоксид кремния (SiO2). Однако в целях миниатюризации транзисторов на определённом этапе потребовался переход к материалам с более высокой, чем у SiO2 (3,9), проницаемостью. Это позволяет получить нужную ёмкость при более толстом[7] слое материала, что полезно, так как для тонких слоёв актуальны проблемы надёжности и туннельных утечек. Примерами применяемых подзатворных «high-k» диэлектриков являются ZrO2, HfO2 (у двух названных материалов 

Проницаемость диэлектрической среды с потерями[править | править код]
Комплексная диэлектрическая проницаемость[править | править код]
При описании колебаний электрического поля методом комплексных амплитуд в случае диэлектрической среды с конечной проводимостью 
Пусть напряженность электрического поля изменяется во времени по гармоническому закону (далее 
Тогда 
Чтобы привести это уравнение к виду, формально совпадающему с видом уравнения для непроводящей среды, величина, стоящая в скобках, интерпретируется как комплексная диэлектрическая проницаемость 



Даже в случаях, когда в постоянном электрическом поле среда обладает очень малой проводимостью, на высоких частотах могут проявиться существенные потери, которые при таком подходе приписываются некоторой «эффективной» диэлектрической проницаемости:
Наличие мнимой части связано с конечной проводимостью 


Без метода комплексных амплитуд подставлять комплексную 






Характеристика диэлектрических потерь[править | править код]
Плотность мощности (Ватт/м3) тепловыделения за счёт диэлектрических потерь составляет:
Подобный механизм разогрева широко используется в микроволновых печах. Для характеристики диэлектрика с поглощением также используется величина «тангенса угла потерь» — отношение мнимой и вещественной частей комплексной диэлектрической проницаемости:
При протекании переменного тока через конденсатор векторы напряжения и тока сдвинуты на угол 
При отсутствии потерь δ = 0. Тангенс угла потерь определяется отношением активной мощности к реактивной при синусоидальном напряжении заданной частоты. Величина, обратная tg δ, называется добротностью конденсатора.
При наличии поглощения взаимосвязь между компонентами комплексной проницаемости и оптическими величинами (показателями преломления и поглощения) устанавливается с использованием соотношений Крамерса — Кронига и имеет вид:
откуда для немагнитных сред следует:
Типичная частотная зависимость проницаемости[править | править код]

Типичное поведение вещественной и мнимой составляющих диэлектрической проницаемости в широком диапазоне частот. Области резкого изменения этих составляющих соответствуют линиям поглощения, которые могут иметь различную природу: дипольная или ионная релаксация, атомные и электронные резонансы на высоких частотах[9]. СВЧ — сверхвысокие частоты, ИК — инфракрасный диапазон, ВД — видимый диапазон, УФ — ультрафиолетовый диапазон.

Зависимость действительной и мнимой составляющих диэлектрической проницаемости воды при 20 °C
Параметры 

Наиболее типичное поведение 











Таблицы неспециализированных справочников обычно содержат данные для статического поля или малых частот вплоть до нескольких единиц кГц (иногда даже без указания данного факта). В то же время значения 



Сведения о поведении относительной диэлектрической проницаемости воды в диапазоне частот от 0 до 1012 (инфракрасная область) можно найти на сайте (англ.).
Измерение диэлектрической проницаемости[править | править код]
Относительная диэлектрическая проницаемость вещества 


Cуществуют и оптические методы получения относительной диэлектрической проницаемости по коэффициенту преломления при помощи эллипсометров и рефрактометров.
Примечания[править | править код]
- ↑ Гольдштейн Л. Д., Зернов Н. В. Электромагнитные поля и волны. М.: Сов. радио, 1971. С. 11.
- ↑ Никольский В. В. , Никольская Т. И. Электродинамика и распространение радиоволн. М.: Наука, 1989. С. 35.
- ↑ Финкельштейн А. В. Физика белка / Птицын О. Б.. — 3-е изд. — М.: КДУ, 2012. — С. 45. — 456 с. — ISBN 5-98227-065-2.
- ↑ Элементы – новости науки: Найдено вещество с гигантским значением диэлектрической проницаемости. elementy.ru. Дата обращения: 11 февраля 2017. Архивировано 11 февраля 2017 года.
- ↑ Наноструктуры, превосходящие сегнетоэлектрики (рус.). Архивировано 11 февраля 2017 года. Дата обращения: 11 февраля 2017.
- ↑ Архивированная копия. Дата обращения: 15 февраля 2017. Архивировано 16 февраля 2017 года.
- ↑ Ёмкость плоского конденсатора
, где d — расстояние между обкладками. Чем больше d, тем меньше ёмкость. Увеличенная проницаемость может это компенсировать.
- ↑ High-k Gate Dielectrics / Michel Houssa. — CRC Press, 2004. — 601 p. — (Series in Material Science and Engineering). — ISBN 0750309067.
- ↑ Dielectric Spectroscopy Архивировано 7 марта 2001 года.
Ссылки[править | править код]
- Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. — М.: Мир, 1965.
- Сивухин Д. В. Общий курс физики. — М.. — Т. III. Электричество.
- Малышкина И. А. Основы метода диэлектрической спектроскопии (учебное пособие) // Изд-во физического ф-та МГУ, М.: 2012 — 81 стр.
- Курс физики для ФМШ при НГУ, раздел «Электромагнитное поле», гл. 2: «Диэлектрики».

A dielectric medium showing orientation of charged particles creating polarization effects. Such a medium can have a lower ratio of electric flux to charge (more permittivity) than empty space
In electromagnetism, the absolute permittivity, often simply called permittivity and denoted by the Greek letter ε (epsilon), is a measure of the electric polarizability of a dielectric. A material with high permittivity polarizes more in response to an applied electric field than a material with low permittivity, thereby storing more energy in the material. In electrostatics, the permittivity plays an important role in determining the capacitance of a capacitor.
In the simplest case, the electric displacement field D resulting from an applied electric field E is
More generally, the permittivity is a thermodynamic function of state.[1] It can depend on the frequency, magnitude, and direction of the applied field. The SI unit for permittivity is farad per meter (F/m).
The permittivity is often represented by the relative permittivity εr which is the ratio of the absolute permittivity ε and the vacuum permittivity ε0
.
This dimensionless quantity is also often and ambiguously referred to as the permittivity. Another common term encountered for both absolute and relative permittivity is the dielectric constant which has been deprecated in physics and engineering[2] as well as in chemistry.[3]
By definition, a perfect vacuum has a relative permittivity of exactly 1 whereas at standard temperature and pressure, air has a relative permittivity of κair ≈ 1.0006.
Relative permittivity is directly related to electric susceptibility (χ) by
otherwise written as
The term “permittivity” was introduced in the 1880s by Oliver Heaviside to complement Thomson’s (1872) “permeability”.[4] Formerly written as p, the designation with ε has been in common use since the 1950s.
Units[edit]
The standard SI unit for permittivity is farad per meter (F/m or F·m−1).[5]
Explanation[edit]
In electromagnetism, the electric displacement field D represents the distribution of electric charges in a given medium resulting from the presence of an electric field E. This distribution includes charge migration and electric dipole reorientation. Its relation to permittivity in the very simple case of linear, homogeneous, isotropic materials with “instantaneous” response to changes in electric field is:
where the permittivity ε is a scalar. If the medium is anisotropic, the permittivity is a second rank tensor.
In general, permittivity is not a constant, as it can vary with the position in the medium, the frequency of the field applied, humidity, temperature, and other parameters. In a nonlinear medium, the permittivity can depend on the strength of the electric field. Permittivity as a function of frequency can take on real or complex values.
In SI units, permittivity is measured in farads per meter (F/m or A2·s4·kg−1·m−3). The displacement field D is measured in units of coulombs per square meter (C/m2), while the electric field E is measured in volts per meter (V/m). D and E describe the interaction between charged objects. D is related to the charge densities associated with this interaction, while E is related to the forces and potential differences.
Vacuum permittivity[edit]
The vacuum permittivity ε0 (also called permittivity of free space or the electric constant) is the ratio D/E in free space. It also appears in the Coulomb force constant,
Its value is[6][7]
where
- c0 is the speed of light in free space,[a]
- µ0 is the vacuum permeability.
The constants c0 and μ0 were both defined in SI units to have exact numerical values until the 2019 redefinition of the SI base units. Therefore, until that date, ε0 could be also stated exactly as a fraction,
even if the result was irrational (because the fraction contained π).[9] In contrast, the ampere was a measured quantity before 2019, but since then the ampere is now exactly defined and it is μ0 that is an experimentally measured quantity (with consequent uncertainty) and therefore so is the new 2019 definition of ε0 (c0 remains exactly defined before and since 2019).
Relative permittivity[edit]
The linear permittivity of a homogeneous material is usually given relative to that of free space, as a relative permittivity εr (also called dielectric constant, although this term is deprecated and sometimes only refers to the static, zero-frequency relative permittivity). In an anisotropic material, the relative permittivity may be a tensor, causing birefringence. The actual permittivity is then calculated by multiplying the relative permittivity by ε0:
where χ (frequently written χe) is the electric susceptibility of the material.
The susceptibility is defined as the constant of proportionality (which may be a tensor) relating an electric field E to the induced dielectric polarization density P such that
where ε0 is the electric permittivity of free space.
The susceptibility of a medium is related to its relative permittivity εr by
So in the case of a vacuum,
The susceptibility is also related to the polarizability of individual particles in the medium by the Clausius-Mossotti relation.
The electric displacement D is related to the polarization density P by
The permittivity ε and permeability µ of a medium together determine the phase velocity v = c/n of electromagnetic radiation through that medium:
Practical applications[edit]
Determining capacitance[edit]
The capacitance of a capacitor is based on its design and architecture, meaning it will not change with charging and discharging. The formula for capacitance in a parallel plate capacitor is written as
where 



Gauss’s law[edit]
Permittivity is connected to electric flux (and by extension electric field) through Gauss’s law. Gauss’s law states that for a closed Gaussian surface, S,
where 



If the Gaussian surface uniformly encloses an insulated, symmetrical charge arrangement, the formula can be simplified to
where 
If all of the electric field lines cross the surface at 90°, the formula can be further simplified to
Because the surface area of a sphere is 

This formula applies to the electric field due to a point charge, outside of a conducting sphere or shell, outside of a uniformly charged insulating sphere, or between the plates of a spherical capacitor.
Dispersion and causality[edit]
In general, a material cannot polarize instantaneously in response to an applied field, and so the more general formulation as a function of time is
That is, the polarization is a convolution of the electric field at previous times with time-dependent susceptibility given by χ(Δt). The upper limit of this integral can be extended to infinity as well if one defines χ(Δt) = 0 for Δt < 0. An instantaneous response would correspond to a Dirac delta function susceptibility χ(Δt) = χδ(Δt).
It is convenient to take the Fourier transform with respect to time and write this relationship as a function of frequency. Because of the convolution theorem, the integral becomes a simple product,
This frequency dependence of the susceptibility leads to frequency dependence of the permittivity. The shape of the susceptibility with respect to frequency characterizes the dispersion properties of the material.
Moreover, the fact that the polarization can only depend on the electric field at previous times (i.e. effectively χ(Δt) = 0 for Δt < 0), a consequence of causality, imposes Kramers–Kronig constraints on the susceptibility χ(0).
Complex permittivity[edit]
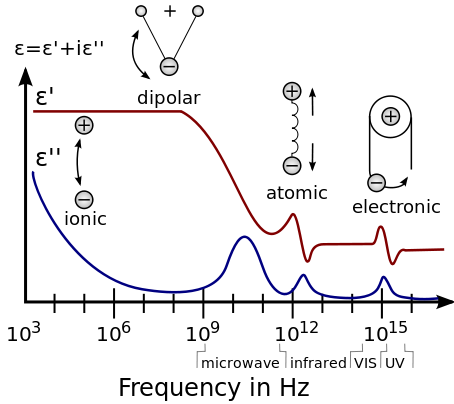
A dielectric permittivity spectrum over a wide range of frequencies. ε′ and ε″ denote the real and the imaginary part of the permittivity, respectively. Various processes are labeled on the image: ionic and dipolar relaxation, and atomic and electronic resonances at higher energies.[10]
As opposed to the response of a vacuum, the response of normal materials to external fields generally depends on the frequency of the field. This frequency dependence reflects the fact that a material’s polarization does not change instantaneously when an electric field is applied. The response must always be causal (arising after the applied field), which can be represented by a phase difference. For this reason, permittivity is often treated as a complex function of the (angular) frequency ω of the applied field:
(since complex numbers allow specification of magnitude and phase). The definition of permittivity therefore becomes
where
- D0 and E0 are the amplitudes of the displacement and electric fields, respectively,
- i is the imaginary unit, i2 = −1.
The response of a medium to static electric fields is described by the low-frequency limit of permittivity, also called the static permittivity εs (also εDC):
At the high-frequency limit (meaning optical frequencies), the complex permittivity is commonly referred to as ε∞ (or sometimes εopt[11]). At the plasma frequency and below, dielectrics behave as ideal metals, with electron gas behavior. The static permittivity is a good approximation for alternating fields of low frequencies, and as the frequency increases a measurable phase difference δ emerges between D and E. The frequency at which the phase shift becomes noticeable depends on temperature and the details of the medium. For moderate field strength (E0), D and E remain proportional, and
Since the response of materials to alternating fields is characterized by a complex permittivity, it is natural to separate its real and imaginary parts, which is done by convention in the following way:
where
- ε′ is the real part of the permittivity;
- ε″ is the imaginary part of the permittivity;
- δ is the loss angle.
The choice of sign for time-dependence, e−iωt, dictates the sign convention for the imaginary part of permittivity. The signs used here correspond to those commonly used in physics, whereas for the engineering convention one should reverse all imaginary quantities.
The complex permittivity is usually a complicated function of frequency ω, since it is a superimposed description of dispersion phenomena occurring at multiple frequencies. The dielectric function ε(ω) must have poles only for frequencies with positive imaginary parts, and therefore satisfies the Kramers–Kronig relations. However, in the narrow frequency ranges that are often studied in practice, the permittivity can be approximated as frequency-independent or by model functions.
At a given frequency, the imaginary part, ε″, leads to absorption loss if it is positive (in the above sign convention) and gain if it is negative. More generally, the imaginary parts of the eigenvalues of the anisotropic dielectric tensor should be considered.
In the case of solids, the complex dielectric function is intimately connected to band structure. The primary quantity that characterizes the electronic structure of any crystalline material is the probability of photon absorption, which is directly related to the imaginary part of the optical dielectric function ε(ω). The optical dielectric function is given by the fundamental expression:[12]
In this expression, Wc,v(E) represents the product of the Brillouin zone-averaged transition probability at the energy E with the joint density of states,[13][14] Jc,v(E); φ is a broadening function, representing the role of scattering in smearing out the energy levels.[15] In general, the broadening is intermediate between Lorentzian and Gaussian;[16][17] for an alloy it is somewhat closer to Gaussian because of strong scattering from statistical fluctuations in the local composition on a nanometer scale.
Tensorial permittivity[edit]
According to the Drude model of magnetized plasma, a more general expression which takes into account the interaction of the carriers with an alternating electric field at millimeter and microwave frequencies in an axially magnetized semiconductor requires the expression of the permittivity as a non-diagonal tensor.[18] (see also Electro-gyration).
If ε2 vanishes, then the tensor is diagonal but not proportional to the identity and the medium is said to be a uniaxial medium, which has similar properties to a uniaxial crystal.
Classification of materials[edit]
| εr″/εr′ | Current conduction | Field propagation |
|---|---|---|
| 0 | perfect dielectric lossless medium |
|
| ≪ 1 | low-conductivity material poor conductor |
low-loss medium good dielectric |
| ≈ 1 | lossy conducting material | lossy propagation medium |
| ≫ 1 | high-conductivity material good conductor |
high-loss medium poor dielectric |
| ∞ | perfect conductor |
Materials can be classified according to their complex-valued permittivity ε, upon comparison of its real ε′ and imaginary ε″ components (or, equivalently, conductivity, σ, when accounted for in the latter). A perfect conductor has infinite conductivity, σ = ∞, while a perfect dielectric is a material that has no conductivity at all, σ = 0; this latter case, of real-valued permittivity (or complex-valued permittivity with zero imaginary component) is also associated with the name lossless media.[19] Generally, when σ/ωε′ ≪ 1 we consider the material to be a low-loss dielectric (although not exactly lossless), whereas σ/ωε′ ≫ 1 is associated with a good conductor; such materials with non-negligible conductivity yield a large amount of loss that inhibit the propagation of electromagnetic waves, thus are also said to be lossy media. Those materials that do not fall under either limit are considered to be general media.
Lossy medium[edit]
In the case of a lossy medium, i.e. when the conduction current is not negligible, the total current density flowing is:
where
Note that this is using the electrical engineering convention of the Complex conjugate ambiguity; the physics/chemistry convention involves the complex conjugate of these equations.
The size of the displacement current is dependent on the frequency ω of the applied field E; there is no displacement current in a constant field.
In this formalism, the complex permittivity is defined as:[20][21]
In general, the absorption of electromagnetic energy by dielectrics is covered by a few different mechanisms that influence the shape of the permittivity as a function of frequency:
- First are the relaxation effects associated with permanent and induced molecular dipoles. At low frequencies the field changes slowly enough to allow dipoles to reach equilibrium before the field has measurably changed. For frequencies at which dipole orientations cannot follow the applied field because of the viscosity of the medium, absorption of the field’s energy leads to energy dissipation. The mechanism of dipoles relaxing is called dielectric relaxation and for ideal dipoles is described by classic Debye relaxation.
- Second are the resonance effects, which arise from the rotations or vibrations of atoms, ions, or electrons. These processes are observed in the neighborhood of their characteristic absorption frequencies.
The above effects often combine to cause non-linear effects within capacitors. For example, dielectric absorption refers to the inability of a capacitor that has been charged for a long time to completely discharge when briefly discharged. Although an ideal capacitor would remain at zero volts after being discharged, real capacitors will develop a small voltage, a phenomenon that is also called soakage or battery action. For some dielectrics, such as many polymer films, the resulting voltage may be less than 1–2% of the original voltage. However, it can be as much as 15–25% in the case of electrolytic capacitors or supercapacitors.
Quantum-mechanical interpretation[edit]
In terms of quantum mechanics, permittivity is explained by atomic and molecular interactions.
At low frequencies, molecules in polar dielectrics are polarized by an applied electric field, which induces periodic rotations. For example, at the microwave frequency, the microwave field causes the periodic rotation of water molecules, sufficient to break hydrogen bonds. The field does work against the bonds and the energy is absorbed by the material as heat. This is why microwave ovens work very well for materials containing water. There are two maxima of the imaginary component (the absorptive index) of water, one at the microwave frequency, and the other at far ultraviolet (UV) frequency. Both of these resonances are at higher frequencies than the operating frequency of microwave ovens.
At moderate frequencies, the energy is too high to cause rotation, yet too low to affect electrons directly, and is absorbed in the form of resonant molecular vibrations. In water, this is where the absorptive index starts to drop sharply, and the minimum of the imaginary permittivity is at the frequency of blue light (optical regime).
At high frequencies (such as UV and above), molecules cannot relax, and the energy is purely absorbed by atoms, exciting electron energy levels. Thus, these frequencies are classified as ionizing radiation.
While carrying out a complete ab initio (that is, first-principles) modelling is now computationally possible, it has not been widely applied yet. Thus, a phenomenological model is accepted as being an adequate method of capturing experimental behaviors. The Debye model and the Lorentz model use a first-order and second-order (respectively) lumped system parameter linear representation (such as an RC and an LRC resonant circuit).
Measurement[edit]
The relative permittivity of a material can be found by a variety of static electrical measurements. The complex permittivity is evaluated over a wide range of frequencies by using different variants of dielectric spectroscopy, covering nearly 21 orders of magnitude from 10−6 to 1015 hertz. Also, by using cryostats and ovens, the dielectric properties of a medium can be characterized over an array of temperatures. In order to study systems for such diverse excitation fields, a number of measurement setups are used, each adequate for a special frequency range.
Various microwave measurement techniques are outlined in Chen et al..[22] Typical errors for the Hakki-Coleman method employing a puck of material between conducting planes are about 0.3%.[23]
- Low-frequency time domain measurements (10−6 to 103 Hz)
- Low-frequency frequency domain measurements (10−5 to 106 Hz)
- Reflective coaxial methods (106 to 1010 Hz)
- Transmission coaxial method (108 to 1011 Hz)
- Quasi-optical methods (109 to 1010 Hz)
- Terahertz time-domain spectroscopy (1011 to 1013 Hz)
- Fourier-transform methods (1011 to 1015 Hz)
At infrared and optical frequencies, a common technique is ellipsometry. Dual polarisation interferometry is also used to measure the complex refractive index for very thin films at optical frequencies.
For the 3D measurement of dielectric tensors at optical frequency, Dielectric tensor tomography [1] can be used.
See also[edit]
- Acoustic attenuation
- Density functional theory
- Electric-field screening
- Green–Kubo relations
- Green’s function (many-body theory)
- Linear response function
- Rotational Brownian motion
- Electromagnetic permeability
Notes[edit]
- ^ Current practice of standards organizations such as NIST and BIPM is to use c0, rather than c, to denote the speed of light in vacuum according to ISO 31. In the original Recommendation of 1983, the symbol c was used for this purpose.[8]
References[edit]
- ^ Landau, L. D.; Lifshitz, E. M.; Pitaevskii, L. P. (2009). Electrodynamics of continuous media. Elsevier Butterworth-Heinemann. ISBN 978-0-7506-2634-7. OCLC 756385298.
- ^ IEEE Standards Board (1997). “IEEE Standard Definitions of Terms for Radio Wave Propagation”. IEEE STD 211-1997: 6.
- ^ Braslavsky, S.E. (2007). “Glossary of terms used in photochemistry (IUPAC recommendations 2006)” (PDF). Pure and Applied Chemistry. 79 (3): 293–465. doi:10.1351/pac200779030293. S2CID 96601716.
- ^ Fleming, John Ambrose (1910). The Principles of Electric Wave Telegraphy. p. 340..
- ^ International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), ISBN 92-822-2213-6, archived (PDF) from the original on 2021-06-04, retrieved 2021-12-16, p. 119
- ^ “2018 CODATA Value: vacuum electric permittivity”. The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ “Latest (2018) values of the constants (NIST)”. Physics.nist.gov. 2019-05-20. Retrieved 2022-02-05.
- ^ “Special Publication 330, Appendix 2″ (PDF). NIST: 45. Archived from the original (PDF) on 2016-06-03..
- ^ “Latest (2006) values of the constants (NIST)”. Physics.nist.gov. 2017-07-01. Retrieved 2018-11-20.
- ^ “Dielectric Spectroscopy”. Archived from the original on 2006-01-18. Retrieved 2018-11-20.
- ^
Hofmann, Philip (2015-05-26). Solid State Physics (2 ed.). Wiley-VCH. p. 194. ISBN 978-3527412822. - ^
Peter Y. Yu; Manuel Cardona (2001). Fundamentals of Semiconductors: Physics and Materials Properties. Berlin: Springer. p. 261. ISBN 978-3-540-25470-6. - ^
José García Solé, Jose Solé, Luisa Bausa (2001). An introduction to the optical spectroscopy of inorganic solids. Wiley. Appendix A1, pp, 263. ISBN 978-0-470-86885-0.{{cite book}}: CS1 maint: multiple names: authors list (link) - ^
John H. Moore; Nicholas D. Spencer (2001). Encyclopedia of chemical physics and physical chemistry. Taylor and Francis. p. 105. ISBN 978-0-7503-0798-7. - ^
Solé, José García; Bausá, Louisa E; Jaque, Daniel (2005-03-22). Solé and Bausa. p. 10. ISBN 978-3-540-25470-6. - ^
Hartmut Haug; Stephan W. Koch (1994). Quantum Theory of the Optical and Electronic Properties of Semiconductors. World Scientific. p. 196. ISBN 978-981-02-1864-5. - ^
Manijeh Razeghi (2006). Fundamentals of Solid State Engineering. Birkhauser. p. 383. ISBN 978-0-387-28152-0. - ^ Prati, E. (2003). “Propagation in Gyroelectromagnetic Guiding Systems”. Journal of Electromagnetic Waves and Applications. 17 (8): 1177–1196. doi:10.1163/156939303322519810. S2CID 121509049.
- ^ Orfanidis, Sophocles J. “1: Maxwell’s Equations” (PDF). Electromagnetic Waves and Antennas. Rutgers University.
- ^ Seybold, John S. (2005). Introduction to RF Propagation. John Wiley & Sons. p. 22, eq. (2.6). ISBN 9780471743682.
- ^ Kaiser, Kenneth L. (2005). Electromagnetic Shielding. CRC Press. pp. 1–28, eqs. (1.80) and (1.81). ISBN 9780849363726.
- ^ Linfeng Chen; V. V. Varadan; C. K. Ong; Chye Poh Neo (2004). “Microwave theory and techniques for materials characterization”. Microwave electronics. Wiley. p. 37. ISBN 978-0-470-84492-2.
- ^ Mailadil T. Sebastian (2008). Dielectric Materials for Wireless Communication. Elsevier. p. 19. ISBN 978-0-08-045330-9.
Further reading[edit]
- C. J. F. Bottcher, O. C. von Belle & Paul Bordewijk (1973) Theory of Electric Polarization: Dielectric Polarization, volume 1, (1978) volume 2, Elsevier ISBN 0-444-41579-3.
- Arthur R. von Hippel (1954) Dielectrics and Waves ISBN 0-89006-803-8
- Arthur von Hippel editor (1966) Dielectric Materials and Applications: papers by 22 contributors ISBN 0-89006-805-4.
External links[edit]
- Electromagnetism, a chapter from an online textbook
Для школьников.
В статье говорится о том, как можно найти диэлектрическую проницаемость диэлектрика и о его роли в увеличении ёмкости конденсатора.
Задача.
Теория вопроса.
При внесении диэлектрика в электрическое поле конденсатора, в диэлектрике происходят изменения.
Представим, что в поле внесли пластину из хлористого натрия
Можно сказать, что его кристаллическая решётка состоит из двух подрешёток, образованных положительными ионами натрия и отрицательными ионами хлора.
Под действием электрического поля положительные ионы смещаются по полю, а отрицательные – против поля.
На гранях диэлектрика образуются связанные поляризационные заряды, которые образуют своё электрическое поле, направленное навстречу поля конденсатора.
Результирующее поле в диэлектрике
направлено в ту же сторону, что и поле конденсатора, но слабее его.
Роль диэлектрика и сводится к тому, чтобы ослабить электрическое поле внутри себя, повысив этим ёмкость конденсатора.
Подробнее см. Занятие 51 ” Почему диэлектрики ослабляют внутри себя электрическое поле? Поляризация диэлектриков.”
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: Как повлияет введение металлической пластины в поле конденсатора на напряжение между его обкладками.
Следующая запись: Какой заряд пройдёт по проводам, соединяющим обкладки заряженного конденсатора, при удалении диэлектрика?
Ссылки на занятия до электростатики даны в Занятии 1.
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45.
Диэлектрическая проницаемость
Вернутся в раздел ⇒ Законы электротехники коротко
 Диэлектрическая проницаемость — величина, характеризующая диэлектрические свойства среды — её реакцию на электрическое поле:
Диэлектрическая проницаемость — величина, характеризующая диэлектрические свойства среды — её реакцию на электрическое поле:
D = εF
В большинстве диэлектриков при не очень сильных полях диэлектрическая проницаемость не зависит от поля Е. В сильных же электрических полях (сравнимых с внутриатомными полями), а в некоторых диэлектриках в обычных полях зависимость D от Е — нелинейная.
Так же диэлектрическая проницаемость показывает, во сколько раз сила взаимодействия F между электрическими зарядами в данной среде меньше их силы взаимодействия Fo в вакууме:
![]()
Относительная диэлектрическая проницаемость вещества может быть определена путем сравнения ёмкости тестового конденсатора с данным диэлектриком (Cx) и ёмкости того же конденсатора в вакууме (Co):
![]()
Таблица значений диэлектрической проницаемости для твердых тел:

Таблица значений диэлектрической проницаемости для жидкостей:

Таблица значений диэлектрической проницаемости для газов:

Обозначение в формуле:
D — электрическая индукция в среде;
ε — диэлектрическая проницаемость среды;
E — напряжённость электрического поля;
F0 — сила взаимодействия между зарядами в среде;
F — сила взаимодействия между зарядами в вакууме;
Cx — ёмкость конденсатора в среде;
C0 — ёмкость конденсатора в вакууме.
Ещё картинки на тему диэлектрическая проницаемость:
























































