Условие задачи:
Найти емкость конденсатора колебательного контура, если при индуктивности 50 мкГн контур настроен на длину волны электромагнитных колебаний 300 м.
Задача №9.13.2 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(L=50) мкГн, (lambda=300) м, (C-?)
Решение задачи:
Частоту колебаний колебательного контура (она равна частоте излучаемых электромагнитных волн) можно определить по формуле:
[nu = frac{1}{{2pi sqrt {LC} }};;;;(1)]
В этой формуле (L) – индуктивность катушки, (C) – электроемкость конденсатора.
Возведем обе части (1) в квадрат, тогда имеем:
[{nu ^2} = frac{1}{{4{pi ^2}LC}}]
Откуда искомая емкость конденсатора (C) равна:
[C = frac{1}{{4{pi ^2}{nu ^2}L}};;;;(2)]
Известно, что электромагнитные волны распространяются со скоростью света (c) (в вакууме она равна 3·108 м/с). Между скоростью распространения электромагнитных волн (скоростью света (c)), частотой их колебаний (nu) и длиной волны (lambda) существует следующее соотношение:
[c = lambda nu ]
Откуда частота колебаний (nu) равна:
[nu = frac{c}{lambda }]
Это выражение подставим в ранее полученную формулу (2):
[C = frac{{{lambda ^2}}}{{4{pi ^2}{c^2}L}}]
Посчитаем численный ответ задачи:
[C = frac{{{{300}^2}}}{{4 cdot {{3,14}^2} cdot {{left( {3 cdot {{10}^8}} right)}^2} cdot 50 cdot {{10}^{ – 6}}}} = 5,1 cdot {10^{ – 10}};Ф = 0,51;нФ]
Ответ: 0,51 нФ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
9.13.1 Колебательный контур имеет емкость 2,6 пФ и индуктивность 0,012 мГн. Какой длины
9.13.3 При изменении тока в катушке индуктивности на 1 А за 0,6 с в ней индуцируется ЭДС
9.13.4 Определите максимальный ток в контуре, если длина электромагнитной волны
Емкость конденсаторов, проводов и других элементов электрической цепи измеряется в фарадах (Ф); индуктивность проводов, катушек и других элементов цепей измеряется в генри (Гн).
Емкость плоского конденсатора, состоящего из п пластин площадью пластины 

где d — расстояние между пластинами, м.
Емкость цилиндрического конденсатора (коаксиального кабеля) длиной / (м), Ф:

где R1 — радиус внутренней обкладки (жилы), м;
R2 — радиус внешней обкладки, м.
Емкость прямолинейного провода длиной / и радиусом поперечного сечения г (м) (второй провод — в бесконечности), Ф:

Индуктивность уединенного прямолинейного провода круглого сечения радиусом г и длиной / (м), Гн:

Индуктивность кольца со средним радиусом R и радиусом сечения кольца г (м), Гн:

Индуктивность многослойной катушки толщиной обмотки d, радиусом обмотки R (от оси до среднего слоя обмотки), длиной / (м) и числом витков w (рис. 1.2, а), Гн


Индуктивность тороидальной катушки кругового сечения (рис. 1.2, б), Гн:

где w — число витков катушки,
D — средний диаметр тора, м;
d — диаметр среднего витка, м.
Взаимная индуктивность двух тороидальных катушек с числами витков w^ и w2, Гн:


Рис. 1.3. Концентрически расположенные катушки индуктивности
Взаимная индуктивность концентрических катушек прямоугольного сечения, имеющих одинаковую длину и примыкающих друг к другу (рис. 1.3), Гн:

где L12 — индуктивность катушки, состоящей из первой и второй катушек;
L1, L2 — собственные индуктивности катушек.
После несложной процедуры регистрации Вы сможете пользоваться всеми сервисами и создать свой веб-сайт.
Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.
Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.
— Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
— Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.
Свободные электрические колебания в параллельном контуре.
Основные свойства индуктивности:
— Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией  .
.
— Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.
Период свободных колебаний контура LC можно описать следующим образом:
Если конденсатор ёмкостью C заряжен до напряжения U, потенциальная энергия его заряда составит .
.
Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток его разряда, создавая магнитное поле в катушке.

Магнитный поток, увеличиваясь от нуля, создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в цепи, поэтому конденсатор разрядится не мгновенно, а через время t1, которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t1 =  .
.
По истечении времени t1, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит .
.
В идеальном рассмотрении, при полном отсутствии потерь в контуре, EC будет равна EL. Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.

Изменение (уменьшение) магнитного потока накопленной энергии катушки создаст в ней ЭДС, которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени t2 = t1, он перезарядит конденсатор от нуля до максимального отрицательного значения (-U).
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.
Описанные интервалы t1 и t2 составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление. Магнитная энергия вновь будет накапливаться в катушке в течении времени t3, сменив полярность полюсов.
В течении заключительного этапа колебания (t4), накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения U (в случае отсутствия потерь) и процесс колебания повторится.
В реальности, при наличии потерь энергии на активном сопротивлении проводников, фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t1 + t2 + t3 + t4 составит период колебаний  .
.
Частота свободных колебаний контура ƒ = 1 / T
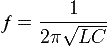
Частота свободных колебаний является частотой резонанса контура, на которой реактивное сопротивление индуктивности XL=2πfL равно реактивному сопротивлению ёмкости XC=1/(2πfC).
Расчёт частоты резонанса LC-контура:
Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Расчёт ёмкости:
Расчёт индуктивности:
Похожие страницы с расчётами:
Замечания и предложения принимаются и приветствуются!

По формуле циклической частоты свободных электромагнитных колебаний , где L — индуктивность катушки (Гн), C — ёмкость конденсатора (Ф). Циклическую частоту расписываем как: , где V — “ню” частота колебаний (Гц). Данную формулу подставляем в формулу циклической частоты свободных электромагнитных колебаний: . Поизводим преобразования и выражаем искомую ёмкость конденсатора:
В системе СИ: 10 МГц = 10*10⁶ Гц; 5,1 мкГн = 5,1*10⁻⁶ Гн. Подставляеи вычисляем:
Расчёт ёмкости колебательного контура
Расчёт ёмкости колебательного контура (L,C)
Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания.
Колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.
Формула расчета ёмкости колебательного контура
- C = 1/(4π²F²L)
Где:
- F – Резонансная частота, Гц)
- L – Индуктивность, (Гн)
- C – Ёмкость, (Ф)
Онлайн-калькулятор для расчёта ёмкости колебательного контура
Индуктивность:
Частота:
Ёмкость:
Поделиться в соц сетях:
Популярные сообщения из этого блога
Найти тангенс фи , если известен косинус фи
Калькулятор коэффициент мощности cos fi в tg fi Как найти тангенс фи, если известен косинус фи формула: tg φ = (√(1-cos²φ))/cos φ Калькулятор онлайн – косинус в тангенс cos φ: tg φ: Поделиться в соц сетях: Найти синус φ, если известен тангенс φ Найти косинус φ, если известен тангенс φ
Индекс Руфье калькулятор
Проба Руфье калькулятор онлайн. Первые упоминания теста относиться к 1950 году. Именно в это время мы находим первое упоминание доктора Диксона о “Использование сердечного индекса Руфье в медико-спортивном контроле”. Проба Руфье – представляет собой нагрузочный комплекс, предназначенный для оценки работоспособности сердца при физической нагрузке. Индекс Руфье для школьников и студентов. У испытуемого, находящегося в положении лежа на спине в течение 5 мин, определяют число пульсаций за 15 сек (P1); После чего в течение 45 сек испытуемый выполняет 30 приседаний. После окончания нагрузки испытуемый ложится, и у него вновь подсчитывается число пульсаций за первые 15 с (Р2); И в завершении за последние 15 сек первой минуты периода восстановления (Р3); Оценку работоспособности сердца производят по формуле: Индекс Руфье = (4(P1+P2+P3)-200)/10; Индекс Руфье для спортсменов Измеряют пульс в положении сидя (Р1); Спортсмен выполняет 30 глубоких приседаний в
Найти косинус фи (cos φ), через тангенс фи (tg φ)
tg фи=… чему равен cos фи? Как перевести тангенс в косинус формула: cos(a)=(+-)1/sqrt(1+(tg(a))^2) Косинус через тангенс, перевести tg в cos, калькулятор – онлайн tg φ: cos φ: ± Поделиться в соц сетях:
Всем доброго времени суток. В прошлой статье я рассказывал о методах расчёта электрических цепей, в которых основным элементом является резистор. Резистор представляет собой один из элементов с сосредоточенными параметрами, в данном случае таким параметром является сопротивление. Однако кроме сопротивления ещё одними из основных параметров элементов цепи являются ёмкость и индуктивность, которые представлены элементами конденсатор и индуктивными элементами (различные дросселя, катушки, трансформаторы и т.д.). В данной статье я рассмотрю такой элемент с сосредоточенными параметрами, как конденсатор.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Проводник в электрическом поле
Помещая проводник в электрическое поле, носители заряда внутри проводника начинают перемещаться. Причем данное перемещение подчиняется двум правилам:
- Напряжённость электрического поля внутри проводника должно равняться нулю
Это означает, что потенциал внутри проводника остается постоянным (φ = const).
- Напряжённость поля на поверхности проводника направлена перпендикулярно к самой поверхности данного проводника. Или другими словами поверхность проводника становится эквипотенциальной, то есть все точки данной поверхности имеют одинаковый потенциал.
Из этих двух правил следует, что когда проводник вносится в электрическое поле его носители заряда (в металлах это электроны, а в жидкостях – ионы) приходят в движение, причем положительные по направлению напряжённости электрического поля, а отрицательные в противоположную сторону. Результатом движения зарядов в проводнике является возникновение зарядов противоположного знака на концах проводника, такие заряды называют индуцированными. Перераспределение заряда в проводнике показано на рисунке ниже

Таким образом, нейтральный проводник, помещённый в электрическое поле, как бы разрывает часть линий электрического поля, а индуцированные заряды распределяются по поверхности проводника.
Практический интерес представляет следующая ситуация, когда внутри проводника имеется некоторая полость. Так как индуцирование зарядов происходит на поверхности проводника, то внутри этого проводника, а значит и во внутренней полости электрическое поле обращается в нуль. На данном явлении основана электростатическая защита, когда необходимо защитить какой-нибудь прибор от воздействия электрического поля, то его помещают внутрь экрана из проводника. Индуцированные заряды на поверхности экрана скомпенсируют электростатическое поле. Вместо сплошного экрана часто используют экран из электропроводящей сетки, что тоже позволяет создать защиту от электростатического поля.
Соленоид
Под этим понятием понимается цилиндрическая обмотка из провода, который может быть намотан в один или несколько слоев. Длина цилиндра значительно больше диаметра. За счет такой особенности при подаче электрического тока в полости соленоида рождается магнитное поле. Скорость изменения магнитного потока пропорциональна изменению тока. Индуктивность соленоида в этом случае рассчитывается следующим образом:
- df : dt = L dl : dt.
Еще эту разновидность катушек называют электромеханическим исполнительным механизмом с втягиваемым сердечником. В данном случае соленоид снабжается внешним ферромагнитным магнитопроводом – ярмом.

- Первая способна контролировать линейное давление.
- Вторая модель отличается от других принудительным управлением блокировки муфты в гидротрансформаторах.
- Третья модель содержит в своем составе регуляторы давления, отвечающие за работу переключения скоростей.
- Четвертая управляется гидравлическим способом или клапанами.
Электроемкость
Если на проводник переместить некоторый заряд q, то он как мы уже знаем, распределится по всей поверхности проводника, так чтобы напряженность электрического поля внутри него была равна нулю. Однако относительно любой точки пространства данный проводник будет обладать некоторым потенциалом φ. Если на данный заряженный проводник переместить ещё один заряд, то опять же он равномерно распределится по всей поверхности проводника, а величина потенциала вырастит на некоторую величину.
Таким образом, между величиной заряда проводника и его потенциалом существует связь, которая определяется следующим выражением
где q – величина заряда, сообщенная проводнику,
φ – потенциал проводника относительно любой точки пространства,
С – коэффициент пропорциональности, называемый электроемкостью проводника, или просто емкостью.
Исходя из этого, электроемкость проводника может быть вычислена из следующего выражения
Таким образом, электроемкость численно равна заряду, передача которого проводнику повышает его потенциал на единицу. Единица измерения электроемкости называется Фарада (обозначается Ф).
Однако емкость уединенного проводника невелика, так емкостью в 1 Ф обладает шар радиусом 9*109 м, что почти в 1500 раз больше радиуса Земли. Поэтому на практике используют специальные устройства для накопления зарядов и обладающие большой емкостью при минимальных размерах. Такие устройства называются конденсаторами.
Как найти индуктивность
Формула, которая является простейшей для нахождения величины, следующая:
- L = F : I,
где F – магнитный поток, I – ток в контуре.
Через индуктивность можно выразить ЭДС самоиндукции:
- Ei = -L х dI : dt.
Из формулы напрашивается вывод о численном равенстве индукции с ЭДС, которое возникает в контуре при изменении силы тока на один амперметр за одну секунду.
Переменная индуктивность дает возможность найти и энергию магнитного поля:
- W = L I2 : 2.
Конденсаторы
Принцип действия конденсатора основывается на явлении индуцирования зарядов на проводнике в электрическом поле или на свойстве диэлектрика поляризоваться под воздействием электрического поля, а также возрастания электроемкости проводника при приближении к нему других тел. Рассмотрим подробнее.
Как известно из предыдущего параграфа, что если к заряженному телу, вокруг которого существует электрическое поле поднести проводник, то на поднесенном проводнике начнут индуцироваться заряды, в результате чего потенциал заряженного проводника будет уменьшаться, а, следовательно, электроемкость возрастать. Поэтому конденсаторы делают в виде двух близкорасположенных проводников, называемых обкладками конденсатора.
Чтобы ограничить влияние посторонних предметов на электрическое поле конденсатора, а следовательно и его емкость, обкладки изготавливают такими, чтобы электрическое поле создаваемое ими было полностью сосредоточенно внутри конденсатора. Такому условию соответствуют плоские, цилиндрические и сферические конденсаторы.
Так как обкладки расположены очень близко, то практически весь заряд обкладок будет сосредоточен на их внутренних поверхностях, то есть обращённых друг к другу, поэтому емкость конденсатора будет определяться следующим выражением
где q – заряд одной из обкладок конденсатора,
φ1 и φ2 – потенциалы обкладок конденсатора.
Самым простым является плоский конденсатор, его мы и рассмотрим в качестве примера.
«Катушка ниток»
Катушка индуктивности представляет собой намотанную изолированную медную проволоку на твердое основание. Что касается изоляции, то выбор материала широк – это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.

Если подать электрический ток на катушку, то в ней возникнет напряжение, противоположное напряжению тока, но оно внезапно исчезает. Такого рода напряжение называется электродвижущей силой самоиндукции. В момент включения напряжения на катушку сила тока меняет свое значение от 0 до некоего числа. Напряжение в этот момент тоже меняет значение, согласно закону Ома:
- I = U : R,
где I характеризует силу тока, U – показывает напряжение, R – сопротивление катушки.
Еще одной особенной чертой катушки является следующий факт: если разомкнуть цепь «катушка – источник тока», то ЭДС добавится к напряжению. Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.
Катушку можно разделить на два вида:
- С магнитным наконечником. В роли материала сердца выступают ферриты и железо. Сердечники служат для повышения индуктивности.
- С немагнитным. Используются в случаях, когда индуктивность не больше пяти миллиГенри.
Устройства различаются и по внешнему виду, и внутреннему строению. В зависимости от таких параметров находится индуктивность катушки. Формула в каждом случае разная. Например, для однослойной катушки индуктивность будет равна:
- L = 10µ0ΠN2R2 : 9R + 10l.
А вот уже для многослойной другая формула:
- L= µ0N2R2 :2Π(6R + 9l + 10w).
Основные выводы, связанные с работой катушек:
- На цилиндрическом феррите самая большая индуктивность возникает в середине.
- Для получения максимальной индуктивности необходимо близко наматывать витки на катушку.
- Индуктивность тем меньше, чем меньше количество витков.
- В тороидальном сердечнике расстояние между витками не играет роли катушки.
- Значение индуктивности зависит от «витков в квадрате».
- Если последовательно соединить индуктивности, то их общее значение равно сумме индуктивностей.
- При параллельном соединении нужно следить, чтобы индуктивности были разнесены на плате. В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.
Плоский конденсатор
Плоский конденсатор представляет собой две одинаковые пластины площадью S, расположенные параллельно, расстояние между пластинами d очень незначительно по отношению к размерам самих пластин, поэтому практически всё электрическое поле сосредоточенно между пластинами-обкладками. Кроме этого между пластинами расположен диэлектрик, который имеет диэлектрическую проницаемость ε, зависящую от свойств диэлектрика.

Тогда разность потенциалов между обкладками конденсатора будет определяться следующим выражением
где S – площадь обкладки конденсатора,
d – расстояние между обкладками,
ε0 – электрическая постоянная, ε0 = 8,85 * 10-12 Кл2/(Н*м2),
ε – относительная диэлектрическая проницаемость диэлектрика, зависящая от его свойств.
Тогда емкость плоского конденсатора будет определяться по следующей формуле
На этом с физикой, пожалуй, закончим и приступим к электронике.
Самоиндукция и измерение индуктивности
Индуктивностью называется величина, которая равна отношению магнитного потока, проходящего по всем виткам контура к силе тока:
- L = N х F : I.
Индуктивность контура находится в зависимости от формы, размеров контура и от магнитных свойств среды, в которой он находится. Если в замкнутом контуре протекает электрический ток, то возникает изменяющееся магнитное поле. Это впоследствии приведет к возникновению ЭДС. Рождение индукционного тока в замкнутом контуре носит название «самоиндукция». По правилу Ленца величина не дает изменяться току в контуре. Если обнаруживается самоиндукция, то можно применять электрическую цепь, в которой параллельно включены резистор и катушка с железным сердечником. Последовательно с ними подсоединены и электрические лампы. В этом случае сопротивление резистора равно сопротивлению на постоянном токе катушки. Результатом будет яркое горение ламп. Явление самоиндукции занимает одно из главных мест в радиотехнике и электротехнике.
Работа на постоянном и переменном токе
Магнитное поле, которое создается внутри катушки, направлено вдоль оси, и равно:
- B= µ0nI,
где µ0 – это магнитная проницаемость вакуума, n – это число витков, а I – значение тока.
Когда ток движется по соленоиду, то катушка запасает энергию, которая равна работе, необходимая для установления тока. Чтобы вычислить в этом случае индуктивность, формула используется следующая:
- E = LI2 :2,
где L показывает значение индуктивности, а E – запасающую энергию.
ЭДС самоиндукции возникает при изменении тока в соленоиде.
В случае работы на переменном токе появляется переменное магнитное поле. Направление силы притяжения может изменяться, а может оставаться неизменным. Первый случай возникает при использовании соленоида как электромагнита. А второй, когда якорь сделан из магнитомягкого материала. Соленоид на переменном токе имеет комплексное сопротивление, в которое включаются сопротивление обмотки и ее индуктивность.
Самое распространенное применение соленоидов первого типа (постоянного тока) — это в роли поступательного силового электропривода. Сила зависит от строения сердечника и корпуса. Примерами использования являются работа ножниц при отрезании чеков в кассовых аппаратах, клапаны в двигателях и гидравлических системах, язычки замков. Соленоиды второго типа применяются как индукторы для индукционного нагрева в тигельных печах.
Колебательный контур
Емкость и индуктивный элемент, соединенные в цепь, образуют колебательный контур с резко выраженными частотными свойствами и будут являться резонансной системой. В качестве системы используется конденсатор, изменяя емкость которого, можно производить коррекцию частотных свойств.

Если измерить резонансную частоту, используя известный конденсатор, то можно определить индуктивность катушки.
Индуктивность – важнейший элемент в разных областях электротехники. Для правильного применения нужно знать все параметры используемых элементов.
Устройство, которое позволяет определить параметры катушек индуктивности, в том числе добротность, может называться L-метр или Q-метр.

Любопытно, что…
…немецкий каноник фон Клейст, независимо от голландского профессора Мушенбрука проведший опыт с лейденской банкой и испытавший ее разряд, пытался, по-видимому, использовать ее для получения электризованной воды, считавшейся полезной для здоровья.
…в 1827 году французский ученый Савар обнаружил, что после разряда лейденской банки через проволоку, намотанную на железную спицу, последняя часто оказывалась намагниченной. Удивительным же было то, что на одном и том же конце спицы появлялся иногда северный, а иногда южный полюс, хотя банка все время заряжалась одинаково. Объяснение пришло позже — вместе с пониманием колебательного характера разряда.
…Герц не только не помышлял о радиосвязи, но даже отрицал ее возможность.
…проблему передачи сигналов на расстояния пытался решить своим, отличным от Попова и Маркони, путем и Резерфорд. Однако, узнав в 1897 году о результатах Маркони, Резерфорд прекратил дальнейшие опыты в этой области и переключился на исследования радиоактивности.
…новый метод получения импульсных сверхсильных магнитных полей Капица предложил во время работы в Кавендишской лаборатории. Вот как описывал работу его установок знаменитый американский математик Норберт Винер: «…мощные генераторы… замыкались накоротко, создавая токи огромной силы, пропускавшиеся по массивным проводам; провода шипели и трещали, как рассерженные змеи, а в окружающем пространстве возникало магнитное поле колоссальной силы».
Что такое электроемкость проводников
Если у нас есть два проводника, изолированных друг от друга, которым мы сообщаем некоторые заряды (обозначим их соответственно q1 и q2), то между ними возникнет определенная разность потенциалов. Ее величина будет зависеть от формы проводников, а также от исходных величин зарядов. Обозначим такую разность Δφ. Если мы говорим о разности, возникающей в электрическом поле между двумя точками, то ее обычно обозначают U.
В рамках темы данной статьи нам больше всего интересна такая разность потенциалов между проводниками, когда их заряды противоположны по знаку, но равны друг другу по модулю. В таком случае мы можем ввести новое понятие – электрическая емкость (электроемкость).
Электрической емкостью системы, состоящей из двух проводников, называется отношение заряда одного проводника (q) к разности потенциалов между этими двумя проводниками.
В виде формулы это записывается так: C=q∆φ=qU.
Для измерения электрической емкости применяется единица, называемая фарад. Она обозначается буквой Ф.
1Φ=1 Кл1 В.
Конфигурации и размеры проводников, а также свойства диэлектрика определяют величину электроемкости заданной системы. Наибольший интерес для нас представляют проводники особой формы, называемые конденсаторами.
Конденсатор – это проводник, конфигурация которого позволяет локализовать (сосредотачивать) электрическое поле в одной выделенной части пространства. Проводники, составляющие конденсатор, называются обкладками.
Если мы возьмем две плоские пластины из проводящего материала, расположим их на небольшом расстоянии друг от друга и проложим между ними слой диэлектрика, то мы получим простейший конденсатор, называемый плоским. При его работе электрическое поле будет располагаться преимущественно в промежутке между пластинами, но небольшая часть этого поля будет рассеиваться вокруг них.
Часть электрического поля вблизи конденсатора называется полем рассеяния.
Иногда в задачах мы можем не учитывать его и работать только с той частью электрического поля, которое расположено между обкладками. Однако пренебрегать полем рассеяния допустимо далеко не всегда, поскольку это может привести к ошибочным расчетам из-за нарушения потенциального характера электрического поля.
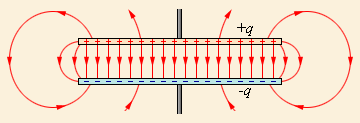
Рисунок 1.6.1. Электрическое поле в плоском конденсаторе.
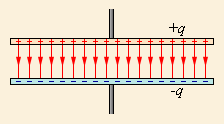
Рисунок 1.6.2. Электрическое поле конденсатора без учета поля рассеяния, не обладающее потенциальностью.
Модуль напряженности электрического поля, которое создает каждая обкладка в плоском конденсаторе, выражается соотношением следующего вида:
E1=σ2ε0.
Исходя из принципа суперпозиции, можно утверждать, что напряженность E→ поля, которое создают обе пластины конденсатора, будет равна сумме напряженностей E+→ и E-→ полей каждой пластины, то есть E→=E+→+E-→.
Векторы напряженностей обеих пластин во внутренней части конденсатора будут параллельны друг другу. Значит, мы можем выразить модуль напряженности их суммарного поля в виде формулы E=2E1=σε0.
Как рассчитать электроемкость конденсатора
Вне пластин векторы напряженности будут направлены в противоположные друг от друга стороны, значит, E будет равно нулю. Если мы обозначим заряд каждой обкладки как q, а ее площадь как S, то соотношение qS даст нам представление о поверхностной плотности. Умножив E на расстояние между обкладками (d), мы получим разность потенциалов между пластинами в однородном электрическом поле. Теперь возьмем оба этих соотношения и выведем из них формулу, по которой может быть рассчитана электрическая емкость конденсатора.
C=q∆φ=σ·SE·d=ε0Sd.
Электрическая емкость плоского конденсатора – величина, обратно пропорциональная расстоянию между обкладками и прямо пропорциональная их площади.
Заполнение пространства между проводниками диэлектрическим материалом может увеличить электроемкость плоского конденсатора в число раз, кратное undefined.
Введем обозначение емкости в виде буквы С и запишем это в виде формулы:
C=εε0Sd.
Данная формула называется формулой электроемкости плоского конденсатора.
Конденсаторы бывают не только плоскими. Возможны и другие конфигурации, также обладающие специфическими свойствами.
Сферическим конденсатором называется система из 2-х концентрических сфер, сделанных из проводящего материала, радиусы которых равны R1 и R2 соответственно.
Цилиндрическим конденсатором называется системы из двух проводников цилиндрической формы, длина которых равна L, а радиусы R1 и R2.
Обозначим проницаемость диэлектрического материала как ε и запишем формулы, по которым можно найти электрическую емкость конденсаторов:
- C=4πε0εR1R2R2-R1(сферический конденсатор),
- C=2πε0εLlnR2R1(цилиндрический конденсатор).
Как рассчитать электроемкость батареи конденсаторов
Если мы соединим несколько проводников между собой, то мы получим конструкцию, называемую батареей.
Способы соединения могут быть разными. Если соединение будет параллельным, то напряжение всех конденсаторов в системе будет одинаково: U1=U2 =U, а заряды можно найти по формулам q1=С1U и q2=C2U. При таком соединении вся система может считаться одним конденсатором, электроемкость которого равна C, заряд – q=q1+q2, а напряжение – U. В виде формулы это выглядит так:
С=q1+q2U или C=C1+C2
Если в батарее конденсаторов элементы соединены параллельно, то для нахождения общей электроемкости нам нужно сложить емкости ее отдельных элементов.
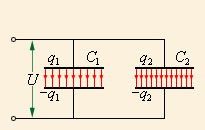
Рисунок 1.6.3. Конденсаторы, соединенные параллельно. C=C1+C2
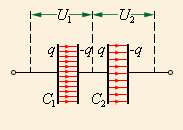
Рисунок 1.6.4. Конденсаторы, соединенные последовательно: 1C=1C1+1C2
Если же батарея состоит из двух последовательно соединенных конденсаторов, то заряды обоих будут одинаковы: q1=q2=q. Найти их напряжения можно так: U1=qC1 и U2=qC2. Такую систему тоже можно считать одним конденсатором, заряд которого равен q, а напряжение U=U1+U2.
C=qU1+U2 или 1C=1C1+1C2
Если конденсаторы в батарее соединены последовательно, то для нахождения общей электроемкости нам нужно сложить величины, обратные емкостям каждого из них.
Справедливость обеих формул, приведенных выше, не зависит от количества конденсаторов в батарее.
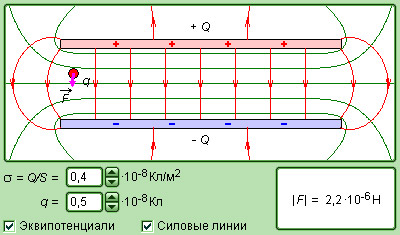
Рисунок 1.6.5. Смоделированное электрическое поле плоского конденсатора.
