Электромагнитные колебания и волны Основные формулы
-
Формула Томсона
Период
собственных колебаний в контуре без
активного сопротивления
![]()
![]()
–
индуктивность контура;
![]()
– электроемкость контура.
-
Связь длины электромагнитной волны с периодом т и частотой колебаний
![]()
![]()
![]()
–
скорость электромагнитной волны в
вакууме.
-
Скорость электромагнитной волны в среде с диэлектрической проницаемостью и магнитной проницаемостью
![]()
Пример.
Колебательный контур,
состоящий из воздушного конденсатора
с двумя пластинами площадью 0,01 м2
каждая и катушки с индуктивностью 1
мкГн. Резонирует на длину волны 10 м.
Определить расстояние между пластинами
конденсатора.
|
Дано: |
Решение: |
|
|
Электроемкость
Из
|
|
|
Из
соотношения
![]()
найдем
![]()
(3)
Подставляя
(3) в (2). А затем полученное выражение в
(1), получим для d
![]()
Вычисления:
![]()
Проверка
размерностей:

Ответ:
![]()
Задачи для самостоятельного решения
-
Катушка
индуктивностью 1 мГн и конденсатор
электроемкостью 500 мкФ соединены
параллельно. Найти период колебаний в
контуре. -
Колебательный
контур состоит из параллельно соединенных
конденсатора электроемкостью 1 мкФ и
катушки индуктивностью 1 мГн. Найти
частоту колебаний. -
Индуктивность
колебательного контура равна 0,5 мГн.
Какова должна быть электроемкость
контура, чтобы он резонировал на длину
волны 300 м.? -
На
какую длину волны будет резонировать
контур, состоящий из катушки индуктивностью
4 мкГн и конденсатора электроемкостью
1 нФ? -
Определить
скорость электромагнитных волн в
парафине, если его диэлектрическая
проницаемость

и магнитная проницаемость
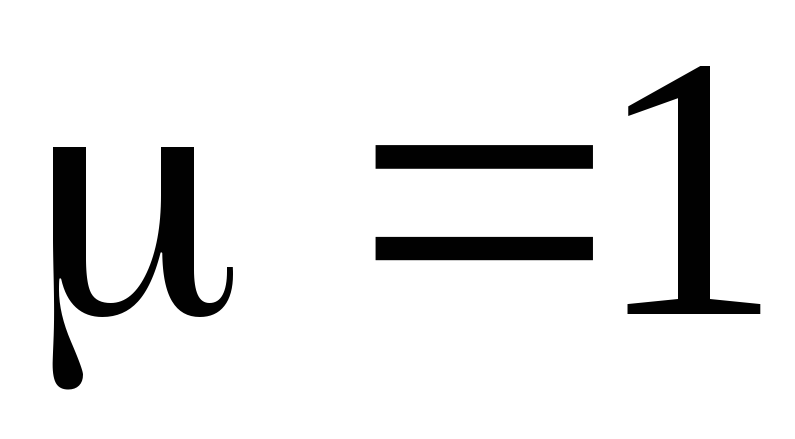 .
. -
Найти
диапазон длин волн радиоприемника,
если во входном колебательном контуре
индуктивность L=0,1 мГн, а
емкость меняется от 10-12 Ф до10-10
Ф.
5.
оптика
Геометрическая оптика и фотометрия Основные формулы

-
Закон
отражения света
![]()
![]()
–
угол падения;
![]()
– угол отражения.
-
Закон
преломления света

![]()
–
угол падения;
![]()
– угол преломления;
![]()
– относительный показатель преломления
второй среды относительно первой;
![]()
и
![]()
– абсолютные показатели преломления
первой и второй сред.
-
Предельный
угол полного внутреннего отражения
![]()
-
Оптическая
сила тонкой линзы D
![]()
![]()
f
– фокусное расстояние линзы;
![]()
– абсолютный показатель преломления
вещества линзы;
![]()
– абсолютный показатель среды;
![]()
– относительный показатель преломления
вещества линзы относительно среды;
радиусы выпуклых поверхностей линзы
![]()
и
![]()
берутся со знаком плюс, вогнутых со
знаком минус.
-
Формула
тонкой линзы
![]()
a
– расстояние от оптического центра
линзы до предмета; b
– расстояние от оптического центра до
изображения; если фокус мнимый (линза
рассеивающая), то фокусное расстояние
f<0.
-
Основные
формулы фотометрии
Полный
световой поток Ф
![]()
![]()
I
– сила света источника.
Освещенность
поверхности Е
![]()
![]()
Ф
– световой поток,
падающий на поверхность S;
S
– площадь поверхности.
Освещенность,
создаваемая изотропным точечным
источником света
![]()
r
– расстояние от поверхности до источника;
![]()
– угол падения лучей.
Сила
света
![]()

Ф
– поток излучения
точечного источника к телесному углу
в пределах которого это излучение
распространяется.
Яркость
В светящейся поверхности в
некотором направлении
![]()
![]()
S
– площадь проекции
светящейся поверхности на плоскость,
перпендикулярную направлению .
Светимость
R
![]()
![]()
Ф
– световой поток,
испускаемый поверхностью; S
– площадь поверхности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Физика,
вопрос задал zavrja,
8 лет назад
Как из формулы Томпсона можно вычислить електроёмкость?
Ответы на вопрос
Ответил Аноним
0
Как из формулы Томпсона можно вычислить електроёмкость?
T= 2pi*√(LC)
T/2pi=√(LC)
(T/2pi)^2=LC
C=(T/2pi)^2/L
Предыдущий вопрос
Следующий вопрос
Новые вопросы
Математика,
5 лет назад
76.x = 38.50
12 · (x + 9x) = 480…
История,
5 лет назад
Какие нравственные уроки дают нам древнеримские басни?
Литература,
8 лет назад
Какие уроки должен был извлечь древнерусский читатель из произведений о ” Житие Сергия Радонежского “?
Алгебра,
8 лет назад
2х+9=13-х решите уравнение…
Физика,
8 лет назад
помогите решить пожалуйста 1. Детский шар,V = 0,003 м. куб. наполнен водородом, m шара+m в =3,4 грамма,какова подъемная сила? 2. зонд V=10 м.куб,наполен водородом,какого веса радиоаппаратуру он может…
Физика,
8 лет назад
1. В чем причина преломления света? 2. Какое среды называют имеющим большую оптическую плотность?
На прошлом уроке мы с вами познакомились с электромагнитными
колебаниями. Напомним, что так называют периодические изменения со временем
электрических и магнитных величин в электрической цепи.
Рассмотрев качественную сторону теории процессов в
колебательном контуре, перейдём к её количественной стороне. Для этого рассмотрим
идеальный колебательный контур, то есть контур, активное сопротивление
которого пренебрежимо мало.
В таком контуре, как мы показали ранее, полная
электромагнитная энергия в любой момент времени равна сумме энергий
электрического и магнитного полей, и она не меняется с течением времени:
А раз энергия контура неизменная, то производная полной
энергии по времени равна нулю:
Напомним, что в записанной формуле заряд и сила тока в цепи
являются функцией времени.
Чтобы понять физический смысл этого уравнения, перепишем его
так:
Из такой записи видно, что скорость изменения магнитного
поля по модулю равна скорости изменения энергии электрического поля. А знак
минус в формуле показывает на то, что увеличение энергии магнитного поля
происходит за счёт убыли энергии поля электрического.
Вычислим производные в записанном уравнении, воспользовавшись
для этого формулой вычисления производной сложной функции.
А теперь вспомним, что производная заряда по времени есть
сила мгновенного тока (то есть сила тока в данный момент времени):
Поэтому предыдущее уравнение можно переписать так, как показано
на экране:
Производная силы тока по времени есть не что иное, как вторая
производная заряда по времени, подобно тому, как производная скорости по
времени (то есть ускорение) есть вторая производная координаты по времени:
Перепишем предыдущее равенство с учётом этой поправки:
Разделив левую и правую части этого уравнения на «Эль И» (Li),
получим основное уравнение, описывающее свободные гармонические
электрические колебания в контуре:
Данное уравнение аналогично уравнению, описывающему
гармонические механические колебания:
Отсюда видно, что величина, обратная квадратному корню из
произведения индуктивности и ёмкости, является циклической частотой свободных
электрических колебаний:
Зная циклическую частоту колебаний, нетрудно найти и их
период, то есть минимальный промежуток времени, через который процесс в
колебательном контуре полностью повторяется:
Эта формула впервые была получена английским физиком Уильямом
Томсоном 1853 году, и в настоящее время носит его имя.
Из формулы видно, что период колебательного контура
определяется параметрами составляющих его элементов: индуктивностью катушки и
ёмкостью конденсатора. Из формулы Томсона также следует, что, например, при
уменьшении ёмкости или индуктивности период колебаний должен уменьшиться, а их
частота — увеличиться и наоборот.
Но вернёмся к уравнению свободных электромагнитных колебаний
в идеальном колебательном контуре. Его решением является уравнение, выражающее
зависимость заряда конденсатора от времени:
В записанной формуле qm — это начальное
(или амплитудное) значение заряда, сообщённому конденсатору. Из этой формулы
следует, что заряд на конденсаторе изменяется со временем по гармоническому
закону.
Если взять первую производную заряда конденсатора по времени,
то мы получим уравнение, описывающее изменение силы тока в контуре:
Величина, равная произведению максимального заряда
конденсатора и циклической частоты колебаний, является амплитудным значением
силы тока:
Перепишем уравнение для силы тока с учётом последнего
равенства, а также воспользовавшись формулой приведения:
Из такой записи хорошо видно, что сила тока в колебательном
контуре также совершает гармонические колебания с той же частотой, но по фазе
она смещена на π/2 относительно колебаний заряда.
Для закрепления материала, решим с вами такую задачу. Конденсатор
ёмкостью 2 мкФ зарядили до напряжения 100 В, а затем замкнули на катушку с
индуктивностью 5 мГн. Определите заряд конденсатора через 0,025π мс после
замыкания.
В заключение отметим, что в реальных колебательных контурах всегда
имеется активное сопротивление, поэтому часть энергии контура всегда превращается
во внутреннюю проводников, которая выделяется в виде излучения. Кроме того,
часть энергии теряется на перемагничивание сердечника и изменение поляризации
диэлектрика. Поэтому полная энергия контура с течением времени уменьшается, в
результате уменьшается и амплитуда колебаний. Следовательно, реальные
электромагнитные колебания в контуре являются затухающими.
