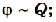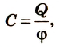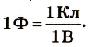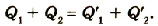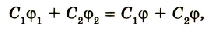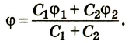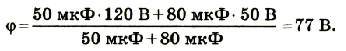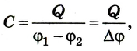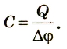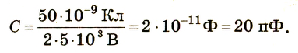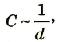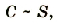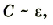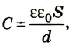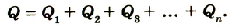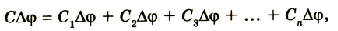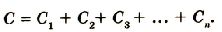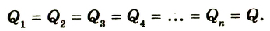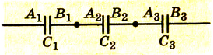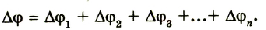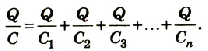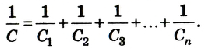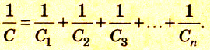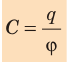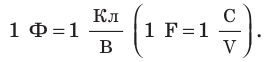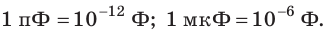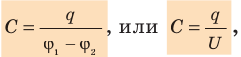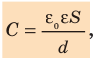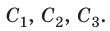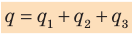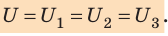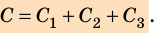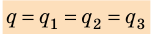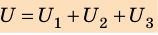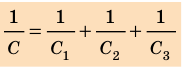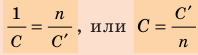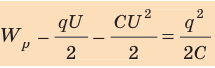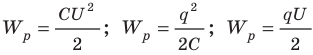Как найти электроемкость по графику

Содержание:

Электроемкость:

Сообщая телу определенный заряд, мы изменяем его потенциал. Это изменение непосредственно связано со значением заряда, сообщаемого телу.

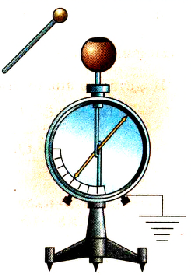
Для исследования зависимости потенциала тела от его заряда проведем опыт с электрометром, корпус которого соединен с поверхностью Земли. ‘Гикая система может измерять потенциал тела относительно Земли. Укрепим на стержне этого электрометра пустотелый металлический шар и будем сообщать ему заряд с помощью маленького металлического шарика на изоляционной ручке. Если коснуться заряженным шариком внутренней поверхности металлического шара, то весь его заряд перейдет на шар, а стрелка электрометра покажет увеличение потенциала шара. Последовательно повторяя опыт с переносом заряда на большой шар, заметим, что каждый раз его потенциал увеличивается (рис. 1.28).

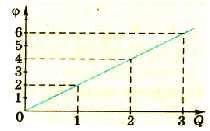
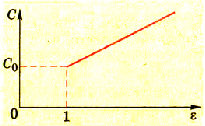
Применяя более точные способы измерения заряда и потенциала, можно установить, что потенциал возрастает пропорционально возрастанию заряда. Потенциал пропорционален заряду шара. Результаты одного из таких опытов отражены на графике (рис 1.29).

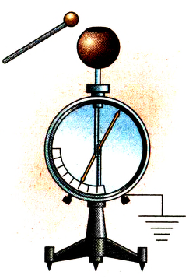
Если ни стержне электрометра укрепим шар большего (меньшего) диаметра и продолжим опыты (рис. 1.31), то увидим, что скорость зарядки изменилась, соответственно уменьшилась (увеличилась).
Процесс электризации шара большего диаметра отображен графиком на рисунке 1.32.

Сопоставив графики, которые иллюстрируют процессы зарядки шаров различных диаметров (рис. 1.30 и 1.32), увидим, что графики имеют различный наклон относительно горизонтальной оси. Это свидетельствует о том, что при одинаковых значениях заряда шары разных диаметров будут иметь разные потенциалы. Оказывается, что на князь между зарядом и потенциалом шара существенно влияют геометрические размеры шаров.

Рис. 130. Электризация шара большего диаметра

Потенциал металлического шара пропорционален его заряду; коэффициент пропорциональности для различных шаров разный.

Анализируя результаты опытов и соответствующие графики, можно сделать выводы:

1. потенциал каждого шара пропорционален его заряду: 
2. для тел различных размеров коэффициент пропорциональности разный.

Установлено, что этот коэффициент для каждого тела имеет вполне определенное значение, что отражает способность тела накапливать электрический заряд. Физическая величина, равная отношению электрического заряда, сообщенного телу, к его потенциалу, называется электроемкостью тела.

где C – электроемкость проводника; Q – заряд; φ – потенциал.

Для измерения электроемкости в физике применяют единицу, которую называют фарад (Ф).

Тело имеет электроемкость в 1 фарад, если при изменении его заряда на 1 кулон потенциал изменяется па 1 вольт:

Электроемкость 1 фарад имеют тела, у которых при изменении заряда на 1 кулон потенциал изменяется на 1 вольт.

• 1Ф – довольно большое значение электроемкости. Например, электроемкость Земли, имеющей радиус 6400 км, составляет всего 7 ∙ 10⁴ Ф. Поэтому на практике используют единицу электроемкости, кратную фараду:
• 1 микрофарад = 1 мкФ = 10^-5 Ф.
• 1 пикофарад = 1 пФ = 10^-12 Ф.

Пример:

Два шара, электроемкости которых 50 мкф и 80 мкФ, а потенциалы 120 В и 50 В соответственно, соединяют проводом. Найти потенциал шаров после соединения.

Дано:  C1 = 50 мкФ, C2 = 80 мкФ, φl = 120 В, φ2 = 50 В.	Решение Заряд каждого шара соответственно равен: Q1 = C1φ1. Q2=c2φ2∙
φ-?

После соединения шаров произойдет перераспределение зарядов между ними так, что их потенциалы станут одинаковыми. Согласно закону сохранения электрических зарядов

Отсюда

или

Подставив значения физических величин и произведя расчеты, получим:

Ответ: после соединения шары будут иметь потенциал 77 В.

Конденсатор

Чтобы экспериментально определить электроемкость проводника, как и его потенциал, нужно создать условия, исключающие влияние всех окружающих тел, которые, влияя па тело, изменяют его потенциал и электроемкость.

Это утверждение можно проверить опытом.
Укрепим на стержне электрометра металлический шар и сообщим ему определенный заряд. Стрелка прибора отклонится от положения равновесия и покажет определенное значение потенциала относительно земли.

Поднесем к шару металлическую пластину, соединенную проводником с землей (рис. 1.32).

Pиc. 132. Заземленная металлическая пластина влияет на электроемкость шара

Показания стрелки электрометра уменьшатся. Поскольку заряд шара в опыте не изменялся, то уменьшение потенциала свидетельствует об увеличении электроемкости шара. Изменение потенциала и соответственно электроемкости шара будет наблюдаться и в случае изменения расстояния между шаром и пластиной.

Таким образом, определяя электроемкость тела, необходимо учитывать также наличие окружающих тел. Поскольку на практике это сделать трудно, то применяют систему из двух или более проводников произвольной формы, разделенных диэлектриком. В этом случае электрические свойства такой системы проводников и диэлектрика не зависят от окружающих тел. Такую систему называют конденсатором. Простейшим для изучения и расчетов является конденсатор из двух металлических пластин, разделенных диэлектриком.

Электроемкость конденсатора, в отличие от обособленного тела, определяется по разности потенциалов между пластинами:

где Q – заряд одной пластины; (φ_l– φ₂) и ∆φ – разность потенциалов между пластинами.

Слово конденсатор обозначает накопитель. В электричестве понимают как «накопитель электрических зарядов».

Пример:

Какую электроемкость имеет конденсатор, если на его обкладках накапливается заряд 50 нКл при разности потенциалов 2,5 кВ?

Дано: Q = 50 нКл, Аφ = 2,5 кВ.	Решение Используем формулу емкости конденсатора:
С-?

Подставим значения физических величин:

Ответ: электроемкость данного конденсатора 20 пФ.

Первый конденсатор был создан в 1745 г. голландским ученым Питером ван Мушенбруком, профессором Лейденского университета. Проводя опыты по электризации различных тел, он опустил проводник от кондуктора электрической машины в стеклянный графин с водой (рис. 1.33).

Питер ван Мушенбрук (1692-1781) – голландский физик; работы посвящены электричеству, теплоте, оптике; изобрел первый конденсатор – лейденскую банку и провел опыты с ней.

Pиc. 133. Из истории открытия простейшего конденсатора лейденской банки

Случайно коснувшись пальцем этого проводника, ученый ощутил сильный электрический удар. В дальнейшем жидкость заменили металлическими проводниками, укрепленными на внутренней и внешней поверхностях банки. Такой конденсатор назвали лейденской банкой. В таком первозданном виде она использовалась в лабораториях более 200 лет.

Более совершенные конденсаторы применяются в современной электротехнике и радиоэлектронике. Их можно найти в преобразователях напряжения (адаптерах), питающих постоянным электрическим током электронные приборы, в радиоприемниках и радиопередатчиках как поставные части колебательных контуров. Они применяются практически во всех функциональных узлах электронной аппаратуры. В фотовспышках конденсаторы накапливают большие заряды, необходимые для действия вспышки.

В электротехнике конденсаторы обеспечивают необходимый режим работы электродвигателей, автоматических и релейных приборов, линий электропередач и т. п.

Во многих широкодиапазонных радиоприемниках конденсаторы переменной емкости (рис. 1.34) позволяют плавно изменять собственную частоту колебательного контура н процессе поиска передачи определенной радиостанции.

Рис. 134. Конденсатор переменной емкости с воздушным диэлектриком

Весьма распространены конденсаторы варикапы, электроемкость которых можно изменять электрическим способом. Конструктивно они весьма схожи с полупроводниковыми диодами.

Конденсаторы могут быть плоскими, трубчатыми, дисковыми. В качестве диэлектрика в них используют парафинированную бумагу, слюду, воздух, пластмассы, керамику (рис. 1.35).

Рис. 1.35. Различные типы конденсаторов

Искусственно созданные диэлектрические материалы позволяют создавать конденсаторы больших емкостей при небольших размерах.

Электроемкость плоского конденсатора

Плоским конденсатором обычно называют систему плоских проводящих пластин – обкладок, разделенных диэлектриком. Благодаря простоте конструкции такого конденсатора легко рассчитывать его емкость и получать значения, подтверждаемые опытами. Для этого достаточно знать его геометрические параметры и электрические свойства диэлектрика между его пластинами. Зависимость электроемкости плоского конденсатора от указанных параметров можно исследовать в школьной лаборатории.

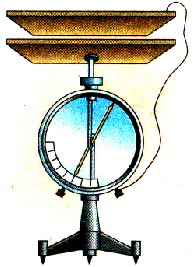
Создадим плоский конденсатор из двух плоских пластин. Для этого одну пластину укрепим на стержне электрометра, я другую — па изоляционной подставке, присоединив ее проводником к корпусу электрометра (рис. 1.36.). В такой системе электрометр будет измерять разность потенциалов между пластинами, образующими плоский конденсатор.

При постоянном значении заряда на пластинах уменьшение разности потенциалов свидетельствует об увеличении электроемкости конденсатора, и наоборот.

Сообщим пластинам некоторый заряд и отметим показания стрелки прибора. Когда начнем сближать пластины, уменьшая расстояние между ними, показания стрелки начнут уменьшаться. Это будет свидетельством того, что при уменьшении расстояния между пластинами электроемкость конденсатора будет увеличиваться. При увеличении расстояния между пластинами показания стрелки будут увеличиваться, что свидетельствует об уменьшении электроемкости.

Электроемкость плоского конденсатора обратно пропорциональна расстоянию между его обкладками.

где d – расстояние между обкладками.

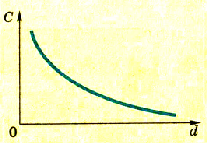
Эту, зависимость можно изобразить на графике как обратно пропорциональную зависимость (рис. 1.37).

Электроемкость плоского конденсатора обратно пропорциональна расстоянию между его обкладками.

Pиc. 137. График зависимости электроемкости и плоского конденсатора от расстояния между пластинами

Будем смещать одну пластину относительно другой в параллельных плоскостях, не изменяя расстояния между ними. При атом площадь перекрытия между пластинами будет изменяться (рис. 1.38). Изменение разности потенциалов, отмеченное электрометром, засвидетельствует изменение электроемкости.

Pиc. 138. При расчетах электроемкости плоского конденсатора учитывают площадь перекрытия пластин

Увеличение площади перекрытия приведет к увеличению электроемкости, при уменьшении – наоборот.

Электроемкость плоского конденсатора пропорциональна площади пластин, которые перекрываются.

где S – площадь пластин, которые перекрываются.

Электроемкость плоского конденсатора пропорциональна площади пластин, которые перекрываются.

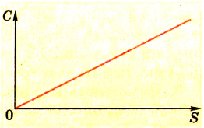
Эту зависимость можно изобразить графиком прямой пропорциональной зависимости (рис. 1.39).

Pиc. 139. График зависимости электроемкости плоского конденсатора от площади его пластин

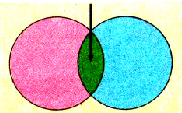
Возвратив пластины в первоначальное положение, внесем в пространство между обкладками пластину из диэлектрика. Электрометр отметит уменьшение разности потенциалов между пластинами, что свидетельствует об увеличении электроемкости. Если внести пластину из другого диэлектрика (другая диэлектрическая проницаемость), то изменение электроемкости будет другим.

Электроемкость плоского конденсатора зависит от диэлектрической проницаемости диэлектрика между обкладками.

где ε – диэлектрическая проницаемость диэлектрика.

Эта зависимость изображена графиком на рисунке 1.40.

Рис. 1.40. График зависимости электроемкости плоского конденсатора от диэлектрической проницаемости диэлектрика

Результаты описанных выше исследований можно обобщить формулой электроемкости плоского конденсатора

где ε – относительная диэлектрическая проницаемость диэлектрика; ε₀– электрическая постоянная; d – расстояние между пластинами; S – площадь пластины.

Электроемкость плоского конденсатора зависит от диэлектрической проницаемости диэлектрика.

Соединение конденсаторов в батареи

Для получения необходимых значений электроемкости конденсаторы соединяют в батареи. На практике встречается параллельное, последовательное и смешанное соединение конденсаторов.

При параллельном соединении конденсаторов все обкладки соединяются в две группы, в каждую из которых входит по одной обкладке каждого конденсатора. На рисунке 1.41 приведена схема такого соединения. При таком соединении каждая группа обкладок имеет одинаковый потенциал.

Pиc 1.41. Схема параллельного соединения конденсаторов

Если батарею параллельно соединенных конденсаторов зарядить, то между обкладками каждого конденсатора будет одинаковая разность потенциалов. Общий заряд батареи будет равен сумме зарядов каждого из конденсаторов, входящих в батарею:

Если учесть, что 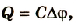 то

или

Электроемкость батареи параллельно соединенных конденсаторов равна сумме электроемкостей всех конденсаторов.

При последовательном соединении конденсаторов соединяются между собой только две пластины разных конденсаторов. Если в каждом конденсаторе пластины обозначить буквами А и В, то при последовательном соединении пластина B₁ будет соединена с пластиной A₂, пластина B₂ -с пластиной А₃ и т. д. (рис. 1.43).

Если цепочку последовательно соединенных конденсаторов присоединить к источнику тока, то об-
кладка A₁ и обкладка B₁ будут иметь одинаковые по значению заряды +Q и -Q. Благодаря этому все обкладки внутри цепочки будут иметь такие же, но попарно противоположные по знаку заряды:

Pиc. 1.42. Последовательное соединение конденсаторов

Вместе с тем общая разность потенциалов на концах цепочки будет равна сумме разностей потенциалов на каждом конденсаторе:

Учитывая, что 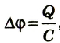 будем иметь

Разделим левую и правую части равенства на Q:

При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно сумме обратных значений электроемкостей каждого из конденсаторов.

При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно с

При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно сумме обратных значений электроемкостей каждого из конденсаторов.

При последовательном соединении конденсаторов разной электроемкости C₁, C₂, C₃, … С_n общая электроемкость С будет меньше электроемкости самого меньшего конденсатора.
Если C₁ < C₇ < C₉ < … < C_n, то C < C₁.

Электроемкость

То, что деньги хранят в банках, знает даже первоклассник. А вот где хранят заряды? И зачем вообще хранить заряды?

Что такое электроемкость

Электроемкость характеризует способность проводника или системы проводников накапливать электрический заряд. Различают электроемкость уединенного проводника и электроемкость системы проводников (например, конденсатора). Уединенным называют проводник, расположенный вдали от других тел так, что они не оказывают на этот проводник никакого влияния.

Электроемкость уединенного проводника (C) — физическая величина, характеризующая способность проводника накапливать заряд и равная отношению электрического заряда q проводника к его потенциалу М:

Единица электроемкости в Си — фарад: [C] = 1 Ф (названа в честь М. Фарадея).

1 Ф — это электроемкость такого проводника, потенциал которого равен 1 В при сообщении ему заряда 1 Кл;

1 Ф — очень большая единица емкости, поэтому используют дольные единицы:

Что такое конденсатор

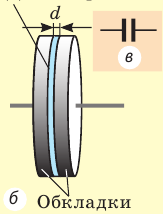
Конденсатор — устройство, представляющее собой систему из двух проводящих обкладок, разделенных тонким слоем диэлектрика (рис. 44.1).

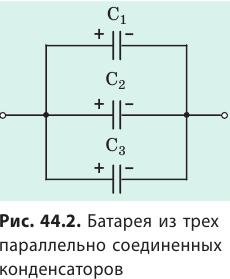
Рис. 44.1. Школьный воздушный конденсатор: а — вид; б — устройство; в — обозначение на схемах

Обкладкам конденсатора передают одинаковые по модулю, но противоположные по знаку заряды, что способствует накоплению зарядов: разноименные заряды притягиваются, а значит, располагаются на внутренних поверхностях обкладок.

Обычно для зарядки конденсатора обе его обкладки соединяют с полюсами батареи аккумуляторов: на обкладках появляются равные по модулю, но противоположные по знаку заряды. Результат не изменится, если соединить с полюсом батареи только одну обкладку, заземлив вторую: вследствие электростатической индукции на заземленной обкладке тоже появится заряд, равный по модулю заряду на другой обкладке, но имеющий противоположный знак.

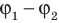
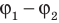
Зарядом конденсатора называют модуль заряда одной из обкладок. Отношение заряда q данного конденсатора к разности потенциалов () между его обкладками не зависит ни от значения q, ни от разности потенциалов (), а значит, может служить характеристикой конденсатора. Такую характеристику называют электроемкостью (емкостью) конденсатора:

где U — напряжение между обкладками: .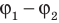

Как показывают исследования, емкость конденсатора увеличится, если увеличить площадь поверхности обкладок или приблизить обкладки друг к другу. На емкость конденсатора влияет также диэлектрик: чем больше его диэлектрическая проницаемость, тем большую емкость имеет конденсатор.

Конденсатор, состоящий из двух параллельных металлических пластин (обкладок), разделенных слоем диэлектрика, называют плоским (см. рис. 44.1). Электроемкость плоского конденсатора вычисляют по формуле:

где 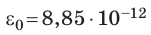Ф/м — электрическая постоянная; ε — диэлектрическая проницаемость диэлектрика; S — площадь пластины конденсатора; d — расстояние между пластинами.

Поле между пластинами плоского конденсатора однородно, поэтому напряженность Е поля связана с напряжением U на конденсаторе формулой U=Ed.

Как рассчитывают электроемкость батареи конденсаторов

Конденсаторы характеризуются емкостью и максимальным рабочим напряжением Umax. Если напряжение, поданное на конденсатор, значительно превысит Umax, произойдет пробой — между обкладками возникнет искра, которая разрушит изоляцию.

Чтобы получить необходимую электроемкость при определенном рабочем напряжении, конденсаторы соединяют в батареи, применяя параллельное, последовательное и смешанное соединения. Рассмотрим батарею из трех конденсаторов электроемкостями

При параллельном соединении конденсаторов положительно заряженные обкладки всех конденсаторов соединяют в один узел, а отрицательно заряженные — в другой узел (рис. 44.2). В таком случае общий заряд q батареи конденсаторов равен алгебраической сумме зарядов отдельных конденсаторов:

Соединенные в один узел обкладки представляют собой один проводник, поэтому потенциалы обкладок, а следовательно, и разность потенциалов (напряжение) между обкладками всех конденсаторов одинаковы:

Таким образом, при параллельном соединении конденсаторов допустимое рабочее напряжение батареи определяется рабочим напряжением одного конденсатора.

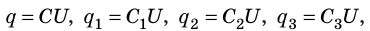
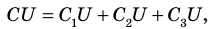
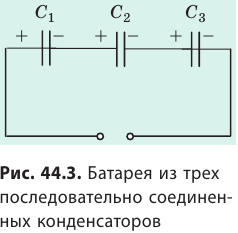
Поскольку то следовательно, электроемкость батареи из трех параллельно соединенных конденсаторов равна:

При последовательном соединении конденсаторы соединяют друг с другом разноименно заряженными обкладками (рис. 44.3). В этом случае заряды всех конденсаторов будут одинаковы и равны заряду батареи:

Напряжение на батарее последовательно соединенных конденсаторов равно сумме напряжений на отдельных конденсаторах:

Таким образом, допустимое рабочее напряжение батареи последовательно соединенных конденсаторов больше допустимого рабочего напряжения отдельного конденсатора. Электроемкость батареи последовательно соединенных конденсаторов вычисляют по формуле:

При последовательном соединении конденсаторов емкость батареи меньше, чем емкость конденсатора с минимальной емкостью.

Приведенные соотношения можно обобщить для любого количества конденсаторов.

Обратите внимание!

• Если батарея содержит n параллельно соединенных конденсаторов электроемкостью C′ каждый, то: C=nC′
• Если батарея содержит n последовательно соединенных конденсаторов электроемкостью C′ каждый, то:

Энергия заряженного конденсатора

Заряженный конденсатор, как и любая другая система заряженных тел, обладает энергией.

Убедимся в этом с помощью простого эксперимента. Присоединим к обкладкам заряженного конденсатора лампочку. Замкнем ключ — лампочка загорится. Теперь измерим напряжение на обкладках конденсатора — оно равно нулю, то есть конденсатор разрядился, а это означает, что заряженный конденсатор обладал энергией, которая частично превратилась в энергию света.

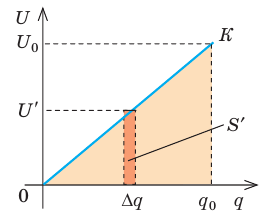
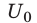
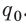
Вычислим энергию заряженного до напряжения конденсатора емкостью С, на котором накоплен заряд . Эту энергию точнее было бы назвать энергией электростатического поля, которое существует между обкладками заряженного конденсатора, поскольку энергия любых заряженных тел сосредоточена в электрическом поле, создаваемом этими телами.

При разрядке конденсатора напряжение U на его обкладках изменяется прямо пропорционально заряду q конденсатора: 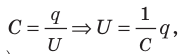поэтому график зависимости U(q) имеет вид, представленный на рис. 44.4.

Рис. 44.4. К определению работы, которую совершает электрическое поле заряженного конденсатора при его разрядке

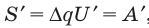
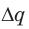
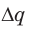
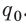
Мысленно разделим весь заряд конденсатора на маленькие «порции» Dq и будем считать, что при потере каждой такой «порции» напряжение на конденсаторе не изменяется. Таким образом получим ряд полос. Площадь S′ каждой полосы равна произведению двух ее сторон: , где U′ — напряжение, при котором конденсатор терял данную «порцию» заряда ; A′ — работа, которую совершило поле при потере конденсатором заряда . Полная работа, которую совершило поле при уменьшении заряда конденсатора от до 0, определяется площадью выделенного на рис. 44.4 треугольника.

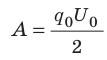
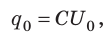
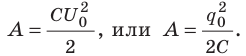
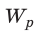
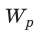
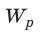
Следовательно,. Учитывая, чтополучим: С другой стороны, данная работа равна уменьшению энергии электрического поля конденсатора от до нуля: A= − 0 = W. Таким образом, энергия заряженного до напряжения U конденсатора, имеющего электроемкость С и заряд q, равна:

Для чего нужны конденсаторы

В современной технике сложно найти отрасль, где не применялись бы конденсаторы. Без них не обходятся радио­ и телеаппаратура (настройка колебательных контуров), радиолокационная и лазерная техника (получение мощных импульсов), телефония и телеграфия (разделение цепей переменного и постоянного токов, тушение искр в контактах), электроизмерительная техника (создание образцов емкости). И это далеко не полный перечень.

В современной электроэнергетике конденсаторы тоже имеют широкое применение: они присутствуют в конструкциях люминесцентных светильников, электросварочных аппаратов, устройств защиты от перенапряжений. Конденсаторы применяют и в других, не электротехнических, областях техники и промышленности (в медицине, фототехнике и т. д.).

Разнообразие областей применения обусловливает большое разнообразие конденсаторов. Наряду с миниатюрными конденсаторами, имеющими массу меньше грамма, а размеры порядка нескольких миллиметров, существуют конденсаторы массой несколько тонн и высотой больше человеческого роста. Емкость современных конденсаторов может составлять от долей, а рабочее напряжение может быть в пределах от нескольких вольт до нескольких сотен киловольт. Конденсаторы можно классифицировать по следующим признакам и свойствам:

• по назначению — постоянной и переменной емкости;
• по форме обкладок — плоские, сферические, цилиндрические и др.;
• по типу диэлектрика — воздушные, бумажные, слюдяные, керамические, электролитические и др.

Выводы:

• Энергию заряженного конденсатора можно вычислить по формулам:
• Конденсаторы классифицируют по назначению (постоянной и переменной емкости); по форме обкладок (плоские, сферические, цилиндрические и др.); по типу диэлектрика (воздушные, бумажные, слюдяные, керамические, электролитические и др.).

Плоским конденсатором обычно называ­ют систему плоских проводящих пластин — обкладок, разделенных диэлектриком. Про­стота конструкции такого конденсатора по­зволяет сравнительно просто рассчитывать его электроемкость и получать значения, совпадающие с результатами эксперимента.

Рис. 4.71. Плоский конденсатор на элект­рометре

Укрепим две металлические пластины на изоляционных подставках и соединим с электрометром так, что одна из пластин будет присоединена к стержню электромет­ра, а вторая — к его металлическому кор­пусу (рис. 4.71). При таком соединении электрометр будет измерять разность по­тенциалов между пластинами, которые об­разуют плоский конденсатор из двух пла­стин. Проводя исследования, необходимо пом­нить, что

при постоянном значении заряда пластин уменьшение разности потенциалов свидетельствует об увеличении электроем­кости конденсатора, и наоборот.

Сообщим пластинам разноименные заря­ды и отметим отклонение стрелки электро­метра. Приближая пластины друг к другу (уменьшая расстояние между ними), заме­тим уменьшение разности потенциалов. Та­ким образом, при уменьшении расстояния между пластинами конденсатора его элект­роемкость увеличивается. При увеличении расстояния показания стрелки электрометра увеличиваются, что является свидетельст­вом уменьшения электроемкости.

Электроемкость плоского конденсатора об­ратно пропорциональна расстоянию между его обкладками.

C ~ 1 / d,

где d — расстояние между обкладками.

Рис. 4.72. График зависимости емкости плоского конденсатора от расстояния между пластинами

Рис. 4.73. При расчетах емкости плоских конденсаторов учитывают площадь пере­крытия пластин

Эту зависимость можно изобразить гра­фиком обратной пропорциональной зависи­мости (рис. 4.72).

Будем смещать пластины одну относи­тельно другой в параллельных плоскостях, не изменяя расстояния между ними.

При этом площадь перекрытия пластин будет уменьшаться (рис. 4.73). Увеличение разности потенциалов, отмеченное электрометром, будет свидетельствовать об умень­шении электроемкости.

Увеличение площади перекрытия пластан приведет к увеличению емкости.

Электроемкость плоского конденсатора про­порциональна площади пластин, которые пере­крываются.

C ~ S,

где S — площадь пластин.

Рис. 4.74. График зависимости емкости плоского конденсатора от площади его пластин

Эту зависимость можно представить гра­фиком прямой пропорциональной зависи­мости (рис. 4.74). 

Возвратив пластины в начальное поло­жение, внесем в пространство между ними плоский диэлектрик. Электрометр отметит уменьшение разности потенциалов между пластинами, что свидетельствует об увели­чении электроемкости конденсатора. Если между пластинами поместить другой диэлек­трик, то изменение электроемкости будет иным.

Электроемкость плоского конденсатора за­висит от диэлектрической проницаемости ди­электрика.

C ~ ε,

где ε — диэлектрическая проницаемость ди­электрика. Материал с сайта http://worldofschool.ru

Рис. 4.75. График зависимости емкости плоского конденсатора от диэлектри­ческой проницаемости диэлектрика

Такая зависимость показана на графике рис. 4.75.

Результаты опытов можно обобщить в ви­де формулы ёмкости плоского конденсатора:

C = εε₀S / d,

где S — площадь пластины; d — расстояние между ними; ε — диэлектрическая прони­цаемость диэлектрика; ε₀ — электрическая постоянная.

Конденсаторы, которые состоят из двух пластин, в практике применяются очень редко. Как правило, конденсаторы имеют много пластин, соединенных между собой по определенной схеме.

Условие задачи:

Определить электроемкость батареи конденсаторов, изображенной на рисунке, если (C_1=2) мкФ, (C_2=4) мкФ.

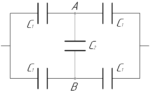
Задача №6.4.43 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(C_1=2) мкФ, (C_2=4) мкФ, (C-?)

Решение задачи:

Обратите Ваше внимание на то, что схема симметричная, а это значит, что потенциалы точек A и B будет одинаковыми. Это означает, что конденсатор с электроемкостью (C_2) будет незаряжен (так как разности потенциалов между его обкладками нет), поэтому этот конденсатор можно легко исключить, и исходная схема примет следующий вид (смотрите рисунок справа).

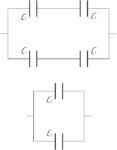
Полученную схему легко преобразовать в другую. Так как два конденсатора в верхней и нижней ветви соединены последовательно, то заменим их эквивалентной электроемкостью (C_3), которую можно найти таким образом:

[frac{1}{{{C_3}}} = frac{1}{{{C_1}}} + frac{1}{{{C_1}}}]

[frac{1}{{{C_3}}} = frac{2}{{{C_1}}}]

[{C_3} = frac{{{C_1}}}{2};;;;(1)]

А так как конденсаторы (C_3) соединены последовательно, то искомая электроемкость (C) равна:

[C = {C_3} + {C_3}]

Учитывая (1), получим:

[C = frac{{{C_1}}}{2} + frac{{{C_1}}}{2}]

[C = {C_1}]

[C = 2;мкФ]

Ответ: 2 мкФ.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.4.42 Найти общую электроемкость соединенных по схеме конденсаторов, если
6.4.44 Батарея из четырех одинаковых конденсаторов включена один раз по схеме A, другой раз по схеме B
6.4.45 Какое количество теплоты выделяется при замыкании пластин конденсатора электроемкостью

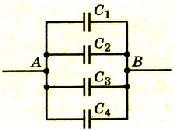
Пусть дана цепь с набором электроёмкостей  (рис. 1).

Проанализируем её: визуально выделяем участки цепи, на которых есть только последовательные или только параллельные соединения конденсаторов. Таких участков три, обозначим их  (рис. 2).

Найдём значения , исходя из параллельности соединения элементов цепи:

(1)

(2)

(3)

Введём обозначения и перерисуем схему (рис. 3).

В полученной схеме опять поищем явно параллельные или последовательные участки. Он один, введём для него обозначение —  (рис. 4).

Найдём значения , пользуясь тем, что элементы цепи соединены последовательно:

(4)

Опять же введём обозначения и перерисуем схему (рис. 5).

И, наконец, последняя схема — классическая: чистое параллельное соединение, общая ёмкость которого:

(5)

Тогда, подставив (1), (2), (3), (4) в (5), получим ответ, только делать мы это не будем, т.к. это громоздко. Получим искомое выражение при условии равенства всех сопротивлений на рисунке 1. Пусть каждое из сопротивлений будет равно . Тогда:

Из (1):

(6)

Из (2):

(7)

Из (3):

(8)

Тогда, при условии (6) и (7), уравнение (4) принимает вид:

=  (9)

Тогда, при условии (8) и (9), уравнение (5) примет вид:

(10)

Таким образом, можно найти полную электроёмкость цепи любой сложности.

Вывод: представленную логику рассуждений можно применять на цепи любой сложности