Электроемкость сферического конденсатора
 Электроемкость сферического конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд.
Электроемкость сферического конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд.
![]() .
.
 Чтобы найти емкость сферического конденсатора, который состоит из двух
Чтобы найти емкость сферического конденсатора, который состоит из двух
концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов будет выглядеть так:
![]() .
.
Подставим данное выражение в формулу электроемкости конденсатора и получим емкость конденсатора для сферического тела:
 .
.
При малой величине зазора, то есть ![]() , а следовательно можно считать, что
, а следовательно можно считать, что ![]() емкость сферического конденсатора будет равна
емкость сферического конденсатора будет равна ![]() . Площадь сферы S = 4πr2 следовательно формула будет совпадать с формулой емкости плоского конденсатора
. Площадь сферы S = 4πr2 следовательно формула будет совпадать с формулой емкости плоского конденсатора ![]() .
.
Формулы:
Энергия конденсатора: ![]() .
.
Ёмкость конденсатора: 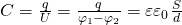 .
.
Ёмкость цилиндрического конденсатора: ![]() .
.
Ёмкость плоского конденсатора: 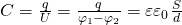 .
.
Обозначения в формулах:
C — электрическая ёмкость (ёмкость конденсатора);
g — заряд;
U — потенциал проводника (напряжение);
φ — потенциал;
ε — относительная диэлектрическая проницаемость;
![]() — электрическая постоянная;
— электрическая постоянная;
S — площадь одной обкладки;
d — расстояние между обкладками;
r2— Больший радиус (от центра, до края конденсатора);
r1 — Малый радиус (Его может и не быть — это пустота).
вернутся в раздел: электрическая ёмкость
Электроемкость сферического конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд.
![]()
Чтобы найти емкость сферического конденсатора, который состоит из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов будет выглядеть так:
![]()
Подставим данное выражение в формулу электроемкости конденсатора и получим емкость конденсатора для сферического тела:
![]()
При малой величине зазора, то есть ![]() , а следовательно можно считать, что
, а следовательно можно считать, что ![]() емкость сферического конденсатора будет равна
емкость сферического конденсатора будет равна ![]() . Площадь сферы
. Площадь сферы ![]() следовательно формула будет совпадать с формулой емкости плоского конденсатора
следовательно формула будет совпадать с формулой емкости плоского конденсатора ![]()
Так же есть:
Энергия конденсатора:![]()
Ёмкость конденсатора : ![]()
Ёмкость цилиндрического конденсатора : ![]()
Емкость плоского конденсатора : ![]() ;
;
В Формуле мы использовали :
![]() — Электроемкость сферического конденсатора
— Электроемкость сферического конденсатора
![]() — Относительная диэлектрическая проницаемость
— Относительная диэлектрическая проницаемость
![]() — Электрическая постоянная
— Электрическая постоянная
![]() — Больший радиус (от центра, до края конденсатора)
— Больший радиус (от центра, до края конденсатора)
![]() — Малый радиус (Его может и не быть — это пустота)
— Малый радиус (Его может и не быть — это пустота)
Конденсатор – это совокупность двух любых проводников, заряды которых одинаковы по значению и противоположны по знаку.
Его конфигурация говорит о том, что поле, созданное зарядами, локализовано между обкладками. Тогда можно записать формулу электроемкости конденсатора:
C=qφ1-φ2=qU.
Значением φ1-φ2=U обозначают разность потенциалов, называемую напряжением, то есть U. По определению емкость положительна. Она зависит только от размерностей обкладок конденсатора их взаиморасположения и диэлектрика. Ее форма и место должны минимизировать воздействие внешнего поля на внутреннее. Силовые линии конденсатора начинаются на проводнике с положительным зарядом, а заканчиваются с отрицательным. Конденсатор может являться проводником, помещенным в полость, окруженным замкнутой оболочкой.
Выделяют три большие группы: плоские, сферические, цилиндрические. Чтобы найти емкость, необходимо обратиться к определению напряжения конденсатора с известными значениями зарядов на обкладках.
Плоский конденсатор
Плоский конденсатор – это две противоположно заряженные пластины, которые разделены тонким слоем диэлектрика, как показано на рисунке 1.
Формула для расчета электроемкости записывается как
C=εε0Sd, где S является площадью обкладки, d – расстоянием между ними, ε – диэлектрической проницаемостью вещества. Меньшее значение d способствует большему совпадению расчетной емкости конденсатора с реальной.
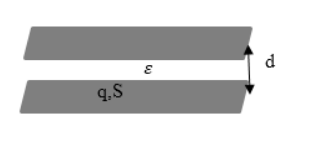
Рисунок 1
При известной электроемкости конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равняется di, вычисление диэлектрической проницаемости этого слоя εi выполняется, исходя из формулы:
C=ε0Sd1ε1+d2ε2+…+dNεN.
Сферический конденсатор
Когда проводник имеет форму шара или сферы, тогда внешняя замкнутая оболочка является концентрической сферой, это означает, что конденсатор сферический.
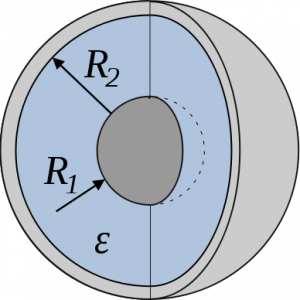
Он состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком, как показано на рисунке 2. Емкость рассчитывается по формуле:
C=4πεε0R1R2R2-R1, где R1 и R2 являются радиусами обкладок.
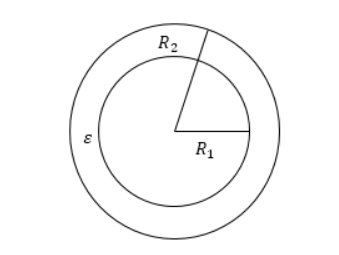
Рисунок 2
Цилиндрический конденсатор
Емкость цилиндрического конденсатора равняется:
C=2πεε0llnR2R1, где l – высота цилиндров, R1 и R2 – радиусы обкладок. Данный вид конденсатора имеет две соосные поверхности проводящих цилиндрических поверхности, как показано на рисунке 3.
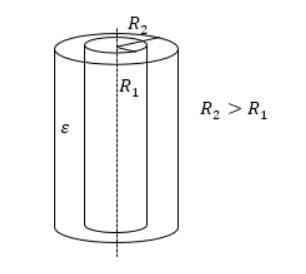
Рисунок 3
Важной характеристикой конденсаторов считается пробивное напряжение – напряжение, при котором происходит электрический разряд через слой диэлектрика.
Umax находится от зависимости от толщины слоя и свойств диэлектрика, конфигурации конденсатора.
Электроемкость плоского конденсатора. Формулы
Кроме отдельных конденсаторов используются их соединения. Наличие параллельного соединения конденсаторов применяют для увеличения его емкости. Тогда поиск результирующей емкости соединения сводится к записи суммы Ci, где Ci- это емкость конденсатора с номером i:
C=∑i=1NCi.
При последовательном соединении конденсаторов суммарная емкость соединения всегда будет по значению меньше, чем минимальная любого конденсатора, входящего в систему. Для расчета результирующей емкости следует сложить величины, обратные к емкостям отдельных конденсаторов:
Произвести вычисление емкости плоского конденсатора при известной площади обкладок
1 см2 с расстоянием между ними 1 мм. Пространство между обкладками находится в вакууме.
Решение
Чтобы рассчитать электроемкость конденсатора, применяется формула:
C=εε0Sd.
Значения:
ε=1, ε0=8,85·10-12 Фм;S=1 см2=10-4 м2;d=1 мм=10-3 м.
Подставим числовые выражения и вычислим:
C=8,85·10-12·10-410-3=8,85·10-13 (Ф).
Ответ: C≈0,9 пФ.
Найти напряженность электростатического поля у сферического конденсатора на расстоянии x=1 см=10-2 м от поверхности внутренней обкладки при внутреннем радиусе обкладки, равном R1=1 см=10-2 м, внешнем – R2=3 см=3·10-2 м. Значение напряжения – 103 В.
Решение
Производящая заряженная сфера создает напряженность поля. Его значение вычисляется по формуле:
E=14πεε0qr2, где q обозначают заряд внутренней сферы, r=R1+x – расстояние от центра сферы.
Нахождение заряда предполагает применение определения емкости конденсатора С:
q=CU.
Для сферического конденсатора предусмотрена формула вида
C=4πεε0R1R2R2-R1 с радиусами обкладок R1 и R2.
Производим подстановку выражений для получения искомой напряженности:
E=14πεε0U(x+R1)24πεε0R1R2R2-R1=U(x+R1)2R1R2R2-R1.
Данные представлены в системе СИ, поэтому достаточно заменить буквы числовыми выражениями:
E=103(1+1)2·10-4·10-2·3·10-23·10-2-10-2=3·10-18·10-6=3,45·104 Вм.
Ответ: E=3,45·104 Вм.
Конденсатор
состоит из двух проводников (обкладок),
которые разделены диэлектриком. На
емкость конденсатора не должны влиять
окружающие тела, поэтому проводникам
придают такую форму, чтобы поле, которое
создавается накапливаемыми зарядами,
было сосредоточено в узком зазоре между
обкладками конденсатора. Этому условию
удовлетворяют: 1) две плоские пластины;
2) две концентрические сферы; 3) два
коаксиальных цилиндра. Поэтому в
зависимости от формы обкладок конденсаторы
делятся на плоские,
сферические и цилиндрические.
Так
как поле сосредоточено внутри конденсатора,
то линии напряженности начинаются на
одной обкладке и кончаются на другой,
поэтому свободные заряды, которые
возникают на разных обкладках, равны
по модулю и противоположны по знаку.
Под емкостьюконденсатора
понимается физическая величина, равная
отношению заряда Q, накопленного в
конденсаторе, к разности потенциалов
(φ1 —
φ2)
между его обкладками:
![]() (1)
(1)
Найдем
емкость плоского конденсатора, который
состоит из двух параллельных металлических
пластин площадью S каждая, расположенных
на расстоянии d друг от друга и имеющих
заряды +Q и –Q. Если считать, что расстояние
между пластинами мало по сравнению с
их линейными размерами, то краевыми
эффектами на пластинах можно пренебречь
и поле между обкладками считать
однородным. Его можно найти используя
формулу потенциала поля двух бесконечных
параллельных разноименно заряженных
плоскостей φ1-φ2=σd/ε0.
Учитывая наличие диэлектрика между
обкладками:
![]() (2)
(2)
где
ε — диэлектрическая проницаемость.
Тогда из формулы (1), заменяя Q=σS, с учетом
(2) найдем выражение для емкости плоского
конденсатора:
![]() (3)
(3)
Для
определения емкости цилиндрического
конденсатора, который состоит из двух
полых коаксиальных цилиндров с радиусами
r1 и
r2(r2 >
r1),
один вставлен в другой, опять пренебрегая
краевыми эффектами, считаем поле
радиально-симметричным и действующим
только между цилиндрическими обкладками.
Разность потенциалов между обкладками
считаем по формуле для разности
потенциалов поля равномерно заряженного
бесконечного цилиндра с линейной
плотностью τ =Q/l (l—длина
обкладок). При наличии диэлектрика между
обкладками разность потенциалов
![]() (4)
(4)
Подставив
(4) в (1), найдем выражение для емкости
цилиндрического конденсатора:
![]() (5)
(5)
Чтобы
найти емкость сферического конденсатора,
который состоит из двух концентрических
обкладок, разделенных сферическим слоем
диэлектрика, используем формулу для
разности потенциалов между двумя
точками, лежащими на расстояниях r1 и
r2 (r2 >
r1)
от центра заряженной сферической
поверхности. При наличии диэлектрика
между обкладками разность потенциалов
![]() (6)
(6)
Подставив
(6) в (1), получим
![]()
Электрическая
ёмкость —
характеристика проводника, мера его
способности накапливать электрический
заряд.
В теории электрических цепей ёмкостью
называют взаимную ёмкость между двумя
проводниками; параметр ёмкостного
элемента электрической схемы,
представленного в виде двухполюсника.
Такая ёмкость определяется как отношение
величины электрического заряда к разности
потенциалов между
этими проводниками.
В
системе СИ ёмкость
измеряется в фарадах.
В системе СГС в сантиметрах.
Для
одиночного проводника ёмкость равна
отношению заряда проводника к его
потенциалу в предположении, что все
другие проводники бесконечно удалены
и что потенциал бесконечно удалённой
точки принят равным нулю. В математической
форме данное определение имеет вид
![]() где
где ![]() — заряд,
— заряд, ![]() —
—
потенциал проводника.
Ёмкость
определяется геометрическими размерами
и формой проводника и электрическими
свойствами окружающей среды (её
диэлектрической проницаемостью) и не
зависит от материала проводника. К
примеру, ёмкость проводящего шара
радиуса Rравна
(в системе СИ):
![]()
где ε0 — электрическая
постоянная, ε — относительная
диэлектрическая проницаемость.
Понятие
ёмкости также относится к системе
проводников, в частности, к системе двух
проводников, разделённых диэлектриком иливакуумом, —
к конденсатору.
В этом случае взаимная
ёмкость этих
проводников (обкладок конденсатора)
будет равна отношению заряда, накопленного
конденсатором, к разности потенциалов
между обкладками. Для плоского конденсатора
ёмкость равна:
![]()
где S —
площадь одной обкладки (подразумевается,
что они равны), d —
расстояние между обкладками, ε — относительная
диэлектрическая проницаемость среды
между обкладками, ε0 =
8.854·10−12 Ф/м — электрическая
постоянная.
Конденса́тор (от лат. condensare —
«уплотнять», «сгущать») — двухполюсник с
определённым значением ёмкости и
малой омической проводимостью;
устройство для накопления заряда и
энергии электрического поля. Конденсатор
является пассивным электронным
компонентом. Обычно состоит из двух
электродов в форме пластин
(называемых обкладками),
разделённых диэлектриком,
толщина которого мала по сравнению с
размерами обкладок.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
2016-12-11 ![]()
Найти электроемкость сферического конденсатора, образованного двумя проводящими концентрическими сферами радиусами $R_{1}$ и $R_{2}$. Рассмотреть также случай, когда пространство между сферами заполнено диэлектриком с диэлектрической проницаемостью $epsilon$.

Решение:
Поместим на внутреннюю сферу заряд $+ q$, на внешнюю — $- q$. Согласно определению электроемкости:
$C = frac{q}{ phi_{A}^{ 0} – phi_{B}^{0}} = frac{q}{U}$, (1)
где $U = phi_{A}^{0} – phi_{B}^{0}$ – разность потенциалов (напряжение) между сферами. Потенциал сферы $R_{1} phi_{A}^{0}$, согласно принципу суперпозиции, складывается из потенциала, создаваемого зарядами $+ q left ( frac{kq}{R_{1}} right )$ и зарядами $- q left ( frac{ – kq}{R_{2}} right )$ в области нахождения сферы $R_{1}$:
$phi_{A}^{0} = frac{kq}{R_{1}} – frac{kq}{R_{2}}$. (2)
Аналогично, потенциал сферы $R_{2} phi_{B}^{0}$ равен:
$phi_{B}^{0} = frac{kq}{R_{2}} – frac{kq}{R_{2}} = 0$. (3)
Из (1—3) находим:
$C = frac{q}{ frac{kq}{R_{1}} – frac{kq}{R_{2}}} = frac{1}{ frac{k}{R_{1}} – frac{k}{R_{2}}}$.
В случае заполнения конденсатора диэлектриком, напряженность электрического поля в каждой точке между сферами уменьшается в в раз. Докажем, что и разность потенциалов так же уменьшается в е раз. Для этого разобьем отрезок радиуса АВ на малые отрезки, такие, что поле на протяжении каждого из них можно считать практически однородным и воспользуемся связью между напряженностью и разностью потенциалов:
$phi_{i} – phi_{i+1} = frac{E_{i}}{ epsilon} Delta d_{i}$, (4)
где $frac{E_{i}}{ epsilon}$ — напряженность электрического поля на участке $Delta d_{i}, E_{i}$ — напряженность в отсутствие диэлектрика. Суммируя (4) по всем $Delta d_{i}$, находим:
$phi_{A} – phi_{B} = frac{1}{ epsilon} sum E_{i} Delta d_{i} = frac{1}{ epsilon} ( phi_{A}^{0} – phi_{B}^{0})$. (5)
Подставляя (5) в определение электроемкости (1), Получаем:
$C = frac{ epsilon}{ frac{k}{R_{1}} – frac{k}{R_{2}}} = frac{4 pi epsilon_{0} epsilon}{ frac{1}{R_{1}} – frac{1}{R_{2}}}$
$C = frac{ epsilon}{ frac{k}{R_{1}} – frac{k}{R_{2}}} = frac{ epsilon}{k} frac{R_{1} R_{2}}{ (R_{1} – R_{2}) }$.
Другой способ вычисления разности потенциалов между сферами при наличии диэлектрика основан на применении результата задачи 1535 с учетом того, что наличие на внешней сфере заряда – $q^{ prime}$ дает одинаковую добавку как к потенциалу внешней сферы, так и внутренней. Таким образом, разность потенциалов, вычисленную с учетом 1535, следует подставить в определение (1).
