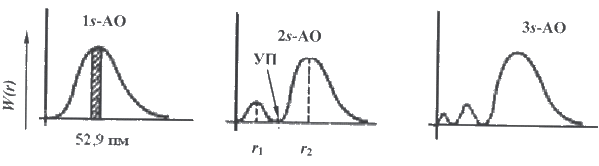Как найти электронную плотность

Электро́нная пло́тность — плотность вероятности обнаружения электрона в данной точке конфигурационного пространства.

Рассмотрим водородоподобный атом — систему из двух зарядов: положительно заряженного тяжёлого ядра, и электрона, вероятность обнаружения которого распределена сферически симметрично вокруг ядра. Таким образом, у атома водорода (и ему подобных) в основном состоянии электронная плотность зависит только от расстояния до ядра и одинакова в любой точке сферы. Это состояние электрона характеризуется нулевым орбитальным моментом импульса (так называемое s-состояние). В возбуждённых состояниях с отличным от нуля орбитальным моментом электрона (p-, d-, f-… состояния) сферическая симметрия электронной плотности отсутствует.
В достаточно сложных молекулах электронная плотность, как правило, несимметрична, а форма электронного облака может меняться. Например, при замещении трёх атомов водорода метильной группы уксусной кислоты на чрезвычайно электроотрицательные атомы хлора её константа диссоциации (pK) снижается с 4,76 до почти 1 в результате индуктивно вызванного снижения силы притяжения H⁺ к карбоксильной группе; сила кислоты возрастает. Существуют две простые, но логичные точки зрения на это явление. По одной из них, увеличение силы кислоты отражает смещение плотности распределения единственного избыточного электрона карбоксильного кислорода в сторону от H+, и сила притяжения протона ослабевает. Согласно другой точке зрения, причиной этого явления служит не смещение, а «разжижение» «облака отрицательного электричества», то есть снижение электронной плотности вокруг однозарядного атома кислорода.

В качестве модели состояния электрона в атоме, в квантовой механике принято представление об электронном облаке, плотность соответствующих участков которого пропорциональна вероятности нахождения там электрона.

Электронное облако часто изображают в виде граничной поверхности. При этом обозначение электронной области при помощи точек опускают. Пространство вокруг ядра, в котором наиболее вероятно пребывание электрона, называют атомной орбиталью (смысл которого вытекает из волнового уравнения Шрёдингера).

Применяются графические изображения распределения электронной плотности относительно ядра.

Кривая радиального распределения вероятности показывает, что электрон находится в тонком концентрическом шаровом слое радиуса r толщины dr вокруг ядра атома водорода^[1].

Проекция максимума кривой соответствует боровскому радиусу α₀=0,53 Å.

Во многих случаях для решения уравнения Шрёдингера используют различные приближения. Вероятностную (статистическую) интерпретацию волновой функции разработал Макс Борн. В 1954 году М.Борн удостоен Нобелевской премии по физике с формулировкой «За фундаментальные исследования в области квантовой механики, особенно, за статистическую интерпретацию волновой функции.»

См. также[править | править код]

Атомная орбиталь
Электронное облако
Индуктивный эффект
Химическая связь
Статистическая интерпретация волновой функции

Примечания[править | править код]

↑ Ахметов Н.С. Неорганическая химия. — издание 2, переработанное и дополненное. — М.: «Высшая школа», 1975. — 672 с.

Источник

From Wikipedia, the free encyclopedia

This article is about the quantum mechanical probability density of an electron. For the number density of electrons in a plasma, also called “electron density”, see Plasma (physics).

Electron density or electronic density is the measure of the probability of an electron being present at an infinitesimal element of space surrounding any given point. It is a scalar quantity depending upon three spatial variables and is typically denoted as either or . The density is determined, through definition, by the normalised -electron wavefunction which itself depends upon variables ( spatial and spin coordinates). Conversely, the density determines the wave function modulo up to a phase factor, providing the formal foundation of density functional theory.

According to quantum mechanics, due to the uncertainty principle on an atomic scale the exact location of an electron cannot be predicted, only the probability of its being at a given position; therefore electrons in atoms and molecules act as if they are “smeared out” in space. For one-electron systems, the electron density at any point is proportional to the square magnitude of the wavefunction.

Definition[edit]

The electronic density corresponding to a normalised -electron wavefunction Psi (with and denoting spatial and spin variables respectively) is defined as^[1]

{displaystyle rho (mathbf {r} )=langle Psi |{hat {rho }}(mathbf {r} )|Psi rangle ,}

where the operator corresponding to the density observable is

${displaystyle {hat {rho }}(mathbf {r} )=sum _{i=1}^{N} delta (mathbf {r} -mathbf {r} _{i}).}$

Computing as defined above we can simplify the expression as follows.

${displaystyle {begin{aligned}rho (mathbf {r} )&=sum _{{s}_{1}}cdots sum _{{s}_{N}}int mathrm {d} mathbf {r} _{1} cdots int mathrm {d} mathbf {r} _{N} left(sum _{i=1}^{N}delta (mathbf {r} -mathbf {r} _{i})right)|Psi (mathbf {r} _{1},s_{1},mathbf {r} _{2},s_{2},...,mathbf {r} _{N},s_{N})|^{2}\&=Nsum _{{s}_{1}}cdots sum _{{s}_{N}}int mathrm {d} mathbf {r} _{2} cdots int mathrm {d} mathbf {r} _{N} |Psi (mathbf {r} ,s_{1},mathbf {r} _{2},s_{2},...,mathbf {r} _{N},s_{N})|^{2}end{aligned}}}$

In words: holding a single electron still in position we sum over all possible arrangements of the other electrons. The factor N arises since all electrons are indistinguishable, and hence all the integrals evaluate to the same value.

In Hartree–Fock and density functional theories, the wave function is typically represented as a single Slater determinant constructed from orbitals, $varphi _{k}$ , with corresponding occupations $n_{k}$ . In these situations, the density simplifies to

$rho ({mathbf {r}})=sum _{{k=1}}^{N}n_{{k}}|varphi _{k}({mathbf {r}})|^{2}.$

General properties[edit]

From its definition, the electron density is a non-negative function integrating to the total number of electrons. Further, for a system with kinetic energy T, the density satisfies the inequalities^[2]

${frac {1}{2}}int {mathrm {d}}{mathbf {r}} {big (}nabla {sqrt {rho ({mathbf {r}})}}{big )}^{{2}}leq T.$

${frac {3}{2}}left({frac {pi }{2}}right)^{{4/3}}left(int {mathrm {d}}{mathbf {r}} rho ^{{3}}({mathbf {r}})right)^{{1/3}}leq T.$

For finite kinetic energies, the first (stronger) inequality places the square root of the density in the Sobolev space ${displaystyle H^{1}(mathbb {R} ^{3})}$ . Together with the normalization and non-negativity this defines a space containing physically acceptable densities as

$mathcal{J}_{N} = left{ rho left| rho(mathbf{r})geq 0, rho^{1/2}(mathbf{r})in H^{1}(mathbf{R}^{3}), intmathrm{d}mathbf{r} rho(mathbf{r}) = N right.right}.$

The second inequality places the density in the L³ space. Together with the normalization property places acceptable densities within the intersection of L¹ and L³ – a superset of ${mathcal {J}}_{{N}}$ .

Topology[edit]

The ground state electronic density of an atom is conjectured to be a monotonically decaying function of the distance from the nucleus.^[3]

Nuclear cusp condition[edit]

The electronic density displays cusps at each nucleus in a molecule as a result of the unbounded electron-nucleus Coulomb potential. This behaviour is quantified by the Kato cusp condition formulated in terms of the spherically averaged density, , about any given nucleus as^[4]

$left.{frac {partial }{partial r_{{alpha }}}}{bar {rho }}(r_{{alpha }})right|_{{r_{{alpha }}=0}}=-2Z_{{alpha }}{bar {rho }}(0).$

That is, the radial derivative of the spherically averaged density, evaluated at any nucleus, is equal to twice the density at that nucleus multiplied by the negative of the atomic number ().

Asymptotic behaviour[edit]

The nuclear cusp condition provides the near-nuclear (small ) density behaviour as

$rho (r)sim e^{{-2Z_{{alpha }}r}},.$

The long-range (large ) behaviour of the density is also known, taking the form^[5]

$rho (r)sim e^{{-2{sqrt {2{mathrm {I}}}}r}},.$

where I is the ionisation energy of the system.

Response density[edit]

Another more-general definition of a density is the “linear-response density”.^[6]^[7] This is the density that when contracted
with any spin-free, one-electron operator yields the associated property defined as the derivative of the energy.
For example, a dipole moment is the derivative of the energy with respect to an external magnetic field and
is not the expectation value of the operator over the wavefunction. For some theories they are the same when
the wavefunction is converged. The occupation numbers are not limited to the range of zero to two, and therefore
sometimes even the response density can be negative in certain regions of space.^[8]

Overview[edit]

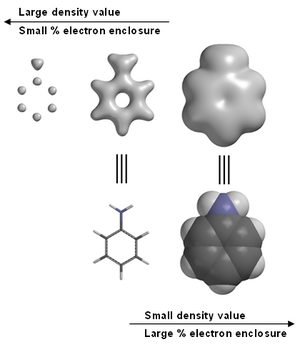
In molecules, regions of large electron density are usually found around the atom, and its bonds. In de-localised or conjugated systems, such as phenol, benzene and compounds such as hemoglobin and chlorophyll, the electron density is significant in an entire region, i.e., in benzene they are found above and below the planar ring. This is sometimes shown diagrammatically as a series of alternating single and double bonds. In the case of phenol and benzene, a circle inside a hexagon shows the delocalised nature of the compound. This is shown below:

In compounds with multiple ring systems which are interconnected, this is no longer accurate, so alternating single and double bonds are used. In compounds such as chlorophyll and phenol, some diagrams show a dotted or dashed line to represent the delocalization of areas where the electron density is higher next to the single bonds.^[9] Conjugated systems can sometimes represent regions where electromagnetic radiation is absorbed at different wavelengths resulting in compounds appearing coloured. In polymers, these areas are known as chromophores.

In quantum chemical calculations, the electron density, ρ(r), is a function of the coordinates r, defined so ρ(r)dr is the number of electrons in a small volume dr. For closed-shell molecules, can be written in terms of a sum of products of basis functions, φ:

$rho ({mathbf {r}})=sum _{mu }sum _{nu }P_{{mu nu }}phi _{mu }({mathbf {r}})phi _{nu }({mathbf {r}})$

Electron density calculated for aniline, high density values indicate atom positions, intermediate density values emphasize bonding, low values provide information on a molecule’s shape and size.

where P is the density matrix. Electron densities are often rendered in terms of an isosurface (an isodensity surface) with the size and shape of the surface determined by the value of the density chosen, or in terms of a percentage of total electrons enclosed.

Molecular modeling software often provides graphical images of electron density. For example, in aniline (see image at right). Graphical models, including electron density are a commonly employed tool in chemistry education.^[10] Note in the left-most image of aniline, high electron densities are associated with the carbons and nitrogen, but the hydrogens with only one proton in their nuclei, are not visible. This is the reason that X-ray diffraction has a difficult time locating hydrogen positions.

Most molecular modeling software packages allow the user to choose a value for the electron density, often called the isovalue. Some software^[11] also allows for specification of the electron density in terms of percentage of total electrons enclosed. Depending on the isovalue (typical units are electrons per cubic bohr), or the percentage of total electrons enclosed, the electron density surface can be used to locate atoms, emphasize electron densities associated with chemical bonds , or to indicate overall molecular size and shape.^[12]

Graphically, the electron density surface also serves as a canvas upon which other electronic properties can be displayed. The electrostatic potential map (the property of electrostatic potential mapped upon the electron density) provides an indicator for charge distribution in a molecule. The local ionisation potential map (the property of local ionisation potential mapped upon the electron density) provides an indicator of electrophilicity. And the LUMO map (lowest unoccupied molecular orbital mapped upon the electron density) can provide an indicatory for nucleophilicity.^[13]

Experiments[edit]

Many experimental techniques can measure electron density. For example, quantum crystallography through X-ray diffraction scanning, where X-rays of a suitable wavelength are targeted towards a sample and measurements are made over time, gives a probabilistic representation of the locations of electrons. From these positions, molecular structures, as well as accurate charge density distributions, can often be determined for crystallised systems. Quantum electrodynamics and some branches of quantum field theory also study and analyse electron superposition and other related phenomena, such as the NCI index which permits the study of non-covalent interactions using electron density. Mulliken population analysis is based on electron densities in molecules and is a way of dividing the density between atoms to give an estimate of atomic charges.

In transmission electron microscopy (TEM) and deep inelastic scattering, as well as other high energy particle experiments, high energy electrons interacts with the electron cloud to give a direct representation of the electron density. TEM, scanning tunneling microscopy (STM) and atomic force microscopy (AFM) can be used to probe the electron density of specific individual atoms.^{[citation needed]}

Spin density[edit]

Spin density is electron density applied to free radicals. It is defined as the total electron density of electrons of one spin minus the total electron density of the electrons of the other spin. One of the ways to measure it experimentally is by electron spin resonance,^[14] neutron diffraction allows direct mapping of the spin density in 3D-space.

References[edit]

^ Parr, Robert G.; Yang, Weitao (1989). Density-Functional Theory of Atoms and Molecules. New York: Oxford University Press. ISBN 978-0-19-509276-9.
^ Lieb, Elliott H. (1983). “Density functionals for coulomb systems”. International Journal of Quantum Chemistry. 24 (3): 243–277. doi:10.1002/qua.560240302.
^ Ayers, Paul W.; Parr, Robert G. (2003). “Sufficient condition for monotonic electron density decay in many-electron systems”. International Journal of Quantum Chemistry. 95 (6): 877–881. doi:10.1002/qua.10622.
^ Kato, Tosio (1957). “On the eigenfunctions of many-particle systems in quantum mechanics”. Communications on Pure and Applied Mathematics. 10 (2): 151–177. doi:10.1002/cpa.3160100201.
^ Morrell, Marilyn M.; Parr, Robert. G.; Levy, Mel (1975). “Calculation of ionization potentials from density matrices and natural functions, and the long-range behavior of natural orbitals and electron density”. Journal of Chemical Physics. 62 (2): 549–554. Bibcode:1975JChPh..62..549M. doi:10.1063/1.430509.
^ Handy, Nicholas C.; Schaefer, Henry F. (1984). “On the evaluation of analytic energy derivatives for correlated wave functions”. The Journal of Chemical Physics. 81 (11): 5031–5033. Bibcode:1984JChPh..81.5031H. doi:10.1063/1.447489.
^ Wiberg, Kenneth B.; Hadad, Christopher M.; Lepage, Teresa J.; Breneman, Curt M.; Frisch, Michael J. (1992). “Analysis of the effect of electron correlation on charge density distributions”. The Journal of Physical Chemistry. 96 (2): 671–679. doi:10.1021/j100181a030.
^ Gordon, Mark S.; Schmidt, Michael W.; Chaban, Galina M.; Glaesemann, Kurt R.; Stevens, Walter J.; Gonzalez, Carlos (1999). “A natural orbital diagnostic for multiconfigurational character in correlated wave functions”. J. Chem. Phys. 110 (9): 4199–4207. Bibcode:1999JChPh.110.4199G. doi:10.1063/1.478301.
^ e.g., the white line in the diagram on Chlorophylls and Carotenoids Archived 2017-08-09 at the Wayback Machine
^ Alan J. Shusterman; Gwendolyn P. Shusterman (1997). “Teaching Chemistry with Electron Density Models”. The Journal of Chemical Education. 74 (7): 771–775. Bibcode:1997JChEd..74..771S. doi:10.1021/ed074p771.
^ or example, the Spartan program from Wavefunction, Inc.
^ Warren J. Hehre, Alan J. Shusterman, Janet E. Nelson (1998). The Molecular Modeling Workbook for Organic Chemistry. Irvine, California: Wavefunction. pp. 61–86. ISBN 978-1-890661-18-2.{{cite book}}: CS1 maint: uses authors parameter (link)
^ Hehre, Warren J. (2003). A Guide to Molecular Mechanics and Quantum Chemical Calculations. Irvine, California: Wavefunction, Inc. pp. 85–100. ISBN 978-1-890661-06-9.
^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the “Gold Book”) (1997). Online corrected version: (2006–) “spin density”. doi:10.1351/goldbook.S05864

Источник

Электронная плотность

Пространственное
распределение заряда электрона называется
электронной плотностью. Исходя из того,
что вероятность нахождения электрона
в элементарном объеме dV равна
|ψ|²dV,
можно рассчитать функцию радиального
распределения электронной плотности.

Если
за элементарный объем принять объем
шарового слоя толщиной dr на
расстоянии r от
ядра атома, то

dV =
4πr²dr
(20.25)

а
функция радиального распределения
вероятности нахождения электрона в
атоме (вероятности электронной плотности),
равна

W_r =
4πr²|ψ|²dr
(20.26)

Она
представляет собой вероятность
обнаружения электрона в сферическом
слое толщиной dr на
определенном расстоянии слоя от ядра
атома.

Рис.
20.7

Для
1s-орбитали
вероятность обнаружения электрона
максимальна в слое, находящемся на
расстоянии 52,9 нм от ядра. По мере удаления
от ядра атома вероятность обнаружения
электрона приближается к нулю. В случае
2s-орбитали
на кривой появляются два максимума и
узловая точка, где вероятность обнаружения
электрона равна нулю. В общем случае
для орбитали, характеризующейся
квантовыми числами n и l,
число узлов на графике функции радиального
распределения вероятности равно (n − l −
1), см. рисунок 20.7.

Собственная
волновая функция, описывающая основное
состояние атома водорода.

Волновая
функция основного состояния атома
водорода

Для
основного состояния атома водорода
квантовые числа n, l,
m_l имеют
следующие значения:

n
= 1, l =
0, m_l =
0.

Это
состояние обозначают 1s. Уравнение
Шредингера имеет для 1s состояния
решение ψ_min = ψ₁₀₀которое
зависит только от расстояния r между
ядром и электроном:

Здесь-первый
боровский радиус.

В
соответствии с вероятностным смыслом
волновой функции вероятность dw обнаружить
электрон в объеме dV:

Отметим,
что dw зависит от выбранной нами
формы элементарного объема dV.

Если
взять dV в форме прямоугольного
параллелепипеда, т.е.

dV
= dxdydz

и
обозначить через dw соответствующую
вероятность.

В
этом случае плотность вероятности
обнаружить электрон в объеме
параллелепипеда dV = dxdydz будет равна

Плотность
вероятности имеет максимальное значение

(1/π₀³)
при r = 0

Так
как волновая функция 1s состояния
зависит только от r, то обычно элемент
объема dV берут в виде сферического
слоя радиуса r и толщиной dr. Как
известно из геометрии, объем такого
сферического слоя dV = 4πr²dr.
Обозначим через dw₀ соответствующую
вероятность.

Эта
функция равна нулю при r = 0 и r →
∞. При r = r₀ она
имеет максимум, положение которого
соответствует первой боровской орбите.

Радиальное
распределение плотности вероятности
обнаружения электрона.

Рис.
20.8

На
рисунке 20.8 представлено радиальное
распределение вероятности нахождения
электрона в атоме водорода в основном
состоянии

Электронное
облако —
наглядная модель, отражающая
распределение функции
плотности
вероятности обнаружения электрона в атоме или молекуле в
зависимости от энергии электрона.

Согласно
теории Бора электрон
в атоме
водорода в
основном состоянии движется вокруг
ядра по круговой орбите с радиусом a₀ =
0,529Å и с постоянной скоростью V₀ =
2,182· 10⁸ см/сек.
Квантово-механическая картина сходна
с этой, но менее определена. Волновая
функция ψ, описывающая движение электрона
в этом атоме, имеет бо́льшую величину
в непосредственной близости от ядра;
на расстоянии 1-2 Å она быстро падает до
нуля. Квадрат волновой функции представляет
собой функцию распределения вероятности
положения электрона, так что ψ²dv
означает вероятность того, что электрон
находится в объёме dv, а 4πr²ψ²dr —
вероятность того, что он будет находиться
на расстоянии от r до r+dr от ядра.

Кривая
радиального распределения вероятности
нахождения электрона в атоме водорода
показывает, что вероятность обнаружения
электрона максимальна в тонком сферическом
слое с центром в точке расположения
протона и радиусом, равным боровскому
радиусу a₀.

Полинг
указывал, что атом водорода в основном
состоянии можно описать, сказав, что
электрон двигается около ядра с переменной
скоростью V₀,
оставаясь обычно на расстоянии около
0,5 Å. «Если рассматривать достаточно
большой период времени, за который может
быть завершено много циклов движения
электрона, то можно описать атом как
ядро, окруженное сферически симметричным
шаром отрицательного электричества».

Чем
прочнее связь электрона с ядром, тем
электронное облако меньше по размерам
и плотнее по распределению заряда.

Электронное
облако наиболее часто изображают в виде
граничной поверхности (охватывающей
примерно 90 % плотности). При этом
обозначение плотности с помощью точек
опускают.

Соседние файлы в папке Физика

#
#
#
16.04.2020396.35 Кб29.docx
#
#
#
#
#

Источник

Электронная плотность

Электро́нная пло́тность, плотность вероятности распределения электронов в квантовой системе (атоме, молекуле, кристалле). Обычно электронную плотность задают как функцию координат одного электрона. В этом случае электронная плотность отражает пространственное распределение заряда и позволяет найти электрические свойства частицы (дипольный момент и т. п.), в связи с чем электронную плотность называют также зарядовой плотностью. Электронную плотность молекулярных систем чаще всего изучают с помощью экспериментальных данных о рассеянии электронов или рентгеновского излучения.

В молекулярных системах с ненулевым суммарным спином (радикалы, триплетные возбуждённые состояния молекул и др.) плотность распределения проекции электронного спина на выделенную ось называют спиновой плотностью. Спиновая плотность может быть изучена экспериментально методами электронного парамагнитного резонанса.

Данные об электронной плотности представляют обычно либо в компактной форме с помощью эффективных «зарядов на атомах», либо картами электронной плотности (похожими на топографические), на которых для определённых сечений трёхмерного пространства задаются линии уровня электронной плотности. Как правило, электронная плотность имеет максимумы лишь в точках пространства, отвечающих положениям ядер. Хотя в целом, электронная плотность – гладкая функция, в указанных точках она имеет особенности, характеризуемые зарядами ядер. Некоторые из ядер на картах электронной плотности соединены «горными хребтами», которые соотносят с химическими связями. Изучение изменений электронных распределений позволяет судить об особенностях перераспределения электронной плотности при образовании молекул или кристаллов из атомов или при других химических реакциях.

Для основного состояния молекулы электронная плотность, согласно теореме Хоэнберга – Кона, отражает всю специфику молекулы. Например, с ростом расстояния от электрона до молекулы электронная плотность экспоненциально спадает, причём показатель экспоненты задаётся ионизационным потенциалом. В рамках методов функционалов плотности делаются попытки соотнести электронную плотность и энергию молекулы.

Электронная плотность – важная физическая характеристика молекулярной системы, анализ которой позволяет соотнести химическое строение молекулы с локальными особенностями электронного распределения. Перераспределение электронной плотности молекулы, по сравнению с электронной плотностью входящих в её состав атомов, отражает характер химической связи и позволяет судить о взаимном влиянии атомов, изменении строения того или иного молекулярного фрагмента в ряду родственных молекул.

Дата публикации: 29 марта 2023 г. в 10:38 (GMT+3)

Источник

Раздел находится в разработке

Рентгеноструктурный анализ

Как проверить качество расшифровки структуры с помощью РСА
— А.Алексеевский

Рентгеноструктурный анализ — метод определения пространственной структуры молекул. Метод широко применяется как для малых органических молекул, так и для макромолекул, прежде всего молекул белков, нуклеиновых кислот и их комплексов друг с другом и различными лигандами (т.е., малыми молекулами).

Основные этапы рентгеноструктурного эксперимента такие:

1) Очистка необходимого количества вещества

2) Кристаллизация вещества — рентгеноструктурный анализ может определять лишь структуру молекул, находящихся в регулярной кристаллической решётке. Чем регулярнее кристалл, тем выше потенциальное качество расшифровки структуры.

3) Собственно рентгеноструктурный эксперимент — получение модулей структурных факторов

4) Решение фазовой проблемы и синтез функции электронной плотности

5) Построение модели

6) Оптимизация модели

Электронная плотность

Определение функции электронной плотности, единицы измерения

Как известно, молекулы состоят из атомов, а атомы — из ядер и электронов. Если ядра можно рассматривать как точки, в которых сосредоточены масса и положительный заряд, то электроны “размазаны” по объёму молекулы. Поскольку рентгеновские лучи рассеиваются прежде всего именно на электронах, для рентгеноструктурного анализа важным является распределение электронной плотности внутри молекулы.

Электронная плотность — это функция, определённая на трёхмерном пространстве и принимающая положительные значения. Физическая размерность значений электронной плотности — количество электронов на единицу объёма; наиболее удобная единица измерения — заряд на квадратный ангстрем. По определению, значение электронной плотности в данной точке пространства равно заряду, приходящемуся на достаточно малую окрестность этой точки, делённому на объём этой окрестности (более точное определение — предел отношения заряда в окрестности к объему окрестности, при стремлении объёма к нулю).

Как задается электронная плотность в компьютере?

Просто большой таблицей: область пространства, включающая молекулу, покрывается достаточно густой “сетью” (решёткой) точек, и для каждой точки решётки указывается значение функции в ней.

Как рассчитать функцию электронной плотности по модели из PDB-файла

Модель макромолекулы в PDB задаётся координатами центров (ядер) атомов. Функция электронной плотности молекулы рассчитывается как сумма электронных плотностей отдельных атомов.

Оказывается, что достаточно хорошей точности описания электронной плотности молекулы можно достичь, считая электронную плотность каждого атома центрально симметричной (то есть зависящей только от расстояния до центра атома). Что касается вида зависимости плотности от расстояния до центра, то она была подобрана для каждого типа атома (углерода, азота, кислорода, серы и т.д.) эмпирически. Как выяснилось, для практических целей можно использовать так называемое пятигауссово приближение. Функция электронной плотности каждого атома представляется как сумма пяти центрально симметричных гауссовых функций с неотрицательными коэффициентами. Каждая такая функция при заданном максимуме (совпадающем с центром атома) задаётся одним параметром; таким образом, нужно было подобрать десять параметров (пять параметров гауссовых функций и столько же коэффициентов) так, чтобы получившаяся линейная комбинация более всего походила на экспериментально определённую электронную плотность данного атома.

Алгоритм визуализации функции электронной плотности

Обычный способ визуализации функции электронной плотности состоит в том, что визуализируется поверхность уровня функции, отвечающее какому-либо её значению. Поверхность уровня — это поверхность, образованная всеми точками пространства, в которых функция принимает данное значение. Естественно, при разных выборах “уровня” получаются разные поверхности и тем самым разные визуализации одной и той же функции.

Чтобы визуализировать поверхность уровня, можно, например, покрыть её достаточно густо точками и показывать эти точки; другой способ — покрыть поверхность сетью треугольников (триангуляцией) и показывать стороны этих треугольников.

Как получить “экспериментальную” электронную плотность для оценки модели из PDB

Что такое кристалл?

Ряд Фурье функции электронной плотности

Теория рассеяния для кристалла

Алгоритм восстановления функции электронной плотности в ячейке

Рефлексы, они же структурные факторы

Разрешение структуры

См. здесь

Определение разрешения структуры методом рентгеноструктурного анализа

“Человеческий фактор” в указании разрешения в модели из PDB

Как соотносятся разрешение структуры и точность определения координат атомов

Как соотносятся разрешение структуры и число ошибок в структуре

Ориентировочные градации разрешения

Теоретический предел разрешения в рентгеноструктурном эксперименте

Оптимизация модели

Фазовая проблема

Популярный конспект методов решения ФП

Источник

См. также[править | править код]

Примечания[править | править код]

Definition[edit]

General properties[edit]