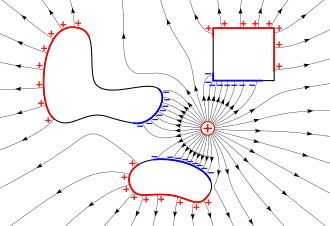
Электростатическая индукция – это явление разделения электрических зарядов и их распределение по поверхности проводника во внешнем электрическом поле.
Простое объяснение
Электростатическая индукция означает перераспределение носителей заряда в объекте, вызванное близлежащими электрическими зарядами. Это означает, что если поместить заряженный объект рядом с нейтральным проводником, то на одном конце проводника образуется положительный электрический заряд, а на другом — отрицательный. Благодаря этому влиянию измеряемый электрический потенциал также одинаков в каждой точке проводника.
Обычная незаряженная среда имеет равное количество положительных и отрицательных электрических зарядов в каждой точке среды. Они расположены близко друг к другу, поэтому преобладает нейтральный электрический заряд. Положительные электрические заряды — имеют ядра атомов. Они неподвижны в структуре вещества и поэтому не могут двигаться. Отрицательные электрические заряды — это электроны, связанные с атомными ядрами. В электропроводящих объектах некоторые из этих электронов могут свободно перемещаться в материале.
Если заряженный объект приблизить к нейтральному проводнику, это приведет к разделению электрических зарядов в проводнике. Это обусловлено действующей силой заряженного объекта, описываемой законом Кулона. То, как электрический заряд распределяется в проводнике, зависит от того, заряжен ли внешний объект положительно или отрицательно.
Если вы поднесете к проводнику положительно заряженный предмет, он притянет к себе отрицательно заряженные электроны проводника. Это приводит к появлению отрицательного электрического заряда в проводнике с той стороны, с которой вы приближаетесь к положительно заряженному объекту. Аналогично этому на противоположной от него стороне возникает скопление положительного электрического заряда. Эти зоны электрического заряда называются индуцированными электрическими зарядами. С другой стороны, если объект, к которому вы приближаетесь, заряжен отрицательно, то происходит обратный процесс.
Обратите внимание, что проводник по-прежнему не заряжен, поскольку число носителей электрического заряда остается прежним. Это всего лишь перераспределение электрического заряда. Процесс является обратимым. Если вы снова удалите внешний объект, электроны вернутся к своему первоначальному распределению.
Физика и формулы, описывающие явление
Самый простой способ показать, что происходит во время электростатический индукции, — это использовать проводящую сферу. Даже если абсолютное число смещённых электронов кажется большим, сдвиг относительно невелик по отношению к общему количеству носителей электрического заряда. Это легче представить, посмотрев на распределение электрического заряда на поверхности сферы.
Если вы проводите эксперимент с электростатической индукцией, вы должны ограничить напряженность электрического поля значениями ниже Emax =105 В/м. Это предотвращает «фальсификацию результата» нежелательными разрядами. Такие разряды возникают в воздухе при значениях Eкрит =107 В/м — 109 В/м. Это напряженность электрического пробоя, которая описывает напряженность электрического поля, выше которой происходит пробой напряжения в изоляторе (диэлектрике). Обычно они имеют форму дуги или искры.
С помощью этого вы можете оценить поверхностную плотность электрического заряда σ на поверхности вашей сферы:
σ = 2 * Emax * ε0 * εr ≈ 1, 789 * 10-6 Кл/м²
Величины ε0 и εr обозначают соответственно абсолютную диэлектрическую проницаемость вакуума и относительную диэлектрическую проницаемость рассматриваемой среды.
Таким образом, на каждом квадратном сантиметре поверхности вашей сферы вы найдете избыточный электрический заряд в 1,8 * 10-10 Кл что соответствует 1,1 * 109 электронов. Количество электронов можно определить по заряду электрона, который равен e=1,602 * 10-19 Кл.
Конечно, теперь вам нужно знать, сколько атомов занимает примерно один квадратный сантиметр, чтобы вы могли определить соотношение. Если ваша сфера сделана из меди, то у вас есть около 8 * 1014 атомов в одном квадратном сантиметре. Каждый из этих атомов дает электрон проводимости. Теперь разделите количество дополнительных атомов в этом квадратном сантиметре на количество существующих.
1,1 * 109 / 8 * 1014 = 1,4 * 10-6 = 1 / 723 000 .
Итак, вы теперь знаете, что на почти 700 000 свободно движущихся электронов приходится еще один из-за электростатической индукции.
Электрические проводники
Как известно из закона Кулона, одноименные электрические заряды отталкиваются друг от друга, а разноименные притягиваются. Благодаря этим знаниям, если вы поместите проводящий материал в электрическое поле или в непосредственной близости от заряженного объекта, вы измените плотность его электрического заряда. Неважно, положительно или отрицательно заряжен объект, потому что он будет отталкивать одноименные носители электрического заряда материала и притягивать разноимённые, как уже говорилось выше. Это создает в материале области с различной плотностью электрического заряда. Общая плотность электрического заряда проводника остается неизменной.
Вывод: электростатическая индукция не изменяет общий электрический заряд проводника .
Такое перераспределение электрического заряда наблюдается только на граничных поверхностях, т.е. на поверхности проводника. Поскольку носители электрического заряда могут свободно перемещаться внутри, электрическое поле в проводнике отсутствует.
Электростатическая индукция и поляризация
В отличие от проводников, носители электрического заряда в изоляторе (диэлектрике) не могут свободно перемещаться. В случае электростатической индукции это приводит к поляризации, то есть к образованию электрических полей на поверхности и внутри диэлектрика. Поляризация на стороне, обращенной в сторону от электрического поля, соответствует внешнему полю, а на стороне, обращенной к нему, имеет противоположный электрический заряд.
Такая форма поляризации называется поляризацией смещения (деформационной поляризацией). В этом процессе положительные атомные ядра смещаются в одном направлении, а отрицательная электронная оболочка — в другом.
В этом процессе электронная оболочка не деформируется. При переменном электрическом поле, можно наблюдать, что электронная оболочка раскачивается взад и вперед, как шарик на ниточке.
Применение
Эффект электростатический индукции используется во многих процессах. Механические эффекты смещения носителей электрического заряда используются, например, в электроскопе. Он используется для измерения электрического напряжения без электрического тока.
В ускорителях частиц, через так называемые пеллетроны, электростатическая индукция используется для достижения высоких напряжений до 32 миллионов вольт.
Список использованной литературы
- Электризация через влияние. // Элементарный учебник физики / Под ред. Г.С. Ландсберга. — 13-е изд. — М.: ФИЗМАТЛИТ, 2003. — Т. 2. Электричество и магнетизм. — С. 24—27.
- Фадеева А. А., Засов А. В., Киселев Д. Ф. Физика 8. – М.: Просвещение.
Для учащихся (для лучшего понимания физики).
Под электростатической индукцией понимается процесс возникновения собственного электрического поля в диэлектриках и проводниках при помещении их во внешнее электрическое поле.
Электростатическая индукция в диэлектриках
Электростатическая индукция в диэлектриках проявляется в том, что оказавшись в электрическом поле диэлектрик поляризуется (см. “Диэлектрик в электрическом поле. Поляризация диэлектрика. Понятие тока поляризации”).
Поляризация диэлектриков заключается в смещении связанных зарядов диэлектрика в пределах его молекулы под действием внешнего электрического поля Ео.
На грани диэлектрика, находящейся вблизи положительно заряженной обкладки конденсатора, появляются отрицательные связанные заряды, а на другой грани диэлектрика, находящейся вблизи вблизи отрицательно заряженной обкладки конденсатора появляются положительные связанные заряды.
Плотность связанных зарядов на рисунке, имеет индекс р (поляризационные) заряды, далее в формулах эта плотность связанных зарядов имеет индекс св (связанные) заряды.
Связанные заряды создают в диэлектрике собственное электрическое поле Есв, направленное навстречу электрическому полю Ео, создаваемому зарядами на обкладках конденсатора (свободными зарядами).
Тогда результирующее поле в диэлектрике Е = Ео – Есв, то есть получается, что диэлектрик ослабляет внешнее электрическое поле Ео и, следовательно, ослабляет напряжение U между обкладками конденсатора.
Эти величины (Ео и U) уменьшаются в “эпсилон”
раз. Ёмкость же конденсатора при этом увеличивается в “эпсилон” раз:
Тогда в присутствие диэлектрика конденсатор способен накопить на своих обкладках больший электрический заряд (чем больше диэлектрическая проницаемость “эпсилон” диэлектрика, тем больший заряд накапливает на себе конденсатор).
Задача 1
Смотрим на предыдущий рисунок, но представляем, что диэлектрик заполнил всё пространство между обкладками конденсатора. Нам известны заряд конденсатора q, диэлектрическая проницаемость “эпсилон” диэлектрика, площадь S. обкладок конденсатора и расстояние между ними d. Надо получить формулу для нахождения плотности связанных зарядов на гранях диэлектрика.
Решение.
Напряжённость поля в диэлектрике Е равна отношению напряжения U между обкладками к расстоянию d между ними:
Е = U /d (1)
Эта формула справедлива для однородного электрического поля (поле конденсатора однородно, его силовые линии идут параллельно друг другу).
Поле, обозначенное в формуле (1) буквой Е, создаётся и свободными, и связанными зарядами.
По определению, ёмкость конденсатора С = q /U, тогда уравнение (1) примет вид:
Е = q / С d.
Но ёмкость конденсатора
Тогда уравнение (1) запишется так:
Но отношение заряда к площади обкладки есть плотность зарядов на обкладках. Тогда уравнение (1) запишется в виде
Обозначим это уравнение цифрой (2).
С другой стороны, напряжённость поля в диэлектрике равна алгебраической сумме напряжённости поля конденсатора Ео и поля связанных зарядов Есв:
Е = Ео – Есв (3)
Воспользуемся формулами для расчёта напряжённости поля плоского воздушного конденсатора:
Параллельные грани поляризованного диэлектрика тоже можно рассматривать как конденсатор, тогда напряжённость поля связанных зарядов:
Подставив два последних уравнения и уравнение (2) в (3), получим выражение для плотности связанных зарядов:
Ответ: Получена зависимость плотности связанных зарядов на гранях диэлектрика с плотностью свободных зарядов на обкладках конденсатора и диэлектрической проницаемостью диэлектрика.
Задача 2
В однородное электрическое поле плоского конденсатора вносится диэлектрик, занимающий часть пространства между обкладками, как показано на рисунке. Как изменится напряжённость поля в областях: до диэлектрика, после диэлектрика и в диэлектрике?
Ответ: Вследствие поляризации диэлектрика напряжённость электрического поля в областях до диэлектрика и после диэлектрика увеличится, а внутри диэлектрика уменьшится.
Задача 3
Плоский конденсатор, пластины которого S велики по сравнению с расстоянием d между ними, присоединён к источнику постоянного напряжения. Изменится ли напряжённость E электрического поля внутри конденсатора, если заполнить пространство между обкладками диэлектриком?
Решение.
Так как конденсатор подключен к источнику постоянного тока, то напряжение U на нём (разность потенциалов между обкладками) не меняется (оно равно напряжению на клеммах источника).
Тогда и напряжённость Е поля между обкладками не меняется, так как
U = Е d.
Но ёмкость конденсатора при заполнении его диэлектриком увеличивается:
то есть от источника к конденсатору будут притекать дополнительные электрические заряды.
Эти заряды будут притекать на обкладки конденсатора в таком количестве, чтобы во время заполнения конденсатора диэлектриком разность потенциалов на обкладках оставалась неизменной.
Такой же она остаётся и после заполнения конденсатора диэлектриком.
Ответ: При внесении диэлектрика в электрическое поле конденсатора, подключенного к источнику постоянного тока, напряжённость электрического поля не изменится, так как напряжение между обкладками при этом не меняется.
Электростатическая индукция в проводниках
Явление электростатической индукции в проводниках заключается в том, что при помещении проводника во внешнее электрическое поле свободные электроны в проводнике смещаются против поля.
В результате этого на одной поверхности проводника оказывается избыток электронов и она заряжается отрицательно, а на противоположной поверхности проводника оказывается недостаток электронов и она заряжается положительно.
Процесс перемещения электронов в проводнике продолжается до тех пор, пока электрическое поле, создаваемое этими индуцированными зарядами, не скомпенсирует напряжённость внешнего электрического поля, то есть пока результирующее поле в проводнике не станет равным нулю (см.”Занятие 52. Явление электростатической индукции”).
На рисунке пунктирными линиями показаны силовые линии внешнего электрического поля (внешнее электрическое поле направлено слева направо).
Применив явление электростатической индукции, можно зарядить конденсатор.
Обычно конденсатор заряжают, подключив его обкладки к полюсам источника постоянного тока.
Но можно поступить иначе: одну из обкладок конденсатора соединить с полюсом источника (на рисунке слева верхняя обкладка конденсатора соединена с положительным полюсом источника, на правом рисунке – с отрицательным), а вторую обкладку конденсатора заземлить, что показано на рисунке ниже.
Тогда на заземлённой обкладке останется заряд, по модулю равный заряду первой обкладки, но противоположный по знаку. Заряд того же знака, что и на первой обкладке, уйдёт в Землю.
Задача 1
В однородное электрическое поле плоского конденсатора помещают хорошо проводящий незаряженный шар. Указать характер изменений в форме и расположении силовых линий поля после внесения шара и указать причины искажения поля. Нарисовать систему эквипотенциальных поверхностей. Указать, где и какие индуцированные заряды появятся на шаре.
Решение.
На шаре появятся индуцированные отрицательные заряды со стороны положительной пластины и положительные – со стороны отрицательно заряженной пластины.
Силовые линии идут под прямым углом к поверхности шара (они начинаются на положительных зарядах и заканчиваются на отрицательных зарядах).
Искажения в форме и расположении силовых линий вызываются наложением на поле конденсатора электрического поля зарядов, индуцированных на поверхности шара.
Линии на рисунке, перпендикулярные к силовым линиям, называются эквипотенциальными поверхностями – в каждой точке одной поверхности потенциал поля имеет одинаковое значение (см. статью “Как графически изображают электростатические поля”).
Вблизи обкладок конденсатора эквипотенциальные поверхности имеют вид близкий к плоскости.
Задача 2
Между двумя разноимёнными одинаковыми по величине точечными зарядами, перпендикулярно к линии их соединяющей, помещаются две достаточно большие, плотно прилегающие друг к другу металлические пластинки.
Что будет происходить с пластинками, если их оставить свободными?
Решение.
Ответ: Пластинки начнут расходиться за счёт взаимодействия точечных зарядов с зарядами, индуцированными на каждой пластинке.
Теперь представим, что показанные на рисунке пластинки не прикасались друг к другу (находились на некотором расстоянии друг от друга). Что произойдёт в этом случае?
Ответ: В этом случае на поверхностях пластинок, обращённых к точечным зарядам тоже появляются индуцированные заряды противоположных знаков, но их плотность будет убывать от А к В (от центра пластинок к их краям).
На внутренних же поверхностях пластинок индуцируемые заряды имеют противоположные знаки, но их плотность одинакова во всех точках, то есть заряды на внутренних поверхностях пластин распределены равномерно.
Задача 3
Расстояние между обкладками заряженного и отключенного от батареи плоского конденсатора равно d = 5 см, напряженность поля Е в нём равна Е = 300 В/см. В конденсатор параллельно его обкладкам вводят незаряженную металлическую пластину толщиной 1 см. Определить разность потенциалов между обкладками до и после введения пластины.
Решение
До внесения металлической пластины напряжение между обкладками конденсатора равно U1 = E d = 1500 B
При внесении металлической пластины между обкладками конденсатора имеет место явление электростатической индукции, то есть напряжённость поля внутри пластинки равна нулю (Е = 0).
Тогда, в соответствии с определением электрического напряжения U (напряжение между обкладками конденсатора численно равно работе, которую надо совершить для переноса единичного заряда с одной обкладки на другую), работу на расстоянии, равном толщине пластинки, совершать не надо.
По условию задачи толщина пластинки равна 1 см, то есть электрическому полю надо совершить работу только на пути (d – 1)см.
Тогда после введения металлической пластины напряжение между обкладками конденсатора уменьшится и станет равным
U2 = E (d – 1) = 1200 В.
Ответ: U1 =1500 B; U2 = 1200 В.
Задача 4
Пластинки плоского конденсатора замкнуты на гальванометр.
Одна из пластин заземлена. Между пластинами продвигают положительный заряд. Что покажет гальванометр?
Решение.
При движении положительного заряда внутри конденсатора на внутренних сторонах пластин конденсатора появляется индуцированные отрицательные заряды, которые будут на них удерживаться.
На наружных сторонах пластин возникают положительные заряды. Эти положительные заряды с заземлённой пластины уйдут в землю.
С другой пластины положительные заряды также уйдёт в землю, пройдя через гальванометр. Поэтому гальванометр даст отброс (отклонение стрелки гальванометра покажет ток).
После этого стекать в Землю начнёт отрицательный заряд – сначала с заземлённой пластины, затем с пластины, соединённой с гальванометром.
При этом стрелка гальванометра отклонится в обратную сторону (гальванометр даст отброс в противоположную сторону).
Ответ: гальванометр покажет проходящий через него заряд (импульс тока).
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Спасибо.
Для школьников предлагаются подборки материала по темам:
!. Механика. Кинематика. Равномерное прямолинейное движение.
2. Равнопеременное прямолинейное движение.
Предыдущая запись: Конденсаторы в электрических цепях постоянного тока.
Следующая запись: Постоянный электрический ток. Методы расчёта сложных цепей постоянного тока.
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 .
Эксперимент с электроскопом показывающий возникновение индуцированного заряда.
Электростатическая индукция — явление наведения собственного электростатического поля при действии на тело внешнего электрического поля. Явление обусловлено перераспределением зарядов внутри проводящих тел, а также поляризацией внутренних микроструктур[1] у непроводящих тел. Внешнее электрическое поле может значительно исказиться вблизи тела с индуцированным электрическим полем.
Электростатическая индукция в проводниках[править | править код]
Перераспределение зарядов в хорошо проводящих металлах при действии внешнего электрического поля происходит до тех пор, пока заряды внутри тела практически полностью не скомпенсируют внешнее электрическое поле. При этом на противоположных сторонах[2] проводящего тела появятся противоположные наведённые (индуцированные) заряды.
Электростатической индукцией в проводниках пользуются при их заряжении. Так, если проводник заземлить и поднести к нему заряженное отрицательно тело, не касаясь им проводника, то некоторое количество отрицательных зарядов перетечёт в землю, заместившись взамен положительными. Если теперь убрать заземление, а затем и заряженное тело, проводник останется положительно заряженным. Если же сделать то же самое, не заземляя проводник, то после убирания заряженного тела индуцированные на проводнике заряды перераспределятся, и все его части вновь станут нейтральными[3].
Электростатическая индукция в диэлектриках[править | править код]
Диэлектрики в электростатическом поле поляризуются.
Применение[править | править код]
Наиболее массовое применение находит основанная на данном явлении электростатическая защита приборов и соединительных цепей.
Эффект электростатической индукции используется в ряде приборов, в частности, в электростатических генераторах: Гольца, Уимсхерста, капельнице Кельвина, генераторе Ван де Граафа, пеллетроне и других.
Примечания[править | править код]
- ↑ атомов, молекул, кристаллических решёток и т.п.
- ↑ относительно внешнего электрического поля
- ↑ § 8. Электризация через влияние. // Элементарный учебник физики / Под ред. Г.С. Ландсберга. — 13-е изд. — М.: ФИЗМАТЛИТ, 2003. — Т. 2. Электричество и магнетизм. — С. 24—27.
Ссылки[править | править код]
- «2.2. Проводник в электростатическом поле. Электрическая ёмкость»
- Электростатическая индукция. — Статья в физической энциклопедии
- Толковый словарь о физике:«Электростатическая индукция» (недоступная ссылка)
Основная
прикладная задача электростатики –
расчет электрических полей, создаваемых
в различных приборах и аппаратах. В
общем виде эта задача решается с помощью
закона Кулона и принципа суперпозиции.
Однако эта задача очень усложняется
при рассмотрении большого числа точечных
или пространственно распределенных
зарядов. Еще большие трудности возникают
при наличии в пространстве диэлектриков
или проводников, когда под действием
внешнего поля Е0происходит
перераспределение микроскопических
зарядов, создающих свое дополнительное
поле Е. Поэтому для практического решения
этих задач используют вспомогательные
методы и приемы, использующие сложный
математический аппарат. Мы рассмотрим
самый простой метод, основанный на
применении теоремы Остроградского –
Гаусса. Чтобы сформулировать эту теорему
введем несколько новых понятий:
А)плотность заряда
Если заряженное тело
велико, то нужно знать распределение
зарядов внутри тела.
Объемная
плотность заряда– измеряется зарядом
единицы объема:
Поверхностная
плотность заряда– измеряется зарядом
единицы поверхности тела (когда заряд
распределяется по поверхности):
Линейная
плотность заряда(распределение
заряда вдоль проводника):
б) вектор
электростатической индукции
Вектором
электростатической индукции
(вектором электрического
смещения) называется векторная величина,
характеризующая электрическое поле.
Вектор
равен произведению вектора
на абсолютную диэлектрическую
проницаемость среды в данной точке:
Проверим
размерность D
в системе единиц СИ:
,
т.к.,
то
размерности D
и Е не совпадают, а также различны и их
численные значения.
Из
определения
следует, что для поля вектора
имеет место тот же принцип суперпозиции,
как и для поля:
Поле
графически изображается линиями
индукции, точно так же как и поле
.
Линии индукции проводятся так, что
касательная в каждой точке совпадает
с направлением
,
а число линий равно численному значениюD
в данном месте.
Чтобы
понять смысл введения
рассмотрим пример.
|
|
|
на границе |
|
Д |
Таким |
в) поток
вектора электростатической индукции
Рассмотрим
в электрическом поле поверхность S
и выберем направление нормали
1.
Если поле однородно, то число силовых
линий через поверхность S:
|
|
N где N |
2.
Если поле неоднородно, то поверхность
разбивают на бесконечно малые элементы
dS,
которые считают плоскими и поле возле
них однородным. Поэтому поток через
элемент поверхности равен: dN
= DndS,
а полный поток через
любую поверхность:
(6)
Поток
индукции N
– величина скалярная; в зависимости от
может быть > 0 или < 0, или = 0.
|
|
N
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
From Wikipedia, the free encyclopedia
Electrostatic induction, also known as “electrostatic influence” or simply “influence” in Europe and Latin America, is a redistribution of electric charge in an object that is caused by the influence of nearby charges.[1] In the presence of a charged body, an insulated conductor develops a positive charge on one end and a negative charge on the other end.[1] Induction was discovered by British scientist John Canton in 1753 and Swedish professor Johan Carl Wilcke in 1762.[2] Electrostatic generators, such as the Wimshurst machine, the Van de Graaff generator and the electrophorus, use this principle. See also Stephen Gray in this context. Due to induction, the electrostatic potential (voltage) is constant at any point throughout a conductor.[3] Electrostatic induction is also responsible for the attraction of light nonconductive objects, such as balloons, paper or styrofoam scraps, to static electric charges. Electrostatic induction laws apply in dynamic situations as far as the quasistatic approximation is valid.
Explanation[edit]
Demonstration of induction, in the 1870s. The positive terminal of an electrostatic machine (right) is placed near an uncharged brass cylinder (left), causing the left end to acquire a positive charge and the right to acquire a negative charge. The small pith ball electroscopes hanging from the bottom show that the charge is concentrated at the ends.
Styrofoam peanuts clinging to a cat’s fur. The static electricity that builds up on the fur causes a polarization of the molecules of the styrofoam due to electrostatic induction, resulting in a slight attraction of the styrofoam to the charged fur.
A normal uncharged piece of matter has equal numbers of positive and negative electric charges in each part of it, located close together, so no part of it has a net electric charge.[4]: p.711-712 The positive charges are the atoms’ nuclei which are bound into the structure of matter and are not free to move. The negative charges are the atoms’ electrons. In electrically conductive objects such as metals, some of the electrons are able to move freely about in the object.
When a charged object is brought near an uncharged, electrically conducting object, such as a piece of metal, the force of the nearby charge due to Coulomb’s law causes a separation of these internal charges.[4]: p.712 For example, if a positive charge is brought near the object (see picture of cylindrical electrode near electrostatic machine), the electrons in the metal will be attracted toward it and move to the side of the object facing it. When the electrons move out of an area, they leave an unbalanced positive charge due to the nuclei. This results in a region of negative charge on the object nearest to the external charge, and a region of positive charge on the part away from it. These are called induced charges. If the external charge is negative, the polarity of the charged regions will be reversed.
Since this process is just a redistribution of the charges that were already in the object, it doesn’t change the total charge on the object; it still has no net charge. This induction effect is reversible; if the nearby charge is removed, the attraction between the positive and negative internal charges causes them to intermingle again.
Charging an object by induction[edit]
Gold-leaf electroscope, showing induction, before the terminal is grounded.
Using an electroscope to show electrostatic induction. The device has leaves/needle that become charged when introducing a charged rod to it. The leaves bend the leave/needle, and the stronger the static introduced, the more bending occurs.
However, the induction effect can also be used to put a net charge on an object.[4]: p.711-713 If, while it is close to the positive charge, the above object is momentarily connected through a conductive path to electrical ground, which is a large reservoir of both positive and negative charges, some of the negative charges in the ground will flow into the object, under the attraction of the nearby positive charge. When the contact with ground is broken, the object is left with a net negative charge.
This method can be demonstrated using a gold-leaf electroscope, which is an instrument for detecting electric charge. The electroscope is first discharged, and a charged object is then brought close to the instrument’s top terminal. Induction causes a separation of the charges inside the electroscope’s metal rod, so that the top terminal gains a net charge of opposite polarity to that of the object, while the gold leaves gain a charge of the same polarity. Since both leaves have the same charge, they repel each other and spread apart. The electroscope has not acquired a net charge: the charge within it has merely been redistributed, so if the charged object were to be moved away from the electroscope the leaves will come together again.
But if an electrical contact is now briefly made between the electroscope terminal and ground, for example by touching the terminal with a finger, this causes charge to flow from ground to the terminal, attracted by the charge on the object close to the terminal. This charge neutralizes the charge in the gold leaves, so the leaves come together again. The electroscope now contains a net charge opposite in polarity to that of the charged object. When the electrical contact to earth is broken, e.g. by lifting the finger, the extra charge that has just flowed into the electroscope cannot escape, and the instrument retains a net charge. The charge is held in the top of the electroscope terminal by the attraction of the inducing charge. But when the inducing charge is moved away, the charge is released and spreads throughout the electroscope terminal to the leaves, so the gold leaves move apart again.
The sign of the charge left on the electroscope after grounding is always opposite in sign to the external inducing charge.[5] The two rules of induction are:[5][6]
- If the object is not grounded, the nearby charge will induce equal and opposite charges in the object.
- If any part of the object is momentarily grounded while the inducing charge is near, a charge opposite in polarity to the inducing charge will be attracted from ground into the object, and it will be left with a charge opposite to the inducing charge.
The electrostatic field inside a conductive object is zero[edit]
Surface charges induced in metal objects by a nearby charge. The electrostatic field (lines with arrows) of a nearby positive charge (+) causes the mobile charges in metal objects to separate. Negative charges (blue) are attracted and move to the surface of the object facing the external charge. Positive charges (red) are repelled and move to the surface facing away. These induced surface charges create an opposing electric field that exactly cancels the field of the external charge throughout the interior of the metal. Therefore electrostatic induction ensures that the electric field everywhere inside a conductive object is zero.
A remaining question is how large the induced charges are. The movement of charges is caused by the force exerted on them by the electric field of the external charged object, by Coulomb’s law. As the charges in the metal object continue to separate, the resulting positive and negative regions create their own electric field, which opposes the field of the external charge.[3] This process continues until very quickly (within a fraction of a second) an equilibrium is reached in which the induced charges are exactly the right size and shape to cancel the external electric field throughout the interior of the metal object.[3][7] Then the remaining mobile charges (electrons) in the interior of the metal no longer feel a force and the net motion of the charges stops.[3]
Induced charge resides on the surface[edit]
Since the mobile charges (electrons) in the interior of a metal object are free to move in any direction, there can never be a static concentration of charge inside the metal; if there was, it would disperse due to its mutual repulsion.[3] Therefore in induction, the mobile charges move through the metal under the influence of the external charge in such a way that they maintain local electrostatic neutrality; in any interior region the negative charge of the electrons balances the positive charge of the nuclei. The electrons move until they reach the surface of the metal and collect there, where they are constrained from moving by the boundary.[3] The surface is the only location where a net electric charge can exist.[4]: p.754
This establishes the principle that electrostatic charges on conductive objects reside on the surface of the object.[3][7] External electric fields induce surface charges on metal objects that exactly cancel the field within.[3]
The voltage throughout a conductive object is constant[edit]
The electrostatic potential or voltage between two points is defined as the energy (work) required to move a small positive charge through an electric field between the two points, divided by the size of the charge. If there is an electric field directed from point 









Since there can be no electric field inside a conductive object to exert force on charges 
Another way of saying this is that in electrostatics, electrostatic induction ensures that the potential (voltage) throughout a conductive object is constant.
Induction in dielectric objects[edit]
Paper snippets attracted by a charged CD
A similar induction effect occurs in nonconductive (dielectric) objects, and is responsible for the attraction of small light nonconductive objects, like balloons, scraps of paper or Styrofoam, to static electric charges[8][9][10] (see cat, above), as well as static cling in clothes.
In nonconductors, the electrons are bound to atoms or molecules and are not free to move about the object as in conductors; however they can move a little within the molecules. If a positive charge is brought near a nonconductive object, the electrons in each molecule are attracted toward it, and move to the side of the molecule facing the charge, while the positive nuclei are repelled and move slightly to the opposite side of the molecule. Since the negative charges are now closer to the external charge than the positive charges, their attraction is greater than the repulsion of the positive charges, resulting in a small net attraction of the molecule toward the charge. This effect is microscopic, but since there are so many molecules, it adds up to enough force to move a light object like Styrofoam.
This change in the distribution of charge in a molecule due to an external electric field is called induced polarization,[8] and the polarized molecules are called dipoles. This should not be confused with a polar molecule, which has a positive and negative end due to its structure, even in the absence of external charge. This is the principle of operation of a pith-ball electroscope.[11]
Notes[edit]
- ^ a b “Electrostatic induction”. Britannica.com Online. Britannica.com Inc. 2008. Retrieved 2008-06-25.
- ^ Fleming, John Ambrose (1911). “Electricity” . In Chisholm, Hugh (ed.). Encyclopædia Britannica. Vol. 9 (11th ed.). Cambridge University Press. pp. 179–193, see page 181, second para, three lines from end.
… the Swede, Johann Karl Wilcke (1732–1796), then resident in Germany, who in 1762 published an account of experiments in which….
- ^ a b c d e f g h i Purcell, Edward M.; David J. Morin (2013). Electricity and Magnetism. Cambridge Univ. Press. pp. 127–128. ISBN 978-1107014022.
- ^ a b c d Halliday, David; Resnick, Robert; Walker, Jearl (2010). Fundamentals of Physics (9 ed.). John Wiley and Sons. ISBN 9780470469118.
- ^ a b Cope, Thomas A. Darlington. Physics. Library of Alexandria. ISBN 1465543724.
- ^ Hadley, Harry Edwin (1899). Magnetism & Electricity for Beginners. Macmillan & Company. p. 182.
- ^ a b Saslow, Wayne M. (2002). Electricity, magnetism, and light. US: Academic Press. pp. 159–161. ISBN 0-12-619455-6.
- ^ a b Sherwood, Bruce A.; Ruth W. Chabay (2011). Matter and Interactions (3rd ed.). USA: John Wiley and Sons. pp. 594–596. ISBN 978-0-470-50347-8.
- ^ Paul E. Tippens, Electric Charge and Electric Force, Powerpoint presentation, p.27-28, 2009, S. Polytechnic State Univ. Archived April 19, 2012, at the Wayback Machine on DocStoc.com website
- ^ Henderson, Tom (2011). “Charge and Charge Interactions”. Static Electricity, Lesson 1. The Physics Classroom. Retrieved 2012-01-01.
- ^ Kaplan MCAT Physics 2010-2011. USA: famous Publishing. 2009. p. 329. ISBN 978-1-4277-9875-6. Archived from the original on 2014-01-31.
External links[edit]
Media related to Electrostatic induction at Wikimedia Commons
- “Charging by electrostatic induction”. Regents exam prep center. Oswego City School District. 1999. Archived from the original on 2008-08-28. Retrieved 2008-06-25.





 ε> 1
ε> 1 ля
ля