Содержание:
- Матрицы: основные определения и понятия
- Умножение матрицы на число
- Сложение и вычитание матриц
- Умножение матриц
- Транспонирование матрицы
- Минор и алгебраическое дополнение
- Вычисление определителя
- Нахождение обратной матрицы
- Нахождение ранга матрицы
Матрицы широко применяются в математике для
компактной записи СЛАУ или систем дифференциальных уравнений. Тогда количество
строк матрицы соответствует количеству уравнений системы, а количество столбцов равно количеству неизвестных. Матричный
аппарат позволяет свести решение громоздких СЛАУ к компактным
операциям над матрицами.
На практике, они позволяют не делать лишних операций и сократить время выполнения задач.
Поэтому, будущим специалистам очень важно понять теорию матриц и научиться решать задачи с ними.
Перед изучением примеров решения задач советуем изучить теоретический материал по матрицам, прочитать
все определения и свойства. Список тем находится в правом меню.
Примеры по темам:
- Матрицы: основные определения и понятия
- Умножение матрицы на число
- Сложение и вычитание матриц
- Умножение матриц
- Транспонирование матрицы
- Минор и алгебраическое дополнение
- Вычисление определителя
- Нахождение обратной матрицы
- Нахождение ранга матрицы
Матрицы: основные определения и понятия
Теоретический материал по теме – основные определения и понятия матриц.
Пример
Задание. Чему равен элемент $ a_{23} $
матрицы $ A=left( begin{array}{rrr}{1} & {4} & {0} \ {-1} & {3} & {7}end{array}right) $ ?
Решение. Находим элемент, который стоит на пересечении второй строки и третьего столбца:
Таким образом, $a_{23}=7$.
Ответ. $a_{23}=7$
Умножение матрицы на число
Теоретический материал по теме – умножение матрицы на число.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Пусть $A=left( begin{array}{r}{3} \ {-1}end{array}right)$ .
Найти матрицу 2$A$.
Решение. $2 A=2 cdot left( begin{array}{r}{3} \ {-1}end{array}right)=left( begin{array}{c}{2 cdot 3} \ {2 cdot(-1)}end{array}right)=left( begin{array}{r}{6} \ {-2}end{array}right)$
Ответ. $2 A=left( begin{array}{r}{6} \ {-2}end{array}right)$
Сложение и вычитание матриц
Теоретический материал по теме – сложение и вычитание матриц.
Пример
Задание. Найти $A+B$, если
$A=left( begin{array}{rrr}{1} & {-2} & {4} \ {2} & {0} & {-1}end{array}right)$,
$B=left( begin{array}{lll}{5} & {2} & {3} \ {4} & {6} & {2}end{array}right)$
Решение. $C=A+B=left( begin{array}{rrr}{1} & {-2} & {4} \ {2} & {0} & {-1}end{array}right)+left( begin{array}{lll}{5} & {2} & {3} \ {4} & {6} & {2}end{array}right)=$
$=left( begin{array}{rrr}{1+5} & {-2+2} & {4+3} \ {2+4} & {0+6} & {-1+2}end{array}right)=left( begin{array}{lll}{6} & {0} & {7} \ {6} & {6} & {1}end{array}right)$
Ответ. $C=left( begin{array}{lll}{6} & {0} & {7} \ {6} & {6} & {1}end{array}right)$
Пример
Задание. Найти матрицу $C=A-3 B$,
если $A=left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right), B=left( begin{array}{rr}{-1} & {1} \ {1} & {2} \ {0} & {0}end{array}right)$
Решение. $C=A-3 B=left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right)-3 cdot left( begin{array}{rr}{-1} & {1} \ {1} & {2} \ {0} & {0}end{array}right)=$
$left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right)-left( begin{array}{rr}{-3} & {3} \ {3} & {6} \ {0} & {0}end{array}right)=left( begin{array}{cc}{1-(-3)} & {2-3} \ {2-3} & {-1-6} \ {3-0} & {0-0}end{array}right)=left( begin{array}{rr}{4} & {-1} \ {-1} & {-7} \ {3} & {0}end{array}right)$
Ответ. $C=left( begin{array}{rr}{4} & {-1} \ {-1} & {-7} \ {3} & {0}end{array}right)$
Умножение матриц
Теоретический материал по теме – умножение матриц.
Пример
Задание. Вычислить $A B$ и $B A$,
если $A=left( begin{array}{rr}{1} & {-1} \ {2} & {0} \ {3} & {0}end{array}right), B=left( begin{array}{ll}{1} & {1} \ {2} & {0}end{array}right)$
Решение. Так как $A=A_{3 times 2}$ , а
$B=B_{2 times 2}$ , то произведение возможно и результатом операции умножения будет матрица
$C=C_{3 times 2}$ , а это матрица вида $C=left( begin{array}{cc}{c_{11}} & {c_{12}} \ {c_{21}} & {c_{22}} \ {c_{31}} & {c_{32}}end{array}right)$ .
Вычисли элементы матрицы $C$ :
$ c_{11}=a_{11} cdot b_{11}+a_{12} cdot b_{21}=1 cdot 1+(-1) cdot 2=-1 $
$ c_{12}=a_{11} cdot b_{12}+a_{12} cdot b_{22}=1 cdot 1+(-1) cdot 0=1 $
$ c_{21}=a_{21} cdot b_{11}+a_{22} cdot b_{21}=2 cdot 1+0 cdot 2=2 $
$ c_{22}=a_{21} cdot b_{12}+a_{22} cdot b_{22}=2 cdot 1+0 cdot 0=2 $
$ c_{31}=a_{31} cdot b_{11}+a_{32} cdot b_{21}=3 cdot 1+0 cdot 2=3 $
$ c_{31}=a_{31} cdot b_{12}+a_{32} cdot b_{22}=3 cdot 1+0 cdot 0=3 $
Итак, $C=A B=left( begin{array}{rl}{-1} & {1} \ {2} & {2} \ {3} & {3}end{array}right)$ .
Выполним произведения в более компактном виде:
$=left( begin{array}{rrr}{1 cdot 1+(-1) cdot 2} & {1 cdot 1+(-1) cdot 0} \ {2 cdot 1+0 cdot 2} & {2 cdot 1+0 cdot 0} \ {3 cdot 1+0 cdot 2} & {3 cdot 1+0 cdot 0}end{array}right)=left( begin{array}{rr}{-1} & {1} \ {2} & {2} \ {3} & {3}end{array}right)$
Найдем теперь произведение $D=B A=B_{2 times 2} cdot A_{3 times 2}$. Так как
количество столбцов матрицы $B$ (первый сомножитель) не совпадает с
количеством строк матрицы $A$ (второй сомножитель), то данное произведение
неопределенно. Умножить матрицы в данном порядке невозможно.
Ответ. $A B=left( begin{array}{rr}{-1} & {1} \ {2} & {2} \ {3} & {3}end{array}right)$ .
В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы
$B$ не совпадает с
количеством строк матрицы $A$ .
Транспонирование матрицы
Теоретический материал по теме – транспонирование матрицы.
Пример
Задание. Найти матрицу $A^{T}$, если
$A=left( begin{array}{rl}{1} & {0} \ {-2} & {3}end{array}right)$
Решение. $A^{T}=left( begin{array}{rr}{1} & {0} \ {-2} & {3}end{array}right)^{T}=left( begin{array}{rr}{1} & {-2} \ {0} & {3}end{array}right)$
Ответ. $A^{T}=left( begin{array}{rr}{1} & {-2} \ {0} & {3}end{array}right)$
Минор и алгебраическое дополнение
Теоретический материал по теме – минор и алгебраическое дополнение.
Пример
Задание. Найти минор
$M_{23}$ к элементу
$a_{23}$ определителя
$left| begin{array}{rrr}{1} & {2} & {-1} \ {1} & {0} & {3} \ {7} & {8} & {4}end{array}right|$ .
Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:
тогда $M_{23}=left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Ответ. $M_{23}=left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Пример
Задание. Найти алгебраическое дополнение
$A_{23}$ к элементу
$a_{23}$ определителя
$left| begin{array}{rrr}{1} & {2} & {-1} \ {1} & {0} & {3} \ {7} & {8} & {4}end{array}right|$ .
Решение. $A_{23}=(-1)^{2+3} cdot M_{23}=(-1)^{5} cdot left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|=-left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Ответ. $A_{23}=-left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Вычисление определителя
Теоретический материал по теме – методы вычисления определителей.
Пример
Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$
Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$
Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.
Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$
$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Пример
Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.
$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{cccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$
$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Пример
Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой – две вторых строки, получаем:
$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:
$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$
$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$
Ответ. $Delta=-80$
Нахождение обратной матрицы
Теоретический материал по теме – нахождение обратной матрицы.
Пример
Задание. Для матрицы $A=left( begin{array}{ll}{7} & {4} \ {5} & {3}end{array}right)$
найти обратную методом присоединенной матрицы.
Решение. Приписываем к заданной матрице
$A$ справа единичную матрицу второго порядка:
$Aleft|E=left( begin{array}{ll|ll}{7} & {4} & {1} & {0} \ {5} & {3} & {0} & {1}end{array}right)right.$
От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):
$Aleft|E sim left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {5} & {3} & {0} & {1}end{array}right)right.$
От второй строки отнимаем две первых:
$Aleft|E sim left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {1} & {1} & {-2} & {3}end{array}right)right.$
Первую и вторую строки меняем местами:
$Aleft|E sim left( begin{array}{rr|r|rr}{1} & {1} & {-2} & {3} \ {2} & {1} & {1} & {-1}end{array}right)right.$
От второй строки отнимаем две первых:
$Aleft|E sim left( begin{array}{rr|rr}{1} & {1} & {-2} & {3} \ {0} & {-1} & {5} & {-7}end{array}right)right.$
Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:
$Aleft|E sim left( begin{array}{rr|rr}{1} & {0} & {3} & {-4} \ {0} & {1} & {-5} & {7}end{array}right)right.$
Итак, слева получили единичную матрицу, а значит матрица, стоящая в
правой части (справа от вертикальной черты), является обратной к исходной.
Таким образом, получаем, что $A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right)$
Ответ. $A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right)$
Пример
Задание. Найти обратную матрицу для $A=left( begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right)$
Решение. Шаг 1. Находим определитель: $Delta=left| begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right|=2-1=1 neq 0$
Шаг 2. $A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right)$
Шаг 3. $A^{-1}=frac{1}{Delta} cdot A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right)$
Ответ. $A^{-1}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right)$
Пример
Задание. Найти обратную матрицу к матрице $A=left( begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right)$
Решение. Вычисляем определитель матрицы:
$Delta=left| begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right|=1 cdot(-1) cdot(-1)+2 cdot 3 cdot 2+0 cdot 1 cdot 1-$
$-1 cdot(-1) cdot 2-3 cdot 1 cdot 1-2 cdot 0 cdot(-1)=1+12+0+2-3+0=12 neq 0$
Так как определитель не равен нулю, то матрица имеет обратную.
Обратная матрица $A^{-1}$ к матрице
$A$ находится по формуле:
$A^{-1}=frac{1}{Delta} cdot widetilde{A}^{T}$
Найдем союзную матрицу $check{A}$ , для этого вычислим алгебраические
дополнения к элементам матрицы $A$ :
$A_{11}=(-1)^{1+1} left| begin{array}{rr}{-1} & {1} \ {3} & {-1}end{array}right|=(-1) cdot(-1)-3 cdot 1=1-3=-2$
$A_{12}=(-1)^{1+2} left| begin{array}{rr}{2} & {1} \ {1} & {-1}end{array}right|=-[2 cdot(-1)-1 cdot 1]=-(-2-1)=3$
$A_{13}=(-1)^{1+3} left| begin{array}{rr}{2} & {-1} \ {1} & {3}end{array}right|=2 cdot 3-1 cdot(-1)=6+1=7$
$A_{21}=(-1)^{2+1} left| begin{array}{rr}{0} & {2} \ {3} & {-1}end{array}right|=-[0 cdot(-1)-3 cdot 2]=-(0-6)=6$
$A_{22}=(-1)^{2+2} left| begin{array}{rr}{1} & {2} \ {1} & {-1}end{array}right|=1 cdot(-1)-1 cdot 2=-1-2=-3$
$A_{23}=(-1)^{2+3} left| begin{array}{cc}{1} & {0} \ {1} & {3}end{array}right|=-[1 cdot 3-1 cdot 0]=-(3-0)=-3$
$A_{31}=(-1)^{3+1} left| begin{array}{rr}{0} & {2} \ {-1} & {1}end{array}right|=0 cdot 1-(-1) cdot 2=0+2=2$
$A_{32}=(-1)^{3+2} left| begin{array}{cc}{1} & {2} \ {2} & {1}end{array}right|=-[1 cdot 1-2 cdot 2]=-(1-4)=3$
$A_{33}=(-1)^{3+3} left| begin{array}{rr}{1} & {0} \ {2} & {-1}end{array}right|=1 cdot(-1)-2 cdot 0=-1-0=-1$
Таким образом, $tilde{A}=left( begin{array}{rrr}{-2} & {3} & {7} \ {6} & {-3} & {-3} \ {2} & {3} & {-1}end{array}right)$
Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):
$widetilde{A}^{T}=left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right)$
Итак, $A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right)$
Ответ. $A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right)$
Нахождение ранга матрицы
Теоретический материал по теме – нахождение ранга матрицы.
Пример
Задание. Найти ранг матрицы $A=left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {4} & {8} & {18} & {7} \ {10} & {18} & {40} & {17} \ {1} & {7} & {17} & {3}end{array}right)$
Решение. С помощью элементарных преобразований над ее строками приведем матрицу $A$ к
ступенчатому виду. Для этого вначале от третьей строки отнимем две вторых:
$A sim left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {4} & {8} & {18} & {7} \ {2} & {2} & {4} & {3} \ {1} & {7} & {17} & {3}end{array}right)$
От второй строки отнимаем четвертую строку, умноженную на 4; от третьей – две четвертых:
$A sim left( begin{array}{rrrr}{0} & {4} & {10} & {1} \ {0} & {-20} & {-50} & {-5} \ {0} & {-12} & {-30} & {-3} \ {1} & {7} & {17} & {3}end{array}right)$
Ко второй строке прибавим пять первых, к третьей – три третьих:
$A sim left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {0} & {0} & {0} & {0} \ {1} & {7} & {17} & {3}end{array}right)$
Меняем местами первую и вторую строчки:
$A sim left( begin{array}{cccc}{0} & {0} & {0} & {0} \ {0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {1} & {7} & {17} & {3}end{array}right)$
Далее четвертую и первую строки:
$A sim left( begin{array}{cccc}{1} & {7} & {17} & {3} \ {0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {0} & {0} & {0} & {0}end{array}right) Rightarrow r a n g A=2$
Ответ. $operatorname{rang} A=2$
Пример
Задание. Найти ранг матрицы $A=left( begin{array}{rrrr}{1} & {2} & {-1} & {-2} \ {2} & {4} & {3} & {0} \ {-1} & {-2} & {6} & {6}end{array}right)$ ,
используя метод окаймления миноров.
Решение. Минорами минимального порядка являются миноры первого порядка, которые равны элементам
матрицы $A$ . Рассмотрим, например, минор
$M_{1}=1 neq 0$ . расположенный в первой строке и первом
столбце. Окаймляем его с помощью второй строки и второго столбца, получаем минор
$M_{2}^{1}=left| begin{array}{ll}{1} & {2} \ {2} & {4}end{array}right|=0$ ; рассмотрим еще один минор второго
порядка, для этого минор $M_{1}$ окаймляем при
помощи второй строки и третьего столбца, тогда имеем минор $M_{2}^{2}=left| begin{array}{rr}{1} & {-1} \ {2} & {3}end{array}right|=5 neq 0$ ,
то есть ранг матрицы не меньше двух. Далее рассматриваем миноры третьего порядка, которые окаймляют минор
$M_{2}^{2}$ . Таких миноров два: комбинация
третьей строки со вторым столбцом или с четвертым столбцом. Вычисляем эти миноры:
$M_{3}^{1}=left| begin{array}{rrr}{1} & {2} & {-1} \ {2} & {4} & {3} \ {-1} & {-2} & {6}end{array}right|=0$
так как содержит два пропорциональных столбца (первый и второй); второй минор
$M_{3}^{2}=left| begin{array}{rrr}{1} & {-1} & {-2} \ {2} & {3} & {0} \ {-1} & {6} & {6}end{array}right|$
преобразуем следующим образом: к первой строке прибавим третью, а ко второй две третьих:
$M_{3}^{2}=left| begin{array}{rrr}{0} & {5} & {4} \ {0} & {15} & {12} \ {-1} & {6} & {6}end{array}right|=0$
И так как первая и вторая строки пропорциональны, то минор равен нулю.
Таким образом, все окаймляющие миноры третьего порядка равны нулю. А, значит, ранг матрицы $A$
равен двум: $operatorname{rang} A=2$
Ответ. $operatorname{rang} A=2$
Читать первую тему – основные определения и понятия матриц,
раздела матрицы.
Равенство матриц
Две матрицы А
= (aij)
и
В = (bij)
называются равными,
если равны элементы, стоящие на одинаковых
местах, т.е. если aij
= bij
при всех i
и j.
При этом число строк и столбцов матриц
А
и В
должно быть одинаковым. Так, матрицы
|
A= |
a11 |
a12 |
и |
B= |
b11 |
b12 |
||
|
a21 |
a22 |
b21 |
b22 |
равны,
если
a11
= b11,
a12
= b12,
a21
= b21,
a22
= b22.
Равные матрицы
имеют одну и ту же структуру: обе они
либо прямоугольные (m
x
n),
либо квадратные одного и того же порядка
n.
Линейные операции над матрицами
Матрицы можно
складывать, умножать на число и друг на
друга. Рассмотрим эти операции.
Суммой двух
матриц А
= (aij)
и В = (bij)
называется матрица С
= (cij),
элементы которой определяются равенством:
aij
+ bij
=
cij
(i
= 1, 2, … m; j = 1, 2, … n).
Аналогично
определяется разность двух матриц.
Складывать можно только матрицы, имеющие
одинаковую структуру: или прямоугольные
типа (m
x
n)
или квадратные порядка n.
Пример 1.
|
a11 |
a12 |
+ |
b11 |
b12 |
= |
a11+b11 |
a12+b12 |
|
a21 |
a22 |
b21 |
b22 |
a21+b21 |
a22+b22 |
Так как сложение
матриц сводится к сложению их элементов,
являющихся числами, то на него
распространяются переместительный
А + В = В + А
(6)
и сочетательный
(А + В) + С = А + (В +
С)
(7)
законы сложения.
Произведением
матрицы
А = (aij)
на число
k
называется матрица, у которой каждый
элемент равен произведению соответствующего
элемента матрицы А
на число k:
kА
= k(aij)
= (kaij)
(i
= 1, 2, … m;
j
= 1, 2, … n)
П
2.
|
k |
a11 |
a12 |
= |
ka11 |
ka12 |
|
a21 |
a22 |
ka21 |
ka22 |
Произведение матриц
Рассмотрим умножение
квадратных матриц второго порядка
|
A= |
a11 |
a12 |
и |
В= |
b11 |
b12 |
|||
|
a21 |
a22 |
b21 |
b22 |
Произведение
обозначается так: A
.
B
= C
(или AB
= C).
Чтобы найти элемент
с11
первой
строки и первого столбца матрицы С,
нужно каждый элемент первой строки
матрицы А
(a11
и а12)
умножить на соответствующий элемент
первого столбца (b11
и b21)
и полученные произведения сложить: c11
= а11b11
+ a12b21;
чтобы найти элемент
с12
первой строки и второго столбца матрицы
С,
нужно умножить все элементы первой
строки (а11
и а12)
на соответствующие элементы второго
столбца (b12
и b22)
и полученные произведения сложить: с12
= а11b12
+ a12b22.
Аналогично находятся
элементы с21
и с22.
|
С |
a11b11 |
a11b12 |
|
a21b11 |
a21b12 |
Сформулируем
правило умножения двух матриц.
Произведением
матрицы
А = (аij),
имеющей m
строк и k
столбцов, на матрицу В
= (bij),
имеющей k
строк и n
столбцов, называется матрица С
= (сij),
имеющая m
строк и n
столбцов, у которой элемент сij
равен сумме произведений элементов
i-ой
строки (ai1,
ai2,
… ain)
матрицы А
на соответствующие элементы j-го
столбца (b1j,
b2j,
… bnj)
матрицы В.
Согласно этому
правилу, число столбцов матрицы А
должно быть
равно числу строк матрицы В.
В противном случае произведение не
определено.
Пример 3.
|
a11 |
a12 |
a13 |
b11 |
b12 |
b13 |
|
a21 |
a22 |
a23 |
b21 |
b22 |
b23 |
|
b31 |
b32 |
b33 |
|
a11b11 |
a11b12 |
a11b13 |
|
a21b11 |
a21b12 |
a21b13 |
Пример 4.
(Кристина Владимирова,
ТШ-062).
Н
произведение матриц
|
А= |
1 |
-3 |
2 |
и |
2 |
5 |
6 |
|
3 |
-4 |
1 |
1 |
2 |
5 |
||
|
2 |
-5 |
3 |
1 |
3 |
2 |
Н
каждый элемент матрицы-произведения:
c11
= a11b11
+ a12b12
+ a13b13
= 1 .2
+ (-3) .1
+ 2 .1
= 1
c12
= a11b12
+ a12b22
+ a13b32
= 1 .5
+ (-3) .2
+2 .3
= 5
c13
= a11b13
+ a12b23
+ a13b33
= 1 .6
+ (-3) .5
+ 2 .2
= -5
c21
= a21b11
+ a22b21
+ a23b31
= 3 .2
+ (-4) .1
+ 1 .1
= 3
c22
= a21b12
+ a22b22
+ a23b32
= 3 .5
+ (-4) .2
+ 1 .3
= 10
c23
= a21b13
+ a22b23
+ a23b33
= 3 .6
+ (-4) .5
+ 1 .2
= 0
c31
= a31b11
+ a32b21
+ a33b31
= 2 .2
+ (-5) .1
+ 3 .1
= 2
c32
=
a31b12
+ a32b22
+ a33b32
= 2 .5
+ (-5) .2
+ 3 .3
=9
c33
= a31b13
+ a32b23
+ a33b33
= 2 .6
+ (-5) .5
+ 3 .2
= -7
С
|
АВ= |
1 |
5 |
-5 |
|
3 |
10 |
0 |
|
|
2 |
9 |
-7 |
Далее Кристина
находит произведение ВА:
|
ВА= |
2 |
2(-3) |
2 |
|
|
1 |
1(-3) |
1 |
= |
|
|
1 |
1(-3) |
1 |
|
= |
29 |
-56 |
27 |
|
17 |
-36 |
1 |
|
|
14 |
-25 |
11 |
Видим, что АВ
≠
ВА.
Этот пример показывает, что произведение
двух матриц, вообще говоря, не подчиняется
переместительному закону.
Путём непосредственной
проверки можно убедиться в справедливости
следующих соотношений для матриц:
(А + В)
.
С = А .
С + В .
С
(8)
С .
(А + В) = С
.
А + С
. В
(9)
А
.
(В .
С) = ( А .
В) .
С (10)
Завершая анализ
операций над матрицами, рассмотрим
пример вычисления матричного многочлена.
Пример 5.
(Маша Куприянова, ТШ-061).
Найти значение
матричного многочлена
3(А2
– В2)
– 2АВ
|
4 |
2 |
1 |
2 |
0 |
2 |
||||||
|
при |
А= |
3 |
-2 |
0 |
и |
В= |
5 |
-7 |
-2 |
||
|
0 |
-1 |
2 |
1 |
0 |
-1 |
||||||
И
|
4 |
2 |
1 |
4 |
2 |
1 |
22 |
3 |
6 |
||
|
А2= |
3 |
-2 |
0 |
3 |
-2 |
0 |
= |
6 |
10 |
3 |
|
0 |
-1 |
2 |
0 |
-1 |
2 |
-3 |
0 |
4 |
||
|
|
||||||||||
|
|
2 |
0 |
2 |
2 |
0 |
2 |
|
6 |
0 |
2 |
|
В2= |
5 |
-7 |
-2 |
5 |
-7 |
-2 |
= |
-27 |
49 |
26 |
|
1 |
0 |
-1 |
1 |
0 |
-1 |
1 |
0 |
3 |
|
16 |
3 |
4 |
48 |
9 |
12 |
||
|
А2 |
33 |
-39 |
-23 |
, |
99 |
-117 |
-69 |
|
-4 |
0 |
1 |
-12 |
0 |
3 |
|
|
4 |
2 |
1 |
2 |
0 |
2 |
1 |
-14 |
3 |
||
|
АВ |
3 |
-2 |
0 |
5 |
-7 |
-2 |
= |
-4 |
14 |
10 |
, |
|
0 |
-1 |
2 |
1 |
0 |
-1 |
-3 |
7 |
0 |
|
3 |
-28 |
6 |
|||||
|
2АВ |
-8 |
28 |
20 |
||||
|
-6 |
14 |
0 |
|
|
10 |
37 |
6 |
||||
|
3(A2 |
107 |
-145 |
-89 |
|
|||
|
-6 |
-14 |
3 |
Соседние файлы в предмете Высшая математика
- #
- #
- #
- #
- #
- #
Калькулятор матриц – действия с матрицами онлайн
С помощью калькулятора матриц вы сможете выполнять различные преобразования матриц, решать СЛАУ, а также находить некоторые характеристики, как, например, определитель, след и ранг. Подробнее о функционале и использовании калькулятора смотрите после блока с самим калькулятором.
Матричный калькулятор
Матрица A
Матрица B
Показатель степени:
Число:
Метод поиска обратной матрицы
Метод Гауса-Жордана
Метод союзной матрицы
Метод решения СЛАУ AX=B
Метод Гауса
Матричный метод
Метод Крамера
Элементарное преобразование
и
Выводить числа в виде
с знаками после запятой
Транспонирование — операция, при которой строки и столбцы матрицы меняются местами: aTij = aji
Выполнено действий:
Также может быть интересно:
- Калькулятор таблицы истинности. СДНФ. СКНФ. Полином Жегалкина
- Калькулятор комплексных чисел
Как пользоваться калькулятором матриц
- Выберите матрицу (или матрицы) с помощью переключателей ()
- Укажите размер с помощью выпадающих списков под матрицей ( × )
- Заполните элементы (нулевые элементы можно не заполнять.)
- Выберите в выпадающем списке требуемую функцию и, если требуется, введите дополнительные параметры.
- Нажмите кнопку .
- Если вывод чисел не устраивает, просто поменяйте его — доступны три варианта представления: правильные дроби (2), неправильные дроби () и десятичные дроби (2.4) с указанием числа знаков после запятой.
Ввод данных и функционал
- В качестве элементов используются обыкновенные правильные дроби (
1/2,29/7,-1/125), десятичные дроби (12,-0.01,3.14), а также числа в экспоненциальной форме (2.5e3,1e-2). - Длина вводимых чисел ничем не ограничена, вводите хоть 1000 цифр, правда, возможно, придётся подождать, пока будут идти вычисления!
- Используйте для работы одну или две матрицы (чтобы выполнять операции с двумя матрицами, передвиньте переключатель второй матрицы).
- Вставляйте результат в A или B с помощью кнопок “Вставить в A” и “Вставить в B”.
- Перетаскивайте (drag-and-drop) матрицы из результата в A или B.
- Используйте стрелки (
←,↑,→,↓) для перемещения по элементам
Что умеет наш калькулятор матриц?
С одной матрицей (только Матрица A или Матрица B)
- Транспонировать;
- Вычислять определитель;
- Находить ранг и след;
- Возводить в степень;
- Умножать на число;
- Вычислять обратную матрицу;
- Приводить к треугольному и ступенчатому вид;
- Находить LU-разложение;
- Выполнять элементарные преобразования;
- Выполнять действия с выражениями, содержащими матрицы.
С двумя матрицами (Матрица A и Матрица B)
- Складывать;
- Вычитать;
- Умножать;
- Решать системы линейных алгебраических уравнений (СЛАУ) вида AX=B;
- Выполнять действия с выражениями, содержащими матрицы.
Вычисление выражений с матрицами
Вы можете вычислять различные арифметические выражения с матрицами, а также с результатами некоторых преобразований этих матриц.
Из чего могут состоять выражения?
- Целые и дробные числа
- Матрицы A, B
- Знаки арифметических действий:
+-*/ - Круглые скобки для изменения приоритета операций:
() - Транспонирование:
^T - Возведение в целую степень:
^
Примеры корректных выражений
- Cложение двух матриц:
A+B,(A)+(B),((A) + B) - Возведение линейной комбинации матриц в степень:
(3A - 0.5B)^5 - Произведение транспонированной матрицы на исходную:
A^TA - Обратная матрица в квадрате для B:
B^-2
Что такое матрица?
Матрицей размера n×m называется прямоугольная таблица специального вида, состоящая из n строк и m столбцов, заполненная числами. Матрицы обозначаются заглавными латинскими буквами. При необходимости размер записывается следующим образом: An×m.
Примеры матриц
Элементы матрицы
Элементы A обозначаются aij, где i – номер строки, в которой находится элемент, j – номер столбца.
Некоторые теоретические сведения
Транспонирование — операция, при которой строки и столбцы матрицы меняются местами: aTij = aji
Главная диагональ квадратной матрицы — диагональ, которая проходит через верхний левый и нижний правый углы. Элементы главной диагонали — aii
Единичная матрица En×n — квадратная матрица из n столбцов и n строк с единицами на главной диагонали и нулями вне её.
Ранг — это максимальное количество линейно независимых строк (столбцов) этой матрицы. Обозначение: rank(A)
След — это сумма элементов, находящихся на её главной диагонали. Обозначение: tr(A) или track(A)
Умножение матрицы на число — матрица такой же размерности, что и исходная, каждый элемент которой является произведением соответствующего элемента исходной матрицы на заданное число.
Возведение в степень — умножение заданной матрицы саму на себя n-ое количество раз, где n – степень, в которую необходимо возвести исходную матрицу. Обозначение: An
Обратная матрица A−1 — матрица, произведение которой на исходную матрицу A равно единичной матрице: A-1×A = A×A-1 = E
Треугольная матрица — квадратная матрица, у которой выше (верхнетреугольная матрица) или ниже (нижнетреугольная матрица) главной диагонали находятся нули.
LU-разложение — представление матрицы в виде произведения двух матриц L и U, где L — нижнетреугольная матрица с еденичной диагональю, а U — верхнетреугольная матрица. A = L·U
Сложение матриц An×m и Bn×m — матрица Cn×m, получаемая попарной суммой соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: сij=aij+bij
Разность матриц An×m и Bn×m — матрица Cn×m, получаемая попарной разностью соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: сij=aij-bij
Умножение матриц An×k и Bk×m — матрица Cn×m, у которой элемент (cij) равен сумме произведений элементов i-той строки матрицы A на соответствующие элементы j-того столбца матрицы B: cij = ai1·b1j + ai2·b2j + ... + aik·bkj
Матрица – это прямоугольная таблица каких-либо элементов. В качестве элементов мы будем рассматривать числа, то есть числовые матрицы.
С помощью этого онлайн калькулятора вы сможете рассчитать: найти определитель матрицы, вычислить ранг матрицы, возвести матрицу в степень, транспонировать матрицу, найти сумму и произведение матриц, вычислить обратную матрицу, умножить матрицу, треугольный и диагональный вид матрицы.
Заполните поля для элементов матрицы и нажмите соответствующую кнопку.
оставляйте лишние ячейки пустыми для ввода не квадратных матриц
элементы матриц – десятичные (конечные и периодические) дроби: 1/23 ,
12.45 ,
-1.3(56) ,
1.2e-4 ; либо арифметические выражения:
2/3+3*(10-4),
(1+x)/y^2,
2^0.5
используйте ввод, пробел, клавиши-стрелки для перемещения по ячейкам
перетаскивайте матрицы из результата (drag-and-drop), или даже из текстового редактора
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

1.
Матрицей А Размера
Называется таблица из Т·п чисел
Часто для краткости пишут А = ||Aij||. Числа, из которых состоит матрица, называются Элементами матрицы. Индексы у элементов матрицы указывают расположение этого элемента в таблице: первый индекс – номер строки, в которой находится элемент, а второй – номер столбца. Например, элемент А23 находится на пересечении второй строки и третьего столбца:
Элементы А11, А22, А33, … называются Главной диагональю матрицы
Если матрица А имеет размер то такую матрицу называют Квадратной матрицей порядка П.
Две матрицы одинакового размера А = ||Aij|| и B = ||Bij|| называют Равными (при этом пишут А = В), если
.
Упражнение 1.

Найти А12 и А23.
Решение.
Элемент А12 располагается в первой строке и втором столбце, то есть это второй элемент первой строки: А12 = -1.
Соответственно А23 – элемент, стоящий во второй строке и в третьем столбце;
А23 = -3.
Упражнение 2.
Даны матрицы

При каких A и B А=В?
Решение.
У равных матриц должны быть равными соответствующие элементы. Для элементов, заданных численно, это условие выполняется: A12 = B12 = 1,
A22 = B22 = 3. Поскольку B11 = 4, a A21 = -2, для равенства матриц А и В должны выполняться условия:

Следовательно, A = ±2, B = -2.
Ответ: A = ±2, B = -2.
| < Предыдущая | Следующая > |
|---|
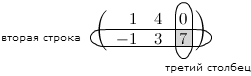
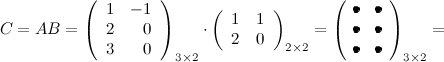
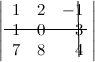















 9
9












 9
9 8
8




