Как найти элемент в выборке

Схемы отбора в выборку

Схема отбора в выборку — это детальное описание того, какие данные и каким способом будут получены. Есть много схем для отбора в выборку, поэтому нужно выбрать для исследований такую, которая даст наиболее репрезентативные результаты. Репрезентативность выборки — это соответствие характеристик выборки характеристикам популяции.

В идеале лучше работать со всей генеральной совокупностью, но это занимает много времени и ресурсов. Поэтому можно исследовать только ее часть, что и называется выборкой. Затем исследуются элементы, которые попали в выборку. На основе полученных значений оцениваются неизвестные элементы выборки.

Основные принципы отбора в выборку

Идея состоит в том, чтобы перенести результаты на всю генеральную совокупность. Поэтому выборка должна быть репрезентативной. Другими словами она пропорциональна как подгруппам, так и всей совокупности, и не исключает каких-либо отдельных групп.

Выборка должна быть настолько большой, насколько это возможно, чтобы избежать ошибочных суждений. По сути выборкой может быть любое подмножество генеральной совокупности.

Если выборка недостаточно репрезентативна — исследование будет считаться предвзятым. Если она будет недостаточно большой — неточным.

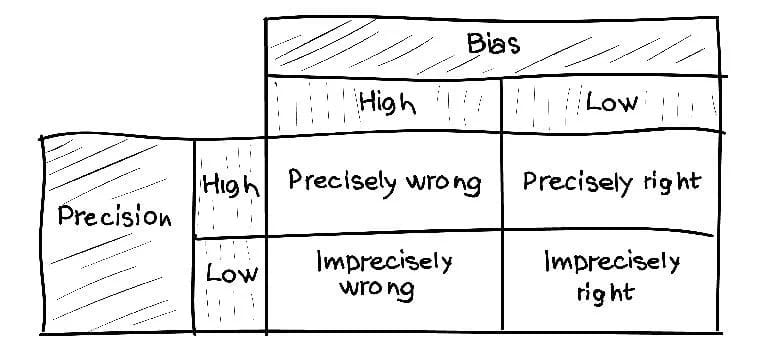
Если правильно подобрать связь между выборкой и совокупностью, тогда можно сделать правильные заключения о природе всей совокупности. Лучше быть возможно правым, чем точно не правым.

Схемы отбора для вероятностных выборок

Вероятностные выборки подразумевают, что исследователь абсолютно уверен в связях выборки с генеральной совокупностью. Если же связи не прослеживаются или в наличии имеются не все элементы генеральной совокупности используется невероятностная выборка.

На основе жеребьевки

Схема отбора состоит в том, чтобы провести ряд испытаний без возвращения элемента в генеральную совокупность. Каждый элемент совокупности имеет одинаковые шансы попасть в выборку.

Из генеральной совокупности N случайным образом отбирается один элемент, вероятность попадания элемента в выборку равна 1/N. Затем из выборки N-1 выбирается второй элемент с вероятностью 1/(N-1) и так далее до n-го элемента с вероятностью 1/(N-n).

Отбор Бернулли

Отбор происходит из упорядоченного списка из N элементов. Пусть наперед задано некоторое число ε (1<ε<0) и набор N независимых реализаций равномерно распределенной на [0,1] случайной величины ε1…εN. Каждому элементу k ставится в соответствие значение. Если εк<π, то этот элемент отбирается, в другом случае — нет. Возможность того, что элемент будет выбран равна π для каждого из N элементов. Таким образом каждый элемент, который попал в выборку является биномиально распределенной величиной.

Систематический отбор

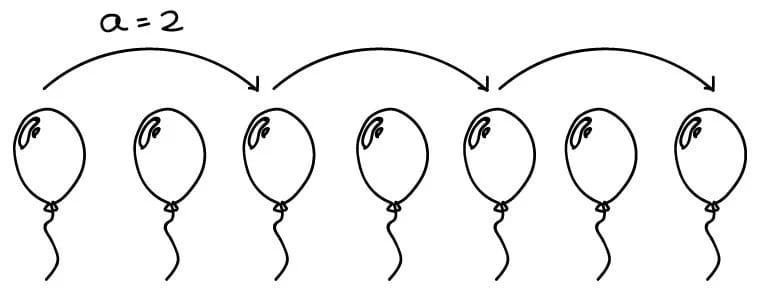
Пусть N — размер генеральной совокупности. а — некоторое фиксированное число. а ∈ N. Первый элемент выборки выбирается случайным образом среди первых a элементов совокупности. Выбранное число r 1≤ r ≤a называется случайным стартом (началом), а число а — выборочным интервалом. Каждый элемент [1,2… а] имеет одинаковую вероятность быть выбранным, равную 1/а. Далее в выборку попадают элементы с шагом а.

Можно получить а разных выборок, каждая из которых имеет одинаковую вероятность быть выбранной.

Простой случайный отбор с возвращением

Во всех вышеизложенных схемах у элемента не было возможности попасть в выборку более 1 раза.
Это логично, так как при повторном включении элемента новая информация не добавляется. Но в этом случае некоторые оценки имеют очень простые статистические свойства, что дает возможность исследовать довольно сложные процедуры отбора.

Например, выполняется m независимых отборов элементов из генеральной совокупности размера N с одинаковыми вероятностями 1/N. Отобранный элемент возвращается в совокупность. Таким образом все N элементов участвуют в отборе постоянно.

Пропорциональный отбор: с возвращением и без

Предполагает, что все числа генеральной совокупности должны быть хорошо перемешаны. Тогда исследователь берет каждый а-й элемент из списка.

Стратифицированный отбор

При этом отборе генеральная совокупность делится на группы, которые не пересекаются. Эти группы называются стратами. Элементы в каждой страте однородны по определенным признакам. В каждой страте проводится отбор элементов. Метод отбора может быть любым, при чем не обязательно одинаковым в каждой страте. Отбор из одной страты не зависит от других страт.

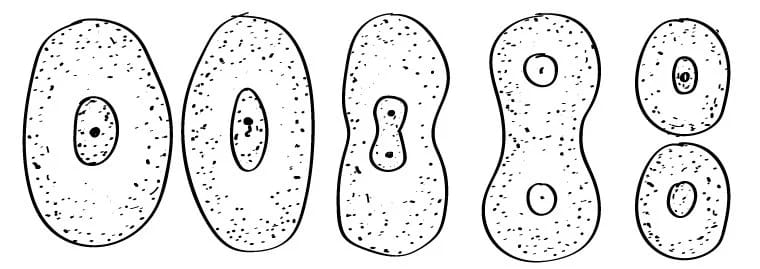
Стратегия отбора в этом случае становится более эффективной. Чем больше изменяется исследуемая характеристика, тем большей будет выборка для более точной оценки. А если разбить совокупность на страты, в которых характеристики мало отличаются, то небольшой выборки из каждой страты будет достаточно для оценки всей совокупности.

Пример: исследование уровня доходов по миру. Вначале весь мир делится на страты, а именно страны. Это области, которые не пересекаются между собой, затем исследование проводится по каждой стране отдельно.

Схемы отбора для невероятностных выборок

В этом случае сложно оценить вероятность попадания каждого элемента совокупности в сэмпл. Исследователи, использующие эти методы, не могут сделать точные выводы о генеральной совокупности.

Кластерный отбор

Если непосредственный отбор из совокупности невозможен, элементы генеральной совокупности объединяются в кластеры.

Кластерный отбор может проходить в одну стадию, тогда сначала отбирают кластеры, а потом исследуют все элементы отобранных кластеров. Например, при исследовании города, кластером может быть семья или жители одного дома.

Если отбор осуществляется в две стадии, то совокупность делят на кластеры, которые состоят из других, более мелких кластеров. На первой стадии получают вероятностную выборку первичных кластеров. На второй стадии — из первичных кластеров отбирают элементы.

Процедура может состоять из трех и более стадий, тогда такая схема называется многостадийной.

Типовой отбор

Элементы отбираются исходя из того, находятся ли они в простом доступе. Такие выборки очень легко составлять, но нет ни единой гарантии что она будет репрезентативной.

Снежный ком

Обычно используется при отборе кандидатов в специфической небольшой группе экспертов. Выбирается один человек для опроса, затем он должен посоветовать несколько других людей и так далее.

Конспект

1. Выборки бывают вероятностные и невероятностные.
2. Если неправильно выбран метод отбора в выборку. исследование может стать предвзятым или неточным.
3. Лучше быть возможно правым, чем точно не правым.

Поиск в выборке

Последнее обновление: 1.11.2015

Для поиска в выборке предназначен метод find. Он имеет следующие варианты использования:

• find(селектор): поиск в выборке объектов, соответствующих селектору

• find(элемент): поиск в выборке объектов, соответствующих данному элементу html

• find(jQuery): поиск в выборке объектов, соответствующих объекту jQuery

Метод find на выходе возвращает новую выборку. Например, у нас есть следующая разметка меню в виде списков:

<ul class="menu">
	<li>Пункт 1</li>
	<li>Пункт 2
		<ul class="submenu">
			<li>Подпункт 2.1</li>
			<li>Подпункт 2.2</li>
		</ul>
	</li>
	<li>Пункт 3
		<ul class="submenu">
			<li>Подпункт 3.1</li>
			<li>Подпункт 3.2</li>
		</ul>
	</li>
</ul>

Теперь последовательно осуществим поиск п селектору, элементу и объекту jQuery:

$(function(){
	// поиск по селектору
	var array0 = $('ul').find('.submenu');
	array0.css('background-color', 'silver');
	
	// поиск по элементу
	// получаем первый элемент выборки
	var elem = $('ul.submenu')[0];
	var array1= $('ul').find(elem);
	array1.css('background-color', 'gray');
	
	// Поиск объекта jQuery
	var jQueryObject = $('ul.submenu');
	var array2= $('ul').find(jQueryObject);
	array2.css('color', 'blue');
});

TurboConf — расширение возможностей Конфигуратора 1С

Поиск в выборке

Здравствуйте! В этом уроке мы  рассмотрим функции Jquery для поиска в выборке (про фильтрацию  выборки  можно почитать  по  ссылке).Для поиска в выборке предназначен метод find. Он имеет следующие варианты использования:

• find(селектор): поиск в выборке объектов, соответствующих селектору
• find(элемент): поиск в выборке объектов, соответствующих данному элементу html
• find(jQuery): поиск в выборке объектов, соответствующих объекту jQuery

Метод find возвращает новую выборку. Например, у нас есть следующая разметка меню в виде списков:

<ul class="menu">
    <li>Пункт 1</li>
    <li>Пункт 2
        <ul class="submenu">
            <li>Подпункт 2.1</li>
            <li>Подпункт 2.2</li>
        </ul>
    </li>
    <li>Пункт 3
        <ul class="submenu">
            <li>Подпункт 3.1</li>
            <li>Подпункт 3.2</li>
        </ul>
    </li>
</ul>

Теперь последовательно осуществим поиск по селектору, элементу и объекту jQuery:

$(function(){
// поиск по селектору
let array0 = $(‘ul’).find(‘.submenu’);
array0.css(‘background-color’, ‘silver’);
// поиск по элементу
// получаем первый элемент выборки
let elem = $(‘ul.submenu’)[0];
let array1= $(‘ul’).find(elem);
array1.css(‘background-color’, ‘gray’);
// Поиск объекта jQuery
let jQueryObject = $(‘ul.submenu’);
let array2= $(‘ul’).find(jQueryObject);
array2.css(‘color’, ‘blue’);
});

(Visited 84 times, 1 visits today)