Как найти элементарный электрический заряд

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 2 июля 2020 года; проверки требуют 3 правки.

Элемента́рный электри́ческий заря́д — фундаментальная физическая постоянная, минимальная порция (квант) электрического заряда, наблюдающегося в природе у свободных долгоживущих частиц. Согласно изменениям определений основных единиц СИ равен точно 1,602 176 634⋅10⁻¹⁹ Кл^[1] в Международной системе единиц (СИ)^[2]. Тесно связан с постоянной тонкой структуры, описывающей электромагнитное взаимодействие^[3].

Квантование электрического заряда[править | править код]

Любой наблюдаемый в эксперименте электрический заряд всегда кратен одному элементарному — такое предположение было высказано Б. Франклином в 1752 году и в дальнейшем неоднократно проверялось экспериментально. Впервые элементарный заряд был экспериментально измерен Милликеном в 1910 году^[3].

Тот факт, что электрический заряд встречается в природе лишь в виде целого числа элементарных зарядов, можно назвать квантованием электрического заряда. При этом в классической электродинамике вопрос о причинах квантования заряда не обсуждается, поскольку заряд является внешним параметром, а не динамической переменной. Удовлетворительного объяснения, почему заряд обязан квантоваться, пока не найдено, однако уже получен ряд интересных наблюдений.

• Если в природе существует магнитный монополь, то, согласно квантовой механике, его магнитный заряд обязан находиться в определённом соотношении с электрическим зарядом любой выбранной элементарной частицы. Отсюда автоматически следует, что существование всего одного магнитного монополя влечёт за собой квантование всех электрических зарядов во Вселенной. Однако обнаружить в природе магнитный монополь не удалось.
• В современной физике элементарных частиц разрабатываются модели наподобие преонной, в которых все известные фундаментальные частицы оказывались бы простыми комбинациями новых, ещё более фундаментальных частиц. В этом случае квантование заряда наблюдаемых частиц не представляется удивительным, поскольку оно возникает «по построению».
• Не исключено также, что все параметры наблюдающихся частиц будут описаны в рамках единой теории поля, подходы к которой разрабатываются в настоящее время. В таких теориях величина электрического заряда частиц должна вычисляться из крайне небольшого числа фундаментальных параметров, возможно, связанных со структурой пространства-времени на сверхмалых расстояниях. Если такая теория будет построена, тогда то, что мы наблюдаем как элементарный электрический заряд, окажется некоторым дискретным инвариантом пространства-времени (скажем, топологическим). Такой подход развивается, например, в модели С. Бильсона-Томпсона^[4], в которой фермионы Стандартной модели интерпретируются, как три ленты пространства-времени, заплетённые в косу (брэд), а электрический заряд (точнее, треть от него) соответствует перекрученной на 180° ленте. Однако несмотря на изящество таких моделей, конкретных общепринятых результатов в этом направлении пока не получено.

Дробный электрический заряд[править | править код]

С открытием кварков стало понятно, что элементарные частицы могут обладать дробным электрическим зарядом, например, ±⅓ и ±⅔ элементарного. Однако подобные частицы существуют только в связанных состояниях (конфайнмент), таким образом, почти все известные свободные частицы (и все стабильные и долгоживущие) имеют электрический заряд, кратный элементарному, хотя рассеяние на частицах с дробным зарядом наблюдалось.

Исключением является t-кварк, его время жизни (~5·10⁻²⁵ с) настолько мало́, что он распадается раньше, чем успевает подвергнуться адронизации, и поэтому встречается только в свободном виде. Заряд t-кварка по прямым измерениям равен +⅔𝑒^[5].

Неоднократные поиски долгоживущих свободных объектов с дробным электрическим зарядом, проводимые различными методиками в течение длительного времени, не дали результата.

Стоит, однако, отметить, что электрический заряд квазичастиц также может быть не кратен целому. В частности, именно квазичастицы с дробным электрическим зарядом отвечают за дробный квантовый эффект Холла.

Экспериментальное определение элементарного электрического заряда[править | править код]

Число Авогадро и постоянная Фарадея[править | править код]

Если известны число Авогадро 𝑁_A и постоянная Фарадея 𝐹, величину элементарного электрического заряда можно вычислить, используя формулу

(другими словами, заряд одного моля электронов, делённый на число электронов в моле, равен заряду одного электрона.)

По сравнению с другими, более точными методами, этот метод не даёт высокой точности, но всё-таки точность его достаточно высока.
Ниже приводятся подробности этого метода.

Значение постоянной Авогадро 𝑁_A было впервые приблизительно измерено Иоганном Йозефом Лошмидтом, который в 1865 году определил на газокинетической основе размер молекул воздуха, что эквивалентно расчету числа частиц в заданном объёме газа^[6]. Сегодня значение 𝑁_A может быть определено с очень высокой точностью с использованием очень чистых кристаллов (как правило — кристаллов кремния) путём измерения расстояния между атомами с использованием дифракции рентгеновских лучей; или другим способом, с точным измерением плотности кристалла. Отсюда можно найти массу (𝑚) одного атома, а так как молярная масса (𝑀) известна, число атомов в моле может быть рассчитано так: 𝑁_A = 𝑀/𝑚.

Величина 𝐹 может быть измерена непосредственно с помощью законов электролиза Фарадея. Законы электролиза Фарадея определяют количественные соотношения, основанные на электрохимических исследованиях, опубликованных Майклом Фарадеем в 1834 году^[7]. В эксперименте электролиза существует взаимно-однозначное соответствие между количеством электронов проходящих между анодом и катодом, и количеством ионов, осевших на пластине электрода. Измеряя изменения массы анода и катода, а также общий заряд, проходящий через электролит (который может быть измерен как интеграл по времени от электрического тока), а также учитывая молярную массу ионов, можно вывести 𝐹.

Ограничения на точность метода заключается в измерении 𝐹. Лучшие экспериментальное значения имеют относительную погрешность 1,6 промилле, что примерно в тридцать раз больше, чем в других современных методах измерения и расчета элементарного заряда.

Опыт Милликена[править | править код]

Известный опыт по измерению заряда электрона e. Маленькая капля масла в электрическом поле будет двигаться с такой скоростью, что будут скомпенсированы сила тяжести, сила Стокса (производная от вязкости воздуха) и электрическая сила. Сила тяжести и Стокса могут быть рассчитаны исходя из размера и скорости падения капли в отсутствие электрического поля, откуда может быть определена и электрическая сила, действующая на каплю. Поскольку электрическая сила, в свою очередь, пропорциональна произведению электрического заряда и известной, заданной в эксперименте, напряжённости электрического поля, электрический заряд капли масла может быть точно вычислен. В этих опытах измеренные заряды различных капель масла оказались всегда целыми кратными одной небольшой величины, а именно e.

Дробовой шум[править | править код]

Любой электрический ток сопровождается электронным шумом от различных источников, одним из которых является дробовой шум. Существование дробового шума связано с тем, что ток является не непрерывным, а состоит из дискретных электронов, которые поочерёдно поступают на электрод. Путём тщательного анализа шума тока может быть вычислен заряд электрона. Этот метод, впервые предложенный Вальтером Шоттки, может давать значение е с точностью до нескольких процентов^[8]. Тем не менее, он был использован в первом прямом наблюдении Лафлином квазичастиц, причастных к дробному квантовому эффекту Холла^[9].

Эффект Джозефсона и константа фон Клитцинга[править | править код]

Другим точным методом измерения элементарного заряда является вычисление его из наблюдения двух эффектов квантовой механики: эффекта Джозефсона, при котором возникают колебания напряжения в определённой сверхпроводящей структуре и квантового эффекта Холла, эффекта квантования холловского сопротивления или проводимости двумерного электронного газа в сильных магнитных полях и при низких температурах. Постоянная Джозефсона

где h — постоянная Планка, может быть измерена непосредственно с помощью эффекта Джозефсона.

Постоянная фон Клитцинга

может быть измерена непосредственно с помощью квантового эффекта Холла.

Из этих двух констант может быть вычислена величина элементарного заряда:

Примечания[править | править код]

Предыдущий урок: Физика для чайников. Урок 16. О вечном двигателе, или законы термодинамики

На бытовом уровне вы представляете, что такое электричество, потому что не раз включали и выключали свет, и, еще наверняка с детства знаете, что пальцы нельзя совать в розетку. Но задумывались ли вы как работает электричество на самом деле? А на самом деле электричество существует благодаря тому, что вещество состоит из атомов, а каждый атом из ядра и «бегающих» округ них электронов. Ядро заряжено положительно, а электроны – отрицательно, и эта разнонаправленность зарядов создает между ними силу притяжения. Не будем пока заморачиватеся над тем вопросов, почему электроны не падают на ядро, это придется углубиться в квантовую механизму.

А вот отрываться электроны от ядра могут. И что тогда получается? А получается, что атом теперь заряжен. Такой заряженный атом называется ион. Если у атома не хватает электрона, то это будет положительно заряженный ион (так как электрон отрицательно заряжен). Можно наоборот, впихнуть в атом лишний электрон. Тогда это будет отрицательно заряженный ион.

Каким же образом можно выбить из атомов электроны? Потоком частиц (в том числе и квантов света – фотоэффект), тепловым воздействием, электрическим полем, химическим способом, и даже от трения. О последнем мы сейчас и поговорим. Вы когда-нибудь замечали, что если ходить в синтетической одежде, то вас начинает бить током, а в темноте такая одежда даже искрит? Вот это и есть то самое явление, когда под действием трения атомы вещества теряют свои электроны. Как правило, электроны «перебегают» с одной трущейся поверхности на другую. Таким образом, накапливаются электрические заряды. В школе для демонстрации подобного явления натирали эбонитовую палочку. Если не помните, напомню. Если эбонитовую палочку натереть специальной шерстяной тряпочкой, она начинала притягивать к себе разные мелкие предметы, например пыль, мелкие бумажки. Если подвесить эбонитовую палочку на тонких ниточках, то видно, что она отталкиваться от другой эбонитовой палочки:

С другой стороны, к заряженному куску шерсти эбонитовая палочка будет наоборот, притягиваться (так как у него заряд с другим знаком). Причем сила взаимодействия зарядов прямо пропорциональная размеру зарядов и обратно пропорционально квадрату расстояния между ними:

В этой формуле F– это сила, в ньютонах, q – заряд, в кулонах, r – расстояние между зарядами в метрах, k – некий коэффициент, равный:

Думаю, в этой формуле все, кроме похожей на букву «Е» закорючки вам знакома. Закорюка эта, называется, кстати, Эпсилон, и обозначит электрическую постоянную, она примерно равна вот таком вот числу:

Число «пи» вы наверняка знаете, но на всякий случай напомню:

Таким образом, значение коэффициента k приближенно равно:

Это коэффициент показывает, что заряд в 1 кулон – это довольно таки большой заряд. То есть, два таких заряда, находящиеся друг от друга на расстоянии 1 метр будет взаимодействовать с силой почти девять миллиардов ньютонов. Примерно с такой силой давит на поверхность Земли груз массой миллиард килограмм, или миллион тонн. Для сравнения, вагон поезда весит «всего» от 22 до 70 тонн.

Но, как ни странно, при токе равном 1 ампер через проводник за секунду проходит заряд в 1 кулон. А ток 1 ампер – это не такой уж и большой ток. Например, через стоваттную лампочку, включённую в розетку на 220 вольт идет ток чуть меньше пол ампера (примерно 0.45А).

Другое определение кулона – это количество элементарных зарядов. Элементарный заряд – это заряд элементарной частицы, например, электрона или протона и равный:

Таким образом, 1 кулон это

Элементарных зарядов (примерно шесть миллиардов миллиардов).

В заключении этого урока расскажу, почему при трении тела могут наэлектризоваться. Электрические силы удерживают электроны внутри тела, будь это хоть эбонитовая палочка, хоть кусок шерсти. Но для разных веществ эти силы разные. И при тесном контакте часть электронов, с тела, у которого сила удерживания меньше, могут перейти на то тело, у которого эти силы больше. Но так как поверхности многих тел далекое не гладки, то площадь касание очень маленькая. А при трении число участков касания увеличивается, соответственно, уваливается и «перебегание» электронов с одного тела на другое.

Следующий урок: Физика для чайников. Урок 18. Электрическое поле

Электрический заряд – физическая
величина, характеризующая способность
тел вступать в электромагнитные
взаимодействия. Измеряется в Кулонах.

Элементарный электрический заряд
– минимальный заряд, который имеют
элементарные частицы (заряд протона и
электрона).

e =
Кл

Тело имеет заряд, значит имеет лишние
или недостающий электроны. Такой заряд
обозначается q = ne.
(он равен числу элементарных зарядов).

Наэлектризовать тело – создать
избыток и недостаток электронов. Способы:
электризация трением и электризация
соприкосновением.

Точечный заряд – заряд тела, которое
можно принять за материальную точку.

Пробный заряд ()
– точечный, малый по величине заряд,
обязательно положительный – используется
для исследования электрического поля.

Закон сохранения заряда: в
изолированной системе алгебраическая
сумма зарядов всех тел сохраняется
постоянной при любых взаимодействиях
этих тел между собой.

Закон Кулона: силы взаимодействия
двух точечных зарядов пропорциональны
произведению этих зарядов, обратно
пропорциональны квадрату расстояния
между ними, зависят от свойств среды и
направлены вдоль прямой, соединяющей
их центры.

,
где Ф/м,
Кл²/нм² – диэлектр. пост.
вакуума

– относит. диэлектрическая проницаемость
(>1)

– абсолютная диэлектрическая прониц.
среды

Электрическое поле – материальная
среда, через которую происходит
взаимодействие электрических зарядов.

Свойства электрического поля:

1. Электрическое поле существует вокруг
   любого заряда. Если заряд неподвижен
   – поле электростатическое.

2. Электрическое поле действует на любой
   помещённый в него заряд согласно закону
   Кулона. Обнаружить электрическое поле
   можно только по его действию на другие
   заряды.

3. Электрическое поле существует в любой
   среде и распространяется с конечной
   скоростью:
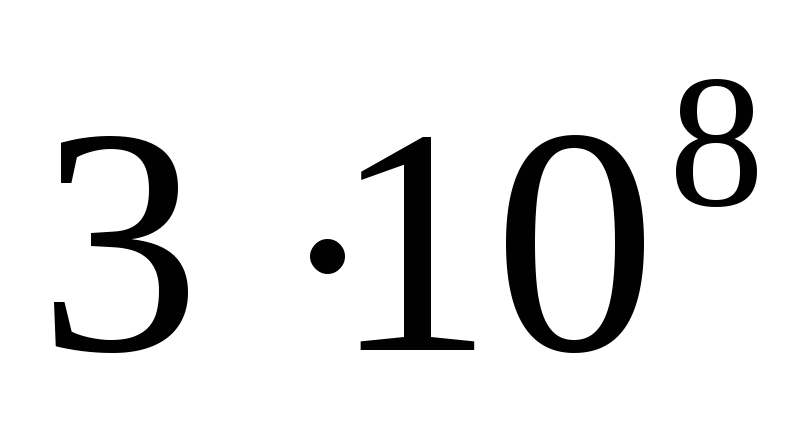   м/с.

4. Электрическое поле не имеет чётких
   границ. Действие его уменьшается при
   увеличении расстояния от заряда, его
   создающего.

Характеристики электрического поля:

1. Напряжённость (E)
   – векторная величина, равная силе,
   действующей на единичный пробный заряд,
   помещённый в данную точку.

Измеряется в Н/Кл.

Направление – такое же, как и у
действующей силы.

Напряжённость не зависит ни от силы,
ни от величины пробного заряда.

Суперпозиция электрических полей:
напряжённость поля, созданного несколькими
зарядами, равна векторной сумме
напряжённостей полей каждого заряда:

Графически электронное поле
изображают с помощью линий напряжённости.

Линия напряжённости – линия,
касательная к которой в каждой точке
совпадает с направлением вектора
напряжённости.

Свойства линий напряжённости: они
не пересекаются, через каждую точку
можно провести лишь одну линию; они не
замкнуты, выходят из положительного
заряда и входят в отрицательный, либо
рассеиваются в бесконечность.

Виды полей:

• Однородное электрическое поле –
  поле, вектор напряжённости которого в
  каждой точке одинаков по модулю и
  направлению.

+ –

+ –

+ –

+ –

• Неоднородное электрическое поле
  – поле, вектор напряжённости которого
  в каждой точке неодинаков по модулю и
  направлению.

• Постоянное электрическое поле –
  вектор напряжённости не изменяется.

• Непостоянное электрическое поле
  – вектор напряжённости изменяется.

1. Работа электрического поля по
   перемещению заряда.

,
где F – сила, S
– перемещение,

– угол между F и S.

Для однородного поля: сила постоянна.

Работа не зависит от формы траектории;
работа по перемещению по замкнутой
траектории равна нулю.

Для неоднородного поля:

1. Потенциал электрического поля –
   отношение работы, которое совершает
   поле, перемещая пробный электрический
   заряд в бесконечность, к величине этого
   заряда.

– потенциал – энергетическая
характеристика поля. Измеряется в
Вольтах

Разность потенциалов:

Если
,
то

,
значит

– градиент потенциала.

Для однородного поля: разность потенциалов
– напряжение:

.
Измеряется в Вольтах, приборы –
вольтметры.

Электроёмкость – способность тел
накапливать электрический заряд;
отношение заряда к потенциалу, которое
для данного проводника всегда постоянно.

.

Не зависит от заряда и не зависит от
потенциала. Но зависит от размеров и
формы проводника; от диэлектрических
свойств среды.

, где r – размер,

– проницаемость среды вокруг тела.

Электроёмкость увеличивается, если
рядом находятся любые тела – проводники
или диэлектрики.

Конденсатор – устройство для
накопления заряда. Электроёмкость:

Плоский конденсатор – две металлические
пластины, между которыми находится
диэлектрик. Электроёмкость плоского
конденсатора:

,
где S – площадь пластин,
d – расстояние между
пластинами.

Энергия заряженного конденсатора
равна работе, которую совершает
электрическое поле при переносе заряда
с одной пластины на другую.

Перенос малого заряда
,
напряжение измениться на
,
совершится работа
.
Так как
,
а С = const,
.
Тогда
.
Интегрируем:

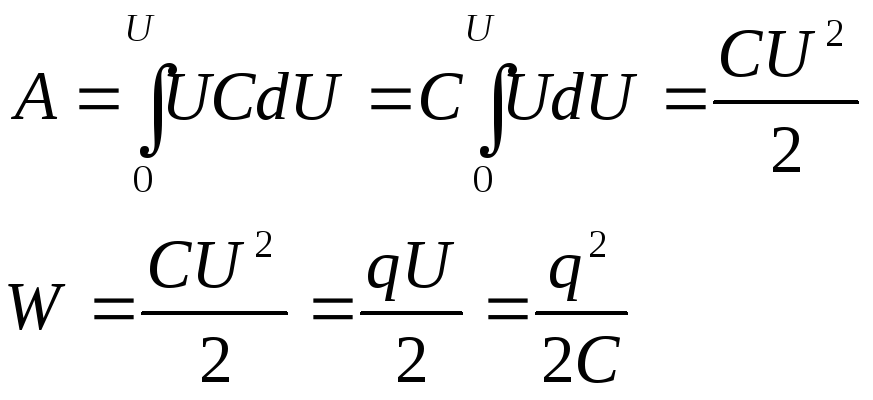
Энергия электрического поля:
,
где V=Sl –
объём, занимаемый электрическим полем

Для неоднородного поля:
.

Объёмная плотность электрического
поля:
.
Измеряется в Дж/м³.

Электрический диполь – система,
состоящая из двух равных, но противоположных
по знаку точечных электрических зарядов,
расположенных на некотором расстоянии
друг от друга (плечо диполя – l).

Основная характеристика диполя –
дипольный момент – вектор, равный
произведению заряда на плечо диполя,
направленный от отрицательного заряда
к положительному. Обозначается
.
Измеряется в Кулон-метрах.

Диполь в однородном электрическом
поле.

На каждый из зарядов диполя действуют
силы:

и
.
Эти силы противоположно направлены и
создают момент пары сил – вращающий
момент:
,
где

М – вращающий момент F –
силы, действующие на диполь

d – плечо сил l
– плечо диполя

p – дипольный момент E
– напряжённость

– угол между p и Е q
– заряд

Под действием вращающего момента,
диполь повернётся и установится по
направлению линий напряжённости. Векторы
p и Е будут параллельны и
однонаправлены.

Диполь в неоднородном электрическом
поле.

Вращающий момент есть, значит диполь
повернётся. Но силы будут неравны, и
диполь будет двигаться туда, где сила
больше.

–
градиент напряжённости. Чем выше
градиент напряжённости, тем выше боковая
сила, которая стаскивает диполь. Диполь
ориентируется вдоль силовых линий.

Собственное поле диполя.

Но
.
Тогда:

.

Пусть диполь находится в точке О, а его
плечо мало. Тогда:

.

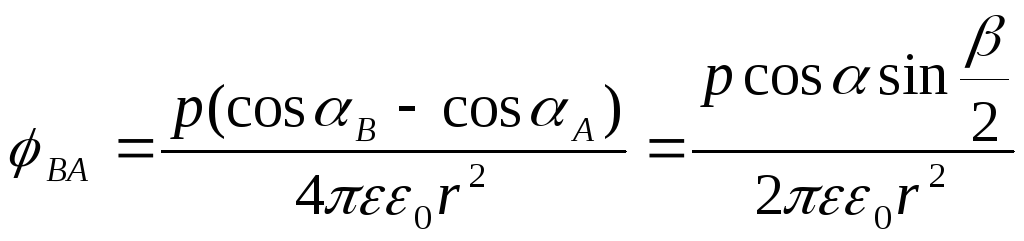Формула получена с учётом:

Таким образом разность потенциалов
зависит от синуса половинного угла, под
которым видны точки диполя, и проекции
дипольного момента на прямую, соединяющие
эти точки.

Диэлектрики в электрическом поле.

Диэлектрик – вещество, не имеющее
свободных зарядов, а значит и не проводящее
электрический ток. Однако на самом же
деле проводимость существует, но она
ничтожно мала.

Классы диэлектриков:

• с полярными молекулами (вода, нитробензол):
  молекулы не симметричны, центры масс
  положительных и отрицательных зарядов
  не совпадают, а значит, они обладают
  дипольным моментом даже в случае, когда
  электрического поля нет.

• с неполярными молекулами (водород,
  кислород): молекулы симметричны, центры
  масс положительных и отрицательных
  зарядов совпадают, а значит, они не
  имеют дипольного момента при отсутствии
  электрического поля.

• кристаллические (хлорид натрия):
  совокупность двух подрешёток, одна из
  которых заряжен положительно, а другая
  – отрицательно; в отсутствии электрического
  поля суммарный дипольный момент равен
  нулю.

Поляризация – процесс пространственного
разделения зарядов, появления связанных
зарядов на поверхности диэлектрика,
что приводит к ослаблению поля внутри
диэлектрика.

Способы поляризации:

1 способ – электрохимическая поляризация:

На электродах – движение к ним катионов
и анионов, нейтрализация веществ;
образуются области положительных и
отрицательных зарядов. Ток постепенно
уменьшается. Скорость установления
механизма нейтрализации характеризуется
временем релаксации – это время, в
течение которого ЭДС поляризации
увеличится от 0 до максимума от момента
наложения поля.

= 10^-3-10^-2 с.

2 способ – ориентационная поляризация:

На поверхности диэлектрика образуются
некомпенсированные полярные, т.е.
происходит явление поляризации.
Напряжённость внутри диэлектрика меньше
внешней напряжённости. Время релаксации:

= 10^-13-10^-7 с. Частота 10 МГц.

3 способ – электронная поляризация:

Характерна для неполярных молекул,
которые становятся диполями. Время
релаксации:
=
10^-16-10^-14 с. Частота 10⁸
МГц.

4 способ – ионная поляризация:

Две решётки (Na и Cl)
смещаются относительно друг друга.

Время релаксации:
=10^-8-10^-3с.
Частота 1 КГц

5 способ – микроструктурная поляризация:

Характерен для биологических структур,
когда чередуются заряженные и незаряженные
слои. Происходит перераспределение
ионов на полупроницаемых или непроницаемых
для ионов перегородках.

Время релаксации:
=10^-8-10^-3с.
Частота 1 КГц

Числовые характеристики степени
поляризации:

1. вектор поляризованности
   .
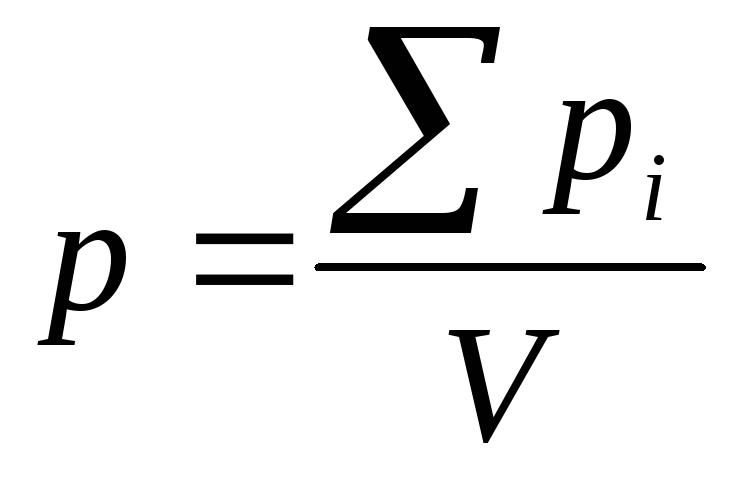   Измеряется в Кл/л

2. относительная диэлектрическая
   проницаемость
   
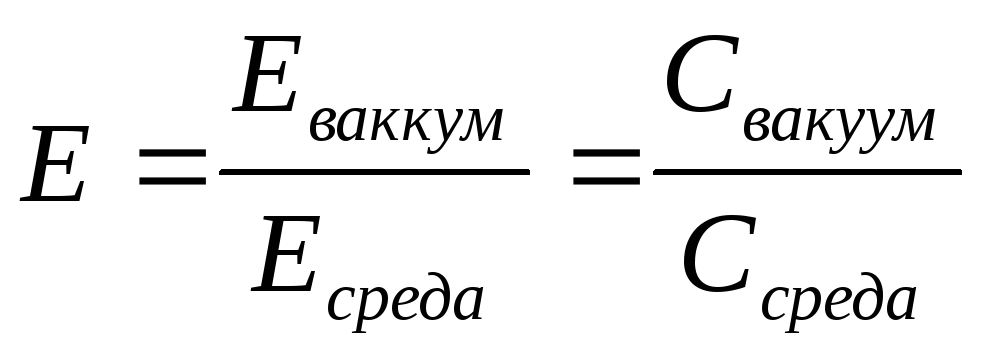
   раз

3. Дисперсия – зависимость от частоты.

Электрический ток – это упорядоченное
движение свободных зарядов в веществе
или в вакууме.

Условия существования электрического
тока:

1. наличие свободных зарядов

2. наличие электрического поля, т.е. сил,
   действующих на эти заряды

Сила тока – величина, равная заряду,
который проходит через любое поперечное
сечение проводника за единицу времени
(1 секунду)

Измеряется в Амперах.

n – концентрация зарядов

q – величина заряда

S – площадь поперечного
сечения проводника

– скорость направленного движения
частиц.

Скорость движения заряженных частиц в
электрическом поле небольшая – 7*10^-5
м/с, скорость распространения электрического
поля 3*10⁸ м/с.

Плотность тока – величина заряда,
проходящего за 1 секунду через сечение
в 1 м².

.
Измеряется в А/м².

– сила, действующая на ион со стороны эл
поля равна силе трения

– подвижность ионов

– скорость направленного движения ионов
=подвижность, напряжённость поля

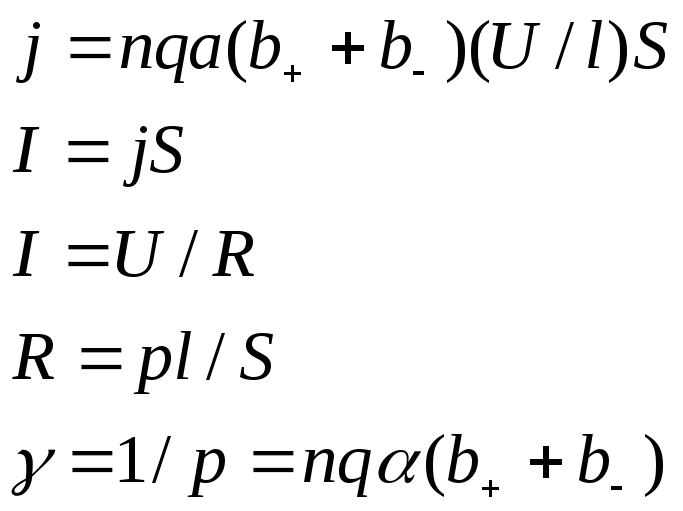
Удельная проводимость электролита тем
больше, чем больше концентрация ионов,
их заряд и подвижность. При повышении
температуры возрастает подвижность
ионов и увеличивается электропроводность.

Соседние файлы в папке Физика лекции

• #
• #
• #
• #
• #
• #
• #

From Wikipedia, the free encyclopedia

Elementary charge
Definition:	charge of a proton
Symbol:	e
SI value:	1.602176634×10−19 C[1]

The elementary charge, usually denoted by e, is the electric charge carried by a single proton or, equivalently, the magnitude of the negative electric charge carried by a single electron, which has charge −1 e.^[2] This elementary charge is a fundamental physical constant.

In the SI system of units, the value of the elementary charge is exactly defined as  = 1.602176634×10⁻¹⁹ coulombs, or 160.2176634 zeptocoulombs (zC).^[1] Since the 2019 redefinition of SI base units, the seven SI base units are defined by seven fundamental physical constants, of which the elementary charge is one.

In the centimetre–gram–second system of units (CGS), the corresponding quantity is 4.8032047…×10⁻¹⁰ statcoulombs.^[3]

Robert A. Millikan and Harvey Fletcher’s oil drop experiment first directly measured the magnitude of the elementary charge in 1909, differing from the modern accepted value by just 0.6%. Under assumptions of the then-disputed atomic theory, the elementary charge had also been indirectly inferred to ~3% accuracy from blackbody spectra by Max Planck in 1901^[4] and (through the Faraday constant) at order-of-magnitude accuracy by Johann Loschmidt’s measurement of the Avogadro number in 1865.

As a unit[edit]

Elementary charge
Unit system	Atomic units
Unit of	electric charge
Symbol	e
Conversions
1 e in …	… is equal to …
coulombs	1.602176634×10−19[5]
(natural units)	0.30282212088
(megaelectronvolt-femtometers)
statC	≘ 4.80320425(10)×10−10

In some natural unit systems, such as the system of atomic units, e functions as the unit of electric charge. The use of elementary charge as a unit was promoted by George Johnstone Stoney in 1874 for the first system of natural units, called Stoney units.^[6] Later, he proposed the name electron for this unit. At the time, the particle we now call the electron was not yet discovered and the difference between the particle electron and the unit of charge electron was still blurred. Later, the name electron was assigned to the particle and the unit of charge e lost its name. However, the unit of energy electronvolt (eV) is a remnant of the fact that the elementary charge was once called electron.

In some other natural unit systems the unit of charge is defined as with the result that

where α is the fine-structure constant, c is the speed of light, ε₀ is the electric constant, and ħ is the reduced Planck constant.

Quantization[edit]

Charge quantization is the principle that the charge of any object is an integer multiple of the elementary charge. Thus, an object’s charge can be exactly 0 e, or exactly 1 e, −1 e, 2 e, etc., but not 1/2 e, or −3.8 e, etc. (There may be exceptions to this statement, depending on how “object” is defined; see below.)

This is the reason for the terminology “elementary charge”: it is meant to imply that it is an indivisible unit of charge.

Fractional elementary charge[edit]

There are two known sorts of exceptions to the indivisibility of the elementary charge: quarks and quasiparticles.

• Quarks, first posited in the 1960s, have quantized charge, but the charge is quantized into multiples of 1/3 e. However, quarks cannot be isolated; they exist only in groupings, and stable groupings of quarks (such as a proton, which consists of three quarks) all have charges that are integer multiples of e. For this reason, either 1 e or 1/3 e can be justifiably considered to be “the quantum of charge”, depending on the context. This charge commensurability, “charge quantization”, has partially motivated Grand unified Theories.
• Quasiparticles are not particles as such, but rather an emergent entity in a complex material system that behaves like a particle. In 1982 Robert Laughlin explained the fractional quantum Hall effect by postulating the existence of fractionally charged quasiparticles. This theory is now widely accepted, but this is not considered to be a violation of the principle of charge quantization, since quasiparticles are not elementary particles.

Quantum of charge[edit]

All known elementary particles, including quarks, have charges that are integer multiples of 1/3 e. Therefore, the “quantum of charge” is 1/3 e. In this case, one says that the “elementary charge” is three times as large as the “quantum of charge”.

On the other hand, all isolatable particles have charges that are integer multiples of e. (Quarks cannot be isolated: they exist only in collective states like protons that have total charges that are integer multiples of e.) Therefore, the “quantum of charge” is e, with the proviso that quarks are not to be included. In this case, “elementary charge” would be synonymous with the “quantum of charge”.

In fact, both terminologies are used.^[7] For this reason, phrases like “the quantum of charge” or “the indivisible unit of charge” can be ambiguous unless further specification is given. On the other hand, the term “elementary charge” is unambiguous: it refers to a quantity of charge equal to that of a proton.

Lack of fractional charges[edit]

Paul Dirac argued in 1931 that if magnetic monopoles exist, then electric charge must be quantized; however, it is unknown whether magnetic monopoles actually exist.^[8][9] It is currently unknown why isolatable particles are restricted to integer charges; much of the string theory landscape appears to admit fractional charges.^[10][11]

Experimental measurements of the elementary charge[edit]

Before reading, it must be remembered that the elementary charge is exactly defined since 20 May 2019 by the International System of Units.

In terms of the Avogadro constant and Faraday constant[edit]

If the Avogadro constant N_A and the Faraday constant F are independently known, the value of the elementary charge can be deduced using the formula

(In other words, the charge of one mole of electrons, divided by the number of electrons in a mole, equals the charge of a single electron.)

This method is not how the most accurate values are measured today. Nevertheless, it is a legitimate and still quite accurate method, and experimental methodologies are described below.

The value of the Avogadro constant N_A was first approximated by Johann Josef Loschmidt who, in 1865, estimated the average diameter of the molecules in air by a method that is equivalent to calculating the number of particles in a given volume of gas.^[12] Today the value of N_A can be measured at very high accuracy by taking an extremely pure crystal (often silicon), measuring how far apart the atoms are spaced using X-ray diffraction or another method, and accurately measuring the density of the crystal. From this information, one can deduce the mass (m) of a single atom; and since the molar mass (M) is known, the number of atoms in a mole can be calculated: N_A = M/m.^[13]

The value of F can be measured directly using Faraday’s laws of electrolysis. Faraday’s laws of electrolysis are quantitative relationships based on the electrochemical researches published by Michael Faraday in 1834.^[14] In an electrolysis experiment, there is a one-to-one correspondence between the electrons passing through the anode-to-cathode wire and the ions that plate onto or off of the anode or cathode. Measuring the mass change of the anode or cathode, and the total charge passing through the wire (which can be measured as the time-integral of electric current), and also taking into account the molar mass of the ions, one can deduce F.^[13]

The limit to the precision of the method is the measurement of F: the best experimental value has a relative uncertainty of 1.6 ppm, about thirty times higher than other modern methods of measuring or calculating the elementary charge.^[13][15]

Oil-drop experiment[edit]

A famous method for measuring e is Millikan’s oil-drop experiment. A small drop of oil in an electric field would move at a rate that balanced the forces of gravity, viscosity (of traveling through the air), and electric force. The forces due to gravity and viscosity could be calculated based on the size and velocity of the oil drop, so electric force could be deduced. Since electric force, in turn, is the product of the electric charge and the known electric field, the electric charge of the oil drop could be accurately computed. By measuring the charges of many different oil drops, it can be seen that the charges are all integer multiples of a single small charge, namely e.

The necessity of measuring the size of the oil droplets can be eliminated by using tiny plastic spheres of a uniform size. The force due to viscosity can be eliminated by adjusting the strength of the electric field so that the sphere hovers motionless.

Shot noise[edit]

Any electric current will be associated with noise from a variety of sources, one of which is shot noise. Shot noise exists because a current is not a smooth continual flow; instead, a current is made up of discrete electrons that pass by one at a time. By carefully analyzing the noise of a current, the charge of an electron can be calculated. This method, first proposed by Walter H. Schottky, can determine a value of e of which the accuracy is limited to a few percent.^[16] However, it was used in the first direct observation of Laughlin quasiparticles, implicated in the fractional quantum Hall effect.^[17]

From the Josephson and von Klitzing constants[edit]

Another accurate method for measuring the elementary charge is by inferring it from measurements of two effects in quantum mechanics: The Josephson effect, voltage oscillations that arise in certain superconducting structures; and the quantum Hall effect, a quantum effect of electrons at low temperatures, strong magnetic fields, and confinement into two dimensions. The Josephson constant is

where h is the Planck constant. It can be measured directly using the Josephson effect.

The von Klitzing constant is

It can be measured directly using the quantum Hall effect.

From these two constants, the elementary charge can be deduced:

CODATA method[edit]

The relation used by CODATA to determine elementary charge was:

where h is the Planck constant, α is the fine-structure constant, μ₀ is the magnetic constant, ε₀ is the electric constant, and c is the speed of light. Presently this equation reflects a relation between ε₀ and α, while all others are fixed values. Thus the relative standard uncertainties of both will be same.

Tests of the universality of elementary charge[edit]

Particle	Expected charge	Experimental constraint	Notes
electron		exact	by definition
proton			by finding no measurable sound when an alternating electric field is applied to SF6 gas in a spherical resonator[18]
positron			by combining the best measured value of the antiproton charge (below) with the low limit placed on antihydrogen’s net charge by the ALPHA Collaboration at CERN.[19]
antiproton			Hori et al.[20] as cited in antiproton/proton charge difference listing of the Particle Data Group[21] The Particle Data Group Wikipedia article has a link to the current online version of the particle data.

See also[edit]

• Committee on Data of the International Science Council

References[edit]

Further reading[edit]

• Fundamentals of Physics, 7th Ed., Halliday, Robert Resnick, and Jearl Walker. Wiley, 2005