Как найти элементы лежащие ниже главной диагонали

Дана квадратная матрица размером nxn. Найти минимальный элемент среди элементов, расположенных ниже главной диагонали, найти максимальный элемент, среди элементов расположенных выше побочной диагонали. Найденные минимальный и максимальный элементы поменять местами и вывести их индексы.

// main_secondary_diagonal.cpp: определяет точку входа для консольного приложения.

#include "stdafx.h"
#include <iostream>
#include <iomanip>
using namespace std;

int main(int argc, char* argv[])
{
    srand(time(NULL));
    int size_array; // размер квадратной матрицы
    setlocale(LC_ALL, "rus");

    cout << "Введите размер квадратной матрицы: ";
    cin >> size_array;

    // динамическое создание двумерного массива
    int **arrayPtr = new int* [size_array];
    for (int count = 0; count < size_array; count++)
        arrayPtr[count] = new int [size_array];

    for (int counter_rows = 0; counter_rows < size_array; counter_rows++)
    {
        for (int counter_columns = 0; counter_columns < size_array; counter_columns++)
        {
            arrayPtr[counter_rows][counter_columns] = rand() % 100; // заполнение массива случайными числами
            cout << setw(2) << arrayPtr[counter_rows][counter_columns] << "  "; // вывод на экран двумерного массива
        }
        cout << endl;
    }
    cout << endl;

    int min = arrayPtr[1][0], // минимальный елемент массива, ниже главной диагонали
        row_min = 1,          // номер строки минимального элемента
        column_min = 0;       // номер столбца минимального элемента

    // поиск минимального элемента в массиве, ниже главной диагонали
    for (int counter_rows = 1; counter_rows < size_array; counter_rows++)
    {
        for (int counter_columns = 0; counter_columns < counter_rows ; counter_columns++)
        {
            if ( arrayPtr[counter_rows][counter_columns] < min )
            {
                min = arrayPtr[counter_rows][counter_columns];
                row_min = counter_rows;
                column_min = counter_columns;
            }
        }
    }

    cout << "min" << "[" << (row_min + 1) << "][" << (column_min + 1) << "]"  << " = " << min << endl; 

    int max = arrayPtr[0][0], // максимальный элемнет массива, выше побочной диагонали
        row_max = 0,              // номер строки максимального элемента
        column_max = 0;           // номер столбца максимального элемента

    for (int counter_rows = 0; counter_rows < size_array - 1; counter_rows++)
    {
        for (int counter_columns = 0; counter_columns < (size_array - counter_rows - 1); counter_columns++)
        {
            if ( arrayPtr[counter_rows][counter_columns] > max )
            {
                max = arrayPtr[counter_rows][counter_columns];
                row_max = counter_rows;
                column_max = counter_columns;
            }
        }
    }

    cout << "max" << "[" << (row_max + 1) << "][" << (column_max + 1) << "]"  << " = " << max << endl; 

    //////////////////перестановка элементов////////////////////////////////////////////////

    arrayPtr[row_min][column_min] = max;
    arrayPtr[row_max][column_max] = min;

    ////////////////////////////////////////////////////////////////////////////////////////

    cout << "nМассив после перестановки максимального и минимального элементов:n";

    for (int counter_rows = 0; counter_rows < size_array; counter_rows++)
    {
        for (int counter_columns = 0; counter_columns < size_array; counter_columns++)
        {
          cout << setw(2) << arrayPtr[counter_rows][counter_columns] << "  "; // вывод на экран двумерного массива
        }
        cout << endl;
    }
    cout << endl;

    cout << "min" << "[" << (row_max + 1) << "][" << (column_max + 1) << "]"  << " = " << min << endl; 
    cout << "max" << "[" << (row_min + 1) << "][" << (column_min + 1) << "]"  << " = " << max << endl; 

    // удаление двумерного динамического массива
    for (int count = 0; count < size_array; count++)
        delete []arrayPtr[count];

    system("pause");
    return 0;
}

Содержание:

Определители II и III порядка

Определение: Определителем порядка n называется число (выражение), записанное в виде квадратной таблицы, имеющей n строк и n столбцов, которая раскрывается по определенному правилу.

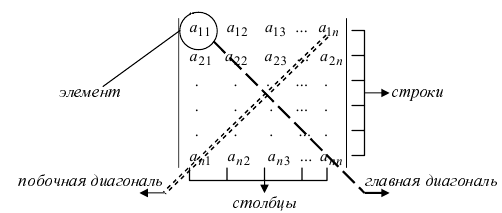
Числа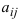

Определение: Определителем II порядка называется число (выражение), записанное в виде квадратной таблицы размером 2×2, т.е. имеющая 2 строки и 2 столбца.

Определение: Определитель II порядка вычисляется по правилу: из произведения элементов, стоящих на главной диагонали, надо вычесть произведение элементов, стоящих на побочной диагонали: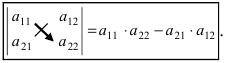

Пример:

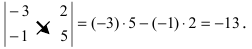
Определение: Определителем III порядка называется число (выражение), записанное в виде квадратной таблицы размером 3×3, то есть имеющей 3 строки и 3 столбца.

Определитель III порядка вычисляется по правилу Саррюса: за определителем выписывают первый и второй столбцы, затем из суммы произведений элементов, стоящих на главной диагонали ей параллельных диагоналях, надо вычесть сумму произведений элементов, стоящих на побочной диагонали и ей параллельных: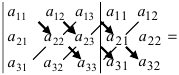

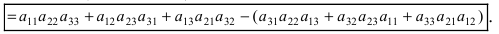
Пример:

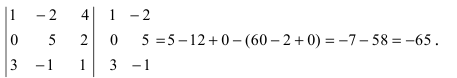
Определение: Минором 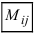элемента 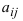называется определитель порядка (n-1), который получается из исходного определителя порядка n путем вычеркивания строки i и столбца j, на пересечении которых стоит элемент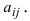

Пример:

Найти миноры элементов 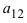и 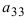определителя из Примера 2. Вычеркивая в определителе строку 1 и столбец 2: 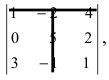получим минор 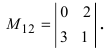Поступая аналогично со строкой 3 и столбцом 3, получим минор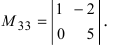

Пример:

Найти миноры элементов 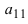и 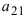определителя 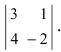Исходя из определения минора 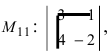получаем 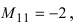аналогично найдем минор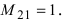

Определение: Алгебраическим дополнением 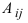элемента 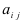называется произведение минора этого элемента на 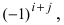т.е.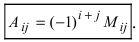

Замечание: Из определения алгебраического дополнения следует, что алгебраическое дополнение совпадает со своим минором, если сумма 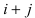является четным числом, и противоположно ему по знаку, если сумма 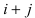– нечетное число.

Определение: Транспонированным определителем n-го порядка называется определитель порядка n, полученный из исходного определителя путем замены строк на соответствующие столбцы, а столбцов на соответствующие строки.

Если

Пример:

Найти определитель, транспонированный к определителю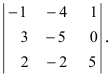 Из определения транспонированного определителя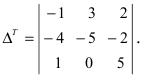

Свойства определителей

1. Величина транспонированного определителя равна величине исходного определителя. Пусть 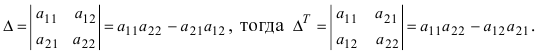Отсюда видно, что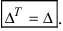

2. Перестановка местами двух строк (столбцов) изменяет знак определителя на противоположный. Пусть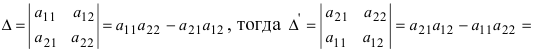

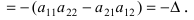
Если поменять местами строки (столбцы) четное число раз, то величина и знак определителя не меняется. Нечетная перестановка местами строк (столбцов) не меняет величину определителя, но изменяет его знак на противоположный.

3. Определитель, содержащий две (или более) одинаковых строки (столбца), равен нулю. Если определитель содержит два одинаковых столбца, то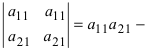

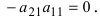
4. Для того чтобы умножить определитель на число k, достаточно умножить на это число все элементы какой-либо одной строки (столбца). Обратно: если все элементы какой-либо строки (столбца) имеют общий множитель k, то его можно вынести за знак определителя.

Докажем это свойство: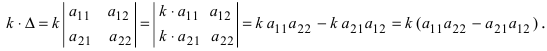

5. Если две каких-либо строки (столбца) пропорциональны, то определитель равен нулю.

Пусть в определителе II порядка первая и вторая строки пропорциональны, тогда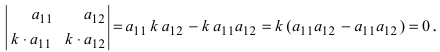

6. Если все элементы какой-либо строки (столбца) равны нулю, то определитель равен нулю.

Пусть в определителе II порядка все элементы первой строки равны нулю, тогда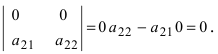

7. Если элементы какой-либо строки (или столбца) можно представить в виде двух слагаемых, то сам определитель можно представить в виде суммы двух определителей. Если 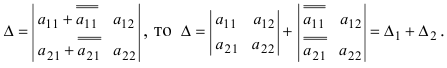Доказать самостоятельно.

8. Если все элементы какой-либо строки (столбца) умножить на вещественное число к и прибавить k соответствующим элементам другой строки (соответственно, столбца), то величина определителя не изменится.

Умножим элементы второго столбца на вещественное число k и прибавим результат умножения к соответствующим элементам первого столбца, получим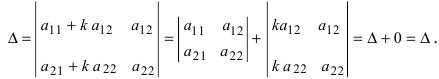

Второй определитель равен нулю по свойству 5.

Замечание: Данное свойство применяется для обнуления всех элементов какой-либо строки (столбца) за исключением одного (метод обнуления), что существенно снижает трудоемкость вычисления определителей порядка выше 3 (см. также свойство 9.).

9. [Метод раскрытия определителя по элементам какой-либо строки (или столбца); универсальный способ вычисления определителя любого порядка]. Определитель любого порядка равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения:

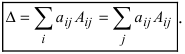
Пример:

Вычислить определитель 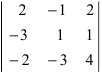по элементам 3 строки и по элементам 2 столбца.

Решение:

Воспользуемся свойством 9.: раскроем определитель по элементам 3 строки 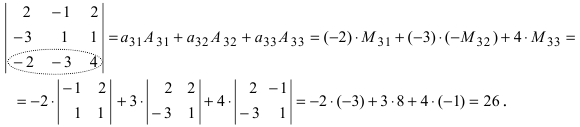Вычислим определитель по элементам 2 столбца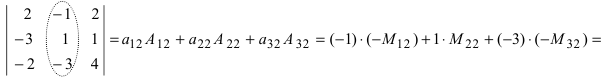

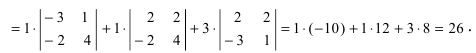
Из полученных результатов видно, что свойство 9. является универсальным методом вычисления любых определителей по элементам любой строки или столбца.

Используя свойство 8. можно обнулить все элементы какой-либо строки (столбца) за исключением одного (метод обнуления), а затем раскрыть определитель по элементам этой строки, воспользовавшись свойством 9.

Пример:

Вычислить определитель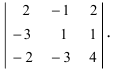

Решение:

Обнулим элементы в третьей строке, для чего выполним следующие действия: (по свойству 4. из третьей строки вынесем множитель 2) 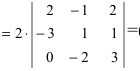используя свойство 8., умножим все элементы второго столбца на 1.5 и прибавим к соответствующим элементам третьего столбца, получим)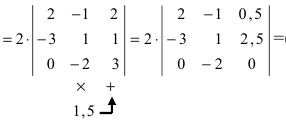

(по свойству 4. из третьего столбца вынесем множитель 0,5, тогда множитель перед определителем станет равным 1)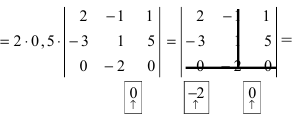

(раскроем определитель по элементам третьей строки: 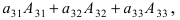выше из определителя третьего порядка вычеркнута третья строка с нулями и второй столбец, т.е. показан необходимый для дальнейших вычислений минор 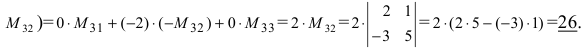Таким образом, метод обнуления позволяет значительно ускорить процесс вычисления любого определителя.

Пример:

Решить уравнение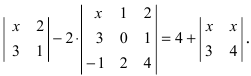

Решение:

Вычислим определители второго и третьего порядков согласно вышеописанным правилам:

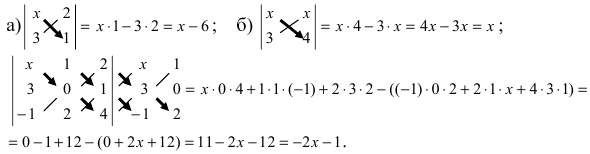
Найденные величины подставим в исходное уравнение

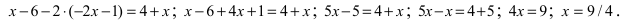
Пример:

Решить неравенство

Решение:

Вычислим определители второго и третьего порядков согласно вышеописанным правилам: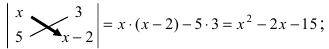

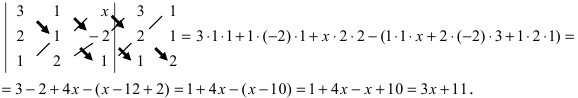
Найденные величины подставим в исходное неравенство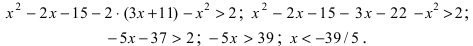

Пример:

Вычислить определитель четвертого порядка (аналогично выполнить такие же действия с определителем третьего порядка), преобразовав его так, чтобы три элемента некоторого ряда равнялись нулю, и вычислить полученный определитель по элементам этого ряда:

Решение:

Во второй строке исходного определителя присутствуют 1 и 0, поэтому обнуление элементов будем производить в этой строке (при обнулении элементов в строке действия производят со столбцами и наоборот): 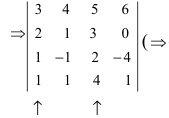– строка обнуления; 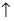– столбцы, с которыми производят действия)=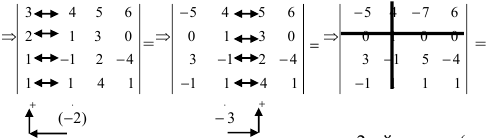

(по методу обнуления раскроем определитель по элементам 2-ой строки ( – цифры, с которыми производятся действия))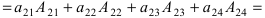

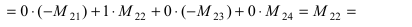
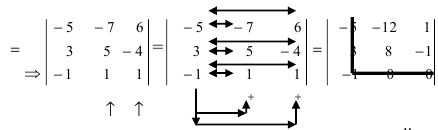(по универсальному методу раскроем определитель по элементам третьей строки)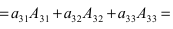

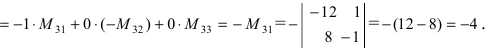
Определители

Перестановкой чисел 1, 2,…, n называется любое расположение этих чисел в определенном порядке. В элементарной алгебре доказывается, что число всех перестановок, которые можно образовать из n чисел, равно 12…n = n!. Например, из трех чисел 1, 2, 3 можно образовать 3!=6 перестановок: 123, 132, 312, 321, 231, 213. Говорят, что в данной перестановке числа i и j составляют инверсию (беспорядок), если i>j, но i стоит в этой перестановке раньше j, то есть если большее число стоит левее меньшего.

Перестановка называется четной (или нечетной), если в ней соответственно четно (нечетно) общее число инверсий. Операция, посредством которой от одной перестановки переходят к другой, составленной из тех же n чисел, называется подстановкой n-ой степени.

Подстановка, переводящая одну перестановку в другую, записывается двумя строками в общих скобках, причем числа, занимающие одинаковые места в рассматриваемых перестановках, называются соответствующими и пишутся одно под другим. Например, символ 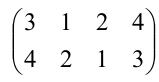обозначает подстановку в которой 3 переходит в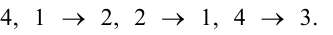

Подстановка называется четной (или нечетной), если общее число инверсий в обеих строках подстановки четно (нечетно). Всякая подстановка n-ой степени может быть записана в виде т.е. с натуральным расположением чисел в верхней строке.

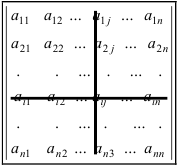
Пусть нам дана квадратная матрица порядка n

Рассмотрим все возможные произведения по n элементов этой матрицы, взятых по одному и только по одному из каждой строки и каждого столбца, т.е. произведений вида:

где индексы 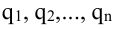составляют некоторую перестановку из чисел 1, 2,…,n. Число таких произведений равно числу различных перестановок из n символов, т.е. равно n!. Знак произведения (4.4) равен (-1)^q где q – число инверсий в перестановке вторых индексов элементов.

Определителем n-го порядка, соответствующим матрице (4.3), называется алгебраическая сумма n! членов вида (4.4). Для записи определителя употребляется символ 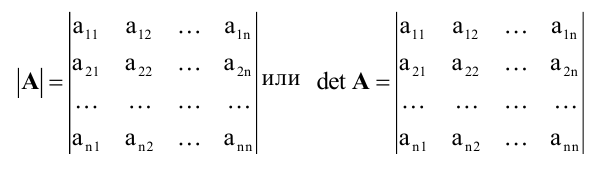(детерминант, или определитель, матрицы А).

Свойства определителей:

1. Определитель не меняется при транспонировании.
2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.
3. Если в определителе переставить две строки, определитель поменяет знак.
4. Определитель, содержащий две одинаковые строки, равен нулю.
5. Если все элементы некоторой строки определителя умножить на некоторое число 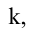то сам определитель умножится на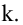
6. Определитель, содержащий две пропорциональные строки, равен нулю.
7. Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых 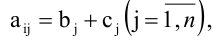то определитель равен сумме определителей, у которых все строки, кроме i-ой, – такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов 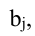в другом – из элементов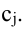
8. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число.

Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы.

Минором 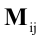элемента 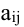определителя d n-го порядка называется определитель порядка n-1, который получается из d вычеркиванием строки и столбца, содержащих данный элемент.

Алгебраическим дополнением элемента 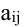определителя d называется его минор 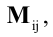взятый со знаком 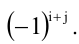Алгебраическое дополнение элемента 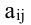будем обозначать 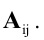Таким образом,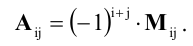

Способы практического вычисления определителей, основанные на том, что определитель порядка n может быть выражен через определители более низких порядков, дает следующая теорема.

• Заказать решение задач по высшей математике

Теорема (разложение определителя по строке или столбцу).

Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки 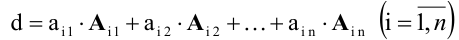или j- го столбца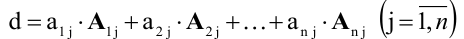

В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.

Пример:

Не вычисляя определителя 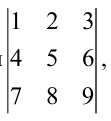показать, что он равен нулю.

Решение:

Вычтем из второй строки первую, получим определитель 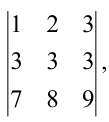равный исходному. Если из третьей строки также вычесть первую, то получится определитель 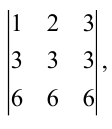в котором две строки пропорциональны.

Такой определитель равен нулю.

Пример:

Вычислить определитель 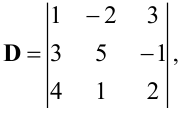разложив его по элементам второго столбца.

Решение:

Разложим определитель по элементам второго столбца: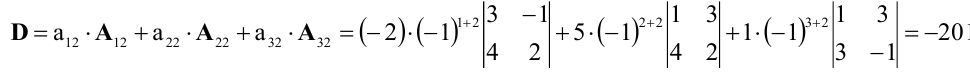

Пример:

Вычислить определитель в котором все элементы по одну сторону от главной диагонали равны нулю.

Решение:

Разложим определитель А по первой строке:

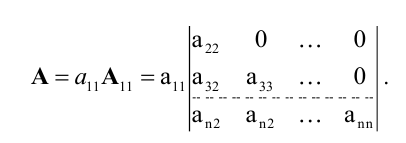
Определитель, стоящий справа, можно снова разложить по первой строке, тогда получим: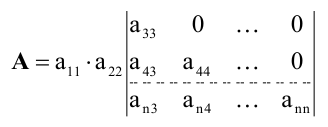

И так далее. После n шагов придем к равенству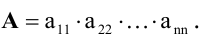

Пример:

Вычислить определитель

Решение:

Если к каждой строке определителя, начиная со второй, прибавить первую строку, то получится определитель, в котором все элементы, находящиеся ниже главной диагонали, будут равны нулю. А именно, получим определитель: равный исходному.

Рассуждая, как в предыдущем примере найдем, что он равен произведению элементов главной диагонали, т.е. n!. Способ, с помощью которого вычислен данный определитель, называется способом приведения к треугольному виду.

——- в вышмате

Определители. Алгебраические дополнения

Внимание! Понятие определителя вводится только для квадратной матрицы.

Матрица называется квадратной порядка n, если количество ее строк совпадает с количеством столбцов и равно n.

Элементы квадратной матрицы, имеющие одинаковые значения индексов, составляют главную диагональ. Элементы квадратной матрицы порядка n, сумма индексов каждого из которых равна n+1, составляют побочную диагональ.

Определитель матрицы 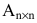обозначается одним из следующих символов: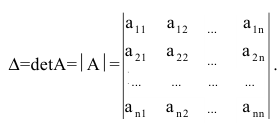

Внимание! Определитель – это число, характеризующее квадратную мат- рицу.

Определитель матрицы второго порядка равен разности элементов главной и побочной диагоналей соответственно:

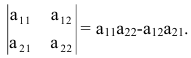
Определитель матрицы третьего порядка равен сумме элементов главной диагонали и элементов, расположенных в вершинах треугольников с основаниями, параллельными главной диагонали, а также разности элементов побочной диагонали и элементов, расположенных в вершинах треугольников с основаниями, параллельными побочной диагонали.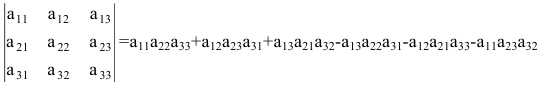

Схематично это правило изображается так (правило треугольника):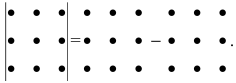

Например,

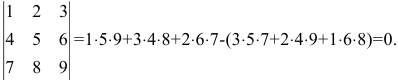Квадратная матрица называется верхней (нижней) треугольной, если все элементы, стоящие под (над) главной диагональю равны нулю.

Отметим некоторые свойства определителя.

1. Определитель треугольной матрицы равен произведению элементов главной диагонали.
2. При транспонировании матрицы ее определитель не изменяется.
3. От перестановки двух рядов (строк или столбцов) определитель меняет знак.
4. Общий множитель всех элементов некоторого ряда определителя можно выносить за знак определителя.
5. Если все элементы какого-нибудь ряда матрицы равны нулю, то определитель равен нулю.
6. Определитель, содержащий два пропорциональных ряда, равен нулю.
7. Определитель не изменится, если к элементам какого-либо ряда прибавить соответствующие элементы другого ряда, умноженные на одно и то же число.
8. Определитель произведения двух матриц одинакового порядка равен произведению определителей этих матриц.

Минором элемента 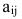определителя n-го порядка называется определитель (n-l)-ro порядка, получаемый вычеркиванием i-й строки и j-ro столбца, на пересечении которых стоит этот элемент. Обозначение: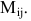

Алгебраическим дополнением элемента 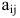называется его минор, умноженный на 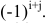Обозначение: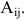

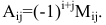
Теорема разложения.

Определитель матрицы равен сумме произведений элементов любого ряда на их алгебраические дополнения.

Пример №2

Вычислить определитель, разлагая его по элементам первой строки: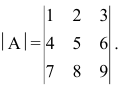

Решение:

По теореме разложения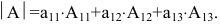

Найдем алгебраические дополнения элементов матрицы А: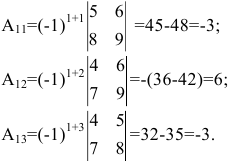

Следовательно,

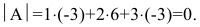
Для вычисления определителя порядка выше третьего удобно пользоваться теоремой разложения (метод понижения порядка) или методом приведения определителя к треугольному виду.

Пример №3

Вычислить определитель, приведя его к треугольному виду:

Решение:

Применяя свойство 6 определителей, преобразуем последовательно второй, третий, четвертый столбцы матрицы.

1. прибавили ко второму столбцу первый, умноженный на -2;
2. прибавили к третьему столбцу первый, умноженный на -3;
3. прибавили к четвертому столбцу первый, умноженный на -4;
4. применили свойство 1 определителей.

Вычисление определителя методом сведения к треугольному виду.

Метод сведения определителя к треугольному виду использует те же преобразования, что и метод эффективного понижения порядка. Только при вычислении определителя методом эффективного понижения порядка мы постепенно уменьшаем порядок определителя, а для метода сведения к треугольному виду порядок определителя остаётся неизменным до конца процесса решения. Суть метода сведения к треугольному виду такова: с помощью действий со строками (или столбцами) преобразовать определитель к виду, когда все элементы, лежащие ниже (или выше) главной диагонали равны нулю. Т.е. после преобразований определитель должен принять одну из двух форм (элементы на главной диагонали выделены синим цветом):

$$
left|begin{array}{ccccc}
normblue{a_{11}} & a_{12} & a_{13} & ldots & a_{1n}\
0 & normblue{a_{22}} & a_{23} & ldots & a_{2n}\
0 & 0 & normblue{a_{33}} & ldots & a_{3n}\
. & . & . & ldots & .\
0 & 0 & 0 & ldots & normblue{a_{nn}}
end{array} right|;;

left|begin{array}{ccccc}
normblue{a_{11}} & 0 & 0 & ldots & 0\
a_{21} & normblue{a_{22}} & 0 & ldots & 0\
a_{31} & a_{32} & normblue{a_{33}} & ldots & 0\
. & . & . & ldots & .\
a_{n1} & a_{n2} & a_{n3} & ldots & normblue{a_{nn}}
end{array} right|.
$$

Хотя разницы и нет, обычно приводят к первому случаю, когда нули расположены под главной диагональю. После преобразований определитель вычисляется простым умножением элементов, расположенных на главной диагонали. Для того, чтобы обнулить требуемые элементы и вычислить определитель, нам пригодятся несколько свойств определителей, которые указаны в теме “Некоторые свойства определителей”. Я запишу ниже несколько свойств, которые нам пригодятся при решении. В примечании после каждого свойства будет указан пример его применения.

1. Если поменять местами две строки (столбца) определителя, то знак определителя изменится на противоположный.

   Пример применения этого свойства: показатьскрыть

2. Определитель не изменится, если ко всем элементам некоей строки (столбца) прибавить соответствующие элементы иной строки (столбца), умноженные на произвольное число.

   Пример применения этого свойства: показатьскрыть

3. Если все элементы строки (столбца) имеют общий множитель, то этот множитель можно вынести за знак определителя.

   Пример применения этого свойства: показатьскрыть

4. Определитель верхней треугольной или нижней треугольной матрицы равен произведению элементов, расположенных на главной диагонали.

   Пример применения этого свойства: показатьскрыть

Буквами $r$ (от слова “row”) станем обозначать строки: $r_1$ – первая строка, $r_2$ – вторая строка и так далее. Буквами $c$ (от слова “column”) станем обозначать столбцы: $c_1$ – первый столбец, $c_2$ – второй столбец и так далее.

Пример №1

Найти определитель $Delta = left|begin{array} {cccc}
-8 & 2 & 9 & 17\
-3 & 1 & 2 & 6\
13 & -3 & -7 & -26\
11 & 1 & 23 & 6end{array}right|$.

Решение

В принципе, начинать решение можно и не преобразовывая определитель. Однако очень удобно, когда первым элементом первой строки является единица (ну, или (-1) на крайний случай). Единицы есть во втором столбце нашего определителя. Сделаем так, чтобы второй столбец стал первым. Для этого просто поменяем местами первый и второй столбцы, используя свойство (1). Не забываем, что при смене мест двух столбцов перед определителем появится знак “минус”:

$$Delta = left|begin{array} {cccc}
-8 & 2 & 9 & 17\
-3 & 1 & 2 & 6\
13 & -3 & -7 & -26\
11 & 1 & 23 & 6end{array}right|=-left|begin{array} {cccc}
2 & -8 & 9 & 17\
1 & -3 & 2 & 6\
-3 & 13 & -7 & -26\
1 & 11 & 23 & 6end{array}right|.$$

Итак, столбцы поменяли, однако единица покамест не вышла на первое место в первой строке, – но это дело поправимое. Поменяем местами первую и вторую строки, при этом перед определителем вновь возникнет знак “минус”. Ну, а так как “минус” на “минус” даёт “плюс”, то получим мы следующее:

$$Delta =-left|begin{array} {cccc}
2 & -8 & 9 & 17\
1 & -3 & 2 & 6\
-3 & 13 & -7 & -26\
1 & 11 & 23 & 6end{array}right|=-left( -left|begin{array} {cccc}
1 & -3 & 2 & 6\
2 & -8 & 9 & 17\
-3 & 13 & -7 & -26\
1 & 11 & 23 & 6end{array}right|right)=
left|begin{array} {cccc}
1 & -3 & 2 & 6\
2 & -8 & 9 & 17\
-3 & 13 & -7 & -26\
1 & 11 & 23 & 6end{array}right|.$$

Начнём решение. Нам нужно получить нули под главной диагональю. Для этого придётся осуществить несколько шагов, на которых будем изменять строки нашего определителя. На первом шаге мы должны сделать так, чтобы все элементы первого столбца стали нулями – кроме элемента на главной диагонали, выделенного красным цветом:

$$
left|begin{array} {cccc}
boldred{1} & -3 & 2 & 6\
normgreen{2} & -8 & 9 & 17\
normblue{-3} & 13 & -7 & -26\
normpurple{1} & 11 & 23 & 6end{array}right|
$$

Преобразования со строками, которые нужно выполнить, чтобы обнулить “серые” элементы, получаются так:

$$
begin{aligned}
&r_2-frac{normgreen{2}}{boldred{1}}cdot{r_1}=r_2-2r_1;\
&r_3-frac{normblue{-3}}{boldred{1}}cdot{r_1}=r_3+3r_1;\
&r_4-frac{normpurple{1}}{boldred{1}}cdot{r_1}=r_4-r_1.
end{aligned}
$$

Запись $r_2-2r_1$ означает, что от элементов второй строки вычли соответствующие элементы первой строки, умноженные на два. Полученный результат записали вместо прежней второй строки. Остальные записи расшифровываются аналогично. Согласно свойству (2) значение определителя от таких действий не изменится. Для наглядности я запишу это действие отдельно:

$$
r_2-2r_1
=(2;;-8;;9;;17)-2cdot(1;;-3;;2;;6)
=(2;;-8;;9;;17)-(2;;-6;;4;;12)
=(0;;-2;;5;;5).
$$

После выполнения всех требуемых операций со строками, мы получим новый определитель. Записывается это так:

$$
Delta=left|begin{array} {cccc}
1 & -3 & 2 & 6\
2 & -8 & 9 & 17\
-3 & 13 & -7 & -26\
1 & 11 & 23 & 6end{array}right|
begin{array} {l} phantom{0} \ r_2-2r_1 \ r_3+3r_1 \ r_4-r_1 end{array}=
left|begin{array} {cccc}
1 & -3 & 2 & 6\
0 & -2 & 5 & 5\
0 & 4 & -1 & -8 \
0 & 14 & 21 & 0end{array}right|.

$$

Перед тем, как мы пойдём дальше, обратим внимание на то, что все элементы четвёртой строки делятся на 7. Согласно свойству (3) число 7 можно вынести за знак определителя:

$$
left|begin{array} {cccc}
1 & -3 & 2 & 6\
0 & -2 & 5 & 5\
0 & 4 & -1 & -8 \
0 & 14 & 21 & 0end{array}right|=7cdot
left|begin{array} {cccc}
1 & -3 & 2 & 6\
0 & -2 & 5 & 5\
0 & 4 & -1 & -8 \
0 & 2 & 3 & 0end{array}right|
$$

Теперь нам нужно обнулить элементы во втором столбце (под главной диагональю). Т.е., обнулению подлежат элементы, выделенные зелёным и синим цветом. Элемент на главной диагонали, который останется без изменений, выделен красным цветом:

$$
left|begin{array} {cccc}
1 & -3 & 2 & 6\
0 & boldred{-2} & 5 & 5\
0 & normblue{4} & -1 & -8 \
0 & normblue{2} & 3 & 0end{array}right|
$$

А если бы вместо числа -2 возник ноль? показатьскрыть

В принципе, мы можем получить (-1) на месте диагонального “красного элемента”. Для этого достаточно поменять местами второй и третий столбцы, а затем поменять местами вторую и третью строки. Однако в нашем случае этого можно и не делать, так как все “синие элементы” нацело делятся на “красный элемент”, т.е. на (-2). Следовательно, никакой работы с дробями не предвидится. Впрочем, тут дело вкуса: можете попробовать для тренировки продолжить решение, поменяв местами строки и столбцы, чтобы “красным элементом” стала (-1). Выполним такие операции со строками:

$$
begin{aligned}
&r_3-frac{normblue{4}}{boldred{-2}}cdot{r_2}=r_3+2r_2;\
&r_4-frac{normblue{2}}{boldred{-2}}cdot{r_2}=r_4+r_2.
end{aligned}
$$

Отдельно выписывать действия со строками не станем, так как они полностью аналогичны рассмотренным ранее. Наш определитель станет таким:

$$
Delta=7cdot
left|begin{array} {cccc}
1 & -3 & 2 & 6\
0 & -2 & 5 & 5\
0 & 4 & -1 & -8 \
0 & 2 & 3 & 0end{array}right|
begin{array} {l} phantom{0} \ phantom{0} \ r_3+2r_2 \ r_4+r_2end{array}=

7cdot left|begin{array} {cccc}
1 & -3 & 2 & 6\
0 & -2 & 5 & 5\
0 & 0 & 9 & 2 \
0 & 0 & 8 & 5end{array}right|.
$$

Осталось последнее действие. Нужно обнулить элемент 8 под главной диагональю:

$$
left|begin{array} {cccc}
1 & -3 & 2 & 6\
0 & -2 & 5 & 5\
0 & 0 & 9 & 2 \
0 & 0 & boldred{8} & 5end{array}right|
$$

Тут уже придется поработать с дробями. Обычно такой работы стараются избегать – и до этого момента нам это удавалось – но теперь уже деваться некуда:

$$
Delta = 7cdot left|begin{array} {cccc}
1 & -3 & 2 & 6\
0 & -2 & 5 & 5\
0 & 0 & 9 & 2 \
0 & 0 & 8 & 5end{array}right|
begin{array} {l} phantom{0} \ phantom{0} \ phantom{0} \ r_4-frac{8}{9}r_3 end{array}=

7cdot left|begin{array} {cccc}
1 & -3 & 2 & 6\
0 & -2 & 5 & 5\
0 & 0 & 9 & 2 \
0 & 0 & 0 & frac{29}{9}end{array}right|.
$$

Преобразования окончены. Осталось лишь использовать свойство (4) и переменожить элементы, расположенные на главной диагонали:

$$
Delta=7cdot 1cdot (-2)cdot 9 cdot frac{29}{9}=-406.
$$

Ответ получен. Полное решение без пояснений выглядит так:

$$
Delta
= left|begin{array} {cccc}
-8 & 2 & 9 & 17\
-3 & 1 & 2 & 6\
13 & -3 & -7 & -26\
11 & 1 & 23 & 6end{array}right|
=[c_1leftrightarrow{c_2}]
=left|begin{array} {cccc}
2 & -8 & 9 & 17\
1 & -3 & 2 & 6\
-3 & 13 & -7 & -26\
1 & 11 & 23 & 6end{array}right|
=[r_1leftrightarrow{r_2}]=\

=left|begin{array} {cccc}
1 & -3 & 2 & 6\
2 & -8 & 9 & 17\
-3 & 13 & -7 & -26\
1 & 11 & 23 & 6end{array}right|
begin{array} {l} phantom{0} \ r_2-2r_1 \ r_3+3r_1 \ r_4-r_1 end{array}=

7cdot left|begin{array} {cccc}
1 & -3 & 2 & 6\
0 & -2 & 5 & 5\
0 & 4 & -1 & -8 \
0 & 2 & 3 & 0end{array}right|
begin{array} {l} phantom{0} \ phantom{0} \ r_3+2r_2 \ r_4+r_2 end{array}=\

=7cdot left|begin{array} {cccc}
1 & -3 & 2 & 6\
0 & -2 & 5 & 5\
0 & 0 & 9 & 2 \
0 & 0 & 8 & 5end{array}right|
begin{array} {l} phantom{0} \ phantom{0} \ phantom{0} \ r_4-frac{8}{9}r_3end{array}

=7cdot left|begin{array} {cccc}
1 & -3 & 2 & 6\
0 & -2 & 5 & 5\
0 & 0 & 9 & 2 \
0 & 0 & 0 & frac{29}{9}end{array}right|

=7cdot 1cdot (-2)cdot 9 cdot frac{29}{9}=-406.
$$

Ответ: $Delta=-406$.

В принципе, преобразования метода сведения к треугольному виду просты, однако стоит иметь в виду свойства определителей, изложенные соответствующей теме. Например, на каком-то шаге может обнулиться строка или столбец, или же окажется, что некие строки или столбцы пропорциональны. Это будет означать, что рассматриваемый определитель равен 0.