Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 марта 2021 года; проверки требуют 4 правки.
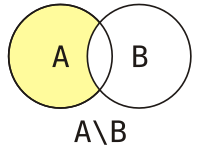
Ра́зность двух мно́жеств — теоретико-множественная операция, результатом которой является множество, в которое входят все элементы первого множества, не входящие во второе множество.
Обычно разность множеств 
и 
обозначается как 
,
но иногда можно встретить обозначение 
и 
.
Пусть и — два указанных в определении множества, тогда их разность определяется (на теоретико-множественном языке):
Это множество часто называют дополнением множества до множества . (только когда множество В полностью принадлежит множеству А)
Обычно предполагается, что рассматриваются подмножества одного и того же множества, которое, в этом случае называют универсумом, скажем, 
. Тогда можно рассматривать вместе с каждым множеством 
и его относительное дополнение 
, при обозначении которого часто опускается значок универсума: 
[источник не указан 2516 дней]; при этом говорится, что — (просто) дополнение множества (без указания, дополнением до чего является данное множество).
С учётом данного замечания, оказывается, что 
, то есть дополнение множества до множества есть пересечение множества и дополнения множества .
Также применяется и операторная запись вида 
, 
или (если опустить универсальное множество) 
, 
, 
.
Операция разности множеств не является по определению симметричной по отношению ко входящим в неё множествам. Симметричный вариант теоретико-множественной разности двух множеств описывается понятием симметрической разности.
Примеры[править | править код]
Свойства[править | править код]
Пусть 
— произвольные множества.
- Вычитание множества из самого себя даёт в результате пустое множество:
- Свойства пустого множества относительно разности:
- Разность двух множеств содержится в уменьшаемом:
- Разность множеств равна пустому множеству тогда и только тогда, когда уменьшаемое содержится в вычитаемом:
- Законы де Моргана в алгебре множеств формулируются следующим образом:
Компьютерные реализации[править | править код]
В пакете Mathematica операция реализована с помощью функции Complement. В пакете MATLAB она же реализована с помощью функции setdiff.
В языке программирования Pascal (а также в его объектном расширении Object Pascal) операция разности множеств представлена оператором «−», обоими операндами и результатом выполнения которого являются значения типа set.
В языке программирования Python операция реализована с помощью метода diff над объектом типа set.
Дополнение множества[править | править код]
Определение[править | править код]
Если из контекста следует, что все рассматриваемые множества являются подмножествами некоторого фиксированного универсума , то определяется операция дополнения:
Свойства[править | править код]
- Операция дополнения является унарной операцией на булеане
. - Законы дополнения:[1]
-
- В частности, если оба и непусты, то является разбиением .
- Операция дополнения является инволюцией:
- Законы де Моргана:
- Законы разности множеств:
Кодировка[править | править код]
| Графема | Название | Юникод | HTML | LaTeX |
|---|---|---|---|---|
| ∁ | COMPLEMENT | U+2201 | ∁
|
complement
|
См. также[править | править код]
- Операции над множествами
Литература[править | править код]
- Лавров И. А., Максимова Л. Л. Задачи по теории множеств, математической логике и теории алгоритмов. — М.: Физматлит, 2004. — 256 с.
- Куратовский К., Мостовский А. Теория множеств / Пер. с англ. М. И. Кратко, под ред. А. Д. Тайманова. — М.: Мир, 1970. — С. 16, 20—22.
Примечания[править | править код]
- ↑ Ильин В. А., Садовничий В. А., Сендов Бл. Х.. Глава 2. Вещественные числа // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 66. — 672 с. — ISBN 5-482-00445-7.
Порой обучение продвигается с трудом. Сложная теория, непонятные задания… Хочется бросить. Не сдавайтесь, все сложности можно преодолеть. Рассказываем, как
Не понятна формулировка, нашли опечатку?
Выделите текст, нажмите ctrl + enter и опишите проблему, затем отправьте нам. В течение нескольких дней мы улучшим формулировку или исправим опечатку
Что-то не получается в уроке?
Загляните в раздел «Обсуждение»:
- Изучите вопросы, которые задавали по уроку другие студенты — возможно, ответ на ваш уже есть
- Если вопросы остались, задайте свой. Расскажите, что непонятно или сложно, дайте ссылку на ваше решение. Обратите внимание — команда поддержки не отвечает на вопросы по коду, но поможет разобраться с заданием или выводом тестов
- Мы отвечаем на сообщения в течение 2-3 дней. К «Обсуждениям» могут подключаться и другие студенты. Возможно, получится решить вопрос быстрее!
Подробнее о том, как задавать вопросы по уроку
Лекция 4. Вычитание
множеств, дополнение подмножества.
Определение. Разностью множеств
А и В называется множество, содержащее те и только те элементы, которые
принадлежат множеству А и не принадлежат множеству В.
Разность множеств А и В обозначают А В. Таким образом, по определению
разности А В = { х | х ∈
А и х ∉В}.
Например, если А = { a , c , k , m , n }
и В = { a , b , c , d , e }, то
А В = { k , m , n }.
Если
изобразить А и В при помощи кругов Эйлера-Венна, то разность данных множеств
является заштрихованная область (рис. 5).
Определение. Пусть В является подмножеством
множества А. В этом случае разность множеств А и В называют дополнением подмножества
В до множества А и обозначают В’А. Дополнение можно изобразить
как показано на рис. 5. Если В – подмножество универсального множества U, то
дополнение подмножества В до U обозначают В’.
Например, если В – множество однозначных
натуральных чисел, то В’– множество неоднозначных натуральных чисел, если С –
множество равнобедренных треугольников, то С’ – множество треугольников, у
которых все стороны имеют разную длину.
Разность множеств и дополнение к подмножеству
обладают рядом свойств.
1) (А В) С = (А С)
В.
2) (А∪В)
С = (А С) ∪ (В С).
3) (А В) ∩ С = (А ∩С)
(В ∩ С).
4) (А ∪
В)’ = А’ ∩ В’.
5) (А ∩ В)’ = А’ ∪В’.
Задания для самостоятельной работы по теме:
1.
Найдите разность множеств А и В, если
а) А = {1,2, 3,4,
5, 6}, В = {2, 4, 6, 8, 10};
б) А =
{1,2,3,4,5,6},В={1,3,5};
в) А =
{1,2,3,4,5,6},В={6,2,3,4,5,1}.
2. В
каких случаях, выполняя упражнение 1, вы находили дополнение множества В до
множества А?
3.
Из каких чисел состоит дополнение:
а) множества натуральных
чисел до множества целых;
б) множества целых чисел
до множества рациональных;
в) множества рациональных
чисел до множества действительных.
Если заданы два
множества, то можно не только найти их
пересечение и объединение, но и вычесть
из одного множества другое. Результат
вычитания называют разностью и
определяют следующим образом.
Определение.
Разностью множеств А и В называют
множество, содержащее все элементы,
которые принадлежат множеству А и не
принадлежат множеству В.
Разность множеств
А и В обозначают А В. По определению: А
В ={х/х∈А
и х∉В}.
В школьном курсе
математики чаще всего приходится
выполнять вычитание множеств в случае,
когда одно из них является подмножеством
другого, при этом разность множеств А
В называют дополнением множества В
до множества А, и обозначают символом
В´А,
а наглядно изображают так:
Определение:
Пусть В⊂ А.
Дополнением множества В до множества
А называется множество, содержащее все
элементы множества А, которые не
принадлежат множеству В.
По определению:
В´А
={х/х∈А
и х∉В}.
Выясним, как
находить дополнение подмножества на
конкретных примерах.
Если элементы
множеств А и В перечислены и В ⊂
А, достаточно перечислить элементы,
принадлежащие множеству А и не
принадлежащие множеству В. Например, А
= {1, 2, 3, 4, 5}, В = {2, 4}, то В´А
= {1, 3, 5}.
В том случае, когда
указаны характеристические свойства
элементов множеств А и В и известно, что
В ⊂ А, то
множество В´А
задают также с помощью характеристического
свойства, общий вид которого «х∈А
и х∉В».
Так, если А – множество четных чисел, а
В – множество кратных 4 чисел, то В´А
– это множество, содержащее такие
четные числа, которые не делятся на 4.
Например, 22∈
В´А.
Вычитание–
это третья операция над множествами.
Условились считать, чтопересечение
– более «сильная» операция, чем вычитание.Что касается вычитания и объединения,
то их считают равноправными.
Вычитание множеств
обладает рядом свойств. В частности
можно доказать, что для любых множеств
А, В и С справедливы следующие равенства:
1) (А
В) С =
(А С) В);
2)
(А∪ В)
С = (А С)∪ (В
С);
-
(А
В)∩ С
= (А∩ С)
(В∩ С); -
А
(В∪ С)
= (А В)
∩(А С); -
А
(В∩ С)
= (А В)
∪(А С).
8. Понятие разбиения множества на классы с помощью одного, двух, трех свойств
Понятия множества
и операций над множествами позволяют
уточнить наше представление о классификации
– действии распределения объектов по
классам.
Классификацию мы
выполняем достаточно часто. Так,
натуральные числа представляем как два
класса – четные и нечетные. Углы на
плоскости разбиваем на три класса:
прямые, острые и тупые.
Любая классификация
связана с разбиением некоторого множества
объектов на подмножества. При этом
считают, что множество Х разбито на
классы Х₁, Х₂,
…, Хn,…, если:
-
подмножества Х₁,
Х₂, …, Хn,…
попарно не пересекаются; -
объединение
подмножеств Х₁,
Х₂, …, Хn,
… совпадает с множеством Х.
Если не выполнено
хотя бы одно из условий, классификацию
считают неправильной. Например, если
из множества Х треугольников выделить
подмножества равнобедренных, равносторонних
и разносторонних треугольников, то
разбиения мы не получим, поскольку
подмножества равнобедренных и
равносторонних треугольников пересекаются
(все равносторонние треугольники
являются равнобедренными). В данном
случае не выполнено первое условие
разбиения множества на классы.
Так как разбиение
множества на классы связано с выделением
его подмножеств, то классификацию можно
выполнять при помощи свойств элементов
множеств.
Рассмотрим,
например, множество натуральных чисел.
Его элементы обладают различными
свойствами.
Положим,.000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000что нас интересуют числа, обладающие
свойством «быть кратным 3». Это свойство
позволяет выделить из множества
натуральных чисел подмножество, состоящее
из чисел, кратных 3. Тогда про остальные
натуральные числа можно сказать, что
они не кратны 3, т.е. получаем еще одно
подмножество множества натуральных
чисел. Так как выделенные подмножества
не пересекаются, а их объединение
совпадает с множеством натуральных
чисел, то имеем разбиение этого множества
на два класса.
NN
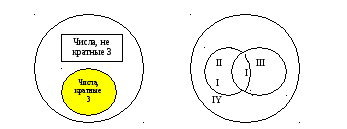
Вообще, если на
множестве Х задано одно свойство, то
это множество разбивается на два класса.
Первый – это класс объектов, обладающий
этим свойством, а второй – дополнение
первого класса до множества Х. Во втором
классе содержатся такие объекты множества
Х, которые заданным свойством не обладают.
Такую классификацию называют
дихотомической.
Рассмотрим ситуацию,
когда для элементов множества заданы
два свойства. Например, «быть кратным
3» и «быть кратным 5». При помощи этих
свойств из множества натуральных чисел
можно выделить два подмножества: А –
подмножество чисел, кратных 3, и В –
подмножество чисел, кратных 5. Эти
множества пересекаются, но ни одно из
них не является подмножеством другого.
Проанализируем получившийся рисунок
(справа). Конечно, разбиения множества
натуральных чисел на подмножества А и
В не произошло. Но круг, изображающий
множество N, можно
рассматривать как состоящий из четырех
непересекающихся областей – на рисунке
они пронумерованы. Каждая область
изображает некоторое подмножество
множестваN. ПодмножествоIсостоит из чисел, кратных
3 и 5; подмножествоII– из
чисел, кратных 3 и не кратных 5; подмножествоIII– из чисел, кратных 5
и не кратных 3; подмножествоIY– из чисел, не кратных 3 и не кратных 5.
Объединение этих четырех подмножеств
есть множествоN.
Таким образом,
выделение двух свойств привело к
разбиению множества Nнатуральных чисел на четыре класса.
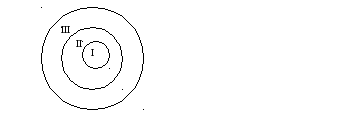
Не следует думать,
что задание двух свойств элементов
множества всегда приводит к разбиению
этого множества на четыре класса.
Например, при помощи двух таких свойств
«быть кратным 3» и «быть кратным 6»
множество натуральных чисел разбивается
на три класса: I– класс
чисел, кратных 6;II– класс
чисел, кратных 3; но не кратных 6;III- класс чисел, не кратных 3.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Начало: Математика для чайников. Глава 1. Что такое математическая абстракция.
Предыдущий выпуск: Математика для чайников. Глава 6. Метод математической индукции
Теория множеств – важный раздел математики, потому что очень многие математические понятия определены именно через множества. Например, как я писал в статье Математика для чайников. Глава 4. Алгебра , алгебра – это множество, в котором содержатся абстракции данной алгебры и операции над ними.
Так что же такое множество? Представьте себе такую «волшебную» коробочку, в которою мы можем поместить сколько угодно много предметов. Хоть бесконечно. Но не факт, что там предметов будет именно бесконечность. Сколько положили, столько и будет. Так вот, эта коробочка со всеми положенными в нее предметами и есть множество. Отсюда сразу запомните, что множества могут быть конечными и бесконечными.
А теперь более строго определение множества. Множество – это математический объект, который является совокупностью (набором) других математических объектов, называемых элементами множества . В качестве элемента множества может быть что угодно, в том числе и множество. Но часто задается конкретно, а что может быть элементом множества. Например, если это множество чисел, то его элементами могут быть только числа.
Как задать множество? Можно просто перечислить его элементы. Например вот так: {1,2,3,4}. Можно задать правило, по которому можно определить, принадлежит элемент множеству или нет. Например «множество натуральных чисел», «множество рациональных чисел», «множество натуральных чисел, больших 2». Как правило, множества обозначаются большими буквами. Элементы – маленькими. Если элемент принадлежит множеству, то используют специальный знак:
Читается как «икс принадлежит A ».
Если элемент не принадлежит множеству, то пишем:
Читается «икс не принадлежит А».
Например:
Порядка элементов в множестве не важен. То есть, множества, содержащие одни и те же элементы, равны, например:
Каждый элемент входит в множество один раз. Если добавить ко множеству элемент, который там уже есть, ничего не меняются. То есть, вот эти два множества равны:
Как я уже говорил, элементом множества может быть что угодно. В том числе и точка на плоскости (или в пространстве). Поэтому с целью проиллюстрировать операции над множествами, их рисуют в виде цветных фигурок. В этом случае элементами множества являться точки внутри этих фигурок. И тут возникает вопрос: а граница фигуры принадлежит множеству или нет? На самом деле может быть и так и так. Помните, я выше писал, что множество можно задать правилом, которое определяет, принадлежит ли элемент множеству или нет. А правило может говорить, что граница принадлежит множеству, а может и говорить, что нет. Запомните это, это важная особенность. Часто такая мелочь используется во всяких определениях в математике.
Рассмотрим пример. Принадлежит ли точка x =2, множеству точек отрезка (2,3]?
Обратите внимание, что тут одна скобка круглая, другая квадратная. Круглая скобка обозначает, что граница не включена в множество, а квадратная – что включена. Фактически, тут имеет место неравенство:
Так как левая граница не включена во множество, то
А вот если взять отрезок [2,3] То точка уже будет принадлежать ему:
Часть элементов какого-либо множества, является его подмножеством. Формально определение звучит так: «Множество A называется подмножеством множества B если все элементы, принадлежащие A , так же принадлежат и B . Это определение записывается в виде формулы:
Первая часть
Читается так « A принадлежит B »
Стрелочка с двумя концами означает, что как из левой части следует правая часть, так и наоборот. То есть, из того, что « A принадлежит B » следует, что «все элементы, принадлежащие множеству A , так же принадлежат и B ». Справедливо и обратное: «Если все элементы множества A принадлежат множеству B , то это значит, что множество A является подмножеством множества B ».
Далее, перевернутая буковка “ A ” обозначает квантор всеобщности. И пусть вас не пугает термин «квантор», он лишь означает, что либо что-то действует для всех чего-то там, либо «существуют такие чего-то там». В данном случае выражение
Следует читать «для всех x ». Ну а полностью выражение
Читается как «для всех x принадлежащих A следует, что x принадлежит так же и B ».
Следует заметить, что подмножество может содержать только те элементы которые содержатся в надмножестве (том множестве, подмножеством которого оно является). Если мы добавим к подмножеству хоть один лишний элемент, то это уже не будет подмножеством. Например, множество {1,2,3} является подмножеством множества {1,2,3,4,5}, а множество {1,2,8} уже не является, потому что элемента 8 нет в надмножестве.
Бывает, что пишут:
Это значит, что A не только является подмножеством множества B , но еще и может равняется ему. Собственно говоря, множество является подмножеством самому себе.
А еще есть такое понятие, как пустое множество, которое обозначают знаком:
Пустое множество не содержит никаких элементов и является подмножеством любого множества, в том числе и самого себя. Но, что характерно, пустое множество не является элементом самого себя, так как оно не содержит никаких элементов.
Теперь поговорим об операциях над множествами. Множества можно объединить . Это значит, что мы просто объединяем их элементы в единое множество. Записывается это так:
Графически операцию объединение множеств можно представить так:
Соответственно, количество элементов в объединенном множестве меньше или равно сумме элементов объединяемых множеств. Почему может быть меньше? Потому что и в том и в другом множестве могут быть одинаковые элементы. А повторы, как я уже сказал выше, не считаются, они идут как один элемент. Если объединить множество с сами собой или с пустым множеством – то будет то же самое множество.
Другая операция – это пересечение множеств. При этой операции мы берем только те элементы, которые есть и в том и в другом множестве. Обозначается эта операция так:
Проиллюстрируем то графически:
Как видим, тут возможны несколько ситуаций:
1. Образуется несколько меньшее множество.
2. Итоговое множество полностью совпадают с одним из пересекающихся множеств – случай, когда оно является подмножество другого.
3. Пустое множество. Это когда множества не имеют общих элементов.
Пересечение множества с сами собой равно этому же множеству. А с пустым множеством – пустому множеству.
Разность множеств. Обозначается как
Разностью множеств A и B являться те элементы, которые есть в A но нет в B . По сути, мы из множества A убираем элементы множества B (поэтому и вычитание множеств). То есть по сути вычесть – значит отнят (из множества A отнять множество B ).
Графически это выглядит так:
Как видим, тут тоже возможны разные случаи. Во-первых, при вычитании можно «отрезать» только часть множества. Во-вторых, можно получить то же самое множество. Это будет в том случае, когда мы вычитаем множество, никак не пересекающееся с нашим (то есть не имеющее с ним общих элементов). Наконец, если мы вычитаем из подмножество его надмножество, то получим пустое множество. То же самое будет, если из множества вычесть само себя.
И четвертая операция над множествами – дополнение . Это по сути вычитание множества из некоторого универсального множества, которое содержит все возможные элементы. Обозначается вот так:
Где U – это универсальное множество. Вот графическая иллюстрация данной операции:
На этом урок закончен, но к теме множеств мы еще вернемся, когда будем подробно рассматривать такой раздел математики, как теорию множеств.
Следующая глава: Математика для чайников. Глава 8. Логарифмы
