Как найти элементы трапеции - Сайт, где вы сможете решить свои вопросы

Трапеция. Формулы, признаки и свойства трапеции

Определение.

Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Параллельные стороны называются основами трапеции, а две другие боковыми сторонами

Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.

Элементы трапеции:

Основы трапеции – параллельные стороны
Боковые стороны – две другие стороны
Средняя линия – отрезок, соединяющий середины боковых сторон.

Виды трапеций:

Равнобедренная трапеция – трапеция, у которой боковые стороны равны
Прямоугольная трапеция – трапеция, у которой одна из боковых сторон перпендикулярна основам

Основные свойства трапеции

1. В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:

AB + CD = BC + AD

2. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:

AK = KB, AM = MC, BN = ND, CL = LD

3. Средняя линия трапеции параллельна основаниям и равна их полусумме:

4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.

5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.

6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:

BC : AD = OC : AO = OB : DO

7. Диагонали трапеции d₁ и d₂ связаны со сторонами соотношением:

d₁² + d₂² = 2ab + c² + d²

Сторона трапеции

Формулы определения длин сторон трапеции:

1. Формула длины оснований трапеции через среднюю линию и другую основу:

a = 2m – b

b = 2m – a

2. Формулы длины основ через высоту и углы при нижнем основании:

a = b + h · (ctg α + ctg β)

b = a – h · (ctg α + ctg β)

3. Формулы длины основ через боковые стороны и углы при нижнем основании:

a = b + c·cos α + d·cos β

b = a – c·cos α – d·cos β

4. Формулы боковых сторон через высоту и углы при нижнем основании:

Средняя линия трапеции

Определение.

Средняя линия – отрезок, соединяющий середины боковых сторон трапеции.

Формулы определения длины средней линии трапеции:

1. Формула определения длины средней линии через длины оснований:

2. Формула определения длины средней линии через площадь и высоту:

Высота трапеции

Формулы определения длины высоты трапеции:

1. Формула высоты через сторону и прилегающий угол при основании:

h = c·sin α = d·sin β

2. Формула высоты через диагонали и углы между ними:

h =	sin γ ·	d₁ d₂	=	sin δ ·	d₁ d₂
a + b	a + b

3. Формула высоты через диагонали, углы между ними и среднюю линию:

h =	sin γ ·	d₁ d₂	=	sin δ ·	d₁ d₂
2m	2m

4. Формула высоты трапеции через площадь и длины оснований:

5. Формула высоты трапеции через площадь и длину средней линии:

Диагонали трапеции

Формулы определения длины диагоналей трапеции:

1. Формулы диагоналей по теореме косинусов:

d₁ = √a² + d² – 2ad·cos β

d₂ = √a² + c² – 2ac·cos α

2. Формулы диагоналей через четыре стороны:

d₁ =	√	d ² + ab –	a(d ² – c²)
a – b

d₂ =	√	c² + ab –	a(c² – d ²)
a – b

3. Формула длины диагоналей через высоту:

d₁ = √h² + (a – h · ctg β)² = √h² + (b + h · ctg α)²

d₂ = √h² + (a – h · ctg α)² = √h² + (b + h · ctg β)²

4. Формулы длины диагонали через сумму квадратов диагоналей:

d₁ = √c² + d ² + 2ab – d₂²

d₂ = √c² + d ² + 2ab – d₁²

Площадь трапеции

Формулы определения площади трапеции:

1. Формула площади через основания и высоту:

2. Формула площади через среднюю линию и высоту:

S = m · h

3. Формула площади через диагонали и угол между ними:

S =	d₁d₂	· sin γ	=	d₁d₂	· sin δ
2	2

4. Формула площади через четыре стороны:

S =	a + b	√	c² –	(	(a – b)² + c² – d ²	)	²
2	2(a – b)

5. Формула Герона для трапеции

S =	a + b	√(p – a)(p – b)(p – a – c)(p – a – d)
\|a – b\|

где

p =	a + b + c + d	– полупериметр трапеции.
2

Периметр трапеции

Формула определения периметра трапеции:

1. Формула периметра через основания:

P = a + b + c + d

Окружность описанная вокруг трапеции

Окружность можно описать только вокруг равнобедренной трапеции!!!

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d₁
4√p(p – a)(p – c)(p – d₁)

где

a – большее основание

Окружность вписанная в трапецию

В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:

a + b = c + d

Формула определения радиуса вписанной в трапецию окружности

1. Формула радиуса вписанной окружности через высоту:

Другие отрезки разносторонней трапеции

Формулы определения длин отрезков проходящих через трапецию:

1. Формула определения длин отрезков проходящих через трапецию:

KM = NL =	b	KN = ML =	a	TO = OQ =	a · b
2	2	a + b

Источник

Виды трапеций

Равнобедренная трапеция — это вид трапеции с равными боковыми сторонами.

Также встречаются такие названия, как равнобокая или равнобочная.

Прямоугольная трапеция — это трапеция, у которой углы при боковой стороне прямые.

Элементы трапеции

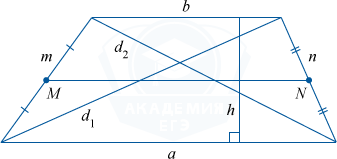
a, b — основания трапеции (a параллельно b),

m, n — боковые стороны трапеции,

d₁, d₂ — диагонали трапеции,

h — высота трапеции (отрезок, соединяющий основания и при этом перпендикулярен им),

MN — средняя линия (отрезок, соединяющий середины боковых сторон).

Площадь трапеции

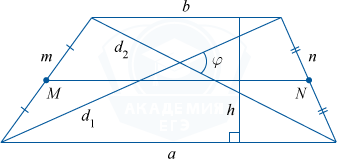
Через полусумму оснований a, b и высоту h: S = frac{a + b}{2}cdot h
Через среднюю линию MN и высоту h: S = MNcdot h
Через диагонали d₁, d₂ и угол (sin varphi) между ними: S = frac{d_{1} d_{2} sin varphi}{2}

Свойства трапеции

Средняя линия трапеции

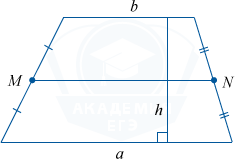
Средняя линия параллельна основаниям, равна их полусумме и разделяет каждый отрезок с концами, находящимися на прямых, которые содержат основания, (к примеру, высоту фигуры) пополам:

MN || a, MN || b, MN = frac{a + b}{2}

Сумма углов трапеции

Сумма углов трапеции, прилежащих к каждой боковой стороне, равна 180^{circ}:

alpha + beta = 180^{circ}

gamma + delta =180^{circ}

Равновеликие треугольники трапеции

Равновеликими, то есть имеющими равные площади, являются отрезки диагоналей и треугольники AOB и DOC, образованные боковыми сторонами.

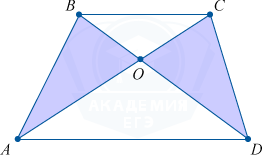
Подобие образованных треугольников трапеции

Подобными треугольниками являются AOD и COB, которые образованы своими основаниями и отрезками диагоналей.

triangle AOD sim triangle COB

Коэффициент подобия k находится по формуле:

k = frac{AD}{BC}

Причем отношение площадей этих треугольников равно k^{2}.

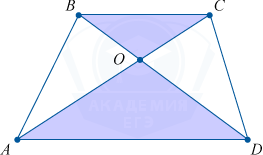
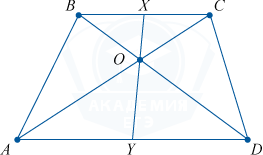
Отношение длин отрезков и оснований

Каждый отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции, поделен этой точкой в отношении:

frac{OX}{OY} = frac{BC}{AD}

Это будет являться справедливым и для высоты с самими диагоналями.

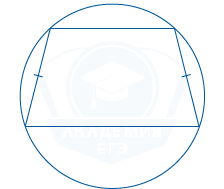
Описанная около трапеции окружность

Каждая равнобокая трапеция может содержать описанную окружность. Только равнобокую трапецию возможно вписать в окружность.

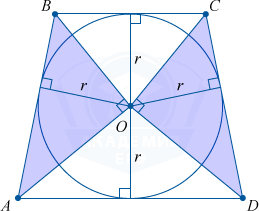
Вписанная в трапецию окружность

Треугольники AOB и DOC являются прямоугольными, если трапеция ABCD описана около окружности. Центром же вписанной окружности будет являться точка O.

Опущенные на гипотенузы, высоты этих треугольников, тождественны радиусу вписанной окружности, а высота трапеции тождественна диаметру вписанной окружности.

Источник

Трапеция, ее свойства, формулы площади, высоты, сторон.

Трапеция – это выпуклый четырехугольник, у которого только одна пара сторон параллельна.

Трапеция (понятие, определение)

Видеоурок “Трапеция”

Виды трапеций

Элементы трапеции: основания, боковые стороны, средняя линия и высота

Свойства трапеции

Свойства равнобедренной трапеции

Формулы трапеции

Трапеция (понятие, определение):

Трапеция (от др.-греч. τραπέζιον – «столик» от τράπεζα – «стол») – это выпуклый четырёхугольник, у которого две стороны параллельны, а другие две стороны не параллельны.

Трапеция – это выпуклый четырехугольник, у которого только одна пара сторон параллельна.

Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, и стороны не равны между собой.

Рис. 1. Трапеция

Выпуклым четырёхугольником называется четырёхугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

@ https://youtu.be/Q4EpXexoMrM

Виды трапеций:

Равнобедренная трапеция или равнобокая трапеция – это трапеция, у которой боковые стороны равны.

Рис. 2. Равнобедренная трапеция

Прямоугольная трапеция – это трапеция, один из углов при боковой стороне которой прямой.

Прямоугольная трапеция – это трапеция, имеющая прямые углы при боковой стороне.

Рис. 3. Прямоугольная трапеция

Элементы трапеции: основания, боковые стороны, средняя линия и высота:

Параллельные стороны трапеции называются основаниями трапеции, а две другие – непараллельные – боковыми сторонами.

Рис. 4. Трапеция

AD и BC – основания трапеции, AB и CD – боковые стороны трапеции.

AD – большее основание трапеции, BC – меньшее основание трапеции.

Отрезок, соединяющий середины боковых сторон трапеции, называется средняя линия.

Рис. 5. Трапеция и срединная линия

Расстояние между основаниями трапеции называется высотой трапеции.

Рис. 6. Трапеция

Высота трапеции (h) определяется формулой:

где b – большее основание трапеции, a – меньшее основание трапеции, c и d – боковые стороны трапеции.

Свойства трапеции:

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

Рис. 7. Трапеция и срединная линия

MN || BC, MN || AD,

l = (a + b) / 2

2. Отрезок, соединяющий середины диагоналей трапеции, равен половине разности оснований и лежит на средней линии.

Рис. 8. Трапеция

MN = (b – a) / 2

3. Сумма внутренних углов трапеции (и любого другого четырёхугольника) равна 360° .

Сумма углов, прилежащих к боковой стороне трапеции, равна 180° .

Рис. 9. Трапеция

4. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

Рис. 9. Трапеция

5. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

Рис. 10. Трапеция

AB = BK

6. Если сумма углов при одном из оснований трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Рис. 11. Трапеция

∠BAD + ∠CDA = 90°, MN = (AD – DC) / 2

7. В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон.

Рис. 12. Трапеция

AB + CD = AD + BC

В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.

Рис. 13. Трапеция

Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований).

Рис. 14. Трапеция

MN = (AB + CD) / 2,

MN = (AD + BC) / 2

8. Диагонали трапеции делят ее на 4 треугольника.

Два из них, прилежащие к основаниям, подобны.

Два других, прилежащие к боковым сторонам, имеют одинаковую площадь.

Рис. 15. Трапеция

Треугольники BCO и AOD подобны. Коэффициент подобия треугольников (k) находится как отношение оснований трапеции. k = AD / BC. Отношение площадей этих подобных треугольников есть k².

Треугольники ABO и CDO имеют одинаковую площадь.

9. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями.

Рис. 16. Трапеция

BC : AD = OC : AO = OB : DO

10. Диагонали трапеции d₁ и d₂ связаны со сторонами соотношением:

d₁² + d₂² = 2ab + c² + d²

где b – большее основание трапеции, a – меньшее основание трапеции, c и d – боковые стороны трапеции.

11. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основания трапеции, так же делит диагонали пополам.

Рис. 17. Трапеция

AK = KB, AM = MC, BN = ND, CL = LD,

KL – средняя линия

Рис. 17. Трапеция

AK = KB, AM = MC, BN = ND, CL = LD,

KL – средняя линия, UV – отрезок, который соединяет основания трапеции

12. Средняя линия разбивает трапецию на две трапеции, площади которых соотносятся как:

где b – большее основание трапеции, a – меньшее основание трапеции, S₁ и S₂ – площади образованных трапеций, в результате разделения средней линией.

Рис. 18. Трапеция

S₁ – площадь трапеции MBCN,

S₂ – площадь трапеции AMND

Свойства равнобедренной трапеции:

1. Прямая, которая проходит через середины оснований, перпендикулярна основаниям, тем самым, является осью симметрии равнобедренной трапеции.

2. Высота, опущенная из вершины на большее основание равнобедренной трапеции, делит его на два отрезка, один из которых равен полусумме оснований, а другой — полуразности оснований.

3. Углы при любом основании равнобедренной трапеции равны.

4. Сумма противоположных углов равнобедренной трапеции равна 180°.

5. Длины диагоналей равнобедренной трапеции равны.

6. Вокруг равнобедренной трапеции можно описать окружность.

7. При перпендикулярности диагоналей в равнобедренной трапеции ее высота равна полусумме оснований.

Формулы трапеции:

Пусть a – большее основание трапеции, b – меньшее основание трапеции, c – левая сторона трапеции, d – правая сторона трапеции, α и β – углы при нижнем основании трапеции, d₁ и d₂– диагонали трапеции, m – средняя линия трапеции, h – высота трапеции, γ и δ – углы между диагоналями трапеции, S – площадь трапеции, P – периметр трапеции.

Формулы для определения сторон трапеции:

Через среднюю линию и одно из оснований трапеции:

a = 2m – b

b = 2m – a

Через высоту и углы при нижнем основании трапеции:

a = b + h · (ctg α + ctg β)

b = a – h · (ctg α + ctg β)

Через боковые стороны и углы при нижнем основании:

a = b + c·cos α + d·cos β

b = a – c·cos α – d·cos β

Через высоту и углы при нижнем основании трапеции:

Формулы для определения средней линии трапеции:

Через длины оснований трапеции:

Через площадь и высоту трапеции:

Формулы для определения высоты трапеции:

Через сторону и прилегающий угол при нижнем основании трапеции:

h = c·sin α = d·sin β

Через диагонали трапеции и углы между ними:

Через диагонали трапеции, углы между ними и среднюю линию трапеции:

Через площадь и длины оснований трапеции:

Через площадь и длину средней линии трапеции:

Формула для определения периметра трапеции:

P = a + b + c + d

Формулы для определения площади трапеции:

Через основания и высоту трапеции:

Через среднюю линию и высоту трапеции:

S = m · h

Через диагонали трапеции и угол между ними:

Через все стороны трапеции:

С помощью формулы Герона для трапеции:

Как называется объемная трапеция?

Если трапецию изобразить в объеме, то такая фигура будет напоминать усеченную пирамиду.

В правильной усеченной пирамиде боковые грани являются равнобокими трапециями.

Квадрат

Овал

Полукруг

Прямой угол

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Ромб

Трапеция

Тупой угол

Шестиугольник

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Видео https://youtu.be/Q4EpXexoMrM

Коэффициент востребованности
6 409

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 ноября 2022 года; проверки требуют 27 правок.

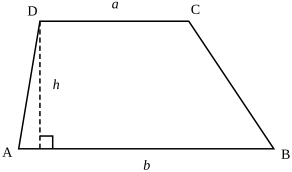
Трапе́ция (от др.-греч. τραπέζιον — «столик» от τράπεζα — «стол») — выпуклый четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны^[1]. Часто в определении трапеции опускают последнее условие (см. ниже). Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами. Средняя линия — отрезок, соединяющий середины боковых сторон.

Варианты определения

Существует и другое определение трапеции.

Трапеция — это выпуклый четырёхугольник, у которого две стороны параллельны^[2]^[3]. Согласно этому определению, параллелограмм и прямоугольник — частные случаи трапеции. Однако при использовании такого определения большинство признаков и свойств равнобедренной трапеции перестают быть верными (так как параллелограмм становится её частным случаем). Приведённые в разделе Общие свойства формулы верны для обоих определений трапеции.

Связанные определения

Элементы трапеции

Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой

Параллельные противоположные стороны называются основаниями трапеции.
Две другие стороны называются боковыми сторонами.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Углом при основании трапеции называется её внутренний угол, образованный основанием с боковой стороной.

Виды трапеций

Трапеция, у которой боковые стороны равны, называется равнобедренной трапецией (реже равнобокой^[4] или равнобочной^[5] трапецией).
Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.

Равнобедренная трапеция
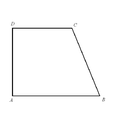
Прямоугольная трапеция

Свойства

Основной источник: ^[6]

Сумма углов, прилежащих к боковой стороне трапеции, равна $180^{circ }$ (как сумма двух внутренних односторонних углов при параллельных прямых, содержащих основания трапеции, и секущей, содержащей боковую сторону).
Средняя линия трапеции параллельна основаниям и равна их полусумме.^[7]
Отрезок, соединяющий середины диагоналей трапеции, равен половине разности оснований и лежит на средней линии.
Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен ${frac {2xy}{x+y}}$ среднему гармоническому длин оснований трапеции.
В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон.
Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
Если сумма углов при одном из оснований трапеции равна 90°, то продолжения боковых сторон пересекаются под прямым углом, а отрезок, соединяющий середины оснований, равен полуразности оснований.
Диагонали трапеции делят её на 4 треугольника. Два из них, прилежащие к основаниям, подобны. Два других, прилежащие к боковым сторонам, являются равновеликими [имеют одинаковую площадь].
Если отношение оснований равно , то отношение площадей треугольников, прилежащих к основаниям, равно $K^{2}$ .
Высота трапеции определяется формулой:

$h={sqrt {c^{2}-{frac {1}{4}}left({frac {c^{2}-d^{2}}{b-a}}+b-aright)^{2}}}$

где

— большее основание,

— меньшее основание,

— боковые стороны.

$d_{1}^{2}+d_{2}^{2}=2ab+c^{2}+d^{2}$

Их можно выразить в явном виде:

$d_{1}=AC={sqrt {ab+d^{2}+{frac {b(c^{2}-d^{2})}{b-a}}}}$

$d_{2}=BD={sqrt {ab+c^{2}-{frac {b(c^{2}-d^{2})}{b-a}}}}$

Если, наоборот, известны боковые стороны и диагонали, то основания выражаются формулами:

${displaystyle a={sqrt {frac {(c^{2}-d_{1}^{2})^{2}-(d^{2}-d_{2}^{2})^{2}}{2(c^{2}-d^{2}+d_{1}^{2}-d_{2}^{2})}}}}$

${displaystyle b={sqrt {frac {(c^{2}-d_{2}^{2})^{2}-(d^{2}-d_{1}^{2})^{2}}{2(c^{2}-d^{2}-d_{1}^{2}+d_{2}^{2})}}}}$

а при известных основаниях и диагоналях боковые стороны следующие:

${displaystyle c={sqrt {frac {a(d_{2}^{2}-b^{2})+b(d_{1}^{2}-a^{2})}{a+b}}}}$

${displaystyle d={sqrt {frac {a(d_{1}^{2}-b^{2})+b(d_{2}^{2}-a^{2})}{a+b}}}}$

Если же известна высота

, то

$d_{1}={sqrt {b^{2}+d^{2}-2b{sqrt {d^{2}-h^{2}}}}}={sqrt {h^{2}+left(b-{sqrt {d^{2}-h^{2}}}right)^{2}}}$

$d_{2}={sqrt {b^{2}+c^{2}-2b{sqrt {c^{2}-h^{2}}}}}={sqrt {h^{2}+left(b-{sqrt {c^{2}-h^{2}}}right)^{2}}}$

Прямая Ньютона для трапеции совпадает с её средней линией.

Неравенства для отрезков в трапеции

Теорема о четырёх точках трапеции

Середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон трапеции лежат на одной прямой.

Равнобедренная трапеция

Трапеция является равнобедренной тогда и только тогда, когда выполнено любое из следующих эквивалентных условий:

прямая, которая проходит через середины оснований, перпендикулярна основаниям (то есть является осью симметрии трапеции)^[8];
высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований;
углы при любом основании равны;
сумма противоположных углов равна 180°;
длины диагоналей равны;
диагонали трапеции образовывали с одним и тем же основание равные углы;
из каждой вершины одного основания другое основание было видно под одним и тем же углом^[9];
вокруг этой трапеции можно описать окружность;
вершинами этой трапеции также являются вершины некоторого антипараллелограмма.

Кроме того

если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Если — равнобочная трапеция (, ), причём — диагональ трапеции, то ${displaystyle {mathcal {{AC}^{2}=ADcdot BC+{AB}^{2}}}}$ .^[10]

Вписанная и описанная окружность

Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований).
В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
Если трапецию можно вписать в окружность — то она равнобедренная.
Радиус описанной окружности равнобедренной трапеции:^{[источник не указан 2873 дня]}

$R={frac {bcd_{1}}{4{sqrt {p(p-b)(p-c)(p-d_{1})}}}}={sqrt {frac {ab+c^{2}}{4-left({frac {b-a}{c}}right)^{2}}}}$

где $p={frac {1}{2}}(b+c+d_{1}),,,c$

— боковая сторона,

— бо́льшее основание,

— меньшее основание, $d_{1}=d_{2}$

— диагонали равнобедренной трапеции.

Если , то в равнобедренную трапецию можно вписать окружность радиуса

${displaystyle r={dfrac {h}{2}}={dfrac {sqrt {ab}}{2}}={dfrac {sqrt {d^{2}-l^{2}}}{2}}}$

Площадь

Здесь приведены формулы, свойственные именно трапеции. См. также формулы для площади произвольных четырёхугольников.

${displaystyle S={dfrac {(a+b)}{2}}h}$

Примечание: Приведённые выше две формулы эквивалентны, так как полусумма оснований равняется средней линии трапеции:

${displaystyle m={dfrac {(a+b)}{2}}}$

${displaystyle S={dfrac {a+b}{4(b-a)}}{sqrt {(a+c+d-b)(a+d-b-c)(a+c-b-d)(b+c+d-a)}}.}$

или

${displaystyle S={dfrac {a+b}{2}}{sqrt {c^{2}-{frac {1}{4}}left({dfrac {c^{2}-d^{2}}{b-a}}+b-aright)^{2}}}}$

Средняя линия разбивает фигуру на две трапеции, площади которых соотносятся как^[11]

${displaystyle {dfrac {S_{1}}{S_{2}}}={dfrac {3a+b}{a+3b}}}$

${displaystyle S={left({sqrt {S_{bigtriangleup AHD}}}+{sqrt {S_{bigtriangleup BHC}}}right)}^{2}.}$

Площадь трапеции равна произведению одной из боковых сторон на длину перпендикуляра, проведённого из середины другой боковой стороны к прямой, содержащей первую боковую сторону.

Формулы площади равнобедренной трапеции

${displaystyle S={dfrac {4r^{2}}{sin {alpha }}}}$

${displaystyle S={dfrac {d^{2}-l^{2}}{sin {alpha }}}}$

Площадь равнобедренной трапеции:

S=(b-ccos {gamma })csin {gamma }=(a+ccos {gamma })csin {gamma }

где

— боковая сторона,

— бо́льшее основание,

— меньшее основание, gamma

— угол между бо́льшим основанием и боковой стороной^[12].

Площадь равнобедренной трапеции через её стороны

$S={frac {a+b}{2}}{sqrt {c^{2}-{frac {1}{4}}(b-a)^{2}}}$

Площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна квадрату её высоты:

${displaystyle S=h^{2}.}$

В этом случае средняя линия совпадает по длине с высотой трапеции, т. е. m=h .

История

Слово «трапеция» происходит от греческого слова др.-греч. τραπέζιον «столик» (уменьш. от τράπεζα «стол»), означающего стол. В русском языке от этого слова происходит слово «трапеза» (еда).

Примечания

↑ Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988. — С. 587.
↑ Вся элементарная математика. Дата обращения: 6 июля 2015. Архивировано 9 июля 2015 года.
↑ Wolfram MathWorld. Дата обращения: 6 июля 2015. Архивировано 19 апреля 2015 года.
↑ Коллектив авторов. Современный справочник школьника. 5-11 классы. Все предметы. — Litres, 2015-09-03. — С. 82. — 482 с. — ISBN 9785457410022.
↑ М. И. Сканави. Элементарная математика. — 2013. — С. 437. — 611 с. — ISBN 9785458254489.
↑ Четырёхугольники. Архивная копия от 16 сентября 2015 на Wayback Machine
↑ Геометрия по Киселёву Архивная копия от 1 марта 2021 на Wayback Machine, § 99.
↑ Эквивалентная формулировка: отрезки, соединяющие середины противоположных сторон трапеции, были взаимно перпендикулярны.
↑ Следствие. В случае перпендикулярности диагоналей боковым сторонам трапеция является равнобедренной.
↑ Комарова В. В. Экзаменационные вопросы и ответы. Геометрия: 9 и 11 выпускные классы. — М.: АСТ-ПРЕСС, 2000. — 448 с. — ISBN 5-7805-0416-4.
↑ Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. 2-е изд., перераб. и доп. — М.: Наука, 1974. — 592 с.
↑ Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов 1986. С. 184

Источник

Трапеция — это выпуклый четырехугольник с двумя параллельными основами и двумя непараллельными
боковыми сторонами.

Иногда фигура определяется как четырёхугольник, у которого пара противолежащих сторон параллельна,
поэтому параллелограмм и прямоугольник являются частными случаями трапеции. Также это
четырехугольник, у которого одна пара противоположных сторон параллельна, а остальные стороны не
равны между собой.
Параллельные стороны называются основами, а остальные боковыми.

Вычисление стороны необходимо для нахождения периметра, площади трапеции, ее диагоналей и других
значимых параметров.

Длина основания через среднию линию и другое известное
основание
Нижнее основание через верхнее основание, высоту и углы при
нижнем основании
Верхнее основание через нижнее основание, высоту и углы при
нижнем основании
Нижнее основание через боковые стороны, верхнее основание и
углы при нижнем основании
Верхнее основание через боковые стороны, нижнее основание и
углы при нижнем основании
Боковую сторону через высоту и угол при нижнем
основании

Длина основания через среднюю линию и известное основание

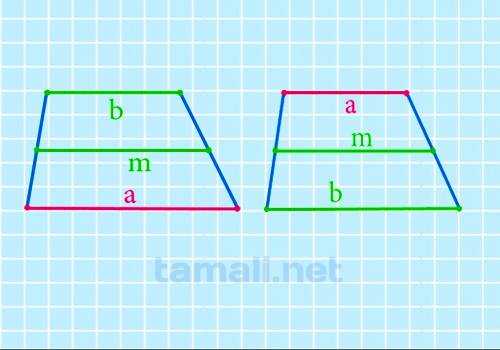
Средняя линия — отрезок, соединяющий середины боковых сторон фигуры. Через её значение
вычисляется одна из основ. Нужно умножить ее на два и вычесть известную:

a = 2m – b

Цифр после
запятой:

Результат в:

Например, средняя линия MN равна 6, а основание а – 9. Соответственно, значения, подставленные в
формулу, показывают, что b = 2*6 – 9 = 3.

Нижнее основание через верхнее основание, высоту и углы при нижнем основании

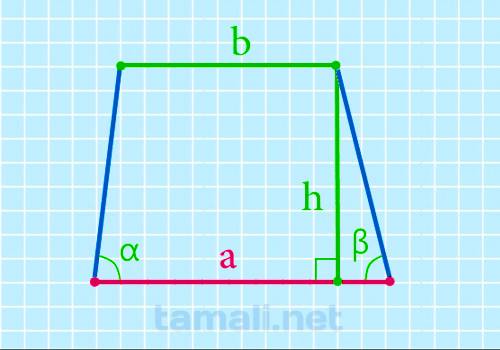
Высота h или BK – перпендикуляр, проведенный от одной основы к другой. Высота проводится в любой их
точке, но удобнее всего это делать из вершины углов при меньшей основе. Чтобы найти нижнее
основание, надо к верхнему прибавить произведение высоты на сумму котангенсов углов при нижнем:

a = b + h*(ctga + ctgb)

Цифр после
запятой:

Результат в:

Дано верхнее основание 10, высота 6 и углы 30 и 45. По формуле а = 10 + 6*(3+1) = 10 + 63 + 6 = 16+63.
Для равнобедренного четырёхугольника выведены две формулы. В первой (a = 2S/h – b) основа выражена с
помощью формулы площади. Пример: Площадь равнобедренной трапеции ABCD = 18, высота = 6, а AD = 5.
Найти BC. BC = 2*18/6 – 5 = 6 – 5 = 1

Второе выражение сформулировано следующим образом: (a = b + 2h*ctga). Высота АН в трапеции ADEF =
10, DE = 4, а DAF = 45 градусам. Найти AF: AF = 4 + 10*2*1 = 24

Верхнее основание через нижнее основание, высоту и углы при нижнем основании

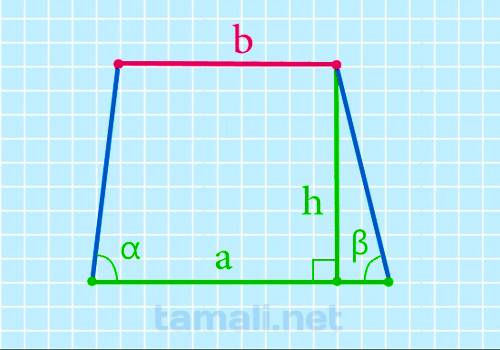
Чтобы найти верхнюю основу, надо из нижней вычесть произведение высоты на сумму котангенсов углов при
ней:

b = a – h*(ctg α + ctg β)

Цифр после
запятой:

Результат в:

Дана трапеция с нижним основанием 15, высотой 8 и углами в 45 градусов. По формуле а = 15 + 8*(1+1) =
15 + 16 = 31

Формулы для равнобедренного четырёхугольника: b = 2S/h – a и b = a – 2h*ctga.

Площадь трапеции KLMN = 44, KL=MN, высота равна 8, KN = 5. Найти LM: LM = 44*2/8 – 5 = 6
Высота трапеции DEFG = 15, DG= 5, а EDG = 45 градусам. Найти EF: EF = 5 + 15*2*1 = 35

Нижнее основание через боковые стороны, верхнее основание и углы при нижнем основании

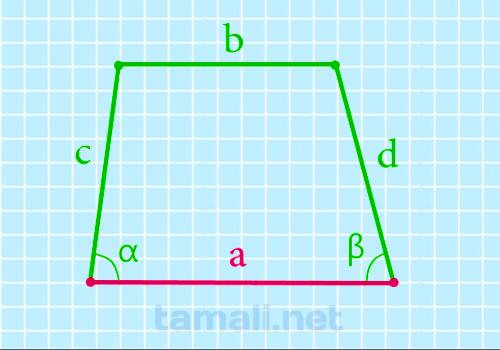
Для нахождения основы а нужно к основе b прибавить произведение одной и другой стороны и косинусов
углов при них

a = b + c * cos α + d * cos β

Цифр после
запятой:

Результат в:

Дана равнобокая трапеция с верхним основанием 6, боковыми сторонами 5 и 11 и углами в 45 градусов.
Найти нижнее основание: а = 6 + 5*2/2 + 11*2/2 = 6 + 162/2 = 6 + 82

Отдельно для подобного типа фигур было выведено два выражения: a = (d1^2 – c^2)/b и a = b +
2c*cosa.

трапеции ABCD AB = CD = 8, диагональ AC = 12, а BC = 4. Вычислить AD: AD = (12*12 – 8*8)/4
= (144 – 64)/4 = 20
В трапеции KLMN KL = MN = 4, LM = 7, а LKN равен 30 градусам. Вычислить KN: KN = 7 +
4*2*3/2 = 7 + 43

Верхнее основание через боковые стороны, нижнее основание и углы при нем

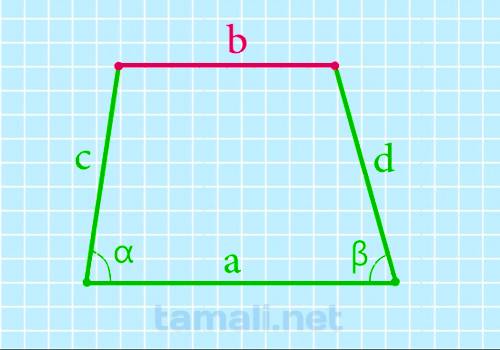
Для нахождения основы b нужно из основы а вычесть произведение одной и другой боковой стороны и углов
при них

b = a – c * cos α – d * cos β

Цифр после
запятой:

Результат в:

Дана трапеция с нижним основанием 27, боковыми сторонами 20 и 14 и углами в 30 и 60 градусов. Найти
верхнее основание: b = 27 — 20*3/2 — 14*1/2 = 27 — 103 — 7 = 20 —
103. Формулы для равнобедренного типа: b = (d1^2 — c^2)/a и b = a — 2c*cosa.

В трапеции DEFG DE и FG = 11, диагональ АС = 13, а EF = 12. Вычислить DG: DG = (13*13 –
11*11)/12= (169 – 121)/12 = 4
Боковые стороны трапеции BCDE BC и DE = 25, BE = 10, а CBE равен 60 градусам. Вычислить CD:
CD = 25 – 10*2*1/2 = 15

Боковая сторона через высоту и угол при нижнем основании

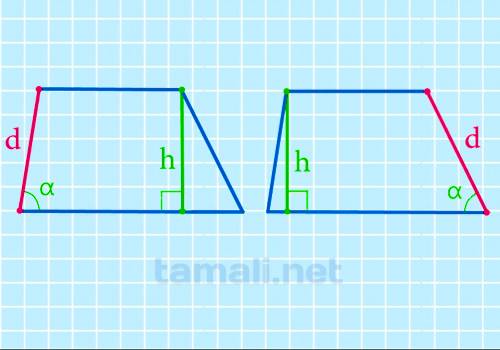
Чтобы найти боковую сторону, надо разделить высоту на синус угла при ней

d = h / sin α

Цифр после
запятой:

Результат в:

Дана трапеция с высотой 12 и углами в 30 и 60 градусов. Найти боковые стороны: c = 12/0,5 =
24, d = 12/3/2 = 243

Для прямоугольного типа формулы несколько отличаются. Самая простая из них связывает высоту и меньшую
боковую сторону: c = h.
Для нее существует еще несколько формул: с = d*sina; c = (a – b)*tga; c
= (d^2 – (a – b)^2)

В прямоугольной трапеции CDEF сторона EF равна 22, а прилежащий угол = 45. Найти CD. CD =
22*2/2 = 112
Прямоугольная трапеция MNOP имеет основания MP и NO, равные 32 и 19 соответственно. NMP равен 60
градусам. Найти MP: MP = (32 – 19)*3 = 133
В прямоугольной трапеции ABCD AD и BC равны 35 и 15 соответственно. Диагональ АС = 26. Найти AB.
AB = (26^2 – (35 – 15)^2) = 676 – 400 = 276 = 269

Первая вытекает из прямоугольного треугольника и свидетельствует о том, что отношение катета к
гипотенузе равно синусу противолежащего угла. В этом треугольнике второй катет равен разности двух
оснований. Отсюда возникает утверждение, приравнивающее тангенс угла к отношению катетов. Третья
формула выведена на основании теоремы Пифагора.

Для второй боковой стороны выведено и записано три выражения: d = (a — b)/cosa; d = c/sina; d =
(c^2 — (a — b)^2). Первое и второе получаются из соотношения сторон в прямоугольном
треугольнике, а третье выводится из теоремы Пифагора.

В прямоугольной трапеции KLMN KN = 28, LM = 13 а прилежащий угол = 30. Найти KL: KL = (28 –
13)/3/2 = 103
В прямоугольной трапеции EFGH EF равна 45. FEH равен 30 градусам. Найти GH: GH = 45/0,5 =
90
В прямоугольной трапеции NOPQ NQ и OP =.36 и 17. Диагональ равна 29. Найти NO: NO = (29^2 –
(36 – 17)^2) = 841 – 361= 480 = 430

Для равнобокой трапеции существуют формулы c = d1^2 – ab; c = (a – b)/2cosa; c = S/m*sina; c =
2S/(a+b)*sina.

В трапеции LMNO LM = NO. LO = 16, MN = 6, диагональ равна 10. Найти LM: LM = 10^2 – 16*6 =
100 – 96 = 4
Трапеция ABCD – равнобокая, AB = CD. AD = 18, BC = 4, а прилежащий угол равен 45 градусам. Найти
AB: AB = (18 – 4)/2/2 = 14/2/2 = 14/2
В трапеции BCDE BC=DE. Площадь фигуры равна 48, BE = 17, CD = 7, а CBE равен 30 градусам.
Вычислить BC: m = (17 – 7)/2 = 5, BC = 48/5*1/2 = 96/5 = 19,2
Площадь равнобедренной трапеции KLMN = 90, основания KN и LM = 32 и 18 соответственно, а LKN =
60 градусов. Вычислить KL: KL = 2*90/(32 + 18)*3/2 = 360/503 = 129600/7500 = 17,28

Виды трапеций

Существуют следующие виды трапеций:

Равнобедренная трапеция — фигура, у которой боковые стороны и углы при основании равны.
Диагонали также равны. Треугольники, образованные диагоналями и основой, являются
равнобедренными. Если диагонали взаимно перпендикулярны, то площадь равна квадрату высоты. Если
разделить обе основы пополам и повести через эти точки линию, то она будет осью геометрической
фигуры. Отрезки, последовательно соединяющие середины смежных сторон, образуют ромб.
Прямоугольная трапеция — фигура, у которой одна из боковых сторон перпендикулярна основам
и равна высоте. Два угла будут равны 90 градусам, и они всегда принадлежат смежным вершинам, а
другие всегда острый и тупой, их сумма всегда будет равна 180 градусам. Каждая диагональ
образует с ее меньшей боковой стороной прямоугольный треугольник. А высота, которая проведена из
вершины с тупым углом, делит фигуру на две. Одна из них прямоугольник, другая прямоугольный
треугольник.
Разносторонняя трапеция — фигура, боковые стороны которой не равны и углы при основании не
являются прямыми. Ее диагонали делят фигуру на четыре треугольника, два из которых подобны, а
остальные — равновелики, то есть имеют одинаковые площади. Сумма углов при боковой стороне 180
градусов.

Свойства трапеции

Средняя линия параллельна основаниям и равна их полусумме.
Любая биссектриса, выведенная из угла четырёхугольника, отсекает на основании (продолжении)
отрезок с длиной боковой стороны.
Треугольники AOD и COD, образованные отрезками диагоналей и основами, подобны.
Коэффициент
подобия – k = AD/BC.
Отношение площадей треугольников — k^2.
Треугольники ABO и DCO, образованные отрезками диагоналей и боковыми сторонами, имеют одинаковую
площадь.
В трапецию можно вписать окружность, если сумма оснований равняется сумме её боковых сторон.
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений
боковых сторон лежат на одной прямой.
Отрезок, соединяющий середины диагоналей, равняется половине разности основ и лежит на средней
линии.

Источник

Трапеция. Формулы, признаки и свойства трапеции

Основные свойства трапеции

Сторона трапеции

Формулы определения длин сторон трапеции:

Средняя линия трапеции

Формулы определения длины средней линии трапеции:

Высота трапеции

Формулы определения длины высоты трапеции:

Диагонали трапеции

Формулы определения длины диагоналей трапеции:

Площадь трапеции

Формулы определения площади трапеции:

Периметр трапеции

Формула определения периметра трапеции:

Окружность описанная вокруг трапеции

Формула определения радиуса описанной вокруг трапеции окружности:

Окружность вписанная в трапецию

Формула определения радиуса вписанной в трапецию окружности

Другие отрезки разносторонней трапеции

Формулы определения длин отрезков проходящих через трапецию:

Виды трапеций

Элементы трапеции

Площадь трапеции

Свойства трапеции

Средняя линия трапеции

Сумма углов трапеции

Равновеликие треугольники трапеции

Подобие образованных треугольников трапеции

Отношение длин отрезков и оснований

Описанная около трапеции окружность

Вписанная в трапецию окружность

Трапеция, ее свойства, формулы площади, высоты, сторон.

Трапеция (понятие, определение):

Виды трапеций:

Элементы трапеции: основания, боковые стороны, средняя линия и высота:

Свойства трапеции:

Свойства равнобедренной трапеции:

Формулы трапеции:

Как называется объемная трапеция?

Варианты определения

Связанные определения

Элементы трапеции

Виды трапеций

Свойства

Неравенства для отрезков в трапеции

Теорема о четырёх точках трапеции

Равнобедренная трапеция

Вписанная и описанная окружность

Площадь

Формулы площади равнобедренной трапеции

История

Примечания

Длина основания через среднюю линию и известное основание

Нижнее основание через верхнее основание, высоту и углы при нижнем основании

Верхнее основание через нижнее основание, высоту и углы при нижнем основании

Нижнее основание через боковые стороны, верхнее основание и углы при нижнем основании

Верхнее основание через боковые стороны, нижнее основание и углы при нем

Боковая сторона через высоту и угол при нижнем основании

Виды трапеций

Свойства трапеции

Вам также может понравиться

Шпон вспучился на столе как исправить

Как найти угол в правильном восьмиугольнике abcdefgh

Как быстро найти матку в многокорпусном улье

Добавить комментарий Отменить ответ