Как найти емкость конденсатора через формулу томсона

На этой странице находится ответ на вопрос Как найти емкость конденсатора через формулу Томпсона?, из категории
Физика, соответствующий программе для 5 – 9 классов. Чтобы посмотреть
другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов
подберите похожие вопросы и ответы в категории Физика. Ответ, полностью
соответствующий критериям вашего поиска, можно найти с помощью простого
интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе.
Обратите внимание на варианты ответов других пользователей, которые можно не
только просмотреть, но и прокомментировать.

Конденсатор – радиоэлектронный прибор, способный накапливать и отдавать заряд. Как правило, на его корпусе дается информация о его емкости, но иногда требуется самому рассчитать этот номинал.

Конденсаторами могут выступать и проводники, они также обладают определенной емкостью. Для расчета существует несколько формул емкости конденсатора, их и рассмотрим.

В чем измеряется емкость конденсатора

Что такое заряд еще проходят в школе, когда эбонитовую палочку натирают о шерстяную ткань и подносят к маленьким кусочкам бумаги.

Под действием электромагнитных сил бумага прилипает к палочке. Подобный заряд накапливается в конденсаторе. Но для начала познакомимся с самим конденсатором.

Простейшим конденсатором являются две металлические пластины, разделенные диэлектриком. От качества диэлектрика зависит, как долго энергия заряженного конденсатора может сохраняться.

На этих пластинах, они еще называются обкладками, накапливается разноименный заряд. Как это происходит?

Электрический заряд, а в случае с металлами это электроны, способен перемещаться под действием электродвижущей силы (э. д. с.).

Подключая металлические пластинки к источнику тока, мы получаем замкнутую цепь, но разделенную диэлектриком. Электростатическое поле проходит этот диэлектрик, замыкая цепь, а электроны, дойдя до препятствия, останавливаются и скапливаются.

Полная статья на блоге “Электрик в доме”:

Получается, на одной обкладке наблюдается избыток электронов, и эта пластина имеет отрицательный знак, а на другой пластине электронов недостает настолько же, знак на этой обкладке, конечно же, будет положительным.

Вот теперь нужна для определения емкости конденсатора формула, определяющая, какой заряд способен разместится на конкретном конденсаторе.

В качестве единицы измерения в международной системе (СИ) емкость определяется в Фарадах.

Много это или мало – емкость в 1Ф? Чтобы конденсатор обладал емкостью в 1Ф, он должен содержать в себе заряд в 1К (кулон) и при этом напряжение между обкладками должно равняться 1 вольту.

Интересно. Что такое заряд в 1 кулон? Если два предмета, каждый из которых имеет заряд в один кулон разместить в вакууме на расстоянии один метр, то сила притяжения между ними будет равна силе притяжения землей тела массой в один миллион тонн.

Как и любая буквальная емкость один и тот же конденсатор может вмещать разное количество заряда.

Рассмотрим пример.

• В трехлитровую банку входит три литра воздуха. Его хватит для дыхания, допустим, на 3 минуты. Но если воздух закачать под каким-то давлением, то емкость так и останется три литра, однако дышать можно будет дольше. Так устроен акваланг для ныряльщиков. Получается, количество воздуха в банке зависит от давления, которое в ней создается. Точно так же есть некая зависимость между различными силами, влияющими на емкость.

Формула емкости плоского конденсатора

Прежде чем узнать, по какой формуле вычисляется емкость плоского конденсатора, рассмотрим формулу для одиночного проводника. Она имеет вид:

• где Q – заряд,
• φ – потенциал.

Как видно емкость конденсатора, формула которого здесь приведена, будет тем больше, чем больший заряд способен накапливаться на нем при незначительном потенциале. Чтобы легче это было понять, рассмотрим получившие широкое распространение плоские конденсаторы разных размеров.

Для получения качественного конденсатора важны любые мелочи:

1. ровная поверхность каждой обкладки;
2. обе пластинки по всей площади должны располагаться на одинаковом расстоянии;
3. размеры обкладок должны быть строго идентичными;
4. от качества диэлектрика, расположенного между пластинками, будет зависеть ток утечки;
5. емкость напрямую зависит от расстояния между обкладками, чем оно меньше, тем больше емкость.

Теперь обратимся к плоскому конденсатору. Формула определения емкости конденсатора несколько отличается от приведенной выше:

• где S – площадь одной обкладки,
• εr – диэлектрическая проницаемость диэлектрика,
• ε0 – электрическая постоянная,
• d – расстояние между обкладками.

Электрическая постоянная выражается числом 8,854187817×10-12.

Внимание! Эта формула справедлива только тогда, когда расстояние между пластинами намного меньше их площади.

Попробуем разобраться с каждой переменной подробнее. Площадь измеряется в м2, точнее, приводится к этой величине. А вот проницаемость диэлектрика может обозначаться по-разному.

В России это εr (также означает относительная проницаемость), в англоязычной литературе встречается εa (также означает абсолютная проницаемость), а то может и вовсе использоваться без индекса, просто ε. О том, что здесь используется диэлектрическая проницаемость диэлектрика можно понять из контекста.

Дальше идет ε0. Это уже вычисленное значение, измеряемое в Ф/м. Последняя переменная – d. Измеренное расстояние также приводится к метру. Емкость конденсатора, формула которого сейчас рассматривается, показывает сильную зависимость от расстояния обкладок. Поэтому стараются это расстояние по возможности сокращать. Почему этот показатель так важен?

Идеальными условиями для получения наибольшей емкости – это отсутствие промежутка между обкладками, чего, конечно, добиться невозможно. Чем ближе находятся разноименные заряды, тем сильнее сила притяжения, но здесь возникает компромисс.

При уменьшении толщины диэлектрика, а именно он разделяет разноименные заряды, возникает вероятность его пробоя из-за разности потенциалов на обкладках. С другой стороны, как уже говорилось, при увеличении напряжения увеличивается количество зарядов. Вот и приходится выбирать между емкостью и рабочим напряжением конденсатора.

Есть другая формула для плоского переменного конденсатора:

Здесь диэлектрическая проницаемость обозначена буквой ε, π = 22/7 ≈ 3,142857142857143, d – толщина диэлектрика. Формула предназначена для конденсатора, состоящего из нескольких пластин.

Допустимая толщина диэлектрика d также зависит от εr, чем выше коэффициент, тем тоньше можно использовать диэлектрик, тем большую емкость будет иметь конденсатор. Это был самый сложный материал, дальше будет легче.

Формула емкости цилиндрического конденсатора

Теперь поговорим о том, как найти емкость конденсатора цилиндрической формы. К ним относятся конденсаторы, состоящие из двух металлических цилиндров, вставленных один в другой.

Для разделения между ними расположен диэлектрик. Формула емкости конденсатора выглядит следующим образом:

Здесь видим несколько новых переменных:

• l – высота цилиндра;
• R1 и R2 – радиус первого и второго (внешнего) цилиндров;
• ln – это не переменная, а математический символ натурального логарифма. На некоторых калькуляторах он имеется.

Всегда нужно помнить, что все величины должны приводиться к единой системе, в приведенной ниже таблице указаны международные системы единиц (СИ).

Из нее видно, что все расстояния нужно приводить к метру.

Еще стоит обращать внимание на качество диэлектрика. Если толщина диэлектрика влияет только на емкость конденсатора, то его качество затрагивает сохранность энергии. Другими словами, конденсатор с качественным диэлектриком будет иметь меньший саморазряд.

Определить качество можно по числу, стоящему возле вещества, чем оно больше, тем лучше качество. Сравнение производится по вакууму, значение которого равно единице.

Формула емкости сферического конденсатора

Последнее что осталось разобрать – формулу определения емкости конденсатора, состоящего из двух сфер. Причем одна сфера находится внутри другой. Формула имеет следующий вид:

Из приведенных переменных здесь все знакомо. Стоит обратить внимание лишь на сам конденсатор.

Кроме своей необычной формы у него есть свои особенности: внутри малой сферы никакого заряда нет, он образуется на внешней части малой сферы и внутренней части большого шара. Также заряд отсутствует и на внешней стороне внешней сферы.

Так же как и все другие конденсаторы, сферы разделены диэлектриком. Толщина и качество диэлектрика оказывают такое же влияние на емкость, как в случае с другими конденсаторами.

После того как были рассмотрены формулы, стоит испробовать их на практике. Рассмотрим, как найти емкость конденсатора каждого вида.

Примеры решения задач

Начнем с плоского конденсатора. Формула для этого вида:

Допустим, у нас есть следующие значения:

• в качестве диэлектрика возьмем слюду толщиной 0,02 мм, ε = 6;
• конденсатор квадратный со сторонами в 7 мм.

Определяем площадь пластин: 7×7 = 49 мм2.

Приводим к единой системе: 4,9×10-5 = 0,000049 м2. Толщина диэлектрика 0,02×10-5 = 0,00002 м. Электрическая постоянная 8,854187817×10-12.

Подставляем в формулу и высчитываем числитель: 6×8,854187817×10-12 ×4,9×10-5, сокращаем и решаем 6×49×8,854187817×10-17 = 2,603131218198×10-14.

Делим на толщину диэлектрика: 2,603131218198×10 / 2×10 = 1301,565609099×10 = 1,301565609099×10. Шесть нулей – это тысячи или приставка «микро», получается округлено 1,3 мкФ.

Возможно, при вычислении была допущена ошибка, но это не экзамен по математике. Важно понять сам метод вычисления.

Формула для цилиндрического конденсатора:

Выбираем значения:

• l = 1 см;
• R1 = 0,25 мм;
• R2 = 0,26 мм;
• ε = 2.

Подгоняем под единую систему: l – 1 см = 1×10-2 = 0,01 м; R1 – 0,25 мм = 0,0025 м; R2 – 0,26 мм = 0,0026 м.

Подставляем значения в числитель: 2×3,142857142857143×8,854187817×10-12×2×0,01 1,11×10-12. Находим знаменатель: 0,26:0,25 = 1,04.

Находим натуральный логарифм, он равен примерно 0,39. Числитель делим на знаменатель: 1,11×10-12/0,39 = 2,85×10-12.

Число с 12 нулями это приставка «пико», получаем 2,85 пФ.

Формула для сферического конденсатора:

Выбираем значения:

• ε= 4;
• r1= 5 см;
• r2= 5,01 см.

Снова все подгоняем: 5 см = 0,05 м; 5,01 см = 0,0501 м. Заполняем числитель. 4×3,142857142857143×4×8,854187817×10-12×0,05×0,0501 1,11×10-12 Вычисляем знаменатель: 0,0501 – 0,05 = 0,01. Производим деление: 1,11×10-12×0,01 = 1,11×10-10. Снова получили пикофарады, а именно 1,11 пФ.

Интересные статьи на канале:

Статья заинтересовала? Лайк, подписка, комментарий!

Друзья ПОДПИСЫВАЙТЕСЬ Дзен на канал, а также заходите на блог https://electricvdome.ru 👍!

#конденсатор #емкость #формула

Что такое плоские конденсаторы

Емкость конденсатора не слишком велика, но энергия при разрядке отдается почти мгновенно. Свойство конденсаторов быстро выдавать импульс большой мощности находит применение в лампах-вспышках для фотографирования, электромагнитных ускорителях, импульсных лазерах.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Примером может служить генератор Ван де Граафа, позволяющий создавать в лабораторных условиях напряжение в миллионы вольт, чтобы моделировать разряды молний. Также конденсаторы используют в радиотехнике.

Описание и технические характеристики

Конденсатор состоит из двух проводников, разделенных слоем диэлектрика.

Простейший конденсатор — две металлические пластины-обкладки, расположенные параллельно, с тонкой прослойкой воздуха между ними. Когда заряды пластин противоположны по знаку, электрическое поле оказывается сосредоточено внутри конденсатора и почти не взаимодействует с внешним миром, что позволяет накапливать на пластинах заряд.

Конденсатор обладает следующими техническими параметрами:

• номинальной и реальной емкостью — заявленной и фактической способностью накапливать заряд;
• удельной емкостью — отношением емкости к массе или объему диэлектрика;
• плотностью энергии;
• номинальным напряжением;
• полярностью — электролитические конденсаторы требуют корректной полярности напряжения для безопасной работы;
• электрическим сопротивлением изоляции диэлектрика;
• временем самостоятельной потери заряда;
• эквивалентным последовательным сопротивлением — внутренним электрическим сопротивлением диэлектрика, материала обкладок, выводов, контактов;
• эквивалентной последовательной индуктивностью и собственной частотой резонанса;
• температурным коэффициентом емкости — относительным изменением емкости при изменении температуры окружающей среды;
• диэлектрической абсорбцией — поглощением и сохранением части заряда при быстрой разрядке;
• пьезоэффектом — генерацией напряжения на обкладках при механических деформациях.

Как найти его емкость, формулы

В СИ напряжение измеряется в вольтах, его обозначение — В.

Емкость измеряется в фарадах и обозначается Ф. Один фарад равен одному кулону, деленному на один вольт. Это очень большая единица: один фарад — примерная электроемкость уединенного металлического шара, радиус которого равен 13 радиусам Солнца.

В системе СГС емкость измеряется в сантиметрах или статфарадах, сокращенно обозначаемых статФ. За единицу измерения берется емкость шара радиусом 1 см в вакууме.

(x = {-b pm sqrt{b^2-4ac} over 2a}1 Ф = 8,9875517873681764;times;10^{11} статФ)

Емкость плоского конденсатора можно вычислить по формуле

(С;=;frac{varepsilon;times;varepsilon_0;times;S}d)

Где S — площадь каждой из пластин, d — расстояние между ними, (varepsilon) — коэффициент диэлектрической проницаемости среды между пластинами, (varepsilon_0) — электрическая постоянная, равная (8,854187817;times;10^{-12};frac Фм).

Таким образом, емкость плоского конденсатора легко изменить, погрузив его в жидкость или иную среду с нужной диэлектрической проницаемостью.

Способы расчета по току и напряжению

Конденсатор — это два проводящих тела, которые разделены диэлектриком. Они несут равные по величине и противоположные по знаку заряды (q_1) и (q_2 ) имеют потенциалы (varphi_1) и (varphi_2).
Электроемкость изолированного проводника С равна отношению изменения заряда q к изменению потенциала проводника (varphi.) Их зависимость выражается формулой:

(С;=;frac qU)

Где U — разность потенциалов тел, т. е. обкладок конденсатора, или напряжение на конденсаторе.

Если порции заряда малы, для простоты расчетов можно предположить, что напряжение между пластинами не меняется. Оно вычисляется по формуле:

( U;=;varphi2;-;varphi_1)

Заряд измеряется в кулонах. Заряд и сила тока связаны следующим соотношением: один кулон равен величине заряда, прошедшего через проводник за одну секунду при силе тока в один ампер. Таким образом, зная силу тока и время зарядки конденсатора в секундах, можно произвести вычисление по формуле:

(q;=;I;times;t)

Когда конденсатор включен в колебательный контур, то, зная период электромагнитных колебаний T и индуктивность катушки контура L, можно вычислить емкость, воспользовавшись формулой Томсона:  

(T;=;2mathrmpisqrt{mathrm{LC}})

При решении задач часто требуется вычислить емкости каждого конденсатора в цепи параллельно или последовательно соединенных, а также напряжение на каждом из них. Чтобы составить необходимые уравнения, нужно воспользоваться формулами для вычисления общей емкости цепи.
При параллельном соединении:

({mathrm С}_{mathrm{общ};};=;{mathrm С}_1;+;{mathrm С}_2;+;{mathrm С}_{3;}+;…;+;{mathrm С}_{mathrm n})

При последовательном:

(frac{1;}{{mathrm С}_{mathrm{общ};}}=;frac1{{mathrm С}_1};+;frac1{{mathrm С}_2};+;frac1{{mathrm С}_{3;}}+;…;+;frac1{{mathrm С}_{mathrm n}})

Конденсатор – пассивный электронный компонент, главной характеристикой которого является емкость. Предназначен в основном для накопления энергии, разделения цепей постоянного тока, фильтрации помех, создания резонансных цепей и т.п. Чтобы применение конденсаторов на практике было осознанным, следует ознакомиться с их основными параметрами, методами измерения и изменения емкости.

От чего зависит и в чем измеряется емкость конденсатора

Конденсатор в общем случае состоит из двух проводящих обкладок, разделенных диэлектриком. Если к обкладкам приложить напряжение, такое устройство запасает электрическую энергию путем накопления заряда. (говорят, что конденсатор заряжается). Количественно запасенная конденсатором электрическая энергия выражается формулой , где W – величина энергии, U – напряжение между обкладками, а С – емкость, то есть, величина, характеризующая способность конденсатора запасать энергию. В целом ёмкость зависит от площади обкладок, расстояния между ними и свойствами разделяющего диэлектрика.

Единицей измерения емкости в СИ является фарад (1 Ф) (устаревшее название – фарада). Для практических целей это слишком большая единица. Так, земной шар имеет ёмкость менее 1 Ф, поэтому в технике используют, в основном, дольные единицы:

• пикофарады – 1 пФ (1 pF) =10^-12 Ф;
• нанофарады – 1 нФ (1 nF) =10^-9 Ф;
• микрофарады – 1мкФ (1 µF) = 10^-6 Ф.

Более крупные единицы до недавнего времени не использовались, так как емкости порядка больших дольных единиц были труднодостижимыми. Лишь с появлением ионисторов появилась возможность оперировать величинами порядка единиц и даже десятков фарад.

Как узнать емкость конденсатора

Чтобы использовать конденсатор для практических целей, надо знать его емкость. Выяснить эту величину можно различными способами.

По маркировке

В первую очередь, надо попробовать определить параметры конденсатора по его маркировке. На оксидные конденсаторы, имеющие емкость которых составляет от долей до нескольких тысяч микрофарад, эта характеристика наносится на корпус в виде цифры, обозначающей емкость в микрофарадах, с индексом uF (для отечественных изделий предыдущих годов выпуска после цифры стоит индекс мкФ).

Конденсаторы, обладающие емкостью от единиц пикофарад до единиц микрофарад маркируют тремя цифрами:

• первые два символа — мантисса;
• третья цифра – множитель.

Попросту говоря, к первым двум цифрам надо приписать количество нулей, обозначаемое третьей цифрой.

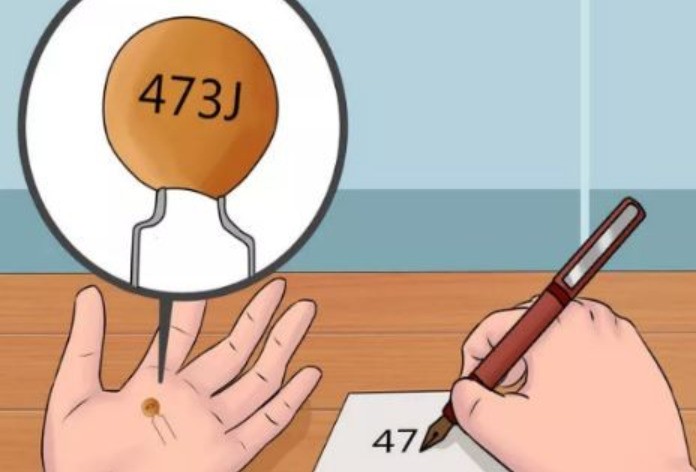
Например, на конденсатор на рисунке нанесено обозначение 473. К цифрам 47 надо приписать три нуля, тогда получится 47000 пФ. Удобнее представить это значение в виде 47нФ или 0,047 мкФ.

Такое обозначение применяется не всегда (особенно, на старых типах отечественных изделий). Иногда на корпусе наносят явное значение ёмкости с единицей измерения.

Но и единицу измерения указывают не всегда. Принцип таков:

• если нет множителя или не указана единица, считается, что ёмкость в пикофарадах;
• если есть множитель, он указывается одной буквой (n – нанофарады, µ — микрофарады и т.п.).

На зарубежных конденсаторах выпуска до 70-х годов можно встретить обозначение µµF. Так маркировалась ёмкость в пикофарадах («микро-микрофарады»).

Если емкость неизвестна, надпись но корпусе отсутствует или есть сомнения, лучше провести измерения одним из известных способов.

Мультиметром

Сделать это можно, например, с помощью цифрового тестера. Многие современные мультиметры имеют функцию измерения емкости конденсаторов. Надо всего лишь выбрать соответствующий режим, обычно обозначаемый символом конденсатора или буквами Cx, и подключить конденсатор к щупам или специально выделенным гнездам. При измерении надо иметь в виду, что:

1. Нижний предел измеряемой величины довольно большой, и для большинства распространенных приборов составляет не менее 1000 пФ.
2. Измерительные провода со щупами имеют собственную ёмкость (до 100 пФ), и ее надо учитывать при измерениях.

Поэтому тестеры, у которых для измерения ёмкости предназначен отдельный выход, измеряют параметры более точно.

Чтобы обмерить конденсатор с меньшей ёмкостью, лучше воспользоваться специализированным тестером (можно приобрести на интернет-площадках, расположенных в Юго-Восточной Азии). Они позволяют измерять ёмкость от десятков или даже единиц пикофарад.

Осциллографом

Если есть два резистора – один с известным сопротивлением R, а другой с неизвестным Rx, их можно соединить последовательно (сделать делитель напряжения), подать на него напряжение, и измерить падение на каждом элементе или на общей цепи. Измерения можно провести тестером в режиме вольтметра. Тогда Rx можно вычислить по одной из формул, указанных на рисунке.

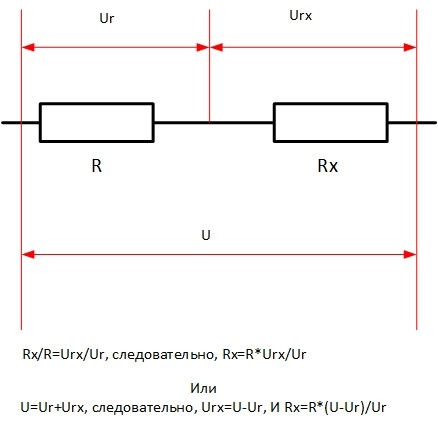
Известно, что конденсатор обладает сопротивлением переменному току, которое зависит от частоты по формуле Xc=1/(2*π*f*C), где:

• f – частота тока в Герцах;
• С – ёмкость конденсатора в Фарадах.

Можно сделать подобный делитель из конденсаторов, и сравнить сопротивление неизвестного прибора Xcx с сопротивлением эталонного конденсатора Xc, откуда легко вычислить неизвестную ёмкость:

откуда

Далее несложно найти С.

При этом возникают две проблемы:

1. Измерения нельзя проводить на постоянном токе – сопротивление реального конденсатора при f=0 близко к бесконечности.
2. При измерении переменного напряжения достаточно высокой частоты тестер будет давать значительную погрешность.

Поэтому в качестве источника тока надо использовать генератор сигнала высокой частоты (чем меньше предполагаемая ёмкость, тем выше должна быть частота, в противном случае точность замеров будет невысокой), а в качестве измерительного прибора – осциллограф.

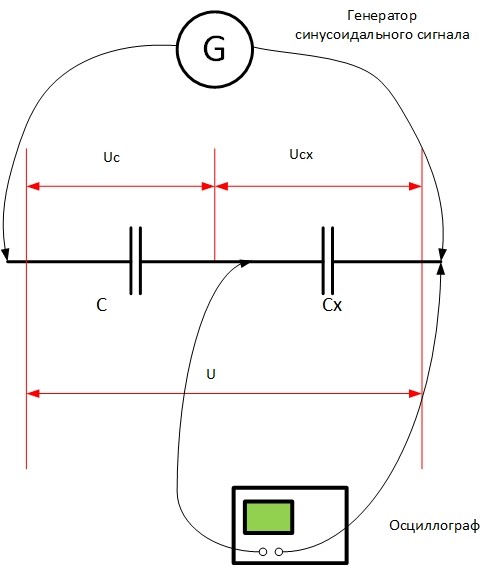
В качестве эталонного элемента для делителя можно взять резистор с известным сопротивлением (вместо Xc в формулу надо подставить R) или катушку (дроссель) с известной индуктивностью. В этом случае вместо Xc в формулу надо подставить X_L (вычисляется, как X_L=2* π*f*L).

Если имеется эталонная индуктивность, можно найти емкость, составив колебательный контур. Его надо подключить по указанной схеме, а затем, перестраивая генератор, найти резонансную частоту (при ней амплитуда сигнала на осциллографе будет максимальной). Ёмкость можно рассчитать по известной формуле Томсона .

Формулы для расчета емкости

Хотя общая зависимость ёмкости от геометрических размеров и свойств диэлектрика определена выше, для конкретных типов конденсаторов удобнее пользоваться приведенными формулами.

Электроемкость плоского конденсатора

Самый распространённый тип конденсатора, применяемый в технике – плоский. Его обкладки состоят из двух параллельных пластин, между которыми находится диэлектрик. Чтобы уменьшить габариты такого прибора, обкладки с диэлектриком между ними сворачивают в рулон или складывают в прямоугольный пакет. Емкость такого конденсатора рассчитывается по формуле , где:

• С – ёмкость, Ф;
• S – площадь обкладок, кв.м;
• d – расстояние между обкладками;
• ε – диэлектрическая проницаемость диэлектрика;
• ε_{0 –} электрическая постоянная, равная 8.85*10^-12 Кл²/Н*м².

Очевидно, что емкость тем больше, чем больше площадь обкладок и меньше расстояние между ними. Кроме того, можно выбрать диэлектрик с высоким ε и пропорционально увеличить ёмкость в тех же габаритах.

Электроемкость сферического конденсатора

Сферическим конденсатором называется устройство, состоящее из двух проводящих сфер – большой радиусом R1 и малой радиусом R2. Малая сфера вложена в большую. Поверхности сфер служат обкладками. Пространство между сферами может заполняться твердым, жидким диэлектриком или воздухом (воздушный сферический конденсатор). Такие приборы используются для лабораторных исследований (например, для изучения фотоэлектрических явлений).

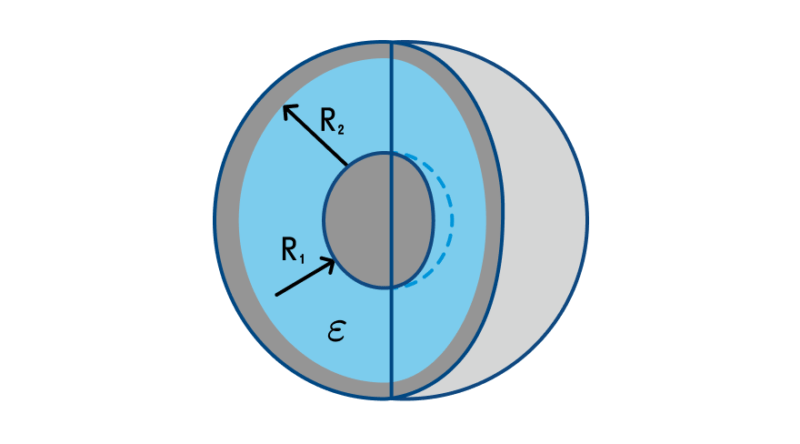
Формула емкости для такого прибора выглядит, как , где:

• С – ёмкость, Ф;
• R1 – радиус внутренней сферы;
• R2 – радиус внешней сферы;
• ε – диэлектрическая проницаемость диэлектрика;
• ε_{0 –} электрическая постоянная, равная 8.85*10^-12 Кл²/Н*м².

Очевидно, что зависимость емкости от геометрии подобна плоскому конденсатору. Емкость увеличивается при увеличении площади поверхностей сфер (которые зависят от квадрата радиусов) и уменьшается при увеличении расстояния между обкладками (R2-R1).

Электроемкость цилиндрического конденсатора

У цилиндрического конденсатора обкладки представляют собой два коаксиальных (расположенных на общей оси) цилиндра длиной l каждый с радиусами R1 (меньший) и R2 (больший). Пространство между ними также может быть заполнено либо воздухом, либо другим диэлектриком. Такие приборы используют в масс-спектрометрии и в некоторых типах счетчиков заряженных частиц. Формула для емкости будет выглядеть, как .

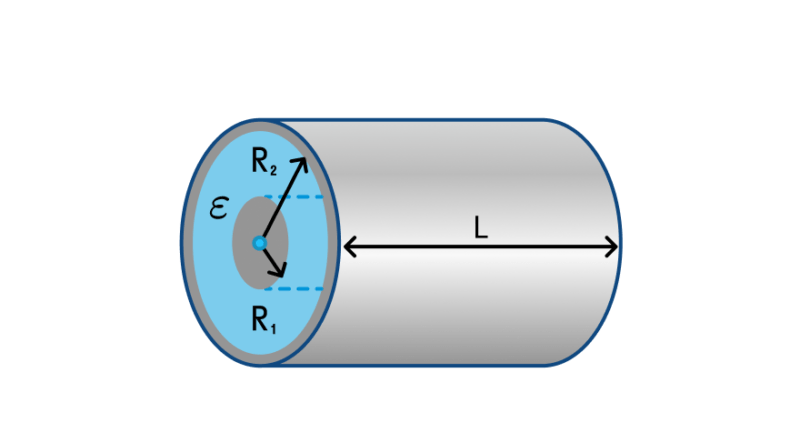
Здесь также прослеживается зависимость от площади (при росте длины увеличивается площадь обкладок, следовательно, растет емкость) и расстояния между обкладками. При росте отношения R2/R1 расстояние увеличивается, а ёмкость падает.

Как изменится емкость при параллельном и последовательном соединении

В реальных схемах конденсаторы могут быть включены последовательно или параллельно. При этом суммарная емкость будет разной.

Если включить n конденсаторов параллельно, то в этом случае:

• к каждой ячейке прикладывается одно и то же напряжение (U₁=U₂=..=U_n=U);
• запасенные в каждом конденсаторе заряды складываются.

Тогда общая емкость равна С=U*q=U*(q₁+q₂+..+q_n)=U*q₁+U*q_2+..+ U*q_n=C1+C2+..+Cn. То есть, при параллельном включении ёмкость батареи равна сумме ёмкостей всех элементов. Это эквивалентно сложению площадей всех пластин.

Батарею можно собрать и последовательно, при этом одна обкладка каждого элемента подключается к выводу соседнего конденсатора, а другая – к выводу другой ячейки. Напряжение подается на свободные выводы крайних элементов.

При этом действуют следующие соотношения (в качестве примера рассмотрена батарея из трех элементов):

• заряды –q1 и q2, -q2 и q3 равны, так как обкладки с этими зарядами соединены между собой;
• заряды q1 и –q1, q2 и –q2, q3 и –q3 равны между собой по модулю, но их знак противоположен.

Заряды каждого конденсатора одинаковы и равны q, но при различной емкости разности потенциалов между обкладками каждого элемента определяются из соотношений:

• U₁=q/ C₁;
• U₂=q/ C₂;
• U₃= q/ C₃.

Следовательно, напряжения на ячейках батареи распределяются пропорционально емкостям. Суммарная емкость равна С=q/(U₁+U₂+U₃), следовательно 1/С=(U₁+U₂+U₃)/q=1/С₁+1/С₂+1/С₃.

Для n элементов, включенных последовательно, выполняется равенcтво:

1/С=1/С₁+1/С₂+..+1/С_n.

Формула достаточно громоздка, но если последовательная цепь состоит из двух элементов, соотношение приводится к виду С= С₁* С₂/( С₁+ С₂).

Последовательное соединение на практике обычно применяется не для снижения общей ёмкости, а для уменьшения напряжения на каждом элементе при использовании конденсаторов в высоковольтных цепях.

Разобравшись с факторами, влияющими на ёмкость конденсатора и способами изменения этого параметра, можно научиться анализировать не только пассивные, но и активные (содержащие полупроводниковые приборы) цепи. Это позволит сделать шаг на пути к развитию навыков и повышению квалификации специалиста.