Условие задачи:
Найти емкость конденсатора колебательного контура, если при индуктивности 50 мкГн контур настроен на длину волны электромагнитных колебаний 300 м.
Задача №9.13.2 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(L=50) мкГн, (lambda=300) м, (C-?)
Решение задачи:
Частоту колебаний колебательного контура (она равна частоте излучаемых электромагнитных волн) можно определить по формуле:
[nu = frac{1}{{2pi sqrt {LC} }};;;;(1)]
В этой формуле (L) – индуктивность катушки, (C) – электроемкость конденсатора.
Возведем обе части (1) в квадрат, тогда имеем:
[{nu ^2} = frac{1}{{4{pi ^2}LC}}]
Откуда искомая емкость конденсатора (C) равна:
[C = frac{1}{{4{pi ^2}{nu ^2}L}};;;;(2)]
Известно, что электромагнитные волны распространяются со скоростью света (c) (в вакууме она равна 3·108 м/с). Между скоростью распространения электромагнитных волн (скоростью света (c)), частотой их колебаний (nu) и длиной волны (lambda) существует следующее соотношение:
[c = lambda nu ]
Откуда частота колебаний (nu) равна:
[nu = frac{c}{lambda }]
Это выражение подставим в ранее полученную формулу (2):
[C = frac{{{lambda ^2}}}{{4{pi ^2}{c^2}L}}]
Посчитаем численный ответ задачи:
[C = frac{{{{300}^2}}}{{4 cdot {{3,14}^2} cdot {{left( {3 cdot {{10}^8}} right)}^2} cdot 50 cdot {{10}^{ – 6}}}} = 5,1 cdot {10^{ – 10}};Ф = 0,51;нФ]
Ответ: 0,51 нФ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
9.13.1 Колебательный контур имеет емкость 2,6 пФ и индуктивность 0,012 мГн. Какой длины
9.13.3 При изменении тока в катушке индуктивности на 1 А за 0,6 с в ней индуцируется ЭДС
9.13.4 Определите максимальный ток в контуре, если длина электромагнитной волны
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,653 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,926 -
разное
16,901
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Емкость конденсаторов, проводов и других элементов электрической цепи измеряется в фарадах (Ф); индуктивность проводов, катушек и других элементов цепей измеряется в генри (Гн).
Емкость плоского конденсатора, состоящего из п пластин площадью пластины 

где d — расстояние между пластинами, м.
Емкость цилиндрического конденсатора (коаксиального кабеля) длиной / (м), Ф:

где R1 — радиус внутренней обкладки (жилы), м;
R2 — радиус внешней обкладки, м.
Емкость прямолинейного провода длиной / и радиусом поперечного сечения г (м) (второй провод — в бесконечности), Ф:

Индуктивность уединенного прямолинейного провода круглого сечения радиусом г и длиной / (м), Гн:

Индуктивность кольца со средним радиусом R и радиусом сечения кольца г (м), Гн:

Индуктивность многослойной катушки толщиной обмотки d, радиусом обмотки R (от оси до среднего слоя обмотки), длиной / (м) и числом витков w (рис. 1.2, а), Гн


Индуктивность тороидальной катушки кругового сечения (рис. 1.2, б), Гн:

где w — число витков катушки,
D — средний диаметр тора, м;
d — диаметр среднего витка, м.
Взаимная индуктивность двух тороидальных катушек с числами витков w^ и w2, Гн:


Рис. 1.3. Концентрически расположенные катушки индуктивности
Взаимная индуктивность концентрических катушек прямоугольного сечения, имеющих одинаковую длину и примыкающих друг к другу (рис. 1.3), Гн:

где L12 — индуктивность катушки, состоящей из первой и второй катушек;
L1, L2 — собственные индуктивности катушек.
После несложной процедуры регистрации Вы сможете пользоваться всеми сервисами и создать свой веб-сайт.
Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.
Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.
— Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
— Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.
Свободные электрические колебания в параллельном контуре.
Основные свойства индуктивности:
— Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией  .
.
— Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.
Период свободных колебаний контура LC можно описать следующим образом:
Если конденсатор ёмкостью C заряжен до напряжения U, потенциальная энергия его заряда составит .
.
Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток его разряда, создавая магнитное поле в катушке.

Магнитный поток, увеличиваясь от нуля, создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в цепи, поэтому конденсатор разрядится не мгновенно, а через время t1, которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t1 =  .
.
По истечении времени t1, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит .
.
В идеальном рассмотрении, при полном отсутствии потерь в контуре, EC будет равна EL. Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.

Изменение (уменьшение) магнитного потока накопленной энергии катушки создаст в ней ЭДС, которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени t2 = t1, он перезарядит конденсатор от нуля до максимального отрицательного значения (-U).
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.
Описанные интервалы t1 и t2 составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление. Магнитная энергия вновь будет накапливаться в катушке в течении времени t3, сменив полярность полюсов.
В течении заключительного этапа колебания (t4), накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения U (в случае отсутствия потерь) и процесс колебания повторится.
В реальности, при наличии потерь энергии на активном сопротивлении проводников, фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t1 + t2 + t3 + t4 составит период колебаний  .
.
Частота свободных колебаний контура ƒ = 1 / T
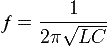
Частота свободных колебаний является частотой резонанса контура, на которой реактивное сопротивление индуктивности XL=2πfL равно реактивному сопротивлению ёмкости XC=1/(2πfC).
Расчёт частоты резонанса LC-контура:
Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Расчёт ёмкости:
Расчёт индуктивности:
Похожие страницы с расчётами:
Замечания и предложения принимаются и приветствуются!

По формуле циклической частоты свободных электромагнитных колебаний , где L — индуктивность катушки (Гн), C — ёмкость конденсатора (Ф). Циклическую частоту расписываем как: , где V — “ню” частота колебаний (Гц). Данную формулу подставляем в формулу циклической частоты свободных электромагнитных колебаний: . Поизводим преобразования и выражаем искомую ёмкость конденсатора:
В системе СИ: 10 МГц = 10*10⁶ Гц; 5,1 мкГн = 5,1*10⁻⁶ Гн. Подставляеи вычисляем:
Итак, для начала немного о конденсаторах. Самый простой из них-две металлические пластины, расположенныена некотором расстоянии друг от друга (рис. 1).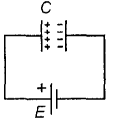 Если к такому элементу подсоединить батарейку, то он через некотороевремя зарядится до того же напряжения, что и батарейка.При этом на пластинах конденсатора будут сосредоточеныэлектрические заряды разного знака (рис. 1). Чем большеенапряжение будет приложено между обкладками, тем больше будет величина электрического заряда пластин. Посколькумежду пластинами находится воздух, а на практике чаще всего какой-либо диэлектрик (непроводящий материал), постоянный ток в цепи на рис. 1 протекать не может. В качестведиэлектрика обычно используются такие материалы, как бумага, слюда, керамика, различные органические пленки и некоторые другие. От типа диэлектрика зависят свойства конденсаторов (в первую очередь частотные), о чем мы дополнительно поговорим в рекомендациях по их выбору. Конечно, на практике через заряженный конденсатор все-таки протекает небольшой ток утечки, вызванный неидеальностью диэлектрика.
Если к такому элементу подсоединить батарейку, то он через некотороевремя зарядится до того же напряжения, что и батарейка.При этом на пластинах конденсатора будут сосредоточеныэлектрические заряды разного знака (рис. 1). Чем большеенапряжение будет приложено между обкладками, тем больше будет величина электрического заряда пластин. Посколькумежду пластинами находится воздух, а на практике чаще всего какой-либо диэлектрик (непроводящий материал), постоянный ток в цепи на рис. 1 протекать не может. В качестведиэлектрика обычно используются такие материалы, как бумага, слюда, керамика, различные органические пленки и некоторые другие. От типа диэлектрика зависят свойства конденсаторов (в первую очередь частотные), о чем мы дополнительно поговорим в рекомендациях по их выбору. Конечно, на практике через заряженный конденсатор все-таки протекает небольшой ток утечки, вызванный неидеальностью диэлектрика.
Рис. 1
Собственно электроемкость есть физическая величина, характеризующая способность конденсатора накапливать (запасать) электрическую энергию. Сухим физико-математическим языком многих учебников говорится, что электроемкость С=q/Uc – это коэффициент пропорциональности между зарядом конденсатора q и напряжением на нем Uc=E, где Е- напряжение источника. Это утверждение, как и многие аналогичные, строго с математической точки зрения, однако, к сожалению, не отражает физической природы явления.
Емкость, как известно, измеряется в долях фарада (единица названа в честь выдающегося физика Майкла Фарадея). При емкости конденсатора в один фарад, электрический заряд на любой из его пластин составил бы один кулон, при напряжении между обкладками в один вольт. На практике емкости, как правило, измеряют в микрофарадах, нанофарадах и пикофарадах.
Емкость конденсатора зависит от формы и геометрических размеров пластин, а также расстояния между ними и параметров диэлектрика. Так, емкость плоского конденсатора, изображенного на рис. 1, определяется как С=ε0εS/d, где ε0 – электрическая постоянная, равная 8,85·1О12 Кл2/(Нм2); ε-диэлектрическая проницаемость диэлектрика; d ~ расстояние между обкладками; S – площадь обкладок. Физический смысл этой формулы вполне очевиден – чем больше площадь пластин и чем ближе друг к другу они расположены, тем больше емкость конденсатора. Отсюда можно сделать важный вывод – при параллельном соединении конденсаторов их емкости складываются, поскольку общая площадь пластин при этом увеличивается. А емкость последовательно соединенных конденсаторов определяется также как сопротивление параллельно включенных резисторов, т.е. итоговая емкость окажется меньше, нежели емкости каждого из последовательно включенных конденсаторов. При этом напряжение распределяется между конденсаторами пропорционально их емкости.
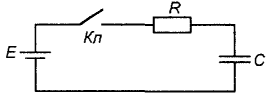
Рис. 2
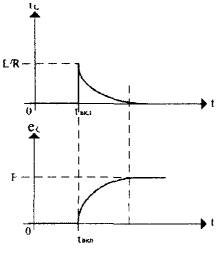
Рис. 3
В заряженном конденсаторе запасена электрическая энергия Wэл = CU2c/2. Однако, накопление электрического заряда и, соответственно, энергии происходит не мгновенно. В электрической цепи, показанной на рис. 2, в момент замыкания ключа начинает протекать ток заряда, ограниченный сопротивлением R, во много раз превосходящем по величине внутренне сопротивление источника, которым в этом случае можно пренебречь. Тогда ток заряда определяется из закона Ома: Iз=E/R. Напряжение на емкости при этом отсутствует Uc=0 (конденсатор до замыкания ключа, естественно, был не заряжен). В процессе заряда конденсатора ток в цепи уменьшается, а напряжение на конденсаторе возрастает и стремится к Uc=Е. Это проиллюстрировано на графиках (рис. 3) Аналогичным образом происходит разряд конденсатора в цепи на рис. 4.
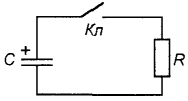
Рис. 4
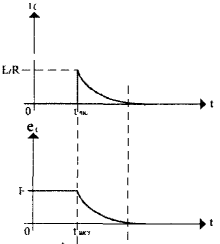
Рис. 5
Здесь ток разряда в момент замыкания ключа скачком возрастает от нуля до величины фаз iраз=E/R, а затем снова плавно падает до нуля. Напряжение на конденсаторе при этом плавно падает от Uc=Е до Uc=0 (рис. 5.). При разряде конденсатора вся энергия, запасенная в нем, переходит в тепловую энергию, рассеиваемую на резисторе. Разряд и соответственно расход энергии, также как и заряд, не происходят мгновенно, а занимают определенное время. Это правило называют законом коммутации, который применительно к цепям с емкостью обычно формулируют так: напряжение на емкости мгновенно измениться не может. Действительно, при разряде конденсатора на резистор, напряжение на нем изменяется плавно:
Uc = E·EXP(-t/RC). Здесь функция ЕХР(х) – показательная функция еx (число Эйлера е=2,718), чаще называемая экспонентой; а величину RC обычно называют постоянной времени и обозначают греческой буквой τ (тау). Действительно, от этой величины зависит длительность разряда. Процессы заряда и разряда конденсатора являются частными случаями переходных процессов.
Теперь переидем к индуктивности. Катушка индуктивности или дроссель также являются накопителями энергии, только здесь, в отличие от конденсатора, энергия электрического тока преобразуется в энергию магнитного поля. Как известно из физики, вокруг проводника с током образуется магнитное поле, т.е. электрическое поле порождает магнитное. Если проводник свернуть в катушку, то магнитное поле возрастет. Это поле пропорционально количеству витков в катушке.
Интенсивность магнитного поля характеризуется величиной магнитного потока Ф и протекающим через катушку током IL. Способность катушки (или проводника с током) накапливать энергию магнитного поля и характеризует величина индуктивности L, которая опять-таки математически строгим языком является коэффициентом пропорциональности между магнитным потоком и протекающим через катушку электрическим током, его порождающим L = Ф/IL Эта величина зависит только от параметров катушки и измеряется в генри (Гн).
 Катушка индуктивностью в один генри при протекании через нее тока в один ампер создает магнитный поток величиной в один веббер (единица измерения магнитного потока). На практике индуктивность катушек обычно намного меньше величины 1 Гн и измеряется в милигенри, микрогенри и наногенри. В цепях постоянного тока сопротивление катушки определяется резистивными потерями в образующем ее проводнике и на ней не падает почти никакого напряжения. При этом, запасенная в катушке энергия магнитного поля может быть вычислена следующим образом: WL=L·IL2/2. Индуктивность (в микрогенри) однослойной катушки (рис. 6) можно рассчитать по следующей известной формуле: L(мкГн)=N2·r2/(9r+10l),где N – число витков, r – радиус витка (каркаса), l – длина намотки Для многослойных катушек существуют свои расчетные формулы. Часто с целью увеличения индуктивности в катушки вводят специальные сердечники из магнито-электриков -феррита, пермалоя, альсифера и т.п.
Катушка индуктивностью в один генри при протекании через нее тока в один ампер создает магнитный поток величиной в один веббер (единица измерения магнитного потока). На практике индуктивность катушек обычно намного меньше величины 1 Гн и измеряется в милигенри, микрогенри и наногенри. В цепях постоянного тока сопротивление катушки определяется резистивными потерями в образующем ее проводнике и на ней не падает почти никакого напряжения. При этом, запасенная в катушке энергия магнитного поля может быть вычислена следующим образом: WL=L·IL2/2. Индуктивность (в микрогенри) однослойной катушки (рис. 6) можно рассчитать по следующей известной формуле: L(мкГн)=N2·r2/(9r+10l),где N – число витков, r – радиус витка (каркаса), l – длина намотки Для многослойных катушек существуют свои расчетные формулы. Часто с целью увеличения индуктивности в катушки вводят специальные сердечники из магнито-электриков -феррита, пермалоя, альсифера и т.п.
Рис. 6
Таким образом, катушка, как и конденсатор, является накопителем энергии. В этом случае на цепи с индуктивностями также должен распространяться закон коммутации, который на сей раз будет звучать так: ток в катушке индуктивности мгновенно изменяться не может. Действительно, при замыкании ключа в цепи на рис. 7 напряжение на катушке изменится скачком до величины E (а затем будет плавно падать до нуля), а ток будет медленно нарастать по тому же закону экспоненты (рис. 8.) от нуля до величины IL= E/R.
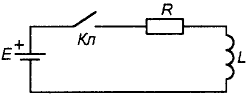
Рис. 7
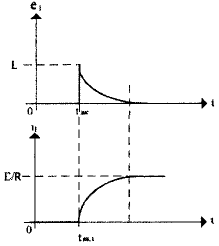
Рис. 8
Так, в цепи на рис. 9 при замыкании ключа сначала загорится лампочка, включенная в ветвь с резистором, а затем, плавно увеличивая яркость, лампочка в индуктивной цепи. Это явление вызвано тем, что аналогично тому как электрическое поле порождает магнитное, так и магнитное, в свою очередь, порождает электрическое. Это утверждение справедливо только для переменного магнитного поля. Это наглядно иллюстрирует известный опыт (рис. 10), когда при перемещении постоянного магнита вдоль катушки в ее внешней цепи протекает ток. Так происходит и в нашем случае: при замыкании ключа через катушку начинает протекать небольшой ток, вызывающий появление около ее витков магнитного потока, изменяющегося пропорционально нарастанию тока. В свою очередь, этот изменяющийся магнитный поток приводит к появлению на катушке электродвижущей силы самоиндукции, включенной согласно закону Ленца встречно силе, вызвавшей ток. Тогда катушка будет оказывать сопротивление нарастанию тока, ровно как и его спаду. Из физики можно привести массу примеров того, когда система противодействует изменению своего стационарного состояния, и сопротивление катушки изменению тока – один из них. В процессе нарастания тока в катушке запасается энергия, а при его спаде, соответственно, тратится. В случае, если резко разомкнуть цепь на рис. 7, через ключ проскочит сильная искра, вызванная ни чем иным, как электродвижущей силой самоиндукции.
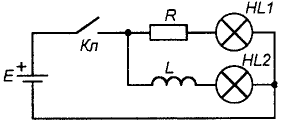
Рис. 9
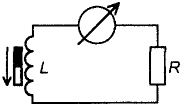
Рис. 10
Рассмотрим, как ведут себя емкость и индуктивность в цепях переменного (синусоидального) тока. Пусть в цепь переменного тока включена емкость (рис. 11). Каждый раз при смене полярности напряжения конденсатор будет перезаряжаться, т.е. знак заряда каждой из его обкладок будет изменяться два раза период переменного напряжения. Если длительность процессов заряда и разряда значительно превосходит период изменения напряжения, ток в цепи также будет изменяться по синусоидальному закону, однако напряжение на конденсаторе отстает по фазе от тока на 90° (рис. 12), что и не удивительно, поскольку конденсатор препятствует резкому изменению напряжения. При этом в процессе каждого заряда-разряда конденсатор будет то накапливать электрическую энергию, то отдавать некоторую ее часть во внешнюю цепь. В большинстве случаев в конденсаторе, включенном в цепь переменного тока, постоянно накоплена определенная электрическая энергия. В цепи с индуктивностью (рис. 13), наоборот, ток отстает по фазе от напряжения на 90° (рис. 14). Это тоже соответствует вышеизложенным рассуждениям -катушка оказывает сопротивление любым изменениям тока. При протекании через катушку переменного тока в ней будет запасаться энергия переменного магнитного поля, приводящая к появлению переменной электродвижущей силы самоиндукции, препятствующей протеканию переменного тока.
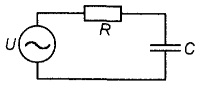
Рис. 11
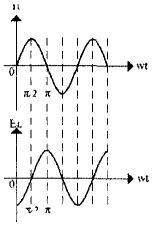
Рис. 12
Итак, катушка в цепи переменного тока оказывает ему сопротивление в результате наведенной переменнои электродвижущей силы самоиндукции. В то же время и конденсатор, запасая в себе электрическую энергию, оказывает сопротивление переменному току. Оба этих сопротивления называют реактивными и обозначают буквой X. В отличие от резистивного (активного) сопротивления, на реактивном не рассеивается никакой тепловой энергии, а лишь запасается энергия в виде электрического или магнитного поля.
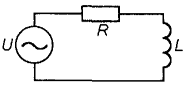
Рис. 13
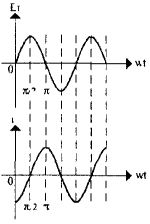
Рис. 14
Реактивные сопротивления катушки XL = j·2πf·L и конденсатора ХC = -j/2πf·C зависят от частоты f протекающего переменного тока. Мнимая единица j учитывает фазовый сдвиг 90° между током и напряжением, а знак “-” показывает, что напряжения на последовательно включенных емкости и индуктивности противофазны. Действительно, при расчете полного комплексного сопротивления цепи, содержащей индуктивности и емкости, индуктивные сопротивления необходимо складывать со знаком “+”, а емкостные, наоборот, со знаком “-“. На рис. 15 показана зависимость реактивных сопротивлений индуктивности и емкости, а также их модулей от частоты. На постоянном токе, как известно, индуктивность не оказывает никакого сопротивления, а сопротивление конденсатора, наоборот, стремиться к бесконечно большому. С ростом частоты картина резко меняется – сопротивление катушки индуктивности возрастает по линейному закону, а сопротивление конденсатора падает согласно кривой, называемой гиперболой.
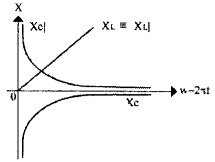
Рис. 15
Вышеупомянутые свойства легко пояснить на примере. На рис. 16 приведена принципиальная схема выходной цепи простейшего радиочастотного усилителя. Здесь в цепь питания коллектора транзистора включен блокировочный дроссель L6n, который на рабочей частоте усилителя имеет очень большое сопротивление. Задача этого дросселя не пропустить переменный ток коллекторной цепи транзистора в источник питания, имеющий очень ма ленькое сопротивление. Этот переменный ток должен протекать в нагрузку через разделительный конденсатор Ср, предотвращающий замыкание источника питания на нагрузку (следующий каскад). Этот конденсатор должен выбираться таким образом, чтобы на рабочей частоте усилителя не оказывать практически никакого сопротивления переменному току, т.е. его реактивное сопротивление должно быть по крайней мере на порядок (в 10 раз) меньше сопротивления нагрузки. Для того, чтобы практически весь переменный ток протекал в нагрузку, нужно, чтобы реактивное сопротивление дросселя, наоборот, по крайней мере на порядок превышало сопротивление нагрузки. Однако, поскольку реактивное сопротивление дросселя не является бесконечно большим, незначительная часть переменного тока все же пройдет через него. Во избежание попадания этого тока в источник питания включен блокировочный конденсатор Сбл, обладающий на рабочей частоте очень маленьким реактивным сопротивлением.
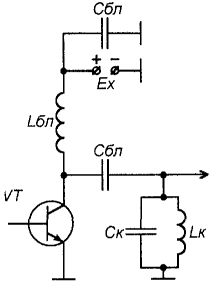
Рис. 16
Катушки, дроссели и конденсаторы находят и много других различных применений в радиоэлектронных устройствах. В частности, на них строятся селективные и иные колебательные цепи, о простейших из которых пойдет речь в следующий раз.
В завершении же сегодняшнего рассказа хотелось отметить еще один важный параметр катушек и конденсаторов. Как мы уже говорили, в катушках и конденсаторах имеются потери. В катушке это конечное сопротивление проводника rL, а в конденсаторе – сопротивление утечки диэлектрика rут. Наличие этих потерь приводит к частичному преобразованию запасаемой в катушке и конденсаторе магнитной и электрической энергии в тепловую. Величина этих потерь характеризуется параметром добротность Q=Х/r, который определяется как отношение запасенной энергии к энергии потерь.
Перейдем к более практическим вещам – как выбрать конденсаторы, дроссели, катушки для своей аппаратуры? Для начала о конденсаторах. Здесь важно знать по крайней мере три параметра – электроемкость, рабочее напряжение (а в ряде случаев и предельную реактивную мощность) и частоту (с точностью до: постоянный ток, звуковые частоты, радиочастоты). Независимо от частоты любые конденсаторы следует выбирать на рабочее напряжение (указывается на корпусе), превосходящее ориентировочно в 1,2 раза максимальное значение напряжения, прикладываемое к этому конденсатору в схеме. Не смотря на то, что напряжение пробоя диэлектрика обычно примерно в 1,5 раза превосходит указанное рабочее, такой запас делать все равно необходимо. Что же касается типа диэлектрика, то на сегодняшний день во все радиочастотные цепи в качестве блокировочных и разделительных конденсаторов, а также емкостей фильтров, необходимо устанавливать керамические конденсаторы, диапазон номиналов которых простирается от единиц пикофорад до десятков нанофарад. Следует особо оговорить, что в качество контурных конденсаторов, а также для других частотоизбирательных цепей (фильтров, цепей согласования и т.п.) следует применять конденсаторы с высокой степенью точности величины их емкости (не хуже ±5%), а вот в качестве блокировочных и разделительных элементов применяют более дешевые детали с меньшей точностью. Подстроечные конденсаторы так же, как правило, керамические, а переменные – с воздушным или твердым синтетическим диэлектриком. Большие значения емкостей, как правило, требуются в низкочастотных цепях, где вполне хорошо работают бумажные конденсаторы – герметизированные и т.п. Разброс значений таких конденсаторов составляет от десятков нанофарад да сотен микрофарад. На смену бумажным конденсаторам (с емкостями, не превышающими единиц микрофарад) все чаще приходят танталовые полупроводниковые. Что же касательно слюдяных, то большинство из них в настоящее время сняты с производства из-за своей нетехнологичности. Эти конденсаторы выпускались с величинами емкостей в пределах от сотен пикофарад до десятков нанофарад. Бумажные конденсаторы устанавливают и в цепи токов промышленной частоты (в качестве сетевых фильтров, пусковых конденсаторов двигателей и неоновых ламп и т.п.). Несколько особняком стоят конденсаторы с диэлектриком на основе различных органических пленок. Их можно применять как в низкочастотной, так и в радиочастотной аппаратуре, однако при частотах, не превышающих примерно 50, в редких случаях 100 МГц. Наконец, в цепях постоянного тока (в фильтрах выпрямителей и т.п.) наиболее предпочтительны электролитические конденсаторы, разброс емкостей которых составляет от единиц микрофарад до десятков милифарад (иногда и более). Эти конденсаторы полярны и в цепях переменного тока очень быстро выходят из строя. В виде исключения, их можно устанавливать в цепи усилителей звуковой частоты в качестве разделительных, а также в цепи смещения маломощных каскадов.
Что касается катушек индуктивности и дросселей, то их при изготовлении любительской аппаратуры, как правило, приходится делать самому. Исключение составляют высокочастотные дроссели, которые выпускаются промышленностью на индуктивности порядка десятков – сотен микро-генри. Эти дроссели низкодобротные и ни в коем случае не могут использоваться в качестве контурных катушек и индуктивностей фильтров. Основное их назначение – блокировочные дроссели каскадов усиления радиочастоты малой и иногда средней мощности (при токах в цепях, не превышающих одного-двух ампер). В мощных каскадах передатчиков и другой генераторной аппаратуры устанавливаются самодельные дроссели, которые наматываются толстым медным проводом, способным выдерживать протекающие в этих цепях токи. Это касается и контурных катушек мощных каскадов. Их следует наматывать на теплостойких каркасах без сердечников, поскольку последние сильно разогреваются вихревыми токами высокой частоты и заметно снижают КПД каскада. А вот при намотке контурных катушек и индуктивносетй фильтров маломощных каскадов передатчиков и приемников обычно используют каркасы с сердечниками – чаще всего ферритовыми. Также иногда применяют альсиферовые и латунные (на УКВ) сердечники. В диапазонах KB и УКВ применяют однослойную намотку, а на более низких частотах – многослойную, причем при многослойной намотке желательно применять метод “универсаль” с перекрещиванием витков (как на бобине с нитками или шпагатом), что позволяет уменьшить собственную емкость катушки. Что же касается низкочастотных дросселей (фильтров выпрямителя и т.п.), то их чаще всего наматывают на сердечниках из трансформаторной стали или используют готовые от промышленной аппаратуры.
В заключение расскажем, как при помощи старенького авометра (стрелочного тестера) определить исправность катушек и конденсаторов. Для испытаний конденсаторов тестер следует перевести на максимальный предел измерения сопротивления. Итак, исправный конденсатор емкостью менее 0,1 микрофарад не должен вызывать никакого отклонения стрелки, – в противном случае конденсатор пробит. При испытании конденсатора емкостью 0,1… 10 микрофарад стрелка должна дернуться вправо и быстро вернуться в область бесконечно большого сопротивления. Наконец, при испытании конденсаторов большой емкости (электролитических и т.п.) стрелка тестера должна резко отклониться вправо (почти до нуля сопротивлений), а затем медленно возвратиться обратно. Слабый бросок свидетельствует о потере емкости. К сожалению, при помощи цифровых мультиметров подобное испытание практически невозможно ввиду отсутствия стрелочного индикатора, однако многие из них “умеют” измерять емкость, что существенно упрощает задачу. Для проверки катушек индуктивности и дросселей тестер необходимо перевести на нижний предел измерения сопротивлений. Контурные катушки и высокочастотные дроссели имеют омическое сопротивление, близкое к нулю, а при испытании низкочастотных дросселей (а также обмоток низкочастотных и силовых трансформаторов) тестер покажет сопротивление порядка десятков – сотен Ом. При испытании низкочастотных индуктивных элементов следует избегать касания проводников незащищенными руками, поскольку в момент подсоединения дросселя или трансформатора к тестеру, на зажимах появляется ЭДС самоиндукции значительной величины.
Содержание
- От чего зависит и в чем измеряется емкость конденсатора
- Как узнать емкость конденсатора
- По маркировке
- Мультиметром
- Осциллографом
- Формулы для расчета емкости
- Электроемкость плоского конденсатора
- Электроемкость сферического конденсатора
- Электроемкость цилиндрического конденсатора
- Как изменится емкость при параллельном и последовательном соединении
Конденсатор – пассивный электронный компонент, главной характеристикой которого является емкость. Предназначен в основном для накопления энергии, разделения цепей постоянного тока, фильтрации помех, создания резонансных цепей и т.п. Чтобы применение конденсаторов на практике было осознанным, следует ознакомиться с их основными параметрами, методами измерения и изменения емкости.
От чего зависит и в чем измеряется емкость конденсатора
Конденсатор в общем случае состоит из двух проводящих обкладок, разделенных диэлектриком. Если к обкладкам приложить напряжение, такое устройство запасает электрическую энергию путем накопления заряда. (говорят, что конденсатор заряжается). Количественно запасенная конденсатором электрическая энергия выражается формулой ![]() , где W – величина энергии, U – напряжение между обкладками, а С – емкость, то есть, величина, характеризующая способность конденсатора запасать энергию. В целом ёмкость зависит от площади обкладок, расстояния между ними и свойствами разделяющего диэлектрика.
, где W – величина энергии, U – напряжение между обкладками, а С – емкость, то есть, величина, характеризующая способность конденсатора запасать энергию. В целом ёмкость зависит от площади обкладок, расстояния между ними и свойствами разделяющего диэлектрика.
Единицей измерения емкости в СИ является фарад (1 Ф) (устаревшее название – фарада). Для практических целей это слишком большая единица. Так, земной шар имеет ёмкость менее 1 Ф, поэтому в технике используют, в основном, дольные единицы:
- пикофарады – 1 пФ (1 pF) =10-12 Ф;
- нанофарады – 1 нФ (1 nF) =10-9 Ф;
- микрофарады – 1мкФ (1 µF) = 10-6 Ф.
Более крупные единицы до недавнего времени не использовались, так как емкости порядка больших дольных единиц были труднодостижимыми. Лишь с появлением ионисторов появилась возможность оперировать величинами порядка единиц и даже десятков фарад.
Как узнать емкость конденсатора
Чтобы использовать конденсатор для практических целей, надо знать его емкость. Выяснить эту величину можно различными способами.
По маркировке
В первую очередь, надо попробовать определить параметры конденсатора по его маркировке. На оксидные конденсаторы, имеющие емкость которых составляет от долей до нескольких тысяч микрофарад, эта характеристика наносится на корпус в виде цифры, обозначающей емкость в микрофарадах, с индексом uF (для отечественных изделий предыдущих годов выпуска после цифры стоит индекс мкФ).
Конденсаторы, обладающие емкостью от единиц пикофарад до единиц микрофарад маркируют тремя цифрами:
- первые два символа — мантисса;
- третья цифра – множитель.
Попросту говоря, к первым двум цифрам надо приписать количество нулей, обозначаемое третьей цифрой.
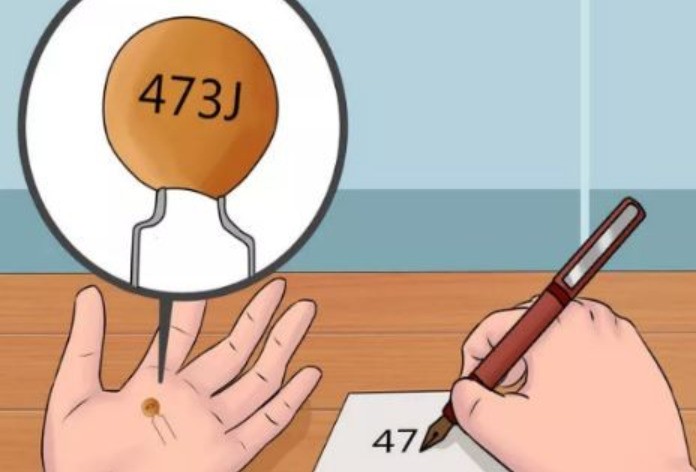
Например, на конденсатор на рисунке нанесено обозначение 473. К цифрам 47 надо приписать три нуля, тогда получится 47000 пФ. Удобнее представить это значение в виде 47нФ или 0,047 мкФ.
Такое обозначение применяется не всегда (особенно, на старых типах отечественных изделий). Иногда на корпусе наносят явное значение ёмкости с единицей измерения.

Но и единицу измерения указывают не всегда. Принцип таков:
- если нет множителя или не указана единица, считается, что ёмкость в пикофарадах;
- если есть множитель, он указывается одной буквой (n – нанофарады, µ — микрофарады и т.п.).
На зарубежных конденсаторах выпуска до 70-х годов можно встретить обозначение µµF. Так маркировалась ёмкость в пикофарадах («микро-микрофарады»).
Если емкость неизвестна, надпись но корпусе отсутствует или есть сомнения, лучше провести измерения одним из известных способов.

Мультиметром

Сделать это можно, например, с помощью цифрового тестера. Многие современные мультиметры имеют функцию измерения емкости конденсаторов. Надо всего лишь выбрать соответствующий режим, обычно обозначаемый символом конденсатора или буквами Cx, и подключить конденсатор к щупам или специально выделенным гнездам. При измерении надо иметь в виду, что:
- Нижний предел измеряемой величины довольно большой, и для большинства распространенных приборов составляет не менее 1000 пФ.
- Измерительные провода со щупами имеют собственную ёмкость (до 100 пФ), и ее надо учитывать при измерениях.
Поэтому тестеры, у которых для измерения ёмкости предназначен отдельный выход, измеряют параметры более точно.
Чтобы обмерить конденсатор с меньшей ёмкостью, лучше воспользоваться специализированным тестером (можно приобрести на интернет-площадках, расположенных в Юго-Восточной Азии). Они позволяют измерять ёмкость от десятков или даже единиц пикофарад.

Осциллографом
Если есть два резистора – один с известным сопротивлением R, а другой с неизвестным Rx, их можно соединить последовательно (сделать делитель напряжения), подать на него напряжение, и измерить падение на каждом элементе или на общей цепи. Измерения можно провести тестером в режиме вольтметра. Тогда Rx можно вычислить по одной из формул, указанных на рисунке.
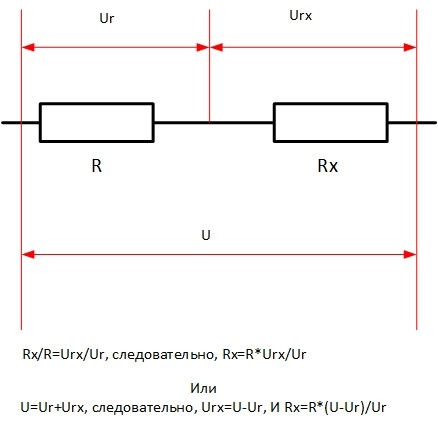
Известно, что конденсатор обладает сопротивлением переменному току, которое зависит от частоты по формуле Xc=1/(2*π*f*C), где:
- f – частота тока в Герцах;
- С – ёмкость конденсатора в Фарадах.
Можно сделать подобный делитель из конденсаторов, и сравнить сопротивление неизвестного прибора Xcx с сопротивлением эталонного конденсатора Xc, откуда легко вычислить неизвестную ёмкость: ![]()
откуда ![]()
Далее несложно найти С.
При этом возникают две проблемы:
- Измерения нельзя проводить на постоянном токе – сопротивление реального конденсатора при f=0 близко к бесконечности.
- При измерении переменного напряжения достаточно высокой частоты тестер будет давать значительную погрешность.
Поэтому в качестве источника тока надо использовать генератор сигнала высокой частоты (чем меньше предполагаемая ёмкость, тем выше должна быть частота, в противном случае точность замеров будет невысокой), а в качестве измерительного прибора – осциллограф.
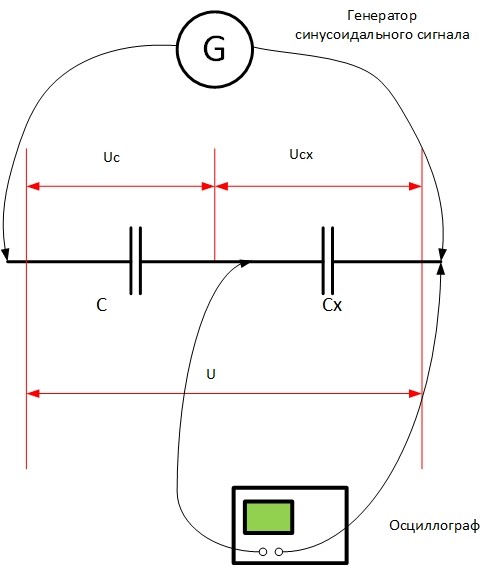
В качестве эталонного элемента для делителя можно взять резистор с известным сопротивлением (вместо Xc в формулу надо подставить R) или катушку (дроссель) с известной индуктивностью. В этом случае вместо Xc в формулу надо подставить XL (вычисляется, как XL=2* π*f*L).
Если имеется эталонная индуктивность, можно найти емкость, составив колебательный контур. Его надо подключить по указанной схеме, а затем, перестраивая генератор, найти резонансную частоту (при ней амплитуда сигнала на осциллографе будет максимальной). Ёмкость можно рассчитать по известной формуле Томсона ![]() .
.

Мнение эксперта
Становой Алексей
Инженер-электроник. Работаю в мастерской по ремонту бытовых приборов. Увлекаюсь схемотехникой.
Задать вопрос
При подключении щупов генератора и осциллографа к измерительным цепям, надо учитывать влияние кабелей (собственная емкость может составлять несколько десятков пикофарад). Чтобы исключить это влияние, измеряемую цепь лучше подключать к щупам через конденсаторы маленькой емкости.
Формулы для расчета емкости
Хотя общая зависимость ёмкости от геометрических размеров и свойств диэлектрика определена выше, для конкретных типов конденсаторов удобнее пользоваться приведенными формулами.
Электроемкость плоского конденсатора
Самый распространённый тип конденсатора, применяемый в технике – плоский. Его обкладки состоят из двух параллельных пластин, между которыми находится диэлектрик. Чтобы уменьшить габариты такого прибора, обкладки с диэлектриком между ними сворачивают в рулон или складывают в прямоугольный пакет. Емкость такого конденсатора рассчитывается по формуле ![]() , где:
, где:
- С – ёмкость, Ф;
- S – площадь обкладок, кв.м;
- d – расстояние между обкладками;
- ε – диэлектрическая проницаемость диэлектрика;
- ε0 – электрическая постоянная, равная 8.85*10-12 Кл2/Н*м2.
Очевидно, что емкость тем больше, чем больше площадь обкладок и меньше расстояние между ними. Кроме того, можно выбрать диэлектрик с высоким ε и пропорционально увеличить ёмкость в тех же габаритах.

Электроемкость сферического конденсатора
Сферическим конденсатором называется устройство, состоящее из двух проводящих сфер – большой радиусом R1 и малой радиусом R2. Малая сфера вложена в большую. Поверхности сфер служат обкладками. Пространство между сферами может заполняться твердым, жидким диэлектриком или воздухом (воздушный сферический конденсатор). Такие приборы используются для лабораторных исследований (например, для изучения фотоэлектрических явлений).
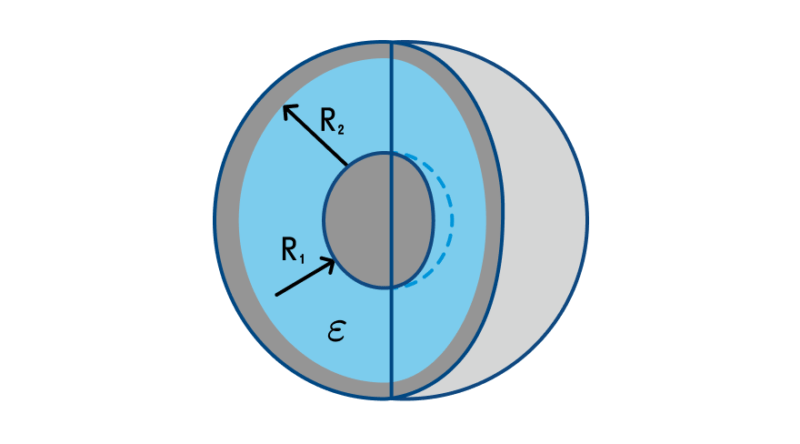
Формула емкости для такого прибора выглядит, как ![]() , где:
, где:
- С – ёмкость, Ф;
- R1 – радиус внутренней сферы;
- R2 – радиус внешней сферы;
- ε – диэлектрическая проницаемость диэлектрика;
- ε0 – электрическая постоянная, равная 8.85*10-12 Кл2/Н*м2.
Очевидно, что зависимость емкости от геометрии подобна плоскому конденсатору. Емкость увеличивается при увеличении площади поверхностей сфер (которые зависят от квадрата радиусов) и уменьшается при увеличении расстояния между обкладками (R2-R1).
Электроемкость цилиндрического конденсатора
У цилиндрического конденсатора обкладки представляют собой два коаксиальных (расположенных на общей оси) цилиндра длиной l каждый с радиусами R1 (меньший) и R2 (больший). Пространство между ними также может быть заполнено либо воздухом, либо другим диэлектриком. Такие приборы используют в масс-спектрометрии и в некоторых типах счетчиков заряженных частиц. Формула для емкости будет выглядеть, как ![]() .
.
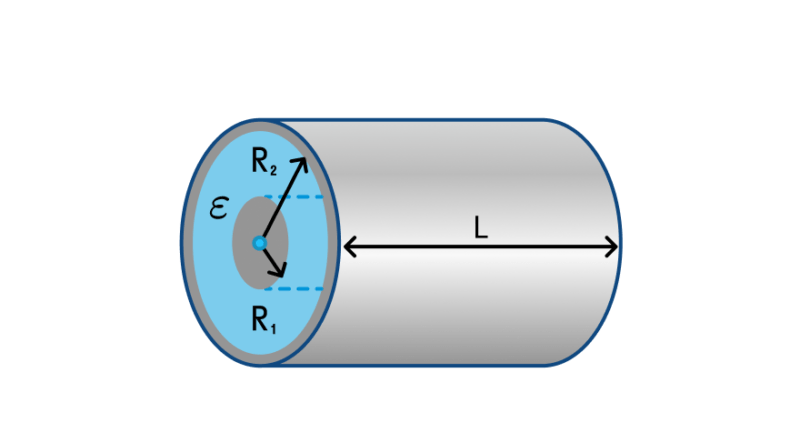
Здесь также прослеживается зависимость от площади (при росте длины увеличивается площадь обкладок, следовательно, растет емкость) и расстояния между обкладками. При росте отношения R2/R1 расстояние увеличивается, а ёмкость падает.
Как изменится емкость при параллельном и последовательном соединении
В реальных схемах конденсаторы могут быть включены последовательно или параллельно. При этом суммарная емкость будет разной.

Если включить n конденсаторов параллельно, то в этом случае:
- к каждой ячейке прикладывается одно и то же напряжение (U1=U2=..=Un=U);
- запасенные в каждом конденсаторе заряды складываются.
Тогда общая емкость равна С=U*q=U*(q1+q2+..+qn)=U*q1+U*q2+..+ U*qn=C1+C2+..+Cn. То есть, при параллельном включении ёмкость батареи равна сумме ёмкостей всех элементов. Это эквивалентно сложению площадей всех пластин.
Батарею можно собрать и последовательно, при этом одна обкладка каждого элемента подключается к выводу соседнего конденсатора, а другая – к выводу другой ячейки. Напряжение подается на свободные выводы крайних элементов.

При этом действуют следующие соотношения (в качестве примера рассмотрена батарея из трех элементов):
- заряды –q1 и q2, -q2 и q3 равны, так как обкладки с этими зарядами соединены между собой;
- заряды q1 и –q1, q2 и –q2, q3 и –q3 равны между собой по модулю, но их знак противоположен.
Заряды каждого конденсатора одинаковы и равны q, но при различной емкости разности потенциалов между обкладками каждого элемента определяются из соотношений:
- U1=q/ C1;
- U2=q/ C2;
- U3= q/ C3.
Следовательно, напряжения на ячейках батареи распределяются пропорционально емкостям. Суммарная емкость равна С=q/(U1+U2+U3), следовательно 1/С=(U1+U2+U3)/q=1/С1+1/С2+1/С3.
Для n элементов, включенных последовательно, выполняется равенcтво:
1/С=1/С1+1/С2+..+1/Сn.
Формула достаточно громоздка, но если последовательная цепь состоит из двух элементов, соотношение приводится к виду С= С1* С2/( С1+ С2).

Последовательное соединение на практике обычно применяется не для снижения общей ёмкости, а для уменьшения напряжения на каждом элементе при использовании конденсаторов в высоковольтных цепях.
Разобравшись с факторами, влияющими на ёмкость конденсатора и способами изменения этого параметра, можно научиться анализировать не только пассивные, но и активные (содержащие полупроводниковые приборы) цепи. Это позволит сделать шаг на пути к развитию навыков и повышению квалификации специалиста.
