Как найти емкость конденсатора колебательного контура

Условие задачи:

Найти емкость конденсатора колебательного контура, если при индуктивности 50 мкГн контур настроен на длину волны электромагнитных колебаний 300 м.

Задача №9.13.2 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(L=50) мкГн, (lambda=300) м, (C-?)

Решение задачи:

Частоту колебаний колебательного контура (она равна частоте излучаемых электромагнитных волн) можно определить по формуле:

[nu = frac{1}{{2pi sqrt {LC} }};;;;(1)]

В этой формуле (L) – индуктивность катушки, (C) – электроемкость конденсатора.

Возведем обе части (1) в квадрат, тогда имеем:

[{nu ^2} = frac{1}{{4{pi ^2}LC}}]

Откуда искомая емкость конденсатора (C) равна:

[C = frac{1}{{4{pi ^2}{nu ^2}L}};;;;(2)]

Известно, что электромагнитные волны распространяются со скоростью света (c) (в вакууме она равна 3·10⁸ м/с). Между скоростью распространения электромагнитных волн (скоростью света (c)), частотой их колебаний (nu) и длиной волны (lambda) существует следующее соотношение:

[c = lambda nu ]

Откуда частота колебаний (nu) равна:

[nu = frac{c}{lambda }]

Это выражение подставим в ранее полученную формулу (2):

[C = frac{{{lambda ^2}}}{{4{pi ^2}{c^2}L}}]

Посчитаем численный ответ задачи:

[C = frac{{{{300}^2}}}{{4 cdot {{3,14}^2} cdot {{left( {3 cdot {{10}^8}} right)}^2} cdot 50 cdot {{10}^{ – 6}}}} = 5,1 cdot {10^{ – 10}};Ф = 0,51;нФ]

Ответ: 0,51 нФ.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

9.13.1 Колебательный контур имеет емкость 2,6 пФ и индуктивность 0,012 мГн. Какой длины
9.13.3 При изменении тока в катушке индуктивности на 1 А за 0,6 с в ней индуцируется ЭДС
9.13.4 Определите максимальный ток в контуре, если длина электромагнитной волны

Популярные сообщения из этого блога

Упражнение 2. Измерение емкости конденсатора

Если индуктивность контура известна, то, измерив резонансную частоту, можно определить емкость конденсатора, включенного в контур. Определим неизвестную емкость конденсатора С₃.

1. Переключатель П_I на стенде поставить в положение III.

2. Найти резонансную частоту , выполнив пункт 5 упр. I.

3. Вычислить емкость конденсатора по формуле

(30)

УПРАЖНЕНИЕ 3. Изучение влияния сердечника на величину индуктивности катушки

В тех случаях, когда необходимо изменять резонансную частоту колебательного контура, обычно используются конденсаторы переменной емкости. Однако иногда удобнее изменять величину индуктивности катушки. Это достигается с помощью сердечников, которые могут перемещаться внутри каркаса, на котором намотана катушка,

В вашем распоряжении имеются латунный и ферритовый сердечники. Выясним, как влияют на индуктивность катушки и на резонансную частоту контура сердечники, изготовленные из различных материалов:

I. Введите латунный сердечник внутрь каркаса катушки.

2. Выполните пункты 4 и 5 упражнения I и определите .

3. Поменяйте латунный сердечник на ферритовый и вновь найдите , выполнив пункт 5 упражнения I.

4. Вычислите индуктивность катушки с латунным и ферритовым сердечниками по формуле

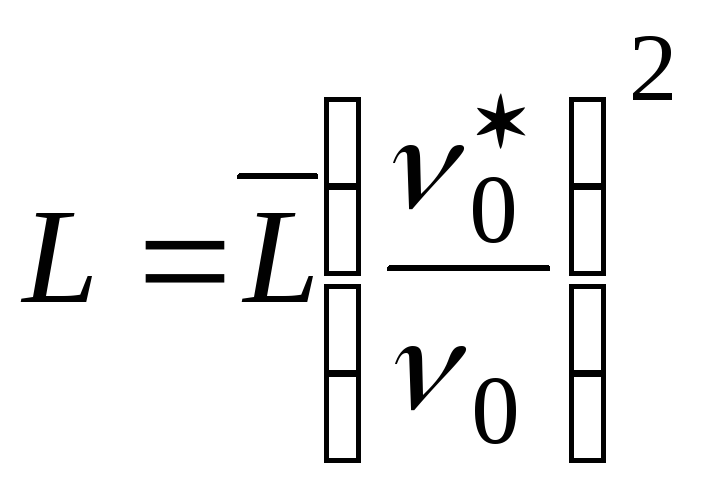(31)

(за взять значениеиз первой строки таблицы I).

5. Заполните таблицу 2.

6. Сделайте выводы о влиянии материала сердечника на величину индуктивности катушки и на резонансную частоту контура.

, МГц

Источник

Колебательный контур LC

Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.

Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.

— Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
— Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.

Рассмотрим, как возникают и поддерживаются свободные электрические колебания в параллельном контуре LC.

Основные свойства индуктивности

— Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией .
— Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.

Природа электромагнитных колебаний в контуре

Период свободных колебаний контура LC можно описать следующим образом:

Если конденсатор ёмкостью C заряжен до напряжения U, потенциальная энергия его заряда составит.
Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток разряда конденсатора, создавая магнитное поле в катушке.

Внешний магнитный поток создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в каждом витке, поэтому конденсатор разрядится не мгновенно, а через время t₁, которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t₁ = .
По истечении времени t₁, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит.
В идеальном рассмотрении, при полном отсутствии потерь в контуре, E_C будет равна E_L. Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.

Далее изменение (уменьшение от максимума) магнитного потока накопленной энергии катушки будет создавать в ней ЭДС, которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени t₂ = t₁, он перезарядит конденсатор от нулевого до максимального отрицательного значения (-U).
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.

Описанные интервалы t₁ и t₂ составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление. Магнитная энергия вновь будет накапливаться в катушке в течении времени t₃, сменив полярность полюсов.

В течении заключительного этапа колебания (t₄), накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения U (в случае отсутствия потерь) и процесс колебания повторится.

В реальности, при наличии потерь энергии на активном сопротивлении проводников, фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t₁ + t₂ + t₃ + t₄ составит период колебаний .
Частота свободных колебаний контура ƒ = 1 / T

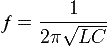
Частота свободных колебаний является частотой резонанса контура, на которой реактивное сопротивление индуктивности X_L=2πfL равно реактивному сопротивлению ёмкости X_C=1/(2πfC).

Расчёт частоты резонанса LC-контура:

Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.

Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

Источник

Как определить емкость конденсатора?

Основной характеристикой конденсатора является его емкость. Очень часто замеры емкости требуется проводить в электролитическом конденсаторе. В отличие от керамических и оксидных конденсаторов, которые редко выходят из строя (разве что в результате пробоя диэлектрика), электролитическим деталям свойственна потеря ёмкости из-за высыхания электролита. Поскольку работа электронных схем сильно зависит от емкостных характеристик, то необходимо знать, как определить емкость конденсатора.

Существуют разные способы определения ёмкости:

• по кодовой или цветной маркировке деталей;
• с помощью измерительных приборов;
• с использованием формулы.

Измерить емкость проще всего с помощью измерителя C и ESR. Для этого контакты измерительных щупов подсоединяют к выводам конденсатора, соблюдая полярность электролитических деталей. При этом результаты измерений выводятся на дисплей. (Рисунок 1). Радиолюбители, которым часто приходится делать измерения, приобретают такой прибор или изготавливают его самостоятельно.

Рис. 1. Измерение ёмкости с помощью измерителя C и ESR

С использованием мультиметра и формул

Если в вашем распоряжении есть мультиметр с функцией измерения параметра «Cx», то измерить ёмкость конденсатора довольно просто: следует переключить прибор в режим «Сх», после чего выбрать оптимальный диапазон измерения, соответствующий параметрам конденсатора. Ножки конденсатора вставляем в соответствующее гнездо (соблюдая полярность подключения) и считываем его параметры.

Режим “Сх” в мультиметре

Менее точно можно определить ёмкость с помощью тестера, у которого нет режима «Сх». Для этого потребуется источник питания, к которому подключают конденсатор по простой схеме (рис. 2).

Рис. 2. Схема подключения конденсатора

Алгоритм измерения следующий:

1. Измерьте напряжение источника питания щупами контактов измерительного прибора.
2. Образуйте RC-цепочку с конденсатором и выводами резистора номиналом 1 – 10 кОм.
3. Закоротите выводы конденсатора и подключите RC-цепочку к источнику питания.
4. Замерьте напряжение образованной цепи с помощью мультиметра.
5. Если напряжение изменилось, необходимо подогнать его до значения, близкого к тому, которое вы получили на выходе источника питания.
6. Вычислите 95% от полученного значения. Запишите показатели измерений.
7. Возьмите секундомер и включите его одновременно с убиранием закоротки.
8. Как только мультиметр покажет значение напряжения, которое вы вычислили (95%), остановите секундомер.
9. По формуле С = t/3R, где t – время падения напряжения, вычисляем ёмкость конденсатора в фарадах, если единицы измерения сопротивление резистора выразили в омах, а время в секундах.

Рис. 3. Измерение с помощью тестера. Проверка

Подчеркнём ещё раз, что точность измерения ёмкости данным способом не слишком высока, но определить работоспособность радиоэлемента на основании такого измерения вполне возможно. Некоторые узлы электронных приборов исправно работают, если есть небольшие отклонения от номинальных емкостей, главное, чтобы не было электрического пробоя.

Таким же методом можно вычислить параметры керамического радиоэлемента. Для этого необходимо подключить RC-цепочку через трансформатор и подать переменное напряжение. Значение ёмкости в данном случае определяем по формуле: C = 0.5*π*f*X_c , где f – частота тока, а X_c – ёмкостное сопротивление.

Осциллографом

С приемлемой точностью можно определить ёмкость конденсатора с помощью цифрового или обычного электронного осциллографа. Принцип похож на метод измерения ёмкости тестером. Разница только в том, что не потребуется секундомер, так как с высокой точностью время зарядки конденсатора отображается на экране осциллографа. Если применить генератор частоты и последовательную RC-цепочку (рис. 4), то ёмкость можно рассчитать по простой формуле: C = U_R / U_C* ( 1 / 2*π*f*R ).

Рис. 4. Простая схема

Алгоритм вычисления простой:

1. Подключите осциллограф к электрической схеме. При подключении щупов прибора к электролитам соблюдайте полярность электрического тока.
2. Измерьте амплитуды напряжений на конденсаторе и на резисторе.
3. Путём подстройки частоты генератора добивайтесь, чтобы значения амплитуд на обоих элементах сравнялись (хотя бы приблизительно).
4. Подставьте полученные значения в формулу и вычислите ёмкость конденсатора.

При измерении ёмкостей неполярных конденсаторов часто вместо RC-цепочки собирают мостовую схему с частотным генератором (показано на рис. 5), а также другие сборки. Сопротивления резисторов подбирают в зависимости от параметров номинальных напряжений измеряемых деталей. Ёмкость вычисляют из соотношения: r₄ / C_x = r₂ / C₀.

Рисунок 5. Мостовая схема

Гальванометром

При наличии баллистического гальванометра также можно определить ёмкость конденсатора. Для этого используют формулу:

C = α * C_q / U , где α – угол отклонения гальванометра, C_q – баллистическая постоянная прибора, U – показания гальванометра.

Из-за падения сопротивления утечки ёмкость конденсаторов уменьшается. Энергия теряется вместе с током утечки.

Описанные выше методики определения ёмкости позволяют определить исправность конденсаторов. Значительное отклонение от номиналов говорит, что конденсаторы неисправны. Пробитый электролитический радиоэлемент легко определяется путём измерения сопротивления. Если сопротивление стремится к 0 – изделие закорочено, а если к бесконечности – значит, есть обрыв.

Следует опасаться сильного электрического разряда при подключениях щупов к большим электролитам. Они могут накапливать мощный электрический заряд от постоянного тока, который молниеносно высвобождается током разряда.

По маркировке

Напомним, что единицей емкости в системе СИ является фарада ( обозначается F или Ф). Это очень большая величина, поэтому на практике используются дольные величины:

• миллифарады (mF, мФ ) = 10 -3 Ф;
• микрофарады (µF, uF, mF, мкФ) = 10 -3 мФ = 10 -6 Ф;
• нанофарады (nF, нФ) = 10 -3 мкФ =10 -9 Ф;
• пикофарады (pF, mmF, uuF) = 1 пФ = 10 -3 нФ = 10 -12 Ф.

Мы перечислили название единиц и их сокращённое обозначение потому, что они часто встречаются в маркировке крупных конденсаторов (см. рис. 6).

Обратите внимание на маркировку плоского конденсатора (второй сверху): после трёхзначной цифры стоит буква М. Данная буква не обозначает единицы измерения «мегафарад» – таких просто не существует. Буквами обозначены допуски, то есть, процент отклонения от ёмкости, обозначенной на корпусе. В нашем случае отклонение составляет 20% в любую сторону. Надпись 102М на большом корпусе можно было бы написать: 102 нФ ± 20%.

Теперь расшифруем надпись на корпусе третьего изделия. 118 – 130 MFD обозначает, что перед нами конденсатор, ёмкость которого находится в пределах 118 – 130 микрофарад. В данном примере буква М уже обозначает «микро». FD – обозначает «фарады», сокращение английского слова «farad».

На этом простом примере видно, какая большая путаница в маркировке. Особенно запутана кодовая маркировка, применяемая для крохотных конденсаторов. Дело в том, что можно встретить конденсаторы, маркировка которых выполнена старым способом и детали с современной кодировкой, в соответствии со стандартом EIA. Одни и те же символы можно по-разному интерпретировать.

По стандарту EIA:

1. Две цифры и одна буква. Цифры обозначают ёмкость, обычно в пикофарадах, а буква – допуски.
2. Если буква стоит на первом или втором месте, то она обозначает либо десятичную запятую (символ R), либо указывает на название единицы измерения («p» – пикофарад, «n» – нанофарад, «u» – микрофарад). Например: 2R4 = 2.4 пФ; N52 = 0,52 нФ; 6u1 = 6,1 мкф.
3. Маркировка тремя цифрами. В данном коде обращайте внимание на третью цифру. Если её значение от 0 до 6, то умножайте первые две на 10 в соответствующей степени. При этом 10 0 =1; 10 1 = 10; 10 2 = 100 и т. д. до 10 6 .

Цифры от 7 до 9 указывают на показатель степени со знаком «минус»: 7 условно = 10 -3 ; 8 = 10 -2 ; 9 = 10 -1 .

• 256 обозначает: 25× 10 5 = 2500 000 пФ = 2,5 мкФ;
• 507 обозначает: 50 × 10 -3 = 50 000 пФ = 0, 05 мкФ.

Возможна и такая надпись: «1B253». При расшифровке необходимо разбить код на две части – «1B» (значение напряжения) и 253 = 25 × 10 3 = 25 000 пФ = 0,025 мкФ.

В кодовой маркировке используются прописные буквы латинского алфавита, указывающие допуски. Один пример мы рассмотрели, анализируя маркировку на рис. 6.

Приводим полный список символов:

• B = ± 0,1 пФ;
• C = ± 0,25 пФ;
• D = ± 0,5 пФ или ± 0,5% (если емкость превышает 10 пФ).
• F = ± 1 пФ или ± 1% (если емкость превышает 10 пФ).
• G = ± 2 пФ или ± 2% (для конденсаторов от 10 пФ»).
• J = ± 5%.
• K = ± 10%.
• M = ± 20%.
• Z = от –20% до + 80%.

Изделия с кодовой маркировкой изображены на рис. 7.

Рис. 7. Пример кодовой маркировки

Если в кодировке отсутствует символ из приведённого выше списка, а стоит другая буква, то она может единицу измерения емкости.

Важным параметром является его рабочее напряжение конденсатора. Но так как в данной статье мы ставим задачу по определению ёмкости, то пропустим описание маркировки напряжений.

Отличить электролитический конденсатор от неполярного можно по наличию символа «+» или «–» на его корпусе.

Цветовая маркировка

Описывать значение каждого цвета не имеет смысла, так как это понятно из следующей таблицы (рис. 8):

Рис. 8. Цветовая маркировка

Запомнить символику кодовой и цветовой маркировки довольно трудно. Если вам не приходится постоянно заниматься подбором конденсаторов, то проще пользоваться справочниками или обратиться к информации, изложенной в данной статье.

Источник

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Емкость конденсаторов, проводов и других элементов электрической цепи измеряется в фарадах (Ф); индуктивность проводов, катушек и других элементов цепей измеряется в генри (Гн).

Емкость плоского конденсатора, состоящего из п пластин площадью пластины

где d — расстояние между пластинами, м.

Емкость цилиндрического конденсатора (коаксиального кабеля) длиной / (м), Ф:

где R1 — радиус внутренней обкладки (жилы), м;

R2 — радиус внешней обкладки, м.

Емкость прямолинейного провода длиной / и радиусом по­перечного сечения г (м) (второй провод — в бесконечности), Ф:

Индуктивность уединенного прямолинейного провода круглого сечения радиусом г и длиной / (м), Гн:

Индуктивность кольца со средним радиусом R и радиусом сечения кольца г (м), Гн:

Индуктивность многослойной катушки толщиной обмот­ки d, радиусом обмотки R (от оси до среднего слоя обмотки), длиной / (м) и числом витков w (рис. 1.2, а), Гн

Индуктивность тороидальной катушки кругового сече­ния (рис. 1.2, б), Гн:

где w — число витков катушки,

D — средний диаметр тора, м;

d — диаметр среднего витка, м.

Взаимная индуктивность двух тороидальных катушек с числами витков w^ и w2, Гн:

Рис. 1.3. Концентрически расположенные катушки индуктивности

Взаимная индуктивность концентрических катушек прямоугольного сечения, имеющих одинаковую длину и примы­кающих друг к другу (рис. 1.3), Гн:

где L12 — индуктивность катушки, состоящей из первой и второй катушек;

L1, L2 — собственные индуктивности катушек.

После несложной процедуры регистрации Вы сможете пользоваться всеми сервисами и создать свой веб-сайт.

Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.

Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.

— Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
— Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.

Свободные электрические колебания в параллельном контуре.

Основные свойства индуктивности:

— Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией .
— Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.

Период свободных колебаний контура LC можно описать следующим образом:

Если конденсатор ёмкостью C заряжен до напряжения U, потенциальная энергия его заряда составит.
Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток его разряда, создавая магнитное поле в катушке.

Магнитный поток, увеличиваясь от нуля, создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в цепи, поэтому конденсатор разрядится не мгновенно, а через время t₁, которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t₁ = .
По истечении времени t₁, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит.
В идеальном рассмотрении, при полном отсутствии потерь в контуре, E_C будет равна E_L. Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.

Изменение (уменьшение) магнитного потока накопленной энергии катушки создаст в ней ЭДС, которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени t₂ = t₁, он перезарядит конденсатор от нуля до максимального отрицательного значения (-U).
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.

Описанные интервалы t₁ и t₂ составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление. Магнитная энергия вновь будет накапливаться в катушке в течении времени t₃, сменив полярность полюсов.

В течении заключительного этапа колебания (t₄), накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения U (в случае отсутствия потерь) и процесс колебания повторится.

В реальности, при наличии потерь энергии на активном сопротивлении проводников, фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t₁ + t₂ + t₃ + t₄ составит период колебаний .
Частота свободных колебаний контура ƒ = 1 / T

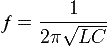
Частота свободных колебаний является частотой резонанса контура, на которой реактивное сопротивление индуктивности X_L=2πfL равно реактивному сопротивлению ёмкости X_C=1/(2πfC).

Расчёт частоты резонанса LC-контура:

Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.

Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

Расчёт ёмкости:

Расчёт индуктивности:

Похожие страницы с расчётами:

Замечания и предложения принимаются и приветствуются!

По формуле циклической частоты свободных электромагнитных колебаний , где L — индуктивность катушки (Гн), C — ёмкость конденсатора (Ф). Циклическую частоту расписываем как: , где V — “ню” частота колебаний (Гц). Данную формулу подставляем в формулу циклической частоты свободных электромагнитных колебаний: . Поизводим преобразования и выражаем искомую ёмкость конденсатора:

В системе СИ: 10 МГц = 10*10⁶ Гц; 5,1 мкГн = 5,1*10⁻⁶ Гн. Подставляеи вычисляем: