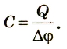-
Конденсаторы.
Емкостью обладают
не только отдельные проводники, но и
системы проводников. Система, состоящая
из двух проводников, разделенных слоем
диэлектрика, называется конденсатором.
Проводники в этом случае называются
обкладками конденсатора. Заряды на
обкладках имеют противоположные знаки,
но по модулю – одинаковы. Практически
все поле конденсатора сосредоточено
между обкладками и.
Емкостью конденсатора
называется величина
С=
![]() ,
,
(1)
где q
– абсолютная величина заряда одной из
обкладок, U
– разность потенциалов (напряжение)
между обкладками.
В зависимости от
формы обкладок, конденсаторы бывают
плоскими, сферическими, цилиндрическими.
Найдем емкость
плоского конденсатора, обкладки которого
имеют площадь S,
расположены на расстоянии d,
а пространство между обкладками заполнено
диэлектриком с диэлектрической
проницаемостью ε.
Если поверхностная
плотность заряда на обкладках равна σ
(σ=
![]() ),
),
то напряженность поля конденсатора
(поле считается однородным) равна:
Е=
![]()
=![]()
Разность потенциалов
между обкладками связана с напряженностью
поля: Е =![]()
, откуда получим U=Ed
=
![]()
=
![]()
Используя формулу
( 1 ), получим для емкости плоского
конденсатора выражение:
С
=![]()
(2)
-
Соединение конденсаторов.
Используются два
основных вида соединения: последовательное
и параллельное.
При параллельном
соединении (рис 1), общая емкость батареи
равна сумме емкостей всех конденсаторов:
Собщ.=
С1
+С2+С3+…=ΣСi
. (3)
При последовательном
соединении (рис.2) величина, обратная
общей емкости, равна сумме величин,
обратных емкостям всех конденсаторов:
![]() .
.
(4)
Если последовательно
соединены n
конденсаторов с одинаковой емкостью
С, то общая емкость: Собщ.=
![]()
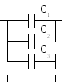

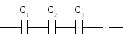




Рис. 1.Параллельное
соединение. Рис. 2.Последовательное
соединение
-
Энергия конденсатора.
Если процесс
зарядки конденсатора является медленным
(квазистационарным), то можно считать,
что в каждый момент времени потенциал
любой из обкладок конденсатора во всех
точках одинаков. При увеличении заряда
на величину dq
совершается работа
![]() ,
,
где u
– мгновенное значение напряжения между
обкладками конденсатора. Учитывая, что
![]() ,
,
получаем:
![]() .
.
Если емкость не зависит от напряжения,
то эта работа идет на увеличение энергии
конденсатора. Интегрируя данное
выражение, получим:
![]() ,
,
где W
– энергия конденсатора, U
– напряжение между обкладками заряженного
конденсатора.
Используя связь
между зарядом, емкостью конденсатора
и напряжением, можно представить
выражение для энергии заряженного
конденсатора в других видах:
![]() .
.
(5)
-
Квазистационарные токи. Процессы зарядки и разрядки конденсатора.
При зарядке или
разрядке конденсатора в цепи конденсатора
течет ток. Если изменения тока происходят
очень медленно, то есть за время
установления электрического равновесия
в цепи изменения токов и э.д.с. малы, то
для определения их мгновенных значений
можно использовать законы постоянного
тока. Такие медленно меняющиеся токи
называют квазистационарными.
Так как скорость
установления электрического равновесия
велика, под понятие квазистационарных
токов подпадают и довольно быстрые в
обычном понимании процессы: переменный
ток, многие электрические колебания,
используемые в радиотехнике.
Квазистационарными являются и токи
зарядки или разрядки конденсатора.
Рассмотрим
электрическую цепь, общее сопротивление
которой обозначим R.
Цепь содержит конденсатор емкостью C,
подключенный к источнику питания с
э.д.с. ε (рис. 3).
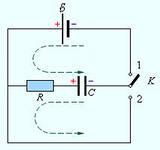
Рис. 3. Процессы
зарядки и разрядки конденсатора.
Зарядка
конденсатора.
Применяя к контуру εRC1ε
второе правило Кирхгофа, получим:
![]() ,
,
где I,
U
– мгновенные значения силы тока и
напряжения на конденсаторе (направление
обхода контура указано стрелкой).
Учитывая, что
![]() ,
,
![]() ,
,
можно привести уравнение к одной
переменной:
![]() .
.
Введем новую
переменную:
![]() .
.
Тогда уравнение запишется:
![]() .
.
Разделив переменные
и проинтегрировав, получим:
![]() .
.
Для определения
постоянной А используем начальные
условия:
t=0,
U=0,
u=
– ε.
Тогда получим: А= – ε.
Возвращаясь к переменной
![]() ,
,
получим окончательно для напряжения
на конденсаторе выражение:
![]() .
.
(6)
С течением времени
напряжение на конденсаторе растет,
асимптотически приближаясь к э.д.с.
источника (рис.4, I.).
Разрядка
конденсатора. Для
контура CR2C
по второму правилу Кирхгофа: RI=U.
Используем также:
![]() ,
,
и
![]()
(ток течет в обратном направлении).
Приведя к переменной
U,
получим:
![]() .
.
Интегрируя, получим:
![]() .
.
Постоянную
интегрирования B
определим из начальных условий: t=0,
U=ε.
Тогда получим: В=ε.
Для напряжения на
конденсаторе получим окончательно:
![]() .
.
(7)
С течением времени
напряжение падает, приближаясь к 0 (рис.
4, II).
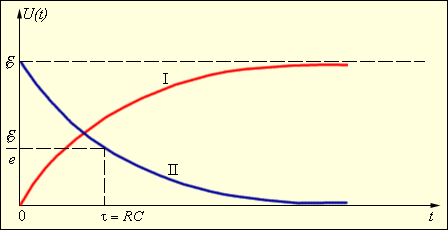
Рис. 4. Графики
зарядки (I)
и разрядки (II)
конденсатора.
-
Постоянная
времени.
Характер протекания процессов зарядки
и разрядки конденсатора (установление
электрического равновесия) зависит от
величины:
![]() ,
,
(8)
которая имеет
размерность времени и называется
постоянной времени электрической цепи.
Постоянная времени показывает, через
какое время после начала разрядки
конденсатора напряжение уменьшается
в e
раз (е=2,71).
Теория метода
Прологарифмируем
выражение (7):
![]()
(учли,
что RC=τ).
График зависимости
lnU
от t
(линейная зависимость) выражается прямой
линией (рис.5), пересекающей ось y
(lnU)
в точке с координатами (0; lnε).
Угловой коэффициент К этого графика и
будет определять постоянную времени
цепи:
![]() ,
,
откуда:
![]() .
.
(9)
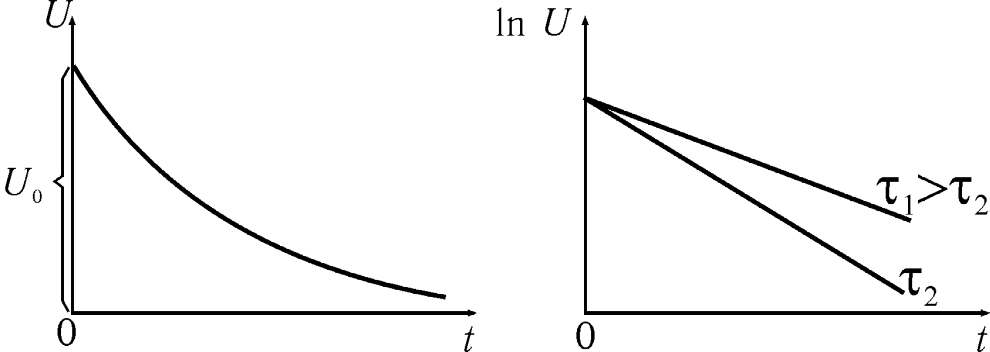
Рис. 5. Зависимость
натурального логарифма напряжения от
времени при разрядке конденсатора
Используя формулы:
![]()
и
![]() ,
,
можно
получить, что для одного и того же
интервала времени
![]() :
:
![]() .
.
Отсюда:
![]() .
.
(10)
Экспериментальная
установка
Установка состоит
из основного блока – измерительного
модуля, имеющего клеммы для подключения
дополнительных элементов, источника
питания, цифрового мультиметра и набора
минимодулей с различными значениями
сопротивления и емкости.
Для выполнения
работы собирается электрическая цепь
в соответствии со схемой, изображенной
на верхней панели модуля. В гнезда «R1»
подключается минимодуль с номиналом
1Мом, в гнезда «R2»
– минимодуль
с номиналом 100Ом. Параметры исследуемого
конденсатора, подключаемого в гнезда
«С», задаются преподавателем. В гнезда
подключения амперметра устанавливается
перемычка. В гнезда вольтметра подключается
цифровой мультиметр в режиме вольтметра.
Следует отметить,
что сопротивления резисторов заряда-разряда
(минимодулей) R
и цифрового вольтметра RV
образуют делитель напряжения, что
приводит к тому, что фактически
максимальное напряжение на конденсаторе
будет равно не ε, а
![]() ,
,
где r0–
сопротивление источника питания.
Соответствующие поправки необходимо
будет вносить и при вычислении постоянной
времени. Однако, если входное сопротивление
вольтметра (107Ом)
значительно превышает сопротивление
резисторов, и сопротивление источника
мало, то данными поправками можно
пренебречь.
Порядок выполнения
работы
-
Собрать электрическую
цепь с заданным преподавателем значением
емкости. Тумблер (переключатель
заряда-разряда) установить в среднее
положение (стоп). Переключатель предела
измерения цифрового мультиметра
установить в положение «20В» (режим
измерения постоянного напряжения). -
Подключить модуль
к сети переменного тока (клавиша
включения на задней панели модуля) и
установить выходное напряжение
 ,
,
заданное преподавателем (6,5В-15В). Включить
цифровой мультиметр. Нажатием кнопки
«Сброс» подготовить модуль к началу
измерений. -
Тумблер перевести
в положение «Заряд». При этом запускается
секундомер, и начинает меняться
напряжение на конденсаторе (показания
вольтметра). Довести напряжение на
конденсаторе до значения примерно
0,8ε. -
Сбросить показания
секундомера нажатием кнопки «Сброс».
Перевести тумблер в положение «Разряд»
и измерять напряжения на конденсаторе
при его разрядке с интервалом времени
5с. Занести данные в таблицу 1. -
Подключить в цепь
конденсатор с неизвестным значением
емкости и повторить измерения по п. 4.
Данные занести в таблицу 2. -
Подключить в цепь
конденсатор и резистор с другим известным
значением емкости. Повторить измерения
по п. 4. Данные занести в таблицу 3. -
Нажать кнопку
«Сброс». Выключить источник питания и
мультиметр. Отключить от сети измерительный
модуль и отсоединить от него дополнительные
элементы.
Таблица
1
|
ε= |
||||||||
|
Разрядка |
t (с) |
|||||||
|
U |
||||||||
|
lnU |
||||||||
|
τ1±Δτ1 |
Таблица
2
|
ε= |
||||||||
|
Разрядка |
t |
|||||||
|
U |
||||||||
|
lnU |
||||||||
|
τх±Δτх |
||||||||
|
Сх±ΔСх |
Таблица
3
|
ε= |
||||||||
|
Разрядка |
t (с) |
|||||||
|
U |
||||||||
|
lnU |
||||||||
|
τ2±Δτ2 |
Обработка
результатов измерения
По результатам
измерений студенты выполняют одно из
следующих заданий (по указанию
преподавателя).
Задание 1.
Построение кривых разрядки конденсаторов
и экспериментальное подтверждение
закона, описывающего данный процесс.
-
Используя данные,
взятые из таблиц 1 и 3, постройте графики
зависимости напряжения от времени при
разрядке конденсаторов С1и
С2.
Проанализируйте их, сравните с
теоретическими (рис. 4). -
Постройте графики
разрядки конденсаторов С1и
С2
в осях (lnU,
t).
Проанализируйте их, сравните с
теоретическими (рис. 5). -
Определите по
графикам угловые коэффициенты К1и
К2.
Среднее значение углового коэффициента
находится как отношение, определяющее
тангенс угла наклона прямой:
![]() .
.
-
Случайные
погрешности графическим методом можно
оценить по отклонению опытных точек
относительно проведенной прямой.
Относительная погрешность углового
коэффициента может быть найдена согласно
формуле:
![]() ,
,
где δ(lnU)
– отклонение (в проекции на ось lnU)
от прямой линии наиболее удаленной
опытной точки,
![]()
– интервал, на котором сделаны измерения.
-
По значениям
угловых коэффициентов определите
постоянные времени τ1
и τ2,
используя формулу (9). Сравните полученные
значения со значениями постоянной
времени, рассчитанными по формуле (8). -
Посчитайте
относительные и абсолютные погрешности
для постоянной времени:
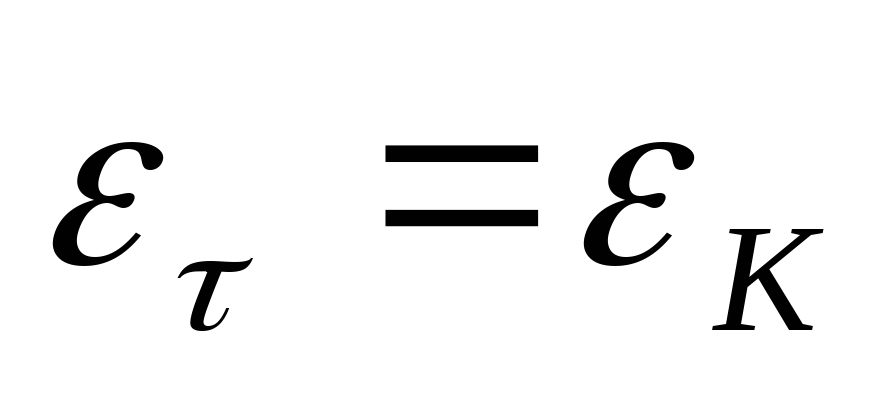 ,
,
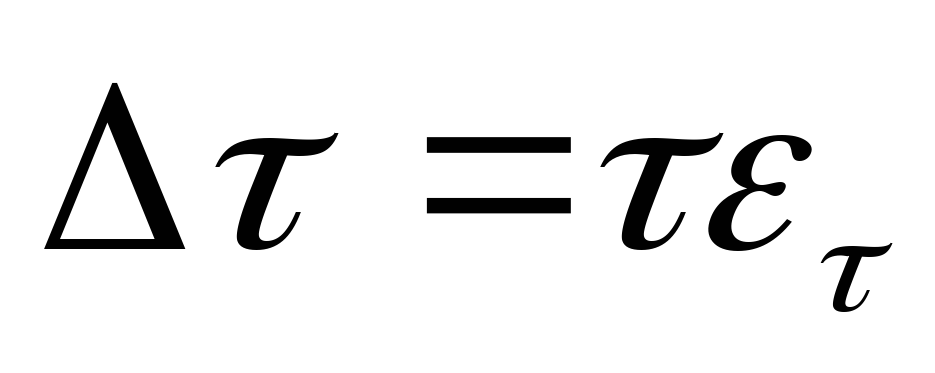 .
. -
Сделайте выводы
о соответствии экспериментальных
графиков экспоненциальному виду
зависимости напряжения от времени, и
о влиянии постоянной времени на
протекание процессов зарядки и разрядки
конденсатора.
Задание 2.
Определение неизвестной емкости
конденсатора.
-
Используя данные,
взятые из таблиц 1 и 2, постройте графики
зависимости напряжения от времени при
разрядке конденсаторов С1
и Сх.
Проанализируйте их, сравните с
теоретическими (рис. 4). -
Постройте графики
разрядки конденсаторов С1
и Сх
в осях (lnU,
t).
Сравните их и сделайте вывод о соотношении
постоянных времени (см. рис.5). -
Определите по
формуле (10) неизвестную емкость, используя
графики и данные таблиц 1 и 2. -
Найдите относительные
погрешности угловых коэффициентов εК1
и εкх
(см. п.4
задания 1). -
Определите
относительную и абсолютную погрешности
емкости:
![]()
,
![]() .
.
-
Сравните полученное
значение Сх
со значением,
измеренным при помощи цифрового
мультиметра в режиме измерения емкости.
Сделайте вывод.
Дополнительное
задание.
Рассчитайте энергию
заряженного конденсатора, используя
формулу (5).
Контрольные
вопросы
-
Что представляет
собой конденсатор? Что называется
емкостью конденсатора? -
Докажите, что
электрическое поле плоского конденсатора
сосредоточено между его обкладками.
2. Сколько надо
взять конденсаторов емкостью 2мкФ и как
их соединить,
чтобы получить
общую емкость 5 мкФ?
-
Как можно найти
энергию заряженного конденсатора? -
Какие токи
называются квазистационарными? Почему
токи зарядки и разрядки конденсатора
можно отнести к квазистационарным? -
По какому закону
изменяется напряжение на конденсаторе
в процессах а) зарядки и б) разрядки? -
Что показывает
постоянная времени цепи? От чего она
зависит? -
Зачем в данной
работе строится график зависимости
lnU
от t? -
Как в данной работе
определяется постоянная времени
электрической цепи?
ЛИТЕРАТУРА
1.Трофимова Т.И.
Курс физики. / Т.И. Трофимова. – М.: Высшая
школа, 2006-2009 г. г. – 544с.
2 Савельев И.В. Курс
физики. В 3-х томах. Том 2. Электричество.
Колебания и волны. Волновая оптика. Изд.
3-е, стереотип. / И.В. Савельев – М.: Лань,
2007. – 480 с.
3. Грабовский Р. И.
Курс физики / Р.И. Грабовский – СПб:
издательство «Лань», 2012. – 608с.
4 Зисман Г. А., Тодес
О. М. Курс общей физики. В 3-х томах. Том
2. Электричество и магнетизм / Г.А. Зисман,
О.М. Тодес – СПб: «Лань», 2007. – 352 c.
Концевой
титул
Учебное
издание
Составитель:
Плотникова
Ольга
Васильевна
Соседние файлы в папке 12-02-2015_08-16-01
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Электроемкость:
Сообщая телу определенный заряд, мы изменяем его потенциал. Это изменение непосредственно связано со значением заряда, сообщаемого телу.
Для исследования зависимости потенциала тела от его заряда проведем опыт с электрометром, корпус которого соединен с поверхностью Земли. ‘Гикая система может измерять потенциал тела относительно Земли. Укрепим на стержне этого электрометра пустотелый металлический шар и будем сообщать ему заряд с помощью маленького металлического шарика на изоляционной ручке. Если коснуться заряженным шариком внутренней поверхности металлического шара, то весь его заряд перейдет на шар, а стрелка электрометра покажет увеличение потенциала шара. Последовательно повторяя опыт с переносом заряда на большой шар, заметим, что каждый раз его потенциал увеличивается (рис. 1.28).
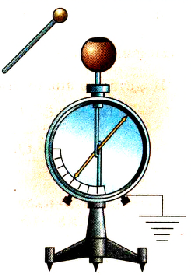
Применяя более точные способы измерения заряда и потенциала, можно установить, что потенциал возрастает пропорционально возрастанию заряда. Потенциал пропорционален заряду шара. Результаты одного из таких опытов отражены на графике (рис 1.29).
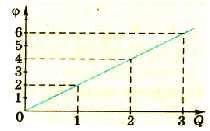
Если ни стержне электрометра укрепим шар большего (меньшего) диаметра и продолжим опыты (рис. 1.31), то увидим, что скорость зарядки изменилась, соответственно уменьшилась (увеличилась).
Процесс электризации шара большего диаметра отображен графиком на рисунке 1.32.
Сопоставив графики, которые иллюстрируют процессы зарядки шаров различных диаметров (рис. 1.30 и 1.32), увидим, что графики имеют различный наклон относительно горизонтальной оси. Это свидетельствует о том, что при одинаковых значениях заряда шары разных диаметров будут иметь разные потенциалы. Оказывается, что на князь между зарядом и потенциалом шара существенно влияют геометрические размеры шаров.
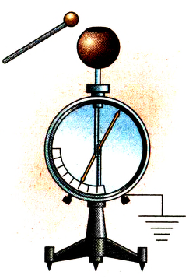
Рис. 130. Электризация шара большего диаметра
Потенциал металлического шара пропорционален его заряду; коэффициент пропорциональности для различных шаров разный.
Анализируя результаты опытов и соответствующие графики, можно сделать выводы:
- потенциал каждого шара пропорционален его заряду:
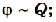
- для тел различных размеров коэффициент пропорциональности разный.
Установлено, что этот коэффициент для каждого тела имеет вполне определенное значение, что отражает способность тела накапливать электрический заряд. Физическая величина, равная отношению электрического заряда, сообщенного телу, к его потенциалу, называется электроемкостью тела.
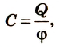
где C – электроемкость проводника; Q – заряд; φ – потенциал.
Для измерения электроемкости в физике применяют единицу, которую называют фарад (Ф).
Тело имеет электроемкость в 1 фарад, если при изменении его заряда на 1 кулон потенциал изменяется па 1 вольт:
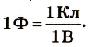
Электроемкость 1 фарад имеют тела, у которых при изменении заряда на 1 кулон потенциал изменяется на 1 вольт.
- 1Ф – довольно большое значение электроемкости. Например, электроемкость Земли, имеющей радиус 6400 км, составляет всего 7 ∙ 104 Ф. Поэтому на практике используют единицу электроемкости, кратную фараду:
- 1 микрофарад = 1 мкФ = 10-5 Ф.
- 1 пикофарад = 1 пФ = 10-12 Ф.
Пример:
Два шара, электроемкости которых 50 мкф и 80 мкФ, а потенциалы 120 В и 50 В соответственно, соединяют проводом. Найти потенциал шаров после соединения.
|
Дано: |
Решение |
| φ-? |
После соединения шаров произойдет перераспределение зарядов между ними так, что их потенциалы станут одинаковыми. Согласно закону сохранения электрических зарядов
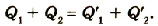
Отсюда
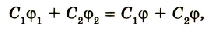
или
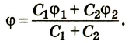
Подставив значения физических величин и произведя расчеты, получим:
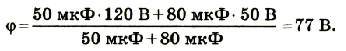
Ответ: после соединения шары будут иметь потенциал 77 В.
Конденсатор
Чтобы экспериментально определить электроемкость проводника, как и его потенциал, нужно создать условия, исключающие влияние всех окружающих тел, которые, влияя па тело, изменяют его потенциал и электроемкость.
Это утверждение можно проверить опытом.
Укрепим на стержне электрометра металлический шар и сообщим ему определенный заряд. Стрелка прибора отклонится от положения равновесия и покажет определенное значение потенциала относительно земли.
Поднесем к шару металлическую пластину, соединенную проводником с землей (рис. 1.32).

Pиc. 132. Заземленная металлическая пластина влияет на электроемкость шара
Показания стрелки электрометра уменьшатся. Поскольку заряд шара в опыте не изменялся, то уменьшение потенциала свидетельствует об увеличении электроемкости шара. Изменение потенциала и соответственно электроемкости шара будет наблюдаться и в случае изменения расстояния между шаром и пластиной.
Таким образом, определяя электроемкость тела, необходимо учитывать также наличие окружающих тел. Поскольку на практике это сделать трудно, то применяют систему из двух или более проводников произвольной формы, разделенных диэлектриком. В этом случае электрические свойства такой системы проводников и диэлектрика не зависят от окружающих тел. Такую систему называют конденсатором. Простейшим для изучения и расчетов является конденсатор из двух металлических пластин, разделенных диэлектриком.
Электроемкость конденсатора, в отличие от обособленного тела, определяется по разности потенциалов между пластинами:
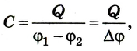
где Q – заряд одной пластины; (φl– φ2) и ∆φ – разность потенциалов между пластинами.
Слово конденсатор обозначает накопитель. В электричестве понимают как «накопитель электрических зарядов».
Пример:
Какую электроемкость имеет конденсатор, если на его обкладках накапливается заряд 50 нКл при разности потенциалов 2,5 кВ?
|
Дано: |
Решение |
| С-? |
Подставим значения физических величин:
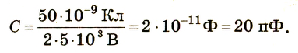
Ответ: электроемкость данного конденсатора 20 пФ.
Первый конденсатор был создан в 1745 г. голландским ученым Питером ван Мушенбруком, профессором Лейденского университета. Проводя опыты по электризации различных тел, он опустил проводник от кондуктора электрической машины в стеклянный графин с водой (рис. 1.33).
 |
Питер ван Мушенбрук (1692-1781) – голландский физик; работы посвящены электричеству, теплоте, оптике; изобрел первый конденсатор – лейденскую банку и провел опыты с ней. |

Pиc. 133. Из истории открытия простейшего конденсатора лейденской банки
Случайно коснувшись пальцем этого проводника, ученый ощутил сильный электрический удар. В дальнейшем жидкость заменили металлическими проводниками, укрепленными на внутренней и внешней поверхностях банки. Такой конденсатор назвали лейденской банкой. В таком первозданном виде она использовалась в лабораториях более 200 лет.
Более совершенные конденсаторы применяются в современной электротехнике и радиоэлектронике. Их можно найти в преобразователях напряжения (адаптерах), питающих постоянным электрическим током электронные приборы, в радиоприемниках и радиопередатчиках как поставные части колебательных контуров. Они применяются практически во всех функциональных узлах электронной аппаратуры. В фотовспышках конденсаторы накапливают большие заряды, необходимые для действия вспышки.
В электротехнике конденсаторы обеспечивают необходимый режим работы электродвигателей, автоматических и релейных приборов, линий электропередач и т. п.
Во многих широкодиапазонных радиоприемниках конденсаторы переменной емкости (рис. 1.34) позволяют плавно изменять собственную частоту колебательного контура н процессе поиска передачи определенной радиостанции.

Рис. 134. Конденсатор переменной емкости с воздушным диэлектриком
Весьма распространены конденсаторы варикапы, электроемкость которых можно изменять электрическим способом. Конструктивно они весьма схожи с полупроводниковыми диодами.
Конденсаторы могут быть плоскими, трубчатыми, дисковыми. В качестве диэлектрика в них используют парафинированную бумагу, слюду, воздух, пластмассы, керамику (рис. 1.35).

Рис. 1.35. Различные типы конденсаторов
Искусственно созданные диэлектрические материалы позволяют создавать конденсаторы больших емкостей при небольших размерах.
Электроемкость плоского конденсатора
Плоским конденсатором обычно называют систему плоских проводящих пластин – обкладок, разделенных диэлектриком. Благодаря простоте конструкции такого конденсатора легко рассчитывать его емкость и получать значения, подтверждаемые опытами. Для этого достаточно знать его геометрические параметры и электрические свойства диэлектрика между его пластинами. Зависимость электроемкости плоского конденсатора от указанных параметров можно исследовать в школьной лаборатории.
Создадим плоский конденсатор из двух плоских пластин. Для этого одну пластину укрепим на стержне электрометра, я другую — па изоляционной подставке, присоединив ее проводником к корпусу электрометра (рис. 1.36.). В такой системе электрометр будет измерять разность потенциалов между пластинами, образующими плоский конденсатор.
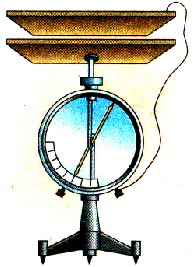
Pиc. 136. Плоский конденсатор, присоединенный к электрометру
Проводя исследования, нужно помнить, что при постоянном значении заряда на пластинах уменьшение разности потенциалов свидетельствует об увеличении электроемкости конденсатора, и наоборот.
При постоянном значении заряда на пластинах уменьшение разности потенциалов свидетельствует об увеличении электроемкости конденсатора, и наоборот.
Сообщим пластинам некоторый заряд и отметим показания стрелки прибора. Когда начнем сближать пластины, уменьшая расстояние между ними, показания стрелки начнут уменьшаться. Это будет свидетельством того, что при уменьшении расстояния между пластинами электроемкость конденсатора будет увеличиваться. При увеличении расстояния между пластинами показания стрелки будут увеличиваться, что свидетельствует об уменьшении электроемкости.
Электроемкость плоского конденсатора обратно пропорциональна расстоянию между его обкладками.
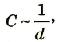
где d – расстояние между обкладками.
Эту, зависимость можно изобразить на графике как обратно пропорциональную зависимость (рис. 1.37).
Электроемкость плоского конденсатора обратно пропорциональна расстоянию между его обкладками.
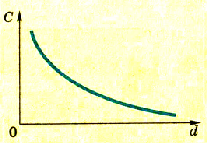
Pиc. 137. График зависимости электроемкости и плоского конденсатора от расстояния между пластинами
Будем смещать одну пластину относительно другой в параллельных плоскостях, не изменяя расстояния между ними. При атом площадь перекрытия между пластинами будет изменяться (рис. 1.38). Изменение разности потенциалов, отмеченное электрометром, засвидетельствует изменение электроемкости.
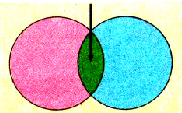
Pиc. 138. При расчетах электроемкости плоского конденсатора учитывают площадь перекрытия пластин
Увеличение площади перекрытия приведет к увеличению электроемкости, при уменьшении – наоборот.
Электроемкость плоского конденсатора пропорциональна площади пластин, которые перекрываются.
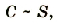
где S – площадь пластин, которые перекрываются.
Электроемкость плоского конденсатора пропорциональна площади пластин, которые перекрываются.
Эту зависимость можно изобразить графиком прямой пропорциональной зависимости (рис. 1.39).
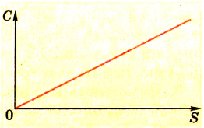
Pиc. 139. График зависимости электроемкости плоского конденсатора от площади его пластин
Возвратив пластины в первоначальное положение, внесем в пространство между обкладками пластину из диэлектрика. Электрометр отметит уменьшение разности потенциалов между пластинами, что свидетельствует об увеличении электроемкости. Если внести пластину из другого диэлектрика (другая диэлектрическая проницаемость), то изменение электроемкости будет другим.
Электроемкость плоского конденсатора зависит от диэлектрической проницаемости диэлектрика между обкладками.
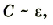
где ε – диэлектрическая проницаемость диэлектрика.
Эта зависимость изображена графиком на рисунке 1.40.
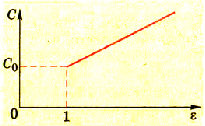
Рис. 1.40. График зависимости электроемкости плоского конденсатора от диэлектрической проницаемости диэлектрика
Результаты описанных выше исследований можно обобщить формулой электроемкости плоского конденсатора
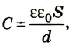
где ε – относительная диэлектрическая проницаемость диэлектрика; ε0– электрическая постоянная; d – расстояние между пластинами; S – площадь пластины.
Электроемкость плоского конденсатора зависит от диэлектрической проницаемости диэлектрика.
Соединение конденсаторов в батареи
Для получения необходимых значений электроемкости конденсаторы соединяют в батареи. На практике встречается параллельное, последовательное и смешанное соединение конденсаторов.
При параллельном соединении конденсаторов все обкладки соединяются в две группы, в каждую из которых входит по одной обкладке каждого конденсатора. На рисунке 1.41 приведена схема такого соединения. При таком соединении каждая группа обкладок имеет одинаковый потенциал.
Pиc 1.41. Схема параллельного соединения конденсаторов
Если батарею параллельно соединенных конденсаторов зарядить, то между обкладками каждого конденсатора будет одинаковая разность потенциалов. Общий заряд батареи будет равен сумме зарядов каждого из конденсаторов, входящих в батарею:
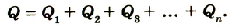
Если учесть, что 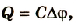 то
то
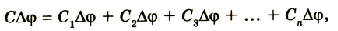
или
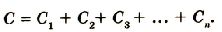
Электроемкость батареи параллельно соединенных конденсаторов равна сумме электроемкостей всех конденсаторов.
При последовательном соединении конденсаторов соединяются между собой только две пластины разных конденсаторов. Если в каждом конденсаторе пластины обозначить буквами А и В, то при последовательном соединении пластина B1 будет соединена с пластиной A2, пластина B2 -с пластиной А3 и т. д. (рис. 1.43).
Если цепочку последовательно соединенных конденсаторов присоединить к источнику тока, то об-
кладка A1 и обкладка B1 будут иметь одинаковые по значению заряды +Q и -Q. Благодаря этому все обкладки внутри цепочки будут иметь такие же, но попарно противоположные по знаку заряды:
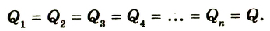
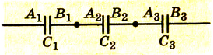
Pиc. 1.42. Последовательное соединение конденсаторов
Вместе с тем общая разность потенциалов на концах цепочки будет равна сумме разностей потенциалов на каждом конденсаторе:
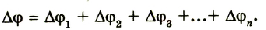
Учитывая, что 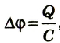 будем иметь
будем иметь
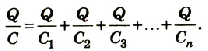
Разделим левую и правую части равенства на Q:
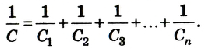
При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно сумме обратных значений электроемкостей каждого из конденсаторов.
При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно с
При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно сумме обратных значений электроемкостей каждого из конденсаторов.
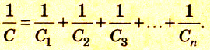
При последовательном соединении конденсаторов разной электроемкости C1, C2, C3, … Сn общая электроемкость С будет меньше электроемкости самого меньшего конденсатора.
Если C1 < C7 < C9 < … < Cn, то C < C1.
Электроемкость
То, что деньги хранят в банках, знает даже первоклассник. А вот где хранят заряды? И зачем вообще хранить заряды?
Что такое электроемкость
Электроемкость характеризует способность проводника или системы проводников накапливать электрический заряд. Различают электроемкость уединенного проводника и электроемкость системы проводников (например, конденсатора). Уединенным называют проводник, расположенный вдали от других тел так, что они не оказывают на этот проводник никакого влияния.
Электроемкость уединенного проводника (C) — физическая величина, характеризующая способность проводника накапливать заряд и равная отношению электрического заряда q проводника к его потенциалу М:
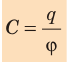
Единица электроемкости в Си — фарад: [C] = 1 Ф (названа в честь М. Фарадея).
1 Ф — это электроемкость такого проводника, потенциал которого равен 1 В при сообщении ему заряда 1 Кл; 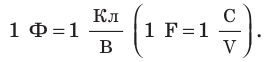
1 Ф — очень большая единица емкости, поэтому используют дольные единицы: 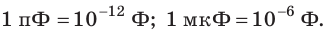
Что такое конденсатор
Конденсатор — устройство, представляющее собой систему из двух проводящих обкладок, разделенных тонким слоем диэлектрика (рис. 44.1).

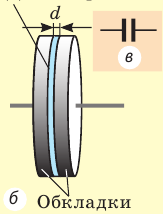
Рис. 44.1. Школьный воздушный конденсатор: а — вид; б — устройство; в — обозначение на схемах
Обкладкам конденсатора передают одинаковые по модулю, но противоположные по знаку заряды, что способствует накоплению зарядов: разноименные заряды притягиваются, а значит, располагаются на внутренних поверхностях обкладок.
Обычно для зарядки конденсатора обе его обкладки соединяют с полюсами батареи аккумуляторов: на обкладках появляются равные по модулю, но противоположные по знаку заряды. Результат не изменится, если соединить с полюсом батареи только одну обкладку, заземлив вторую: вследствие электростатической индукции на заземленной обкладке тоже появится заряд, равный по модулю заряду на другой обкладке, но имеющий противоположный знак.
Зарядом конденсатора называют модуль заряда одной из обкладок. Отношение заряда q данного конденсатора к разности потенциалов (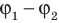 ) между его обкладками не зависит ни от значения q, ни от разности потенциалов (
) между его обкладками не зависит ни от значения q, ни от разности потенциалов (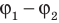 ), а значит, может служить характеристикой конденсатора. Такую характеристику называют электроемкостью (емкостью) конденсатора:
), а значит, может служить характеристикой конденсатора. Такую характеристику называют электроемкостью (емкостью) конденсатора:
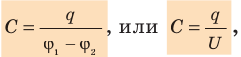
где U — напряжение между обкладками: 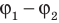 .
.
Как показывают исследования, емкость конденсатора увеличится, если увеличить площадь поверхности обкладок или приблизить обкладки друг к другу. На емкость конденсатора влияет также диэлектрик: чем больше его диэлектрическая проницаемость, тем большую емкость имеет конденсатор.
Конденсатор, состоящий из двух параллельных металлических пластин (обкладок), разделенных слоем диэлектрика, называют плоским (см. рис. 44.1). Электроемкость плоского конденсатора вычисляют по формуле:
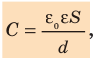
где 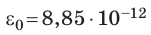 Ф/м — электрическая постоянная; ε — диэлектрическая проницаемость диэлектрика; S — площадь пластины конденсатора; d — расстояние между пластинами.
Ф/м — электрическая постоянная; ε — диэлектрическая проницаемость диэлектрика; S — площадь пластины конденсатора; d — расстояние между пластинами.
Поле между пластинами плоского конденсатора однородно, поэтому напряженность Е поля связана с напряжением U на конденсаторе формулой U=Ed.
Как рассчитывают электроемкость батареи конденсаторов
Конденсаторы характеризуются емкостью и максимальным рабочим напряжением Umax. Если напряжение, поданное на конденсатор, значительно превысит Umax, произойдет пробой — между обкладками возникнет искра, которая разрушит изоляцию.
Чтобы получить необходимую электроемкость при определенном рабочем напряжении, конденсаторы соединяют в батареи, применяя параллельное, последовательное и смешанное соединения. Рассмотрим батарею из трех конденсаторов электроемкостями 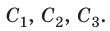
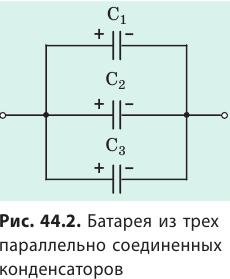
При параллельном соединении конденсаторов положительно заряженные обкладки всех конденсаторов соединяют в один узел, а отрицательно заряженные — в другой узел (рис. 44.2). В таком случае общий заряд q батареи конденсаторов равен алгебраической сумме зарядов отдельных конденсаторов:
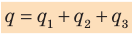
Соединенные в один узел обкладки представляют собой один проводник, поэтому потенциалы обкладок, а следовательно, и разность потенциалов (напряжение) между обкладками всех конденсаторов одинаковы:
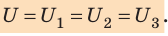
Таким образом, при параллельном соединении конденсаторов допустимое рабочее напряжение батареи определяется рабочим напряжением одного конденсатора.
Поскольку 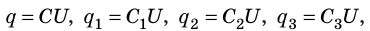 то
то 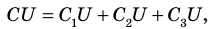 следовательно, электроемкость батареи из трех параллельно соединенных конденсаторов равна:
следовательно, электроемкость батареи из трех параллельно соединенных конденсаторов равна:
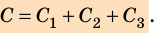
При последовательном соединении конденсаторы соединяют друг с другом разноименно заряженными обкладками (рис. 44.3). В этом случае заряды всех конденсаторов будут одинаковы и равны заряду батареи:
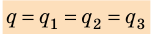
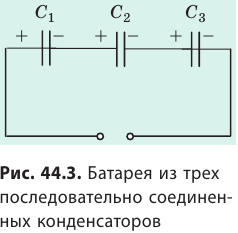
Напряжение на батарее последовательно соединенных конденсаторов равно сумме напряжений на отдельных конденсаторах:
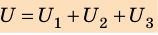
Таким образом, допустимое рабочее напряжение батареи последовательно соединенных конденсаторов больше допустимого рабочего напряжения отдельного конденсатора. Электроемкость батареи последовательно соединенных конденсаторов вычисляют по формуле:
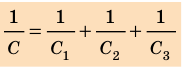
При последовательном соединении конденсаторов емкость батареи меньше, чем емкость конденсатора с минимальной емкостью.
Приведенные соотношения можно обобщить для любого количества конденсаторов.
Обратите внимание!
- Если батарея содержит n параллельно соединенных конденсаторов электроемкостью C′ каждый, то: C=nC′
- Если батарея содержит n последовательно соединенных конденсаторов электроемкостью C′ каждый, то:
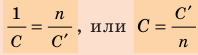
Энергия заряженного конденсатора
Заряженный конденсатор, как и любая другая система заряженных тел, обладает энергией.
Убедимся в этом с помощью простого эксперимента. Присоединим к обкладкам заряженного конденсатора лампочку. Замкнем ключ — лампочка загорится. Теперь измерим напряжение на обкладках конденсатора — оно равно нулю, то есть конденсатор разрядился, а это означает, что заряженный конденсатор обладал энергией, которая частично превратилась в энергию света.
Вычислим энергию заряженного до напряжения 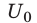 конденсатора емкостью С, на котором накоплен заряд
конденсатора емкостью С, на котором накоплен заряд 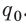 . Эту энергию точнее было бы назвать энергией электростатического поля, которое существует между обкладками заряженного конденсатора, поскольку энергия любых заряженных тел сосредоточена в электрическом поле, создаваемом этими телами.
. Эту энергию точнее было бы назвать энергией электростатического поля, которое существует между обкладками заряженного конденсатора, поскольку энергия любых заряженных тел сосредоточена в электрическом поле, создаваемом этими телами.
При разрядке конденсатора напряжение U на его обкладках изменяется прямо пропорционально заряду q конденсатора: 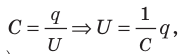 поэтому график зависимости U(q) имеет вид, представленный на рис. 44.4.
поэтому график зависимости U(q) имеет вид, представленный на рис. 44.4.
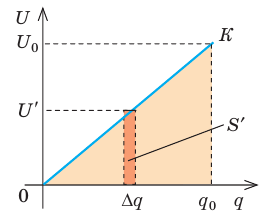
Рис. 44.4. К определению работы, которую совершает электрическое поле заряженного конденсатора при его разрядке
Мысленно разделим весь заряд конденсатора на маленькие «порции» Dq и будем считать, что при потере каждой такой «порции» напряжение на конденсаторе не изменяется. Таким образом получим ряд полос. Площадь S′ каждой полосы равна произведению двух ее сторон: 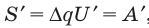 , где U′ — напряжение, при котором конденсатор терял данную «порцию» заряда
, где U′ — напряжение, при котором конденсатор терял данную «порцию» заряда 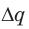 ; A′ — работа, которую совершило поле при потере конденсатором заряда
; A′ — работа, которую совершило поле при потере конденсатором заряда 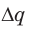 . Полная работа, которую совершило поле при уменьшении заряда конденсатора от
. Полная работа, которую совершило поле при уменьшении заряда конденсатора от 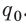 до 0, определяется площадью выделенного на рис. 44.4 треугольника.
до 0, определяется площадью выделенного на рис. 44.4 треугольника.
Следовательно,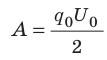 . Учитывая, что
. Учитывая, что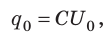 получим:
получим: 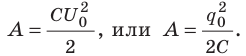 С другой стороны, данная работа равна уменьшению энергии электрического поля конденсатора от
С другой стороны, данная работа равна уменьшению энергии электрического поля конденсатора от 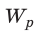 до нуля: A=
до нуля: A=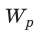 − 0 = W. Таким образом, энергия
− 0 = W. Таким образом, энергия 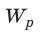 заряженного до напряжения U конденсатора, имеющего электроемкость С и заряд q, равна:
заряженного до напряжения U конденсатора, имеющего электроемкость С и заряд q, равна:
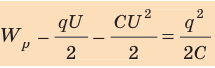
Для чего нужны конденсаторы
В современной технике сложно найти отрасль, где не применялись бы конденсаторы. Без них не обходятся радио и телеаппаратура (настройка колебательных контуров), радиолокационная и лазерная техника (получение мощных импульсов), телефония и телеграфия (разделение цепей переменного и постоянного токов, тушение искр в контактах), электроизмерительная техника (создание образцов емкости). И это далеко не полный перечень.
В современной электроэнергетике конденсаторы тоже имеют широкое применение: они присутствуют в конструкциях люминесцентных светильников, электросварочных аппаратов, устройств защиты от перенапряжений. Конденсаторы применяют и в других, не электротехнических, областях техники и промышленности (в медицине, фототехнике и т. д.).
Разнообразие областей применения обусловливает большое разнообразие конденсаторов. Наряду с миниатюрными конденсаторами, имеющими массу меньше грамма, а размеры порядка нескольких миллиметров, существуют конденсаторы массой несколько тонн и высотой больше человеческого роста. Емкость современных конденсаторов может составлять от долей, а рабочее напряжение может быть в пределах от нескольких вольт до нескольких сотен киловольт. Конденсаторы можно классифицировать по следующим признакам и свойствам:
- по назначению — постоянной и переменной емкости;
- по форме обкладок — плоские, сферические, цилиндрические и др.;
- по типу диэлектрика — воздушные, бумажные, слюдяные, керамические, электролитические и др.
Выводы:

- Энергию заряженного конденсатора можно вычислить по формулам:
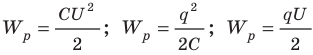
- Конденсаторы классифицируют по назначению (постоянной и переменной емкости); по форме обкладок (плоские, сферические, цилиндрические и др.); по типу диэлектрика (воздушные, бумажные, слюдяные, керамические, электролитические и др.).
- Полупроводники
- Потенциал электрического поля
- Постоянный электрический ток
- Законы постоянного тока
- Принцип суперпозиции электрических полей
- Проводники в электрическом поле
- Диэлектрики в электрическом поле
- Закон Кулона
Главная
→
Примеры решения задач ТОЭ
→
Электроемкость. Емкость конденсатора
Электроемкость. Емкость конденсатора

Электроемкость. Емкость конденсатора
Основные положения и соотношения
1. Закон Кулона
F= Q 1 ⋅ Q 2 4π⋅ ε a ⋅ R 2 , (1)
здесь
F — сила взаимодействия между зарядами;
Q1 и Q2 — точечные заряды;
R — расстояние между ними;
εa — абсолютная диэлектрическая проницаемость среды, равная ε0·εr;
εr — относительная диэлектрическая проницаемость;
– электрическая постоянная.
2. Напряженность электростатического поля точечного заряда Q на расстоянии R от него
E= Q 4π⋅ ε a ⋅ R 2 . (2)
Напряженность поля в любой точке между пластинами плоского конденсатора вдалеке от краев
E= U d , (3)
здесь d — расстояние между пластинами конденсатора, U — напряжение.
Напряженность поля в точке, отстоящей на расстоянии r от бесконечно длинной заряженной оси с линейной плотностью τ
E= τ 2π⋅ ε a ⋅r . (4)
Напряженность поля в точке, отстоящей на расстоянии r от оси цилиндрического конденсатора (r1 <r < r2)
E= U r⋅ln r 2 r 1 , (5)
здесь U — напряжение конденсатора, r1 и r2 — соответственно внутренний и внешний радиусы конденсатора.
Напряженность поля в точке, отстоящей на расстоянии R от центра сферического конденсатора (R1 < R < R2)
E= U⋅ R 1 ⋅ R 2 R 2 ⋅( R 2 − R 1 ) , (6)
здесь U — напряжение конденсатора, R1 и R2 — соответственно внутренний и внешний радиусы конденсатора.
3. Вектор электрического смещения
D → = ε a ⋅ E → . (7)
4. Общее выражение емкости конденсатора
C= Q U . (8)
Емкость плоского конденсатора
C= ε a ⋅S d = ε r ⋅ ε 0 ⋅S d , (9)
здесь S — поверхность каждой пластины конденсатора; d — расстояние между ними.
Скачать статью Вывод формулы емкости плоского конденсатора
Емкость цилиндрического конденсатора
C= 2π⋅ ε a ⋅l ln r 2 r 1 , (10)
здесь l — длина конденсатора, r1 и r2 — соответственно внутренний и внешний радиусы конденсатора.
Скачать статью Вывод формулы емкости коаксиального кабеля
Емкость сферического конденсатора
C= 4π⋅ ε a ⋅ R 1 ⋅ R 2 R 2 − R 1 , (11)
здесь R1 и R2 — соответственно внутренний и внешний радиусы конденсатора.
Скачать статью Вывод формулы емкости сферического конденсатора
Емкость двухпроводной линии
C= π⋅ ε a ⋅l ln[ D 2a + ( D 2a ) 2 −1 ] , (12)
здесь l — длина линии, D — расстояние между осями проводов, a — радиус проводов.
Емкость однопроводной линии
C= 2π⋅ ε a ⋅l ln[ h a + ( h a ) 2 −1 ] , (13)
здесь l — длина линии, h — высота подвеса провода над землей, a — радиус провода.
5. При параллельном соединении конденсаторов С1, С2, …, Сn эквивалентная емкость равна
C= C 1 + C 2 +…+ C n = ∑ k=1 n C k . (14)
При последовательном соединении конденсаторов эквивалентная емкость определяется из формулы
1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k . (15)
Для двух последовательно соединенных конденсаторов эквивалентная емкость составляет
C= C 1 ⋅ C 2 C 1 + C 2 , (16)
а напряжения между отдельными конденсаторами распределяются обратно пропорционально их емкостям
U 1 =U⋅ C 2 C 1 + C 2 ; U 2 =U⋅ C 1 C 1 + C 2 . (17)
6. Энергия электростатического поля конденсатора
W= C⋅ U 2 2 = Q⋅U 2 = Q 2 2C . (18)
Удельная энергия электростатического поля (на единицу объема диэлектрика) выражается следующим образом
w= dW dV = E⋅D 2 = ε a ⋅ E 2 2 . (19)
Общая величина энергии электростатического поля выражается интегралом величины удельной энергии по всему объему диэлектрика конденсатора
W= ∫ V ε a ⋅ E 2 2 dV . (20)
7. Расчет распределения зарядов в сложных цепях, содержащих источники э. д. с. и конденсаторы, производится путем составления уравнений по двум законам:
1) По закону сохранения электричества (закон сохранения электрического заряда): алгебраическая сумма зарядов на обкладках конденсаторов, соединенных в узел и не подключенных к источнику энергии, равна алгебраической сумме зарядов, имевшихся на этих обкладках до их соединения:
ΣQ=Σ Q ′ . (21)
2) По второму закону Кирхгофа: алгебраическая сумма э. д. с. в замкнутом контуре равна алгебраической сумме напряжений на участках контура, в том числе на входящих в него конденсаторах:
∑ k=1 n E k = ∑ k=1 n U C k = ∑ k=1 n Q k C k . (22)
Задача 1. Имеется конденсатор переменной емкости от 500 до 1500 пФ. Указать, какой добавочный конденсатор с минимальным диапазоном переменной емкости следует взять и как его включить, чтобы эквивалентная емкость изменялась от 100 до 250 пФ.
Ответ: 125 — 300 пФ, включить параллельно.
Смотрите key54.ru ремонт замка зажигания.
Задача 2. Емкость плоского конденсатора, имеющего слюдяной диэлектрик, равна 44,3 пФ. Площадь каждой пластины конденсатора составляет 25 см2, расстояние между пластинами равно 3 мм.
Чему равна относительная диэлектрическая проницаемость слюды? Принимая пробивное напряжение слюды равным 80 кВ/мм, определить, при каком максимальном напряжении может работать этот конденсатор, чтобы он имел трехкратный запас прочности.
Начертить график изменения потенциала между пластинами конденсатора.
Ответ: εr = 6; Umax = 80 кВ; график падения потенциала вычерчивается по уравнению φ = U·(1 — x/d), здесь U — потенциал положительно заряженной обкладки, принятый равным напряжению конденсатора, d — расстояние между пластинами, x — переменное расстояние до положительной обкладки конденсатора.
Задача 3. Доказать, что многопластинчатый конденсатор (рис. 1), состоящий из n одинаковых пластин, площадью S каждая, с рас стоянием между двумя соседними пластинами d, с диэлектриком, абсолютная диэлектрическая проницаемость которого ε, имеет емкость, равную
C= ε a ⋅S⋅( n−1 ) d .
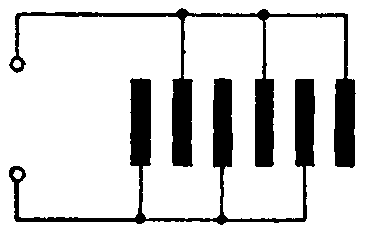
Рис. 1
Подсчитать, сколько надо взять листов станиоля, каждый площадью S = 40 см2, чтобы получить многопластинчатый конденсатор емкостью 0,5 мкФ при условии, что диэлектриком является парафинированная бумага (εr = 1,8) толщиною 0,05 мм.
Ответ: 393 листа.
Задача 4. Плоский слоистый конденсатор (рис. 2), поверхность каждой пластины которого S = 12 см2, имеет диэлектрик, состоящий из слюды (εr1 = 6) толщиною d1 = 0,3 мм и стекла (εr2 = 7) толщиною d2 =0,4 мм.
Пробивные напряженности слюды и стекла соответственно равны E1 = 77 кВ/мм, E2 = 36 кВ/мм.
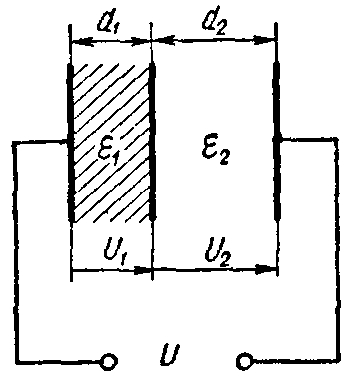
Рис. 2
Вычислить емкость конденсатора и предельное напряжение, на которое его можно включать, принимая для более слабого слоя двойной запас электрической прочности.
Решение
Эквивалентная емкость слоистого конденсатора определится как емкость двух последовательно соединенных конденсаторов
C= C 1 ⋅ C 2 C 1 + C 2 = ε a1 ⋅S d 1 ⋅ ε a2 ⋅S d 2 ε a1 ⋅S d 1 + ε a2 ⋅S d 2 = ε a1 ⋅ ε a2 ⋅S ε a1 ⋅ d 2 + ε a2 ⋅ d 1 .
Подставляя сюда числовые значения, предварительно заменив εa1 = ε0εr1 и εa2 = ε0εr2, получим
C= ε 0 ⋅ ε r1 ⋅ ε r2 ⋅S ε r1 ⋅ d 2 + ε r2 ⋅ d 1 =8,85⋅ 10 −12 ⋅ 6⋅7⋅12⋅ 10 −4 6⋅0,4⋅ 10 −3 +7⋅0,3⋅ 10 −3 =99⋅ 10 −12 Ф.
Обозначим общее напряжение, подключаемое к слоистому конденсатору, через Uпр, при этом заряд конденсатора будет равен
Q = C·Uпр.
Напряжения на каждом слое будут равны
U 1 = Q C 1 = C⋅ U пр ε a1 ⋅S d 1 = ε a2 ⋅ d 1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр ; U 2 = Q C 2 = C⋅ U пр ε a2 ⋅S d 2 = ε a1 ⋅ d 2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр .
Напряженности электростатического поля в каждом слое
E 1 = U 1 d 1 = ε a2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ′ пр ; E 2 = U 2 d 2 = ε a1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ″ пр .
Здесь U’np — общее напряжение, подключаемое к конденсатору, при котором пробивается первый слой, a U”np — общее напряжение, при котором происходит пробой второго слоя.
Из последнего выражения находим
U ′ пр = E 1 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a2 =49,5 кВ; U ″ пр = E 2 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a1 =27,0 кВ.
Таким образом, более слабым слоем является второй; согласно условию, принимая для него двойной запас прочности, находим, что конденсатор может быть включен на напряжение, равное
27,0 кВ / 2 = 13,5 кВ.
Задача 5. Вычислить емкость 1 км коаксиального кабеля типа 2,6/9,4. В этом кабеле изоляция осуществлена с помощью полиэтиленовых шайб (εr = 2,2) толщиною a = 2,2 мм, размещенных через равные промежутки b = 25 мм, остальное пространство между шайбами заполнено воздухом (рис. 3). Диаметр жилы d = 2,6 мм, внутренний диаметр наружного провода D = 9,4 мм.
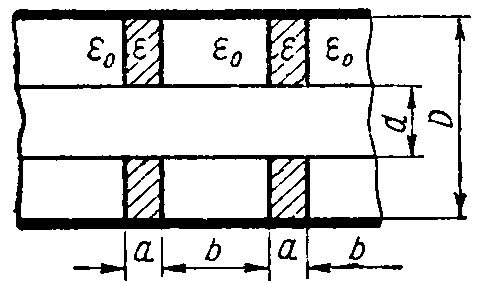
Рис. 3
Указание. Емкость кабеля может быть подсчитана, исходя из того, что отдельные его участки соединены параллельно.
Ответ: 48·10–9 Ф/км = 48 нФ/км.
Задача 6. Силовой одножильный кабель с резиновой изоляцией в свинцовой оболочке марки СРГ имеет сечение жилы 25 мм2. Известно, что наибольшая напряженность электростатического поля в изоляции кабеля не должна превышать 6 кВ/мм. Определить толщину слоя резиновой изоляции, если при испытании кабеля между жилой и оболочкой включают напряжение, равное 10 кВ.
Принимая потенциал жилы кабеля равным U = 10 кВ, построить график падения потенциала в диэлектрике кабеля в зависимости от расстояния до центра кабеля.
Ответ: 2,25 мм. График строится по уравнению φ( r )= U⋅ln r 2 r ln r 2 r 1 .
Задача 7. Цилиндрический конденсатор длиною l = 5 см имеет двухслойный диэлектрик (рис. 4).
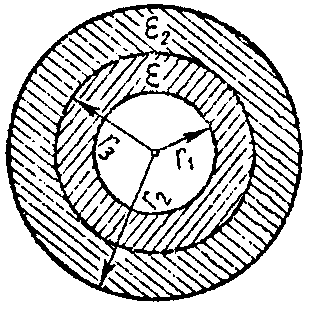
Рис. 4
Внутренний радиус r1 = 1 см, внешний — r2 = 3 см, радиус разграничения слоев диэлектриков r3 = 1.5 см. Относительные диэлектрические проницаемости: внутреннего слоя изоляции εr1 = 2, наружного εr2 = 4.
Вычислить емкость конденсатора и начертить кривые изменения напряженностей и потенциалов в каждом из слоев, если конденсатор находится под напряжением U = 2 кВ.
Указание. При помощи теоремы Гаусса находятся напряженности электростатического поля в каждом из слоев
E 1 = τ 2π⋅ ε a1 ⋅r ; E 2 = τ 2π⋅ ε a2 ⋅r ,
где τ — линейная плотность заряда (заряд на единицу длины конденсатора). Затем вычисляется напряжение между обкладками конденсатора по формуле
U= ∫ r 1 r 3 E 1 dr + ∫ r 3 r 2 E 2 dr .
Отсюда определяется линейная плотность заряда
τ= 2π⋅U 1 ε a1 ln r 3 r 1 + 1 ε a2 ln r 2 r 3 .
Емкость конденсатора вычисляется по формуле (8). Потенциал φ1 в любой точке области первого слоя диэлектрика (r3 > r > r1) определяется из выражения
φ r 1 − φ 1 = ∫ r 1 r E 1 dr ,
а потенциал φ2 в любой точке области второго слоя (r2 > r > r3) диэлектрика вычисляется из выражения
φ r 2 − φ 2 = ∫ r 2 r E 2 dr .
В последних формулах φr1 = U — потенциал внутренней обкладки конденсатора, φr2 — потенциал на границе раздела диэлектриков. Внешняя оболочка заземлена: φ2(r2) = 0.
Ответ:
C= 2π⋅l 1 ε a1 ln r 3 r 1 + 1 ε a2 ln r 2 r 3 ; E 1 ( r )= U r⋅( ln r 3 r 1 + ε a1 ε a2 ln r 2 r 3 ) ; E 2 ( r )= U r⋅( ε a2 ε a1 ln r 3 r 1 +ln r 2 r 3 ) ; φ 1 ( r )=U⋅( 1− ln r r 1 ln r 3 r 1 + ε a1 ε a2 ln r 2 r 3 ); φ 2 ( r )= U⋅ ε a1 ε a2 ln r 2 r ln r 3 r 1 + ε a1 ε a2 ln r 2 r 3 .
Пример вывода формулы емкости двухслойного цилиндрического конденсатора при помощи теоремы Гаусса
Задача 8. Чему равен внешний радиус сферического конденсатора емкостью 20 пФ, внутренний радиус которого 2 см. а относительная Диэлектрическая проницаемость изоляции εr = 3. При каком напряжении конденсатор будет пробит, если пробивное напряжение изоляции равно 15 кВ/мм?
Ответ: 3 см, 100 кВ.
Задача 9. Найти емкость сферического конденсатора, изображенного на рис. 5.
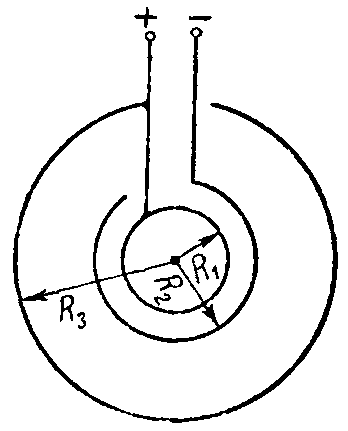
Рис. 5
Даны радиусы R1, R2 и R3; изоляция однородная, ее абсолютная диэлектрическая проницаемость равна ε.
Указание. Данный конденсатор может быть рассмотрен как два Параллельно соединенных конденсатора.
Ответ: C= 4π⋅ ε a ⋅ R 2 2 ⋅( R 3 − R 1 ) ( R 3 − R 2 )( R 2 − R 1 ) .
Задача 10. К пластинам плоского двухслойного конденсатора приложено напряжение 3 кВ. Площадь пластины равна 5 см2. Толщины первого и второго слоев конденсатора равны соответственно 4 и 6 мм, а диэлектрические проницаемости — 6 и 1.
Построить графики изменения напряженности и потенциала между пластинами в зависимости от расстояния до положительной пластины, потенциал которой принять равным + 3 кв.
Задача 11. Имеется два одинаковых конденсатора переменной емкости. Емкость каждого конденсатора можно плавно изменять от 20 до 200 пФ.
Какие границы изменения емкости можно получить при различном соединении этих конденсаторов между собой?
Ответ: от 10 до 400 пФ.
Задача 12. Определить емкость воздушной двухпроводной линии длиной 2 км, если диаметр проводов равен 3 мм и расстояние между осями проводов составляет 30 см.
Задача 13. Определить емкость однопроводной телеграфной линии длиною 180 км, если диаметр провода равен 3 мм, а средняя высота подвеса провода над землей составляет 7 м.
Начертить кривую зависимости емкости этого провода в функции расстояния от земли.
Ответ: 1,1 мкФ.
Задача 14. Обкладки плоского конденсатора с воздушным диэлектриком расположены на расстоянии d1 = 1 см друг от друга. Площадь обкладок S = 50 см2. Конденсатор заряжается до напряжения U = 120 В и затем отсоединяется от источника электрической энергии.
Определить, какую надо совершить работу, если увеличить расстояние между пластинами до d2 = 10 см. Краевым эффектом можно пренебречь; другими словами, емкость конденсатора можно считать обратно пропорциональной расстоянию между обкладками.
Решение
Энергия заряженного плоского конденсатора равна
W 1 = C 1 ⋅ U 2 2 = ε 0 ⋅S d 1 ⋅ U 2 2 ,
где С1 — емкость до раздвижения обкладок.
Так как конденсатор отключен от источника, то при изменении расстояния между обкладками его заряд остается постоянным. Поэтому из~ соотношения
Q = C2·U2,
где C2 — емкость конденсатора после раздвижения обкладок, следует, что, так как C 2 = ε 0 ⋅S d 2 стало меньше в 10 раз (d2 увеличилось в 10 раз), то напряжение на конденсаторе U2 увеличилось в 10 раз, т. е. U2 = 10U.
Таким образом, энергия конденсатора после отключения и раздвижения обкладок на расстояние d2 будет больше первоначальной
W 2 = ε 0 ⋅S d 2 ⋅ U 2 2 2 = ε 0 ⋅S 10 d 1 ⋅ ( 10U ) 2 2 =10⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =10⋅ W 1 .
Увеличение энергии произошло за счет работы внешних сил, затраченной на раздвижение обкладок.
Таким образом, надо совершить работу, равную
W 2 − W 1 =9⋅ W 1 =9⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =2,86⋅ 10 −7 Дж.
Задача 15. Плоский конденсатор с воздушным диэлектриком заряжается от источника электрической энергии с напряжением U.
Определить, как изменится энергия конденсатора, если после отключения его от источника энергии расстояние между обкладками увеличить вдвое.
Ответ: энергия увеличится в два раза.
Задача 16. Плоский конденсатор с диэлектриком из эбонита (εr = 2,5) в виде пластинки толщиной d = 5 см присоединен к полюсам батареи. После зарядки эбонитовая пластинка вынимается. Как нужно изменить расстояние между обкладками конденсатора, чтобы энергия конденсатора осталась без изменения?
Задачу решить в двух случаях: 1) если конденсатор остается присоединенным к батарее и 2) если конденсатор отключить от батареи.
Ответ: в обоих случаях пластины должны отстоять друг от друга на расстоянии 2 см.
Задача 17. Конденсатор емкостью C1 = 40 мкФ заряжен от сети до напряжения U1 = 220 В; другой конденсатор емкостью C2 = 10 мкФ заряжен от другой сети до напряжения U2 = 110 В.
Положительные зажимы конденсаторов после отсоединения от источников соединяются вместе:
а) Чему равна разность потенциалов между отрицательными зажимами конденсаторов?
б) Чему равны заряды до и после последующего соединения друг с другом отрицательных зажимов конденсаторов?
в) Чему равны напряжения на конденсаторах после соединения их отрицательных зажимов?
г) Чему равна энергия каждого конденсатора до. и после соединения отрицательных зажимов?
Ответ: а) 110 В, б) до соединения: Q1 = 8800 мкКл, Q2 = 1100 мкКл; после соединения: Q′1 = 7920 мкКл, Q′2 = 1980 мкКл, в) 198 В, г) до соединения: W1 = 0,97 Дж, W2 = 0,06 Дж; после соединения: W′1 = 0,784 Дж, W′2 = 0,196 Дж.
Задача 18. Три последовательно соединенных конденсатора, емкости которых 2, 10 и 15 мкФ, заряжаются от сети с напряжением 120 В. После отключения от сети конденсаторы разъединяются друг от друга без потери заряда. Если затем конденсаторы соединить параллельно, то чему будет равно напряжение на их зажимах?
Ответ: 20 В.
Список литературы
1. Бессонов Л.А. Теоретические основы электротехники. Электромагнитное поле. — М.: Гардарики, 2001.– 317 с.
2. Демирчян К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники: в 3-х тт.: Учебник для вузов. Том 3. –4-е изд. — СПб.: Питер, 2003. — 377 с.
3. Купалян С.Д. Теоретические основы электротехники / Под ред. Г.И. Атабекова. — М.-Л.: Госэнергоиздат, 1963. — ч. 3. Электромагнитное поле. — 112 с.
4. Теоретические основы электротехники. т. 2. Нелинейные цепи и основы теории электромагнитного поля. Под ред. П.А. Ионкина. Учебник для электротехн. вузов. Изд. 2-е, перераб. и доп. — М.: Высш. шк., 1976. — 383 с.
5. Поливанов, К.М. Теоретические основы электротехники: в 3-х ч. / К.М. Поливанов. ч. 3: Теория электромагнитного поля. — М.: Энергия, 1969. — 352 с.
6. Бессонов Л.А. Сборник задач по теоретическим основам электротехники: Учебное пособие для вузов / Бессонов Л.А., Демидова И.Г. и др.; Под ред. Л.А. Бессонова. — М., Высшая школа, 2000. — 528с.: ил.
7. Колли Я.Н. и др. Задачник по теоретическим основам электротехники (теория поля). Уч. пособие для вузов. Под ред. Поливанова К.М. — М., «Энергия», 1972.
8. Ионкин П.А. Сборник задач и упражнений по теоретическим основам электротехники: Учебное пособие. — М., Энергоиздат, 1982. — 768с.
9. Татур Т.А. Основы теории электромагнитного поля: Справочное пособие. — М.: Высш. шк., 1989 . — 270 с.
 электрическая постоянная,
электрическая постоянная,
емкость конденсатора,
электроемкость,
емкость плоского конденсатора,
емкость цилиндрического конденсатора,
сферический конденсатор,
емкость двухпроводной линии,
емкость однопроводной линии,
емкость коаксиального кабеля
Для учащихся (для лучшего понимания физики).
Вспомним основное из предыдущей статьи.
Плоский конденсатор представляет собой устройство, состоящее из двух металлических пластин (обкладок), между которыми находится диэлектрик.
На практике конденсаторы нашли очень широкое применение благодаря их способности накапливать на обкладках значительные электрические заряды. При этом между обкладками возникает разность потенциалов (напряжение).
Конденсаторы характеризуются электрической ёмкостью С:
Ёмкость конденсатора численно равна отношению заряда на одной из обкладок к напряжению между обкладками
или
ёмкость конденсатора численно равна заряду, который надо сообщить обкладке конденсатора, чтобы повысить напряжение между обкладками на единицу напряжения.
Надо помнить, что заряд конденсатора и его напряжение зависят друг от друга, а ёмкость конденсатора не зависит ни от заряда, ни от напряжения, она только численно равна их отношению.
Ёмкость плоского конденсатора зависит лишь от его размеров (от площади пластин, расстояния между ними) и от диэлектрической проницаемости среды между обкладками:
Заряжаются конденсаторы от источников постоянного тока (см. статью “Зарядка конденсатора. Зарядный и разрядный ток проводимости”
На рисунке ниже показана электрическая цепь, состоящая из источника постоянного напряжения, конденсатора и сопротивления:
В момент замыкания ключа К возникший в цепи ток (рисунок справа) имеет максимальное значение, так как разность потенциалов между полюсом источника и обкладкой конденсатора (она не была заряжена) максимальна.
По мере роста заряда на обкладке ток в цепи уменьшается, обращаясь в нуль в момент, когда напряжение на конденсаторе станет равным напряжению на клеммах источника:
Если заряженный конденсатор отключить от источника (следующий рисунок) и замкнуть его обкладки через сопротивление, то по цепи пойдёт разрядный ток, направленный в сторону обратную зарядному току.
Ниже на одном рисунке показаны кривые зависимости зарядного и разрядного тока от времени, из которого видно, что и зарядный, и разрядный токи имеют максимальные значения в моменты замыкания цепей.
При разрядке конденсатор является источником электрической энергии, отдаваемой во внешнюю цепь.
Чтобы энергия конденсаторов постоянно пополнялась, их включают в электрические цепи, содержащие источники постоянного тока. Такие цепи называют ещё конденсаторными цепями.
Дальше рассмотрим некоторые задачи на расчёт таких цепей. Расчёт сводится, как правило, к нахождению заряда конденсаторов или напряжения на конденсаторах.
Задача.
При решении задач на конденсаторные цепи можно кроме способов, применённых при решении рассмотренных выше задач, пользоваться первым, вторым, третьим и четвёртым правилами.
Сейчас на примере качественного решения следующей задачи рассмотрим перечисленные правила.
Задача
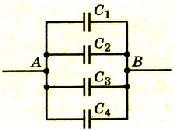
Найти заряд каждого конденсатора в изображённой на рисунке цепи, если известны ЭДС источников постоянного тока и ёмкости конденсаторов.
Сначала подумаем, какие обкладки конденсаторов заряжены положительно, а какие – отрицательно.
Левая обкладка первого конденсатора и правая обкладка третьего конденсатора заряжены отрицательно, так как они соединены с отрицательными полюсами источников. По этой же причине верхняя обкладка второго конденсатора заряжена положительно. Другие обкладки конденсаторов имеют противоположные знаки.
Первое правило
Если в цепи есть точки, в которых сходятся провода обкладок конденсаторов, не соединённых с источником, то их общий заряд равен нулю.
В нашей задаче такой точкой является точка В.
Второе правило
В цепи находим точки равного потенциала и соединяем их в узлы. Потенциал одного из узлов принимаем за нуль. Заряд каждого конденсатора выражаем через его ёмкость и разность потенциалов (напряжение).
Наша цепь содержит два узла А и В. Примем потенциал узла В за нуль.
Третье правило
Для любого замкнутого контура в конденсаторной цепи алгебраическая сумма ЭДС, входящих в контур, равна алгебраической сумме напряжений на конденсаторах в контурах.
В статье “Как найти заряды конденсаторов в цепи …” всё это проделано для нашей задачи и получен ответ.
Все четыре правила расчёта конденсаторных цепей подробно с примерами рассмотрены в статье Занятии 54 и следующих за ней четырёх статьях.
Итак, пользуясь изложенными здесь методами и правилами можно решать сложные задачи на расчёт цепей постоянного тока, содержащих конденсаторы.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Спасибо.
Для школьников предлагаются подборки материала по темам:
!. Механика. Кинематика. Равномерное прямолинейное движение.
2. Равнопеременное прямолинейное движение.
Предыдущая запись: Ёмкость уединённого проводника. Ёмкость конденсатора. Почему диэлектрик повышает ёмкость конденсатора?
Следующая запись: Явление электростатической индукции в задачах.
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 .