Как найти емкость конденсатора все формулы - Сайт, где вы сможете решить свои вопросы

Определение 1

Конденсатор – это совокупность двух любых проводников, заряды которых одинаковы по значению и противоположны по знаку.

Его конфигурация говорит о том, что поле, созданное зарядами, локализовано между обкладками. Тогда можно записать формулу электроемкости конденсатора:

C=qφ1-φ2=qU.

Значением φ1-φ2=U обозначают разность потенциалов, называемую напряжением, то есть U. По определению емкость положительна. Она зависит только от размерностей обкладок конденсатора их взаиморасположения и диэлектрика. Ее форма и место должны минимизировать воздействие внешнего поля на внутреннее. Силовые линии конденсатора начинаются на проводнике с положительным зарядом, а заканчиваются с отрицательным. Конденсатор может являться проводником, помещенным в полость, окруженным замкнутой оболочкой.

Выделяют три большие группы: плоские, сферические, цилиндрические. Чтобы найти емкость, необходимо обратиться к определению напряжения конденсатора с известными значениями зарядов на обкладках.

Плоский конденсатор

Определение 2

Плоский конденсатор – это две противоположно заряженные пластины, которые разделены тонким слоем диэлектрика, как показано на рисунке 1.

Формула для расчета электроемкости записывается как

C=εε0Sd, где S является площадью обкладки, d – расстоянием между ними, ε – диэлектрической проницаемостью вещества. Меньшее значение d способствует большему совпадению расчетной емкости конденсатора с реальной.

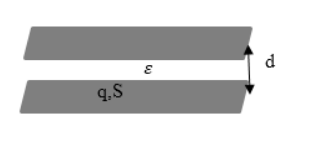
Рисунок 1

При известной электроемкости конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равняется di, вычисление диэлектрической проницаемости этого слоя εi выполняется, исходя из формулы:

C=ε0Sd1ε1+d2ε2+…+dNεN.

Сферический конденсатор

Определение 3

Когда проводник имеет форму шара или сферы, тогда внешняя замкнутая оболочка является концентрической сферой, это означает, что конденсатор сферический.

Он состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком, как показано на рисунке 2. Емкость рассчитывается по формуле:

C=4πεε0R1R2R2-R1, где R1 и R2 являются радиусами обкладок.

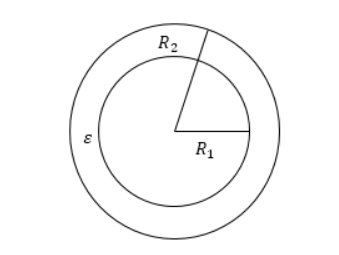
Рисунок 2

Цилиндрический конденсатор

Емкость цилиндрического конденсатора равняется:

C=2πεε0llnR2R1, где l – высота цилиндров, R1 и R2 – радиусы обкладок. Данный вид конденсатора имеет две соосные поверхности проводящих цилиндрических поверхности, как показано на рисунке 3.

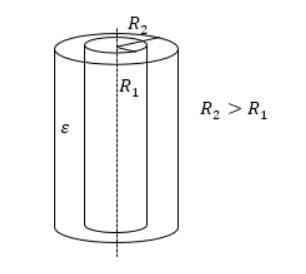
Рисунок 3

Определение 4

Важной характеристикой конденсаторов считается пробивное напряжение – напряжение, при котором происходит электрический разряд через слой диэлектрика.

Umax находится от зависимости от толщины слоя и свойств диэлектрика, конфигурации конденсатора.

Электроемкость плоского конденсатора. Формулы

Кроме отдельных конденсаторов используются их соединения. Наличие параллельного соединения конденсаторов применяют для увеличения его емкости. Тогда поиск результирующей емкости соединения сводится к записи суммы Ci, где Ci- это емкость конденсатора с номером i:

C=∑i=1NCi.

При последовательном соединении конденсаторов суммарная емкость соединения всегда будет по значению меньше, чем минимальная любого конденсатора, входящего в систему. Для расчета результирующей емкости следует сложить величины, обратные к емкостям отдельных конденсаторов:

Пример 1

Произвести вычисление емкости плоского конденсатора при известной площади обкладок
1 см2 с расстоянием между ними 1 мм. Пространство между обкладками находится в вакууме.

Решение

Чтобы рассчитать электроемкость конденсатора, применяется формула:

C=εε0Sd.

Значения:

ε=1, ε0=8,85·10-12 Фм;S=1 см2=10-4 м2;d=1 мм=10-3 м.

Подставим числовые выражения и вычислим:

C=8,85·10-12·10-410-3=8,85·10-13 (Ф).

Ответ: C≈0,9 пФ.

Пример 2

Найти напряженность электростатического поля у сферического конденсатора на расстоянии x=1 см=10-2 м от поверхности внутренней обкладки при внутреннем радиусе обкладки, равном R1=1 см=10-2 м, внешнем – R2=3 см=3·10-2 м. Значение напряжения – 103 В.

Решение

Производящая заряженная сфера создает напряженность поля. Его значение вычисляется по формуле:

E=14πεε0qr2, где q обозначают заряд внутренней сферы, r=R1+x – расстояние от центра сферы.

Нахождение заряда предполагает применение определения емкости конденсатора С:

q=CU.

Для сферического конденсатора предусмотрена формула вида

C=4πεε0R1R2R2-R1 с радиусами обкладок R1 и R2.

Производим подстановку выражений для получения искомой напряженности:

E=14πεε0U(x+R1)24πεε0R1R2R2-R1=U(x+R1)2R1R2R2-R1.

Данные представлены в системе СИ, поэтому достаточно заменить буквы числовыми выражениями:

E=103(1+1)2·10-4·10-2·3·10-23·10-2-10-2=3·10-18·10-6=3,45·104 Вм.

Ответ: E=3,45·104 Вм.

Источник

Конденсатор – радиоэлектронный прибор, способный накапливать и отдавать заряд. Как правило, на его корпусе дается информация о его емкости, но иногда требуется самому рассчитать этот номинал.

Конденсаторами могут выступать и проводники, они также обладают определенной емкостью. Для расчета существует несколько формул емкости конденсатора, их и рассмотрим.

В чем измеряется емкость конденсатора

Что такое заряд еще проходят в школе, когда эбонитовую палочку натирают о шерстяную ткань и подносят к маленьким кусочкам бумаги.

Под действием электромагнитных сил бумага прилипает к палочке. Подобный заряд накапливается в конденсаторе. Но для начала познакомимся с самим конденсатором.

Простейшим конденсатором являются две металлические пластины, разделенные диэлектриком. От качества диэлектрика зависит, как долго энергия заряженного конденсатора может сохраняться.

На этих пластинах, они еще называются обкладками, накапливается разноименный заряд. Как это происходит?

как найти емкость конденсатора

Электрический заряд, а в случае с металлами это электроны, способен перемещаться под действием электродвижущей силы (э. д. с.).

Подключая металлические пластинки к источнику тока, мы получаем замкнутую цепь, но разделенную диэлектриком. Электростатическое поле проходит этот диэлектрик, замыкая цепь, а электроны, дойдя до препятствия, останавливаются и скапливаются.

Полная статья на блоге “Электрик в доме”:

Получается, на одной обкладке наблюдается избыток электронов, и эта пластина имеет отрицательный знак, а на другой пластине электронов недостает настолько же, знак на этой обкладке, конечно же, будет положительным.

Вот теперь нужна для определения емкости конденсатора формула, определяющая, какой заряд способен разместится на конкретном конденсаторе.

В качестве единицы измерения в международной системе (СИ) емкость определяется в Фарадах.

Много это или мало – емкость в 1Ф? Чтобы конденсатор обладал емкостью в 1Ф, он должен содержать в себе заряд в 1К (кулон) и при этом напряжение между обкладками должно равняться 1 вольту.

Интересно. Что такое заряд в 1 кулон? Если два предмета, каждый из которых имеет заряд в один кулон разместить в вакууме на расстоянии один метр, то сила притяжения между ними будет равна силе притяжения землей тела массой в один миллион тонн.

Как и любая буквальная емкость один и тот же конденсатор может вмещать разное количество заряда.

устройство конденсатора

Рассмотрим пример.

В трехлитровую банку входит три литра воздуха. Его хватит для дыхания, допустим, на 3 минуты. Но если воздух закачать под каким-то давлением, то емкость так и останется три литра, однако дышать можно будет дольше. Так устроен акваланг для ныряльщиков. Получается, количество воздуха в банке зависит от давления, которое в ней создается. Точно так же есть некая зависимость между различными силами, влияющими на емкость.

Формула емкости плоского конденсатора

Прежде чем узнать, по какой формуле вычисляется емкость плоского конденсатора, рассмотрим формулу для одиночного проводника. Она имеет вид:

формула емкости плоского конденсатора

где Q – заряд,
φ – потенциал.

Как видно емкость конденсатора, формула которого здесь приведена, будет тем больше, чем больший заряд способен накапливаться на нем при незначительном потенциале. Чтобы легче это было понять, рассмотрим получившие широкое распространение плоские конденсаторы разных размеров.

Для получения качественного конденсатора важны любые мелочи:

ровная поверхность каждой обкладки;
обе пластинки по всей площади должны располагаться на одинаковом расстоянии;
размеры обкладок должны быть строго идентичными;
от качества диэлектрика, расположенного между пластинками, будет зависеть ток утечки;
емкость напрямую зависит от расстояния между обкладками, чем оно меньше, тем больше емкость.

Теперь обратимся к плоскому конденсатору. Формула определения емкости конденсатора несколько отличается от приведенной выше:

емкость конденсатора формула

где S – площадь одной обкладки,
εr – диэлектрическая проницаемость диэлектрика,
ε0 – электрическая постоянная,
d – расстояние между обкладками.

Электрическая постоянная выражается числом 8,854187817×10-12.

емкость конденсатора

Внимание! Эта формула справедлива только тогда, когда расстояние между пластинами намного меньше их площади.

Попробуем разобраться с каждой переменной подробнее. Площадь измеряется в м2, точнее, приводится к этой величине. А вот проницаемость диэлектрика может обозначаться по-разному.

В России это εr (также означает относительная проницаемость), в англоязычной литературе встречается εa (также означает абсолютная проницаемость), а то может и вовсе использоваться без индекса, просто ε. О том, что здесь используется диэлектрическая проницаемость диэлектрика можно понять из контекста.

Дальше идет ε0. Это уже вычисленное значение, измеряемое в Ф/м. Последняя переменная – d. Измеренное расстояние также приводится к метру. Емкость конденсатора, формула которого сейчас рассматривается, показывает сильную зависимость от расстояния обкладок. Поэтому стараются это расстояние по возможности сокращать. Почему этот показатель так важен?

Идеальными условиями для получения наибольшей емкости – это отсутствие промежутка между обкладками, чего, конечно, добиться невозможно. Чем ближе находятся разноименные заряды, тем сильнее сила притяжения, но здесь возникает компромисс.

При уменьшении толщины диэлектрика, а именно он разделяет разноименные заряды, возникает вероятность его пробоя из-за разности потенциалов на обкладках. С другой стороны, как уже говорилось, при увеличении напряжения увеличивается количество зарядов. Вот и приходится выбирать между емкостью и рабочим напряжением конденсатора.

Есть другая формула для плоского переменного конденсатора:

Формула для расчета емкости плоского конденсатора

Здесь диэлектрическая проницаемость обозначена буквой ε, π = 22/7 ≈ 3,142857142857143, d – толщина диэлектрика. Формула предназначена для конденсатора, состоящего из нескольких пластин.

Допустимая толщина диэлектрика d также зависит от εr, чем выше коэффициент, тем тоньше можно использовать диэлектрик, тем большую емкость будет иметь конденсатор. Это был самый сложный материал, дальше будет легче.

Формула емкости цилиндрического конденсатора

Теперь поговорим о том, как найти емкость конденсатора цилиндрической формы. К ним относятся конденсаторы, состоящие из двух металлических цилиндров, вставленных один в другой.

Для разделения между ними расположен диэлектрик. Формула емкости конденсатора выглядит следующим образом:

Формула электрической емкости цилиндрического конденсатора

Здесь видим несколько новых переменных:

l – высота цилиндра;
R1 и R2 – радиус первого и второго (внешнего) цилиндров;
ln – это не переменная, а математический символ натурального логарифма. На некоторых калькуляторах он имеется.

Всегда нужно помнить, что все величины должны приводиться к единой системе, в приведенной ниже таблице указаны международные системы единиц (СИ).

международные системы единиц (СИ)

Из нее видно, что все расстояния нужно приводить к метру.

Формулы для расчета емкости конденсаторов

Еще стоит обращать внимание на качество диэлектрика. Если толщина диэлектрика влияет только на емкость конденсатора, то его качество затрагивает сохранность энергии. Другими словами, конденсатор с качественным диэлектриком будет иметь меньший саморазряд.

Определить качество можно по числу, стоящему возле вещества, чем оно больше, тем лучше качество. Сравнение производится по вакууму, значение которого равно единице.

Формула емкости сферического конденсатора

Последнее что осталось разобрать – формулу определения емкости конденсатора, состоящего из двух сфер. Причем одна сфера находится внутри другой. Формула имеет следующий вид:

Формула расчета емкости сферического конденсатора

Из приведенных переменных здесь все знакомо. Стоит обратить внимание лишь на сам конденсатор.

Кроме своей необычной формы у него есть свои особенности: внутри малой сферы никакого заряда нет, он образуется на внешней части малой сферы и внутренней части большого шара. Также заряд отсутствует и на внешней стороне внешней сферы.

Так же как и все другие конденсаторы, сферы разделены диэлектриком. Толщина и качество диэлектрика оказывают такое же влияние на емкость, как в случае с другими конденсаторами.

После того как были рассмотрены формулы, стоит испробовать их на практике. Рассмотрим, как найти емкость конденсатора каждого вида.

Примеры решения задач

Начнем с плоского конденсатора. Формула для этого вида:

формула емкости плоского конденсатора

Допустим, у нас есть следующие значения:

в качестве диэлектрика возьмем слюду толщиной 0,02 мм, ε = 6;
конденсатор квадратный со сторонами в 7 мм.

Определяем площадь пластин: 7×7 = 49 мм2.

Приводим к единой системе: 4,9×10-5 = 0,000049 м2. Толщина диэлектрика 0,02×10-5 = 0,00002 м. Электрическая постоянная 8,854187817×10-12.

Подставляем в формулу и высчитываем числитель: 6×8,854187817×10-12 ×4,9×10-5, сокращаем и решаем 6×49×8,854187817×10-17 = 2,603131218198×10-14.

Делим на толщину диэлектрика: 2,603131218198×10 / 2×10 = 1301,565609099×10 = 1,301565609099×10. Шесть нулей – это тысячи или приставка «микро», получается округлено 1,3 мкФ.

Возможно, при вычислении была допущена ошибка, но это не экзамен по математике. Важно понять сам метод вычисления.

Формула для цилиндрического конденсатора:

Электроемкость цилиндрического конденсатора

Выбираем значения:

l = 1 см;
R1 = 0,25 мм;
R2 = 0,26 мм;
ε = 2.

Подгоняем под единую систему: l – 1 см = 1×10-2 = 0,01 м; R1 – 0,25 мм = 0,0025 м; R2 – 0,26 мм = 0,0026 м.

Подставляем значения в числитель: 2×3,142857142857143×8,854187817×10-12×2×0,01 1,11×10-12. Находим знаменатель: 0,26:0,25 = 1,04.

Находим натуральный логарифм, он равен примерно 0,39. Числитель делим на знаменатель: 1,11×10-12/0,39 = 2,85×10-12.

Число с 12 нулями это приставка «пико», получаем 2,85 пФ.

Формула для сферического конденсатора:

Электроемкость цилиндрического конденсатора

Выбираем значения:

ε= 4;
r1= 5 см;
r2= 5,01 см.

Снова все подгоняем: 5 см = 0,05 м; 5,01 см = 0,0501 м. Заполняем числитель. 4×3,142857142857143×4×8,854187817×10-12×0,05×0,0501 1,11×10-12 Вычисляем знаменатель: 0,0501 – 0,05 = 0,01. Производим деление: 1,11×10-12×0,01 = 1,11×10-10. Снова получили пикофарады, а именно 1,11 пФ.

Интересные статьи на канале:

Статья заинтересовала? Лайк, подписка, комментарий!

Друзья ПОДПИСЫВАЙТЕСЬ Дзен на канал, а также заходите на блог https://electricvdome.ru 👍!

#конденсатор #емкость #формула

Источник

Расчёт ёмкости конденсатора

Содержание

1 Конденсатор
2 Емкость
3 Зависимость
4 Расчет
- 4.1 Плоский конденсатор
- 4.2 Электроемкость
- 4.3 Сферический конденсатор
- 4.4 Цилиндрический
5 Проверка
6 Заключение
7 Видео по теме

Конденсаторы нашли в наше время очень широкое применение в электронике и электротехнике, ведь они являются основными элементами большинства электрических цепей и схем. Постараемся подробно в данной статье рассказать — что такое электроемкость конденсатора. Так же будут приведены применяемые формулы расчета, описаны различные виды таких устройств и рассказано об их маркировке. Кроме того будет затронуто влияние различных факторов на емкость конденсатора.

Конденсатор

Прежде чем разобраться с тем, что такое емкость простейшего конденсатора, необходимо определиться, что из себя представляет этот электроэлемент. Конденсатором является радиоэлектронная деталь, которая может накапливать и отдавать определенную порцию электрического заряда. Состоит устройство из следующих элементов:

Корпуса. Зачастую выполняется из алюминия. По форме он может быть плоским, сферическим и цилиндрическим.
Обкладок (2 и более). Их делают из металлических пластинок или фольги.
Диэлектрической прокладки. Устанавливается между обкладками и служит в качестве изолятора.
Двух или более выводных контактов для подключения устройства в электроцепь.

Работает такой накопитель электрического заряда следующим образом.

В момент подключения элемента к источнику электрического тока, он выступает в роли проводника. В этот момент электроток имеет максимальное значение, а напряжение — минимальное.
На обкладках элемента начинают скапливаться положительные и отрицательные заряды (электроны и ионы). Таким образом происходит зарядка самого устройства. На момент заряда сила электротока постепенно уменьшается, а напряжение наоборот — увеличивается.
После того как количество заряда в конденсаторе станет больше допустимого предела, он разряжается и процесс опять начинает повторяться циклически.

Основой работоспособности данного устройства является его емкость. Именно от этого параметра зависит время накопления заряда и общая «вместимость» устройства. О том, как на схемах обозначается простейший конденсатор, поможет понять следующий рисунок ниже.

Электрическая емкость, как и сами конденсаторы, нашли широкую область применения. Их используют в качестве:

Частотных фильтров.
Источника импульсов для различной фотоаппаратуры.
Сглаживателей пульсирующих токов в выпрямителях.
Фазосдвигающих элементов для электрических двигателей.

Применение конденсаторов в различных сферах основано именно на способности устройства накапливать электрический заряд. В более сложной электроаппаратуре эти устройства используются для бесперебойного поддержания определенного напряжения в разных накопителях данных.

Емкость

Емкостью конденсатора является физическая величина, которая определяет отношение между накопленным зарядом на обкладках и разностью потенциалов между ними.

В системе «СИ» емкость конденсатора и ее единица измерения — Фарад. В формулах для ее обозначения используется буква Ф (F). Однако емкость конденсатора редко измеряется в Фарадах, потому что это довольно большая величина. Чаще всего применяют ее кратные и дольные значения.

Значение электроемкости конденсатора всегда можно найти в маркировке устройства, которая нанесена на его корпус.

На схеме элемент обозначается буквой «С». Обозначение емкости является обязательным условием, ведь это позволит упростить процесс подбора необходимой электродетали для схемы.

Зависимость

Благодаря приведенному ранее описанию, мы узнали — что такое емкость. Далее попытаемся разобраться, от чего зависит эта характеристика. Емкость конденсатора зависит от расстояния между обкладками, их площади, а так же от самого материала диэлектрика. Благодаря этому можно сказать, от чего зависит емкость устройства: она прямопропорциональна площади пластины конденсатора и обратно пропорциональна расстоянию между пластинами.

Рассмотрим, как найти данную величину. Для плоского конденсатора формула расчета емкости выглядит следующим образом:

Зависимость способности устройства накапливать заряд от площади его обкладок и толщины диэлектрической прослойки так же указывает на то, что на данную величину оказывают влияние и общие размеры элемента.

Расчет

Расчет емкости конденсатора делается по довольно простой формуле:

В этой формуле:

q — величина заряда, накопленного конденсатором.
φ1−φ2 — разница потенциалов между его обкладками.

Данное выражение помогает довольно легко рассчитать емкость любого плоского конденсатора. Как и говорилось ранее в статье, этот величина электроёмкости конденсаторов всегда зависит от его геометрических размеров.

Плоский конденсатор

Отличительная особенность плоского конденсатора — наличие двух параллельно расположенных обкладок. Такие устройства могут иметь квадратную, круглую или прямоугольную форму.

Рассмотрим далее, как определить емкость данного вида конденсаторов. Найти емкость такого типа конденсаторов всегда поможет следующая формула:

Электроемкость

Зачастую применение конденсаторов подразумевает подключение в цепь сразу нескольких таких элементов. Благодаря этому можно увеличить общую емкость. Формула для определения электроемкости плоского конденсатора при параллельном подключении выглядит следующим образом:

Определение общей емкости для такой электроцепи делается следующим образом: C=C₁+C₂

Величина заряда и напряжение для такой схемы соединения определяется следующим образом:

q_общ=q₁+q₂

U_общ=U₁=U₂

Определить емкость конденсатора для последовательного соединения элементов позволит формула:

То есть в этом случае общую электроемкость плоского конденсатора находят с помощью выражения:

1/C_общ=1/C₁+1/C₁

Благодаря данным выражениям найдем общее напряжение и определим величину заряда для последовательного соединения элементов:

q_общ=q₁=q₂

U_общ=U₁+U₂

Емкость конденсатора и применяемые формулы расчетов для различных вариантов соединения плоских устройств приведены на рисунке ниже. Можно сказать, что она очень наглядная и удобная для использования:

Сферический конденсатор

Сферическое устройство имеет две обкладки в форме концентрических сфер, между которыми расположен диэлектрик. Емкость сферического конденсатора можно определить следующим образом:

В данном выражении значение «4π» определяет коэффициент рассеивания зарядов на поверхности сферических плоскостей.

Расчет емкости сферического конденсатора можно сделать по формуле для плоского устройства в том случае, если зазор по сравнению с радиусом сферы имеет довольно маленькое значение.

Цилиндрический

Цилиндрическое устройство немного схоже с ранее описанным сферическим. В них применяются схожие по форме обкладки. Они имеют так же круглую форму, а значит на расчет емкости цилиндрического устройства так же будет влиять такой параметр, как радиус обкладок. Отличием заключается только в самой вытянутой форме пластин цилиндрического конденсатора. Емкость цилиндрического конденсатора определяется по формуле:

Сферические и цилиндрические типы элементов сильно зависимы от толщины слоя диэлектрика. Чем он толще, тем меньше будет объем заряда, а значит у него повысится устойчивость к воздействию пробивного напряжения.

Проверка

Как отмечалось ранее, емкость устройства проставляется на его корпусе. Проверить паспортную величину и имеющуюся емкость устройства можно при помощи тестера с режимом «СХ». Например, для этого подойдут популярные модели M890D, AM-1083, DT9205A, UT139C, другие. Далее надо будет:

Выпаять и разрядить устройство. Разрядка проводится строго изолированным металлическим предметом.
Вставить ножки конденсатора в пазы «СХ», соблюдая полярность.
Прибор отобразит на табло результат измерений. Его нужно будет сравнить с тем, который прописан в маркировке на его корпусе. Если значения между собой сильно отличаются, то это говорит о том, что элемент неисправный и требует замены.

Если мультиметр показал наличие бесконечной емкости, то это говорит о коротком замыкании внутри корпуса устройства и оно так же признается неисправным, требующим замены. Кроме того неисправность всегда можно определить визуально по трещинам или вздутию корпуса.

Заключение

В статье было описано — что такое конденсатор, как определить его емкость, от чего зависит этот параметр и основные формулы для расчета емкости различных типов таких устройств. Устройства всегда имеют на корпусе специальную маркировку, поэтому довольно просто выбрать наиболее подходящий по значению накопитель электрозаряда. Кроме того был приведен способ проверки устройства, который позволяет определить возможные его неисправности.

Видео по теме

Источник

Мы все знаем об электрическом токе, проводимости и сопротивлении. Но емкость является еще одной важной частью понимания концепции электричества. Возможно, вы слышали, что ничто не может хранить электричество. Однако это не так — конденсаторы способны накапливать электрический заряд. Давайте подробнее рассмотрим концепцию конденсаторов и емкости. Начнем с конденсатора.

Конденсатор образован двумя обращенными друг к другу проводниками, между которыми вставлен диэлектрик, то есть изолирующий материал. Эти два проводника называются обкладками конденсатора.

Главной характеристикой конденсаторов является величина емкости.

Емкость конденсатора — формула

Определение

Емкость конденсатора — это ничто иное, как умение конденсатора накапливать энергию в виде электрического заряда. Другими словами, емкость — это запоминающая способность конденсатора. Измеряется емкость в фарадах.

Емкость может быть рассчитана, когда известны заряд Q и напряжение V конденсатора:

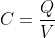
Емкость используется для описания того, сколько заряда может удерживать любой проводник. Он представляет собой отношение заряда к приложенному потенциалу.

Любой объект, который может быть электрически заряжен, показывает емкость. Конденсатор с двумя параллельными пластинами — это обычная форма накопителя энергии. Емкость отображается параллельным расположением пластин и определяется с точки зрения накопления заряда. Когда конденсатор заряжен полностью, между его пластинами имеется разность потенциалов, и чем больше площадь пластин и чем меньше расстояние между ними, тем больше будет заряд конденсатора и тем больше будет его Емкость.

Если конденсаторы соединены последовательно, формула емкости выражается следующим образом:

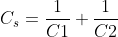
Если конденсаторы подключены параллельно, формула емкости выражается следующим образом:

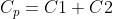
Где C1, C2, C3 ……. Cn — конденсаторы, а емкость выражается в фарадах.

Примеры решения:

Пример 1

Определите емкость конденсатора, если течет 5 кулонов заряда и приложен потенциал 2 В.

Решение

Приведенные параметры

Заряд Q составляет 5 C,

Приложенное напряжение V равно 2 В.

Формула емкости определяется как

C=Q/V

= 5/2

= 2,5 F

Пример 2

Определите емкость, если подключены конденсаторы 6 Ф и 5 Ф.

a) последовательно;

b) параллельно

Решение

Формула последовательной емкости определяется как

Cs = 1 / C1 + 1 / C2

= C1 + C2 / C1C2

= 6 + 5/30

Cs = 0,367 F

Емкость в параллельной формуле определяется как

Ср = С1 + С2

= 6 + 5

Cp = 11 F

Различают три вида конденсаторов:

Конденсатор плоский;
Конденсатор цилиндрический
Конденсатор сферический.

Конденсатор плоский

Данный конденсатор образован двумя металлическими пластинами, которые мы называем A и B, расположенными на расстоянии d.

Две проводящие пластины A и B являются пластинами конденсатора, d — их расстояние, более того, поскольку две пластины параллельны, их поверхности равны.

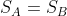
Мы знаем, что внутри двух поверхностей электрическое поле однородно, а снаружи равно нулю

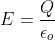
Рассчитываем разность потенциалов между двумя пластинами

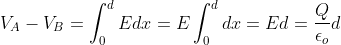
Как только разность потенциалов известна, мы можем рассчитать емкость плоского конденсатора.

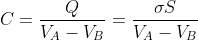
Заменим найденную ранее разность потенциалов

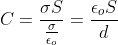
Конденсатор цилиндрический

Конденсатор используется для хранения большого количества электрического тока в небольшом пространстве. Цилиндрический конденсатор включает полый или сплошной цилиндрический проводник, окруженный концентрическим полым сферическим цилиндром. Конденсаторы широко используются в электродвигателях, мельницах, электрических соковыжималках и других электрических инструментах. Разность потенциалов между конденсаторами различна. Существует множество электрических цепей, в которых конденсаторы должны быть сгруппированы соответствующим образом, чтобы получить желаемую емкость. Есть два общих режима, включая конденсаторы, включенные последовательно, и конденсаторы, подключенные параллельно. Единица измерения емкости — Фарад (Ф).

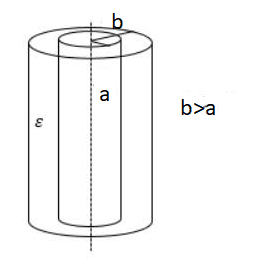
Его часто используют для хранения электрического заряда. Цилиндрический конденсатор — это тип конденсатора, который имеет форму цилиндра, имеющую внутренний радиус как a и внешний радиус как b.

Формула для цилиндрического конденсатора:

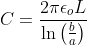
C = емкость цилиндра
L = длина цилиндра
a = внутренний радиус цилиндра,
b = внешний радиус
εₒ= диэлектрическая проницаемость свободного пространства (8.85×10ˉ¹²)

Пример

Цилиндрический конденсатор длиной 8 см состоит из двух колец с внутренним радиусом 3 см и внешним радиусом 6 см. Найдите емкость конденсатора.

Дано:

Длина L = 8 см

внутренний радиус a = 3 см

внешний радиус b = 6 см

Решение

Формула для конденсатора цилиндрического:

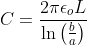
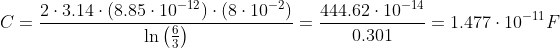
Конденсатор сферический

Данный конденсатор состоит из сплошного или полого сферического проводника, окруженного другой полой концентрической сферической формой другого радиуса.

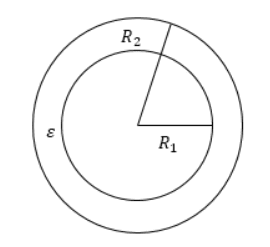
Формула для определения емкости сферического конденсатора

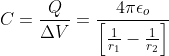
Где,

C = емкость

Q = заряд

V = напряжение

r ₁ = внутренний радиус

r ₂ = внешний радиус

ε ₀ = диэлектрический потенциал (8,85 x ^10-12 Ф / м)

Значение емкости двух разных конденсаторов может быть одинаковым, а номинальное напряжение двух конденсаторов может быть разным. Возьмем два конденсатора — один с малым номинальным напряжением, а другой с высоким. Если мы заменим конденсатор с меньшим номинальным напряжением на конденсатор с более высоким номинальным напряжением, то получится конденсатор меньшего размера. Это может произойти из-за неожиданного повышения напряжения.

Нет времени решать самому?

Наши эксперты помогут!

Влияние диэлектрика на емкость

Плотности поверхностного заряда равны σ _p и — σ _p. Когда мы полностью помещаем диэлектрик между двумя пластинами конденсатора, его диэлектрическая проницаемость увеличивается по сравнению с вакуумным значением.

Внутри конденсатора следующее электрическое поле:

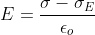
Следовательно, мы имеем:

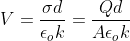
а именно:

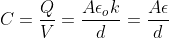
Ɛ — диэлектрическая проницаемость. Разность потенциалов между пластинами задаются

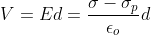
Для линейных диэлектриков:

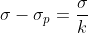
Где k — диэлектрическая проницаемость вещества, K = 1.

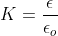
Электрическое поле между пластинами конденсатора прямо пропорционально емкости конденсатора. Напряжение электрического поля снижается из-за наличия диэлектрика. Если общий заряд на пластинах поддерживается постоянным, то уменьшается разность потенциалов на пластинах конденсатора. Таким образом, диэлектрик увеличивает емкость конденсатора.

Источник

Электрическая ёмкость — характеристика проводника (конденсатора), мера его способности накапливать электрический заряд.

$Large C=frac{q}{U}=frac{q}{varphi_1-varphi _2} =varepsilon varepsilon _0frac{S}{d}$

Конденсатор состоит из двух проводников (обкладок), которые разделены диэлектриком. На емкость конденсатора не должны влиять окружающие тела, поэтому проводникам придают такую форму, чтобы поле, которое создается накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) две концентрические сферы; 3) два коаксиальных цилиндра. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, сферические и цилиндрические.

Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками

$Large C=frac{q}{U}=frac{q}{varphi_1-varphi _2}$

Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею.