Конденсатор – радиоэлектронный прибор, способный накапливать и отдавать заряд. Как правило, на его корпусе дается информация о его емкости, но иногда требуется самому рассчитать этот номинал.
Конденсаторами могут выступать и проводники, они также обладают определенной емкостью. Для расчета существует несколько формул емкости конденсатора, их и рассмотрим.
В чем измеряется емкость конденсатора
Что такое заряд еще проходят в школе, когда эбонитовую палочку натирают о шерстяную ткань и подносят к маленьким кусочкам бумаги.
Под действием электромагнитных сил бумага прилипает к палочке. Подобный заряд накапливается в конденсаторе. Но для начала познакомимся с самим конденсатором.
Простейшим конденсатором являются две металлические пластины, разделенные диэлектриком. От качества диэлектрика зависит, как долго энергия заряженного конденсатора может сохраняться.
На этих пластинах, они еще называются обкладками, накапливается разноименный заряд. Как это происходит?
Электрический заряд, а в случае с металлами это электроны, способен перемещаться под действием электродвижущей силы (э. д. с.).
Подключая металлические пластинки к источнику тока, мы получаем замкнутую цепь, но разделенную диэлектриком. Электростатическое поле проходит этот диэлектрик, замыкая цепь, а электроны, дойдя до препятствия, останавливаются и скапливаются.
Полная статья на блоге “Электрик в доме”:
Получается, на одной обкладке наблюдается избыток электронов, и эта пластина имеет отрицательный знак, а на другой пластине электронов недостает настолько же, знак на этой обкладке, конечно же, будет положительным.
Вот теперь нужна для определения емкости конденсатора формула, определяющая, какой заряд способен разместится на конкретном конденсаторе.
В качестве единицы измерения в международной системе (СИ) емкость определяется в Фарадах.
Много это или мало – емкость в 1Ф? Чтобы конденсатор обладал емкостью в 1Ф, он должен содержать в себе заряд в 1К (кулон) и при этом напряжение между обкладками должно равняться 1 вольту.
Интересно. Что такое заряд в 1 кулон? Если два предмета, каждый из которых имеет заряд в один кулон разместить в вакууме на расстоянии один метр, то сила притяжения между ними будет равна силе притяжения землей тела массой в один миллион тонн.
Как и любая буквальная емкость один и тот же конденсатор может вмещать разное количество заряда.
Рассмотрим пример.
- В трехлитровую банку входит три литра воздуха. Его хватит для дыхания, допустим, на 3 минуты. Но если воздух закачать под каким-то давлением, то емкость так и останется три литра, однако дышать можно будет дольше. Так устроен акваланг для ныряльщиков. Получается, количество воздуха в банке зависит от давления, которое в ней создается. Точно так же есть некая зависимость между различными силами, влияющими на емкость.
Формула емкости плоского конденсатора
Прежде чем узнать, по какой формуле вычисляется емкость плоского конденсатора, рассмотрим формулу для одиночного проводника. Она имеет вид:
- где Q – заряд,
- φ – потенциал.
Как видно емкость конденсатора, формула которого здесь приведена, будет тем больше, чем больший заряд способен накапливаться на нем при незначительном потенциале. Чтобы легче это было понять, рассмотрим получившие широкое распространение плоские конденсаторы разных размеров.
Для получения качественного конденсатора важны любые мелочи:
- ровная поверхность каждой обкладки;
- обе пластинки по всей площади должны располагаться на одинаковом расстоянии;
- размеры обкладок должны быть строго идентичными;
- от качества диэлектрика, расположенного между пластинками, будет зависеть ток утечки;
- емкость напрямую зависит от расстояния между обкладками, чем оно меньше, тем больше емкость.
Теперь обратимся к плоскому конденсатору. Формула определения емкости конденсатора несколько отличается от приведенной выше:
- где S – площадь одной обкладки,
- εr – диэлектрическая проницаемость диэлектрика,
- ε0 – электрическая постоянная,
- d – расстояние между обкладками.
Электрическая постоянная выражается числом 8,854187817×10-12.
Внимание! Эта формула справедлива только тогда, когда расстояние между пластинами намного меньше их площади.
Попробуем разобраться с каждой переменной подробнее. Площадь измеряется в м2, точнее, приводится к этой величине. А вот проницаемость диэлектрика может обозначаться по-разному.
В России это εr (также означает относительная проницаемость), в англоязычной литературе встречается εa (также означает абсолютная проницаемость), а то может и вовсе использоваться без индекса, просто ε. О том, что здесь используется диэлектрическая проницаемость диэлектрика можно понять из контекста.
Дальше идет ε0. Это уже вычисленное значение, измеряемое в Ф/м. Последняя переменная – d. Измеренное расстояние также приводится к метру. Емкость конденсатора, формула которого сейчас рассматривается, показывает сильную зависимость от расстояния обкладок. Поэтому стараются это расстояние по возможности сокращать. Почему этот показатель так важен?
Идеальными условиями для получения наибольшей емкости – это отсутствие промежутка между обкладками, чего, конечно, добиться невозможно. Чем ближе находятся разноименные заряды, тем сильнее сила притяжения, но здесь возникает компромисс.
При уменьшении толщины диэлектрика, а именно он разделяет разноименные заряды, возникает вероятность его пробоя из-за разности потенциалов на обкладках. С другой стороны, как уже говорилось, при увеличении напряжения увеличивается количество зарядов. Вот и приходится выбирать между емкостью и рабочим напряжением конденсатора.
Есть другая формула для плоского переменного конденсатора:
Здесь диэлектрическая проницаемость обозначена буквой ε, π = 22/7 ≈ 3,142857142857143, d – толщина диэлектрика. Формула предназначена для конденсатора, состоящего из нескольких пластин.
Допустимая толщина диэлектрика d также зависит от εr, чем выше коэффициент, тем тоньше можно использовать диэлектрик, тем большую емкость будет иметь конденсатор. Это был самый сложный материал, дальше будет легче.
Формула емкости цилиндрического конденсатора
Теперь поговорим о том, как найти емкость конденсатора цилиндрической формы. К ним относятся конденсаторы, состоящие из двух металлических цилиндров, вставленных один в другой.
Для разделения между ними расположен диэлектрик. Формула емкости конденсатора выглядит следующим образом:
Здесь видим несколько новых переменных:
- l – высота цилиндра;
- R1 и R2 – радиус первого и второго (внешнего) цилиндров;
- ln – это не переменная, а математический символ натурального логарифма. На некоторых калькуляторах он имеется.
Всегда нужно помнить, что все величины должны приводиться к единой системе, в приведенной ниже таблице указаны международные системы единиц (СИ).
Из нее видно, что все расстояния нужно приводить к метру.
Еще стоит обращать внимание на качество диэлектрика. Если толщина диэлектрика влияет только на емкость конденсатора, то его качество затрагивает сохранность энергии. Другими словами, конденсатор с качественным диэлектриком будет иметь меньший саморазряд.
Определить качество можно по числу, стоящему возле вещества, чем оно больше, тем лучше качество. Сравнение производится по вакууму, значение которого равно единице.
Формула емкости сферического конденсатора
Последнее что осталось разобрать – формулу определения емкости конденсатора, состоящего из двух сфер. Причем одна сфера находится внутри другой. Формула имеет следующий вид:
Из приведенных переменных здесь все знакомо. Стоит обратить внимание лишь на сам конденсатор.
Кроме своей необычной формы у него есть свои особенности: внутри малой сферы никакого заряда нет, он образуется на внешней части малой сферы и внутренней части большого шара. Также заряд отсутствует и на внешней стороне внешней сферы.
Так же как и все другие конденсаторы, сферы разделены диэлектриком. Толщина и качество диэлектрика оказывают такое же влияние на емкость, как в случае с другими конденсаторами.
После того как были рассмотрены формулы, стоит испробовать их на практике. Рассмотрим, как найти емкость конденсатора каждого вида.
Примеры решения задач
Начнем с плоского конденсатора. Формула для этого вида:
Допустим, у нас есть следующие значения:
- в качестве диэлектрика возьмем слюду толщиной 0,02 мм, ε = 6;
- конденсатор квадратный со сторонами в 7 мм.
Определяем площадь пластин: 7×7 = 49 мм2.
Приводим к единой системе: 4,9×10-5 = 0,000049 м2. Толщина диэлектрика 0,02×10-5 = 0,00002 м. Электрическая постоянная 8,854187817×10-12.
Подставляем в формулу и высчитываем числитель: 6×8,854187817×10-12 ×4,9×10-5, сокращаем и решаем 6×49×8,854187817×10-17 = 2,603131218198×10-14.
Делим на толщину диэлектрика: 2,603131218198×10 / 2×10 = 1301,565609099×10 = 1,301565609099×10. Шесть нулей – это тысячи или приставка «микро», получается округлено 1,3 мкФ.
Возможно, при вычислении была допущена ошибка, но это не экзамен по математике. Важно понять сам метод вычисления.
Формула для цилиндрического конденсатора:
Выбираем значения:
- l = 1 см;
- R1 = 0,25 мм;
- R2 = 0,26 мм;
- ε = 2.
Подгоняем под единую систему: l – 1 см = 1×10-2 = 0,01 м; R1 – 0,25 мм = 0,0025 м; R2 – 0,26 мм = 0,0026 м.
Подставляем значения в числитель: 2×3,142857142857143×8,854187817×10-12×2×0,01 1,11×10-12. Находим знаменатель: 0,26:0,25 = 1,04.
Находим натуральный логарифм, он равен примерно 0,39. Числитель делим на знаменатель: 1,11×10-12/0,39 = 2,85×10-12.
Число с 12 нулями это приставка «пико», получаем 2,85 пФ.
Формула для сферического конденсатора:
Выбираем значения:
- ε= 4;
- r1= 5 см;
- r2= 5,01 см.
Снова все подгоняем: 5 см = 0,05 м; 5,01 см = 0,0501 м. Заполняем числитель. 4×3,142857142857143×4×8,854187817×10-12×0,05×0,0501 1,11×10-12 Вычисляем знаменатель: 0,0501 – 0,05 = 0,01. Производим деление: 1,11×10-12×0,01 = 1,11×10-10. Снова получили пикофарады, а именно 1,11 пФ.
Интересные статьи на канале:
Статья заинтересовала? Лайк, подписка, комментарий!
Друзья ПОДПИСЫВАЙТЕСЬ Дзен на канал, а также заходите на блог https://electricvdome.ru 👍!
#конденсатор #емкость #формула
Конденсатор – это совокупность двух любых проводников, заряды которых одинаковы по значению и противоположны по знаку.
Его конфигурация говорит о том, что поле, созданное зарядами, локализовано между обкладками. Тогда можно записать формулу электроемкости конденсатора:
C=qφ1-φ2=qU.
Значением φ1-φ2=U обозначают разность потенциалов, называемую напряжением, то есть U. По определению емкость положительна. Она зависит только от размерностей обкладок конденсатора их взаиморасположения и диэлектрика. Ее форма и место должны минимизировать воздействие внешнего поля на внутреннее. Силовые линии конденсатора начинаются на проводнике с положительным зарядом, а заканчиваются с отрицательным. Конденсатор может являться проводником, помещенным в полость, окруженным замкнутой оболочкой.
Выделяют три большие группы: плоские, сферические, цилиндрические. Чтобы найти емкость, необходимо обратиться к определению напряжения конденсатора с известными значениями зарядов на обкладках.
Плоский конденсатор
Плоский конденсатор – это две противоположно заряженные пластины, которые разделены тонким слоем диэлектрика, как показано на рисунке 1.
Формула для расчета электроемкости записывается как
C=εε0Sd, где S является площадью обкладки, d – расстоянием между ними, ε – диэлектрической проницаемостью вещества. Меньшее значение d способствует большему совпадению расчетной емкости конденсатора с реальной.
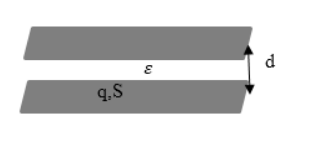
Рисунок 1
При известной электроемкости конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равняется di, вычисление диэлектрической проницаемости этого слоя εi выполняется, исходя из формулы:
C=ε0Sd1ε1+d2ε2+…+dNεN.
Сферический конденсатор
Когда проводник имеет форму шара или сферы, тогда внешняя замкнутая оболочка является концентрической сферой, это означает, что конденсатор сферический.
Он состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком, как показано на рисунке 2. Емкость рассчитывается по формуле:
C=4πεε0R1R2R2-R1, где R1 и R2 являются радиусами обкладок.
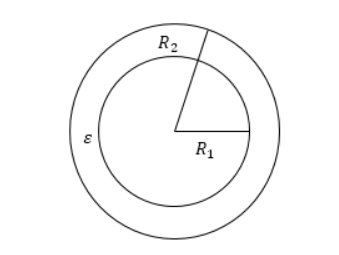
Рисунок 2
Цилиндрический конденсатор
Емкость цилиндрического конденсатора равняется:
C=2πεε0llnR2R1, где l – высота цилиндров, R1 и R2 – радиусы обкладок. Данный вид конденсатора имеет две соосные поверхности проводящих цилиндрических поверхности, как показано на рисунке 3.
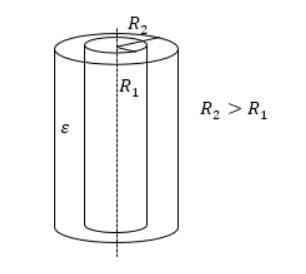
Рисунок 3
Важной характеристикой конденсаторов считается пробивное напряжение – напряжение, при котором происходит электрический разряд через слой диэлектрика.
Umax находится от зависимости от толщины слоя и свойств диэлектрика, конфигурации конденсатора.
Электроемкость плоского конденсатора. Формулы
Кроме отдельных конденсаторов используются их соединения. Наличие параллельного соединения конденсаторов применяют для увеличения его емкости. Тогда поиск результирующей емкости соединения сводится к записи суммы Ci, где Ci- это емкость конденсатора с номером i:
C=∑i=1NCi.
При последовательном соединении конденсаторов суммарная емкость соединения всегда будет по значению меньше, чем минимальная любого конденсатора, входящего в систему. Для расчета результирующей емкости следует сложить величины, обратные к емкостям отдельных конденсаторов:
Произвести вычисление емкости плоского конденсатора при известной площади обкладок
1 см2 с расстоянием между ними 1 мм. Пространство между обкладками находится в вакууме.
Решение
Чтобы рассчитать электроемкость конденсатора, применяется формула:
C=εε0Sd.
Значения:
ε=1, ε0=8,85·10-12 Фм;S=1 см2=10-4 м2;d=1 мм=10-3 м.
Подставим числовые выражения и вычислим:
C=8,85·10-12·10-410-3=8,85·10-13 (Ф).
Ответ: C≈0,9 пФ.
Найти напряженность электростатического поля у сферического конденсатора на расстоянии x=1 см=10-2 м от поверхности внутренней обкладки при внутреннем радиусе обкладки, равном R1=1 см=10-2 м, внешнем – R2=3 см=3·10-2 м. Значение напряжения – 103 В.
Решение
Производящая заряженная сфера создает напряженность поля. Его значение вычисляется по формуле:
E=14πεε0qr2, где q обозначают заряд внутренней сферы, r=R1+x – расстояние от центра сферы.
Нахождение заряда предполагает применение определения емкости конденсатора С:
q=CU.
Для сферического конденсатора предусмотрена формула вида
C=4πεε0R1R2R2-R1 с радиусами обкладок R1 и R2.
Производим подстановку выражений для получения искомой напряженности:
E=14πεε0U(x+R1)24πεε0R1R2R2-R1=U(x+R1)2R1R2R2-R1.
Данные представлены в системе СИ, поэтому достаточно заменить буквы числовыми выражениями:
E=103(1+1)2·10-4·10-2·3·10-23·10-2-10-2=3·10-18·10-6=3,45·104 Вм.
Ответ: E=3,45·104 Вм.
Как найти емкость батареи конденсатора?
Лариса Александрова
Ученик
(2),
закрыт
12 лет назад
Если два соединены параллельно, а с третьим последовательно?
Лучший ответ
Марат Сунагатуллин
Мыслитель
(7614)
12 лет назад
2 паралельных кондёра складываешь
1с=1(с1+с2)+1с3
с-это общая суммарная ёмкость
Остальные ответы
Александр Агольцов
Гуру
(4391)
12 лет назад
пр паралельном соединение ёмкости складываются, т. е. С0=С1+С2+С3…
при последовательном соединение:
1/С0=(1/С1)+(1/С2)+(1/С3) …
само С=q/U, где q-заряд, u – напряжение.
Валентин Дульша
Гуру
(3556)
12 лет назад
Найди по формуле емкости емкость двух левых конденсаторов С=(Е0*Е*S)/d. Потом сплюсуйте их и все готово.
–
Ученик
(107)
1 месяц назад
емкость батареи конденсаторов находятся c из формулы
Похожие вопросы
Основной характеристикой конденсатора является его емкость. Очень часто замеры емкости требуется проводить в электролитическом конденсаторе. В отличие от керамических и оксидных конденсаторов, которые редко выходят из строя (разве что в результате пробоя диэлектрика), электролитическим деталям свойственна потеря ёмкости из-за высыхания электролита. Поскольку работа электронных схем сильно зависит от емкостных характеристик, то необходимо знать, как определить емкость конденсатора.
Существуют разные способы определения ёмкости:
- по кодовой или цветной маркировке деталей;
- с помощью измерительных приборов;
- с использованием формулы.
Измерить емкость проще всего с помощью измерителя C и ESR. Для этого контакты измерительных щупов подсоединяют к выводам конденсатора, соблюдая полярность электролитических деталей. При этом результаты измерений выводятся на дисплей. (Рисунок 1). Радиолюбители, которым часто приходится делать измерения, приобретают такой прибор или изготавливают его самостоятельно.

С использованием мультиметра и формул
Если в вашем распоряжении есть мультиметр с функцией измерения параметра «Cx», то измерить ёмкость конденсатора довольно просто: следует переключить прибор в режим «Сх», после чего выбрать оптимальный диапазон измерения, соответствующий параметрам конденсатора. Ножки конденсатора вставляем в соответствующее гнездо (соблюдая полярность подключения) и считываем его параметры.

Менее точно можно определить ёмкость с помощью тестера, у которого нет режима «Сх». Для этого потребуется источник питания, к которому подключают конденсатор по простой схеме (рис. 2).

Алгоритм измерения следующий:
- Измерьте напряжение источника питания щупами контактов измерительного прибора.
- Образуйте RC-цепочку с конденсатором и выводами резистора номиналом 1 – 10 кОм.
- Закоротите выводы конденсатора и подключите RC-цепочку к источнику питания.
- Замерьте напряжение образованной цепи с помощью мультиметра.
- Если напряжение изменилось, необходимо подогнать его до значения, близкого к тому, которое вы получили на выходе источника питания.
- Вычислите 95% от полученного значения. Запишите показатели измерений.
- Возьмите секундомер и включите его одновременно с убиранием закоротки.
- Как только мультиметр покажет значение напряжения, которое вы вычислили (95%), остановите секундомер.
- По формуле С = t/3R, где t – время падения напряжения, вычисляем ёмкость конденсатора в фарадах, если единицы измерения сопротивление резистора выразили в омах, а время в секундах.

Подчеркнём ещё раз, что точность измерения ёмкости данным способом не слишком высока, но определить работоспособность радиоэлемента на основании такого измерения вполне возможно. Некоторые узлы электронных приборов исправно работают, если есть небольшие отклонения от номинальных емкостей, главное, чтобы не было электрического пробоя.
Таким же методом можно вычислить параметры керамического радиоэлемента. Для этого необходимо подключить RC-цепочку через трансформатор и подать переменное напряжение. Значение ёмкости в данном случае определяем по формуле: C = 0.5*π*f*Xc , где f – частота тока, а Xc – ёмкостное сопротивление.
Осциллографом
С приемлемой точностью можно определить ёмкость конденсатора с помощью цифрового или обычного электронного осциллографа. Принцип похож на метод измерения ёмкости тестером. Разница только в том, что не потребуется секундомер, так как с высокой точностью время зарядки конденсатора отображается на экране осциллографа. Если применить генератор частоты и последовательную RC-цепочку (рис. 4), то ёмкость можно рассчитать по простой формуле: C = UR / UC* ( 1 / 2*π*f*R ).

Алгоритм вычисления простой:
- Подключите осциллограф к электрической схеме. При подключении щупов прибора к электролитам соблюдайте полярность электрического тока.
- Измерьте амплитуды напряжений на конденсаторе и на резисторе.
- Путём подстройки частоты генератора добивайтесь, чтобы значения амплитуд на обоих элементах сравнялись (хотя бы приблизительно).
- Подставьте полученные значения в формулу и вычислите ёмкость конденсатора.
При измерении ёмкостей неполярных конденсаторов часто вместо RC-цепочки собирают мостовую схему с частотным генератором (показано на рис. 5), а также другие сборки. Сопротивления резисторов подбирают в зависимости от параметров номинальных напряжений измеряемых деталей. Ёмкость вычисляют из соотношения: r4 / Cx = r2 / C0.

Гальванометром
При наличии баллистического гальванометра также можно определить ёмкость конденсатора. Для этого используют формулу:
C = α * Cq / U , где α – угол отклонения гальванометра, Cq – баллистическая постоянная прибора, U – показания гальванометра.
Из-за падения сопротивления утечки ёмкость конденсаторов уменьшается. Энергия теряется вместе с током утечки.
Описанные выше методики определения ёмкости позволяют определить исправность конденсаторов. Значительное отклонение от номиналов говорит, что конденсаторы неисправны. Пробитый электролитический радиоэлемент легко определяется путём измерения сопротивления. Если сопротивление стремится к 0 – изделие закорочено, а если к бесконечности – значит, есть обрыв.
Следует опасаться сильного электрического разряда при подключениях щупов к большим электролитам. Они могут накапливать мощный электрический заряд от постоянного тока, который молниеносно высвобождается током разряда.
По маркировке
Напомним, что единицей емкости в системе СИ является фарада ( обозначается F или Ф). Это очень большая величина, поэтому на практике используются дольные величины:
- миллифарады (mF, мФ ) = 10-3 Ф;
- микрофарады (µF, uF, mF, мкФ) = 10-3 мФ = 10-6 Ф;
- нанофарады (nF, нФ) = 10-3 мкФ =10-9 Ф;
- пикофарады (pF, mmF, uuF) = 1 пФ = 10-3 нФ = 10-12 Ф.
Мы перечислили название единиц и их сокращённое обозначение потому, что они часто встречаются в маркировке крупных конденсаторов (см. рис. 6).

Обратите внимание на маркировку плоского конденсатора (второй сверху): после трёхзначной цифры стоит буква М. Данная буква не обозначает единицы измерения «мегафарад» – таких просто не существует. Буквами обозначены допуски, то есть, процент отклонения от ёмкости, обозначенной на корпусе. В нашем случае отклонение составляет 20% в любую сторону. Надпись 102М на большом корпусе можно было бы написать: 102 нФ ± 20%.
Теперь расшифруем надпись на корпусе третьего изделия. 118 – 130 MFD обозначает, что перед нами конденсатор, ёмкость которого находится в пределах 118 – 130 микрофарад. В данном примере буква М уже обозначает «микро». FD – обозначает «фарады», сокращение английского слова «farad».
На этом простом примере видно, какая большая путаница в маркировке. Особенно запутана кодовая маркировка, применяемая для крохотных конденсаторов. Дело в том, что можно встретить конденсаторы, маркировка которых выполнена старым способом и детали с современной кодировкой, в соответствии со стандартом EIA. Одни и те же символы можно по-разному интерпретировать.
По стандарту EIA:
- Две цифры и одна буква. Цифры обозначают ёмкость, обычно в пикофарадах, а буква – допуски.
- Если буква стоит на первом или втором месте, то она обозначает либо десятичную запятую (символ R), либо указывает на название единицы измерения («p» – пикофарад, «n» – нанофарад, «u» – микрофарад). Например: 2R4 = 2.4 пФ; N52 = 0,52 нФ; 6u1 = 6,1 мкф.
- Маркировка тремя цифрами. В данном коде обращайте внимание на третью цифру. Если её значение от 0 до 6, то умножайте первые две на 10 в соответствующей степени. При этом 100 =1; 101 = 10; 102 = 100 и т. д. до 106.
Цифры от 7 до 9 указывают на показатель степени со знаком «минус»: 7 условно = 10-3; 8 = 10-2; 9 = 10-1.
Пример:
- 256 обозначает: 25× 105 = 2500 000 пФ = 2,5 мкФ;
- 507 обозначает: 50 × 10-3 = 50 000 пФ = 0, 05 мкФ.
Возможна и такая надпись: «1B253». При расшифровке необходимо разбить код на две части – «1B» (значение напряжения) и 253 = 25 × 103 = 25 000 пФ = 0,025 мкФ.
В кодовой маркировке используются прописные буквы латинского алфавита, указывающие допуски. Один пример мы рассмотрели, анализируя маркировку на рис. 6.
Приводим полный список символов:
- B = ± 0,1 пФ;
- C = ± 0,25 пФ;
- D = ± 0,5 пФ или ± 0,5% (если емкость превышает 10 пФ).
- F = ± 1 пФ или ± 1% (если емкость превышает 10 пФ).
- G = ± 2 пФ или ± 2% (для конденсаторов от 10 пФ»).
- J = ± 5%.
- K = ± 10%.
- M = ± 20%.
- Z = от –20% до + 80%.
Изделия с кодовой маркировкой изображены на рис. 7.

Если в кодировке отсутствует символ из приведённого выше списка, а стоит другая буква, то она может единицу измерения емкости.
Важным параметром является его рабочее напряжение конденсатора. Но так как в данной статье мы ставим задачу по определению ёмкости, то пропустим описание маркировки напряжений.
Отличить электролитический конденсатор от неполярного можно по наличию символа «+» или «–» на его корпусе.
Цветовая маркировка
Описывать значение каждого цвета не имеет смысла, так как это понятно из следующей таблицы (рис. 8):

Запомнить символику кодовой и цветовой маркировки довольно трудно. Если вам не приходится постоянно заниматься подбором конденсаторов, то проще пользоваться справочниками или обратиться к информации, изложенной в данной статье.
Видео в помощь
Содержание
- От чего зависит и в чем измеряется емкость конденсатора
- Как узнать емкость конденсатора
- По маркировке
- Мультиметром
- Осциллографом
- Формулы для расчета емкости
- Электроемкость плоского конденсатора
- Электроемкость сферического конденсатора
- Электроемкость цилиндрического конденсатора
- Как изменится емкость при параллельном и последовательном соединении
Конденсатор – пассивный электронный компонент, главной характеристикой которого является емкость. Предназначен в основном для накопления энергии, разделения цепей постоянного тока, фильтрации помех, создания резонансных цепей и т.п. Чтобы применение конденсаторов на практике было осознанным, следует ознакомиться с их основными параметрами, методами измерения и изменения емкости.
От чего зависит и в чем измеряется емкость конденсатора
Конденсатор в общем случае состоит из двух проводящих обкладок, разделенных диэлектриком. Если к обкладкам приложить напряжение, такое устройство запасает электрическую энергию путем накопления заряда. (говорят, что конденсатор заряжается). Количественно запасенная конденсатором электрическая энергия выражается формулой ![]() , где W – величина энергии, U – напряжение между обкладками, а С – емкость, то есть, величина, характеризующая способность конденсатора запасать энергию. В целом ёмкость зависит от площади обкладок, расстояния между ними и свойствами разделяющего диэлектрика.
, где W – величина энергии, U – напряжение между обкладками, а С – емкость, то есть, величина, характеризующая способность конденсатора запасать энергию. В целом ёмкость зависит от площади обкладок, расстояния между ними и свойствами разделяющего диэлектрика.
Единицей измерения емкости в СИ является фарад (1 Ф) (устаревшее название – фарада). Для практических целей это слишком большая единица. Так, земной шар имеет ёмкость менее 1 Ф, поэтому в технике используют, в основном, дольные единицы:
- пикофарады – 1 пФ (1 pF) =10-12 Ф;
- нанофарады – 1 нФ (1 nF) =10-9 Ф;
- микрофарады – 1мкФ (1 µF) = 10-6 Ф.
Более крупные единицы до недавнего времени не использовались, так как емкости порядка больших дольных единиц были труднодостижимыми. Лишь с появлением ионисторов появилась возможность оперировать величинами порядка единиц и даже десятков фарад.
Как узнать емкость конденсатора
Чтобы использовать конденсатор для практических целей, надо знать его емкость. Выяснить эту величину можно различными способами.
По маркировке
В первую очередь, надо попробовать определить параметры конденсатора по его маркировке. На оксидные конденсаторы, имеющие емкость которых составляет от долей до нескольких тысяч микрофарад, эта характеристика наносится на корпус в виде цифры, обозначающей емкость в микрофарадах, с индексом uF (для отечественных изделий предыдущих годов выпуска после цифры стоит индекс мкФ).
Конденсаторы, обладающие емкостью от единиц пикофарад до единиц микрофарад маркируют тремя цифрами:
- первые два символа — мантисса;
- третья цифра – множитель.
Попросту говоря, к первым двум цифрам надо приписать количество нулей, обозначаемое третьей цифрой.
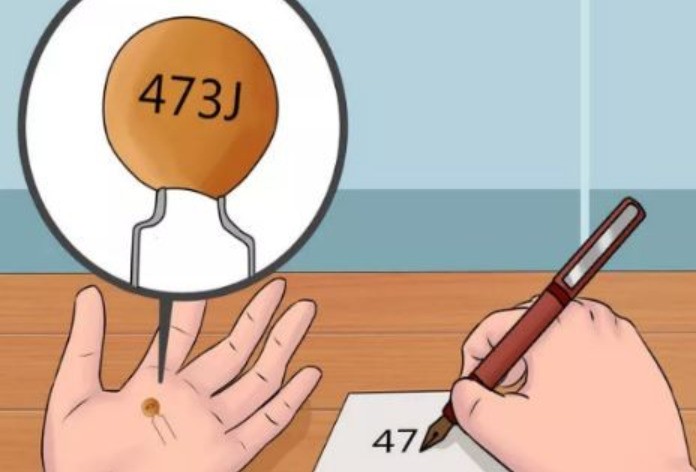
Например, на конденсатор на рисунке нанесено обозначение 473. К цифрам 47 надо приписать три нуля, тогда получится 47000 пФ. Удобнее представить это значение в виде 47нФ или 0,047 мкФ.
Такое обозначение применяется не всегда (особенно, на старых типах отечественных изделий). Иногда на корпусе наносят явное значение ёмкости с единицей измерения.

Но и единицу измерения указывают не всегда. Принцип таков:
- если нет множителя или не указана единица, считается, что ёмкость в пикофарадах;
- если есть множитель, он указывается одной буквой (n – нанофарады, µ — микрофарады и т.п.).
На зарубежных конденсаторах выпуска до 70-х годов можно встретить обозначение µµF. Так маркировалась ёмкость в пикофарадах («микро-микрофарады»).
Если емкость неизвестна, надпись но корпусе отсутствует или есть сомнения, лучше провести измерения одним из известных способов.

Мультиметром

Сделать это можно, например, с помощью цифрового тестера. Многие современные мультиметры имеют функцию измерения емкости конденсаторов. Надо всего лишь выбрать соответствующий режим, обычно обозначаемый символом конденсатора или буквами Cx, и подключить конденсатор к щупам или специально выделенным гнездам. При измерении надо иметь в виду, что:
- Нижний предел измеряемой величины довольно большой, и для большинства распространенных приборов составляет не менее 1000 пФ.
- Измерительные провода со щупами имеют собственную ёмкость (до 100 пФ), и ее надо учитывать при измерениях.
Поэтому тестеры, у которых для измерения ёмкости предназначен отдельный выход, измеряют параметры более точно.
Чтобы обмерить конденсатор с меньшей ёмкостью, лучше воспользоваться специализированным тестером (можно приобрести на интернет-площадках, расположенных в Юго-Восточной Азии). Они позволяют измерять ёмкость от десятков или даже единиц пикофарад.

Осциллографом
Если есть два резистора – один с известным сопротивлением R, а другой с неизвестным Rx, их можно соединить последовательно (сделать делитель напряжения), подать на него напряжение, и измерить падение на каждом элементе или на общей цепи. Измерения можно провести тестером в режиме вольтметра. Тогда Rx можно вычислить по одной из формул, указанных на рисунке.
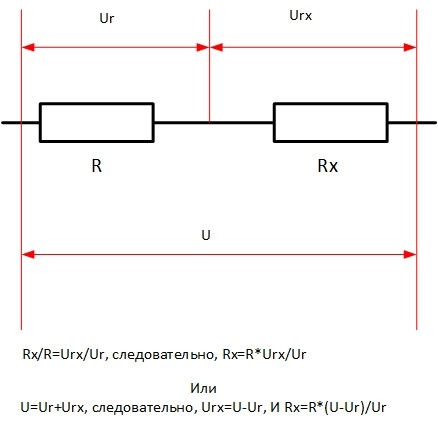
Известно, что конденсатор обладает сопротивлением переменному току, которое зависит от частоты по формуле Xc=1/(2*π*f*C), где:
- f – частота тока в Герцах;
- С – ёмкость конденсатора в Фарадах.
Можно сделать подобный делитель из конденсаторов, и сравнить сопротивление неизвестного прибора Xcx с сопротивлением эталонного конденсатора Xc, откуда легко вычислить неизвестную ёмкость: ![]()
откуда ![]()
Далее несложно найти С.
При этом возникают две проблемы:
- Измерения нельзя проводить на постоянном токе – сопротивление реального конденсатора при f=0 близко к бесконечности.
- При измерении переменного напряжения достаточно высокой частоты тестер будет давать значительную погрешность.
Поэтому в качестве источника тока надо использовать генератор сигнала высокой частоты (чем меньше предполагаемая ёмкость, тем выше должна быть частота, в противном случае точность замеров будет невысокой), а в качестве измерительного прибора – осциллограф.
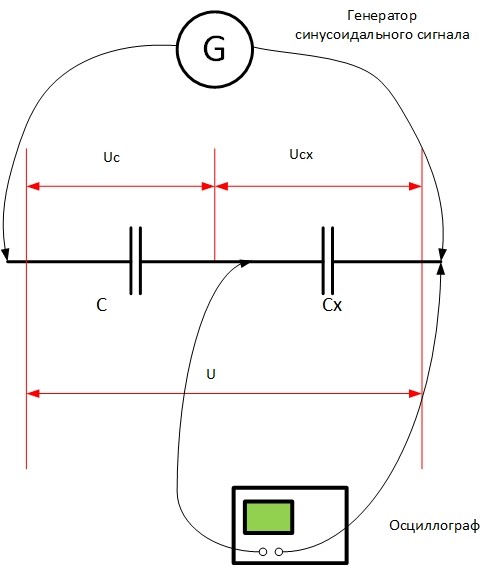
В качестве эталонного элемента для делителя можно взять резистор с известным сопротивлением (вместо Xc в формулу надо подставить R) или катушку (дроссель) с известной индуктивностью. В этом случае вместо Xc в формулу надо подставить XL (вычисляется, как XL=2* π*f*L).
Если имеется эталонная индуктивность, можно найти емкость, составив колебательный контур. Его надо подключить по указанной схеме, а затем, перестраивая генератор, найти резонансную частоту (при ней амплитуда сигнала на осциллографе будет максимальной). Ёмкость можно рассчитать по известной формуле Томсона ![]() .
.

Мнение эксперта
Становой Алексей
Инженер-электроник. Работаю в мастерской по ремонту бытовых приборов. Увлекаюсь схемотехникой.
Задать вопрос
При подключении щупов генератора и осциллографа к измерительным цепям, надо учитывать влияние кабелей (собственная емкость может составлять несколько десятков пикофарад). Чтобы исключить это влияние, измеряемую цепь лучше подключать к щупам через конденсаторы маленькой емкости.
Формулы для расчета емкости
Хотя общая зависимость ёмкости от геометрических размеров и свойств диэлектрика определена выше, для конкретных типов конденсаторов удобнее пользоваться приведенными формулами.
Электроемкость плоского конденсатора
Самый распространённый тип конденсатора, применяемый в технике – плоский. Его обкладки состоят из двух параллельных пластин, между которыми находится диэлектрик. Чтобы уменьшить габариты такого прибора, обкладки с диэлектриком между ними сворачивают в рулон или складывают в прямоугольный пакет. Емкость такого конденсатора рассчитывается по формуле ![]() , где:
, где:
- С – ёмкость, Ф;
- S – площадь обкладок, кв.м;
- d – расстояние между обкладками;
- ε – диэлектрическая проницаемость диэлектрика;
- ε0 – электрическая постоянная, равная 8.85*10-12 Кл2/Н*м2.
Очевидно, что емкость тем больше, чем больше площадь обкладок и меньше расстояние между ними. Кроме того, можно выбрать диэлектрик с высоким ε и пропорционально увеличить ёмкость в тех же габаритах.

Электроемкость сферического конденсатора
Сферическим конденсатором называется устройство, состоящее из двух проводящих сфер – большой радиусом R1 и малой радиусом R2. Малая сфера вложена в большую. Поверхности сфер служат обкладками. Пространство между сферами может заполняться твердым, жидким диэлектриком или воздухом (воздушный сферический конденсатор). Такие приборы используются для лабораторных исследований (например, для изучения фотоэлектрических явлений).
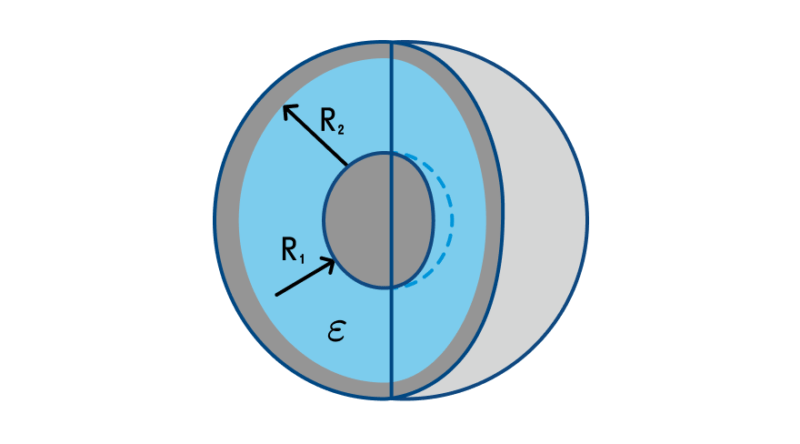
Формула емкости для такого прибора выглядит, как ![]() , где:
, где:
- С – ёмкость, Ф;
- R1 – радиус внутренней сферы;
- R2 – радиус внешней сферы;
- ε – диэлектрическая проницаемость диэлектрика;
- ε0 – электрическая постоянная, равная 8.85*10-12 Кл2/Н*м2.
Очевидно, что зависимость емкости от геометрии подобна плоскому конденсатору. Емкость увеличивается при увеличении площади поверхностей сфер (которые зависят от квадрата радиусов) и уменьшается при увеличении расстояния между обкладками (R2-R1).
Электроемкость цилиндрического конденсатора
У цилиндрического конденсатора обкладки представляют собой два коаксиальных (расположенных на общей оси) цилиндра длиной l каждый с радиусами R1 (меньший) и R2 (больший). Пространство между ними также может быть заполнено либо воздухом, либо другим диэлектриком. Такие приборы используют в масс-спектрометрии и в некоторых типах счетчиков заряженных частиц. Формула для емкости будет выглядеть, как ![]() .
.
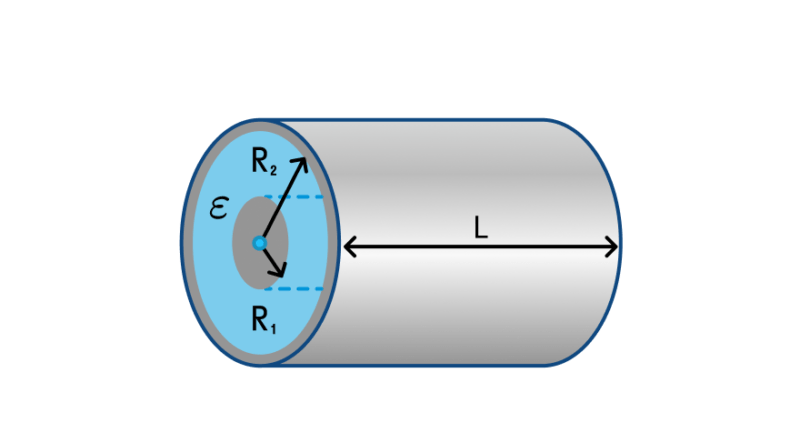
Здесь также прослеживается зависимость от площади (при росте длины увеличивается площадь обкладок, следовательно, растет емкость) и расстояния между обкладками. При росте отношения R2/R1 расстояние увеличивается, а ёмкость падает.
Как изменится емкость при параллельном и последовательном соединении
В реальных схемах конденсаторы могут быть включены последовательно или параллельно. При этом суммарная емкость будет разной.

Если включить n конденсаторов параллельно, то в этом случае:
- к каждой ячейке прикладывается одно и то же напряжение (U1=U2=..=Un=U);
- запасенные в каждом конденсаторе заряды складываются.
Тогда общая емкость равна С=U*q=U*(q1+q2+..+qn)=U*q1+U*q2+..+ U*qn=C1+C2+..+Cn. То есть, при параллельном включении ёмкость батареи равна сумме ёмкостей всех элементов. Это эквивалентно сложению площадей всех пластин.
Батарею можно собрать и последовательно, при этом одна обкладка каждого элемента подключается к выводу соседнего конденсатора, а другая – к выводу другой ячейки. Напряжение подается на свободные выводы крайних элементов.

При этом действуют следующие соотношения (в качестве примера рассмотрена батарея из трех элементов):
- заряды –q1 и q2, -q2 и q3 равны, так как обкладки с этими зарядами соединены между собой;
- заряды q1 и –q1, q2 и –q2, q3 и –q3 равны между собой по модулю, но их знак противоположен.
Заряды каждого конденсатора одинаковы и равны q, но при различной емкости разности потенциалов между обкладками каждого элемента определяются из соотношений:
- U1=q/ C1;
- U2=q/ C2;
- U3= q/ C3.
Следовательно, напряжения на ячейках батареи распределяются пропорционально емкостям. Суммарная емкость равна С=q/(U1+U2+U3), следовательно 1/С=(U1+U2+U3)/q=1/С1+1/С2+1/С3.
Для n элементов, включенных последовательно, выполняется равенcтво:
1/С=1/С1+1/С2+..+1/Сn.
Формула достаточно громоздка, но если последовательная цепь состоит из двух элементов, соотношение приводится к виду С= С1* С2/( С1+ С2).

Последовательное соединение на практике обычно применяется не для снижения общей ёмкости, а для уменьшения напряжения на каждом элементе при использовании конденсаторов в высоковольтных цепях.
Разобравшись с факторами, влияющими на ёмкость конденсатора и способами изменения этого параметра, можно научиться анализировать не только пассивные, но и активные (содержащие полупроводниковые приборы) цепи. Это позволит сделать шаг на пути к развитию навыков и повышению квалификации специалиста.
