Электроемкость сферического конденсатора

.

концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов будет выглядеть так:
.
Подставим данное выражение в формулу электроемкости конденсатора и получим емкость конденсатора для сферического тела:

При малой величине зазора, то есть , а следовательно можно считать, что
емкость сферического конденсатора будет равна
. Площадь сферы S = 4πr2 следовательно формула будет совпадать с формулой емкости плоского конденсатора
.
Формулы:
Энергия конденсатора: .
Ёмкость конденсатора: 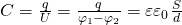
Ёмкость цилиндрического конденсатора: .
Ёмкость плоского конденсатора: 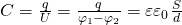
Обозначения в формулах:
C — электрическая ёмкость (ёмкость конденсатора);
g — заряд;
U — потенциал проводника (напряжение);
φ — потенциал;
ε — относительная диэлектрическая проницаемость;
— электрическая постоянная;
S — площадь одной обкладки;
d — расстояние между обкладками;
r2— Больший радиус (от центра, до края конденсатора);
r1 — Малый радиус (Его может и не быть — это пустота).
вернутся в раздел: электрическая ёмкость
Конденсатор – радиоэлектронный прибор, способный накапливать и отдавать заряд. Как правило, на его корпусе дается информация о его емкости, но иногда требуется самому рассчитать этот номинал.
Конденсаторами могут выступать и проводники, они также обладают определенной емкостью. Для расчета существует несколько формул емкости конденсатора, их и рассмотрим.
В чем измеряется емкость конденсатора
Что такое заряд еще проходят в школе, когда эбонитовую палочку натирают о шерстяную ткань и подносят к маленьким кусочкам бумаги.
Под действием электромагнитных сил бумага прилипает к палочке. Подобный заряд накапливается в конденсаторе. Но для начала познакомимся с самим конденсатором.
Простейшим конденсатором являются две металлические пластины, разделенные диэлектриком. От качества диэлектрика зависит, как долго энергия заряженного конденсатора может сохраняться.
На этих пластинах, они еще называются обкладками, накапливается разноименный заряд. Как это происходит?
Электрический заряд, а в случае с металлами это электроны, способен перемещаться под действием электродвижущей силы (э. д. с.).
Подключая металлические пластинки к источнику тока, мы получаем замкнутую цепь, но разделенную диэлектриком. Электростатическое поле проходит этот диэлектрик, замыкая цепь, а электроны, дойдя до препятствия, останавливаются и скапливаются.
Полная статья на блоге “Электрик в доме”:
Получается, на одной обкладке наблюдается избыток электронов, и эта пластина имеет отрицательный знак, а на другой пластине электронов недостает настолько же, знак на этой обкладке, конечно же, будет положительным.
Вот теперь нужна для определения емкости конденсатора формула, определяющая, какой заряд способен разместится на конкретном конденсаторе.
В качестве единицы измерения в международной системе (СИ) емкость определяется в Фарадах.
Много это или мало – емкость в 1Ф? Чтобы конденсатор обладал емкостью в 1Ф, он должен содержать в себе заряд в 1К (кулон) и при этом напряжение между обкладками должно равняться 1 вольту.
Интересно. Что такое заряд в 1 кулон? Если два предмета, каждый из которых имеет заряд в один кулон разместить в вакууме на расстоянии один метр, то сила притяжения между ними будет равна силе притяжения землей тела массой в один миллион тонн.
Как и любая буквальная емкость один и тот же конденсатор может вмещать разное количество заряда.
Рассмотрим пример.
- В трехлитровую банку входит три литра воздуха. Его хватит для дыхания, допустим, на 3 минуты. Но если воздух закачать под каким-то давлением, то емкость так и останется три литра, однако дышать можно будет дольше. Так устроен акваланг для ныряльщиков. Получается, количество воздуха в банке зависит от давления, которое в ней создается. Точно так же есть некая зависимость между различными силами, влияющими на емкость.
Формула емкости плоского конденсатора
Прежде чем узнать, по какой формуле вычисляется емкость плоского конденсатора, рассмотрим формулу для одиночного проводника. Она имеет вид:
- где Q – заряд,
- φ – потенциал.
Как видно емкость конденсатора, формула которого здесь приведена, будет тем больше, чем больший заряд способен накапливаться на нем при незначительном потенциале. Чтобы легче это было понять, рассмотрим получившие широкое распространение плоские конденсаторы разных размеров.
Для получения качественного конденсатора важны любые мелочи:
- ровная поверхность каждой обкладки;
- обе пластинки по всей площади должны располагаться на одинаковом расстоянии;
- размеры обкладок должны быть строго идентичными;
- от качества диэлектрика, расположенного между пластинками, будет зависеть ток утечки;
- емкость напрямую зависит от расстояния между обкладками, чем оно меньше, тем больше емкость.
Теперь обратимся к плоскому конденсатору. Формула определения емкости конденсатора несколько отличается от приведенной выше:
- где S – площадь одной обкладки,
- εr – диэлектрическая проницаемость диэлектрика,
- ε0 – электрическая постоянная,
- d – расстояние между обкладками.
Электрическая постоянная выражается числом 8,854187817×10-12.
Внимание! Эта формула справедлива только тогда, когда расстояние между пластинами намного меньше их площади.
Попробуем разобраться с каждой переменной подробнее. Площадь измеряется в м2, точнее, приводится к этой величине. А вот проницаемость диэлектрика может обозначаться по-разному.
В России это εr (также означает относительная проницаемость), в англоязычной литературе встречается εa (также означает абсолютная проницаемость), а то может и вовсе использоваться без индекса, просто ε. О том, что здесь используется диэлектрическая проницаемость диэлектрика можно понять из контекста.
Дальше идет ε0. Это уже вычисленное значение, измеряемое в Ф/м. Последняя переменная – d. Измеренное расстояние также приводится к метру. Емкость конденсатора, формула которого сейчас рассматривается, показывает сильную зависимость от расстояния обкладок. Поэтому стараются это расстояние по возможности сокращать. Почему этот показатель так важен?
Идеальными условиями для получения наибольшей емкости – это отсутствие промежутка между обкладками, чего, конечно, добиться невозможно. Чем ближе находятся разноименные заряды, тем сильнее сила притяжения, но здесь возникает компромисс.
При уменьшении толщины диэлектрика, а именно он разделяет разноименные заряды, возникает вероятность его пробоя из-за разности потенциалов на обкладках. С другой стороны, как уже говорилось, при увеличении напряжения увеличивается количество зарядов. Вот и приходится выбирать между емкостью и рабочим напряжением конденсатора.
Есть другая формула для плоского переменного конденсатора:
Здесь диэлектрическая проницаемость обозначена буквой ε, π = 22/7 ≈ 3,142857142857143, d – толщина диэлектрика. Формула предназначена для конденсатора, состоящего из нескольких пластин.
Допустимая толщина диэлектрика d также зависит от εr, чем выше коэффициент, тем тоньше можно использовать диэлектрик, тем большую емкость будет иметь конденсатор. Это был самый сложный материал, дальше будет легче.
Формула емкости цилиндрического конденсатора
Теперь поговорим о том, как найти емкость конденсатора цилиндрической формы. К ним относятся конденсаторы, состоящие из двух металлических цилиндров, вставленных один в другой.
Для разделения между ними расположен диэлектрик. Формула емкости конденсатора выглядит следующим образом:
Здесь видим несколько новых переменных:
- l – высота цилиндра;
- R1 и R2 – радиус первого и второго (внешнего) цилиндров;
- ln – это не переменная, а математический символ натурального логарифма. На некоторых калькуляторах он имеется.
Всегда нужно помнить, что все величины должны приводиться к единой системе, в приведенной ниже таблице указаны международные системы единиц (СИ).
Из нее видно, что все расстояния нужно приводить к метру.
Еще стоит обращать внимание на качество диэлектрика. Если толщина диэлектрика влияет только на емкость конденсатора, то его качество затрагивает сохранность энергии. Другими словами, конденсатор с качественным диэлектриком будет иметь меньший саморазряд.
Определить качество можно по числу, стоящему возле вещества, чем оно больше, тем лучше качество. Сравнение производится по вакууму, значение которого равно единице.
Формула емкости сферического конденсатора
Последнее что осталось разобрать – формулу определения емкости конденсатора, состоящего из двух сфер. Причем одна сфера находится внутри другой. Формула имеет следующий вид:
Из приведенных переменных здесь все знакомо. Стоит обратить внимание лишь на сам конденсатор.
Кроме своей необычной формы у него есть свои особенности: внутри малой сферы никакого заряда нет, он образуется на внешней части малой сферы и внутренней части большого шара. Также заряд отсутствует и на внешней стороне внешней сферы.
Так же как и все другие конденсаторы, сферы разделены диэлектриком. Толщина и качество диэлектрика оказывают такое же влияние на емкость, как в случае с другими конденсаторами.
После того как были рассмотрены формулы, стоит испробовать их на практике. Рассмотрим, как найти емкость конденсатора каждого вида.
Примеры решения задач
Начнем с плоского конденсатора. Формула для этого вида:
Допустим, у нас есть следующие значения:
- в качестве диэлектрика возьмем слюду толщиной 0,02 мм, ε = 6;
- конденсатор квадратный со сторонами в 7 мм.
Определяем площадь пластин: 7×7 = 49 мм2.
Приводим к единой системе: 4,9×10-5 = 0,000049 м2. Толщина диэлектрика 0,02×10-5 = 0,00002 м. Электрическая постоянная 8,854187817×10-12.
Подставляем в формулу и высчитываем числитель: 6×8,854187817×10-12 ×4,9×10-5, сокращаем и решаем 6×49×8,854187817×10-17 = 2,603131218198×10-14.
Делим на толщину диэлектрика: 2,603131218198×10 / 2×10 = 1301,565609099×10 = 1,301565609099×10. Шесть нулей – это тысячи или приставка «микро», получается округлено 1,3 мкФ.
Возможно, при вычислении была допущена ошибка, но это не экзамен по математике. Важно понять сам метод вычисления.
Формула для цилиндрического конденсатора:
Выбираем значения:
- l = 1 см;
- R1 = 0,25 мм;
- R2 = 0,26 мм;
- ε = 2.
Подгоняем под единую систему: l – 1 см = 1×10-2 = 0,01 м; R1 – 0,25 мм = 0,0025 м; R2 – 0,26 мм = 0,0026 м.
Подставляем значения в числитель: 2×3,142857142857143×8,854187817×10-12×2×0,01 1,11×10-12. Находим знаменатель: 0,26:0,25 = 1,04.
Находим натуральный логарифм, он равен примерно 0,39. Числитель делим на знаменатель: 1,11×10-12/0,39 = 2,85×10-12.
Число с 12 нулями это приставка «пико», получаем 2,85 пФ.
Формула для сферического конденсатора:
Выбираем значения:
- ε= 4;
- r1= 5 см;
- r2= 5,01 см.
Снова все подгоняем: 5 см = 0,05 м; 5,01 см = 0,0501 м. Заполняем числитель. 4×3,142857142857143×4×8,854187817×10-12×0,05×0,0501 1,11×10-12 Вычисляем знаменатель: 0,0501 – 0,05 = 0,01. Производим деление: 1,11×10-12×0,01 = 1,11×10-10. Снова получили пикофарады, а именно 1,11 пФ.
Интересные статьи на канале:
Статья заинтересовала? Лайк, подписка, комментарий!
Друзья ПОДПИСЫВАЙТЕСЬ Дзен на канал, а также заходите на блог https://electricvdome.ru 👍!
#конденсатор #емкость #формула
Электроемкость сферического конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд.
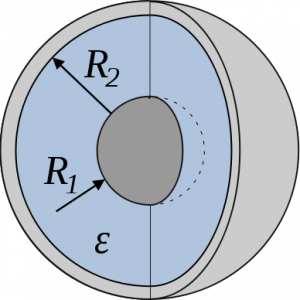
Чтобы найти емкость сферического конденсатора, который состоит из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов будет выглядеть так:
Подставим данное выражение в формулу электроемкости конденсатора и получим емкость конденсатора для сферического тела:
При малой величине зазора, то есть , а следовательно можно считать, что
емкость сферического конденсатора будет равна
. Площадь сферы
следовательно формула будет совпадать с формулой емкости плоского конденсатора
Так же есть:
Энергия конденсатора:
Ёмкость конденсатора :
Ёмкость цилиндрического конденсатора :
Емкость плоского конденсатора : ;
В Формуле мы использовали :
— Электроемкость сферического конденсатора
— Относительная диэлектрическая проницаемость
— Электрическая постоянная
— Больший радиус (от центра, до края конденсатора)
— Малый радиус (Его может и не быть — это пустота)
Ёмкость плоского конденсатора.
Плоский конденсатор состоит из двух
параллельных пластин, разделённых
небольшим зазором шириной
,
заполненным однородным диэлектриком.
Нам известно, что поле между двумя
разноимённо заряженными пластинами с
одинаковой по величине поверхностной
плотностью
равно
,
где,S– площадь каждой пластины.
Напряжение между обкладками:
.
Используя определение емкости
конденсатора, получаем:
Отметим, что полученная формула является
приближенной, так как выведена без учета
искажения поля у краев пластин. Расчет
по этой формуле дает завышенное значение
ёмкости и тем точнее, чем меньше зазор
по сравнению с линейными размерами
пластин.
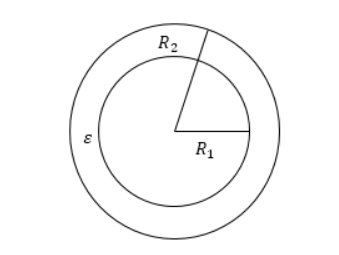
Ёмкость сферического конденсатора.
С
конденсатор представляет собой систему
двух концентрических сфер с радиусами
и.
Электрическое поле между обкладками
сферического конденсатора согласно
теореме Гаусса определяется зарядом
внутренней сферы. Напряжение между
обкладками равно:
.
Для ёмкости сферического конденсатора
получаем:
.
Это формула точная.
Если
,
полученная формула переходит в выражение
для ёмкости плоского конденсатора.
Ёмкость цилиндрического
конденсатора.
Цилиндрический конденсатор составляет
систему двух коаксиальных цилиндров с
радиусами
и
,
длиной.
Рассуждая аналогично выводу ёмкости
сферического конденсатора, получаем:
.

Полученная формула является приближенной
и при малом зазоре
переходит в формулу емкости плоского
конденсатора.
Соединение конденсаторов.
В практике для получения необходимых
значений емкости используют соединения
конденсаторов: а) последовательное, б)
параллельное, в) смешанное (см. рисунок).
Ёмкость последовательного
соединения конденсаторов.
Заряды последовательно соединенных
конденсаторов равны
,
а напряжение на батарее.
Из определения емкости следует:
или

Если
,
то(ёмкость последовательного соединения
меньше наименьшей ёмкости в последовательном
соединении).
Для
последовательно соединенных конденсаторов
емкость вычисляется по формуле:
.
В случае одинаковых конденсаторов:
.
Ёмкость параллельного
соединения конденсаторов.
Заряд батареи равен сумме зарядов:
,
а напряжение
.
По определению емкости получаем:
.
Для
параллельно соединенных конденсаторов:
.
В случае одинаковых конденсаторов:
.
Пример.
О
емкость батареи (см. рисунок).
.
Ответ:.
Используя свойство бесконечности можно
представить цепь в виде соединения (см.
рисунок).
Д
расчета ёмкости батареи получаем:
,
.
Откуда:
,
так как,
то.
Лекция 7.
Диэлектрики в электрическом
поле.
Диэлектриками (изоляторами) называют
вещества, не проводящие постоянного
электрического тока. Это означает, что
в диэлектриках отсутствуют «свободные»
заряды, способные перемещаться на
значительные расстояния.
Диэлектрики состоят либо из нейтральных
молекул, либо из ионов, находящихся в
узлах кристаллической решетки. Сами же
молекулы могут быть полярнымиинеполярными.Полярные молекулы
обладают дипольным моментом, у неполярных
молекул дипольный момент равен нулю.
Поляризация.
В электрическом поле диэлектрики
поляризуются. Это явление связано с
появлением в объеме и на поверхности
диэлектрика «связанных» зарядов.
При этом конечный объем диэлектрика
приобретает дипольный момент. Механизм
поляризации связан с конкретным строением
диэлектрика. Если диэлектрик состоит
из неполярных молекул, то в пределах
каждой молекулы происходит смещение
зарядов – положительных по полю,
отрицательных против поля, т.е. молекулы,
приобретают дипольный момент. У
диэлектрика с полярными молекулами в
отсутствии внешнего электрического
поля их дипольные моменты ориентированы
хаотично.
П
действием электрического поля диполи
ориентируются преимущественно в
направлении поля. Рассмотрим подробнее
этот механизм (см. рисунок). Пара сили
создает
вращательный момент равный,
где–
дипольный момент молекулы. Этот момент
стремится ориентировать диполь вдоль
поля. В ионных кристаллах под действием
электрического поля все положительные
ионы смещаются по полю, отрицательные
– против поля. Отметим, что смещение
зарядов очень малы даже по сравнению с
размерами молекул. Это связано с тем,
что напряженность внешнего электрического
поля обычно много меньше напряженности
внутренних электрических полей в
молекулах.
Отметим, что существуют диэлектрики,
поляризованные даже при отсутствии
внешнего поля (электреты, сегнетоэлектрики).
Мы остановимся на рассмотрении только
однородных диэлектриков, в которых
отсутствует остаточная поляризация, а
объемный и «связанный» заряд всегда
равен нулю
.
Соседние файлы в папке Физика2
- #
- #
- #
- #
- #
- #
Конденсатор – это совокупность двух любых проводников, заряды которых одинаковы по значению и противоположны по знаку.
Его конфигурация говорит о том, что поле, созданное зарядами, локализовано между обкладками. Тогда можно записать формулу электроемкости конденсатора:
C=qφ1-φ2=qU.
Значением φ1-φ2=U обозначают разность потенциалов, называемую напряжением, то есть U. По определению емкость положительна. Она зависит только от размерностей обкладок конденсатора их взаиморасположения и диэлектрика. Ее форма и место должны минимизировать воздействие внешнего поля на внутреннее. Силовые линии конденсатора начинаются на проводнике с положительным зарядом, а заканчиваются с отрицательным. Конденсатор может являться проводником, помещенным в полость, окруженным замкнутой оболочкой.
Выделяют три большие группы: плоские, сферические, цилиндрические. Чтобы найти емкость, необходимо обратиться к определению напряжения конденсатора с известными значениями зарядов на обкладках.
Плоский конденсатор
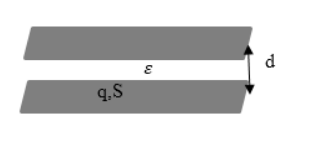
Плоский конденсатор – это две противоположно заряженные пластины, которые разделены тонким слоем диэлектрика, как показано на рисунке 1.
Формула для расчета электроемкости записывается как
C=εε0Sd, где S является площадью обкладки, d – расстоянием между ними, ε – диэлектрической проницаемостью вещества. Меньшее значение d способствует большему совпадению расчетной емкости конденсатора с реальной.
Рисунок 1
При известной электроемкости конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равняется di, вычисление диэлектрической проницаемости этого слоя εi выполняется, исходя из формулы:
C=ε0Sd1ε1+d2ε2+…+dNεN.
Сферический конденсатор
Когда проводник имеет форму шара или сферы, тогда внешняя замкнутая оболочка является концентрической сферой, это означает, что конденсатор сферический.
Он состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком, как показано на рисунке 2. Емкость рассчитывается по формуле:
C=4πεε0R1R2R2-R1, где R1 и R2 являются радиусами обкладок.
Рисунок 2
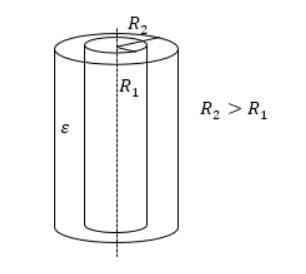
Цилиндрический конденсатор
Емкость цилиндрического конденсатора равняется:
C=2πεε0llnR2R1, где l – высота цилиндров, R1 и R2 – радиусы обкладок. Данный вид конденсатора имеет две соосные поверхности проводящих цилиндрических поверхности, как показано на рисунке 3.
Рисунок 3
Важной характеристикой конденсаторов считается пробивное напряжение – напряжение, при котором происходит электрический разряд через слой диэлектрика.
Umax находится от зависимости от толщины слоя и свойств диэлектрика, конфигурации конденсатора.
Электроемкость плоского конденсатора. Формулы
Кроме отдельных конденсаторов используются их соединения. Наличие параллельного соединения конденсаторов применяют для увеличения его емкости. Тогда поиск результирующей емкости соединения сводится к записи суммы Ci, где Ci- это емкость конденсатора с номером i:
C=∑i=1NCi.
При последовательном соединении конденсаторов суммарная емкость соединения всегда будет по значению меньше, чем минимальная любого конденсатора, входящего в систему. Для расчета результирующей емкости следует сложить величины, обратные к емкостям отдельных конденсаторов:
Произвести вычисление емкости плоского конденсатора при известной площади обкладок
1 см2 с расстоянием между ними 1 мм. Пространство между обкладками находится в вакууме.
Решение
Чтобы рассчитать электроемкость конденсатора, применяется формула:
C=εε0Sd.
Значения:
ε=1, ε0=8,85·10-12 Фм;S=1 см2=10-4 м2;d=1 мм=10-3 м.
Подставим числовые выражения и вычислим:
C=8,85·10-12·10-410-3=8,85·10-13 (Ф).
Ответ: C≈0,9 пФ.
Найти напряженность электростатического поля у сферического конденсатора на расстоянии x=1 см=10-2 м от поверхности внутренней обкладки при внутреннем радиусе обкладки, равном R1=1 см=10-2 м, внешнем – R2=3 см=3·10-2 м. Значение напряжения – 103 В.
Решение
Производящая заряженная сфера создает напряженность поля. Его значение вычисляется по формуле:
E=14πεε0qr2, где q обозначают заряд внутренней сферы, r=R1+x – расстояние от центра сферы.
Нахождение заряда предполагает применение определения емкости конденсатора С:
q=CU.
Для сферического конденсатора предусмотрена формула вида
C=4πεε0R1R2R2-R1 с радиусами обкладок R1 и R2.
Производим подстановку выражений для получения искомой напряженности:
E=14πεε0U(x+R1)24πεε0R1R2R2-R1=U(x+R1)2R1R2R2-R1.
Данные представлены в системе СИ, поэтому достаточно заменить буквы числовыми выражениями:
E=103(1+1)2·10-4·10-2·3·10-23·10-2-10-2=3·10-18·10-6=3,45·104 Вм.
Ответ: E=3,45·104 Вм.