Как найти емкость земного шара

Для школьников.

Тело человека является проводником. Как и для любого проводника, для него характерно следующее:

• избыточные заряды распределяются по поверхности тела;
• максимальная плотность заряда находится на “остриях” (см. Электрометр) – на пальцах рук. На практике наблюдаем проскакивание искры именно между пальцем и наэлектризованным предметом;

• поверхность тела человека является эквипотенциальной поверхностью, то есть в любой точке тела человека потенциал одинаков (хотя плотность заряда в разных точках на поверхности тела различна), именно поэтому мы не ощущаем электрическое поле Земли;

• внутри тела человека электрическое поле отсутствует (напряжённость поля равна нулю);
• тело человека обладает электроёмкостью.

Точное значение электроёмкости тела человека найти невозможно, но можно найти примерное её значение (порядок величины).

Воспользовавшись формулой плотности

можем найти объём тела человека.

Пусть масса человека равна 70 кг.

Средняя плотность тела человека равна 1070 кг/м3.

Разделив массу на плотность, найдём объём тела человека

– он равен 0,07 м3.

Сведём объём тела человека к объёму шара

Приравняв объём шара к 0,07 м3, получим радиус шара – он равен примерно 0,26 м.

Ёмкость этого шара (примерную ёмкость тела человека) найдём по формуле

Таким образом, электроёмкость тела человека составляет примерно 3,3 пФ.

По этой же формуле найдём электроёмкость Земли. Радиус Земли равен 6400 км. Электрическая постоянная равна

Получается, что электроёмкость Земли равна 711 мкФ.

К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.

Предыдущая запись: Что означает понятие “электрическая ёмкость“?

Следующая запись: Что произойдёт, если два шара разной ёмкости, заряженных до разных потенциалов, соединить тонкой проволокой?

Ссылки на занятия до электростатики даны в Занятии 1.

Ссылки на занятия (начиная с электростатики) даны в Занятии 45.

С увеличением размеров тела возрастает и его электрическая ем­кость.

Если тело имеет
форму шара, то оказывается, что сто электрическая
емкость зависит только от радиуса: во сколько раз радиус од­ного шара больше радиуса второго шара, во столько
же раз первого шара больше емкости
второго шара.

Та Снаиример, шар,
радиусом 0,5 м, обладает электрнчеекоа ем­костью в 50 см, так как радиус этбф
шара равен 50 см.

Следует заметить., что «сантиметр емкости является абсолютной единицей емкости.

Существуют еще другие практические единицы для измерена электрической
емкости:- 1 микрофарада ==|Ш
000 см.                                                                         .

1 фарада =г 1 000 000 микрофарад.

Фарада представляет
весьма большую единицу, что видно что емкость
земного шара равна только 707 микрофарадам, т. в.. 0,000707 фарады.¹

Шар, обладающий
ёмкость» в 1 фараду, должен был бы иметь ра­диус в 9″миллионов километров.

Подобно тому как емкость всякого сосуда указывает на то количе­ство жидкости,
которое можно налить в этот сосуд, электрическая ем­кость тела указывает
на его способность воспринять электрический заряд, т. е. на то количество электричества,
которое можно иметь на поверхности данного тела.

Однако количество жидкости, налитой в сосуд, зависит еще от уровня, до
которого жидкость налита. Подобно этому количество электричества, находящееся на заряженном теле, зависит от
электрического уровня, т. е. от
электрического потенциала (напряжения) тела.

Чем больше
электрическая емкость тела и чем выше напряжение (потенциал) заряда, тем больше будет количество электричества на этом теле.

Бели обозначить
буквами: а — количество электричества (эл. заряд), С
— электрическую емкость тела, , V—электрический потенциал (напряжение), то можно написать следующую
Формулу:

В этой
формуле qдолжно быть выражено в кулонах, емкость С
— в фарадах, а напряжение У—в вольтах.²

Теперь становится понятным, почему такую большую единицу, как фарада, приняли, за
единицу, так как отношение числа вольт к числу кулонов равно числу фарад:,

Однако в практической жизни пользуются не фарадами, а болоо удобными для применения единицами —
микрофарадами.

Пример 2.
Имеется шар, радиусом 1,5 м, заряженный до электрического потенциала. 10000
вольт. Определить количество электричества на этом шаре.

, См. пример 3 на следующей
странице.

Веди же в формуле,
связывающей количество электричества д с емкостью С и напряжением У, выразить количество
электричества в абсолютных единицах, а емкость С — в сантиметрах,
то не следует забывать, что в этом случае яапряжс-

ние У должно
быть выражено в абсолютных единицах.

ЭЛЕКТРИЧЕСКАЯ ИНДУКЦИЯ

Решение.
Емкость шара равна числу
сантиметра* радиусу а потому,

Количество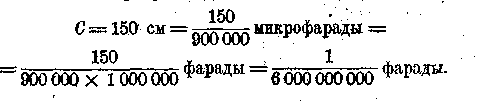электричества:

Пример3. Найти емкость земного шара.

Решение. Известно,
что 1 метр равен одной десятимиллионной части чет­верти меридиана.
Следовательно, 1 м меньше окружности земного шара (меридиана) в 40 миллионов
раз; отсюда следует, что длина окружности земного шара равна 40 миллионам
Метров:

откуда радиус земного шара равен:

Емкость земного шара равна числу сантиметров его радиуса, а потому: или

§ 10.
Электрическая индукция.

Произведем любопытный опыт: возьмем шар А и наэлектризуем его, допустим, положительным электричеством
(рис. 24)’. Возьмем еще другой шар В, который перед опытом не был заряжен;
оказывается, что шар В, находясь от
шара А на некотором расстоянии, сам электризуется, причем на одной стороне шара В, обращенной к заряженному шару, получается
или, как говорят, индуктируется отрицательное
электричество, а на противоположной стороне — положительное электричество. При этом шар А, возбуждая, или индуктируя, электричество на шаре В, сам нисколько не теряет своего собственного
заряда. Следовательно, электричество на
шаре В возникло под влиянием шара А; такое явление называется электрический
индукцией, или электризацией”* через
влияние._;                                                                .

Итак, явление электрической индукции состоит в том, что под влия­нием заряженного
тела на приближенном к нему другом проводящем толп одновременно индуктируются оба
рода электричества: электриче­ство, разноименное с заряженным телом,
притягивается на сторону, ближайшую к заряженному телу, а одноименное
электричество отталкивается заряженным телом в противоположную сторону.

Если
удалить шар В от шара А, то положительное электричество • на шаре
В снова соединится с отрицательным; они друг друга уничтожат, и на шаре В не будет
обнаруживаться никакого присутствия электрического
заряда.

Другая картина получится, если мы, приблизив шар В к заряжен­ному шару А, дотронемся
до него рукой или вообще соединим его с землей (рис. 25). При этом только часть электричества на теле В
уйдет в землю; это электричество
называется свободным электричеством. Другая же часть, называемая связанным электричеством, в землю
уйти не может, так как будет притягиваться зарядом тела А. Уничто­жим теперь соединение с землей и удалим шар В от
шара А; тогда шар В останется
наэлектризованным отрицательным электричеством, так как ему не с чем соединиться.

Совершенно подобная картина получилась бы, если бы шар А был
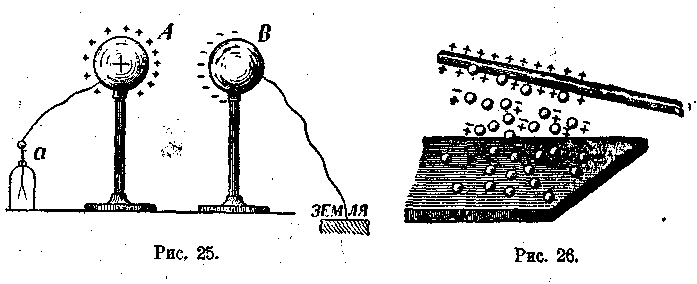
заряжен отрицательным электричеством; в этом случае на поверхности шара В также появилось бы два рода
электричества: связано — по­ложительное и свободное — отрицательное
электричество.: При соединении шара В
с землей свободное отрицательное электричество уйдет в землю, а связанное положительное электричество
останется на поверх­ности шара В.

Явлением электрической индукции можно объяснить причину при­тяжения
наэлектризованными телами различных легких предметов. Дей­ствительно, возьмем
стеклянную палочку, наэлектризованную положи­тельным электричеством (рис. 26), и приблизим к шарикам,
сделан­ным из пробил. Под влиянием
электрической индукции в каждом, ша­рике
возникнут два рода электричества: отрицательное и положитель­ное. Отрицательный заряд будет притягиваться к
палочке, а положи­тельный
будет от нее отталкиваться, но притяжение окажется сильнее отталкивания, так как отрицательный заряд
расположен к наэлектри­зованной палочке ближе, чем положительный.

Содержание книги

Предыдующая страница

§16. Превращение энергии в электрических и магнитных явлениях

В многочисленных электротехнических устройствах происходят постоянные переходы энергии из одной формы в другую. В данном параграфе мы рассмотрим некоторые примеры таких превращений и покажем, что во многих случаях эти переходы связаны с преобразованиями электрических и магнитных полей. Начнем обсуждение этих проблем с устройств, способных накапливать электрический заряд, сохранять его и создаваемое ими электрическое поле в течение длительного промежутка времени.

16.1 Электроемкость.

16.1.1 Электроемкость уединенного проводника.

Любое тело способно накапливать электрический заряд. На первый взгляд, кажется, что любому телу можно сообщить сколь угодно большой заряд. Однако существует ряд причин, которые ограничивают величину максимального заряда. С ростом электрического заряда возрастает напряженность поля, создаваемого телом. Если тело находится в воздухе или другой среде, то может начаться электрический разряд, посредством которого заряд начнет стекать с тела. Даже если рассматриваемое тело находится в вакууме, то электростатическое взаимодействие заряженных частиц внутри вещества приведет к испусканию, эмиссии частиц (чаще всего электронов), что тоже приведет к уменьшению заряда тела. Поэтому необходимо ввести некоторую характеристику тела, описывающую его возможность накапливать электрический заряд. Такой характеристикой является электроемкость тела C : отношение заряда тела к его потенциалу

(~C = frac{Q}{varphi}) . (1)

В этом определении необходимо оговорить, относительно какой точки определяется потенциал. Как правило, для уединенного тела его потенциал отсчитывается относительно бесконечности. Можно дать и несколько иное определение, свободное от указанной неопределенности значения потенциала: электроемкость тела равна заряду, который необходимо сообщить телу, чтобы увеличить его потенциал на единицу

(~C = frac{Delta Q}{Delta varphi}) . (2)

Вспомним другую «емкость»: теплоемкость тела равна количеству теплоты, которое необходимо сообщить телу, чтобы увеличить его температуру на один градус (~C = frac{Delta Q}{Delta t^circ}). Как видите, определение электроемкости полностью аналогично.

Можно дать аналогичное определение емкости сосуда: объем жидкости, который необходимо влить в сосуд, чтобы увеличит высоту его уровня на единицу, то придется признать, что емкость цилиндрического сосуда равна площади его дна (~C = frac{Delta V}{Delta h}). В этом примере аналогом электрического заряда является объем жидкости, налитой в сосуд, аналогом изменения потенциала – изменение уровня жидкости.

Электроемкость является размерной физической величиной. В системе единиц СИ единицей электроемкости является фарад^[1] (сокращенно Ф). Емкостью в 1 фарад обладает тело, потенциал которого возрастает на 1 вольт при увеличении его заряда на 1 кулон. Один фарад очень большая емкость, поэтому чаще используются дольные единицы: микрофарад (мкФ, 1 мкФ = 10^-6 Ф), нанофарад (нФ, 1 нФ = 10^-9 Ф), пикофарад (пФ, 1 пФ = 10^-12 Ф).

Для расчета электроемкости следует задать электрический заряд тела и рассчитать его потенциал, после чего вычислить их отношение. Так потенциал тела всегда пропорционален его заряду, то емкость тела не зависит от его заряда, а полностью определяется его размерами, формой и диэлектрическими свойствами среды, в которой находится тело.

Для примера найдем электрическую емкость уединенного шара радиуса R, находящегося в вакууме. Если заряд шара равен Q, то его потенциал (относительно бесконечности) равен

(~varphi = frac{Q}{4 pi varepsilon_0 R}) .

Следовательно, электрическая емкость шара равна

(~C = frac{Q}{varphi} = 4 pi varepsilon_0 R) . (3)

Так электрическая емкость земного шара (R ≈ 6350 км) равна С ≈ 7·10^-4 Ф – действительно 1 фарад очень большая емкость.

Если поместить шар в бесконечную среду из однородного диэлектрика с проницаемостью ε, то напряженность поля уменьшится в ε раз, потенциал шара также уменьшится, поэтому его емкость возрастет в ε раз:

(~C = 4 pi varepsilon_0 varepsilon R) . (4)

16.1.2 Конденсаторы.

Мы показали, что уединенные тела малопригодны как накопители электрического заряда. Еще в середине XVIII века было изобретено устройство, способное накапливать и длительное время сохранять большие электрические заряды – конденсатор.

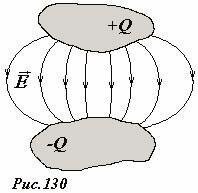
Конденсатор представляет собой два проводника (которые называются обкладками), разделенными диэлектриком (Рис. 130). Как правило, на обкладки подают разноименные электрические заряды, равные по величине. В этом случае электрическое поле практически полностью локализуется в пространстве между обкладками. Емкостью конденсатора называется отношение заряда одной из обкладок к разности потенциалов между обкладками

(~C = frac{Delta Q}{Delta varphi}) . (5)

В этом определении фигурирует разность потенциалов, которая не зависит от выбора нулевого уровня потенциала, поэтому нет необходимости в дополнительных оговорках. Часто зарядом конденсатора называют заряд одной из его обкладок (ясно, что полный заряд конденсатора на двух обкладках равен нулю), вместо разности потенциалов между обкладками чаще говорят о напряжении конденсатора U, которое, конечно, равно разности потенциалов U = Δϕ, так в пространстве между обкладками не действуют сторонние силы.

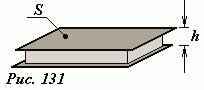
Простейший конденсатор состоит из двух проводящих параллельных пластин, разделенных слоем диэлектрика, причем расстояние между пластинами значительно меньше их размеров – такой конденсатор называется плоским (Рис. 131). Найдем емкость такого конденсатора. Будем считать, что на обкладки конденсатора (проводящие пластины) поданы разноименные электрические заряды, модули которых равны Q. Если площадь каждой пластины равна S , то поверхностная плотность заряда на них равна (~sigma = frac{Q}{S}). Эти заряды создают в пространстве между пластинами электрическое поле напряженности (~E = frac{sigma}{varepsilon varepsilon_0} = frac{Q}{varepsilon varepsilon_0 S}), где ε – диэлектрическая проницаемость вещества между пластинами. Разность потенциалов между обкладками конденсатора равна (~Delta varphi = Eh = frac{Qh}{varepsilon varepsilon_0 S}). По определению емкость плоского конденсатора рассчитывается по формуле

(~C = frac{Q}{Delta varphi} = frac{varepsilon varepsilon_0 S}{h}) . (6)

Таким образом, емкость конденсатора пропорциональна проницаемости диэлектрика, площади пластин и обратно пропорциональна расстоянию между ними. Если расстояние между пластинами сделать малым, а площади пластин большими, то такой конденсатор может иметь большую емкость (даже превосходящую емкость земного шара).

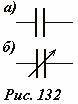
Конденсаторы широко используются не только для накопления электрического заряда, но и в цепях переменного электрического тока (эти вопросы мы рассмотрим позднее). На электрических схемах конденсаторы изображаются в виде двух параллельных отрезков (Рис. 132).

Промышленностью выпускаются конденсаторы различных типов, которые различаются своей конструкцией. Емкости промышленно выпускаемых конденсаторов изменяются в широких пределах от нескольких пикофарад, до единиц фарад. Часто пластины таких конденсаторов изготавливают из тонкой металлической фольги, которую скручивают в рулоны и помещают в корпус. В качестве диэлектрика используется воздух (в этом случае с высокой точностью можно считать ε = 1), слюда, сухая бумага, и другие материалы.

Большой электрической емкостью обладают электролитические конденсаторы. Одной обкладкой такого конденсатора служит тонкая полоска фольги большой площади, покрытая слоем окисла (который играет роль диэлектрика), второй обкладкой является раствор электролита. Так как толщина оксидного слоя может быть малой (порядка нескольких микрон), то емкость такого конденсатора весьма велика. При использовании таких конденсаторов следует внимательно следить за полярностью их включения в электрическую цепь, так как при ошибочном подключении оксидный слой быстро разрушается, что приводит к выходу конденсатора из строя.

Широко используются также конденсаторы переменной емкости, в котором наборы пластин могут двигаться друг относительно друга, при этом изменяется площадь их перекрытия, вследствие чего изменяется и емкость конденсатора. На схемах переменные конденсаторы отмечаются стрелкой (Рис. 132б).

16.1.3 Соединение конденсаторов.

Установим правила для расчета электроемкости системы конденсаторов, подобно правилам расчета сопротивлений соединенных резисторов.

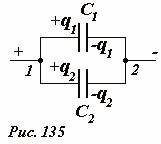
При параллельном соединении конденсаторов (Рис. 135) емкости которых равны C₁ и C₂ напряжения на обоих конденсаторах одинаковы и равны разности потенциалов между точками соединения U₁ = U₂ = Δϕ, что является следствием потенциальности электростатического поля. Суммарный заряд конденсатора равен сумме зарядов конденсаторов q = q₁ + q₂.

По определению емкость такого составного конденсатора равна отношению его суммарного заряда к напряжению, следовательно,

(~C = frac{q_1 + q_2}{U} = frac{q_1}{U} + frac{q_2}{U} = C_1 + C_2) . (1)

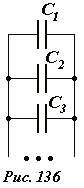
Это правило легко обобщается: общая емкость системы параллельно соединенных конденсаторов (Рис. 136) равна сумме емкостей всех конденсаторов

(~C_o = C_1 + C_2 + C_3 + ldots = sum_k C_k) . (2)

В частном случае плоских конденсаторов с одинаковыми расстояниями между пластинами установленное правило утверждает, что суммарная площадь пластин равна сумме площадей отдельных обкладок

(~S_o = S_1 + S_2 + S_3 + ldots) .

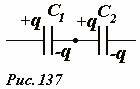
При последовательном соединении конденсаторов (Рис. 137) суммарное напряжение на батарее конденсаторов равно сумме напряжений на отдельных конденсаторах

(~U_o = U_1 + U_2) . (3)

Электрические заряды на всех конденсаторах одинаковы

(~q_o = q_1 = q_2) .

Для доказательства этого утверждения достаточно рассмотреть две соединенных внутренних обкладки, которые изолированы от внешних источников – их суммарный заряд остается равным нулю. Поэтому если на обкладке первого конденсатора индуцируется заряд − q, то на соединенной с ней обкладке второго конденсатора возникнет такой же по модулю заряд противоположного знака.

Выразим напряжения на конденсаторах через их заряды и емкости (~U = frac{q}{C}) и подставим их в уравнение (3)

(~frac{q_o}{C_o} = frac{q_1}{C_1} + frac{q_2}{C_2}) ,

принимая во внимание равенство всех зарядов, получим правило расчета емкости последовательно соединенных конденсаторов (Рис. 138):

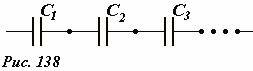
величина обратная емкости батареи последовательно соединенных конденсаторов равна сумме величин, обратных емкости каждого конденсатора,

(~frac{1}{C_o} = frac{1}{C_1} + frac{1}{C_2} + frac{1}{C_3} + ldots = sum_k frac{1}{C_k}) . (4)

Для плоских конденсаторов с одинаковыми площадями пластин это правило утверждает, что суммарное расстояние между пластинами равно сумме этих расстояний всех конденсаторов.

Интересно отметить, что правила расчетов емкости батареи конденсаторов противоположны правилам расчета сопротивлений соединений резисторов: при последовательном соединении складываются сопротивления; при параллельном – складываются величины обратные сопротивлениям (проводимости), а для конденсаторов наоборот: при параллельном соединении складываются емкости, а при последовательном – складываются обратные величины.

Примечания

1. ↑ Названа в честь выдающегося английского физика Майкла Фарадея.

Следующая страница