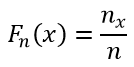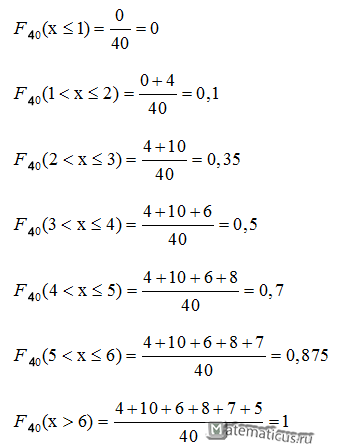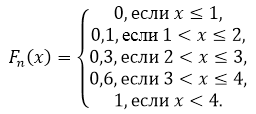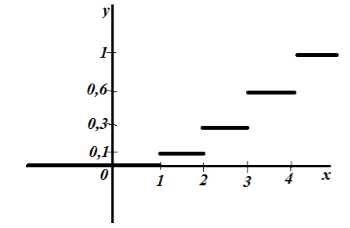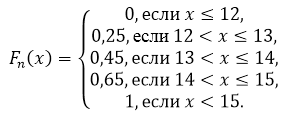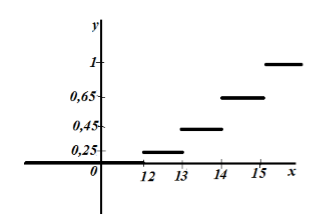Выборочная функция распределения
Калькулятор строит график выборочной (эмпирической) функции распределения по заданной выборке случайной величины
Выборочная функция распределения
Значения случайной величины
| Значение измерения | ||
|---|---|---|
Точность вычисления
Знаков после запятой: 2
Выборочная функция распределения
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Этот калькулятор использует следующие справочники
- Вспомогательный для построения гистограмм
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Функция распределения дискретной случайной величины
- • Логнормальное распределение
- • Биномиальное распределение. Функция плотности вероятности, кумулятивная функция распределения, математическое ожидание и дисперсия
- • Генератор нормально распределенных случайных чисел
- • Нормальное распределение
- • Раздел: Статистика ( 32 калькуляторов )
PLANETCALC, Выборочная функция распределения
Skip to content
Эмпирической (опытной) функцией распределения или функцией распределения выборки называют такую функцию, которая определяет для каждого значения x частоту событий X<x и предназначена для оценке теоретической функции распределения генеральной совокупности в математической статистике.
Эмпирическая функция распределения находится по формуле:
n — объем выборки;
nx — количество наблюдений (вариантов) меньше x.
Пример
Дана таблица функции распределения выборки. Требуется построить эмпирическую функцию распределения
| xi | 1 | 2 | 3 | 4 | 5 | 6 |
| ni | 4 | 10 | 6 | 8 | 7 | 5 |
Решение
Из таблицы n=40, т.е.
n=4+10+6+8+7+5=40
Вычислим функцию распределения выборки
Эмпирическая функция распределения имеет вид
Построим график кусочно-постоянной эмпирической функции распределения
таким образом, по данным выборки можно приближенно построить функцию для неизвестной функции выборки.
72286
Эмпирическая функция распределения
Содержание:
- Что называют эмпирической функции распределения
- Свойства функции
- Как найти
- Как построить график
- Примеры задач
Что называют эмпирической функции распределения
Допустим, известно статистическое распределение частот количественного признака Х. Обозначим nх – количество наблюдений со значением меньше x1, n – всего наблюдений. Очевидно, что относительная частота события Х<x будет равна nх/n.
Определение
Эмпирическая функция распределения – это функция F*(x), которая определяет для каждого значения x относительную частоту события X
Данное понятие можно записать в виде формулы:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(Fast(x)=frac{n_x}n)
В этой записи nx – количество вариантов, меньших x; n – объем выборочной совокупности.
Существует также теоретическая функция распределения (функция распределения генеральной совокупности). Ее отличие от выборочной функции распределения состоит в определении объективной возможности или вероятности события X<x.
Свойства функции
Функция распределения выборки обладает рядом свойств, которые следуют из определения понятия.
- Значения рассматриваемой функции F*(x) располагаются на отрезке [0; 1].
- Функция имеет неубывающий характер.
- При минимальной варианте x1 верно равенство F*(x)=0 при условии, что х<х1. При максимальной варианте хk верно равенство F*(x)=1 при условии х>xk.
Таким образом, функция распределения выборки помогает оценить теоретическую функцию распределения.
Как найти
Выборочная функция распределения для случайной величины рассчитывается по формуле:
(F(x)=P(xi<x))
Данное равенство читается так: функция распределения равна вероятности события, при котором случайная величина будем меньше x.
Поскольку при условии, что x меньше или равно 1, событие ξ20<1 невозможно (ξ20 не принимает значение менее 1, вероятность невозможного события равна 0), верно следующее выражение:
(F(x)=P(xi20<1)=0)
При принадлежности x отрезку (1; 2] событие ξ20<2 представляет собой равенство ξ20=1, значит, вероятность этого события равно 0,1. В записи это выглядит так:
(F(x)=P(xi20<2)=0,1)
Когда x принадлежит отрезку (2; 4], событие ξ20<4 состоит в равенстве ξ20 значению 1 или 2, то есть вероятность рассматриваемого события равна 0,1+0,2=0,3 или:
(F(x)=P(xi20<4)=0,3)
Если 4 < x ≤ 5, то событие ξ20<5 означает, что ξ20 принимает значение либо 1, либо 2, либо 4. Следовательно, вероятность данного события вычисляется так: 0,1+0,2+0,35=0,65, то есть:
(F(x)=P(xi20<5)=0,65)
При 5 < x ≤ 6 событие ξ20<6 заключается в том, что ξ20 принимает значение 1, 2, 4 или 5. Значит его вероятность равно 0,1+0,2+0,35+0,1=0,75 или:
(F(x)=P(xi20<6)=0,75)
И так далее.
Итак, эмпирическая функция распределения имеет следующий вид:
Как построить график
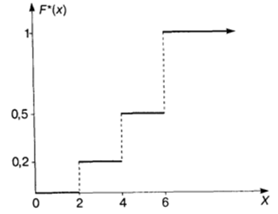
Построение графика эмпирической функции распределения возможно после вычисления ее значений на всей числовой оси. Для рассмотренного примера схематическое изображение будет выглядеть так:
График ступенчатого вида, построенный на отрезках. Совпадение графика с горизонтальной осью означает, что левее минимального значения x=1 функция приобретает значение нуля. Увеличение в каждой следующей точке xi происходит на величину вероятности νi. Правее максимального значения х8=13 функция равна 1. Стрелки и точки на концах отрезков указывают на определение функции на полуинтервалах.
Примеры задач
Задача
В таблице даны значения эмпирического распределения:
Необходимо найти объем выборочной совокупности, составить выборочную функцию распределения, построить ее график.
Решение
- Вычислим объем выборки: n=5+10+15+20=50.
- Из свойства эмпирической функции распределения: Fn(x)=0 при x≤1, Fn(x)=1 при x>4.
Выходит, что:
По полученным значениям построим график:
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение эмпирической функции распределения
Пусть $X$ — случайная величина. $F(x)$ – функция распределения данной случайной величины. Будем проводить в одних и тех же независимых друг от друга условий $n$ опытов над данной случайной величиной. При этом получим последовательность значений $x_1, x_2 $, … ,$ x_n$, которая и называется выборкой.
Определение 1
Каждое значение $x_i$ ($i=1,2 $, … ,$ n$) называется вариантой.
Определение 2
Функция распределения $F(x)$ генеральной совокупности называется теоретической функцией распределения.
Одной из оценок теоретической функции распределения является эмпирическая функция распределения.
Определение 3
Эмпирической функцией распределения $F_n(x)$ называется функция, которая определяет для каждого значения $x$ относительную частоту события $X
[F_nleft(xright)=frac{n_x}{n}]
где $n_x$ – число вариант, меньших $x$, $n$ — объем выборки.
Отличие эмпирической функции от теоретической состоит том, что теоретическая функция определяет вероятность события $X
Свойства эмпирической функции распределения
Рассмотрим теперь несколько основных свойств функции распределения.
-
Область значений функции $F_nleft(xright)$ — отрезок $[0,1]$.
-
$F_nleft(xright)$ неубывающая функция.
-
$F_nleft(xright)$ непрерывная слева функция.
-
$F_nleft(xright)$ кусочно-постоянная функция и возрастает только в точках значений случайной величины $X$
-
Пусть $X_1$ — наименьшая, а $X_n$ — наибольшая варианта. Тогда $F_nleft(xright)=0$ при ${xle X}_1$и $F_nleft(xright)=1$ при $xge X_n$.
«Эмпирическая функция распределения» 👇
Введем теорему, которая связывает между собой теоретическую и эмпирическую функции.
Пусть $F_nleft(xright)$ — эмпирическая функция распределения, а $Fleft(xright)$ — теоретическая функция распределения генеральной выборки. Тогда выполняется равенство:
[{mathop{lim}_{nto infty } {|F}_nleft(xright)-Fleft(xright)|=0 }]
Примеры задач на нахождение эмпирической функции распределения
Пример 1
Пусть распределение выборки имеет следующие данные, записанные с помощью таблицы:
Рисунок 1.
Найти объем выборки, составить эмпирическую функцию распределения и построить её график.
Решение:
Объем выборки: $n=5+10+15+20=50$.
По свойству 5, имеем, что при $xle 1$ $F_nleft(xright)=0$, а при $x>4$ $F_nleft(xright)=1$.
Значение $x
Значение $x
Значение $x
Таким образом, получаем:
Рисунок 2.
Построим график эмпирического распределения:
Рисунок 3.
Пример 2
Из городов центральной части России случайным образом выбрано 20 городов, для которых получены следующие данные по стоимости проезда в общественном транспорте: 14, 15, 12, 12, 13, 15, 15, 13, 15, 12, 15, 14, 15, 13, 13, 12, 12, 15, 14, 14.
Составить эмпирическую функцию распределения данной выборки и построить её график.
Решение:
Запишем значения выборки в порядке возрастания и посчитаем частоту каждого значения. Получаем следующую таблицу:
Рисунок 4.
Объем выборки: $n=20$.
По свойству 5, имеем, что при $xle 12$ $F_nleft(xright)=0$, а при $x>15$ $F_nleft(xright)=1$.
Значение $x
Значение $x
Значение $x
Таким образом, получаем:
Рисунок 5.
Построим график эмпирического распределения:
Рисунок 6.
Оригинальность: $92,12%$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Содержание:
- Формулы и свойства эмпирической функции распределения
- Примеры расчёта с таблицей и графиком
При рассмотрении различных разделов теории вероятности непрерывно встречается такое понятие как функция распределения. Она может быть задана для разных типов случайных величин. Через её посредство задаются также и все ключевые параметры случайных величин, такие как матожидание, дисперсия среднеквадратическое отклонение и другие.
Чаще всего, при решении примеров и задач функция распределения является теоретической, а при работе в рамках матстатистики, в общем случае — неизвестной. Однако, на практике с помощью имеющейся выборки, можно создать выражение, которое будет максимально приближено к виду неизвестной функции распределения.
Чтобы определить вид такого, приближенного, выражения, вводится представление об эмпирической функции распределения (выборки). Она позволяет структурировать статистические данные, выявить необходимые закономерности, определить все нужные характеристики случайной величины.
Формулы и свойства эмпирической функции распределения
Определение 1
Для существующей выборки $x=(x_1, x_2,…x_n)$ и ряда частот, каждая из которых соответствует каждому элементу выборки, существует такая функция $F^*(x)$, которая и определяет конкретное значение частоты события для любого из компонентов выборки.
Используемая формула, для вычисления эмпирической функции распределения
$F^*(x)=frac {n_x}{n}=sum_{x_i<x}^{}p_i$
Здесь $n_x$ — количество наблюдений (вариантов) меньше x, n – размер выборки, х – произвольное значение величин.
Либо более общая, но абсолютно идентичная запись:
$F_n^*(t)=frac {|i:x_ileq t|}{n}$
Термин «эмпирическая», употреблённый в определении значит, что функция определяется по результатам опыта (эмпирического опыта), то есть, по набору значений, составленных из итогов испытаний — по выборке. Именно из-за такого принципа формирования используемых данных также применимо и другое наименование — «выборочная функция распределения».
Из определения становится ясно, что в точках рассматриваемая функция будет зависеть от значений выборки, поэтому уточненное и более точное её обозначение могло бы иметь вид: $F^*_n(t;x_1…x_n)$. Тогда в данном виде параметр t будет являться основным, а другие представляют собой фиксированные величины. Иной подход позволяет представить значения выборки x в виде независимых, а также одинаковым образом распределяемых случайных величин, для которых определена функция распределения — F. Исходя из такой интерпретации, $F^*_n(t)$ является случайной величиной. Получаем, что в пределе $nrightarrowinfty$ функция распределения выборки обладает свойством равномерной сходимости к своему теоретическому значению:
$P(sup_{t in R}|F^*_n(t)-F(t)|rightarrow 0)=1$
Данный факт представляет собой общую закономерность, которая, в свою очередь, носит наименование теорема Гливенко.
Свойство 1
Одно из свойств функции $F^*(x)$ заключается в том, что все её значения лежат в пределах интервала [0;1].
Свойство 2
$F^*(x)$- неубывающая функция.
Не трудно уловить закономерность, заключающуюся в том, что функция $F_n^*(t)$ представляет собой кусочно-постоянную, а также неубывающую и непрерывную справа функцию. В том случае, если $x_i$ различные, тогда для каждой точке $x_i$ функция получает скачок величины своего значения. В случае, когда $frac {1}{n}$ из $x_i$ совпадают, скачки будут складываться.
Свойство 3
Если $х_1$ – наименьшая варианта, то $F^*(x)=0 при x leq x1$.
Свойство 4
Если $х_k$ – наибольшая варианта, то $F^*(x)=1 при x > x_k$.
Примеры расчёта с таблицей и графиком
Пример 1
Пусть существует таблица, с помощью которой задана функция распределения выборки. Необходимо произвести вычисления и установить каков графический вид эмпирической функции распределения
| Xi | 2 | 3 | 4 | 5 | 6 | |
| Ni | 4 | 10 | 6 | 8 | 7 | 5 |
Решение
Из таблицы n=40, т.е. n=4+10+6+8+7+5=40
Вычислим функцию распределения выборки
$F_{40}(xleq1)=frac{0}{40}=0$
$F_{40}(1< xleq2)=frac{0+4}{40}=0.1$
$F_{40}(2< xleq3)=frac{4+10}{40}=0,35$
$F_{40}(3< xleq4)=frac{4+10+6}{40}=0,5$
$F_{40}(4< xleq5)=frac{4+10+6+8}{40}=0,7$
$F_{40}(5< xleq6)=frac{4+10+6+8+7}{40}=0,875$
$F_{40}(x>6)=frac{4+10+6+8+7+5}{40}=1$
Для эмпирической функции распределения $F_n(x)$ можно записать её значения в интервалах:
0, если $ xleq1$,
0,1, если $ 1< xleq2$,
0,35, если $ 2< xleq3$,
0,5, если $ 3< xleq4$,
0,7, если $ 4< xleq5$,
0,875, если $ 5< xleq6$,
1, если $ x>6$.
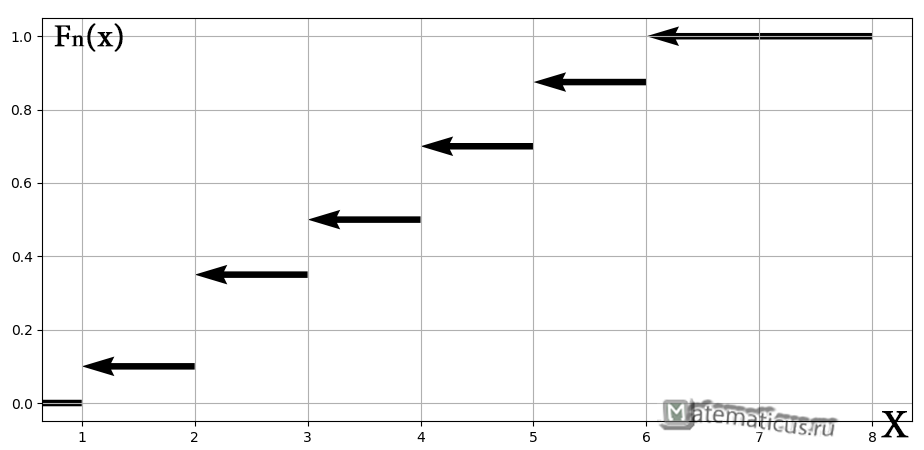
Изобразим на графике внешний вид кусочно-постоянной эмпирической функции распределения
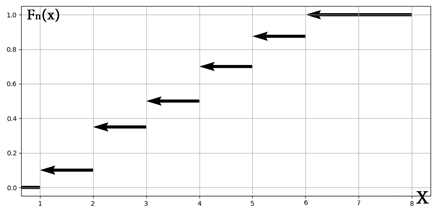

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример 2
Требуется нарисовать график для эмпирической функции, если известно распределение выборки.
Решение
Рассчитаем размер выборки: n = 10 + 15 + 25 = 50. Значение самой маленькой варианты составляет 2. Тогда имеем F*(X) = 0 при Х ≤ 2. При этом случай Х < 4 (или X1 = 2) наблюдался 10 раз, значит, F*(X) = 10/50 = 0,2 при 2 < Х < 4. Значения X < 6 (а именно X1 = 2 и X2 = 4) наблюдались 10 + 15 = 25 раз, значит, при 4 < Х < 6 функция F*(X) = 25/50 = 0,5. Поскольку X = 6 — максимальная варианта, то F*(X) = 1 при Х > 6. Далее выведем формулу той самой эмпирической функции, которую требуется найти.
График этой функции показан на следующем рисунке: