Сергей Сергеевич Соев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Используя формулу Планка для спектральной плотности энергии ($w_{nu }$), которая имеет вид:
где $beta =frac{1}{kT}$, k — постоянная Больцмана, $hbar =1,05{cdot 10}^{-34}Джcdot с,$ с=$3{cdot 10}^8frac{м}{с}cdot $- скорость света в вакууме можно рассчитать полную плотность энергии излучения (w), если взять интеграл от плотности энергии ${(w}_{nu })$ по всем частотам излучения ($0
[w=intlimits^{infty }_0{w_{nu }}dnu =frac{hbar }{{pi }^2c^3}intlimits^{infty }_0{frac{{nu }^3dnu }{{exp left(frac{hbar nu }{kT}right) }-1}}=frac{hbar }{{pi }^2c^3}{left(frac{kT}{hbar }right)}^4intlimits^{infty }_0{frac{{xi }^3dxi }{{exp left(xi right) }-1} left(2right),}]
где мы произвели замену переменных в подынтегральном выражении, а именно заменили:
Интеграл $intlimits^{infty }_0{frac{{xi }^3dxi }{{exp left(xi right) }-1}=frac{{pi }^4}{15},}$ подставим в выражение (2), получим:
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
где коэффициент, стоящий перед температурой в четвертой степени ($T^4$) можно вычислить:
Интегральная энергетическая светимость
Гораздо чаще вместо полной плотности энергии равновесного излучения пользуются понятием интегральной энергетической светимости абсолютно черного тела (интегральной излучательной способности абсолютно черного тела) (${varepsilon }_T$). Интегральная энергетическая светимость характеризует плотность потока излучения с поверхности по всем направлениям (пространственный угол $2pi $). Объемная плотность энергии абсолютно черного тела или полная плотность энергии равновесного излучения одинакова во всех точках и зависит только от температуры. С плотностью интегральная излучательная способность абсолютно черного тела связана формулой:
Следовательно, из формул (4) и (5), получаем:
Уравнение Стефана-Больцмана
[{varepsilon }_T=sigma T^4left(6right),]
где $ sigma =frac{ccdot a}{4}=7,6•{10}^{-16}frac{3•{10}^8}{4}=5,7{cdot 10}^{-8}(Втcdot м^{-2}cdot К^{-4})$- постоянная Стефана — Больцмана. Более точное значение постоянной равно $sigma =5,67{cdot 10}^{-8}Втcdot м^{-2}cdot К^{-4}$. А уравнение (6) называется уравнением Стефана — Больцмана.
«Закон Стефана-Больцмана» 👇
Закон Стефана – Больцмана для серого тела
Для серого тела закон Стефана — Больцмана можно записать следующим образом:
[{varepsilon }_s=alpha sigma T^4left(7right),]
где ${varepsilon }_s$ — энергетическая светимость серого тела, $alpha $- коэффициент теплового излучения (степень черноты) серого тела.
Давление, которое производит черное излучение на стенки полости, выразится следующим образом:
[p=frac{w}{3}=frac{4}{3c}sigma T^4left(8right).]
Спектральная плотность объемной плотности энергии поля черного тела излучения имеет вид:
[w_{nu }=frac{dw}{dnu }=frac{4}{c}{varepsilon }_{nu ,T }left(9right),]
где $dw$- объемная плотность энергии поля излучения в интервале частот от $nu до nu +dnu $, ${varepsilon }_{nu ,T }$– излучательная способность абсолютно черного тела.
Пример 1
Задание: Поток энергии, который излучается из смотрового окошка плавильной печи, равен Ф. Найдите температуру в печи, если площадь отверстия S.
Решение:
Будем считать, что плавильная печь является эквивалентной модели абсолютно черного тела.
За основу решения задачи примем формулу, которая определяет поток энергии через отверстие печи:
[Ф={varepsilon }_{T }Sleft(1.1right),]
где ${varepsilon }_{T }$- излучательная способность абсолютно черного тела, и она может быть найдена по закону Стефана — Больцмана:
[{varepsilon }_{T }=sigma T^4 left(1.2right),]
где $sigma$- постоянная Стефана – Больцмана.
Подставим (1.2) в (1.1), получим:
[Ф=sigma T^4Sto T^4=frac{sigma S}{Ф}to T=sqrt[4]{frac{sigma S}{Ф}}left(1.3right),]
Ответ: Температура в плавильной печи может быть рассчитана по формуле: $T=sqrt[4]{frac{sigma S}{Ф}}.$
Пример 2
Задание: Во сколько раз необходимо увеличить термодинамическую температуру абсолютно черного тела, чтобы его энергетическая светимость возросла в n раз?
Решение:
За основу решение примем закон Стефана — Больцмана:
[{varepsilon }_{T }=sigma T^4 left(2.1right).]
Запишем его дважды для состояния (1) с температурой $T_1$ и энергетической светимостью ${varepsilon }_{T 1}$, получим выражение:
[{varepsilon }_{T1 }=sigma {T_1}^4 left(2.2right).]
Для состояния (2) с температурой $T_2$ и энергетической светимостью ${varepsilon }_{T 2}$, получим выражение:
[{varepsilon }_{T2 }=sigma {T_2}^4 left(2.3right).]
Найдем отношение выражений (2.3) и (2.2), учитывая, что по условию задачи $frac{{varepsilon }_{T2 }}{{varepsilon }_{T1 }}=n$, получим:
[frac{{varepsilon }_{T2 }}{{varepsilon }_{T1 }}=frac{sigma {T_2}^4}{sigma {T_1}^4}=frac{{T_2}^4}{{T_1}^4}=n left(2.4right).]
Из (2.4) следует, что
[frac{T_2}{T_1}=sqrt[4]{n} left(2.5right).]
Ответ: Полученное равенство (2.5) означает, что термодинамическую температуру абсолютно черного тела необходимо увеличить в $sqrt[4]{n}$ раз, чтобы его энергетическая светимость возросла в n раз.
Пример 3
Задание: Энергетическая светимость серого тела при температуре T равна ${varepsilon }_s$. Определите коэффициент теплового излучения данного тела.
Решение:
В качестве основы для решения примем закон Стефана — Больцмана для серого тела:
[{varepsilon }_s=alpha sigma T^4left(3.1right).]
Из этого закона выразим коэффициент $alpha ,$ так как именно он является коэффициент теплового излучения тела в условиях задачи:
[alpha =frac{е_s}{sigma T^4}.]
Ответ: Коэффициент теплового излучения тела равен $alpha =frac{{varepsilon }_s}{sigma T^4}.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Энергетическая
светимость тела
RТ,
численно равна энергии W, излучаемой
телом во всем диапазоне длин волн (0<<)
с единицы поверхности тела, в единицу
времени, при температуре тела Т,
т.е.
(1)
Испускательная
способность тела
r,Т
численно равна энергии тела dW,
излучаемой телом c единицы поверхности
тела, за единицу времени при температуре
тела Т, в диапазоне длин волн от
до +d,
т.е.
(2)
Эту
величину называют также спектральной
плотностью энергетической светимости
тела.
Энергетическая
светимость связана с испускательной
способностью формулой
(3)
Поглощательная
способность
тела ,T
– число, показывающее, какая доля энергии
излучения, падающего на поверхность
тела, поглощается им в диапазоне длин
волн от
до +d,
т.е.
.
(4)
Тело,
для которого ,T
= 1
во всем диапазоне длин волн, называется
абсолютно
черным телом (АЧТ).
Тело,
для которого ,T=const<1
во всем
диапазоне длин волн называют серым.
7.3. Закон Кирхгофа
Отношение
испускательной способности тела r,Т
к его
поглощательной способности
,T
не зависит
от природы тела и является для всех тел
универсальной функцией длины волны и
температуры, равной испускательной
способности АЧТ, т.е.
.
(5)
Отсюда
следует, что тело, которое сильнее
поглощает какие-либо лучи, будет сильнее
эти лучи и испускать.
7.4. Распределение энергии в спектре абсолютно черного тела

черных тел в природе не существует. Его
функции может выполнять малое отверстие
в почти замкнутой полости (см. рис. 1).
Излучение, прошедшее внутрь этого
отверстия, прежде чем выйти обратно из
отверстия претерпевает многократные
отражения и практически полностью
поглощается. Поэтому поглощательная
способность для него,T
= 1
и по закону
Кирхгофа (5) испускательная способность
r,Т
такого
устройства очень близка к испускательной
способности АЧТ
.
Таким образом,
если стенки полости поддерживать при
некоторой температуре Т, то из отверстия
выйдет излучение, весьма близкое к
излучению AЧТ.
Разлагая полученное
излучение в спектр с помощью дифракционной
решетки и измеряя интенсивность разных
участков спектра, можно найти
экспериментально вид функции
от
(рис. 2).
Площадь, охватываемая кривой, дает
энергетическую светимость АЧТ [см.
формулу (3)]. Из рис. 2 следует, что
энергетическая светимость АЧТ сильно
возрастает с ростом температуры, а длина
волны, соответствующая максимуму
испускательной способности АЧТ, с ростом
температуры сдвигается в сторону более
коротких волн.
7.5. Закон Стефана-Больцмана
Энергетическая
светимость АЧТ пропорциональна четвертой
степени термодинамической температуры
,
(6)
где =5.6710-8
Вт/(м2К4)
– постоянная Стефана-Больцмана.
7.6. Закон смещения Вина
Длина
волны, соответствующая максимальному
значению испускательной способности
АЧТ, с ростом температуры смещается в
сторону меньших длин волн:
, (7)
где b=2.910-3
мК
– постоянная Вина.
Соседние файлы в папке Методичка Беланов А.С.
- #
- #
- #
- #
Закономерности теплового излучения: Учебно-методическое обеспечение практического занятия
Страницы работы
Содержание работы
5. основы квантовой физики
5.1. закономерности
Теплового излучения (4 часа)
5.1.1. Учебная цель занятия
Научить студентов применять следующие понятия и законы:
Тепловое излучение. Закон Кирхгофа. Модель абсолютно черного тела. Закон Стефана-Больцмана.
Закон смещения Вина.
5.1.2. Методические указания к проведению
занятия
При решении задач по данному разделу подчеркнуть, что тепловое излучение
это электромагнитное излучение, испускаемое телами за счет их внутренней
энергии и отметить, что только тепловое излучение может находиться в равновесии
с излучающими телами. Остановиться на таких понятиях как поток (мощность)
излучения, энергетическая светимость, интегральный коэффициент черноты и
абсолютно черное тело.
При использовании для решения задач законов Стефана-Больцмана, смещения
Вина, важно подчеркнуть согласие классической теории с опытом в области малых
частот и катастрофическое расхождение в области больших частот, что позволяет
привести гипотезу Планка о том, что электромагнитное излучение испускается в
виде отдельных порций энергии (квантов) пропорциональных частоте излучения.
5.1.3. Рекомендуемая литература
[4] , Т.4, гл. 1, [8] стр. 4-8.
5.1.4. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1. Энергетическая светимость абсолютно
черного тела . Найти температуру поверхности
этого тела.
|
Дано: |
Решение |
|
|
В соответствии с законом Стефана–Больцмана энергетическая |
,
где – постоянная Стефана–Больцмана;
– термодинамическая температура.
Из этой формулы получаем выражение для искомой величины:
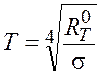
Подставив значения величин, найдем
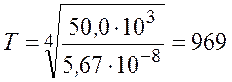
Ответ: = 969 К.
Пример 2. Энергетическая светимость серого тела
составляет ; интегральный коэффициент черноты 0,345.
Найти температуру поверхности этого тела.
|
Дано: |
Решение |
|
|
Энергетическая светимость |
,
где – интегральный коэффициент
черноты; – постоянная Стефана–Больцмана;
– термодинамическая температура.
Из этой формулы получаем выражение для искомой величины:
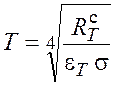
Подставив значения величин, найдем
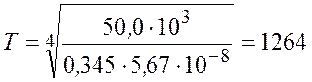
Ответ: К.
Пример 3. Энергетическая светимость абсолютно
черного тела . Найти длину волны, на которую
приходится максимум испускательной способности этого тела.
|
Дано: |
Решение |
|
|
В соответствии с законом Стефана–Больцмана энергетическая |
, (3.1)
где – постоянная Стефана–Больцмана;
– термодинамическая температура.
Температура связана с длиной волны
, приходящейся на максимум испускательной
способности тела, законом смещения
Вина:
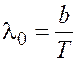
где – постоянная закона смещения
Вина.
Из формулы (3.2) с учетом (3.1) получаем выражение для
искомой величины:
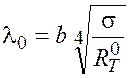
Подставив значения величин в формулу (3.3), найдем
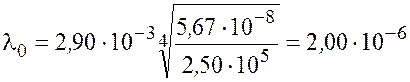
,00 мкм.
Ответ: мкм.
Пример 4. Пластина, площадь которой 15,0 , имеет температуру 500 К.
Интегральный коэффициент черноты пластины 0,368. Определить, какую энергию
теряет пластина за счет излучения в течение 2 мин.
|
Дано: |
Решение |
|
|
Энергия излучения связана с энергетической светимостью
где коэффициент 2 учитывает две стороны поверхности пластины |
Энергетическая светимость серого
тела выражается формулой
, (4.2)
где – интегральный коэффициент
черноты; – постоянная Стефана–Больцмана;
– термодинамическая температура.
Из выражений (4.1) и (4.2) получим формулу для энергии излучения:
. (4.3)
Подставив значения величин в формулу (4.3), найдем
Дж.
Ответ: Дж.
Пример 5. Найти мощность излучения с площади
15,0 абсолютно черного тела, которое имеет
температуру 1000 К.
|
Дано: |
Решение |
|
|
Мощность излучения, т. е. поток излучения, связана с
|
Энергетическая светимость абсолютно
черного тела выражается формулой
Похожие материалы
- Механические колебания: Учебно-методическое обеспечение практического занятия
- Электрическая емкость. Энергия электростатического поля: Учебно-методическое обеспечение практического занятия
- Законы постоянного тока. Правила Кирхгофа: Учебно-методическое обеспечение практического занятия
Информация о работе
Тип:
Методические указания и пособия
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
- IvanPetrov
- 24.10.202018.11.2021
Уважаемые пользователи сайта oldfiz! Вы можете помочь проекту, пожертвовав на продление домена:
Определите энергетическую светимость тела человека при температуре t=36 ͦ, принимая его за серое тело с коэффициентом поглощения α=0,9. // Ремизов А.Н., Максина А.Г. «Сборник задач по медицинской и биологической физике», 2001 г.


Список решённых на данный момент задач из сборника Ремизова находится тут
Испускание и поглощение
света. Тепловое излучение
Нагретые
тела начинают светиться. Чем выше температура тела, тем интенсивнее и богаче
становится спектральный состав излучения. С понижением температуры уменьшается
интенсивность излучения и изменяется его спектральный состав: в свечении
начинает преобладать красное излучение. При дальнейшем охлаждении свечение не
прекращается, тела испускают невидимые инфракрасное излучение. Электромагнитное
излучение за счет только внутренней энергии тела и зависящее только от
температуры называется тепловым излучением. Если в процессе излучения
внутренняя энергия тела, затрачиваемая на излучение, не восполняется,
температура тела понижается.
Тепловое
излучение является единственным излучением, способным находиться в равновесии с
излучающим веществом. Если в теплоизолированную полость с абсолютно отражающими
стенками поместить нагретое тело, то тело вначале охлаждается из-за потери
внутренней энергии на излучение. Одновременно тело начнет и поглощать энергию
из поля излучения и за счет поглощенной энергии нагреваться. Однако с
увеличением плотности энергии в поле излучения наступит такое состояние, когда
энергия, теряемая телом на излучение за данный промежуток времени, сравняется
с энергией, поглощаемой им за тот же промежуток времени. Между телом и полем
излучения наступит равновесие, подобное равновесию между жидкостью и ее
насыщенным паром в герметичном сосуде.
Поток
энергии, испускаемой единицей поверхности излучающего тела по всем
направлениям, называется энергетической
светимостью или интегральной интенсивностью R. Излучение состоит
из волн различных частот или длин волн и ее интенсивность не одинакова для всех
частот (или длин волн). Поэтому для характеристики спектрального состава
излучения вводится понятие испускательной
способности или спектральной
плотности, определяемой, как энергия, приходящаяся на единичный
интервал частот (или длин волн) в интервале частот (или
длин волн):
,
или (33)
Спектральной
характеристикой поглощения является коэффициент поглощения
или
,
(34)
определямый как энергия,
поглощаемая в единичном интервале частот (или длин волн), находящемся в
интервале частот (или длин волн
).
Тело,
которое поглощает все падающее на него электромагнитное излучение всех частот
(или длин волн) называвется абсолютно черным
телом. Коэффициент поглощения абсолютно черного тела равен единице.
Излучательная способность абсолютно черного тела зависит только от частоты (или
длины волны) и температуры.
Все реальные
черные тела не являются абсолютно черными. Однако некоторые из них в
определенных интервалах частот приближаются к абсолютно черному телу (сажа,
платиновая чернь, черный бархат). Наиболее хорошей моделью абсолютно черного
тела можно считать небольшое отверстие в замкнутой полости. Луч, попадая в
полость через отверстие, практически не выйдет из полости, полностью поглотится
при многократных отражениях от стенок полости (рис.39).
Рис.39
Испускательная
и поглощательная способности тел взаимосвязаны. Пусть в некоторой
теплоизолированной полости с абсолютно отражающими стенками находится несколько
различных тел с различными испускательными и поглощательными способностями
(рис.40).
Рис.40
Если начальные
температуры тел различны, то спустя некоторое время, благодаря обмену энергией
посредством излучения тела придут в тепловое равновесие как с полем излучения,
так и между собой. Температуры тел станут одинаковыми и неизменными во времени.
Тем не менее тела, у которых больше испускательная способность, охлаждаются
сильнее, испуская большее количество энергии за единицу времени. Однако
тепловое равновесие между телами не должно нарушаться. Для этого необходимо,
чтобы те тела, которые испускают больше энергии, должны ее больше и поглощать.
Другими словами, чем больше испускательная способность тел, тем больше их
поглощательная способность. Это условие может быть выражено математическим
соотношением
,
где индексы 1,2,…,n
относятся к разным телам. Это условие Кирхгоф сформулировал как закон: отношение испускательной способности и поглощательной
способности тел не зависит от природы тела, оно для всех тел одинаково и
является функцией частоты (или
длины волны) и температуры
.
(35)
Функцияназывается функцией Кирхгофа
Если среди перечисленных тел какое-либо
тело, например, второе является абсолютно черным, то. испускательная способность
этого тела станет равной функции Кирхгофа.
Значит, функция Кирхгофа это испускательная способность абсолютно черного тела.
Широко
используется понятие серого тела. Серым называется тело, коэффициент
поглощения которого одинаков для всех частот и зависит только от температуры,
материала и состояния поверхности. Энергетическая светимость серого тела
связана с энергетической светимостью абсолютно черного тела
,
где Rc,
Rч
– энергетические светимости серого и абсолютно черного тела, ас –коэффициент черноты.
Испускательная
способность абсолютно черного тела и объемная плотность энергии излучения связаны
соотношением
.
(36)
Законы теплового
излучения абсолютно черного тела
После
установления закона Кирхгофа перед теорией возникла задача найти явный вид
зависимости излучательной способности абсолютно черного тела от частоты и
температуры. Сначала удалось решить более скромную задачу.
Больцман
(1884), применив термодинамический метод показал, что установленный Стефаном
(1879) эмпирический закон справедлив только для абсолютно черного тела
(37)
где σ
– постоянная Стефана-Больцмана (σ =5,77·10-8
Вт/м2К4). Эта формула носит название закона
Стефана-Больцмана.
Эксперименты
показали, что зависимость излучательной способности абсолютно черного тела от
частоты при разных температурах имеет вид, показанный на рис.41.
Рис.41
Существование
максимума на кривых спектральной плотности свидетельствует. что энергия
излучения по спектру распределена неравномерно, черное тело излучает мало
энергии в области малых и больших частот. Площадь, охватываемая кривой
распределения энергии дает энергетическую светимость абсолютно черного тела R0
и эта площадь возрастает пропорционально Т4.
Значительно
трудной оказалось решение задачи по установлению явного вида функции Кирхгофа ,
описывающей кривые, представленные на рис. 41. Важный шаг в этом направлении
сделал Вин (1893), рассмотревший излучение абсолютно черного тела с
термодинамической точки зрения. Для функции Кирхгофа он получил выражение вида
.
(38)
Ему не удалось
выразить явный вид функции, зависящей от отношения частоты к абсолютной
температуре .
Тем не менее, из такой зависимости были получены важные выводы. Из (38) можно
вывести закон Стефана-Больцмана
,
где –
постоянный коэффициент,.
Из
формулы Вина следует, что частота, соответствующая максимуму кривой
спектральной плотности νm,
выражается формулой
,
(38)
где b1
– постоянная величина. Эту формулу называют законом смещения Вина: частота, соответствующая максимуму спектральной
плотности абсолютно черного тела, прямо пропорционально его абсолютной
температуре. Из этой формулы легко получить более известную формулу
,
(39)
где b
– постоянная Вина (b =2,898·10-3м·К).
Длина волны, соответствующая максимуму
спектральной плотности абсолютно черного тела, обратно пропорционально его
абсолютной температуре. Из формулы Вина можно получить выражение для
максимальной спектральной плотности
,
которая
показывает, что она пропорциональна пятой степени абсолютной температуры.
Максимум кривой с
температурой растет пропорционально Т5.
Дальнейший
поиск функции Кирхгофа осуществили
Релей и Джинс. В отличие от остальных исследователей для этого они применили
методы классической статистической физики. Они рассчитывали распределение
энергии электромагнитных волн по частотам в закрытой полости, в которой в
результате интерференции падающих на стенки полости и отраженных волн
образуются стоячие волны. Определяли число независимых пучностей волн и затем
применяли к ним закон о равномерном распределении энергии по степеням свободы.
В результате они получили формулу
.
(40)
Кривая
Релея и Джинса изображена на рис.42 линией 1.
Рис.
42
Видно,
что кривая Релея-Джинса 1 согласуется с данными опыта лишь в области малых
частот (длинных волн). В области больших частот она сильно расходится с
экспериментальной кривой 2, показывая свою непригодность для описания
излучательной способности абсолютно черного тела. Формула Релея и Джинса
расходилась с законами смещения Вина и Стефана-Больцмана. Она приводила к
абсурдному результату, что при любой температуре энергетическая светимость
обращается в бесконечность.
.
Все
эти затруднения, которые образно были названы «ультрафиолетовой катастрофой»
указывали на непригодность принципов классической физики для описания процесса
излучения атомов и на необходимость их пересмотра. Этот пересмотр был выполнен
М. Планком. В1900 г. Планк предложил рассматривать атомы как осциллирующие
диполи. Он показал, что правильное выражение для можно
получить лишь предположив, что излучение испускается атомами не непрерывно, как
полагает классическая физика, а в виде отдельных порций энергии ε1,
ε2,
ε3,….
Такая порция энергии пропорциональна частоте
,
где h
– универсальная постоянная по всему спектру, получившая название постоянной
Планка, в системе «СИ» она равна h
= 6,62·10-34 Дж·с.
Полученная
на этом основании формула Планка

(41)
очень точно
описывала экспериментальную кривую, изображенную на рис. 41. Заметим, что в
области малых частот формула Планка переходит в формулу Релея и Джинса.
Интегрирование формулы Планка по частоте приводит к выражению
.
Найденное
из этой формулы значение σ
= =5,77·10-8
Вт/м2К4 хорошо согласуется с экспериментальным значением.
Решение
задачи на экстремум функции распределения Планка приводит к закону Вина
T·lmax =
hc/4,965k =
b.
Найденная из этого
выражения постоянная Вина равна b=2,90·10-3м·К
и хорошо согласуется с результатом эксперимента.
Таким
образом, формула Планка дает исчерпывающее описание равновесного излучения
абсолютно черного тела. С этой формулы началось дальнейшее развитие квантовой
физики.






