Как найти энергию частицы через скорость

Как найти энергию частицы через скорость

О, это очень интересная формула.

Во-первых, сложно сказать, в какой системе подразумеваемая частица обретает релятивистскую энергию и импульс. В формуле присутствует скорость света, и скорость v. Но не уточняется – это любая движущаяся со скоростью v частица в нашей системе, или покоящаяся частица в какой-то другой системе, движущейся относительно нашей со скоростью v. А у покоящейся частицы, и нет никакого импульса.

Во-вторых, каждая частица вроде бы имеет внутреннюю энергию Е=mc^2, которая никак не зависит от движения частицы. «Достать» эту энергию можно только разрушив частицу. C другой стороны, эта энергия напрямую зависит от скорости движения частицы, согласно имеющейся формуле:

И.В. Савельев, "Курс общей физики", "Наука", 1982г
И.В. Савельев, “Курс общей физики”, “Наука”, 1982г

То есть, внутренних энергий – две. Покоя и релятивистская. Ну, тут намек на не подтвердившуюся растущую массу.

Если что, то импульсов вообще четыре:

Про выражение полной энергии частицы через импульс.

Классический импульс – это когда частица движется в нашей системе.

Релятивистский импульс – это когда частица движется.

«Внутренний» импульс – это такой инвариант у частицы в покое.

Внутренний релятивистский импульс – это такой неинвариант инварианта.

И смотрим уже на выражение полной энергии частицы через импульс.

И.В. Савельев, "Курс общей физики", "Наука", 1982г
И.В. Савельев, “Курс общей физики”, “Наука”, 1982г

И попробуем эту формулу немного преобразовать.

Про выражение полной энергии частицы через импульс.

Ничего не напоминает? Ну, да это теорема Пифагора. Три стороны представлены разнообразными импульсами в квадрате.

Про выражение полной энергии частицы через импульс.

И представляете, совершенно волшебным образом, из этого треугольника, если известна гипотенуза и один катет – можно найти второй катет!

И.В. Савельев, "Курс общей физики", "Наука", 1982г
И.В. Савельев, “Курс общей физики”, “Наука”, 1982г

Одно только непонятно, если эксперименты над быстрыми частицами, то есть, движущимися, подтверждают инвариантность величины (68.11), то откуда mc – релятивистская?

Источник

Мы уже ввели релятивистскую частицу и эффекты, связанные с релятивистским движением. Напомним, что прилагательное «релятивистское» обозначает движение тел с близкими к световой скоростями. Большинство соотношений в данной теме вывести достаточно сложно, поэтому просто верим.

Итак, введённый нами импульс (displaystyle p=mupsilon ) при условии релятивистской массы (displaystyle m=frac{{{m}_{0}}}{sqrt{1-frac{{{upsilon }^{2}}}{{{c}^{2}}}}}) может быть записан как:

displaystyle p=frac{{{m}_{0}}}{sqrt{1-frac{{{upsilon }^{2}}}{{{c}^{2}}}}}upsilon (1)

  • где

Немного о displaystyle {{m}_{0}} — массе неподвижного в данной системе тела, называемой массой покоя.

Великим Эйнштейном было получено уникальное соотношение, характеризующее полную энергию движущейся частицы:

displaystyle E=m{{c}^{2}} (2)

Логично предположить, что наименьшей энергией обладает тело, которое покоится в данной системе, назовём эту энергию энергией покоя:

displaystyle {{E}_{0}}={{m}_{0}}{{c}^{2}} (3)

Тогда кинетическая энергия движущегося тела может быть найдена как разность между полной энергией и энергией покоя:

displaystyle {{E}_{k}}=E-{{E}_{0}} (4)

Или:

displaystyle m{{c}^{2}}(1-sqrt{1-frac{{{upsilon }^{2}}}{{{c}^{2}}}})=frac{{{m}_{0}}{{c}^{2}}}{sqrt{1-frac{{{upsilon }^{2}}}{{{c}^{2}}}}}(1-sqrt{1-frac{{{upsilon }^{2}}}{{{c}^{2}}}})=displaystyle frac{{{m}_{0}}{{upsilon }^{2}}}{1+sqrt{1-frac{{{upsilon }^{2}}}{{{c}^{2}}}}}displaystyle frac{{{m}_{0}}{{upsilon }^{2}}}{1+sqrt{1-frac{{{upsilon }^{2}}}{{{c}^{2}}}}} (5)

При условии displaystyle frac{{{upsilon }^{2}}}{{{c}^{2}}}to 0 (скорость тела очень мала по сравнению со скоростью света) получим displaystyle {{E}_{k}}=frac{m{{upsilon }^{2}}}{2} (отношение скорости тела к скорости света стремиться к нулю), и соотношение (5) принимает вид displaystyle {{E}_{k}}=frac{m{{upsilon }^{2}}}{2} — т.е. вид кинетической энергии в классической механике.

Вывод: в случае релятивистской механики (скорость частицы велика) достаточно помнить, что энергетические характеристики тела выражаются через более сложные соотношения (1) — (5). С точки зрения энергии, главное понять по задаче, какую энергию нам необходимо найти — покоя, полную или кинетическую.

Источник

Если скорость релятивистской частицы меньше скорости света, то она называется массовой. Её собственная энергия, то есть энергия при (v=0):
(boxed{E_0=m_0cdot c^2}),  ((1))
где (m_0) — масса покоя частицы, (E_0) — энергия покоя частицы.
Масса движущейся релятивистской частицы:
(boxed{m=frac{m_0}{sqrt{1-frac{v^2}{c^2}}}}).  ((2))
Полная (релятивистская) энергия, или энергия свободной (невзаимодействующей) движущейся релятивистской частицы (сформулировал А. Эйнштейн):
(boxed{E=frac{m_0 c^2}{sqrt{1-frac{v^2}{c^2}}}}).  ((3))
Кинетическая энергия массовой частицы:
(boxed{E_k=E-E_0}).  ((4))
Импульс частицы:
(boxed{vec{p}=frac{m_0 vec{v}}{sqrt{1-frac{v^2}{c^2}}}}).  ((5))
Если скорость частицы равна скорости света, то такую частицу называют безмассовой (фотон и нейтрино). В таком случае энергия и импульс свободной частицы связаны соотношением:
(boxed{E^2-p^2c^2=0}).  ((6))
Таким образом, для всех свободных частиц в любой инерциальной системе можно записать:
(boxed{E^2-p^2c^2=m_0^2c^4}).  ((7))

Источник

Содержание:

  • Определение и формула кинетической энергии
  • Кинетическая энергия материальной точки и тела
  • Единицы измерения кинетической энергии
  • Теорема Кенига
  • Примеры решения задач

Определение и формула кинетической энергии

Определение

Кинетическую энергию тела определяют при помощи работы, которая совершается телом при его торможении от начальной скорости, до скорости, равной нулю.

Кинетическая энергия тела – мера механического движения тела. Она зависит от относительной скорости тел.

Встречаются следующие обозначения кинетической энергии: Ek,Wk,T.

Работу, которую производят над телом (A’) можно связать с изменением его кинетической энергии:

$$A^{prime}=E_{k 2}-E_{k 1}(1)$$

Кинетическая энергия материальной точки и тела

Кинетическая энергия материальной точки равна:

$$E_{k}=frac{m v^{2}}{2}=frac{p^{2}}{2 m}=frac{p v}{2}(2)$$

где m – масса материальной точки, p – импульс материальной точки, v – скорость ее движения. Кинетическая энергия является скалярной физической величиной.

Если тело нельзя принять за материальную точку, то его кинетическая энергия рассчитывается как сумма кинетических энергий всех материальных точек, которые составляют исследуемое тело:

$$E_{k}=frac{1}{2} int_{m} v^{2} d m=frac{1}{2} int_{m} rho v^{2} d V(3)$$

где dm – элементарный участок тела, который можно считать материальной точкой, dV – объем выделенного элементарного участка тела,
v – скорость перемещения рассматриваемого элемента, $rho$ – плотность участка, m–масса всего рассматриваемого тела, V – объем тела.

В том случае, если тело (отличное от материальной точки) движется поступательно, то его кинетическую энергию можно рассчитать, применяя формулу (2), в которой все параметры отнесены к телу в целом.

При вращении тело вокруг неподвижной оси его кинетическую энергию можно вычислить, применяя формулу:

$$E_{k}=frac{J omega^{2}}{2}=frac{omega^{2}}{2} int_{m} r^{2} d m=frac{L^{2}}{2 J}=frac{L omega}{2}(4)$$

где J – момент инерции тела по отношению к оси вращения, ?–модуль угловой скорости вращения тела,
r – расстояние от элементарного участка тела до оси вращения,
L – проекция момента импульса вращающегося тела на ось во круг которой идет вращение.

Если твердое тело совершает вращение относительно неподвижной точки (например, точки O), то его кинетическую энергию находят как:

$$E_{k}=frac{bar{L} bar{omega}}{2}(5)$$

$bar{L}$ – момент импульса рассматриваемого тела относительно точки О.

Единицы измерения кинетической энергии

Основной единицей измерения кинетической энергии (как и любого другого вида энергии) в системе СИ служит:

[Ek]=Дж (джоуль),

в системе СГС –[Ek]= эрг.

При этом: 1 дж= 107 эрг.

Теорема Кенига

Для самого общего случая при расчете кинетической энергии применяют теорему Кенига. В соответствии с которой,
кинетическая энергия совокупности материальных точек есть сумма кинетической энергии поступательного перемещения
системы со скоростью центра масс (vc) и кинетической энергии
(E’k) системы при ее относительном движении к поступательному перемещению системы отсчета.
При этом начало системы отсчета связывают с центром масс системы. Математически данную теорему можно записать как:

$$E_{k}=sum_{i=1}^{n} frac{m_{i} v_{i}^{2}}{2}=frac{m v_{c}^{2}}{2}+E_{k}^{prime}$$

где $mathrm{E}_{k}^{prime}=sum_{i=1}^{n} frac{m_{i} v_{i}^{prime 2}}{2}, v_{i}^{prime}=v_{i}-v_{c}, m=sum_{i=1}^{n} m_{i}$ –суммарная масса системы материальных точек.

Так, если рассматривать твердое тело, то его кинетическую энергию можно представить как:

$$E_{k}=frac{m v_{c}^{2}}{2}+frac{J_{c} omega^{2}}{2}(7)$$

где Jc – момент инерции тела по отношению к оси вращения, проходящей через центр масс. В частности, при плоском движении
Jc=const.В общем случае, ось (она называется мгновенной) перемещается в теле, тогда момент инерции является переменным во времени.

Примеры решения задач

Пример

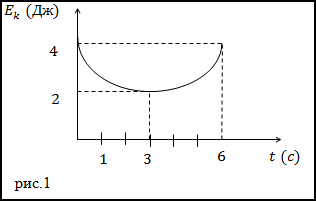
Задание. Какова работа, которая производится над телом за t=3 c (с начала отсчета времени),
при силовом взаимодействии, если изменение кинетической энергии исследуемого тела задано графиком (рис.1)?

Решение. По определению изменение кинетической энергии равно работе (A’),
которая производится над телом при силовом взаимодействии, то есть можно записать, что:

$$A^{prime}=Delta E_{k}(1.1)$$

Исследуя график, приведенный на рис.1 мы видим, что за время t=3 c кинетическая энергия тела изменяется от 4 Дж до 2 Дж, следовательно:

$A^{prime}=2-4=-2$ (Дж)

Ответ. A’=-2 Дж.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Материальная точка движется по окружности, радиус которой равен R. Кинетическая
энергия частицы связана c величиной пути (s), пройденного ей в соответствии с формулой:
$E_{k}=alpha s^{2}(alpha=$const$)$. Какое уравнение связывает силу (F), действующую на точку и путь s?

Решение. В качестве основы для решения задачи используем формулу, определяющую кинетическую энергию материальной точки:

$$E_{k}=frac{m v^{2}}{2}(2.1)$$

Но по условию задачи:

$$E_{k}=alpha s^{2}(2.2)$$

Следовательно, можно приравнять правые части выражений (2.1) и (2.2), и получить:

$$frac{m v^{2}}{2}=alpha s^{2} rightarrow v^{2}=frac{2 alpha s^{2}}{m} rightarrow v=s sqrt{frac{2 alpha}{m}}(2.3)$$

Из второго закона Ньютона нам известно, что сила, действующая на частицу, будет равна:

$$bar{F}=m bar{a}(2.4)$$

где

$$a=sqrt{a_{n}^{2}+a_{tau}^{2}}(2.5)$$

При этом нормальное ускорение частицы (an), перемещающейся по окружности найдем как:

$$a_{n}=frac{v^{2}}{R}=frac{2 alpha s^{2}}{R m}(2.6)$$

Тангенциальную составляющую ускорения (aт)используя определение тангенциального ускорения, определение скорости
($v=frac{d s}{d t}$) и выражение v(s) (2.3) вычислим как:

$$a_{tau}=frac{d v}{d t}=frac{d v}{d s} cdot frac{d s}{d t}=sqrt{frac{2 a}{m}} cdot v=s frac{2 a}{m}(2.7)$$

Используем выражения: (2.5), (2.6), (2.7), окончательно получаем для модуля силы:

$$F=m a=m sqrt{frac{4 alpha^{2} s^{4}}{R^{2} m^{2}}+s^{2} frac{4 alpha^{2}}{m^{2}}}=2 alpha s sqrt{frac{s^{2}}{R^{2}}+1}$$

Ответ. $F=2 alpha s sqrt{frac{s^{2}}{R^{2}}+1}$

Читать дальше: Формула массы тела.

Источник

Физика > Релятивистская кинетическая энергия

Изучите формулу для кинетической энергии релятивистской частицы. Узнайте, как определить релятивистскую кинетическую энергию, связь с импульсом, полная энергия.

В виде формулы релятивистская кинетическая энергия задается как: (m – масса покоя, v – скорость, c – скорость света).

Задача обучения

  • Сопоставьте классическую и кинетическую релятивистские энергии для объектов, чья скорость меньше или приближается к световой.

Основные пункты

  • В формуле видно, что энергия объекта близится к бесконечности, если скорость приближается к световой. Поэтому нельзя ускорить объект на границе.
  • Расчеты кинетической энергии проводят по формуле: Eпокоя = E0 = mc2.
  • При низком скоростном показателе релятивистская кинетическая энергия может быть аппроксимирована классической. Поэтому полная энергия делится на энергию массы в состоянии покоя с добавлением традиционной кинетической.

Термины

  • Коэффициент Лоренца – фактор для определения степени временного замедления, сокращения длины и релятивистской массы перемещающегося объекта.
  • Классическая механика – все физические законы природы, характеризующие поведение обычного мира.
  • Специальная теория относительности: скорость света остается стабильной в любой системе отсчета.

Кинетическая энергия основывается на массе тела и скорости. Задается формулой: (m – масса, v – скорость тела).

Классическая кинетическая энергия связана с импульсом уравнением:

(р – импульс).

Если скорость объекта составляет примечательную часть световой, то для определения кинетической энергии нужно воспользоваться специальной теорией относительности. Здесь необходимо изменить выражение для линейного импульса. Формула:

p = mγv, где γ – коэффициент Лоренца:

Кинетическая энергия обладает связью с импульсом, поэтому релятивистское выражение отличается от классического:

Из формулы видно, что энергия объекта подходит к бесконечности, когда скорость приближается к световой. Поэтому нельзя ускорить объект на этой черте.

Математическим побочным результатом выступает уравнение эквивалентности массы-энергии. Тело в позиции покоя обязано обладать энергией:

Популярную связь между Эйнштейном, E = mc2 и атомной бомбой отобразили на обложке журнала

Eпокоя = E0 = mc2.

Общая формула для энергии объекта, не пребывающего в позиции покоя:

KE = mc2 – m0c2 (m – релятивистская масса объекта, а m0 – масса объекта в состоянии покоя).

При низких скоростях релятивистская кинетическая энергия может аппроксимироваться классической. Это показывают на разложении Тейлора:

Eк ≈ mc2 (1 + 0.5 v2/с2) – mc2 = 0.5 mv2.

Выходит, что полную энергию можно поделить на энергию массы покоя с добавлением классический кинетической при небольших скоростных показателях.

Источник

Добавить комментарий