Необходимо рассмотреть диполь, находящийся в неоднородном поле, симметричном относительно Х. Объяснить, как будет вести себя диполь в таком поле с точки зрения действующих на него сил.
Решение
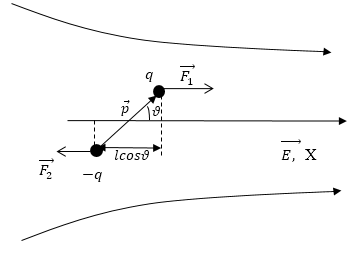
Предположим, что центр диполя лежит на оси Х, как показано на рисунке 2. Тогда угол между плечом диполя и осью Х равняется υ≠π2. Из условия видно, что F1≠F2. На диполь будет действовать вращательный момент и сила, стремящаяся переместить диполь по оси Х.
Рисунок 2
Для нахождения модуля этой силы применяются формулы:
Fx=-∂W∂x, Fy=-∂W∂y, Fz=-∂W∂z.
Опираясь на уравнение для потенциальной энергии диполя, получаем:
W(x, y, z)=-pE(x, y, z)cos υ.
Обозначим, что υ=const.
Для точек, располагаемых на оси Х:
Fy=-∂W∂y=0, Fz=-∂W∂z=0;Fx=-∂W∂x=p∂E∂xcos υ.
Если υ=0, то диполь начинает втягиваться в область более сильного поля. При υ>π2Fx.
Когда -∂W∂x=Fx, т.е. производная потенциальной энергии дает проекцию силы на соответствующую ось, тогда производная выражения -∂W∂υ=Mυ выдает проекцию вращательного момента на ось:
-∂W∂υ=Mυ=-pEsin υ.
Ответ: Наличие отрицательного результата говорит о том, что момент стремится уменьшить угол между электрическим моментом диполя и вектором напряженности поля. Стремление диполя в электрическом поле стремится повернуться таким образом, чтобы электрический момент диполя стал параллельным полю p→↑↑E→. При p→↑↑E→ вращающий момент также равняется нулю, но такое равновесие считается неустойчивым.
Энергия диполя в поле
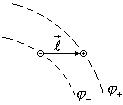
Поместим диполь во внешнее
электрическое поле. Мы знаем, что энергия
точечного заряда q во
внешнем поле равна
,
где
— потенциал поля в точке нахождения
заряда q. Диполь — это
система из двух зарядов, поэтому его
энергия во внешнем поле
,
где
и
— потенциал внешнего поля в точках
расположения зарядов
и
.
Изменение потенциала
при
перемещении в направлении вектора
на величину
можно найти как произведение производной
потенциала по направлению вектора
на величину перемещения
;
.
Тогда энергия диполя во внешнем
электрическом поле будет равна
.
Учитывая, что
и
,
где
— проекция вектора напряженности поля
на направление
,
запишем
.
То есть
.
Из этой
формулы следует, что минимальную энергию
(
)
диполь имеет в положении
(положение устойчивого равновесия). При
отклонении из этого положения возникает
момент внешних сил, возвращающий диполь
к положению равновесия.
Момент сил, действующих на диполь. Сила, действующая на диполь в неоднородном поле.
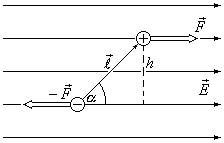
Если диполь поместить в однородное
электрическое поле, то полная действующая
на него сила будет равна нулю. Действующие
на заряды диполя силы равны по модулю
и противоположны по направлению
Эти силы приложены в разных точках,
образуя, так называемую пару сил. Пара
сил создает вращающий момент. Модуль
момента пары сил равен произведению
силы на плечо, т. е.
,
где h — есть плечо пары
сил (кратчайшее расстояние между линиями
действия сил). Учитывая, что сила,
действующая на заряд со стороны поля
равна
,
а плечо пары сил
(см. рисунок,
— угол между векторами
и
),
запишем
.
Произведение
равно дипольному моменту
,
тогда
.
.Вектора
,
и
образуют правовинтовую систему, что
позволяет нам записать выражение для
вращающего момента в векторном виде:
.
При
двух ориентациях диполя — по полю (
)
и против поля (
)
момент сил обращается в нуль. Первая
ориентация (
)
соответствует устойчивому равновесию,
вторая (
)
— неустойчивому. Момент сил стремится
повернуть диполь так, чтобы его
электрический момент
установился по направлению внешнего
поля
.
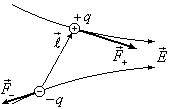
В неоднородном электрическом поле
на диполь кроме ориентирующего момента
сил будет действовать результирующая
сила, втягивающая диполь в область с
большей напряженностью. Пусть
и
— напряженности внешнего поля в точках,
где расположены положительный и
отрицательный заряды диполя. Тогда
результирующая сила
,
действующая на диполь равна (см. рисунок)
, (1)
где
— сила, действующая на заряд
диполя,
— сила, действующая на отрицательный
заряд
диполя. Разность
— это приращение вектора
на отрезке, равном длине диполя
в направлении вектора
.
Вследствие малости этого отрезка можно
записать
, (2)
где
— есть производная вектора
по направлению
,
характеризующая изменение вектора
на единицу длины в этом направлении.
После подстановки (2) в (1) и учитывая, что
получим,
.
Электрическое поле в диэлектриках
В диэлектриках в отличии от проводников
нет свободных зарядов. Удельное
сопротивление идеального диэлектрика
= ∞.
В реальных диэлектриках
Ом·м.
В идеальных диэлектриках заряды
неразрывно связаны с атомами и молекулами
(связанные заряды). Под действием поля
они могут лишь смещаться от положения
равновесия на микроскопические
расстояния. Процесс смещения связанных
зарядов под действием поля называется
поляризацией диэлектрика. Это означает,
что результирующий дипольный момент
диэлектрика становится отличным от
нуля.
В качестве величины, характеризующей
степень поляризации диэлектрика
естественно взять дипольный момент
молекул единицы объёма. Если поле и
диэлектрик неоднородны, то вектор
поляризации диэлектрика в данной точке
,
где V — физически
малый объем, включающий в себя данную
точку,
— векторная
сумма дипольных моментов всех молекул
в этом объёме.
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сергей Сергеевич Соев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Потенциальная энергия жесткого диполя
Рассмотрим так называемый жесткий диполь — это диполь, у которого расстояние между зарядами не изменяется ($l=const$). Определим, какова потенциальная энергия, которую имеет диполь во внешнем электростатическом поле. Если заряд $q$, который находится в точке поля с потенциалом $varphi $, имеет потенциальную энергию равную:
то энергия диполя равна:
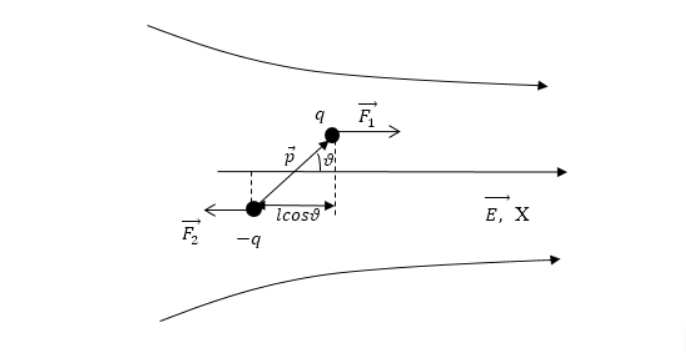
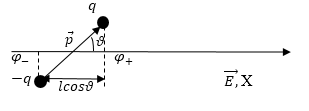
где ${varphi }_+;{varphi }_-$ – потенциалы внешнего поля в точках нахождения зарядов $q$ и $-q$. Потенциал электростатического поля убывает линейно, если поле однородно в направлении вектора напряженности поля. Направим ось X вдоль поля (рис.1). Тогда получим:
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Рис. 1
Из рис. 1 видим, что изменение потенциала от ${varphi }_+до {varphi }_-$происходит на отрезке $triangle x=lcos vartheta$, поэтому:
Электрический момент диполя
Подставим (4) в (2), получим:
где $overrightarrow{p}$=$qoverrightarrow{l}$ — электрический момент диполя. Уравнение (6) не учитывает энергию взаимодействия зарядов диполя. Формула (6) получена при условии, что поле однородно, однако, она справедлива и для неоднородного поля.
Пример 1
Задание: Рассмотрите диполь, который находится в неоднородном поле, которое симметрично относительно оси X. Объясните, как поведет себя диполь в таком поле с точки зрения действующих на него сил.
Решение:
Пусть центр диполя лежит на оси X (рис.2). Угол между плечом диполя и осью X равен $vartheta ne frac{pi }{2}$. В нашем случае силы $F_1ne F_2$.На диполь будет действовать вращательный момент и
Рис. 2
сила, которая стремится переместить диполь по оси X. Чтобы найти модуль этой силы используем формулы:
[F_x=-frac{partial W}{partial x}, F_y=-frac{partial W}{partial y}, F_z=-frac{partial W}{partial z}(1.1).]
В соответствии с уравнением для потенциальной энергии диполя имеем:
[W(x,y,z)=-pE(x,y,z)cos vartheta left(1.2right),]
считаем, что $vartheta=const$
Для точек оси X имеем:
[F_y=-frac{partial W}{partial y}=0, F_z=-frac{partial W}{partial z}=0]
[F_x=-frac{partial W}{partial x}=pfrac{partial E}{partial x}cos vartheta(1.3).]
При $vartheta 0$, значит, диполь втягивается в область более сильного поля. При $vartheta >frac{pi }{2}$ $F_x
Заметим, что если $-frac{partial W}{partial x}=F_x$, производная от потенциальной энергии дает проекцию силы на соответствующую ось, то производная $-frac{partial W}{partial vartheta}=M_vartheta$ дает проекцию вращательного момента на ось $?$:
[-frac{partial W}{partial vartheta}=M_vartheta=-pEsin vartheta (1.4.)]
В формуле (1.4) минус означает, что момент стремится уменьшить угол меду электрическим моментом диполя и вектором напряженности поля. Диполь в электрическом поле стремится повернуться так, чтобы электрический момент диполя, был параллельно полю ($overrightarrow{p}uparrow uparrow overrightarrow{E}$). При $overrightarrow{p}uparrow downarrow overrightarrow{E}$ вращающий момент тоже будет равен нулю, но такое равновесие не устойчиво.
«Энергия электрического диполя во внешнем поле» 👇
Пример 2
Задание: Два диполя находятся на расстоянии $r$ друг от друга. Их оси лежат на одной прямой. Электрические моменты равны соответственно: $p_1$ и $p_2$. Вычислите потенциальную энергию любого из диполей, которая будет соответствовать положению устойчивого равновесия.
Решение:
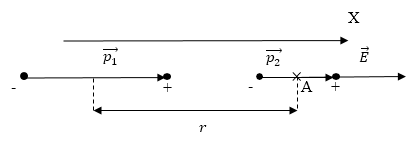
Система будет находиться в состоянии равновесия, когда диполи ориентированы, как показано на рис. 3, вдоль поля, противоположными по знаку зарядами друг к другу.
Рис. 3
Будем считать, что поле создаёт диполь с моментом $p_1$, будем искать потенциальную энергию диполя, который обладает электрическим моментом $p_2$ в точке поля (A) на расстоянии r от первого диполя. Примем, что плечи диполя малы по сравнению с расстоянием между диполями ($lll r$). Диполи можно будет принять за точечные (так считаем, что диполь с моментом $p_2 находится в точке А$). Напряжённость поля, которое создает диполь на его оси в точке А по модулю равна (при $varepsilon =1$):
[E=frac{p_1}{2pi {varepsilon }_0r^3}left(2.1right).]
Потенциальная энергия диполя с моментом $p_2$ в точке А может быть выражена формулой:
[W=-p_2E left(2.2right),]
где мы учли, что векторы напряженности и электрического момента диполя сонаправлены в состоянии устойчивого равновесия. В таком случае потенциальная энергия второго диполя будет равна:
[W=-p_2frac{p_1}{2pi {varepsilon }_0r^3} left(2.3right).]
Ответ: Потенциальные энергии диполей будут равны по величине $W=-p_2frac{p_1}{2pi {varepsilon }_0r^3}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 17 марта 2022 года; проверки требуют 5 правок.
У этого термина существуют и другие значения, см. Диполь.
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
Дипо́ль (фр. dipôle, от греч. di(s) «дважды» + polos «ось», «полюс», буквально — «дву(х)полюсность») — идеализированная система, служащая для приближённого описания поля, создаваемого более сложными системами зарядов, а также для приближенного описания действия внешнего слоя поля на такие системы.
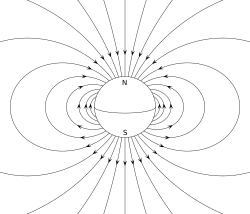
Магнитное поле Земли примерно совпадает с полем диполя. Однако «N» и «S» (северный и южный) полюса отмечены «географически», то есть противоположно принятому обозначению для полюсов магнитного диполя.
Типичный и стандартный пример диполя — два заряда, равные по величине и противоположные по знаку, находящиеся друг от друга на расстоянии, очень малом по сравнению с расстоянием до точки наблюдения. Поле такой системы полностью описывается дипольным приближением при стремлении расстояния между зарядами к нулю при сохранении произведения величины заряда на расстояние между зарядами — постоянным (или стремящимся к конечному пределу; эта константа или этот предел будет дипольным моментом такой системы).
Эквипотенциальные поверхности электрического диполя
Силовые линии электрического диполя
Дипольное приближение, выполнение которого обычно подразумевается, когда говорится о поле диполя, основано на разложении потенциалов поля в ряд по степеням радиус-вектора, характеризующего положение зарядов-источников, и отбрасывании всех членов выше первого порядка[1].
Полученные функции будут эффективно описывать поле в случае, если:
- размеры создающей или излучающей поле системы (области, содержащей заряды) малы по сравнению с рассматриваемыми расстояниями, так что отношение характерного размера системы к длине радиус-вектора является малой величиной и имеет смысл рассмотрение лишь первых членов разложения потенциалов в ряд;
- член первого порядка в разложении не равен 0, в противном случае нужно использовать приближение более высокой мультипольности;
- в уравнениях рассматриваются градиенты потенциалов не выше первого порядка.
Дипольный момент системы[править | править код]
Электрический диполь[править | править код]
Электрический диполь — идеализированная электронейтральная система, состоящая из точечных и равных по абсолютной величине положительного и отрицательного электрических зарядов.
Другими словами, электрический диполь представляет собой совокупность двух равных по абсолютной величине разноимённых точечных зарядов, находящихся на некотором расстоянии друг от друга.
Произведение вектора 


Во внешнем электрическом поле 

Потенциальная энергия электрического диполя в (постоянном) электрическом поле равна 
Вдали от электрического диполя напряжённость его электрического поля убывает с расстоянием 


Дипольное приближение для электростатического поля нейтральной системы[править | править код]
Любая в целом электронейтральная система, содержащая электрические заряды, в некотором приближении (то есть собственно в дипольном приближении) может рассматриваться как электрический диполь с моментом 



В точечном приближении, поле, создаваемое диполем в точке с радиус-вектором 
Дипольное приближение для электростатического поля не-нейтральной системы[править | править код]
Не электрически нейтральная система очевидным образом может быть представлена как сумма (суперпозиция) электрически нейтральной системы и точечного заряда. Для этого достаточно поместить куда-то внутрь системы точечный заряд, противоположный ее суммарному заряду, и в ту же точку еще один точечный заряд, равный ее суммарному заряду. После чего рассматривать первый заряд вместе с остальной системой (ее дипольный момент будет очевидно равен дипольному моменту, вычисленному по формуле, приведенной выше, если за начало координат взять положение добавленного точечного заряда: тогда сам добавленный заряд не войдет в выражение). Второй же точечный заряд даст кулоновское поле.
То есть, вдалеке от такой системы электростатическое поле, создаваемое ею, в дипольном приближении будет суммой (суперпозицией) кулоновского поля, создаваемого зарядом этой системы 






Магнитный диполь[править | править код]
Магнитный диполь — аналог электрического, который можно представить себе как систему двух «магнитных зарядов» — магнитных монополей. Эта аналогия условна, так как магнитные заряды не обнаружены. В качестве модели магнитного диполя можно рассматривать небольшую (по сравнению с расстояниями, на которых излучается генерируемое диполем магнитное поле) плоскую замкнутую проводящую рамку площади 



Выражения для вращающего момента 



Поле колеблющегося диполя[править | править код]
В этом разделе рассматривается поле, создаваемое точечным электрическим диполем 
Поле на близких расстояниях (ближняя зона)[править | править код]
Поле точечного диполя, колеблющегося в вакууме, имеет вид
где 

Этим выражениям можно придать несколько другую форму, если ввести вектор Герца
Напомним, что диполь покоится в начале координат, так что 
При этом потенциалы поля можно выбрать в виде
Указанные формулы можно применять всегда, когда применимо дипольное приближение.
Дипольное излучение (излучение в волновой зоне или дальней зоне)[править | править код]
Приведённые формулы существенно упрощаются, если размеры системы много меньше длины излучаемой волны, то есть скорости зарядов много меньше c, а поле рассматривается на расстояниях много больших, чем длина волны. Такую область поля называют волновой зоной. Распространяющуюся волну можно в этой области считать практически плоской. Из всех членов в выражениях для 


Выражения для полей в системе СГС принимают вид
В плоской волне интенсивность излучения в телесный угол 
поэтому для дипольного излучения
где 






Укажем спектральный состав излучения. Он получается заменой вектора 
См. также[править | править код]
- Мультиполь
- Квадруполь
- Октуполь
- Дипольный момент
- Магнитный дипольный момент
- Диполярная система координат
Примечания[править | править код]
- ↑ Для случая электростатики, магнитостатики и т.п. это означает сохранение в потенциале членов со степенями радиус-вектора от диполя к точке наблюдения −1 и −2; в случае же чисто дипольного поля (когда система источников имеет нулевой суммарный заряд) только степени −2.
Литература[править | править код]
- Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7.
- Ахманов С. А., Никитин С. Ю., «Физическая оптика», 2004.
До сих пор мы изучали свойства электромагнитных волн в пустом пространстве, основываясь на уравнениях Максвелла с равными нулю источниками r и . Такие уравнения без источников описывают распространение волн в пустоте, но не позволяют понять, как возникают электромагнитные волны, что является источником этих волн. Ответы на эти вопросы может дать только квантовая теория. Однако исследование именно этих вопросов и привело к открытию квантовых законов природы. Само понятие “квант” было впервые введено Максом Планком в связи с исследованием излучения нагретых тел.
Первоначально излучение ЭМВ было получено с помощью так называемого “вибратора Герца”. Частота излучения вибратора Герца составляет 107 – 108 Гц. Частота видимого света порядка 1014 – 1015 Гц. Существуют ли вибраторы Герца с такими частотами? Поскольку частота излучения возрастает при уменьшении размеров вибратора, можно предположить, что элементарный источник света обладает чрезвычайно малыми размерами. Была высказана идея, что таким источником может быть атом или молекула. Обсуждение физики излучения можно провести на основе классической модели атома как системы заряженных частиц, связанных упругими силами.
Достоинство этой модели – простота и наглядность, возможность объяснись излучение света исходя из законов электродинамики макроскопических тел. Многие выводы классической теории находят качественное и даже количественное подтверждение в квантовой теории излучения.
Классическая модель атома позволяет дать теорию целого ряда явлений, возникающих при взаимодействии света с веществом: поглощение и дисперсия света, разнообразные нелинейные процессы (генерация оптических гармоник, самофокусировка света и т. д.).
Классический образ атома – пара разноименных зарядов, связанных между собой упругой силой. Как могла бы выглядеть такая система? Согласно модели, предложенной Дж. Дж. Томсоном, атом представляет собой непрерывно распределенный в некотором объеме положительный заряд, внутри которого находился электрон, удерживаемый в положении равновесия упругой электростатической силой. Будучи выведенным из положения равновесия, электрон совершает гармонические колебания, частота которых w0 определяемся зарядом и массой электрона, а также размером атома. Конкретный пример системы подобного типа (для атома водорода) показан на рис. 1а. Здесь точечный отрицательно заряженный электрон находится внутри однородного положительно заряженного шара. На рис. 1б. показана аналогичная модель, которая в большей степени соответствует современным представлениям о строении атома. В этой модели точечное положительно заряженное атомное ядро окружено “электронным облаком”, которое в простейшем случае имеет вид однородно заряженного шара.
В обеих моделях при смещении центра распределенного заряда относительно точечного заряда противоположного знака возникает кулоновская возвращающая сила F = Kx, пропорциональная величине смещения X.Т. о., заряды взаимодействуют подобно шарикам, связанным пружинкой (рис. 1в).
Как известно из механики, в этом случае ускоренное движение заряда описывается уравнением гармонического осциллятора.
,
Если
X = ACosw0T,
То
(1)
Собственная частота осциллятора определяется массой электрона M и силовой постоянной K. Нетрудно вычислить эту постоянную для случая, когда распределенный заряд представляет собой однородно заряженный шар с радиусом A0 и зарядом Q. Зная напряженность электрического поля внутри шара (


Следовательно, частота колебаний электрона в атоме Томсона определяется формулой

Полагая Q = 1,6×10–19 Кл, M = 9,1×10–31 кг, A0 = 0,5×10–10 м, получим w0 = 4,5×1016 с–1 , или в герцах n0 = 7,2×1015 Гц. Таким образом, частота атомного осциллятора в модели Томсона, вычисленная исходя из известных параметров атома (заряд, масса электрона, размер атома), оказывается близкой к частоте оптических колебаний.
Излучение диполя
Имея в виду классическую модель атома, рассмотрим излучение пары электрических зарядов +Q и –Q, связанных между собой упругой силой. Такую систему будем называть диполем. Основной характеристикой диполя является дипольный момент, определяемый в общем случае формулой , где
и
– радиус-векторы зарядов. Причем осцилляции дипольного момента обусловлены изменением расстояния между зарядами по гармоническому закону.
Строгое решение задачи об излучении диполя может быть получено путем решения уравнений Максвелла с учетом переменного тока, вызванного ускоренным движением зарядов. В курсе электродинамики показано, что это решение имеет вид

В формулах (2) – радиус-вектор, проведенный от диполя в точку наблюдения поля,
– единичный вектор вдоль этого направления, C – скорость света, точка над буквой обозначает дифференцирование по времени. Решение (2) справедливо для так называемой дальней зоны, т. е. области пространства, находящейся от диполя на расстоянии много больше размера диполя и длины волны излучения.
Поле излучения диполя представляет собой сферическую волну и имеет структуру, представленную на рис. 2.
Если для каждой точки наблюдения ввести волновой вектор , направленный из начала координат вдоль вектора
, то вектора
,
и
в этой точке образуют правую тройку. Притом индукция
магнитного поля сферической электромагнитной волны в каждой точке связана с напряженностью
электрического поля в этой же точке тем же соотношением, что и для плоской волны.
Гармонические колебания диполя
Вычислим энергетические характеристики излучения диполя, считая, что диполь совершает гармонические колебания с амплитудой A и с частотой w0:
Так что
(3)
– единичный вектор, направленный вдоль линии, соединяющей заряды (рис. 2). Используя формулы (2) и (3), получим

– единичный вектор вдоль вектора
.

Формулы (4,5) показывают, что излучение диполя линейно поляризовано, причем вектор Лежит в плоскости векторов
и
, а вектор
перпендикулярен этой плоскости (рис. 2). Запишем вектор потока энергии
Учитывая формулы (4,5), можно записать
Из определения единичного вектора следует, что
, т. к.
,
. Поток энергии в волновой зоне

Совпадает с направлением радиус-вектора (рис. 2). Усредняя выражение (6) по времени, получаем интенсивность излучения диполя на расстоянии R

Зависимость интенсивности от направления выражается в (7) множителем Sin2q. Максимальная интенсивность наблюдается при q = p/2 т. е. в экваториальной плоскости: максимум интенсивности соответствует направлению, перпендикулярному оси диполя. Вдоль оси диполя (q = 0) энергия не излучается. Угловое распределение излучаемой осциллирующим диполем энергии показано на рис. 3. с помощью “диаграммы направленности”. Длина отрезка, проведенного из начала координат до пересечения с линией R = Sin2q, пропорциональна интенсивности распространяющейся в данном направлении волны. Распределение интенсивности по направлениям в пространстве характеризуется поверхностью, которая получается вращением кривой на рис. 3 вокруг оси OX.
Полную энергию, излучаемую диполем за 1 с по всем направлениям (мощность излучения) можно найти, вычисляя <S> через поверхность сферы радиусом R с центром в начале координат. Разобьем сферу на кольца координатными поверхностями q = Const и q + DQ = Const. Площадь такого кольца равна 2pR2SinQDQ, а значение <S> во всех его точках можно считать одинаковым. Поэтому полная излучаемая мощность

Согласно формуле (8), излучаемая осциллятором мощность пропорциональна квадрату амплитуды его дипольного момента и четвертой степени частоты (обратно пропорциональна четвертой степени длины волны). Этот закон играет большую роль в теории рассеяния света. Короткие волны рассеиваются сильнее чем длинные. Этим объясняется голубой цвет неба и красный цвет Солнца на закате.
Выражаемый формулой (8) поток излучения осциллятора через поверхность сферы не зависит от ее радиуса, т. е. через любую охватывающую осциллятор замкнутую поверхность протекает за 1 с одинаковая энергия. Этот факт объясняет характер зависимости напряженности электрического поля в формуле (2).
Радиационное затухание
Осциллятор совершает незатухающие колебания лишь в том случае, когда эти колебания поддерживаются каким-либо внешним источником. Без такого источника колебания будут затухать даже при движении в абсолютно пустом пространстве, так как осциллятор теряет энергию на излучение. Затухание колебаний атомного осциллятора, связанное с потерей энергии на излучение, получило название Радиационного затухания. Затухание колебаний можно описать, вводя в уравнение движения излучающего заряда некоторую эффективную “силу трения” таким образом, чтобы потеря энергии на излучение могла быть представлена как средняя работа этой силы. Полагая эту силу пропорциональной скорости движения заряда , уравнение движения заряда запишем в виде
Надо помнить, однако, что никаких сил сопротивления, никакой “вязкости” в обычном смысле этого слова здесь нет.
Используя полученное выше выражение (8) для излучаемой осциллятором мощности, можно сделать оценку времени жизни атома в возбужденном состоянии.
Энергия осциллятора состоит из кинетической () и потенциальной (
), средние значения которых равны между собой. Полная энергия осциллятора
(9)
Пропорциональна квадрату амплитуды. Излучаемая осциллятором мощность Pизл, представляющая собой скорость уменьшения энергии (–DW/Dt) в соответствии с (8) также пропорциональна квадрату амплитуды. Выражая A2 через энергию W из (9) и подставляя в правую часть (8), получаем, что скорость уменьшения энергии осциллятора пропорциональна его энергии:
, (10)
Где

Из уравнения (10) следует, что энергия возбуждения осциллятора уменьшается вследствие потерь на излучение по экспоненциальному закону:
Здесь tЭ = 1/2g – время радиационного затухания, в течение которого энергия осциллятора уменьшаемся в E = 2,72 раз. Амплитуда A колебаний осциллятора также убывает экспоненциально:
(12)
Длительность этого процесса характеризуемся временем t затухания амплитуды: t = 1/g (время жизни колебаний), которое в два раза превышает время затухания энергии: t = 2tэ. Принимая в формуле (11) для w0 = 2pC/l0 значение, соответствующее l0 = 0,5 мкм (видимый свет), находим, что g»108 с–1, поэтому время жизни возбужденного состояния атома, обусловленное радиационным затуханием, по порядку величины равно 10–8 с. Этот результат согласуется с опытными данными. Затухание колебаний излучающего электрона, описываемое формулой
,
Представлено на рис. 4 в искаженном масштабе. За время затухания осциллятор совершает около 107 полных колебаний, период которых T»10–15 с. Время t определяет продолжительность цуга волн, испускаемых возбужденным осциллятором (неподвижным изолированным атомом).
Зависимость поля излучения E(T) отдельного атома от времени подобна зависимости, показанной на рис. 4.
В фиксированной точке пространства поле излучения имеет вид модулированного колебания и его можно приближенно записать в виде
, (13)
Где E0 и j – начальные амплитуда и фаза колебаний электрического поля в точке наблюдения, w0 и t – частота и время затухания свободных электронных колебаний.
Рассмотрим спектральный состав модулированного колебания (13), т. е. спектральный состав излучения, представляющего собой одиночный затухающий волновой цуг конечной длительности.
Естественная ширина линии излучения
Полагая в (13) начальную фазу равной нулю, напряженность поля в волне, испускаемой затухающим осциллятором, представим в виде

Где постоянная g = 1/t определяется соотношением (11). Для нахождения спектра излучения выполним обратное преобразование Фурье

Для вычисления интеграла (15) удобно CosW0T выразить через показательные функции
,
Тогда

Рассчитаем первый интеграл
И рассмотрим функцию – спектральную плотность энергии с учетом только одного слагаемого

Согласно (17), S(w) имеет максимум в точке w = w0. При g << w0 максимум очень острый. Поэтому в интересующей нас области положительных частот вкладом второго слагаемого из (16) в функцию S(w) можно пренебречь. Описываемая выражением (17) форма спектральной линии излучения называется Лоренцевским контуром (рис. 5).
Пунктиром представлен контур линии в области отрицательных частот с максимумом при w = –w0 , обусловленный вторым слагаемым формулы (16). Как видно из рис. 5, кривая имеет максимум при w = w0 (в области положительных частот, т. е. на частоте собственных колебаний в отсутствие затухания. Уширение спектра излучаемых частот обусловлено радиационным затуханием свободных колебаний осциллятора. Плотность энергии уменьшается вдвое для частот, отличающихся от w0 на g = 1/t. Отсюда для ширины линии на половине высоты находим Dw = 2g = 2/t. Это значит, что ширина полосы излучаемых частот Dn связана с характерной длительностью цуга t соотношением: Dnt~1: чем меньше длительность процесса испускания, тем шире спектр частот. Так как Dw = 2g<<w0, то излучаемый свет можно назвать Квазимонохроматическим.
Рассмотренный пример позволяет оценить обусловленную радиационным затуханием естественную ширину спектральных линий излучения свободных атомов. Так как время жизни возбужденного состояния составляет около 10‑8 с, то для естественной ширины получаем Dn ~ 108 Гц. В шкале длин волн оценка естественной ширины спектральной линии дает Dl ~ 10–5 нм. На практике, однако, редко можно наблюдать столь узкие спектральные линии. Обычно естественное уширение маскируется другими, более сильными механизмами уширения.
Как видно из формулы (15) частотный спектр излучения определяется характером изменения во времени напряженности светового поля E(T). Вид этой зависимости, в свою очередь, определяется наряду с радиационным затуханием колебаний такими физическими факторами как тепловое движение осцилляторов (атомов), столкновения, сбивающие фазу колебаний, разброс осцилляторов по частотам и т. п. Каждый из этих факторов обусловливает свой механизм уширения спектральной линии: доплеровское, столкновительное, неоднородное уширение и т. п. Прежде чем рассмотреть некоторые механизмы уширения, остановимся на описании излучения реальных источников света, состоящих из огромного числа отдельных осцилляторов (атомов и молекул).







![{displaystyle mathbf {B} =left[{frac {dot {mathbf {d} }}{cR^{2}}}+{frac {ddot {mathbf {d} }}{Rc^{2}}},mathbf {n} right]=left[mathbf {n} ,mathbf {E} +{frac {mathbf {d} }{R^{3}}}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7a5116d7a27a9b77d37a2c68a88a56b17ee0409)






![{mathbf {H}}={frac {1}{c^{2}R}}[{ddot {{mathbf {d}}}},{mathbf {n}}],~~{mathbf {H}}=[{mathbf {n}},{mathbf {E}}],](https://wikimedia.org/api/rest_v1/media/math/render/svg/84bd71646576efdf7b568ca73f3fdfda274c2016)
![mathbf{E} = frac{1}{c^2 R}left[ [ddot{mathbf{d}},mathbf{n}] , mathbf{n} right], ~~ mathbf{E} = [mathbf{B} , mathbf{n}].](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddd81cd25579185d582c5b37412b7dba1031b2fd)

![{displaystyle dI={frac {1}{4pi c^{3}}}[{ddot {mathbf {d} }},mathbf {n} ]^{2}dOmega ={frac {{ddot {mathbf {d} }}^{2}}{4pi c^{3}}}sin ^{2}{theta }dOmega .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3aeed50c002be6da19c971e846b937ea1619c953)









