Конденсатор. Энергия электрического поля
-
Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.
-
Ёмкость уединённого проводника
-
Ёмкость плоского конденсатора
-
Энергия заряженного конденсатора
-
Энергия электрического поля
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.
Предыдущие две статьи были посвящены отдельному рассмотрению того, каким образом ведут себя в электрическом поле проводники и каким образом — диэлектрики. Сейчас нам понадобится объединить эти знания. Дело в том, что большое практическое значение имеет совместное использование проводников и диэлектриков в специальных устройствах — конденсаторах.
Но прежде введём понятие электрической ёмкости.
к оглавлению ▴
Ёмкость уединённого проводника
Предположим, что заряженный проводник расположен настолько далеко от всех остальных тел, что взаимодействие зарядов проводника с окружающими телами можно не принимать во внимание. В таком случае проводник называется уединённым.
Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду. Коэффициент пропорциональности принято обозначать
, так что
Величина называется электрической ёмкостью проводника и равна отношению заряда проводника к его потенциалу:
(1)
Например, потенциал уединённого шара в вакууме равен:
где — заряд шара,
— его радиус. Отсюда ёмкость шара:
(2)
Если шар окружён средой-диэлектриком с диэлектрической проницаемостью , то его потенциал уменьшается в
раз:
Соответственно, ёмкость шара в раз увеличивается:
(3)
Увеличение ёмкости при наличии диэлектрика — важнейший факт. Мы ещё встретимся с ним при рассмотрении конденсаторов.
Из формул (2) и (3) мы видим, что ёмкость шара зависит только от его радиуса и диэлектрической проницаемости окружающей среды. То же самое будет и в общем случае: ёмкость уединённого проводника не зависит от его заряда; она определяется лишь размерами и формой проводника, а также диэлектрической проницаемостью среды, окружающей проводник. От вещества проводника ёмкость также не зависит.
В чём смысл понятия ёмкости? Ёмкость показывает, какой заряд нужно сообщить проводнику, чтобы увеличить его потенциал на В. Чем больше ёмкость — тем, соответственно, больший заряд требуется поместить для этого на проводник.
Единицей измерения ёмкости служит фарад (Ф). Из определения ёмкости (1) видно, что Ф = Кл/В.
Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным км.
мкФ.
Как видите, Ф — это очень большая ёмкость.
Единица измерения ёмкости полезна ещё и тем, что позволяет сильно сэкономить на обозначении размерности диэлектрической постоянной . В самом деле, выразим
из формулы (2):
Следовательно, диэлектрическая постоянная может измеряться в Ф/м:
Ф.
Так легче запомнить, не правда ли?
к оглавлению ▴
Ёмкость плоского конденсатора
Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.
Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости — но на сей раз о ёмкости этой системы проводников.
Наиболее простым и важным примером такой системы является плоский конденсатор. Он состоит из двух параллельных металлических пластин (называемых обкладками), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров.
Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух
Пусть заряды обкладок равны и
. Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина
— заряд положительной обкладки — называется зарядом конденсатора.
Пусть — площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.
Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости:
Здесь — напряжённость поля положительной обкладки,
— напряженность поля отрицательной обкладки,
— поверхностная плотность зарядов на обкладке:
На рис. 1 (слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора.

Рис. 1. Электрическое поле плоского конденсатора
Согласно принципу суперпозиции, для результирующего поля имеем:
Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга):
Внутри конденсатора поле удваивается:
или
(4)
Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак:
Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4). Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.
Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты: поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.
Пусть расстояние между обкладками конденсатора равно . Поскольку поле внутри конденсатора является однородным, разность потенциалов
между обкладками равна произведению
на
(вспомните связь напряжения и напряжённости в однородном поле!):
(5)
Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками:
(6)
Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на В. Формула (6), таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.
Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора:
(7)
Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними.
Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Как изменится ёмкость конденсатора?
Напряжённость поля внутри конденсатора уменьшится в раз, так что вместо формулы (4) теперь имеем:
(8)
Соответственно, напряжение на конденсаторе:
(9)
Отсюда ёмкость плоского конденсатора с диэлектриком:
(10)
Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор.
Важное следствие формулы (10): заполнение конденсатора диэлектриком увеличивает его ёмкость.
к оглавлению ▴
Энергия заряженного конденсатора
Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится.
Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке. Нетрудно понять, что этой энергией является потенциальная энергия взаимодействия обкладок конденсатора — ведь обкладки, будучи заряжены разноимённо, притягиваются друг к другу.
Мы сейчас вычислим эту энергию, а затем увидим, что существует и более глубокое понимание происхождения энергии заряженного конденсатора.
Начнём с плоского воздушного конденсатора. Ответим на такой вопрос: какова сила притяжения его обкладок друг к другу? Величины используем те же: заряд конденсатора , площадь обкладок
.
Возьмём на второй обкладке настолько маленькую площадку, что заряд этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой
где — напряжённость поля первой обкладки:
Следовательно,
Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам).
Результирующая сила притяжения второй обкладки к первой складывается из всех этих сил
, с которыми притягиваются к первой обкладке всевозможные маленькие заряды
второй обкладки. При этом суммировании постоянный множитель
вынесется за скобку, а в скобке просуммируются все
и дадут
. В результате получим:
(11)
Предположим теперь, что расстояние между обкладками изменилось от начальной величины до конечной величины
. Сила притяжения пластин совершает при этом работу:
Знак правильный: если пластины сближаются , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины
, то работа силы притяжения получается отрицательной, как и должно быть.
С учётом формул (11) и (7) имеем:
где
Это можно переписать следующим образом:
где
(12)
Работа потенциальной силы притяжения обкладок оказалась равна изменению со знаком минус величины
. Это как раз и означает, что
— потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора.
Используя соотношение , из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):
(13)
(14)
Особенно полезными являются формулы (12) и (14).
Допустим теперь, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью . Сила притяжения обкладок уменьшится в
раз, и вместо (11) получим:
При вычислении работы силы , как нетрудно видеть, величина
войдёт в ёмкость
, и формулы (12) — (14) останутся неизменными. Ёмкость конденсатора в них теперь будет выражаться по формуле (10).
Итак, формулы (12) — (14) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.
к оглавлению ▴
Энергия электрического поля
Мы обещали, что после вычисления энергии конденсатора дадим более глубокое истолкование происхождения этой энергии. Что ж, приступим.
Рассмотрим воздушный конденсатор и преобразуем формулу (14) для его энергии:
Но — объём конденсатора. Получаем:
(15)
Посмотрите внимательно на эту формулу. Она уже не содержит ничего, что являлось бы специфическим для конденсатора! Мы видим энергию электрического поля , сосредоточенного в некотором объёме
.
Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.
Итак, электрическое поле само по себе обладает энергией. Ничего удивительного для нас тут нет. Радиоволны, солнечный свет — это примеры распространения энергии, переносимой в пространстве электромагнитными волнами.
Величина — энергия единицы объёма поля — называется объёмной плотностью энергии. Из формулы (15) получим:
(16)
В этой формуле не осталось вообще никаких геометрических величин. Она даёт максимально чистую связь энергии электрического поля и его напряжённости.
Если конденсатор заполнен диэлектриком, то его ёмкость увеличивается в раз, и вместо формул (15) и (16) будем иметь:
(17)
(18)
Как видим, энергия электрического поля зависит ещё и от диэлектрической проницаемости среды, в которой поле находится.
Замечательно, что полученные формулы для энергии и плотности энергии выходят далеко за пределы электростатики: они справедливы не только для электростатического поля, но и для электрических полей, меняющихся во времени.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Конденсатор. Энергия электрического поля» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Содержание:
Энергия электрического поля:
Для зарядки проводника выполняется работа по преодолению силы отталкивания между зарядами. За счет этой работы проводник получает энергию. Полученная энергия заряженного тела количественно равна работе, выполненной при его зарядке, т.е. 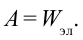

Среднее значение потенциала тела равно среднему арифметическому его начальных и конечных значений, т.е.

Поставляя значении 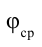 в уравнение (7.21), получим следующее выражение:
в уравнение (7.21), получим следующее выражение:

Значит, работа, выполненная при зарядке тела, равняется половине произведения его заряда на потенциал. При зарядке тела его потенциал плавно, т.е. линейно изменяется согласно формуле 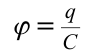 . Здесь
. Здесь 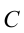 – электрическая емкость проводника. Тогда выражение (7.23) можно записать следующим образом:
– электрическая емкость проводника. Тогда выражение (7.23) можно записать следующим образом:

Согласно соотношению 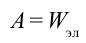 , формулу для расчета энергии электрического поля изолированного заряженного тела можно записать в виде
, формулу для расчета энергии электрического поля изолированного заряженного тела можно записать в виде
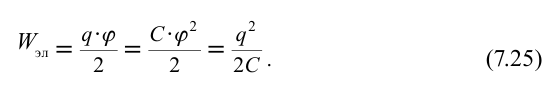
Если заряженное тело является конденсатором, то при расчете энергии (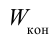 ) его электрического поля величину заряда в формуле (7.25) нужно заменить на величину зарядов на одной обкладке конденсатора, а потенциал заменить на разницу потенциалов между обкладками, т.е., можно записать:
) его электрического поля величину заряда в формуле (7.25) нужно заменить на величину зарядов на одной обкладке конденсатора, а потенциал заменить на разницу потенциалов между обкладками, т.е., можно записать:
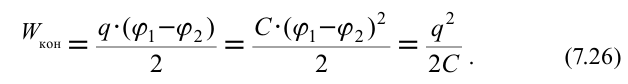
Исходя из этого, формулу определения электрической энергии конденсатора можно записать в виде:
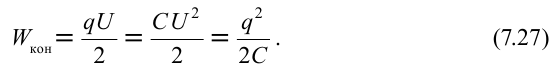
Энергия заряженного тела сосредоточена в электрическом поле, созданном вокруг него, величина энергии зависит от объема пространства, занимаемого полем и напряженности поля.
Рассмотрим частный случай плоского заряженного конденсатора.
Электрическое поле, созданное зарядами обкладок плоского конденсатора, сосредоточено в среде между его обкладками. Объем пространства можно вычислить по формуле 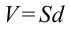 .
.
Учитывая емкость заряженного плоского конденсатора 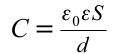 и зависимость между разницей потенциалов обкладок и напряженностью поля конденсатора, с учетом формулы (7.27), получим следующее соотношение:
и зависимость между разницей потенциалов обкладок и напряженностью поля конденсатора, с учетом формулы (7.27), получим следующее соотношение:
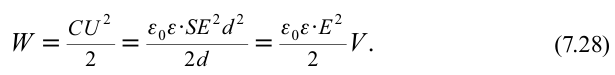
Энергия заряженного плоского конденсатора прямо пропорциональна квадрату напряженности созданного им поля и объему пространства, занимаемого этим полем. Энергия, приходящаяся на удельную единицу поля, называется объемной плотностью энергии. То есть:
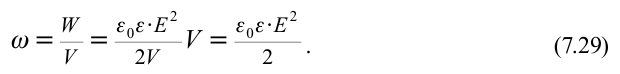
Каждый конденсатор имеет свойство накапливать в себе не только заряд, но и энергию. Энергия, полученная конденсатором, сосредоточена в среде между его обкладками. Эту энергию невозможно хранить длительное время. Конденсатор с течением времени передает полученный заряд в окружающую среду, т.е. разряжается.
При разрядке конденсатора через цепь с маленьким электрическим сопротивлением энергия передается практически мгновенно.
Образец решения задачи:
Емкость плоского воздушного конденсатора равна 0,1 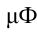 , разность потенциалов 200 В. Вычислите энергию электрического поля в конденсаторе.
, разность потенциалов 200 В. Вычислите энергию электрического поля в конденсаторе.
Дано:
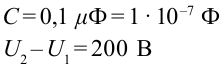
Найти:
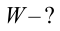
Формула:
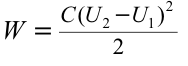
Решение:
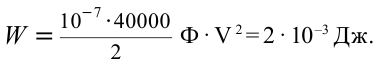
Ответ: 2 мДж.
Основные понятия, правила и законы:
| Закон сохранения зарядов | Алгебраическая сумма зарядов всех тел внутри любой закрытой системы не меняется, т.е.: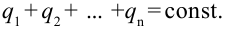 |
| Силовые линии электрического поля |
Линии, показывающие направления силы, действующие со стороны поля на положительный заряд, введенный в электрическое поле. Силовые линии электрического поля, образованного положительным зарядом, направлены от заряда, а в случае отрицательного заряда – направлены к нему. |
| Напряженность электрического поля |
Напряженность электрического поля – векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы 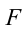 , действующей на , действующей нанеподвижный заряд, помещенный в данную точку поля, к величине этого заряда 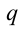 : :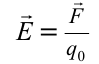 |
| Напряженность поля, создаваемого точечным зарядом 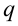 на расстоянии на расстоянии 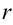 . . |
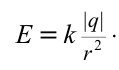 |
| Принцип суперпозиции электрического поля. |
Напряженность электростатического поля, создаваемого в данной точке системой зарядов, равна векторной сумме напряженностей полей, создаваемых в этой точке каждым зарядом в отдельности: 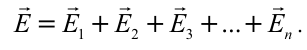 |
| Напряженность электрического поля в точках внутри заряженного шара (сферы) и за его пределами |
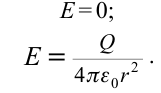 |
| Поляризация диэлектрика. |
Деформация электронной оболочки атомов (молекул) диэлектрика под воздействием электрического поля, в результате чего центры положительных и отрицательных зарядов атома не накладываются друг на друга. |
| Диэлектрическая восприимчивость. |
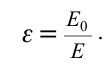 |
| Напряженность поля в точке на расстоянии 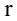 от точечного заряда, от точечного заряда,расположенного внутри диэлектрика. |
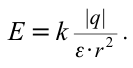 |
Потенциальная энергия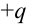 заряда, находящегося заряда, находящегосяна расстоянии 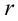 от неподвижного положительного от неподвижного положительногозаряда 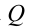 |
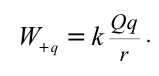 |
| Потенциал точечного заряда 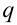 . . |
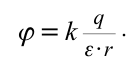 |
| Электрическое напряжение. |
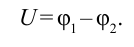 |
| Консервативная сила. | Сила, работа которой не зависит от траектории перемещения. |
| Объемная плотность энергии. |
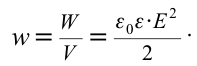 |
Энергия электрического поля
В заряженном конденсаторе обкладки имеют разноименные .заряды и взаимодействуют благодаря наличию электрического поля. О телах, которые взаимодействуют, говорят, что они имеют энергию. Таким образом можно утверждать, что заряженный конденсатор имеет энергию.
Наличие энергии в заряженном конденсаторе можно подтвердить опытами. Для этого возьмем конденсатор довольно большой емкости, источник тока, лампочку и составим цепь, показанную на рисунке 1.44. Сначала переведем переключатель в положение 1, зарядив таким образом конденсатор от источника тока.
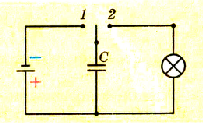
Pиc. 1.44. Схема цепь, в которой лампочка вспыхивает за счет энергии заряженного конденсатора
Если после этого перевести переключатель в положение 2, то увидим кратковременную вспышку света вследствие накала нити лампочки.
Наблюдаемое явление можно объяснить тем, что заряженный конденсатор имел энергию, благодаря которой была выполнена работа по накалу спирали лампочки.
Согласно закону сохранения энергии работа, выполненная при разрядке конденсатора, равна работе, выполненной при его зарядке. Расчет этой работы и соответственно потенциальной энергии заряженного конденсатора должен учитывать особенности процесса зарядки конденсатора. Зависимость заряда Q от времени зарядки t показана на графике (рис. 1.45).
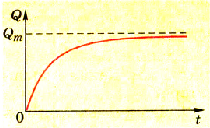
Pиc. 1.45. Изменение заряда конденсатора при его зарядке
Поскольку заряд конденсатора изменяется не пропорционально времени, вести расчет на основании формулы A = QEd нельзя, ведь напряженность поля также все время изменяется. Вместе с тем разность потенциалов между обкладками при зарядке линейно изменяется от нуля до определенного максимального значения (рис. 1.46).
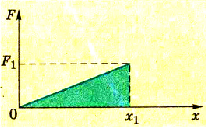
Рис. 1.46. К расчету работы электрического поля в конденсаторе
Поэтому работа, которая выполняется при зарядке конденсатора, равна:
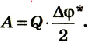
Если учесть, что 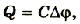 то
то
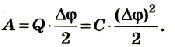
Таким образом, энергия электрического поля в конденсаторе равна:
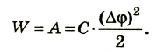
Приняв во внимание, что 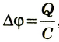 , получим:
, получим: 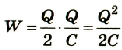 .
.
Задача:
Импульсную контактную сварку медной проволоки совершают при помощи разряда конденсатора электроемкостью 1000 мкФ при разности потенциалов между обкладками 1500 В. Какова средняя мощность импульсного разряда, если его дли тельность 2 мкс и КПД установки равен 4 %?
|
Дано: |
Решение |
| N – ? |
Средняя полезная мощность определяется с учетом времени выполнения работы:
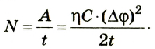
Подставив значения физических величин, получим:
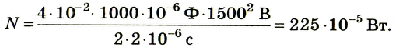
Ответ: полезная мощность, которую развивает сварочная установка, равна 225 ∙ 10-5 Вт.
Влияние электрического поля на живые организмы
Многие люди понятие электричества и электрического поля связывают только с электризацией различных тел, мощными электрическими машинами, средствами электроники и т. п. Вместе с тем электрические явления происходят и в живой природе. И это не только электризация шерсти кошки или собаки, когда их гладят рукой, но и более сложные формы, связанные с их жизнедеятельностью. В природе существуют живые организмы, способные генерировать электричество и использовать его для охоты, защиты и ориентирования в пространстве.
Одним из таких живых существ является электрический угорь (рис. 1.47). Он может генерировать разность потенциалов между отдельными частями своего тела до 360 В. Разряды, которые создает эта рыба, живые существа ощущают на расстоянии до 20 см.

Рис. 1.47 Электрический угорь
Свойства электрического угря использовали древние врачи для лечения подагры, мигрени, эпилепсии и т. п.
Аналогичные свойства и у электрического ската-торпедо (рис. 1.48). Он может на протяжении 15 с генерировать до 150 разрядов за секунду по 80 В каждый.

Pиc. 1.48 Электрический скат
Электрические явления играют существенную роль и в физиологии человека. Одним из мощных генераторов человека является сердце. На рисунке 1.49 показаны о к ни потенциальные поверхности тела человека при активной работе сердца.
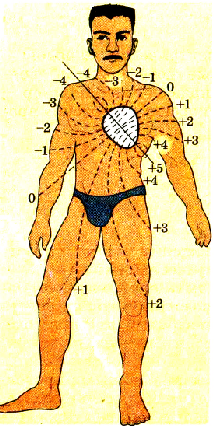
Рис. 1.49. Эквипотенциальные растений.
Хотя эти потенциалы сравнительно невелики – несколько милливольт, но их используют для диагностирования болезней сердца. Записывая эти потенциалы, специальные аппараты создают кардиограммы, по которым врач определяет состояние человека.
В физиотерапевтических кабинетах используют лечебный метод -фарадизацию, когда человека подвергают действию электрического поля и таким образом лечат некоторые болезни.
Исследования ученых показали, что под действием электрического поля улучшаются свойства семян растений. Растения, выращенные поверхности человека из таких семян, существенно улучшают спою урожайность. Даже трава растет интенсивнее под линиями электропередач, где существует сильное электрическое поле.
Если человека определенным образом изолировать от действия электрического поля «Земли, то его состояние существенно ухудшается. Некоторые люди чувствуют себя не комфортно в цельнометаллических вагонах, самолетах, автомобилях, где электрическое поле Земли экранируется металлическими корпусами транспортных средств.
- Электрическое поле заряженных неподвижных тел
- Напряженность электрического поля
- Принцип суперпозиции электрических полей
- Проводники в электрическом поле
- Электрическое поле заряженного шара
- Электрические явления в физике
- Потенциал поля точечного заряда в физике
- Работа электрического поля при перемещении заряда в физике
Исходя из опытов, заряженный конденсатор имеет запас энергии.
Энергия заряженного конденсатора равняется работе внешних сил, которая необходима для его зарядки.
Его заряжение представляется как последовательный перенос малых порций заряда ∆q>0 с одной обкладки на другую, как изображено на рисунке 1.7.1 Одна из них заряжается положительным зарядом, другая – отрицательным. Процесс производится при уже имеющемся некотором заряде q, тогда как между обкладками существует разность потенциалов U=qC, а при переносе ∆q внешние силы совершают работу ∆A=U∆q=q∆qC.
Нахождение энергии We конденсатора с емкостью С и с зарядом Q производится с помощью интегрирования в переделах от 0 до Q. Формула примет вид:
We=A=Q22C.
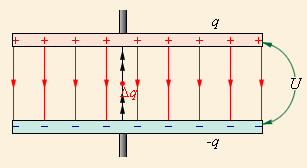
Рисунок 1.7.1. Процесс зарядки конденсатора.
Энергия заряженного конденсатора
Существует еще одна эквивалентная запись заряженного конденсатора при использовании соотношения Q=CU:
We=Q22C=CU22=QU2.
Электрическая энергия We рассматривается как потенциальная. Формулы для We аналогичны формулам потенциальной энергии Ep деформированной пружины, а именно:
Ep=kx22=F22k=Fx2, где k является жесткостью пружины, х – деформацией, F=kx – внешней силой.
Современные представления электрической энергии говорят о том, что она сосредоточена между пластинами конденсатора. В связи с этим и получила название энергии электрического поля. Это объяснимо с помощью иллюстрирования заряженного плоского конденсатора.
Объемная плотность электрической энергии
Напряженность однородного поля плоского конденсатора равняется E=Ud, его емкость – C=ε0εSd.
Отсюда следует, что We=C·U22=ε0·ε·S·E2·d22d=ε0·ε·E22V, где V=Sd обозначает объем пространства между обкладками с наличием электрического поля. Данное соотношение приводит к формуле следующей физической величины.
Физическая величина We=ε0·ε·E22 – это электрическая энергия на единицу объема пространства, в котором создается электрическое поле. Ее называют объемной плотностью данной электрической энергии.
Энергия поля конденсатора, создаваемая любыми распределениями электрических зарядов в пространстве, находится путем интегрирования We по всему объему, в котором было создано электрическое поле.
1.Энергия системы точечных зарядов.
Энергия системы из двух неподвижных
точечных зарядов в вакууме определяется
формулой (3.20). В диэлектрической среде
с проницаемостью
она принимает вид:
![]()
(7.1)
Если в поле зарядов q1
и q2
внести третий точечный заряд q3,
то энергия системы увеличится на величину
работы внесения третьего заряда
A(q3) = q3
[(q1) + (q2)],
(7.2)
г
де
(q1)
и (q2)
потенциалы полей зарядов q1
и q2
в точке А, куда вносится третий заряд
(рис.40). Отсюда
![]()
(7.3)
Полная энергия
системы из трёх зарядов равна сумме
![]()
(7.4)
Количество зарядов в системе можно
увеличивать таким образом неограниченно.
Энергия системы каждый раз будет
прирастать на величину работы внесения
очередного заряда в поле имеющихся
зарядов. В общем случае при n
зарядах энергия системы определяется
формулой

(7.5)
Коэффициент ½ позволяет учитывать
энергию каждой пары зарядов 1 раз.
2.Электрическая ёмкость проводников
это мера способности проводников
собирать на себе свободные заряды и
аккумулировать вокруг себя энергию
электрического поля. Если постепенно
увеличивать заряд на проводнике, то,
как показывает опыт, для проводника
любой конфигурации и при любом
распределении вокруг него других
проводников и диэлектриков всякое
изменение заряда q
неизбежно вызывает пропорциональное
изменение потенциала проводника ,
так что q = С
(7.6)
Здесь
это потенциал проводника относительно
тех тел, на которых замыкаются силовые
линии поля проводника. Коэффициент
пропорциональности С называют
электрической ёмкостью проводника. Из
выражения
![]()
следует, что чем больше ёмкость проводника
С, тем медленнее увеличивается
потенциал проводника
с ростом заряда q.
Ёмкость проводника не зависит от его
электрических свойств, а определяется
его размерами, геометрической конфигурацией
и диэлектрическими свойствами среды,
в которой находится электрическое поле.
Единица ёмкости в СИ фарад (Ф). Один фарад
это ёмкость такого проводника, изменение
заряда на котором в 1 Кл приводит к
изменению потенциала в 1 В.
Пример 7.1 Электрическая ёмкость
уединённого шара.
Выразив заряд q из
формулы потенциала поверхности заряжённой
сферы (4.10) и подставив его в формулу
(7.6) получаем:
![]()
(7.7)
Вычислим в качестве примера электрическую
ёмкость земного шара в вакууме, где
= 1.
Так как радиус земного шара R = 6,4·106 м,
то C=40R=4·3,14·8,85·1012·6,4·106=
=7,1·104 Ф.
Как видно из этого примера единица
ёмкости фарад очень большая величина.
На практике чаще используются производные
единицы микрофарад(106
Ф), нанофарад(109
Ф), и пикофарад(1012Ф).
3.Конденсаторы
технические устройства, позволяющие
накапливать заряд и аккумулировать
электрическое поле в сравнительно
небольших замкнутых объемах. Первый
конденсатор изобрёл Питер Мушенбрук в
г. Лейдене в 1745 г. (лейденская банка).
Как следует из примера 7.1, электрическая
ёмкость уединённых проводников очень
мала. Даже у столь грандиозного тела
как Земля она не превышает одного
миллифарада. Поэтому электрические
конденсаторы
устройства для накапливания электрического
заряда конструируются
в виде системы из двух проводников,
имеющих, как правило, одинаковую
геометрическую конфигурацию и разделённых
прослойкой диэлектрика.
В зависимости от формы этих двух
проводников их
называют обкладками конденсатора,
различают плоские, сферические и
цилиндрические конденсаторы.
4.Плоский конденсатор. Представляет
собой два плоских параллельных друг
другу проводника, разделённых тонким
слоем диэлектрика (рис.41). Расстояние
между обкладками d
обычно много меньше их площади S.
В электрических устройствах обкладки
конденсатора всегда заряжаются
одинаковыми по величине, но противоположными
по знаку зарядами.
Найдём поле в плоском конденсаторе и
вычислим его электрическую ёмкость.
а. Поле в конденсаторе Пусть на
обкладках конденсатора одинаковые по
величине, но разные по знаку заряды с
поверхностной плотностью σ, так что
|σ+| = |σ|.
Левая обкладка на рис.41 заряжена
положительно, правая
отрицательно.
П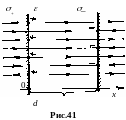
ри
малом расстоянии d
между обкладками их можно считать
бесконечно протяжёнными заряженными
плоскос-тями. Поля обкладок внутри
конденсатора складываются, вне
взаимно уничтожаются. Из формулы поля
бесконечной заряжённой плоскости
(4.18), учитывая, что между обкладками
находится диэлектрик с проницаемостью
ε, получаем:

(7.8)
Д
ля
вычисления потенциала точек поля внутри
конденсатора полагаем потенциал
отрицательной пластины равным 0.
Ориентируем ось х по направлению
силовых линий, начало совместим с
положительной пластиной, тогда положение
отрицательной пластины соответствует
x = d.
Проинтегрируем выражение d
=Edx от произвольной
точки 0 < x < d
до точки d.
![]()
(7.9)
Напряжение
U между обкладками
![]()
(7.10)
Н
а
рисунке 42 показано поле Е внутри и
вне плоского конденсатора (вверху) и
потенциал поля
(внизу). На рис.43 показаны силовые линии
и сечения плоскостью рисунка
эквипотенциальных поверхностей
(штриховые линии). Поле в
плоском конденсаторе однородно. Лишь
на краях обкладок наблюдается нарушение
однородности из-за провисания поля
наружу.
б. Электрическая ёмкость плоского
конденсатора найдётся из формулы
(7.6), где = U
напряжение между обкладками, определяемое
формулой (7.10)

.
(7.11)
Для увеличения ёмкости конденсатора
надо увеличивать площадь обкладок S,
уменьшать расстояние d
между ними и выбирать диэлектрик с
максимально большой проницаемостью ε.
5.Сферический конденсатор образуется
двумя проводящими концентрическими
сферами(рис.44-а). Поле в пространстве
между сферами создаётся только внутренней
сферой. Поэтому напряжённость и потенциал
поля в интервале R1< r < R2
определяется формулами (4.9) и (4.10),
записанными для случая ε ≠ 1(вместо
0
входит произведение 0).
Поле внутри малой сферы и вне большой
равно 0 (рис.44-б).
Н
апряжение
U между обкладками
есть разность потенциалов поля точечного
заряда между точками R1
и R2
(формула 4.10).
![]()
(7.12)
Ёмкость
сферического конденсатора
![]()
.
(7.13)
При R2
получаем ёмкость уединённого шара
(формула 7.7).
Сферические
конденсаторы не имеют широкого
технического применения. В основном
они используются в научных исследованиях,
например, при изучении внешнего
фотоэффекта.
6.Цилиндрический конденсатор
образуется двумя проводящими коаксиальными
цилиндрами (рис.45-а). Как и в сферическом
конденсаторе поле между цилиндрами
создаётся только внутренним цилиндром.
Напряжённость и потенциал в пространстве
R1> r >R2
определяется формулами (4.23) и (4.25),
записанными для случая диэлектрической
сферы (вместо 0
в формулы входит произведение
0)(рис.45-б).
Н
апряжение
между обкладками найдётся из формулы
(4.25), где r0 = R2,
r = R1.
![]()
(7.14)
Здесь
заряд, приходящийся на единицу длины
цилиндров. Ёмкость
цилиндрического конденсатора на каждую
единицу длины равна
![]()
(7.15)
Цилиндрические конденсаторы широко
применяются в технических устройствах.
Обычно они представляют собой керамическую
трубку, на поверхности которой нанесены
металлические слои, играющие роль
обкладок. Формула (7.15) используется при
вычислении волнового сопротивления
коаксиальных кабелей.
Электрическая ёмкость элементов
электрических устройств имеет часто
большое значение для их нормального
функционирования. Поэтому необходимо
знание ёмкостей систем, не являющихся
в обычном смысле конденсаторами. Примером
такой системы является двухпроводная
линия.
П
ример
7.2. Ёмкость двухпроводной линии. Пусть
2 параллельных провода имеют каждый
диаметр 2R и расположены
на расстоянии l друг
от друга. Полагаем, что диаметр проводов
много меньше расстояния между ними,
2R<< l.
Это позволяет считать распределение
заряда на каждом проводе равномерным,
а поле невозмущённым и определяющимся
формулами (4.23) и (4.25).
Пусть оба провода заряжены противоположными
зарядами с одинаковой линейной плотностью
. Для вычисления
напряжения между проводами направим
ось х через центры проводов, начало
оси выберем на левом положительном
проводе (рис.46). Потенциал отрицательного
провода примем за 0.
Напряжённость поля в любой его точке
на оси х есть сумма
![]()
, (7.16)
где
диэлектрическая проницаемость сферы.
Проинтегрировав уравнение –d = Edx
от R до l R,
получаем напряжение между проводниками

(7.17)
Ёмкость двухпроводных линий увеличивает
потери в энергосистемах и ограничивает
максимальную частоту электрического
поля в линиях связи.
7
.
Энергия заряженного конденсатора.
Рассмотрим процесс зарядки конденсатора
путём переноса одноимённых зарядов с
одной обкладки на другую. Пусть с левой
обкладки конденсатора на рис.47 переносятся
положительные заряды. Перенос зарядов
приводит к появлению поля в конденсаторе
и должен совершаться за счёт работы
внешних сил. Эта работа идёт на увеличение
энергии электрического поля W.
dA = dW = Udq
(7.19)
Но U = qС,
где q – заряд на правой
по рис.47 обкладке, а С – ёмкость
конденсатора. После интегрирования
получаем :

(7.20)
Используя формулу q = СU,
можно получить три выражения энергии
![]()
(7.21)
8. Плотность энергии электрического
поля. Если площадь пластин конденсатора
велика, по сравнению с расстоянием между
ними, то есть S >>d2,
то поле в плоском конденсаторе практически
однородно и полностью заключено в объёме
конденсатора V = Sd.
Разделив энергию поля W
на объем V, получаем
плотность энергии электрического поля.
![]()
(7.22)
Полученная формула определяет плотность
энергии в зависимости от «точечной»
характеристики поля напряжённости Е,
поэтому применима не только к однородным,
но и к неоднородным полям.
Пример 7.3. Размер электрона. Вычислим
энергию электрического поля уединённой
сферы, имеющей заряд q
и радиус R, воспользовавшись
формулой плотности энергии (7.22).
Проинтегрируем энергию по всему объёму
пространства вне шара.

(7.23)
С уменьшением радиуса сферы R
энергия её поля стремится в бесконечность.
Это обстоятельство ограничивает размер
реальных зарядов снизу.
Например, если полагать, что вся масса
покоя электрона m
обусловлена его электрическим полем,
то W = mc2,
где с скорость света в вакууме.
Отсюда

Это минимально возможный радиус
электрона.
У частиц с большой массой, например, у
протона, радиус может быть и меньше. Но
предположение о том, что масса покоя
частицы обусловлена исключительно её
электрическим полем остаётся всего
лишь гипотезой, которая не может объяснить
массу нейтральных частиц, например,
нейтронов.
9
.
Притяжение обкладок конденсатора.
Поскольку обкладки имеют разный по
знаку заряд, то они притягиваются друг
к другу. Найдём силу притяжения обкладок
плоского конденсатора, предположив,
что одна из них смещается на расстояние
dl за счёт энергии поля
(рис.48).
Изменение энергии dW = dA = Fdl.
Отсюда
![]()
.
Но
![]()
.
Тогда
![]()
.
(7.24)
Знак «минус» означает, что пластины
притягиваются.
10. Неустойчивость электростатических
систем. В 1839 г.
английский математик С. Ирншоу
сформулировал и доказал теорему:
совокупность неподвижных частиц,
взаимодействующих между собой с силой,
обратно пропорциональной квадрату
расстояния (притягивающихся или
отталкивающихся) не может образовывать
устойчивой равновесной системы.
Доказательство
теоремы Ирншоу основано на том, что
потенциальная энергия системы электрически
заряженных частиц не имеет минимума.
Это значит, что совокупность неподвижных
электрических зарядов, находящихся на
конечном расстоянии друг от друга, не
может находиться в устойчивом равновесии.
Теорема
Ирншоу сыграла большую роль в развитии
теории строения атома, поскольку из нее
следует динамическая модель атома.
Стационарный атом не может быть построен
из неподвижных зарядов, связанных только
электрическими силами.
Глава.
2. Законы
постоянного тока и его природа в
разных средах.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Энергия заряженного конденсатора. Калькулятор онлайн для любых конденсаторов.
Онлайн калькулятор вычисления энергии электростатического поля заряженного конденсатора, позволит найти энергию заряженного конденсатора через напряжение, емкость и электрический заряд на одной из обкладок. Калькулятор произведет вычисление и даст подробное решение. Единицы измерения, могут включать любые приставки Си. Калькулятор автоматически переведет одни единицы в другие.
Калькулятор вычислит:
Энергию заряженного конденсатора через напряжение (разность потенциалов), до которого заряжен конденсатор и емкость.
Энергию заряженного конденсатора через напряжение (разность потенциалов), до которого заряжен конденсатор и электрический заряд на одной из обкладок
Энергию заряженного конденсатора через электрический заряд на одной из обкладок и емкость
Так же для вычисления энергии электростатического поля плоского, цилиндрического и сферического конденсаторов, можно воспользоваться
калькулятором вычисления энергии заряженного конденсатора для плоского, цилиндрического и сферического конденсаторов.
Энергия заряженного конденсатора через напряжение (разность потенциалов), до которого заряжен конденсатор и емкость
Энергия заряженного конденсатора через напряжение (разность потенциалов), до которого заряжен конденсатор и емкость определяется формулой, где
C – емкость конденсатора
U – напряжение (разность потенциалов), до которого заряжен конденсатор
Единицей измерения энергии является – Джоуль (Дж, J).
Электроемкость C =
Напряжение U =
Единица измерения энергии W
Энергия заряженного конденсатора через напряжение (разность потенциалов), до которого заряжен конденсатор и электрический заряд на одной из обкладок
Энергия заряженного конденсатора через напряжение (разность потенциалов), до которого заряжен конденсатор и электрический заряд на одной из обкладок определяется формулой, где
q – электрический заряд на одной из обкладок
U – напряжение (разность потенциалов), до которого заряжен конденсатор
Единицей измерения энергии является – Джоуль (Дж, J).
Заряд q =
Напряжение U =
Единица измерения энергии W
Энергия заряженного конденсатора через электрический заряд на одной из обкладок и емкость
Энергия заряженного конденсатора через электрический заряд на одной из обкладок и емкость определяется формулой, где
q – электрический заряд на одной из обкладок
C – емкость конденсатора
Единицей измерения энергии является – Джоуль (Дж, J).
Заряд q =
Электроемкость C =
Единица измерения энергии W
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (физика) |
|
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
|
Оптика |
| Калькулятор отражения и преломления света |
|
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
|
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер по математике |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
| Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |