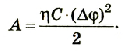Конденсатор. Энергия электрического поля
-
Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.
-
Ёмкость уединённого проводника
-
Ёмкость плоского конденсатора
-
Энергия заряженного конденсатора
-
Энергия электрического поля
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.
Предыдущие две статьи были посвящены отдельному рассмотрению того, каким образом ведут себя в электрическом поле проводники и каким образом — диэлектрики. Сейчас нам понадобится объединить эти знания. Дело в том, что большое практическое значение имеет совместное использование проводников и диэлектриков в специальных устройствах — конденсаторах.
Но прежде введём понятие электрической ёмкости.
к оглавлению ▴
Ёмкость уединённого проводника
Предположим, что заряженный проводник расположен настолько далеко от всех остальных тел, что взаимодействие зарядов проводника с окружающими телами можно не принимать во внимание. В таком случае проводник называется уединённым.
Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду. Коэффициент пропорциональности принято обозначать
, так что
Величина называется электрической ёмкостью проводника и равна отношению заряда проводника к его потенциалу:
(1)
Например, потенциал уединённого шара в вакууме равен:
где — заряд шара,
— его радиус. Отсюда ёмкость шара:
(2)
Если шар окружён средой-диэлектриком с диэлектрической проницаемостью , то его потенциал уменьшается в
раз:
Соответственно, ёмкость шара в раз увеличивается:
(3)
Увеличение ёмкости при наличии диэлектрика — важнейший факт. Мы ещё встретимся с ним при рассмотрении конденсаторов.
Из формул (2) и (3) мы видим, что ёмкость шара зависит только от его радиуса и диэлектрической проницаемости окружающей среды. То же самое будет и в общем случае: ёмкость уединённого проводника не зависит от его заряда; она определяется лишь размерами и формой проводника, а также диэлектрической проницаемостью среды, окружающей проводник. От вещества проводника ёмкость также не зависит.
В чём смысл понятия ёмкости? Ёмкость показывает, какой заряд нужно сообщить проводнику, чтобы увеличить его потенциал на В. Чем больше ёмкость — тем, соответственно, больший заряд требуется поместить для этого на проводник.
Единицей измерения ёмкости служит фарад (Ф). Из определения ёмкости (1) видно, что Ф = Кл/В.
Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным км.
мкФ.
Как видите, Ф — это очень большая ёмкость.
Единица измерения ёмкости полезна ещё и тем, что позволяет сильно сэкономить на обозначении размерности диэлектрической постоянной . В самом деле, выразим
из формулы (2):
Следовательно, диэлектрическая постоянная может измеряться в Ф/м:
Ф.
Так легче запомнить, не правда ли?
к оглавлению ▴
Ёмкость плоского конденсатора
Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.
Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости — но на сей раз о ёмкости этой системы проводников.
Наиболее простым и важным примером такой системы является плоский конденсатор. Он состоит из двух параллельных металлических пластин (называемых обкладками), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров.
Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух
Пусть заряды обкладок равны и
. Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина
— заряд положительной обкладки — называется зарядом конденсатора.
Пусть — площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.
Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости:
Здесь — напряжённость поля положительной обкладки,
— напряженность поля отрицательной обкладки,
— поверхностная плотность зарядов на обкладке:
На рис. 1 (слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора.

Рис. 1. Электрическое поле плоского конденсатора
Согласно принципу суперпозиции, для результирующего поля имеем:
Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга):
Внутри конденсатора поле удваивается:
или
(4)
Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак:
Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4). Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.
Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты: поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.
Пусть расстояние между обкладками конденсатора равно . Поскольку поле внутри конденсатора является однородным, разность потенциалов
между обкладками равна произведению
на
(вспомните связь напряжения и напряжённости в однородном поле!):
(5)
Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками:
(6)
Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на В. Формула (6), таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.
Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора:
(7)
Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними.
Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Как изменится ёмкость конденсатора?
Напряжённость поля внутри конденсатора уменьшится в раз, так что вместо формулы (4) теперь имеем:
(8)
Соответственно, напряжение на конденсаторе:
(9)
Отсюда ёмкость плоского конденсатора с диэлектриком:
(10)
Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор.
Важное следствие формулы (10): заполнение конденсатора диэлектриком увеличивает его ёмкость.
к оглавлению ▴
Энергия заряженного конденсатора
Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится.
Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке. Нетрудно понять, что этой энергией является потенциальная энергия взаимодействия обкладок конденсатора — ведь обкладки, будучи заряжены разноимённо, притягиваются друг к другу.
Мы сейчас вычислим эту энергию, а затем увидим, что существует и более глубокое понимание происхождения энергии заряженного конденсатора.
Начнём с плоского воздушного конденсатора. Ответим на такой вопрос: какова сила притяжения его обкладок друг к другу? Величины используем те же: заряд конденсатора , площадь обкладок
.
Возьмём на второй обкладке настолько маленькую площадку, что заряд этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой
где — напряжённость поля первой обкладки:
Следовательно,
Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам).
Результирующая сила притяжения второй обкладки к первой складывается из всех этих сил
, с которыми притягиваются к первой обкладке всевозможные маленькие заряды
второй обкладки. При этом суммировании постоянный множитель
вынесется за скобку, а в скобке просуммируются все
и дадут
. В результате получим:
(11)
Предположим теперь, что расстояние между обкладками изменилось от начальной величины до конечной величины
. Сила притяжения пластин совершает при этом работу:
Знак правильный: если пластины сближаются , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины
, то работа силы притяжения получается отрицательной, как и должно быть.
С учётом формул (11) и (7) имеем:
где
Это можно переписать следующим образом:
где
(12)
Работа потенциальной силы притяжения обкладок оказалась равна изменению со знаком минус величины
. Это как раз и означает, что
— потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора.
Используя соотношение , из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):
(13)
(14)
Особенно полезными являются формулы (12) и (14).
Допустим теперь, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью . Сила притяжения обкладок уменьшится в
раз, и вместо (11) получим:
При вычислении работы силы , как нетрудно видеть, величина
войдёт в ёмкость
, и формулы (12) — (14) останутся неизменными. Ёмкость конденсатора в них теперь будет выражаться по формуле (10).
Итак, формулы (12) — (14) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.
к оглавлению ▴
Энергия электрического поля
Мы обещали, что после вычисления энергии конденсатора дадим более глубокое истолкование происхождения этой энергии. Что ж, приступим.
Рассмотрим воздушный конденсатор и преобразуем формулу (14) для его энергии:
Но — объём конденсатора. Получаем:
(15)
Посмотрите внимательно на эту формулу. Она уже не содержит ничего, что являлось бы специфическим для конденсатора! Мы видим энергию электрического поля , сосредоточенного в некотором объёме
.
Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.
Итак, электрическое поле само по себе обладает энергией. Ничего удивительного для нас тут нет. Радиоволны, солнечный свет — это примеры распространения энергии, переносимой в пространстве электромагнитными волнами.
Величина — энергия единицы объёма поля — называется объёмной плотностью энергии. Из формулы (15) получим:
(16)
В этой формуле не осталось вообще никаких геометрических величин. Она даёт максимально чистую связь энергии электрического поля и его напряжённости.
Если конденсатор заполнен диэлектриком, то его ёмкость увеличивается в раз, и вместо формул (15) и (16) будем иметь:
(17)
(18)
Как видим, энергия электрического поля зависит ещё и от диэлектрической проницаемости среды, в которой поле находится.
Замечательно, что полученные формулы для энергии и плотности энергии выходят далеко за пределы электростатики: они справедливы не только для электростатического поля, но и для электрических полей, меняющихся во времени.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Конденсатор. Энергия электрического поля» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023
1 Энергия системы точечных зарядов
Формулу
![]() можно рассматривать как взаимную
можно рассматривать как взаимную
потенциальную энергию зарядов![]() и
и![]() ,
,
находящихся на расстоянии![]() (рис.1).
(рис.1).

Рис.1
Если мы теперь в поле двух зарядов
![]() и
и![]() внесем
внесем
третий заряд![]() ,
,
то благодаря свойству аддитивности
энергии взаимодействий, получим:
![]() .
.
Преобразуем эту сумму следующим образом.
Представим каждое слагаемое
![]() в симметричном виде:
в симметричном виде:![]() ,
,
поскольку![]() .
.
Тогда
![]() .
.
Сгруппируем члены с одинаковыми первыми
индексами:
![]()
Каждая сумма в круглых скобках – это
энергия
![]() взаимодействия
взаимодействия![]() -го
-го
заряда с остальными зарядами.
Поэтому можно последнее выражение
переписать так:
![]()
Обобщим это выражение на систему,
состоящую из
![]() точечных зарядов
точечных зарядов![]() .
.
Итак, энергия взаимодействия системы
точечных зарядов
![]() (3.1)
(3.1)
Имея в виду, что
![]() ,
,
где![]() -i-ый заряд системы,
-i-ый заряд системы,![]() – потенциал, создаваемый всеми зарядами,
– потенциал, создаваемый всеми зарядами,
кроме![]() ,
,
в той точке, где находится заряд![]() ,
,
получим окончательное выражение:
![]() (3.2)
(3.2)
Если заряды распределены непрерывно,
то, разлагая систему зарядов на
совокупность элементарных зарядов
![]() и переходя от суммирования в (3.2) к
и переходя от суммирования в (3.2) к
интегрированию, получаем
![]() ,
,
(3.3)
где
![]() – потенциал, создаваемый всеми зарядами
– потенциал, создаваемый всеми зарядами
системы в элементе объемом![]() .
.
2 Энергия заряженных проводника и конденсатора
Энергия уединенного проводника.
Пусть проводник имеет заряд![]() и потенциал
и потенциал![]() .
.
Поскольку![]() на поверхности проводника, получим
на поверхности проводника, получим
![]()
Учитывая, что
![]()
![]() (3.4)
(3.4)
Любое из этих выражений определяет
энергию заряженного проводника.
Энергия заряженного конденсатора.
Предположим, что (+![]() )
)
и![]() – заряд и потенциал положительно
– заряд и потенциал положительно
заряженной обкладки конденсатора, (-![]() )
)
и![]() – отрицательно заряженной обкладки
– отрицательно заряженной обкладки
(рис. 2).

Рис. 2
Согласно формуле (3.3) интеграл можно
разбить на две части – для одной и другой
обкладок. Тогда
![]() .
.
Приняв во внимание, что
![]() ,
,
получим для энергии заряженного
конденсатора три выражения:
![]() (3.5)
(3.5)
3 Энергия и плотность энергии электрического поля
Выразим энергию заряженного плоского
конденсатора через напряженность
![]() электрического поля. Подставим в формулу
электрического поля. Подставим в формулу
![]() выражение
выражение![]() ,
,
получим
![]() .
.
Поскольку
![]() и
и![]() (объем между обкладками конденсатора),
(объем между обкладками конденсатора),
то
![]() .
.
Как будет показано в следующей главе,
вспомогательной характеристикой поля
в веществе является вектор электрического
смещения
![]() ,
,
который связан с вектором напряженности
электрического поля![]() соотношением
соотношением![]() .
.
С учетом этого соотношения полученную
формулу можно представить в виде:
 (3.6)
(3.6)
Эти формулы справедливы для однородного
поля, заполняющего объем
![]() .
.
Энергия распределена по объему
конденсатора равномерно. Следовательно,
в единице объема поля содержится энергия
![]() (3.7)
(3.7)
Выражения (3.7) определяют плотность
энергии электрического поля.
Формулы (3.7) справедливы для любого
электрического поля. Если поле неоднородно,
то плотность энергии в некоторой точке
определяется по формулам (3.7) подстановкой
значений
![]() (или
(или![]() )
)
и![]() в этой точке.
в этой точке.
Зная плотность энергии в каждой точке,
можно найти энергию поля, заключенную
в любом объеме
![]() .
.
Для этого нужно вычислить интеграл
![]() (3.8)
(3.8)
Примеры решения задач
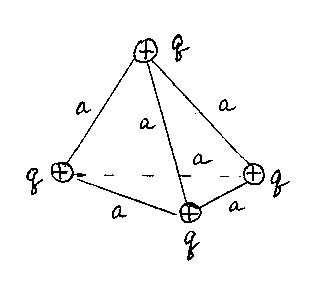
Задача 1Четыре одинаковых точечных
заряда![]() находятся
находятся
в вершинах тетраэдра с ребром![]() .
.
Найти энергию взаимодействия зарядов
этой системы.
Решение:
-
способ. Энергия взаимодействия каждой
пары зарядов здесь одинакова и равна
![]() .
.
Как видно из рисунка, всего таких
взаимодействующих пар шесть, поэтому
энергия взаимодействия всех точечных
зарядов данной системы
![]() .
.
2. способ.
![]() ,
,
где потенциал![]() в месте нахождения одного из зарядов,
в месте нахождения одного из зарядов,
равен![]() .
.
Поэтому
![]() .
.
Задача 2(С.3.114)Точечный заряд![]() = 1 мкКл помещается в центре шарового
= 1 мкКл помещается в центре шарового
слоя из однородного и изотропного
диэлектрика с![]() = 3. Внутренний радиус слоя
= 3. Внутренний радиус слоя![]() = 100 мм, внешний
= 100 мм, внешний![]() = 200 мм. Найти энергию
= 200 мм. Найти энергию![]() ,
,
заключенную в пределах диэлектрика.
Решение:
Напряженность поля в диэлектрике
![]() .
.
Разобьем диэлектрик на шаровые слои
радиуса
![]() и толщины
и толщины![]() .
.
Объем слоя![]() .
.
Плотность энергии в слое
![]()
Энергия, заключенная в слое
![]() :
:
![]()
Проинтегрировав это выражение по
![]() в пределах от
в пределах от![]() до
до![]() ,
,
найдем энергию, заключенную в диэлектрике:
![]() Дж.
Дж.
Задача 3Найдем работу, которую надо
совершить против электрических сил,
чтобы удалить диэлектрическую пластинку
из плоского заряженного конденсатора.
Предполагается, что заряд![]() конденсатора
конденсатора
остается постоянным. Емкость конденсатора
без диэлектрика равна![]() .
.
Решение:
Работа против электростатических сил
в этой системе пойдет на приращение ее
электрической энергии:
![]() ,
,
где
![]() – энергия поля между обкладками
– энергия поля между обкладками
конденсатора при наличии диэлектрика,![]() – при отсутствии диэлектрика. Отсюда
– при отсутствии диэлектрика. Отсюда
![]() .
.
Задача 4(С 3.111)Заряд![]() распределен равномерно по объему шара
распределен равномерно по объему шара
радиусом![]() .
.
Полагая![]() =1, найти электрическую энергию шара
=1, найти электрическую энергию шара![]() ,
,
а также отношение энергии![]() ,
,
локализованной внутри шара, к энергии![]() в окружающем пространстве.
в окружающем пространстве.
Решение:
Прежде всего найдем с помощью теоремы
Гаусса поле внутри и вне шара:
![]() (
(![]() );
);![]() (
(![]() ).
).
Теперь вычислим электрическую энергию
шара:
 .
.
Отсюда следует:
![]() ;
;![]() .
.
Тесты
1.
Емкость плоского конденсатора
пропорциональна:
1.
расстоянию между его пластинами. 2.
отношению площади его пластин к расстоянию
между ними. 3. произведению площади его
пластин на расстояние между ними. 4.
заряду пластин. 5. потенциалу пластин.
2.
Напряженность электрического поля
внутри проводника:
1.
определяется объемной плотностью заряда
в проводнике. 2. равняется нулю. 3.
определяется зарядом на поверхности
проводника. 4. определяется потенциалом
проводника. 5. зависит от напряженности
электрического поля в пространстве,
окружающем проводник.
3.
Три конденсатора одинаковой емкости
соединены параллельно. Результирующая
емкость получается
1.
равной емкости каждого из конденсаторов.
2. в три раза меньше емкости каждого из
конденсаторов. 3. в три раза больше
емкости каждого из конденсаторов.
4. Электроемкость проводника зависит
от:
1. формы и размеров, 2. площади
поверхности, 3. массы и рода вещества,
4. заряда и напряжения, 5. свойств
окружающей среды.
1.1., 2., 3. 2. 3., 4., 5. 3. 1., 2., 5.
4. 2., 3., 5.
5. Емкость батареи состоящей из пяти
одинаковых конденсаторов емкостью 1
мкФ, изображенной на рисунке равна:
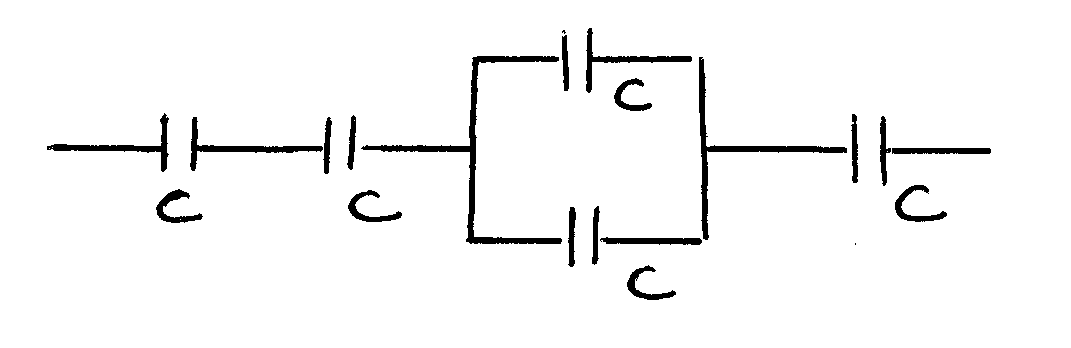
1. 3,5 мкФ 2. 0,286 мкФ 3. 5 мкФ
4. 0,2 мкФ
6. Взаимной электроемкостью тел называют:
-
 2.
2.
 3.
3.
 .
.
7. Плоский воздушный конденсатор
подключили к источнику тока, а затем не
отключая от источника, погрузили в
керосин с диэлектрической проницаемостью,
равной 2. Найти отношение заряда,
первоначально находившегося на обкладках
конденсатора, к конечному заряду.
1. 0,5 2. 1 3. 2 4. 4.
8. Разность
потенциалов между обкладками конденсаторов
емкостью![]() мкФ
мкФ
изменилась на 175 В. Определите изменение
заряда конденсатора.
1.![]() Кл
Кл
2.![]() Кл
Кл
3.![]() Кл
Кл
4.0.
9. Указать неправильнуюформулу для
электроемкости плоского конденсатора
.
1.
![]() 2.
2.![]() 3.
3.![]() 4.
4.![]() ;
;
10. Конденсатор имеет емкость
![]() пФ.
пФ.
Какой заряд находится на каждой из его
обкладок, если разность потенциалов
между ними![]() В?
В?
1.![]() Кл 2.
Кл 2.![]() Кл
Кл
3.![]() Кл
Кл
4.![]() эВ.
эВ.
11. Потенциал φ, заряд qи
емкость
![]() уединенного проводника связаны
уединенного проводника связаны
соотношением:
1.![]() 2.
2.![]() 3.
3.![]() 4.
4.![]() .
.
12. Изменится ли
заряд конденсатора, подключенного к
источнику напряжения, если раздвинуть
его пластины?
1. заряд конденсатора
увеличится 2. заряд конденсатора не
изменится 3. заряд конденсатора
уменьшится 4. заряд конденсатора
не зависит от его емкости 5. заряд
конденсатора не зависит от
расстояния между пластинами.
13. Вектор напряженности электростатического
поля:
1. ортогонален эквипотенциальной
поверхности 2. направлен по касательной
к эквипотенциальной поверхности 3.
направлен под углом π./4 к эквипотенциальной
поверхности, 4. может иметь любое
направление.
14. Внутри полой проводящей сферы помещен
электрический заряд. Электрическое
поле будет существовать:
1. и вне и внутри сферы 2. только
вне сферы 3. только внутри сферы
4. ни там, ни там.
15. Электроемкость С уединенной сферы
радиуcаRв
среде равна:
1.![]()
2.![]()
3.![]()
4.![]()
16. Между обкладками конденсатора, на
концах которого поддерживается постоянная
разность потенциалов, поместили слой
диэлектрика с диэлектрической
проницаемостью ε. Напряженность поля
в диэлектрике по отношению к напряженности
поля вне его:
1.увеличилась в ε раз 2. уменьшилась
в ε раз 3.обратилась в нуль 4. не
изменилась.
17. Для проводника,
помещенного в электростатическое поле,
характерно:
1. отсутствие поля
внутри проводника 2. усиление поля
внутри проводника 3. ослабление поля
вблизи острия проводника 4. силовые
линии поля направлены по касательной
к поверхности проводника 5. потенциал
проводника максимален на его поверхности.
18. Изменится ли энергия заряженного
воздушного конденсатора, если, при
отключенном источнике, раздвинуть его
пластины?
1. Изменится за счет энергии внешних
сил, совершающих работу по раздвижению
пластин. 2.Не изменится, так как заряд
на конденсаторе не изменяется
3.Нельзя дать однозначный ответ, так как
не известны численные значения исходных
данных 4.Энергия уменьшится.
19. Потенциальная энергия взаимодействия
пластин заряженного плоского конденсатора
(указать неверныйответ):
1.
![]() 2.
2.![]() 3.
3.![]() 4.
4.![]() ,
,
где
![]() и
и![]() – заряд и потенциал первой пластины,
– заряд и потенциал первой пластины,![]() и
и![]() – заряд и потенциал второй пластины;
– заряд и потенциал второй пластины;
5. все перечисленные варианты правильные.
20. Как изменится
энергия заряженного конденсатора, не
отключенного от источника, если уменьшить
расстояние между обкладками в два раза?
.
1. уменьшится в 2
раза 2. увеличится в 2 раза 3. не
изменится 4. увеличится в 4 раза
5. уменьшится в 4 раза.
21. Плотность энергии wэлектростатического поля с напряженностьюEв среде с диэлектрической
проницаемостью ε равна:
1.
![]() 2.
2.![]() 3.
3.![]() 4.
4.![]() .
.
22. Какую из формул нельзя использовать
для расчета энергии заряженного
конденсатора?
1.
![]() 2.
2.![]() 3.
3.![]() 4.
4.![]()
15
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Энергия электрического поля:
Для зарядки проводника выполняется работа по преодолению силы отталкивания между зарядами. За счет этой работы проводник получает энергию. Полученная энергия заряженного тела количественно равна работе, выполненной при его зарядке, т.е. 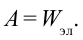

Среднее значение потенциала тела равно среднему арифметическому его начальных и конечных значений, т.е.

Поставляя значении 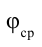 в уравнение (7.21), получим следующее выражение:
в уравнение (7.21), получим следующее выражение:

Значит, работа, выполненная при зарядке тела, равняется половине произведения его заряда на потенциал. При зарядке тела его потенциал плавно, т.е. линейно изменяется согласно формуле 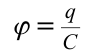 . Здесь
. Здесь 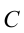 – электрическая емкость проводника. Тогда выражение (7.23) можно записать следующим образом:
– электрическая емкость проводника. Тогда выражение (7.23) можно записать следующим образом:

Согласно соотношению 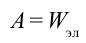 , формулу для расчета энергии электрического поля изолированного заряженного тела можно записать в виде
, формулу для расчета энергии электрического поля изолированного заряженного тела можно записать в виде
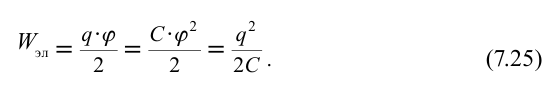
Если заряженное тело является конденсатором, то при расчете энергии (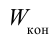 ) его электрического поля величину заряда в формуле (7.25) нужно заменить на величину зарядов на одной обкладке конденсатора, а потенциал заменить на разницу потенциалов между обкладками, т.е., можно записать:
) его электрического поля величину заряда в формуле (7.25) нужно заменить на величину зарядов на одной обкладке конденсатора, а потенциал заменить на разницу потенциалов между обкладками, т.е., можно записать:
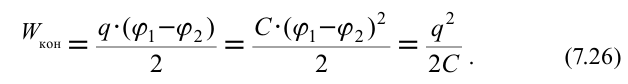
Исходя из этого, формулу определения электрической энергии конденсатора можно записать в виде:
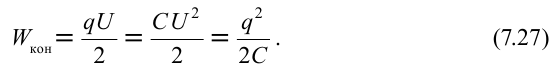
Энергия заряженного тела сосредоточена в электрическом поле, созданном вокруг него, величина энергии зависит от объема пространства, занимаемого полем и напряженности поля.
Рассмотрим частный случай плоского заряженного конденсатора.
Электрическое поле, созданное зарядами обкладок плоского конденсатора, сосредоточено в среде между его обкладками. Объем пространства можно вычислить по формуле 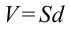 .
.
Учитывая емкость заряженного плоского конденсатора 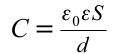 и зависимость между разницей потенциалов обкладок и напряженностью поля конденсатора, с учетом формулы (7.27), получим следующее соотношение:
и зависимость между разницей потенциалов обкладок и напряженностью поля конденсатора, с учетом формулы (7.27), получим следующее соотношение:
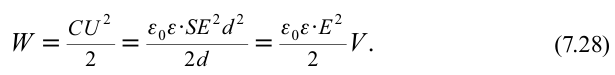
Энергия заряженного плоского конденсатора прямо пропорциональна квадрату напряженности созданного им поля и объему пространства, занимаемого этим полем. Энергия, приходящаяся на удельную единицу поля, называется объемной плотностью энергии. То есть:
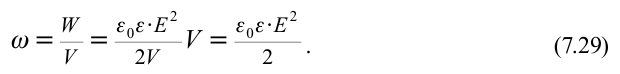
Каждый конденсатор имеет свойство накапливать в себе не только заряд, но и энергию. Энергия, полученная конденсатором, сосредоточена в среде между его обкладками. Эту энергию невозможно хранить длительное время. Конденсатор с течением времени передает полученный заряд в окружающую среду, т.е. разряжается.
При разрядке конденсатора через цепь с маленьким электрическим сопротивлением энергия передается практически мгновенно.
Образец решения задачи:
Емкость плоского воздушного конденсатора равна 0,1 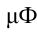 , разность потенциалов 200 В. Вычислите энергию электрического поля в конденсаторе.
, разность потенциалов 200 В. Вычислите энергию электрического поля в конденсаторе.
Дано:
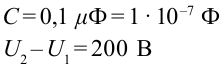
Найти:
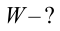
Формула:
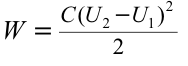
Решение:
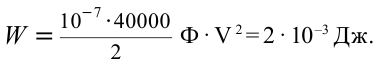
Ответ: 2 мДж.
Основные понятия, правила и законы:
| Закон сохранения зарядов | Алгебраическая сумма зарядов всех тел внутри любой закрытой системы не меняется, т.е.: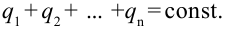 |
| Силовые линии электрического поля |
Линии, показывающие направления силы, действующие со стороны поля на положительный заряд, введенный в электрическое поле. Силовые линии электрического поля, образованного положительным зарядом, направлены от заряда, а в случае отрицательного заряда – направлены к нему. |
| Напряженность электрического поля |
Напряженность электрического поля – векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы 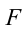 , действующей на , действующей нанеподвижный заряд, помещенный в данную точку поля, к величине этого заряда 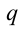 : :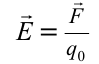 |
| Напряженность поля, создаваемого точечным зарядом 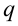 на расстоянии на расстоянии 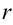 . . |
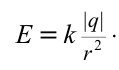 |
| Принцип суперпозиции электрического поля. |
Напряженность электростатического поля, создаваемого в данной точке системой зарядов, равна векторной сумме напряженностей полей, создаваемых в этой точке каждым зарядом в отдельности: 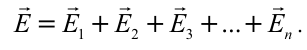 |
| Напряженность электрического поля в точках внутри заряженного шара (сферы) и за его пределами |
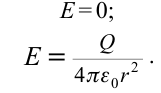 |
| Поляризация диэлектрика. |
Деформация электронной оболочки атомов (молекул) диэлектрика под воздействием электрического поля, в результате чего центры положительных и отрицательных зарядов атома не накладываются друг на друга. |
| Диэлектрическая восприимчивость. |
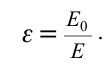 |
| Напряженность поля в точке на расстоянии 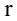 от точечного заряда, от точечного заряда,расположенного внутри диэлектрика. |
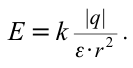 |
Потенциальная энергия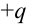 заряда, находящегося заряда, находящегосяна расстоянии 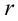 от неподвижного положительного от неподвижного положительногозаряда 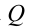 |
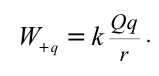 |
| Потенциал точечного заряда 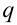 . . |
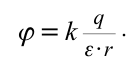 |
| Электрическое напряжение. |
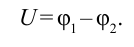 |
| Консервативная сила. | Сила, работа которой не зависит от траектории перемещения. |
| Объемная плотность энергии. |
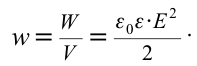 |
Энергия электрического поля
В заряженном конденсаторе обкладки имеют разноименные .заряды и взаимодействуют благодаря наличию электрического поля. О телах, которые взаимодействуют, говорят, что они имеют энергию. Таким образом можно утверждать, что заряженный конденсатор имеет энергию.
Наличие энергии в заряженном конденсаторе можно подтвердить опытами. Для этого возьмем конденсатор довольно большой емкости, источник тока, лампочку и составим цепь, показанную на рисунке 1.44. Сначала переведем переключатель в положение 1, зарядив таким образом конденсатор от источника тока.
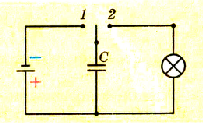
Pиc. 1.44. Схема цепь, в которой лампочка вспыхивает за счет энергии заряженного конденсатора
Если после этого перевести переключатель в положение 2, то увидим кратковременную вспышку света вследствие накала нити лампочки.
Наблюдаемое явление можно объяснить тем, что заряженный конденсатор имел энергию, благодаря которой была выполнена работа по накалу спирали лампочки.
Согласно закону сохранения энергии работа, выполненная при разрядке конденсатора, равна работе, выполненной при его зарядке. Расчет этой работы и соответственно потенциальной энергии заряженного конденсатора должен учитывать особенности процесса зарядки конденсатора. Зависимость заряда Q от времени зарядки t показана на графике (рис. 1.45).
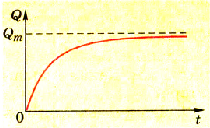
Pиc. 1.45. Изменение заряда конденсатора при его зарядке
Поскольку заряд конденсатора изменяется не пропорционально времени, вести расчет на основании формулы A = QEd нельзя, ведь напряженность поля также все время изменяется. Вместе с тем разность потенциалов между обкладками при зарядке линейно изменяется от нуля до определенного максимального значения (рис. 1.46).
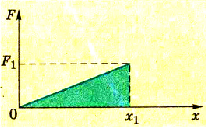
Рис. 1.46. К расчету работы электрического поля в конденсаторе
Поэтому работа, которая выполняется при зарядке конденсатора, равна:
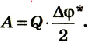
Если учесть, что 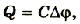 то
то
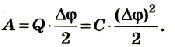
Таким образом, энергия электрического поля в конденсаторе равна:
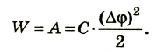
Приняв во внимание, что 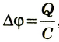 , получим:
, получим: 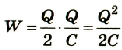 .
.
Задача:
Импульсную контактную сварку медной проволоки совершают при помощи разряда конденсатора электроемкостью 1000 мкФ при разности потенциалов между обкладками 1500 В. Какова средняя мощность импульсного разряда, если его дли тельность 2 мкс и КПД установки равен 4 %?
|
Дано: |
Решение |
| N – ? |
Средняя полезная мощность определяется с учетом времени выполнения работы:
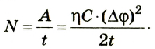
Подставив значения физических величин, получим:
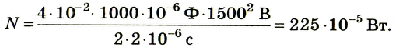
Ответ: полезная мощность, которую развивает сварочная установка, равна 225 ∙ 10-5 Вт.
Влияние электрического поля на живые организмы
Многие люди понятие электричества и электрического поля связывают только с электризацией различных тел, мощными электрическими машинами, средствами электроники и т. п. Вместе с тем электрические явления происходят и в живой природе. И это не только электризация шерсти кошки или собаки, когда их гладят рукой, но и более сложные формы, связанные с их жизнедеятельностью. В природе существуют живые организмы, способные генерировать электричество и использовать его для охоты, защиты и ориентирования в пространстве.
Одним из таких живых существ является электрический угорь (рис. 1.47). Он может генерировать разность потенциалов между отдельными частями своего тела до 360 В. Разряды, которые создает эта рыба, живые существа ощущают на расстоянии до 20 см.

Рис. 1.47 Электрический угорь
Свойства электрического угря использовали древние врачи для лечения подагры, мигрени, эпилепсии и т. п.
Аналогичные свойства и у электрического ската-торпедо (рис. 1.48). Он может на протяжении 15 с генерировать до 150 разрядов за секунду по 80 В каждый.

Pиc. 1.48 Электрический скат
Электрические явления играют существенную роль и в физиологии человека. Одним из мощных генераторов человека является сердце. На рисунке 1.49 показаны о к ни потенциальные поверхности тела человека при активной работе сердца.
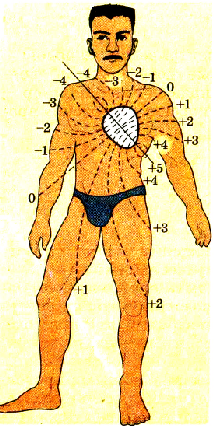
Рис. 1.49. Эквипотенциальные растений.
Хотя эти потенциалы сравнительно невелики – несколько милливольт, но их используют для диагностирования болезней сердца. Записывая эти потенциалы, специальные аппараты создают кардиограммы, по которым врач определяет состояние человека.
В физиотерапевтических кабинетах используют лечебный метод -фарадизацию, когда человека подвергают действию электрического поля и таким образом лечат некоторые болезни.
Исследования ученых показали, что под действием электрического поля улучшаются свойства семян растений. Растения, выращенные поверхности человека из таких семян, существенно улучшают спою урожайность. Даже трава растет интенсивнее под линиями электропередач, где существует сильное электрическое поле.
Если человека определенным образом изолировать от действия электрического поля «Земли, то его состояние существенно ухудшается. Некоторые люди чувствуют себя не комфортно в цельнометаллических вагонах, самолетах, автомобилях, где электрическое поле Земли экранируется металлическими корпусами транспортных средств.
- Электрическое поле заряженных неподвижных тел
- Напряженность электрического поля
- Принцип суперпозиции электрических полей
- Проводники в электрическом поле
- Электрическое поле заряженного шара
- Электрические явления в физике
- Потенциал поля точечного заряда в физике
- Работа электрического поля при перемещении заряда в физике
Электростатика: элементы учебной физики
Продолжение. См. № 17,
18, 19, 20,
21, 22, 23/07
В.В.МАЙЕР,
ГОУ ВПО ГГПИ им. В.Г.Короленко, г. Глазов,
Республика Удмуртия
varaksina_ei@list.ru
Электростатика: элементы учебной
физики
Понятие энергии электрического поля
неразрывно связано с понятиями её накопления и
расходования. Отсюда следует, что должны быть
рассмотрены и накопители этой энергии –
электрические конденсаторы. Существенно при
этом понимание школьниками, насколько большая
энергия может быть сосредоточена в сравнительно
небольшом объёме современного конденсатора.
Особую значимость имеют эксперименты,
показывающие, в каких процессах эта энергия
может быть использована для практических нужд.
Изучение электрической ёмкости и
конденсаторов позволяет сопоставить
примитивные, но принципиально важные методы
электростатики с возможностями современных
электроизмерительных приборов. К ним, в
частности, относятся широко распространённые в
быту цифровые мультиметры, позволяющие измерять
ёмкости от единиц пикофарад. Поэтому можно
сначала оценивать ёмкость и диэлектрическую
проницаемостьметодами электростатики, а затем
более точно измерять эти величины с помощью
мультиметра.
Интересной методической проблемой
является обоснование целесообразности введения
понятия электроёмкости уединённого проводника и
разработка оптимальной методики формирования
этого понятия.
Сформировать понятие энергии
электрического поля в полном объёме на уроках
физики вряд ли удастся. Поэтому в классах
профильного обучения необходимы внеурочные
исследования учащихся.
8.1. Электроёмкость уединённого
проводника
Выполняя исследования, учащиеся,
конечно, заметили, что проводники могут
накапливать и сохранять электрические заряды.
Это свойство проводников характеризуется
электрической ёмкостью. Выясним, как зависит
потенциал уединённого проводника от его заряда.
Потенциал 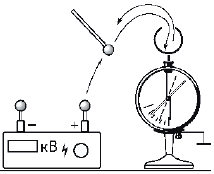 можно измерять относительно бесконечно
можно измерять относительно бесконечно
удалённой точки. На практике удобнее измерять
потенциалы заряженных тел относительно земли.
На стержень электрометра наденем
полый проводящий шар, и корпус электрометра
соединим с заземлением. Электрометр будем
использовать в качестве электростатического
вольт-метра, измеряющего потенциал шара
относительно земли или, что то же самое, разность
потенциалов между шаром и землёй. 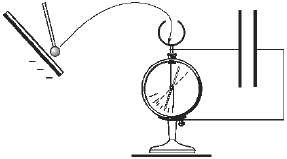
Пробным шариком, прикоснувшись к
кондуктору источника электричества, перенесём
внутрь шара некоторый заряд q. Стрелка
электростатического вольтметра отклонится,
показывая определённый потенциал ![]() . Повторим опыт, сообщая
. Повторим опыт, сообщая
полому шару заряды 2q, 3q… Обнаруживаем,
что стрелка вольтметра отклоняется, показывая
значения 2![]() , 3
, 3![]() …
…
Таким образом, отношение заряда Q
проводящего тела к его потенциалу ![]() остаётся постоянным и
остаётся постоянным и
характеризует электроёмкость проводника: ![]()
Заменим полый шар электрометра другим,
например, меньшего размера, и повторим опыт.
Наблюдаем, что при сообщении ему тех же зарядов q,
2q, 3q, … вольтметр показывает значения,
растущие пропорционально заряду, но б![]() льшие, чем в предыдущей
льшие, чем в предыдущей
серии опытов. Значит, ёмкость C = Q/![]() этого шара меньше.
этого шара меньше.
В системе СИ электрическая ёмкость
выражается в фарадах: 1 Ф = 1 Кл/1 В.
8.2. Электроёмкость сферического
проводника
Пусть в среде с диэлектрической проницаемостью
![]() находится
находится
сферический проводник радиусом R. Если
потенциал в бесконечности считать равным нулю,
то потенциал заряженной сферы ![]()
Тогда электрическая ёмкость сферы радиусом R
есть ![]() Таким
Таким
образом, ёмкость уединённого проводящего шара
пропорциональна его радиусу.
Простые опыты показывают, что тела,
несущие электрический заряд, можно считать
уединёнными в том случае, если окружающие тела не
вызывают значительного перераспределения
заряда на них.
8.3. Конденсатор
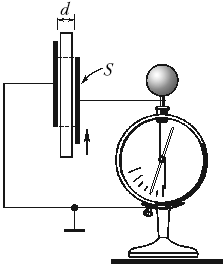
Изготовим конденсатор из двух
одинаковых проводящих пластин, расположенных
параллельно, и соединим его с электрометром,
выполняющим функцию вольтметра. На стержень
электрометра насадим полую проводящую сферу.
Зарядим одну из пластин пробным шариком,
перенеся им заряд q с наэлектризованной
эбонитовой палочки или иного источника
электричества. При этом вольтметр покажет
некоторое напряжение U между пластинами.
Будем переносить внутрь полой сферы, а
значит, и на пластину конденсатора равные заряды.
При этом увидим, что показания вольтметра
увеличиваются на равные значения. Значит,
система двух проводящих пластин обладает
ёмкостью
![]()
(8.1)
и может выполнять функцию
конденсатора – накопителя электрического
заряда. Подчеркнём, что здесь q – заряд одной
из пластин конденсатора.
8.4. Ёмкость плоского конденсатора
Вычислим теоретически электрическую ёмкость
плоского конденсатора. Напряжён ность поля,
создаваемого одной из его пластин ![]() где
где ![]() – поверхностная плотность заряда на
– поверхностная плотность заряда на
пластине. Согласно принципу суперпозиции
напряжённость электрического поля между
пластинами конденсатора в два раза больше (см.
исследование 5.7): ![]()
Так как поле однородное, то разность
потенциалов между пластинами, расположенными на
расстоянии d друг от друга, равна ![]() Отсюда ёмкость плоского
Отсюда ёмкость плоского
конденсатора есть ![]() :
:
![]()
(8.2)
Подтвердим теорию экспериментом. Для
этого соберём плоский конденсатор, зарядим его и
соединим пластины с электростатическим
вольтметром. Оставив заряд конденсатора
неизменным, будем менять остальные его
параметры, наблюдая за вольтметром, показания
которого обратно пропорциональны ёмкости
конденсатора: ![]()
Увеличение расстояния d между
пластинами конденсатора ведёт к
пропорциональному увеличению напряжения между
ними, значит, ёмкость конденсатора С ~ 1/d.
Смещая пластины друг относительно друга так,
чтобы они оставались параллельными, будем
увеличивать площадь перекрытия пластин S.
При этом в той же степени уменьшается напряжение
между ними, т.е. растёт ёмкость конденсатора: С
~ S. Заполним промежуток между пластинами
диэлектриком с диэлектрической проницаемостью ![]() и увидим, что
и увидим, что
показания вольтметра уменьшатся в ![]() раз, т.е. С ~
раз, т.е. С ~ ![]() .
.
Так как заряд системы оставался
неизменным, то можно сделать вывод, что ёмкость
конденсатора прямо пропорциональна площади
перекрытия пластин, обратно пропорциональна
расстоянию между ними и зависит от свойств среды,
т.е. С ~ ![]() S/d,
S/d,
что и подтверждает формулу (8.2). Значение
электрической постоянной ![]() 0 получаем, измерив в опытах U,
0 получаем, измерив в опытах U,
q, d, S, ![]() и вычислив ёмкость один раз по формуле
и вычислив ёмкость один раз по формуле
(8.1), а другой – по формуле (8.2).
8.5. Параллельное соединение
конденсаторов
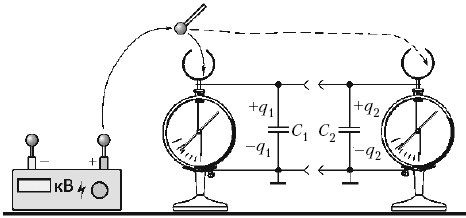
При параллельном соединении двух
конденсаторов ёмкостями С1 и С2
напряжения на них одинаковы и равны U, а
заряды q1 и q2 различны.
Понятно, что общий заряд батареи равен сумме
зарядов конденсаторов q = q1 + q2,
а её ёмкость:
![]()
(8.3)
8.6. Последовательное соединение
конденсаторов
К батарее из двух последовательно
соединённых конденсаторов подключим
электростатический вольтметр с полой сферой.
Сообщим соединённой с вольтметром обкладке
первого конденсатора заряд +q. По индукции
вторая обкладка этого конденсатора приобретёт
заряд –q, а соединённая с ней проводником
обкладка второго конденсатора – заряд +q. В
результате оба конденсатора будут нести
одинаковый заряд q. При этом напряжения на
конденсаторах различны. Понятно, что сумма
напряжений на каждом из конденсаторов равна
общему напряжению батареи:
![]()
Но U = q/С, U1 = q/С1,
U2 = q/С2, поэтому ёмкость
батареи определяется формулой
![]()
(8.4)
8.7. Энергия плоского конденсатора
Сообщим одной из пластин плоского
конденсатора заряд q такой величины, чтобы
разность потенциалов между пластинами стала
равна U. Если расстояние между пластинами d,
то напряжённость электрического поля в
конденсаторе Е = U/d.
Одна из пластин конденсатора с зарядом
q находится в созданном второй пластиной
однородном электрическом поле напряжённостью Е/2,
поэтому на неё действует сила притяжения ко
второй пластине f = qE/2. Потенциальная
энергия заряда q в этом поле равна работе,
которую совершает электрическое поле при
сближении пластин конденсатора вплотную:
![]()
Подставляя в это равенство значение Ed
= U и пользуясь формулой (8.1), получаем, что
энергия электрического поля между пластинами
конденсатора: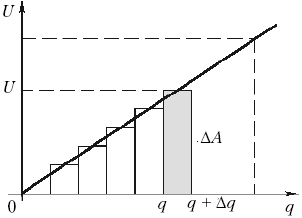
![]()
(8.5)
8.8. Энергия произвольного
конденсатора
Полученная формула справедлива не
только для плоского, но и вообще для любого
конденсатора. Действительно, напряжение на
конденсаторе данной ёмкости прямо
пропорционально его заряду U = q/C. Если заряд
изменился на малую величину ![]() q, то электрическое поле
q, то электрическое поле
совершило работу ![]() А = U
А = U![]() q. Полная работа поля, очевидно,
q. Полная работа поля, очевидно,
равна площади под графиком:
![]()
Ситуация не изменится, если вместо
конденсатора использовать уединённый проводник.
Его потенциал (относительно бесконечности) равен
![]() = q/С,
= q/С,
поэтому энергия электрического поля
![]()
8.9. Экспериментальное определение
энергии, запасённой конденсатором
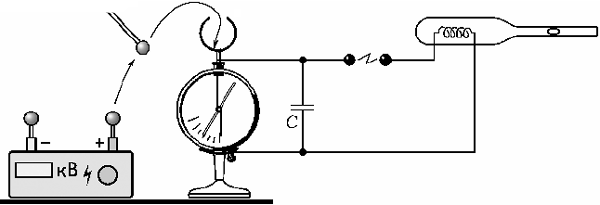
Энергию конденсатора будем измерять
по тепловому действию. В пробирке расположим
тонкую металлическую спираль. Пробирку закроем
пробкой с капиллярной трубкой, внутри которой
находится капля воды. Мы получили газовый
термометр – прибор, в котором смещение капли в
трубке пропорционально количеству теплоты,
выделившемуся в пробирке. К спирали через
разрядный промежуток из двух металлических
шариков подключим конденсатор, параллельно
которому подсоединим электрометр с полым шаром.
Для заряда конденсатора будем использовать
любой источник электричества и металлический
шарик на изолирующей ручке.
Зарядим конденсатор до некоторого
напряжения и, сблизив шарики, разрядим его через
спираль. При этом капля в трубке переместится на
определённое расстояние. Так как разряд
происходит быстро, то процесс нагревания воздуха
в пробирке можно считать адиабатическим, т.е.
происходящим без теплообмена с окружающей
средой.
Подождём, пока воздух в пробирке
охладится, а капля вернётся в исходное положение.
Увеличим напряжение в два, а затем в три раза.
После разрядов капля переместится на расстояние,
соответственно в четыре и девять раз превышающее
первоначальное. Заменим конденсатор на другой,
ёмкость которого в два раза больше, и зарядим его
до исходного напряжения. Тогда при разряде капля
переместится в два раза дальше.
Таким образом, опыт подтверждает
справедливость формулы (8.5) W = СU2/2,
согласно которой энергия, запасённая в
конденсаторе, пропорциональна его ёмкости и
квадрату напряжения.
8.10. Плотность энергии
электрического поля
Выразим энергию электрического поля
между обкладками конденсатора такой формулой,
чтобы в ней не было величин, характеризующих сам
конденсатор, и остались бы только величины,
характеризующие поле. Понятно, что этого можно
достичь только одним способом: вычислить энергию
поля, приходящуюся на единицу объёма. Так как
напряжение на конденсаторе U = Ed, а его
ёмкость ![]() то
то
подстановка этих выражений в формулу (8.5) даёт:
![]()
Величина Sd представляет собой объём V
электрического поля в конденсаторе. Поэтому
плотность энергии электрического поля ![]() пропорциональна
пропорциональна
квадрату его напряжённости.
Исследование 8.1. Измерение
ёмкости плоского конденсатора с помощью
мультиметра
Информация. В последние годы
стали доступны цифровые мультиметры самых
различных типов. Эти приборы в принципе
позволяют измерять напряжение, силу тока,
сопротивление, температуру, ёмкость,
индуктивность, определять параметры
транзисторов. Перечень измеряемых мультиметром
величин определяется типом мультиметра. Нас
сейчас интересуют мультиметры, допускающие
измерение ёмкости; к ним относятся, например,
приборы типов М890G и DТ9208А. Для определённости в
дальнейшем мы будем иметь в виду последний
прибор.
Проблема. Как экспериментально
подтвердить справедливость теоретически
полученной формулы для ёмкости конденсатора?
Задание. Разработайте
демонстрационный эксперимент, позволяющий на
уроке подтвердить справедливость формулы (8.2) для
ёмкости плоского конденсатора с воздушным
диэлектриком.
Вариант выполнения. 
Соберите плоский конденсатор из
круглых пластин, входящих в комплект приборов по
электростатике, и подключите к нему мультиметр.
Линейкой измерьте диаметр пластин и расстояние
между ними. По формуле (8.2) вычислите ёмкость
конденсатора и сравните получившееся значение с
измеренным. В демонстрационном опыте могут
получиться, например, следующие результаты:
диаметр пластин конденсатора D = 0,23 м,
расстояние между пластинами d = 0,01 м,
вычисленная по формуле ёмкость: ![]() мультиметр показывает
мультиметр показывает
такое же значение.
Изменяйте расстояние между
пластинами, площадь перекрытия пластин
конденсатора и вводите между ними различные
диэлектрики. При этом соответствующим образом
изменяются измеренные мультиметром значения
ёмкости конденсатора. Вместе с учащимися
проанализируйте результаты опыта и сделайте
вывод относительно справедливости формулы (8.2).
Исследование 8.2. Определение
диэлектрической проницаемости методом
измерения ёмкости
Задание. Используя цифровой
мультиметр, определите диэлектрические
проницаемости различных веществ.
Вариант выполнения. Соберите
плоский конденсатор с воздушным диэлектриком,
измерьте расстояние d между обкладками и
ёмкость С0 конденсатора. Измерьте
толщину l плоскопараллельной пластины
диэлектрика, аккуратно введите диэлектрик между
обкладками и мультиметром измерьте ёмкость С.
По формуле 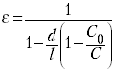
вычислите диэлектрическую проницаемость
вещества. Подскажите учащимся, как выводится эта
формула. Измерьте диэлектрические проницаемости
стекла, оргстекла, винипласта, текстолита,
полиэтилена и т.д. Сравните получившиеся
значения с табличными.
Исследование 8.3. Параллельное и
последовательное соединения конденсаторов
Задание. Используя цифровой
мультиметр, подтвердите справедливость формул
(8.3) и (8.4) для ёмкости параллельно и
последовательно соединённых конденсаторов.
Вариант выполнения. 
Подберите радиотехнические
конденсаторы ёмкостью от десятков пикофарад до
десятков нанофарад и с помощью мультиметра
определите их ёмкости. Обратите внимание на то,
что измеренные значения, как правило, не
совпадают с обозначенными на корпусах
конденсаторов. Это объясняется тем, что
допустимая погрешность ёмкости
радиотехнических конденсаторов достигает 20%.
Конденсаторы соедините параллельно, измерьте
результирующую ёмкость и убедитесь, что она
равна сумме ёмкостей каждого из конденсаторов.
Затем соедините конденсаторы последовательно и
убедитесь, что величина, обратная результирующей
ёмкости, равна сумме величин, обратных ёмкостям
соединённых конденсаторов.
Учащимся можно предложить
количественные задачи по вычислению ёмкости
различных батарей конденсаторов с последующей
проверкой решения в реальном эксперименте.
Исследование 8.4. Работа
электрического поля
Задание. При поднесении
заряженного тела к лежащим на поверхности лёгким
шарикам они начинают подпрыгивать. Используя это
явление, экспериментально покажите, что работа
электрического поля по перемещению заряда
пропорциональна разности потенциалов, которую
прошёл этот заряд: А = qU.
Вариант выполнения. 
Возле дна пластиковой бутылки
горизонтально закрепите неподвижный плоский
электрод, а над ним параллельно – подвижный
электрод. К стенке бутылки приклейте шкалу с
миллиметровыми делениями. Между электродами
поместите пенопластовый шарик, обёрнутый тонкой
алюминиевой фольгой. Электроды подключите к
высоковольтному источнику. При подаче
напряжения на электроды шарик начнёт
подпрыгивать. Увеличивая напряжение, добейтесь
того, чтобы шарик подпрыгивал на высоту h,
равную расстоянию d между электродами. В
этом случае работа электрического поля по
перемещению заряженного шарика А = qU = mgh.
Увеличьте напряжение в два раза и убедитесь, что
высота h также возрастёт в два раза. Сделайте
вывод из опыта.
Заметьте, что разность потенциалов
выражается через напряжённость электрического
поля формулой U = Ed. Так как, по условиям
опыта, h = d, то на оторвавшийся от
нижнего электрода шарик со стороны
электрического поля действует постоянная по
модулю сила F = Eq = mg.
Исследование 8.5.
Электростатический двигатель
Задание. Используйте явление
электрического ветра (см. исследование 7.7) для
построения действующей модели
электростатического двигателя.
Вариант выполнения. Первым
изготовил электростатический двигатель один из
основоположников учения об электричестве,
выдающийся американский учёный Б.Франклин. Так
называемое колесо Франклина имеется в любом
кабинете физики (фото вверху).
Дома школьники могут изготовить
простейшую модель такого двигателя, если на один
из электродов пьезоэлектрического источника
наденут вырезанную из алюминиевой фольги фигуру
в форме сегнерова колеса (фото внизу).
Периодически нажимая на рычаг источника, они
смогут привести получившееся колесо Франклина в
непрерывное вращение.

На фотографии гораздо более мощный
электростатический двигатель, который способен
вращать даже крыльчатку вентилятора. Прибор
собран на пластиковой бутылке.
Исследование 8.6. Энергия
заряженного конденсатора
Задание. Учащиеся надолго
запомнят свойство конденсатора накапливать
электрическую энергию, если прямо на их глазах
собрать конденсатор и продемонстрировать его в
работе. Предложите простой способ изготовления
такого конденсатора, который способен поразить
воображение школьников.
Вариант выполнения. Приготовьте
две дюралевые пластины размером, например, 15 ![]() 15 см. Из толстой
15 см. Из толстой
полиэтиленовой плёнки вырежьте прямоугольник
размером примерно 20 ![]() 20 см и, проложив его между пластинами,
20 см и, проложив его между пластинами,
соберите конденсатор. Включите высоковольтный
источник, установите напряжение 10 кВ и, сблизив
электроды источника, покажите проскакивающую
между ними искру. Затем от того же источника при
том же напряжении зарядите собранный на
демонстрационном столе конденсатор. Разрядите
конденсатор и покажите, что получается гораздо
более мощная искра, чем при разряде между
электродами источника. Обратите внимание на
необходимость соблюдения правил техники
безопасности при работе с конденсаторами.
Исследование 8.7. Батарея
гальванических элементов
Проблема. Учащимся хорошо знакомы
отдельные элементы и батареи гальванических
элементов, которые широко используются в быту.
Школьники знают, что эти приборы характеризуются
напряжением и способны давать электрический ток.
Однако напряжение указанных источников не
превышает нескольких вольт, а в электростатике
используются напряжения в тысячи и десятки тысяч
вольт. Поэтому заряды на электродах
гальванических источников практически никак
себя не проявляют. Как экспериментально
доказать, что на выводах батарей гальванических
элементов действительно имеются электрические
заряды, физическая природа которых такая же, как
тех, которые обнаруживаются в опытах
электростатики?
Задание. Поставьте эксперимент,
позволяющий обнаружить заряды на выводах
батареи гальванических элементов и определить
их знак.
Вариант выполнения. 
В комплект к электрометрам входит
дисковый конденсатор, представляющий собой два
металлических диска диаметром 100 мм, рабочие
поверхности которых покрыты тонким слоем лака.
Один из дисков имеет крепление для насадки на
стержень электрометра, второй снабжён
изолирующей ручкой.
Используя указанное оборудование и
ориентируясь по фотографии, выполните задание.
Исследование 8.8. Оценка энергии
заряженного конденсатора
Информация. Выполняя
исследование 2.7, вы убедились, что энергию
электрического поля можно оценить по вспышке
лампы накаливания, происходящей при разряде
создающих поле заряженных тел. Действительно,
при разряде потенциальная энергия неподвижных
зарядов переходит в кинетическую энергию
движущихся зарядов, заряды нейтрализуются, и
поле исчезает. Движение свободных зарядов по
проводнику вызывает его нагревание.
Задание. Приготовьте две
батарейки по 4,5 В, два электролитических
конденсатора ёмкостью по 1000 мкФ, рассчитанных
на рабочее напряжение не ниже 12 В, и четыре
лампочки для карманного фонаря на напряжение 1 В.
Докажите, что энергия заряженного конденсатора
пропорциональна его ёмкости и квадрату
напряжения.
Вопросы для самоконтроля
1. Какова методика введения и
формирования понятия электрической ёмкости
проводника и системы проводников?
2. Как в демонстрационном эксперименте
можно обосновать справедливость формулы для
ёмкости плоского конденсатора?
3. Насколько целесообразна
демонстрация непосредственно на уроке сущности
метода определения диэлектрической
проницаемости вещества?
4. Предложите методику введения и
формирования понятия плотности энергии
электрического поля.
5. Разработайте серию
исследовательских заданий учащимся по
экспериментальному обоснованию построения
электростатических двигателей.
6. Перечислите наиболее яркие опыты,
демонстрирующие накопление электрической
энергии конденсаторами.
7. Как доказать, что используемые в быту
батареи гальванических элементов принципиально
ничем не отличаются от электростатических
источников электричества?
8. Какими экспериментами можно
подтвердить, что энергия, запасённая в
конденсаторе, пропорциональна его ёмкости и
квадрату напряжения?
Литература
Бутиков Е.И., Кондратьев А.С.
Физика: Учеб. пособие: В 3 кн. Кн. 2.
Электродинамика. Оптика. – М.: Физматлит, 2004.
Демонстрационный эксперимент по
физике в старших классах средней школы. Т. 2.
Электричество. Оптика. Физика атома: Под ред.
А.А.Покровского. – М.: Просвещение, 1972.
Майер В.В., Майер Р.В. Электричество.
Учебные исследования: Библиотека учителя и
школьника. – М.: ФМЛ, 2007.
Шилов В.Ф. О первоочередных мерах по
материально-техническому обновлению кабинета
физики. – Учебная физика, 2000, № 4.