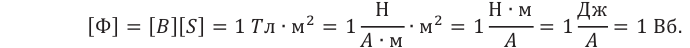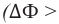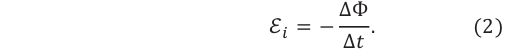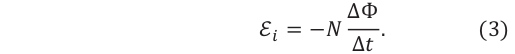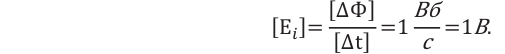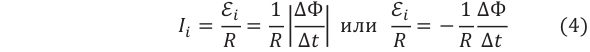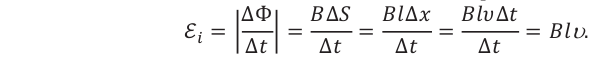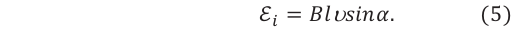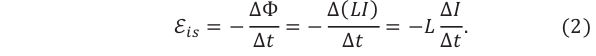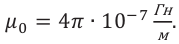Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 января 2022 года; проверки требует 1 правка.
Эне́ргия электромагни́тного по́ля — энергия, заключенная в электромагнитном поле[источник не указан 3862 дня]. Сюда же относятся частные случаи чистого электрического и чистого магнитного поля.
| Виды энергии: | ||
|---|---|---|
| Механическая | Потенциальная Кинетическая |
|
| ‹♦› | Внутренняя | |
| Электромагнитная | Электрическая Магнитная |
|
| Химическая | ||
| Ядерная | ||
 |
Гравитационная | |
 |
Вакуума | |
| Гипотетические: | ||
 |
Тёмная | |
| См. также: Закон сохранения энергии |
Работа электрического поля по перемещению заряда[править | править код]
Понятие работы 


где 
Во многих задачах рассматривается непрерывный перенос заряда в течение некоторого времени между точками с заданной разностью потенциалов 
где 
Мощность электрического тока в цепи[править | править код]
Мощность 

Это наиболее общее выражение для мощности в электрической цепи.
С учётом закона Ома
электрическую мощность, выделяемую на сопротивлении 
так и через напряжение:
Соответственно, работа (выделившаяся теплота) является интегралом мощности по времени:
Энергия электрического и магнитного поля[править | править код]
Для электрического и магнитного полей их энергия пропорциональна квадрату напряжённости поля. Строго говоря, термин «энергия электромагнитного поля» является не вполне корректным. Вместо него в физике обычно используют понятие плотности энергии электромагнитного поля (в определённой точке пространства). Общая энергия поля равняется интегралу плотности энергии по всему пространству.
Плотность энергии электромагнитного поля является суммой плотностей энергий электрического и магнитного полей.
В системе СИ:
В вакууме (а также в веществе при рассмотрении микрополей):
где E — напряжённость электрического поля, B — магнитная индукция, D — электрическая индукция, H — напряжённость магнитного поля, с — скорость света, 



В системе СГС:[1]
Энергия электромагнитного поля в колебательном контуре[править | править код]
Энергия электромагнитного поля в колебательном контуре:
где:
- U — электрическое напряжение в цепи,
- C — электроемкость конденсатора,
- I — сила тока,
- L — индуктивность катушки или витка с током.
Потоки энергии электромагнитного поля[править | править код]
Для электромагнитной волны плотность потока энергии определяется вектором Пойнтинга S (в русской научной традиции — вектор Умова — Пойнтинга).
В системе СИ вектор Пойнтинга равен 
Вместе с тем, формула для плотности потока энергии может быть обобщена для случая стационарных электрических и магнитных полей и имеет тот же вид: 
Факт существования потоков энергии в постоянных электрических и магнитных полях может выглядеть странно, но не приводит к каким-либо парадоксам; более того, такие потоки обнаруживаются в эксперименте.
См. также[править | править код]
- Электричество
- Коэффициент мощности
- Счётчик электрической энергии
Примечания[править | править код]
- ↑ С. А. Ахманов, С. Ю. Никитин. Физическая оптика. — М.: Изд-во МГУ, 1998. ISBN 5-211-04858-X, ISBN 978-5-211-04858-4, на стр. 47
Энергией называется общая количественная
мера различных форм движения материи,
амощностью называется работа,
производимая в единицу времени.
Электромагнитное поле обладает энергией,
значит, ее можно определить. При этом
векторы поля и электродинамические
характеристики среды считаем
известными.
4.1. Баланс энергии электромагнитного поля
Вначале сформулируем
уравнение баланса энергии в общем виде.
Для этого рассмотрим объем V,
заполненный однородной
изотропной средой и ограниченный
поверхностью S.
Пусть в этом объеме за счет действия
сторонних источников выделяется
электромагнитная энергия. Очевидно,
что мощность, выделяемая сторонними
источниками, может расходоваться на
потери в среде, на изменение запаса
энергии внутри объема и на излучение в
окружающую среду через
поверхность S.
При этом должно выполняться следующее
равенство:
|
|
(4.1) |
|
где |
Рст |
|
Рп |
|
|
PΣ |
|
|
W |
|
|
dW/dt |
Уравнение (4.1) дает качественное
представление об энергетических
соотношениях в электромагнитном поле.
Для определения количественных
характеристик воспользуемся уравнениями
Максвелла.
Рассмотрим первое уравнение
Максвелла с учетом сторонних токов из
системы (2.23). Все
члены этого уравнения – векторные
величины, имеющие размерность ампер на
квадратный метр (А/м2).
Чтобы сравнить его с уравнением (4.1)
нужно преобразовать все слагаемые в
скалярные величины, измеряющиеся в
ваттах. Для этого достаточно скалярно
умножить их на вектор Е
и
проинтегрировать
полученное выражение по объему V.
После скалярного умножения получим:
|
|
(4.2) |
Далее необходимо использовать
формулу векторного анализа (1.26) [6] и
выразить из нее произведение Е
rot
Н,
стоящие в правой части уравнения (4.2):
|
|
(4.3) |
Подставим это выражение в
формулу (4.2) и перенесем произведение
вектора напряженности электрического
поля на вектор плотности сторонних
токов в левую часть, а все остальные
слагаемые – в правую. Кроме того, с
помощью второго уравнения Максвелла
заменим rot
Е
на производную по времени от вектора
магнитной индукции с обратным знаком
и с помощью формул (1.9), (1.14) выразим
векторы индукции через соответствующие
векторы напряженности поля и проницаемости.
Получим:
|
|
(4.4) |
Векторное произведение
векторов Е
и Н
обозначается буквой П
и называется вектор
Пойнтинга:
|
|
(4.5) |
Осталось проинтегрировать
уравнение (4.4) по объему V.
В результате получим:
|
|
(4.6) |
В преобразовании уравнения (4.6) использована
теорема Остроградского-Гаусса (1.33) [6].
Кроме того, в последнем слагаемом правой
части уравнения изменен порядок операций
интегрирования и дифференцирования.
Левая часть уравнения (4.6)
определяет мощность, отдаваемую
сторонними токами в объеме V.
Сторонний ток проводимости
– это упорядоченное движение заряженных
частиц. Для простоты положим, что векторы
напряженности электрического поля и
плотности сторонних токов коллинеарны.
Если частицы тормозятся полем, ток
отдает ему свою энергию. Для этого
требуется, чтобы векторы напряженности
электрического поля и плотности
стороннего тока были направлены
противоположно. Значит, скалярное
произведение векторов Е
и Jст
будет отрицательным и левая часть
уравнения (4.5) станет положительной
величиной. Такая ситуация характерна
для работы некоторых передающих антенн.
Если векторы плотности стороннего тока
и напряженности электрического поля
направлены в одну сторону, заряженные
частицы будут ускоряться полем, и ток
станет отбирать у него энергию. Эту
процедуру осуществляют разного рода
приемные антенны, однако энергия, которую
они могут отнять у поля в свободном
пространстве, невелика.
Иначе обстоит дело в волноводах, которые
служат для передачи энергии от источника
к потребителю. На входном конце волновода
сторонние силы реализуют процедуру
возбуждения поля. Когда энергия достигает
конца волновода, ее надо полностью
отобрать у поля и передать потребителю.
Для этого используются приемные
устройства, преобразующие энергию
электрической или магнитной составляющей
поля в ток проводимости и передающие
его дальше. В этом случае требуется
отбирать у поля максимум энергии.
Реальная среда всегда обладает
электропроводностью. Поэтому, зная
напряженность электрического поля и
электропроводность среды, можно найти
мощность тепловых потерь, т. е. энергию,
теряемую электромагнитным процессом
за единицу времени.
|
|
|
Рис. 4.1. К определению |
Электрическая мощность
– это произведение тока на напряжение.
Нам известна напряженность электрического
поля и электропроводность среды. Значит,
можно определить плотность тока
проводимости, создаваемого полем.
Напряженность электрического поля
имеет размерность В/м, а плотность тока
проводимости – А/м2.
Их произведение будет иметь размерность
Вт/м3,
то есть плотности
мощности. Значит,
первое слагаемое в правой части формулы
(4.6), интеграл от плотности мощности,
описывает мощность
потерь.
Обратимся к рис. 4.1, на котором
изображена картина линий вектора
плотности тока проводимости. В объеме
протекания тока выделена цилиндрическая
область V.
Этот цилиндр имеет длину l
и площадь основания S,
а ось его совпадает с направлением
вектора плотности тока проводимости.
Для упрощения решения задачи область
должна быть так мала, чтобы вектор
плотности тока внутри нее можно было
бы считать не зависящим от координат.
В этом случае в соответствии с первым
слагаемым правой части формулы (4.6)
получим:
|
|
(4.7) |
Так как плотность тока
проводимости и напряженность поля не
зависят от координат, они вынесены
из-под знака интеграла. Там остался
только скалярный дифференциал объема.
Его интегрирование по объему дает
величину объема. В средней части формулы
(4.7) объем цилиндра представлен как
произведение площади его основания S
на длину l,
а параллельные векторы
плотности тока и напряженности поля
заменены их модулями. Ток I
в последней части формулы определен
как произведение площади основания
цилиндра на плотность тока, а напряжение
U
– как произведение длины цилиндра на
напряженность электрического поля.
Равенство (4.7) эквивалентно
закону Джоуля – Ленца.
Для выяснения физического
смысла последнего слагаемого в правой
части уравнения (4.6) рассмотрим частный
случай. Предположим, что объем V
окружен идеальной
проводящей оболочкой, совпадающей с
поверхностью S.
Такая оболочка блокирует обмен энергией
с внешней средой, и объем становится
энергетически
изолированным. В
этом случае тангенциальная (касательная)
составляющая напряженности
электрического поля на поверхности S
будет равна нулю. Векторный дифференциал
поверхности dS
совпадает по направлению с ортом внешней
нормали n0.
Следовательно, поверхностный интеграл
в уравнении (4.6) будет равен нулю из-за
того, что нормальная компонента
векторного произведения [Е,
Н] определяется
тангенциальными составляющими
входящих в него векторов.
Предположим, кроме того,
что электропроводность среды в объеме
V
равна нулю. Значит,
тепловые потери исчезнут, и первый
интеграл в правой части уравнения (4.6)
также будет равен нулю. Получим:
|
|
(4.8) |
В таком изолированном объеме
без потерь мощность сторонних источников
может расходоваться только на изменение
запаса энергии электромагнитного поля.
Значит, правая часть уравнения (4.8) равна
скорости изменения энергии электромагнитного
поля, запасенной в объеме V,
а интеграл
в правой части этого уравнения равен
энергии электромагнитного поля в объеме
V:
|
|
(4.9) |
Осталось выяснить физическую
сущность поверхностного интеграла
в уравнении (4.6). Предположим, что потери
внутри объема V
отсутствуют и,
кроме того, величина электромагнитной
энергии остается
постоянной. B
этом случае уравнение (4.6) примет следующий
вид:
|
|
(4.10) |
Потерь в объеме нет, и запас
энергии не меняется, значит, вся мощность
сторонних источников должна излучаться
в окружающее пространство. Следовательно,
поток вектора Пойнтинга П
через поверхность S
равен излучаемой мощности, которую в
уравнении (4.1) мы обозначили РΣ.
Таким образом, качественное
уравнение (4.1) преобразовано в уравнение
(4.6) с помощью которого можно проводить
количественные оценки составляющих
баланса мощности.
Рассмотрим частный случай
отбора энергии электромагнитного поля
сторонними источниками. Пусть энергия
поступает в объем V
из окружающего
пространства. Часть ее преобразуется
в тепло, а другая отбирается сторонними
источниками. При этом количество
электромагнитной энергии, запасенной
в объеме V,
не изменяется. Уравнение
(4.6) в этом случае надо переписать в
следующем виде:
|
|
(4.11) |
Левая часть уравнения (4.11)
определяет мощность, поступающую в
объем V
извне, а правая часть –
мощность, расходуемую в
этом объеме. Это
уравнение было получено Пойнтингом и
носит название теоремы
Пойнтинга в интегральной форме.
Так как левая часть уравнения
(4.11) представляет собой поток энергии,
то вектор Пойнтинга является вектором
плотности потока энергии.
Направление вектора
Пойнтинга в изотропной среде совпадает
с направлением распространения энергии.
Соседние файлы в папке пособия
- #
- #
- #
- #
- #
Раздел 4 Энергия электромагнитного поля.
4.1. Баланс энергий электромагнитного поля.
Как и любая форма материи, электромагнитное поле обладает энергией, которая может распространяться в пространстве и преобразоваться в другие виды энергии.
Сформулируем уравнение баланса электромагнитного поля применительно к некоторому объему V, ограниченному поверхностью S. Пусть, в этом объеме, за счет сторонних источников, выделяется электромагнитная энергия. Из общефизических соображений, очевидно, что мощность сторонних источников будет расходоваться на потери, на изменение энергии и частично будет рассеиваться на поверхности S, уходя во внешнее пространство.
Будем полагать, что среда в объеме V однородная и изотропная. Мощность в объеме V выделяется за счет протекания сторонних токов, в дальнейшем будем пользоваться известными материальными уравнениями:





Материальные уравнения в форме (2) не позволяют учесть потери связанные с явлением поляризации и намагничивания вещества. Уравнение баланса в форме (1) дает качественное представление о балансе энергии. Для получения уравнения необходимо перейти к векторам электромагнитного поля, т.е. воспользоваться уравнениями Максвелла. Для получения количественного соотношения обратимся к уравнениям Максвелла.
Рекомендуемые материалы
-52%
Вариант 14 – ДЗ №2 – Задачи 6.1.14 и 6.2.14
В плоский воздушный конденсатор вдвинули стеклянную пластинку так, что она образовала так, что она образовала с пластинами конденсатора угол α=45º. Определить на какой угол β от своего первоначального направления отклонятся силовые линии электрическо
FREE
К-5, К-11, К-69, К-65, К-4, К-70
Лабораторная работа – Кинетика ядерных реакторов (Лаб 1+2+3+4)
Тонкое плоское кольцо, внутренний и внешний радиусы которого равны 20 и 40 см, соответственно, равномерно заряжено до 0.6 мкКл. Определить потенциал поля в точке, лежащей на перпендикуляре, проведенном через центр кольца, и отстоящей на 25 см от ц
Запишем первое уравнение Максвелла с учетом сторонних токов:

Размерность входящих в (3) составляющих 
Для получения уравнения, аналогичного (1), надо уравнение (3) преобразовать в скалярное и обеспечить размерность слагаемых в Ваттах. Указанный алгоритм можно реализовать, если каждое из слагаемых умножить скалярно на 
Умножим все составляющие на Е, получим:

Преобразовав левую часть (4) используем известное векторное тождество:

Выразим, 


Подставляя правую часть (6) в левую часть (4) получим:

Преобразуем предыдущее выражение следующим образом:
Также (7) можно записать следующим образом:



В последнем соотношении (9) мы сделаем следующее:
1) поменяем порядок дифференцирования по времени, и интегрирования по объему.
2) При интегрировании по объему воспользуемся теоремой Остроградского – Гаусса.
Для цилиндрического проводника с током I: 
Для элементарного цилиндрического проводника, концы которого перпендикулярны линиям тока:

Для произвольного объема:

В выражении (11) первый интеграл это мощность потерь.
В левой части (9) стоит мощность, выделяемая сторонними токами в объеме V. Ток проводимости, который представляет собой упорядоченное движение заряженных частиц, отдает энергию электромагнитного поля, если частицы попадают в тормозящее электромагнитное поле.
Для того, чтобы электромагнитное поле было тормозящим необходимо чтобы скалярное произведение удовлетворяло следующему условию: 
При этом левая часть (9) становится положительной величиной.
Рассмотрим второе слагаемое правой части. Будем полагать, что поверхность S окружающая V является идеально проводящей

и проводимость среды в объеме равна нулю.



По условию поверхность S является идеально проводящей.
При этом уравнение баланса имеет следующий вид:

т.е. в рассматриваемом случае мощность сторонних источников может расходоваться на изменение энергии внутри объема. В правой части выражения (12) мы получили скорость изменения энергии 
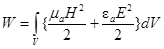



В этом случае мощность сторонних токов рассеиваясь на поверхности S уходит во внешнее пространство. Таким образом, мы получили, что уравнение (9) полностью идентично формуле (1).
Соотношение (9) было сформулировано Поинтингом (уравнение баланса энергии электромагнитного поля – теорема Пойнтинга).
Проанализируем несколько частных случаев,
которые следуют из теоремы Пойнтинга.
1.Энергия может поступать в объем V не только за счет сторонних источников. Поток энергии, определяемой интегралом 
2. Сторонние источники могут не только отдавать энергию, а также вбирать энергию электромагнитного поля. Поток заряженных частиц вбирает энергию электромагнитного поля, если этот поток попадает в ускоряющее электрическое поле. При этом скалярное произведение 
3. Пусть, поток энергии, определяемой последним слагаемым в соотношении (9), направлен внутрь объема, причем, мощность, которая поступает, таким образом, расходуется на джоулевы потери и вбирается сторонним источником так, что энергия внутри объема V остается неизменной. В этом случае соотношение (9) преобразуется к виду (15)

Так как слева стоит полная поступающая через поверхность энергия, то вектор 
Вектор Пойнтинга равняется пределу отношения энергии, проходящей за время DТ, через поверхность DS, перпендикулярно направлению распространения энергии, при DS и DТ стремящихся к нулю. В изотропных средах направление 
4.2. Плотность энергии электромагнитного поля.
Из предыдущего параграфа известно, что запас электромагнитного поля в объеме V:
Правую часть можно представить в виде двух слагаемых, одно из которых зависит только от электрического поля, а другое только от магнитного.


Так как энергии представлены в виде интегралов по объему, то подынтегральные выражения можно трактовать как объемную плотность энергий, а их сумму — как объемную плотность энергии электромагнитного поля.



Принцип суперпозиции, которому удовлетворяют векторы электромагнитного поля, не распространяется на энергию электромагнитного поля.
Пусть в объеме V существует независимо два электромагнитных поля. Энергия суммарного электромагнитного поля:



где W12 — взаимная энергия электромагнитного поля. Она может быть как положительной, так и отрицательной, т.е. суммирование электромагнитных полей может приводить как к увеличению энергии результирующего поля, так и к уменьшению ее. Если электрический и магнитный вектора, суммируемых полей, взаимно ортогональны, то очевидно, что взаимная энергия будет равна нулю. В случае переменных процессов электромагнитная энергия непрерывно изменяется. Эти изменения в каждой точке можно описать следующим соотношением:

Так как левая часть и первое слагаемое есть подынтегральные выражения, то их можно трактовать объемной плотностью мощности сторонних источников и сторонних потерь.


Соотношение (8) есть дифференциальная форма теоремы Пойнтинга.
4.3. Скорость распространения энергии электромагнитных волн.
В пространстве, в котором распространяется электромагнитная энергия, выделим энергетическую трубку (некий протяжный объем, на боковой поверхности которого вектор Пойнтинга равен нулю).
Пусть, за время Dt через боковую поверхность DS прошла энергия DW и оказалась сосредоточенной между сечениями DS и DS1 , между которыми, расстояние Dl. Направление единичного вектора 
Тогда скорость распространения энергии:

Энергию, заключенную между торцами DS и DS1:

где w — объемная плотность энергии, а DS’ — среднее сечение.
Если промежуток Dt взять достаточно малым, чтобы 

Приравняем (2) к (3) и выразим 

Найдем предел от соотношения (4) при Dt®0. Получим:

Получили общее выражение для величины скорости распространения энергии. Если предположить, что векторы 






4.4. Уравнения Максвелла для монохроматического поля.
4. Метод комплексных амплитуд.
Любые переменные электромагнитные процессы можно представить в виде дискретного или непрерывного спектра гармонических электромагнитных полей. Поэтому в дальнейшем будем анализировать гармонические электромагнитные процессы (монохроматические), так как сигнал любой сложности можно представить как суперпозицию гармонических процессов. Обычно используют метод комплексных амплитуд.
Пусть имеется некоторый гармонический процесс:

ему в соответствие ставится: 

Аналогично и для векторных величин. Пусть, есть вектор 

Ему соответствует комплексная величина:

или 

Если, мгновенные скалярные и векторные функции удовлетворяют некоторым линейным уравнениям, то этим же уравнениям удовлетворяют и их комплексные аналоги.
Использование метода комплексных амплитуд существенно упрощает решение задач с геометрическими электромагнитными процессами. Причина этого: дифференцирование по времени от комплексных амплитуд эквивалентно просто домножению на jw, а интегрирование по времени эквивалентно делению на jw.
5. 4.5. Система уравнений монохроматического (гармонического) поля.
Известно, что уравнения Максвелла относятся к линейным дифференциальным уравнениям. Поэтому в случае гармонических электромагнитных полей в уравнениях Максвелла можно перейти к комплексным амплитудам.

Т.е. если 


Используя понятие комплексных амплитуд, получим:







Входящее в соотношение (5) отношение 

Комплексная диэлектрическая проницаемость в форме (5) справедлива для сред, в которых имеются только джоулевы потери. В общем случае, когда необходимо учесть диэлектрические потери 


Этот общий случай позволяет также учесть потери, связанные с эффектом поляризации в переменном электрическом поле. Наличие диэлектрических потерь приводит к появлению фазового сдвига между электрическими векторами D и Е. Величина которого: 
Переходя во втором уравнении Максвелла к комплексным амплитудам получим: 



Магнитные потери связаны с эффектом периодического изменения намагниченности вещества во внешнем поле. Наличие магнитных потерь приводит к фазовому запаздыванию вектора В относительно вектора Н (явление Гистерезиса) в электромагнитных средах.
В случае гармонического поля при использовании метода комплексных амплитуд, возникает дополнительная возможность учесть потери, связанные с эффектами поляризации и намагничивания вещества.
В случае гармонических полей при использовании метода комплексных амплитуд 3 и 4 уравнения Максвелла являются следствием первых двух.
Поясним это:
В средах с проводимостью неравной нулю объемная плотность убывает и в случае установившегося электромагнитного процесса (к ним относятся гармонические колебания). Можно считать, что объемная плотность электрического заряда равна нулю. В этом случае третье уравнение Максвелла запишется следующим образом:

Это соотношение для среды с конечной проводимостью. Оно является справедливым и для не проводящих сред. Если в непроводящей среде рассмотрим гармонический процесс, то:
Всякое изменение свободных электрических зарядов сопровождается появлением в среде электрического тока, но при 
Переходя в уравнении (13) к комплексным амплитудам, получим:

Покажем, что оно является следствием (4). Возьмем дивергенцию от правой и левой части. Аналогично и для 4 уравнения Максвелла:

В случае гармонических полей они полностью описываются соотношениями(4), (11). Будем предполагать, что в рассмотренной области имеются сторонние источники. В этом случае выражения (4), (11) не применимы. Для получения справедливых соотношений воспользуемся 1 уравнением Максвелла:


Рассмотрим 3 уравнение Максвелла. Возьмем дивергенцию от соотношения (16).
Для сторонних токов:
Окончательно получим: 
В случае гармонических электромагнитных полей мы должны воспользоваться соотношением (17) и (18), при этом (4) и (11) останутся без изменений.
Итак, когда имеются сторонние источники:
Уравнения Максвелла без учета сторонних источников:
Подставляя вторую систему в первую, с использованием метода комплексных амплитуд, получим:
В дальнейшем индекс m будем формально опускать.
5.6. Уравнения баланса для средней за период мощности.
Теорема Умова-Пойнтинга и соответствующее ей аналитическое соотношение

были сформулированы для мгновенных значений и остаются справедливыми в последний момент времени. Это соотношение — важнейшее в классе электродинамики.
При анализе гармонических электромагнитных процессов особый интерес представляют энергетические параметры, усредненные по периоду. Среднее за период значение: 
Получим уравнение баланса для средней за период значения мощности гармонического электромагнитного процесса. Необходимо для каждого из слагаемых уравнения (1) получить величину, определяемую соотношением (2). Т. к. в соотношении (2) осуществляется интегрирование по времени, а анализируется гармонический электромагнитных процесс, то, естественно, надо воспользоваться методом комплексных амплитуд. Непосредственная замена мгновенных функций, соответствующими комплексными аналогами возможна только в линейных уравнениях. В данном случае непосредственная замена мгновенных векторов электромагнитного поля невозможна, так как выполняются следующие неравенства:
В случае нелинейных уравнений, переход к комплексным амплитудам осуществляют с помощью следующего соотношения:

Получим уравнение баланса для средней за период значения мощности гармонического электромагнитного поля. Сначала определим среднее за период значения функций входящие в (1).
Для начала получим среднее за период значение вектора Пойнтинга:
раскроем векторное произведение: 
Таким образом, сумму можно записать как удвоенную действительную часть любого из слагаемых:

Величина 

Подставим (6) в (2). Два последних слагаемых, в соотношении (6), меняются с удвоенной частотой, т.е. половину периода принимают положительную величину, а другую половину — отрицательную. Поэтому и среднее за период значение равно нулю.

Величина, от которой берется действительная часть 


Итак, (7) определяет среднее за период значение плотности потока энергии через поверхность S. Среднее за период значение потока мощности:

Рассмотрим каждое из слагаемых выражения (1).




Таким образом, в результате проделанных нами вычислений, получили:


В среднем за период, мощность сторонних источников расходуется на потери внутри объема и частично уходит во внешнее пространство, через поверхность S.
6. 4.7. Уравнения баланса для комплексной мощности.
В радиотехнике часто пользуются понятием комплексной мощности. Так, если рассматривается гармонический процесс, то комплексную мощность сторонних источников можно записать:
Получим уравнение баланса для комплексных мощностей гармонического электромагнитного процесса. Уравнение баланса для комплексной мощности получается аналогично уравнению баланса для среднего за период значения. Удобно записать уравнение Максвелла сразу для комплексно-сопряженных величин:

Вновь полагаем, что потери в среде обусловлены конечной проводимостью:

Возьмем комплексное сопряжение от всех комплексных величин:

Умножим скалярно правую и левую части соотношения (1) на 

Воспользуемся векторным тождеством, из которого следует:
Выразим из тождества 

Будем предполагать, что магнитные потери в среде отсутствуют, тогда 


7. Проинтегрируем по объему:

Поделим на 2 и учтем, что во втором слагаемом стоит разность энергий


Выражение (7) запишем в виде системы из 2-х уравнений: одно устанавливает связь между активными мощностями, другое — между реактивными.
Получим: 

Как мы и ожидали, соотношение (8) совпадает с уравнением для средних за период мощностей. Из (9) следует, что реактивная мощность сторонних источников равна умноженной на 2w разности средних за период значений энергий + реактивный поток энергии, через поверхность S. Рассмотрим важное приложение к (8) и (9). Будем предполагать, что объем V, для которого составлено уравнение баланса, является изолированной системой. В этом случае комплексный поток мощности, через поверхность S, равен нулю и уравнение баланса:

В этом случае происходит колебательный обмен энергией между электрическим и магнитным полями, т.е. один момент существует только электрическое поле, потом и то и другое, потом только магнитное и т.д. В том случае когда

мощность сторонних источников становится чисто активной:

и обмен энергиями происходит без участия сторонних источников. Если (11) не соблюдается, то для этого обмена необходимо участие сторонних источников. Изолированная система, в которой мощность сторонних источников чисто активна, т.е. выполняется равенство (11), называется резонирующей изолированной системой, а условие (11) называется условием резонанса. Для характеристики изолированной колебательной системы вводят понятие добротности.
Под добротностью Q понимают:


Средняя за период энергия электрического поля:
При резонансе 
Соотношения (6), (7) были получены при условии, что 
В этом случае общее выражение для баланса комплексных мощностей остается неизменным, но конкретное, аналитическое выражение для слагаемых, изменится. Мощность потерь записывается следующим образом:
В заключение этого параграфа приведем выражение для скорости распределения энергии, записанное через комплексные амплитуды:

В том случае, когда составляющие неизменны, получаем:
8. 4.8. Теорема единственности для внутренней и внешней задач электродинамики.
Уравнения Максвелла являются дифференциальными уравнениями в частных производных, поэтому они допускают множество решений. Из общефизических соображений, очевидно, что если полностью повторять условия опытов, то будем получать одно и то же распространение электромагнитного поля. Для обеспечения единственности решения электродинамических задач электромагнитное поле должно удовлетворять не только уравнениям Максвелла, но также должно удовлетворять ряду дополнительных условий. Они называются условиями единственности решения уравнений Максвелла. Выводы и доказательства формулируются теоремой единственности. Теорема единственности отдельно формулируется двух основных видов задач:
для внутренней и внешней задач электродинамики.
Требуется определить распределение электромагнитного поля внутри поверхности S (внутренняя задача). Определим распространение электромагнитного поля в пространстве, внешнем по отношению к объему V, ограниченному поверхностью S. (
9. 4.9. Единственность решения внутренних задач.
Внутренние задачи электродинамики имеют единственное решение, если выполняется одно из следующих условий:
1.Если в каждой точке М поверхности S задана проекция вектора 

2. Если в каждой точке M поверхности S задана проекция вектора 

3. Если на части поверхности S в каждой точке задана проекция вектора 


4. Если в каждой точке поверхности S задано соотношение между проекциями векторов 

Рекомендация для Вас – 4.1 Постановка задачи синтеза самонастраивающихся систем.
10. 4.10. Условия единственности внешних задач электродинамики.
Для обеспечения единственности решения внешних задач электродинамики необходимо выполнение одного из условий 1-4, плюс к этому должно выполнятся одно из условий, описывающее поведение электромагнитного поля при бесконечно удаленных точках (при r®¥).
1. Принцип предельного поглощения (



2. Если в среде отсутствуют потери и принцип предельного поглощения не применим, в этом случае векторы электромагнитного поля должны удовлетворять следующим соотношениям:

Физически эти условия означают, что электромагнитные волны при r®¥ имеют вид сферических волн, расходящихся от источника электромагнитного поля.
Содержание:
Электромагнитное поле:
Сильное электромагнитное поле отрицательно действует на человеческий организм – повреждается центральная нервная система, может возникнуть рак головного мозга, уровень гемоглобина в крови понижается, нарушается память и понижается внимание.
Карта электромагнитного поля:
Электрический заряд и электромагнитное поле
При трении тел друг о друга на них возникают электрические заряды. В этом случае говорят, что тело наэлектризовано, оно получило электрический заряд, или оно потеряло электрический заряд.
Электрическое взаимодействие между наэлектризованными телами в зависимости от знаков их зарядов может носить характер притяжения или отталкивания:
- – тела, обладающие зарядами одинакового знака, отталкиваются друг от друга;
- – тела, обладающие зарядами противоположного знака, притягиваются друг к другу.
В природе существуют заряды двух видов: положительный электрический заряд (+) и отрицательный электрический заряд (-). Заряды одинакового знака отталкиваются друг от друга, а заряды разного знака притягиваются друг к другу. Тела, не обладающие избытком электрического заряда, называют электрически нейтральными, или незаряженными телами.
Электрический заряд обозначают буквой q. За единицу измерения электрического заряда в СИ принят 1 кулон, названный так в честь французского ученого Шарля Кулона: [q] = 1 Кл.
Электростатическое поле – вид материи, который создается неподвижными электрическими зарядами.
Напряженность электрического поля – силовая характеристика этого поля. Являясь векторной величиной, напряженность электрического поля направлена так же, как и электрическая сила, действующая на положительный заряд.
Вещества, продолжительное время сохраняющие свои магнитные свойства, называются постоянными магнитами или просто магнитами. Каждый магнит имеет два полюса: северный (N) и южный (S). Одноименные полюсы магнита отталкиваются, разноименные полюсы магнита притягиваются.
Магнитное поле – вид материи, который создается движущимися зарядами.
Индукция магнитного поля (или магнитная индукция) является силовой характеристикой этого поля. Направление вектора магнитной индукции в данной точке магнитного поля совпадает с направлением северного полюса магнитной стрелки, помещенной в эту точку поля.
Кстати:
Было выяснено, что при полете пчела заряжается положительно. А цветы обладают отрицательным зарядом. Поэтому, когда пчела садится на цветок, ее пыльца прилипает к пчеле. Самым интересным является то, что после контакта пчелы с цветком электромагнитное поле растения меняется. Это изменение как будто подает знаки другим пчелам, находящимся в воздухе: “На этом цветке нет пыльцы!”.
Электрический заряд
Электрический заряд — это свойство тел и частиц создавать вокруг себя электромагнитное ноле. Электрический заряд принят также количественной мерой измерения этого свойства тел.
Взаимодействие между заряженными частицами называется электромагнитным взаимодействием. Например, когда говорят, что протон несет положительный заряд, а электрон несет отрицательный заряд, то можно с уверенностью говорить о наличии электромагнитного взаимодействия между ними. Между незаряженными (электрически нейтральными) частицами не существует электромагнитного взаимодействия. Поэтому говорят: Электрический заряд определяет интенсивность электромагнитного взаимодействия.
Электрический заряд обладает следующими особенностями:
1. Электрический заряд дискретен (не непрерывен, делим) — электрический заряд любого тела кратен целому числу элементарных зарядов:
Здесь N – число приобретенных или потерянных телом электронов.
Абсолютное значение наименьшего электрического заряда в природе называют элементарным зарядом. Элементарный заряд обозначают буквой е, численное его значение равно абсолютному значению заряда электрона или протона:
Кроме электрона и протона в природе существуют ещё несколько видов элементарных частиц. Однако только электроны и протоны могут существовать в свободном состоянии неограниченно долго. Время жизни остальных заряженных частиц очень мало – миллионные доли секунды. Они образуются в результате столкновений быстрых элементарных частиц, и через ничтожно малое время превращаются в другие частицы.
Дискретность заряда позволяет ему равномерно распределяться по поверхности проводника. Предположим, что заряд равномерно распределился по поверхности площадью S.
Величина, численно равная электрическому заряду, приходящемуся на единицу площади поверхности, называется поверхностной плотностью электрического заряда (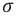
Единицей поверхностной плотности электрического заряда в СИ является:
2. Для электрического заряда выполняется закон сохранения – алгебраическая сумма электрических зарядов частиц (или тел) замкнутой системы остается неизменной:
3. Электрический заряд является аддитивной величиной – электрический заряд системы равен алгебраической сумме электрических зарядов частиц (или тел) этой системы.
4. Электрический заряд является инвариантной величиной – электрический заряд частиц (или тел) одинаков во всех инерциальных системах отсчета.
Электромагнитное поле
Раздел физики, в котором изучаются электрические и магнитные явления, проявляющиеся при движении и взаимодействии электрических зарядов, называется электродинамикой.
Электродинамика – раздел физики, изучающий закономерности взаимодействия между электрическими зарядами посредством электромагнитного поля.
Электромагнитное поле – вид материи, осуществляющий взаимодействие между электрически заряженными частицами и телами.
Электрическое и магнитное поля являются особыми формами проявления электромагнитного поля. Поэтому состояние электромагнитного поля в произвольной точке пространства и в любой момент времени характеризуется двумя величинами – напряженностью электрического поля 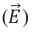
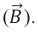
Силу, с которой электромагнитное поле действует на заряд, покоящийся в данной инерциальной системе отсчета, называют электрической. Электрическая сила всегда прямо пропорциональна количественному значению заряда, помещенного в данную точку поля:
На электрический заряд, движущийся в данной инерциальной системе отсчета, электромагнитное поле действует, кроме электрической силы, ещё с силой, называемой магнитной силой. Магнитная сила прямо пропорциональна и значению движущегося заряда, и проекции скорости заряда, перпендикулярной вектору магнитной индукции:
Поэтому на электрический заряд, движущийся в электромагнитном поле, действует результирующая сила, равная сумме электрической и магнитной сил. Эту силу называют обобщенной силой Лоренца:
Напряженность электростатического поля
Поле, созданное неподвижными электрическими зарядами, называется электростатическим.
Напряженность электрического поля – векторная физическая величина, равная отношению электрической силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку поля, к величине этого заряда:
Единица измерения напряженности электрического поля в СИ:
Электрическая сила равна произведению напряженности электрического поля на величину помещенного в поле заряда:
Закон Кулона: сила взаимодействия двух неподвижных точечных электрических зарядов в вакууме прямо пропорциональна произведению модулей этих зарядов и обратно пропорциональна квадрату расстояния между ними:
Учитывая кулоновскую силу в формуле напряженности, выясняем, от каких величин зависит напряженность электрического поля.
Модуль напряженности электрического поля, создаваемого точечным зарядом 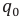
Одной из задач электродинамики является определение силовой характеристики электростатического поля, созданного данным электрическим зарядом. Одним из особых состояний электромагнитного поля является создаваемое неподвижным зарядом электростатическое поле.
Электрическое поле — это электромагнитное поле, в котором 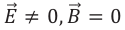
Электрическое иоле может быть однородным и неоднородным.
Однородное электрическое поле — поле, в каждой точке которого численное значение и направление напряженности электрического поля одинаковы. В противном случае поле неоднородное.
Например, поле между двумя параллельными пластинами, одна из которых обладает положительным, а другая таким же но модулю отрицательным зарядом, является однородным (а), а электрическое поле, создаваемое точечным зарядом, является неоднородным (b).
Напряженность электрического поля, создаваемого точечным электрическим зарядом в вакууме и в среде. Известно, что при внесении пробного заряда в электрическое поле точечного заряда 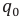
Силы взаимодействия двух точечных электрических зарядов прямо пропорциональны произведению модулей зарядов, обратно пропорциональны квадрату расстояния между ними и направлены вдоль прямой, соединяющей эти заряды (с).
Здесь 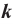
Эта постоянная показывает, что два точечных заряда по 1 Кл каждый, находящиеся в вакууме на расстоянии 1 м друг от друга, взаимодействуют с силой 9•109 Н.
Здесь 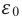
Таким образом, на основе закона Кулона можно определить модуль напряженности электрического поля, созданного в вакууме зарядом 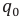
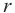
Напряженность в данной точке электрического поля, созданного точечным зарядом в вакууме, прямо пропорциональна величине этого заряда и обратно пропорциональна квадрату расстояния от источника поля до этой точки.
Если заряд 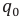
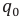
Для электрических полей выполняется принцип суперпозиции.
Напряженность результирующего электрического поля в данной точке пространства, создаваемого несколькими электрическими зарядами, равна геометрической сумме напряженностей отдельных полей:
На рисунке изображена схема определения напряженности результирующего ноля в точке А, созданного двумя точечными зарядами (е).
В среде (внутри однородного диэлектрика) кулоновская сила взаимодействия зарядов слабее по сравнению с силой их взаимодействия в вакууме в 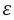
Здесь 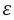
Напряженность электрического поля в среде меньше, чем в вакууме, в 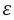
Значит, диэлектрическая проницаемость среды также является физической величиной, показывающей, во сколько раз напряженность электрического поля, созданного электрическим зарядом в данной точке внутри однородного диэлектрика, меньше, чем в вакууме:
Диэлектрическая проницаемость различных сред различна. Например, для дистиллированной воды 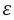
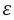
Работа однородного электрического поля
Энергетическая характеристика электрического поля называется электрическим напряжением или просто напряжением.
Скалярная величина, показывающая, какую работу совершило электрическое поле при перемещении единичного заряда из одной точки поля в другую, называется электрическим напряжением между этими точками поля:
Единицей измерения напряжения в СИ является вольт:
Механическая работа — скалярная физическая величина, равная произведению модуля силы, действующей на тело, модуля перемещения тела и косинуса угла между векторами силы и перемещения:
Работа силы тяжести в гравитационном поле Земли:
Работа силы тяжести не зависит от формы траектории движения тела, она зависит от разности уровней начального и конечного положений центра тяжести тела.
Силы, работа которых не зависит от формы траектории движения тела, называются консервативными. Значит, сила тяжести — консервативная сила.
Это положение позволяет вывести понятие “потенциальной энергии” для системы тел, взаимодействующих с силами гравитационного взаимодействия. Так, выражение mgh в последней формуле является потенциальной энергией взаимодействия Земли и тела, находящегося на высоте h от поверхности Земли:
Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:
Проведенные учеными исследования показали, что Земля обладает отрицательным электрическим зарядом, а слой ионосферы в её атмосфере – положительным зарядом. Слои атмосферы, лежащие между ними, играют роль изолятора.
Работа однородного электрического поля:
Работа однородного электрического поля, в котором положительный пробный заряд под действием постоянной электрической силы 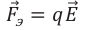
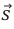
Здесь 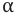
Так как проекция вектора перемещения на силовую линию равна 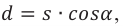
Работа однородного электрического поля при перемещении пробного положительного заряда равна произведению модуля этого заряда на модуль напряженности электрического поля и на проекцию его перемещения на направление силовых линий.
Выражение (1) можно написать и так:
Здесь 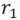
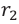
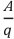
Так как работа электрической силы при переносе пробного заряда из одной точки электрического поля в другую не зависит от формы траектории, то электрическая сила является консервативной, а электрическое поле — потенциальным.
Скалярная физическая величина, равная отношению работы электрического поля при переносе электрического заряда из одной точки поля в другую к величине этого заряда, называется разностью потенциалов между этими точками, или напряжением между ними:
Здесь 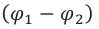
поля, между которыми перемещается заряд. Единицей измерения разности потенциалов в СИ является вольт:
Из выражения (3) можно определить работу поля при перемещении заряда между двумя его точками:
Работа электрического поля при перемещении заряда между двумя его точками равна произведению заряда на разность потенциалов (напряжение) между ними :
Сравнивая (1) и (3), получим формулу, связывающую напряженность и напряжение:
Напряженность электрического поля направлена от точки поля с большим потенциалом к точке с меньшим потенциалом.
Потенциал электрического поля
Для выражения энергетической характеристики электрического ноля в произвольной точке используется физическая величина, называемая потенциалом. Разность потенциалов между любой точкой электрического поля и точкой, принятой за нулевой потенциал, называют потенциалом поля в этой точке. Обычно вычисление потенциала производится относительно бесконечности.
Потенциал – скалярная величина, численно равная работе поля по перемещению единичного положительного заряда в бесконечность при его отталкивании от положительного заряда q:
Потенциал обозначается символом 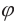
является вольт:
Потенциальная энергия заряда в электрическом поле. Так как электрическое поле является потенциальным, то к замкнутой системе заряд-электрическое поле можно применить теорему о потенциальной энергии.
Работа, совершенная в потенциальном поле, равна изменению потенциальной энергии системы, взятому с противоположным знаком:
Здесь 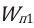
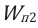
Сравнив выражения (4) и (7), получим:
Отсюда
Значит, величина, определяемая отношением потенциальной энергии пробного заряда в данной точке поля к величине заряда, равна потенциалу поля.
Эквипотенциальные поверхности
Поверхность, во всех точках которой потенциал поля принимает одинаковые значения, называется эквипотенциальной. Для точечного заряда эквипотенциальными являются концентрические сферы, центры которых совпадают с местонахождением заряда (с). Для однородного электрического поля — это поверхности, перпендикулярные силовым линиям поля (d).
Конденсатор и электрическая емкость
Конденсатор-устройство, используемое для накопления электрических зарядов. Его название происходит от латинского слова “kondensare”, что означает сгущение.
Самый простой конденсатор — плоский конденсатор, состоит из двух близко расположенных параллельных металлических пластин с тонким слоем диэлектрика (например, воздуха) между ними (а). На схемах электрических цепей конденсатор обозначают как 
Пластины конденсатора электризуются равными по модулю зарядами противоположных знаков.
Способность конденсатора накапливать электрический заряд характеризуется физической величиной, называемой электрической ёмкостью.
Для разделения, накопления и передачи большого количества электрического заряда разных знаков используются устройства, называемые электрофорной машиной (b).
Быстро вращаясь, диски электрофорной машины трутся о воздух между ни-ми и электризуются зарядами разного знака. Заряды пластин снимаются с помощью металлических щеток и накапливаются в двух лейденских банках (1), а оттуда передаются на сферические металлические кондукторы (2). В результате на одном из кондукторов накапливается положительный, а на другом — отрицательный заряд.
Известный сербский ученый Никола Тесла (1856-1943) выдвинул идею о том, что система Земля – атмосфера представляет собой гигантский конденсатор, который является источником дешевой электрической энергии. Согласно этой идее, совпадение частоты слабого электромагнитного излучения, посылаемого в ионосферу Земли, с собственной частотой заряженных частиц ионосферы вызовет в ней резонанс. В результате возникнет очень сильное излучение, окружающее Землю. В это время достаточно будет в любой точке поверхности Земли воткнуть длинный металлический стержень, чтобы непрерывно получать из неба бесплатную электрическую энергию. Главной проблемой было построение башни для создания возбуждающих ионосферу импульсов – резонатора. Американский миллиардер Морган принял решение о финансировании постройки этой башни в Лонг-Айленде (США). Однако незадолго до завершения работы он приостановил и отменил этот проект в целях предотвращения возможной экологической катастрофы.
Известно, что простейшим конденсатором является плоский конденсатор, состоящий из двух параллельных пластин. Характеристикой конденсатора является электрическая ёмкость.
Электрическая ёмкость конденсатора (С) – скалярная физическая величина, равная отношению заряда конденсатора к разности потенциалов (напряжению) между его пластинами:
Единицей измерения электрической ёмкости в СИ является фарад (1Ф):
1 фарад – это электрическая емкость конденсатора, когда заряд пластин 1 Кл создает между ними напряжение 1В:
Фарад – очень большая ёмкость, поэтому на практике используются его дольные единицы (микрофарад, нанофарад, пикофарад и др.):
Заряд конденсатора равен модулю заряда одной из пластин конденсатора. Этот заряд прямо пропорционален напряжению на концах источника, подключенного к конденсатору:
Значит, электроёмкость является коэффициентом пропорциональности между зарядом и напряжением и не зависит ни от заряда, ни от напряжения. От чего же зависит электроёмкость?
Электрическая ёмкость плоского конденсатора зависит от площади его пластин, расстояния между пластинами и диэлектрической проницаемости вещества, находящегося между ними:
Здесь S – площадь одной из пластин конденсатора, d – расстояние между пластинами, 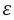
Энергия электрического поля конденсатора
Энергия однородного электрического поля между пластинами плоского заряженного конденсатора определяется нижеприведенной формулой:
Примечание. Множитель 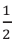
Если учесть здесь выражение (2), то получаются выражения, отражающие зависимость энергии конденсатора от ёмкости и заряда конденсатора:
или
Если учесть выражение (3) в выражениях (6) и (7), то можно получить следующие выражения для энергии электрического поля плоского конденсатора:
Распределение энергии электрического ноля в пространстве выражается физической величиной, называемой плотностью энергии электрического поля:
Плотность энергии электрического поля – физическая величина, численно равная энергии электрического поля, приходящейся на единицу объёма:
Здесь 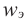
Если в последнем выражении учесть формулу (8), выражения 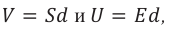
Примечание. Конденсатор не может служить аккумулятором, длительное время сохраняющим в себе электрическую энергию (из-за утечки заряда). Однако он, в отличие от аккумулятора, способен мгновенно разряжаться в цепи с малым сопротивлением. Это свойство конденсатора широко используется на практике (например, во вспышках фотоаппаратов и лампах мобильных телефонов).
Соединение конденсаторов
Электрическая цепь может состоять из различных элементов: источник тока, потребители (лампа, электрический звонок, электрический нагреватель, телевизор и др.), ключ, соединительные провода. Одной из простейших цепей является последовательное соединение этих элементов.
При последовательном соединении конец каждого проводника соединяется с началом последующего.
При последовательном соединении силы токов одинаковы в любой части цепи:
Общее напряжение цепи при последовательном соединении равно сумме напряжений отдельных участков этой цепи:
Общее сопротивление при последовательном соединении равно сумме сопротивлений отдельных ее участков:
Общее сопротивление 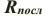
Параллельным называется соединение проводников, при котором начапа всех проводников соединяются в одной точке (например, в точке А), а концы в другой (например, в точке В).
Напряжения на концах параллельно соединенных проводников одинаковы:
При параллельном соединении сила тока в неразветвленной части цепи равна сумме сил токов в отдельных ветвях цепи:
Величина, обратная общему сопротивлению параллельно соединенных проводников, равна сумме величин, обратных сопротивлению каждого проводника:
Общее сопротивление участка цепи, состоящей из двух параллельно соединенных проводников, равно:
В соответствии с этим общее сопротивление участка цепи, состоящей из n числа параллельно соединенных проводников с одинаковым сопротивлением R, меньше сопротивления каждого из них в n раз:
На практике часто случается, что при выходе из строя бытовых приборов для срочного их ремонта отсутствуют конденсаторы с необходимым номиналом электроёмкости и напряжения. В таких случаях приходится получить необходимый номинал, используя конденсаторы различного номинала. А для этого необходимо знать правила их соединений.
С целью получения различных значений электроёмкости собирают батареи конденсаторов, соединяя их либо последовательно, либо параллельно.
Последовательное соединение конденсаторов
При последовательном соединении конденсаторов отрицательно заряженная пластина первого конденсатора соединена с положительно заряженной пластиной второго и т.д. (с).
Заряды последовательно соединенных конденсаторов одинаковы:
Общее напряжение на концах цепи, состоящей из последовательно соединенных конденсаторов, равно сумме напряжений отдельных конденсаторов:
Величина, обратная общей электроемкости батареи последовательно соединенных конденсаторов, равна сумме величин, обратных значениям электроёмкостей отдельных конденсаторов:
Общая ёмкость цепи, состоящей из последовательно соединенных n конденсаторов одинаковой ёмкости, в n раз меньше ёмкости одного конденсатора:
Напряжение и энергия последовательно соединенных конденсаторов обратно пропорциональны их электрическим ёмкостям:
Параллельное соединение конденсаторов
При параллельном соединении положительно заряженные пластины всех конденсаторов соединяют в одной точке, а отрицательно заряженные пластины в другой точке (d).
Общий заряд параллельно соединенных конденсаторов равен сумме зарядов отдельных конденсаторов:
Напряжения на концах параллельно соединенных конденсаторов одинаковы:
Общая электроёмкость батареи параллельно соединенных конденсаторов равна сумме электроёмкостей отдельных конденсаторов:
Общая электроёмкость n числа параллельно соединенных одинаковых конденсаторов в n раз больше электроёмкости одного конденсатора:
Электрические заряды и энергии параллельно соединенных конденсаторов прямо пропорциональны их электроёмкостям:
Движение заряженных частиц в магнитном поле
При равномерном движении по окружности линейная скорость материальной точки численно равна отношению пройденного пути ко времени, за которое этот путь пройден:
При равномерном движении по окружности модуль центростремительного ускорения материальной точки равен отношению квадрата линейной скорости к радиусу окружности:
Сила, с которой магнитное поле действует на движущуюся заряженную частицу, называется силой Лоренца:
Если заряженная частица влетает в магнитное поле в направлении, перпендикулярном линиям индукции, то сила Лоренца принимает максимальное значение:
Сила Лоренца перпендикулярна векторам 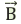
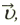
Правило левой руки для определения направления силы Лоренца
Правило левой руки для определения направления силы Лоренца: левую руку следует расположить в магнитном поле так, чтобы вектор магнитной индукции 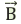
Вблизи Северного и Южного полюсов Земли наблюдаются очень красивые природные явления, называемые “полярным сиянием”. Причиной возникновения полярного сияния является действие магнитного поля Земли на поток заряженных частиц в атмосфере.
Магнитное поле — это электромагнитное поле, индукция магнитного поля которого относительно данной системы отсчета отлична от нуля 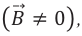
На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца:
Так как направление силы Лоренца перпендикулярно направлению скорости частицы 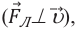
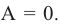
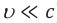
Если частица влетает в поле в направлении, перпендикулярном силовым линиям поля 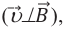
В этом случае уравнение движения частицы:
Сообщая телу центростремительное ускорение (так как 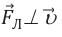
Уравнение движения частицы преобразуется:
Из выражения (4) можно выяснить, от каких величин зависит радиус окружности, по которой вращается частица:
Здесь р и Ек – соответственно модуль импульса и кинетическая энергия частицы.
Радиус окружности, которую описывает заряженная частица в однородном магнитном поле, прямо пропорционален модулю скорости его движения (импульса) и обратно пропорционален модулю вектора магнитной индукции поля.
Период обращения частицы по окружности зависит от массы частицы, величины заряда и модуля индукции магнитного поля:
Кстати:
Прибор, используемый для определения массы частицы, называется “масс-спектрограф”. Принцип его работы заключается в следующем: вакуумная камера прибора помещается в однородное магнитное поле (вектор его индукции направлен к нам перпендикулярно плоскости рисунка). Заряженные частицы сначала ускоряются электрическим полем, а затем, отклоняясь магнитным полем, описывают дугу, оставляя след на фотопластинке (с). Радиус кривизны дуги измеряется. Это позволяет точно вычислить массу частицы с известным значением заряда.
Действие магнитного поля на проводник с током
Направление вектора индукции магнитного поля, созданного электрическим током, удобно определять правилом правого буравчика: если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика показывает направление вектора индукции магнитного поля, созданного этим током (1). Направление вектора индукции магнитного поля кругового тока также определяется правилом правого буравчика: если вращать рукоятку буравчика по направлению кругового тока, то направление поступательного движения буравчика покажет направление вектора индукции магнитного поля, созданного током (2).
При помещении проводника с током в однородное магнитное поле модуль действующей на него силы Ампера равен произведению модуля индукции магнитного поля, длины этого проводника, силы тока в нем и синуса угла между направлением тока и вектором магнитной индукции:
Направление силы Ампера определяется правилом левой руки: если расположить левую руку в магнитном поле так, чтобы линии магнитной индукции были направлены в ладонь, а четыре пальца были вытянуты по направлению тока, то отведенный под 90о большой палец укажет направление силы Ампера.
В начале XIX века один из основоположников математической теории электромагнетизма, немецкий математик и физик Карл Фридрих Гаусс (1777-1855) разработал теорию электромагнитной пушки, называемой “пушкой Гаусса”. Принцип её работы основан на взаимодействии катушки с током и железного снаряда (постоянный магнит). На рисунке изображены модель пушки Гаусса и схема принципа его работы (а).
После того, как датский ученый X. Эрстед экспериментально установил существование взаимодействия проводника с током и магнитной стрелки, французский физик А. Ампер выяснил, что два параллельных проводника с током взаимодействуют как два постоянных магнита. Стало известно, что между параллельными проводниками с токами одинакового направления взаимодействие носит характер притяжения, а между проводниками с токами противоположного направления -характер отталкивания. Так как электрический ток является упорядоченным движением заряженных частиц, то магнитное взаимодействие является взаимодействием магнитных полей, созданных движущимися заряженными частицами в пространстве.
Магнитное поле действует с определенной силой на любой проводник с током (пробный ток), помещенный в это поле. Модуль этой силы, называемой силой Ампера, равен произведению силы тока в проводнике, модуля вектора магнитной индукции, длины проводника и синуса угла между направлением тока и вектором индукции магнитного поля:
Известно, что направление силы Ампера определяется правилом левой руки. Если проводник с током перпендикулярен вектору магнитной индукции (sin90°=l), то сила Ампера принимает максимальное значение:
С помощью этой формулы можно выразить физическую суть силовой характеристики магнитного поля – индукции магнитного поля.
Индукция магнитного поля — векторная величина, численно равная максимальной силе, действующей на элемент тока (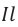
За направление вектора магнитной индукции в данной точке поля принимают направление, которое указывает северный полюс свободной магнитной стрелки, помещенной в эту точку поля (с). Единицей измерения магнитной индукции в СИ является тесла (Тл):
1 тесла — индукция такого магнитного поля, которое на проводник длиной 1 м, расположенный перпендикулярно линиям магнитной индукции, и силой тока 1 А, действует с силой 1 Н.
Магнитное поле, в каждой точке которого числовое значение и направление вектора магнитной индукции 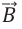
Для магнитного поля выполняется принцип суперпозиции: вектор индукции результирующего магнитного поля, созданного несколькими проводниками с током, равен геометрической сумме векторов индукции отдельных магнитных полей, созданных этими проводниками:
С целью визуализации магнитного поля его изображают с помощью линий магнитной индукции (силовые линии поля) (d):
Линия индукции магнитного поля – линия, касательная к каждой точке которой совпадает с вектором магнитной индукции в этой точке.
Линии индукции магнитного поля замкнутые, они не имеют ни начала, ни конца.
Поле, силовые линии которого являются замкнутыми, называют вихревым.
Применение силы Ампера в электроизмерительных приборах
Известно, что существуют различные системы электроизмерительных приборов – амперметра, вольтметра и ваттметра. Это магнитоэлектрические, электромагнитные и электродинамические системы. Принцип работы всех этих систем основан на действии магнитного поля на проводник с током.
Принцип работы приборов магнитоэлектрической системы основан на взаимодействии магнитного поля постоянного магнита с магнитным полем, возникающим вследствие прохождения измеряемого тока через проводящую рамку (е).
Принцип работы прибора электромагнитной системы основан на взаимодействии магнитного поля, возникающего в результате прохождения измеряемого тока через неподвижную катушку, с подвижным стальным сердечником, помещенным в это поле (f).
Принцип действия прибора электродинамической системы основан на взаимодействии магнитных полей токов, протекающих по неподвижной и подвижной катушкам (или системам катушек) (g).
Магнитный поток и явление электромагнитной индукции
После проведения многочисленных опытов М. Фарадей в 1831 году установил, что изменения магнитного поля приводят к возникновению электрического тока в замкнутом проводящем контуре.
Явление возникновения электрического тока в замкнутом проводящем контуре, помещенном в изменяющееся магнитное поле, называют электромагнитной индукцией, а возникающий ток – индукционным током.
Возникновение переменного магнитного поля всегда сопровождается созданием в окружающем пространстве вихревого электрического поля.
Вихревое электрическое поле отличается от электростатического:
- a) электростатическое поле создается неподвижным электрическим зарядом, а вихревое электрическое поле создается переменным магнитным полем;
- b) линии напряженности электростатического поля не замкнуты: они начинаются на положительных зарядах и заканчиваются на отрицательных зарядах. Линии напряженности вихревого электрического поля не имеют ни начала, ни конца — эти линии замкнуты.
В 1833 году русский физик Э. Ленц установил общее правило определения направления индукционного тока, так называемое правило Ленца:
Индукционный ток принимает такое направление, что созданное им магнитное поле противодействует тому изменению внешнего магнитного поля, которое стало причиной возникновения тока.
При усилении внешнего магнитного поля магнитное поле индукционного тока ослабляет это изменение — вектор индукции магнитного поля индукционного тока направлен против вектора индукции внешнего магнитного поля (1).
При ослаблении внешнего магнитного поля магнитное поле индукционного тока препятствует изменению, то есть стремится к тому, чтобы это поле не ослабло. Вектор индукции магнитного поля индукционного тока направлен так же, как и вектор индукции внешнего магнитного поля (2).
Магнитный поток
Если поместить замкнутый контур (рамку) в однородное магнитное поле, то через площадь S, ограниченную этим контуром, проходит определенное количество линий магнитной индукции (с). Величину, прямо пропорциональную числу этих линий индукции, называют потоком магнитной индукции, или просто магнитным потоком.
Поток магнитной индукции (Ф) – скалярная физическая величина, равная произведению модуля вектора магнитной индукции, площади контура и косинуса угла между вектором магнитной индукции и нормалью к площади контура:
Магнитный поток относится к скалярным величинам, которые могут принимать положительные, отрицательные значения, а также равняться нулю:
- — если угол между вектором индукции и нормалью к плоскости контура острый, то магнитный поток принимает положительные значения, а если этот угол тупой – отрицательные;
- — если вектор индукции перпендикулярен плоскости контура, то есть параллелен нормали к плоскости, то
тогда магнитный поток, пронизывающий плоскость контура, принимает максимальное значение:
Единицей измерения магнитного потока в СИ является вебер (1 Вб):
1 Вебер — магнитный поток, пронизывающий поверхность площадью 1 м2, ограниченную проводящим контуром, расположенным в магнитном поле с индукцией 1 Тл перпендикулярно линиям индукции поля.
Явление электромагнитной индукции
В 1831 году английский ученый Майкл Фарадей (1791-1867) открыл явление электромагнитной индукции и показал существование взаимосвязи между электрическим и магнитным полем.
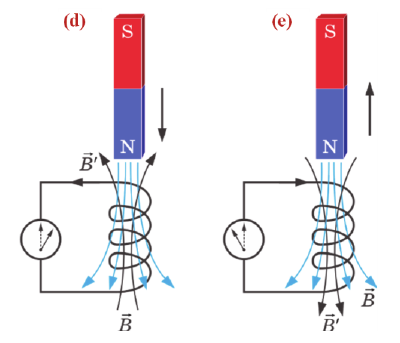
Вы знаете, что при введении в катушку, соединенную с гальванометром, постоянного магнита, и выведении его из катушки в витках катушки возникает индукционный ток. А если магнит неподвижен внутри катушки или совершает вращательное движение внутри катушки, то ток не возникает. Значит, причиной возникновения индукционного тока является изменение магнитного потока, пронизывающего контур (d и е).
Возникновение электрического тока в проводящем контуре в результате изменений магнитного потока, пронизывающего площадь, ограниченную этим контуром, называют явлением электромагнитной индукции.
Направление индукционного тока зависит от того, увеличивается или уменьшается пронизывающий контур магнитный поток.
1. Магнитный поток увеличивается 
Правило правого буравчика для кругового тока
Правило правого буравчика для кругового тока: при вращении рукоятки буравчика по направлению кругового тока направление его поступательного движения совпадает с направлением вектора индукции магнитного поля внутри кругового тока (f).
2. Магнитный поток уменьшается 
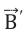
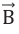
Итак, возникающий в замкнутом проводящем контуре индукционный ток всегда направлен так, что его собственное магнитное поле препятствует тем изменениям внешнего магнитного поля, которые стали причиной возникновения этого тока.
Это правило Ленца, позволяющее определить направление индукционного тока.
Закон электромагнитном индукции
Упорядоченное движение заряженных частиц называется электрическим током.
Для существования непрерывного электрического тока в проводнике необходимо выполнение следующих условий: наличие в проводнике заряженных частиц (носителей заряда), способных свободно перемещаться по проводнику; действие электрической силы, способной перемещать эти частицы в определенном направлении; проводник (цепь, состоящая из проводников), по которому проходит электрический ток, должен быть замкнутым.
За направление электрического тока условно принято направление вектора напряженности электрического поля внутри проводника.
За направление электрического тока принято направление движения положительных зарядов (против направления движения свободных электронов).
Зависимость силы тока в данном проводнике от напряжения на его концах проводника и от его сопротивления выражается законом Ома для участка цепи постоянного тока.
Сила тока на участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению:
Индукционный ток, как и любой другой, создается электрическим полем.
Существование переменного магнитного поля всегда сопровождается появлением в окружающем пространстве вихревого электрического поля. Именно вихревое электрическое поле (а не переменное магнитное) действует на свободные электроны в замкнутом контуре и способствует возникновению индукционного тока в нем.
Вихревое электрическое поле существенно отличается от электростатического:
- а) Электростатическое поле создается покоящимися зарядами, а вихревое электрическое переменным магнитным полем;
- b) Линии напряженности электростатического поля не замкнуты: они начинаются на положительных зарядах и заканчиваются на отрицательных зарядах. Линии напряженности вихревого электрического поля не имеют ни начала, ни конца, они замкнуты как линии индукции магнитного поля.
Кстати:
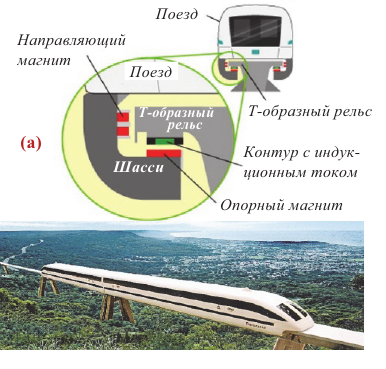
Одним из современных видов общественного транспорта является поезд на воздушной подушке, движущийся в подвешенном состоянии левитации -без непосредственного контакта с дорогой. Вместо колес шасси этого поезда, называемого МагЛев, оснащено электромагнитной опорой и направляющими магнитами. Железная дорога состоит из проводящего рельса Т-образной формы, оснащенного электромагнитом, создающим мощный индукционный ток. Такой поезд, испытания которого проводились в Японии вблизи города Фудзияма, показал рекордную скорость 603 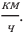
Вихревое электрическое поле и ЭДС индукции
Причиной возникновения индукционного тока в замкнутом проводящем контуре является возникновение вихревого электрического поля вокруг переменного магнитного ноля, которое, действуя на свободные электроны в контуре, приводит их в упорядоченное движение -создает индукционный электрический ток. Работа вихревого электрического поля по перемещению положительного единичного заряда по замкнутому проводнику характеризуется физической величиной, называемой электродвижущей силой индукции (ЭДС индукции).
Электродвижущая сила индукции — скалярная физическая величина, равная отношению работы, совершенной вихревым электрическим полем при перемещении положительного единичного заряда вдоль замкнутого контура, к величине этого заряда:
В проведенном исследовании явления электромагнитной индукции вы определили, что значение возникшего в замкнутом контуре индукционного тока пропорционально скорости изменения магнитного потока, проходящего через поверхность, ограниченную этим контуром. Значит, и электродвижущая сила индукции, создающая индукционный ток в проводящем контуре, зависит от скорости изменения внешнего магнитного потока.
Если за очень малый промежуток времени 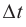
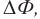
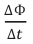
Закон электромагнитной индукции
На основе вышесказанного можно выразить закон электромагнитной индукции:
ЭДС индукции, возникающая в замкнутом проводящем контуре, прямо пропорциональна скорости изменения магнитного потока, проходящего через ограниченную этим контуром поверхность:
Знак минус в выражении (2) указывает на то, что магнитный поток индукционного тока препятствует изменению внешнего магнитного потока, породившего индукционный ток.
Если контур состоит из N числа витков, го выражение (2) принимает вид:
Здесь 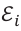
Сила индукционного тока, возникающего в замкнутом проводящем контуре, определяется согласно закону Ома для участка цепи:
Здесь R – сопротивление контура.
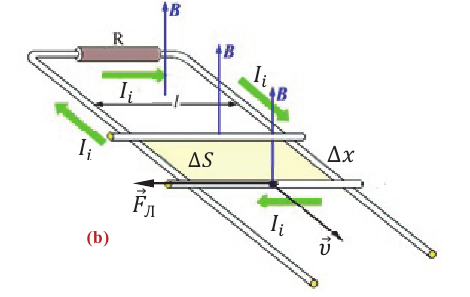
ЭДС индукции в движущихся в магнитном поле проводниках. При движении проводника в магнитном поле находящиеся внутри него свободные заряженные частицы движутся вместе с ним. По этой причине на каждую частицу действует сила Лоренца. В результате свободные заряды, перемещаясь внутри проводника, совершают упорядоченное движение – в проводнике возникает ЭДС индукции.
Возникающая ЭДС индукции зависит от скорости проводника, длины части проводника, находящейся в поле, и модуля вектора магнитной индукции. Это легко доказывается на основе закона электромагнитной индукции.
Представим, что проводник длиной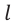
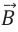
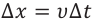
Здесь принято во внимание, что 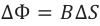
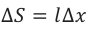
Направление индукционного тока в проводнике, движущегося в магнитном иоле, удобно определять правилом правой руки:
Правую руку следует держать в магнитном поле так, чтобы вектор 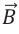
Кстати:
Принцип работы электронных счетчиков потребления, используемых в быту, основан на применении закона электромагнитной индукции. Например, в электронных счетчиках потребления воды в проводящем электрический ток потоке жидкости возникает ЭДС индукции, пропорциональная скорости жидкости. Индукционный ток в электронной части прибора преобразуется в цифровой сигнал.
ЭДС самоиндукции и энергия магнитного поля
Инертность – одно из важнейших свойств тела (происходит от латинского слова “inertia” – бездеятельность, ленивость).
Инертность — это свойство тел, выражающееся в том, что на изменение скорости тела всегда требуется определенное время. Явление сохранения телом состояния покоя или прямолинейного равномерного движения при отсутствии действия на тело других тел (когда действующие на тело силы уравновешивают друг друга) называется инерцией.
Мера инертности тела — его масса.
Энергия, которой обладает тело вследствие своего движения, называется кинетической энергией. Кинетическая энергия тела зависит от массы тела и модуля его скорости (не от направления):
Так как магнитные свойства разных веществ различны, то индукция магнитного поля, созданного в них одним и тем же источником поля, будет различна. Магнитные свойства веществ характеризуются величиной, называемой магнитной проницаемостью вещества.
Магнитная проницаемость вещества показывает, во сколько раз модуль индукции однородного магнитного поля В в веществе отличается от индукции этого магнитного поля в вакууме Во:
Здесь 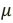
Прохождение электрического тока через газ при отсутствии внешнего воздействия называется самостоятельным разрядом. Одним из видов самостоятельного газового разряда является искровой разряд.
Искровой разряд возникает в воздухе при высоком напряжении между электродами и наблюдается в виде светящихся узких каналов зигзагообразной формы. Температура в канале разряда может достигать 10 ООО °С, сила тока до 5000 А, напряжение до 104 В.
Кстати:
Наверно, каждый из вас наблюдал появление кратковременной искры при вынимании вилки прибора в рабочем режиме из электрической розетки. Это значит, что в воздухе между вилкой прибора и электрической розеткой возник самостоятельный разряд с напряжением несколько тысяч вольт. Такая искра иногда приводит к выводу из строя вилки или розетки.
ЭДС самоиндукции
Электрический ток, существующий в любом замкнутом контуре, создает собственное магнитное поле (находится в собственном магнитном поле). При изменении силы тока в контуре одновременно происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока приводит к возникновению вихревого электрического поля, и в результате в этом контуре возникает ЭДС индукции.
Явление возникновения ЭДС индукции в замкнутом проводящем контуре в результате изменения силы тока в нем называют самоиндукцией.
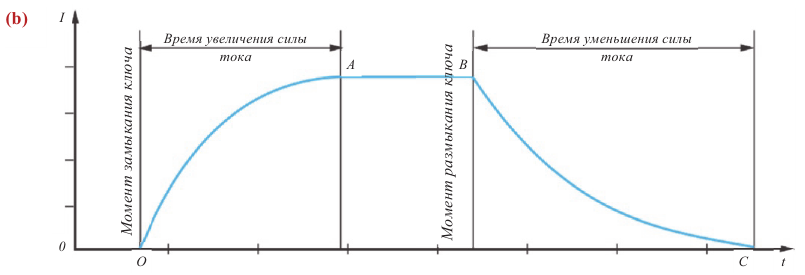
При увеличении силы тока в замкнутом контуре от нуля до определенного значения увеличивается и проходящий через этот контур магнитный поток. Возникающая в контуре в результате увеличения магнитного потока ЭДС самоиндукции создает индукционный ток, направленный против проходящего по контуру основного тока – индукционный ток замедляет рост основного тока и достижение им максимального значения – на увеличение силы тока до максимального значения уходит определенное время (кривая OA, b).
При размыкании цепи сила тока уменьшается от максимального значения до нуля, вместе с этим уменьшается магнитный поток. Уменьшение магнитного потока приводит к возникновению в контуре ЭДС самоиндукции, которая в свою очередь создает в этом контуре индукционный ток, направленный, согласно правилу Ленца, так же, как и основной ток, и замедляющий его уменьшение (кривая ВС, b).
Из вышесказанного становится ясно, что возникающий в контуре собственный магнитный поток прямо пропорционален силе проходящего через контур тока –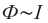
Здесь L является коэффициентом пропорциональности (между 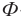
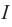
Индуктивность зависит от геометрических размеров контура (катушки), от магнитной проницаемости среды внутри него, от числа витков. Она не зависит от силы тока в контуре и магнитного потока.
Индуктивность – скалярная величина, единица ее измерения в СИ названа генри (1 Гн), в честь американского ученого Джозефа Генри:
1 Гн — индуктивность такого контура (катушки), в которой при силе тока 1 А через контур проходит собственный магнитный поток 1 Вб.
Если учесть выражение (1) в законе электромагнитной индукции, то получим, что ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока, проходящего через контур:
Здесь 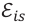
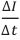
Энергия магнитного поля
Согласно закону сохранения энергии, работа, совершенная при создании ЭДС индукции, будет равна энергии магнитного поля, создавшего его. Для определения этой энергии удобно воспользоваться схожестью явления самоиндукции с явлением инерции. Так, индуктивность L играет такую же роль при изменениях силы тока 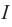
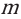
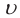
Если в этом выражении учесть формулу (1), получим ещё две формулы для энергии магнитного поля:
Из теоретических вычислений получено, что плотность энергии магнитного поля прямо пропорциональна квадрату магнитной индукции и обратно пропорциональна магнитным свойствам среды:
Здесь 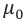
- Опыты Фарадея в физике
- Электромагниты и их применение в физике
- Колебательный контур в физике
- Исследовательские методы в физике
- Свободные и вынужденные колебания в физике
- Вынужденные электромагнитные колебания
- Резонанс в физике
- Распространение механических волн в средах
Магнитное поле, связанное с электрическим током, характеризуется определенной энергией.
Если через проводник или катушку проходит ток, то часть электроэнергии расходуется на преодоление сопротивления проводника и превращается в тепло, а часть образует магнитное поле, в котором накапливается некоторая часть энергии, превращается в потенциальную энергию.
Определение магнитной энергии
Магнитная энергия и электростатическая потенциальная энергия связаны уравнениями Максвелла. Потенциальная энергия магнитного момента mm в магнитном поле BB определяется как механическая работа магнитной силы (фактически магнитного момента) на повторное выравнивание вектора магнитного дипольного момента и равна:
E=−m⋅BE = – m cdot B
в то время как энергия, запасенная в катушке индуктивности (с индуктивностью LL) при прохождении через нее тока II, определяется как:
E=1/2LI2E = 1/2 LI^2
Это выражение лежит в основе сверхпроводящего накопления магнитной энергии.
Энергия также хранится в магнитном поле. Энергия на единицу объема в области пространства проницаемости μ0μ0, содержащей магнитное поле BB, равна:
U=B2/2μ0U = B^2/2μ_0
В более широком смысле, если мы предположим, что среда является парамагнитной или диамагнитной и существует линейное определяющее уравнение, связывающее BB, то можно показать, что магнитное поле хранит энергию
E=12∫HBdV,E=frac{1}{2}int{HBdV},
где интеграл оценивается по всей области, где существует магнитное поле.
Аналогично энергию магнитного поля тока можно определить также через работу тока против ЭДС самоиндукции, которая выполняется при замыкании цепи.
Сравнивая выражение энергии магнитного поля через индукцию и силу тока с формулой для определения кинетической энергии, делаем вывод, что индуктивность в электромагнитных явлениях играет такую же роль, как масса в механических явлениях, и является мерой инертности электрической цепи.
Энергия магнитного поля соленоида
Физическая величина, определяемая удвоенной энергией магнитного поля, сформированного единичным током в этом контуре.
Определим энергию магнитного поля соленоида, индуктивность которого LL:
L=μμ0n02VL=mu {{mu }_{0}}n_{0}^{2}V
Wm=12μμ0n02I2V{{W}_{m}}=frac{1}{2}mu {{mu }_{0}}n_{0}^{2}{{I}^{2}}V.
Индукция магнитного поля внутри соленоида:
B=μμ0n0IB=mu {{mu }_{0}}{{n}_{0}}I
откуда
I=Bμμ0n0I=frac{B}{mu {{mu }_{0}}{{n}_{0}}}
Из данных формул получаем
Wm=12B2Vμμ0,{{W}_{m}}=frac{1}{2}frac{{{B}^{2}}V}{mu {{mu }_{0}}},
где VV –объем соленоида.
Поскольку поле соленоида однородно и почти полностью локализовано в его объеме, можно определить плотность энергии магнитного поля, то есть энергию, рассчитанную на единицу объема поля:
wm=WmV=12B2μμ0=BH2=μμ0H22{{w}_{m}}=frac{{{W}_{m}}}{V}=frac{1}{2}frac{{{B}^{2}}}{mu {{mu }_{0}}}=frac{BH}{2}=frac{mu {{mu }_{0}}{{H}^{2}}}{2}
Плотность энергии магнитного поля как характеристику поля относят к любой точке поля, в которых заданы векторы BB или HH.
Зная энергию магнитного поля, можно по теории относительности найти подходящую массу поля:
m=Wmc2m=frac{{{W}_{m}}}{{{c}^{2}}}
Итак, как электрическое, так и магнитное поля имеют не только энергию, но и массу. Эти поля так же материальны, как и вещества.











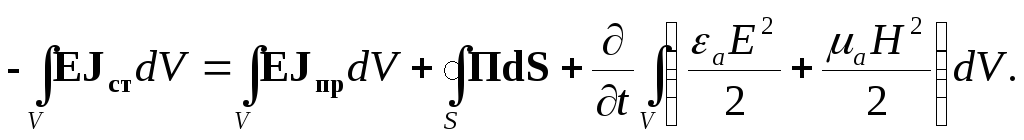
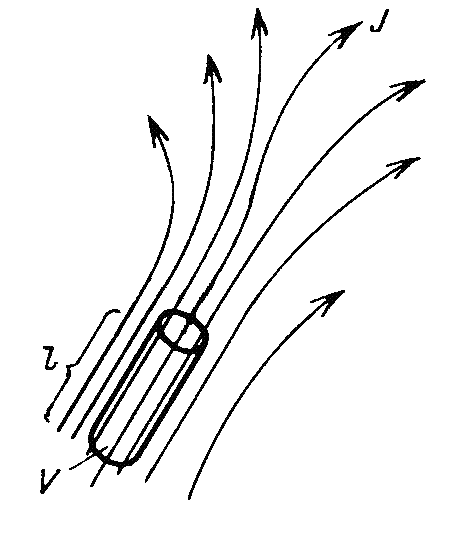
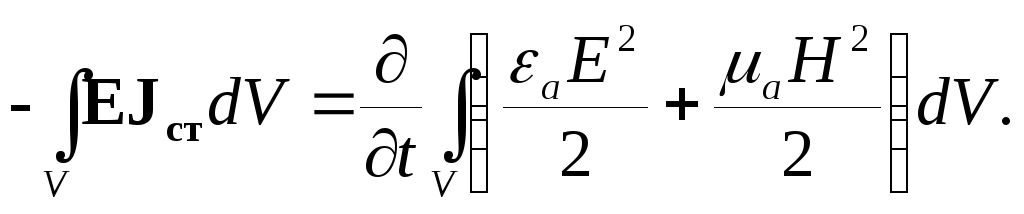











































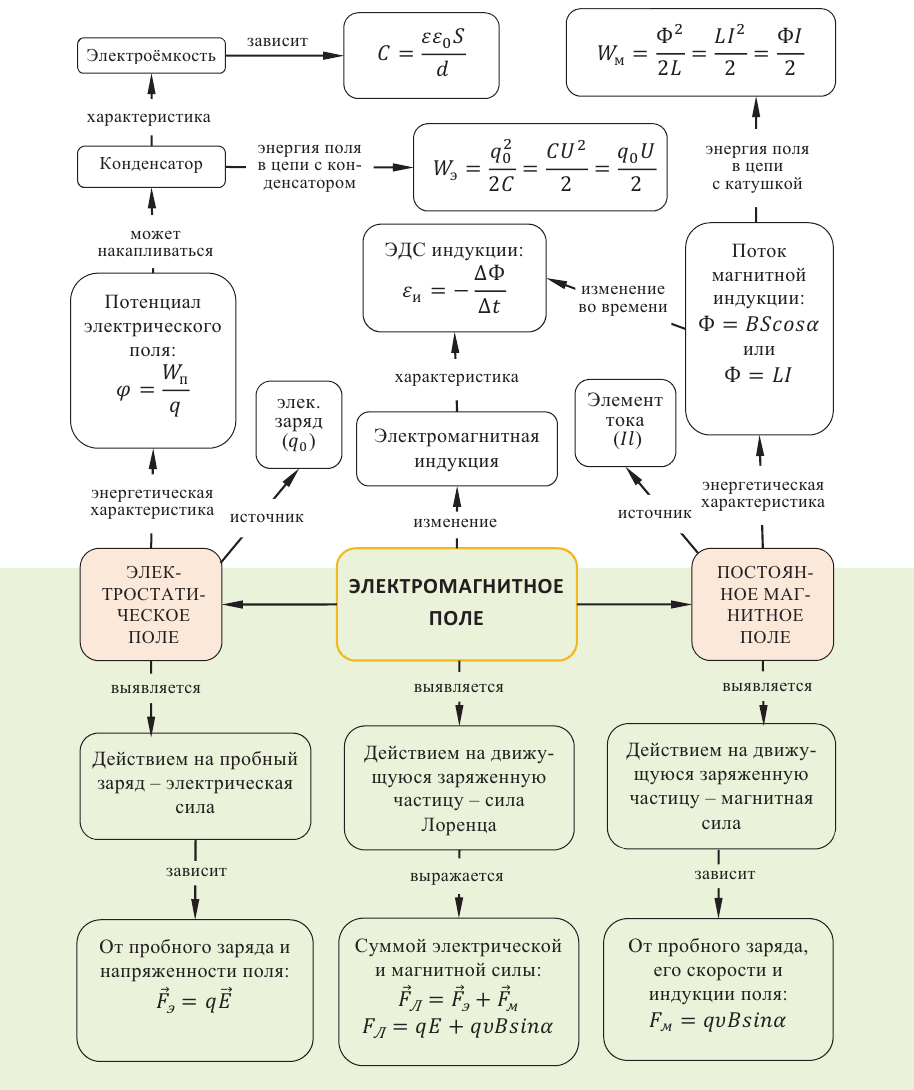



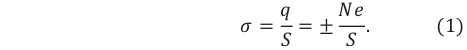

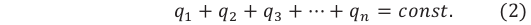
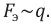
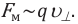
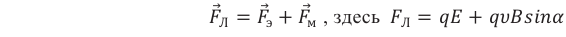
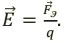
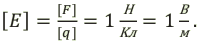
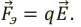


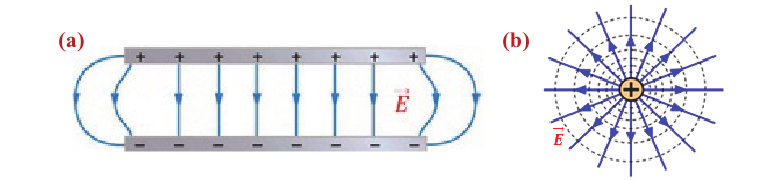
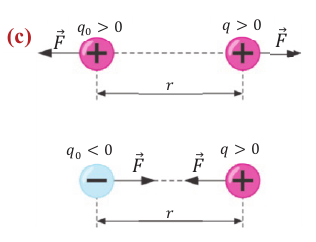
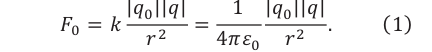
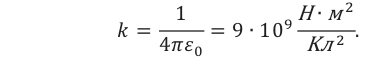
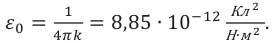
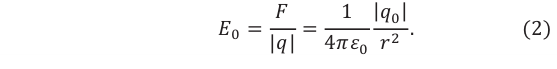
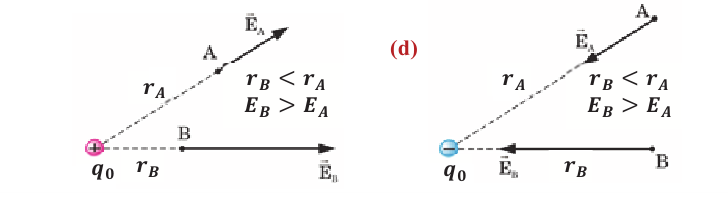
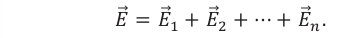
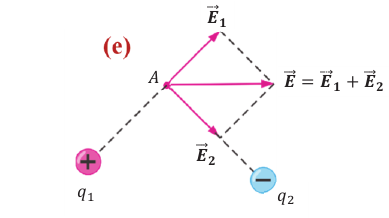
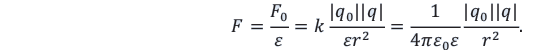




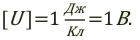

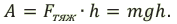



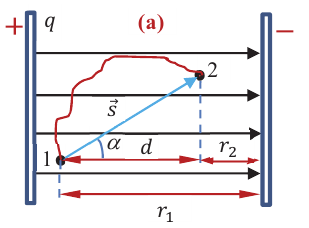
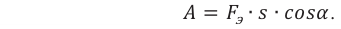

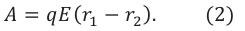
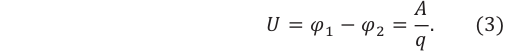
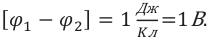
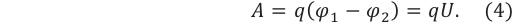
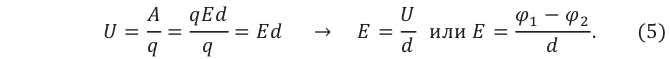
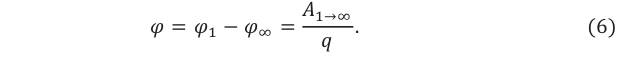
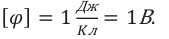
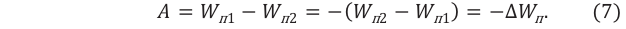

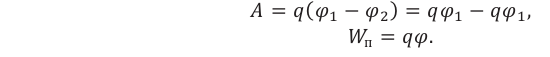

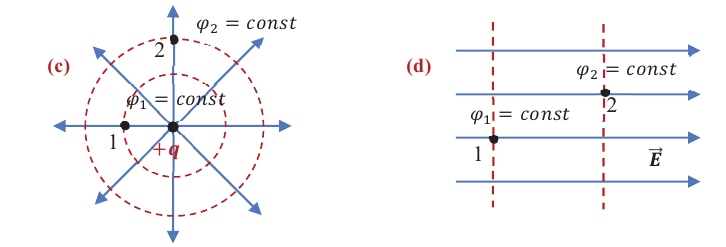


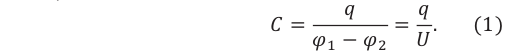

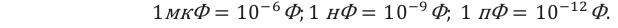

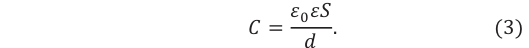
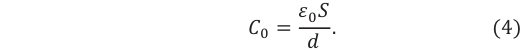
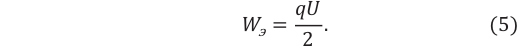
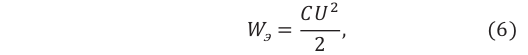
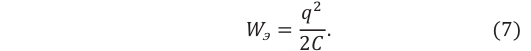
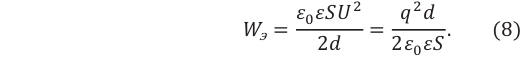
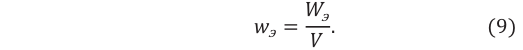
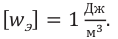
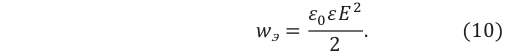
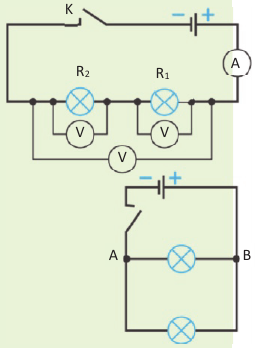
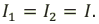


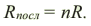
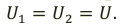
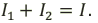



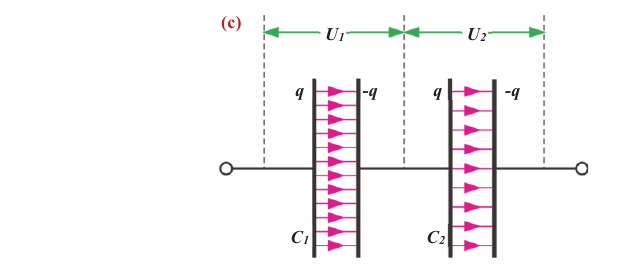


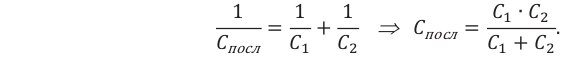

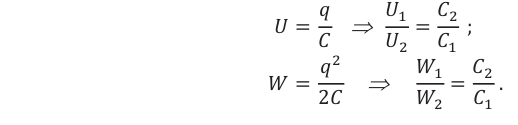
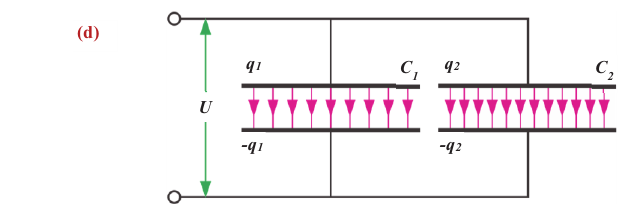




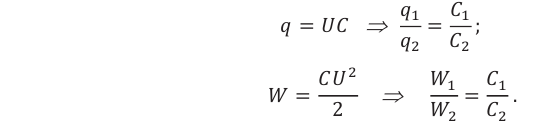
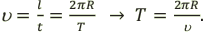
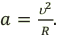
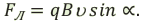


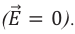

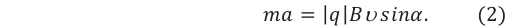

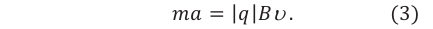
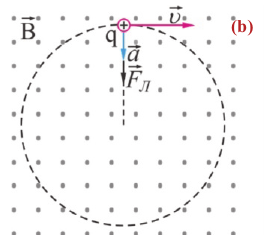

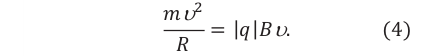
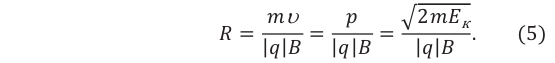
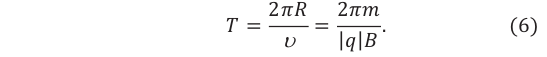
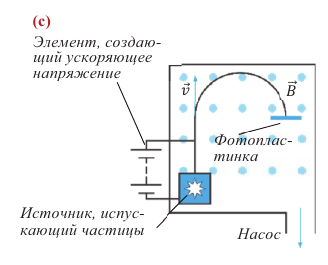
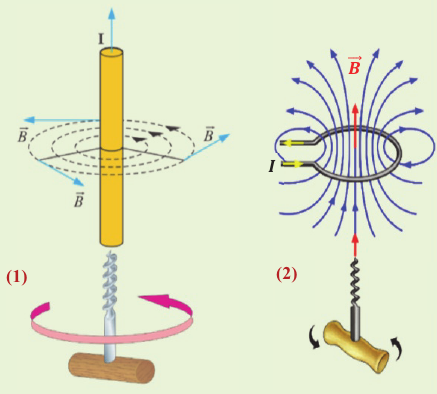
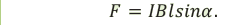
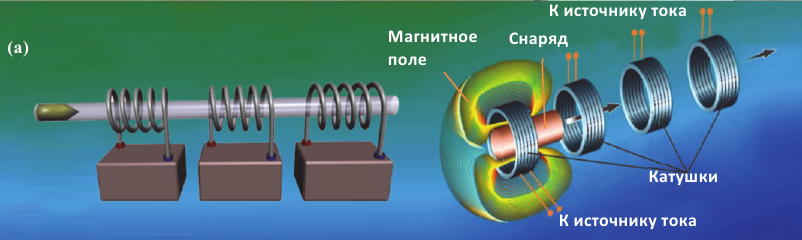



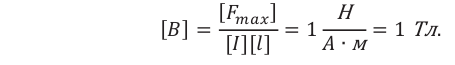
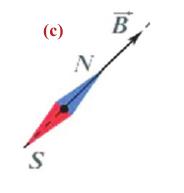
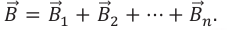
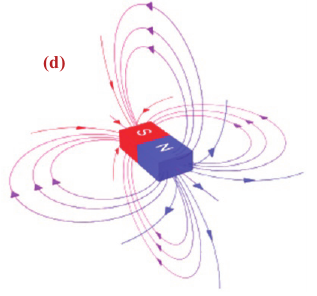
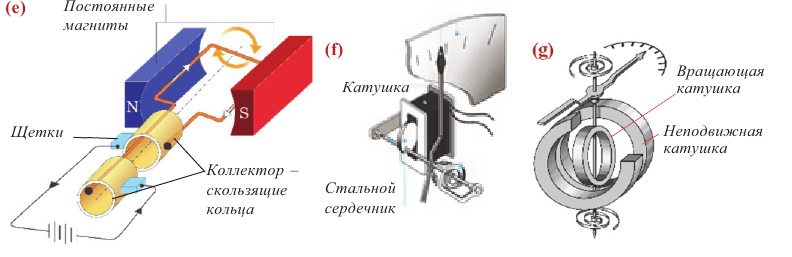
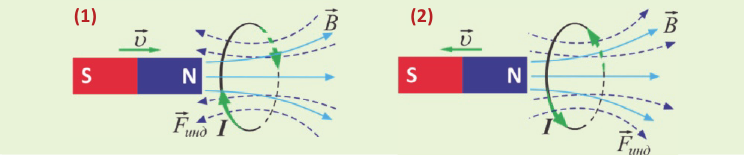
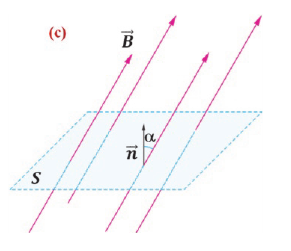

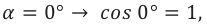 тогда магнитный поток, пронизывающий плоскость контура, принимает максимальное значение:
тогда магнитный поток, пронизывающий плоскость контура, принимает максимальное значение: