Электрон — это стабильная отрицательно заряженная элементарная частица.
Электроны играют важную роль почти во всех физических эффектах. Поскольку электроны несут заряд, они также генерируют электрическое поле. Если привести электрон в движение, то возникнет магнитное поле. Если электрон проходит через другое внешнее электрическое поле, его путь изменяется под действием силы Лоренца.
Электрон принадлежит к лептонному семейству частиц. Существует несколько различных семейств частиц, перечисленных в стандартной модели физики частиц.
Спин электрона и магнитный момент электрона.
Согласно современному уровню знаний, лептоны являются элементарными частицами. По сравнению с другими лептонами, электрон имеет самую низкую массу среди лептонов, несущих заряд. Он принадлежит к первому поколению лептонов. Второе и третье поколения — мюон и тауон. Эти две частицы имеют одинаковые с электроном заряды и спин, но отличаются от него большей массой.
Лептоны отличаются от других фундаментальных частиц, таких как кварки, отсутствием сильного взаимодействия. Все лептоны принадлежат к семейству фермионов, поэтому электрон имеет собственный вращательный момент ( спин ) s = ½ в единицах ℏ, где ℏ — приведённая постоянная Планка).
« Как и любая заряженная частица со спином, электрон обладает магнитным моментом, причём магнитный момент делится на нормальную часть и аномальный магнитный момент (добавка примерно 0,116 %). Магнитный момент электрона μe = -9,2847647043(28)⋅10−24 Дж/Тл. »
Википедия
Атомы и молекулы.
Электроны связаны с ядрами атомов «притягивающей» кулоновской силой. Такой состав из атомного ядра и одного или нескольких электронов называется атомом. Электроны движутся вокруг ядра атома. Если число электронов отличается от заряда ядра, то это ион.
Волновая природа связанных электронов описывается атомными орбиталями. Каждая из этих орбиталей имеет ряд квантовых чисел, таких как энергия и момент. Кроме того, у атома может быть только дискретное число орбиталей. В силу принципа Паули на орбитали может находиться максимум два электрона, спин которых имеет разные знаки.
Химическая связь между атомами возникает благодаря электромагнитным взаимодействиям, которые описываются с помощью квантовой физики. Самые прочные связи создаются путем обмена или передачи электронов. Это позволяет образовывать молекулы. В молекулах электроны движутся аналогично атомам и занимают молекулярные орбитали. Однако фундаментальным отличием является образование пар электронов с разными спинами. Это позволяет нескольким электронам занимать одну орбиталь без нарушения принципа Паули.
Делимость электрического заряда
Хорошо известно, что молекулы и атомы в их нормальном состоянии не имеют электрического заряда. Поэтому мы не можем объяснить электризацию их движением. Однако если мы предположим, что частицы с электрическим зарядом существуют в природе, то мы должны обнаружить, что существует предел деления электрического заряда.
Согласно различным экспериментам, проведенным советским ученым Абрамом Федоровичем Иоффе и американским ученым Робертом Милликеном, было обнаружено, что существует заряженная частица с минимальным зарядом, который невозможно разделить.
В своих экспериментах они электризовали маленькие частицы цинковой пыли. Заряд пылинок меняли и вычисляли. Это было проделано несколько раз. При этом заряд оказывался каждый раз другим. Однако все изменения были кратны целому числу, большему, чем некоторый минимальный заряд (т.е. 2, 3, 4 и т.д.). Этот результат можно интерпретировать только следующим образом. Только наименьший заряд (или целое число таких зарядов) присоединяется к пылинке цинка или отсоединяется от нее. Этот заряд дальше уже не делится. Частица с наименьшим зарядом называется электроном.
Также в ходе опытов было установлено, что любая частица вещества либо электрически нейтральна, либо имеет заряд, кратный по модулю заряду электрона.
Свойства электрона
Электрон характеризуется и другими важными свойствами, помимо спина и магнитного момента. Рассмотрим их.
Масса электрона
Электроны очень малы. Масса электрона составляет me = 9,109 • 10-31 кг или 5, 489 • 10-4 атомных единиц массы (а. е. м). Эта масса примерно в 3700 раз меньше массы молекулы водорода, которая является самой маленькой из всех молекул. Из-за эквивалентности массы и энергии в соответствии с принципом относительности это приводит к энергии покоя 0,511 МэВ (мегаэлектронвольт).
Отношение массы протона к массе электрона равно 1836, то есть протон в 1836 раз «тяжелее» электрона.
Заряд электрона
Электрический заряд — одно из основных свойств электрона. Невозможно представить, что с электронов можно снять заряд. Они неотделимы друг от друга.
Электрический заряд — это физическая величина. Она обозначается буквой q. Единицей электрического заряда является кулон (Кл). Эта единица названа в честь французского физика Шарля Кулона. Электрон — это частица с наименьшим отрицательным зарядом. Его заряд равен e0 = — 1,6 • 10-19 Кл.
Модуль заряда электрона назвали элементарным электрическим зарядом. Его обозначают е. Измерения показали, что e = 1,6 • 1019 Кл.
Обратите внимание, что любой, даже самый малый, заряд тела содержит целое число элементарных зарядов. Так как заряд тела обозначается буквой q, то получаем: q = eN, где N — целое число (N = 1, 2, 3, … ).
Элементарный заряд может показаться очень малым, однако вспомним: в любом теле, видимом невооружённым глазом, содержится невообразимо большое число заряженных частиц. Так, суммарный заряд электронов в одной столовой ложке воды равен по модулю примерно миллиону кулонов (а вы уже знаете, как велик заряд всего в 1 Кл).
Важно! Термин элементарный заряд был придуман, когда предположили, что этот заряд является наименьшим электрическим зарядом в природе. Сегодня мы знаем, что 1/3 элементарного заряда также приходится на кварки.
Энергия покоя электрона
Энергия электрона рассчитывается из эквивалентности массы и энергии. Вы знаете это как формулу из теории относительности E=mc2. E означает энергию, m — массу, а c — скорость света. Как было уже сказано выше в этой статье: «из-за эквивалентности массы и энергии в соответствии с принципом относительности это приводит к энергии покоя 0,511 МэВ (мегаэлектронвольт)».
В формуле это можно рассчитать следующим образом: E = mec2 = 9,109 • 10-31 • (3 • 108 )2 = 8,2 • 10-14 Дж = 0,511 • 106 эВ ≈ 0,511 МэВ
Список литературы
Список литературы
- Тихомирова С. А., Яворский Б. М. Физика (базовый уровень) – М.: Мнемозина, 2012.
- Перышкин А. В. Физика 8. – М.: Дрофа, 2010.
- Бронштейн М. П. Атомы и электроны. — М.: Наука. — 1980. — 152 с., Библиотечка «Квант», вып. 1. Тир. 150000 экз.
|
|
Макеты страниц
Проблема собственной энергии электрона не является новой: она появилась в классической физике. Если предположить, что электрон является шариком радиуса 
, причем весь его заряд расположен на поверхности, то полная электростатическая энергия равна 
. Возможно, что масса электрона 
соответствует этой энергии. Однако, если вы сосчитаете импульс 
поля, когда электрон движется со скоростью v (с учетом лоренцева сокращения шарика), то получите 
. Эта величина соответствует частице с массой 
. Пуанкаре предположил, что какие-то силы должны удерживать части шарика и что эти силы должны давать добавки в энергию. Однако не существует надежной теории таких сил.
Эта собственная энергия происходит от энергии, необходимой для того, чтобы «собрать» заряд. Можно считать, что это есть энергия взаимодействия одной части заряда электрона с другой.
Казалось бы, что возможный способ избавиться от подобных эффектов состоит в том, чтобы запретить электрону воздействовать на самого себя — т. е. предположить, что электроны действуют только друг на друга. (Тогда электрон мог бы быть точечным зарядом.) Однако действие электрона самого на себя необходимо для объяснения реального явления, явления радиационного трения. Ускоряемый заряд излучает, теряя энергию, поэтому ускоряющая сила должна производить работу. Против каких сил? Согласно классической физике — против силы, создаваемой действием одной части заряда на другую.
Вы можете рассчитать силу F, действующую на движущийся заряженный шарик, благодаря действию электромагнитного поля одной части шарика на его другие части. Эта сила равна
Первый член согласуется с массой, вычисленной из импульса поля. Второй член есть сила реакции излучения, испущенного электроном, и не зависит от 
. Однако было бы непоследовательным устремить а к нулю. Распределенный заряд никогда не был тщательно проанализирован. Возникают вопросы, связанные с внутренними движениями и т. п.
В действительности эти вопросы в классической физике решались различными путями, но ни один из них не был успешно перенесен в квантовую механику (ссылки см. в работе Фейнмана [10]).
Перенормировка массы.
Обсудим теперь аналог этой задачи в квантовой механике — перенормировку массы. Рассмотрим амплитуду электрона, движущегося между точками X и Y. Диаграмма низшего порядка дает
Возможно также, что при движении от X к Y электрон испустит и поглотит виртуальный фотон. В этом случае
где величина
является инвариантной функцией вида 
. Каков ее физический смысл? Допустим, что С мала. Тогда первые два члена могут быть записаны в виде
благодаря тому, что
(Последняя формула является частным случаем более общего операторного соотношения
Если бы С была числом, мы могли бы рассматривать ее как поправку к массе. Первый и второй члены этого ряда суть амплитуды движения электрона без и с одним виртуальным фотоном соответственно.
Легко проверить, что третий член соответствует вкладу с двумя фотонами
четвертый член — вкладу с тремя фотонами и т. д. Однако такие диаграммы содержат лишь процессы, в которых в каждый данный момент содержится не более одного фотона.
Рис. 28-1.
Примеры диаграмм другого типа с двумя виртуальными фотонами приведены на рис. 28-1. Мы не будем сейчас принимать во внимание такие диаграммы, так как они добавляют в С члены порядка 
, когда мы записываем полную амплитуду распространения электрона между X и Y в виде
где А и В — функции от 
. Полюс этого пропагатора дает соотношение между энергией и импульсом свободной частицы и поэтому определяет экспериментально наблюдаемую массу 
.
Избавляясь от матриц в знаменателе
мы получаем, что положение полюса определяется решением уравнения
Заметим здесь, что наличие второго полюса может быть истолковано как существование другой частицы (вероятно, 
-мезона). Предполагая, что 
и 
, мы можем положить 
и 
. Тогда
или
где
Таким образом, пропагатор имеет полюс при 
и для 
, близких к 
, ведет себя как некоторая константа (вычет в полюсе), умноженная на 
. Обозначим вычет при 
через 
. Можно теперь переписать пропагатор следующим образом:
(
может быть выражено через А, В и их производные 
, 
в точке 
. Отклонение от обычной формы 
можно интерпретировать как поправку к константе связи фотона [11] (поскольку множитель 
в пропагаторе можно получить, умножая каждую фотонную вершину на 
). Следующий шаг заключается в том, чтобы вычислить функции А и В. Для этой цели следует вычислить интеграл
Используя соотношения
избавляемся от 
. При вычислении 
можно положить 
, тогда получаем
Этот интеграл расходится. При больших значениях 
первый знаменатель может быть заменен на 
. Тогда член, содержащий 
, исчезает в силу соображений симметрии. Остальная часть подынтегрального выражения ведет себя при больших 
как 
, и поэтому интеграл логарифмически расходится. Квантовая электродинамика ударила лицом в грязь!
Бете заметил, что данная бесконечность является единственно существенной в электродинамике (за исключением еще одной, которую мы обсудим позднее). Пусть у нас есть способ сделать этот интеграл «на время» сходящимся. Допустим, например, что пропагатор 
всегда следует умножать на релятивистски-инвариантный множитель 
, обеспечивающий сходимость.
Если положить
(такой 
обрезает интеграл при больших 
), то интеграл может быть вычислен. Получаем (методы вычисления см. в ссылке [11])
пренебрегая членами, исчезающими вместе с 
.
Если вам придется вычислять любой процесс в высшем порядке, 
вы встретите член, пропорциональный 
(для частиц со спином 
— электронов, взаимодействующих лишь с фотонами, не встретится ничего более плохого, чем логарифмические расходимости). Затем, где бы вы ни встретили m, подставьте вместо него 
разложите до первой степени по 
. Чудо заключается в том, что полный коэффициент при 
обратится в нуль. Остальные члены имеют определенный предел при 
. Другими словами, значение параметра обрезания не появляется в окончательном выражении, если мы всегда выражаем ответ через экспериментальную массу и устремляем 
при фиксированном 
.
Используя подобные идеи, Бете попробовал вычислить смещение энергетических уровней в атоме водорода, обусловленное собственной энергией связанного электтрона. Толчок был дан экспериментом Резерфорда и Лэмба, которые обнаружили, используя микроволновую технику, расщепление примерно в 1000 МГц между уровнями 
и 
в водороде. Если пренебречь взаимодействием с полем излучения, то эти уровни должны быть полностью вырождены. Бете произвел неполное вычисление, используя нерелятивистское приближение. Быстрое развитие квантовой электродинамики в 1948—1949 гг. последовало в результате усилий сформулировать его и Вайскопфа идеи в релятивистски-инвариантной форме и закончить его вычисления.
Итак, мы нашли еще одно правило, которое должно быть включено в квантовую электродинамику: (1) введите произвольный фактор обрезания
к каждому пропагатору 
; (2) выразите ответ через 
; (3) перейдите к пределу 
при фиксированном 
.
Швингер вычитал бесконечности из подынтегрального выражения, но его метод чрезвычайно сложен с практической точки зрения. Оказывается также, что он совершенно эквивалентен сформулированному правилу.
Все ли в порядке в описанной процедуре? Это, разумеется, весьма сомнительный рецепт. Вайскопф заметил однажды, что только, если бы Господь снабдил нас и заряженным, и нейтральным электронами, введение 
было бы оправдано.
В действительности в природе встречаются примеры, в которых техника обрезания не работает; например, 
и 
. Массы 
и 
отличаются, но вычисления приводят к квадратичным расходимостям. При проведении подобных расчетов частицы считаются точечными. В действительности следует учитывать облако нуклонных пар, и некоторые считают, что такой учет приведет к устранению расжодимостей. Однако подобные утверждения никогда не были доказаны.
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА СЕРИИ
- ПРЕДИСЛОВИЕ
- 1. ОБЗОР ПРИНЦИПОВ КВАНТОВОЙ МЕХАНИКИ
- 2. СПИН И СТАТИСТИКА
- 3. ВРАЩЕНИЯ И МОМЕНТ
- 4. ПРАВИЛА СЛОЖЕНИЯ МОМЕНТОВ
- 5. РЕЛЯТИВИЗМ
- 6. ЭЛЕКТРОМАГНИТНОЕ И ФЕРМИЕВСКОЕ ВЗАИМОДЕЙСТВИЯ
- 7. ФЕРМИЕВСКИЕ ВЗАИМОДЕЙСТВИЯ И НИСПРОВЕРЖЕНИЕ ЧЕТНОСТИ
- 8. ПИОН-НУКЛОННАЯ СВЯЗЬ
- 9. СТРАННЫЕ ЧАСТИЦЫ
- 10. НЕКОТОРЫЕ СЛЕДСТВИЯ СТРАННОСТИ
- 11. СХЕМЫ СИЛЬНОЙ СВЯЗИ
- 12. РАСПАДЫ СТРАННЫХ ЧАСТИЦ
- 13. ВОПРОС ОБ УНИВЕРСАЛЬНОМ КОЭФФИЦИЕНТЕ
- 14. ЗАКОНОМЕРНОСТИ РАСПАДОВ С ИЗМЕНЕНИЕМ СТРАННОСТИ: ДАННЫЕ ОПЫТОВ
- 15. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРОМАГНИТНЫХ И СЛАБЫХ ВЗАИМОДЕЙСТВИЙ
- 16. ПЛОТНОСТЬ КОНЕЧНЫХ СОСТОЯНИЙ
- 17. ПРОПАГАТОР СКАЛЯРНОЙ ЧАСТИЦЫ
- 18. ПРОПАГАТОР В КОНФИГУРАЦИОННОМ ПРОСТРАНСТВЕ
- 19. ЧАСТИЦЫ СО СПИНОМ 1
- 20. ВИРТУАЛЬНЫЕ И РЕАЛЬНЫЕ ФОТОНЫ
- 21. ЗАДАЧИ
- 22. ЧАСТИЦЫ СО СПИНОМ 1/2
- 23. ОБОБЩЕНИЕ НА КОНЕЧНУЮ МАССУ
- 24. СВОЙСТВА ЧЕТЫРЕХКОМПОНЕНТНОГО СПИНОРА
- 25. ЭФФЕКТ КОМПТОНА
- 26. ПРЯМОЕ РОЖДЕНИЕ ПАР МЮОНАМИ
- 27. ПРОЦЕССЫ ВЫСШИХ ПОРЯДКОВ
- 28. СОБСТВЕННАЯ ЭНЕРГИЯ ЭЛЕКТРОНА
- 29. КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
- 30. МЕЗОННАЯ ТЕОРИЯ
- 31. ТЕОРИЯ B-РАСПАДА
- 32. СВОЙСТВА B-ВЗАИМОДЕЙСТВИЙ
- 33. ИТОГИ КУРСА
- ФУНДАМЕНТАЛЬНЫЕ ЧАСТИЦЫ
- ЛИТЕРАТУРА
- ПОСЛЕСЛОВИЕ ПЕРЕВОДЧИКА
Квантовые постулаты Бора – это два основных допущения, введённые Н.Бором для объяснения устойчивости атома и спектральных закономерностей (в рамках модели атома Резерфорда).
Планетарная модель атома Резерфорда позволила объяснить результаты опытов по рассеянию α-частиц вещества, но она не способна объяснить факт существования атома и его устойчивость.
В соответствии с планетарной моделью электроны атома должны двигаться вокруг неподвижного ядра. Двигаясь вокруг ядра с центростремительным ускорением под действием силы притяжения к ядру, электрон должен, как и всякий ускоренно движущийся электрический заряд, излучать электромагнитные волны с частотой, равной частоте обращения электрона вокруг ядра.
Энергия электрона в атоме должна при этом непрерывно уменьшаться за счёт излучения. Сам электрон должен с каждым оборотом приближаться по спирали к ядру и упасть на него под действием электрической силы притяжения. При этом атом потеряет всю электронную оболочку, а также присущие ему физические и химические свойства. Кроме того, атом должен потерять спектр излучения частоты, то есть атом должен давать излучение с непрерывным (сплошным) спектром частот.
Эти результаты, полученные с помощью классической механики и электродинамики, находятся в резком противоречии с опытом, который показывает, что
- Атомы являются весьма устойчивыми системами и в невозбуждённом состоянии могут существовать неограниченно долго, не излучая при этом электромагнитные волны
- Спектр излучения атома является линейчатым (дискретным) – образованным из отдельных линий (от латинского discretus – прерывистый, состоящий из отдельных значений)
Всё это свидетельствует о том, что законы классический физики применить к электронам в атомах нельзя, поэтому необходимы новые представления о механизме излучения и поглощения атомами электромагнитных волн. В основе современной теории атома лежитквантовая механика – теория, устанавливающая способ описания и законы движения микрочастиц (элементарных частиц, атомов, молекул, атомных ядер) и их систем (например, кристаллов), а также связь величин, которые характеризуют частицы и системы, с физическими величинами, измеряемыми опытным путём.
В 1913 году датский физик Нильс Бор (1885 – 1962) ввёл идеи квантовой теории в ядерную модель атома Резерфорда и разработал теорию атома водорода, которая подтвердилась всеми известными тогда опытами. Бор сформулировал в виде постулатов основные положения новой теории, которые налагали лишь некоторые ограничения на допускаемые классической физикой движения. Однако последовательной теории атома Бор не дал. Впоследствии теория Бора была включена как частный случай в квантовую механику. В основе теории Бора лежат два постулата.
Первый постулат Бора: постулат стационарных состояний
Атомная система может находиться только в особых стационарных, или квантовых, состояниях, каждому из которых соответствует определённая энергия En. В стационарном состоянии атом не излучает.
Второй постулат Бора: правило частотe
Излучение света происходит при переходе атома из стационарного состояния с большей энергией Ek в стационарное состояние с меньшей энергией En. Энергия излученного фотона равна разности энергий стационарных состояний:
hvkn = Ek — En
Частота излучения равна:
vkn = (Ek — En) / h = (Ek / h) — (En / h)
Или, длина волны излучения λ равна:
1 / λkn = (1 / hc) (Ek — En)
Где h – постоянная Планка, с – скорость света в вакууме.
Если Ek > En, то происходит излучение фотона, если Ek < En, то происходит поглощение фотона, при котором атом переходит из стационарного состояния с меньшей энергией в стационарное состояние с большей энергией. Таким образом, для каждого атома имеется ряд строго определённых дискретных значений энергии, которыми он может обладать. Физические величины, например энергия и импульс, которые могут принимать лишь дискретные (квантовые) значения, носят название квантованные физические величины (квантование физических величин). При этом энергетические уровни атома – это возможные значения энергии атома.
Правило квантования орбит позволяет определить радиусы стационарных орбит:
mvnrn = nh’
где n = 1, 2, 3…, m – масса электрона, rn – радиус n-ой орбиты, vn – скорость электрона на этой орбите.
Число n – положительное число, которое называется главное квантовое число.
Величина (mvn)rn – момент импульса электрона.
h’ – это величина, которая равна:
h’ = h/2π = 1,05445887•10-34 Дж•с
где h – постоянная Планка.
Главное квантовое число указывает номер орбиты, по которой может обращаться электрон.
Свои постулаты Н.Бор применил для построения теории простейшей атомной системы – атома водорода, состоящего из ядра – протона, и одного электрона. Эта теория также применима для водородоподобных ионов, то есть атомов с зарядом ядра Ze и потерявших все электроны, кроме одного (например, Li2+, Be3+ и т.п.). В предположении, что электрон движется по круговой орбите, постулаты Бора позволяют найти радиусы rn стационарных, возможных орбит электрона. На электрон действует кулоновская сила:
Fk = (1 / 4πε0) (ε2 / rn2)
Где е – модуль заряда электрона, равный заряду ядра, ε0 = 8,85418782 * 10-12 Ф/м – электрическая постоянная в единицах СИ.
Кулоновская сила сообщает электрону на орбите центростремительное ускорение:
aцс = (vn2) / rn
Согласно второму закону Ньютона:
Fk = maцс
Поэтому
(mvn2) / rn = e2 / (4πε0rn2)
Или
mvn2rn = e2 / (4πε0)
Используя правило квантования орбит mvnrn = nh’, можно получить выражения для возможных радиусов орбит. Исключая скорость vn из предыдущего выражения, получим:
rn = 4πε0n2h’ / me2 (так как h’ = h / 2π)
Таким образом, радиусы орбит электрона в атоме водорода прямо пропорциональны квадратам главного квантового числа n.
Наименьший радиус орбит при n = 1, то есть радиус первой орбиты в атоме водорода равен:
r1 = 4πε0h’ / me2 = 0,528 * 10-10 м = 0,528 Å
Радиус первой орбиты в атоме водорода носит название первый Боровский радиус и служит единицей длины в атомной физике.
Полная энергия Е электрона в атоме водорода, согласно механике Ньютона, равна сумме кинетической энергии Еk и потенциальной энергии П взаимодействия электрона с ядром:
E = Еk — П = (mvn2 / 2) — (e2 / 4πε0rn)
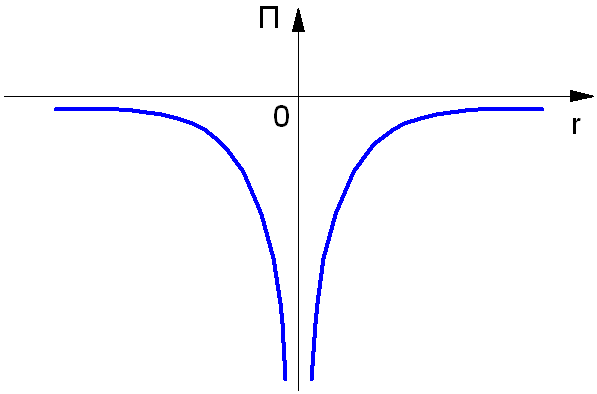
Потенциальная энергия электрона в атоме отрицательна:
П = — (e2 / 4πε0rn)
Так как нулевой уровень отсчёта берётся на бесконечности (рис. 1.3), а по мере приближения электрона к ядру его потенциальная энергия уменьшается. Взаимодействующие частицы – ядро и электрон – имеют заряды противоположных знаков.
Рис. 1.3. Потенциальная энергия электрона в атоме.
Подставляя значение скорости
vn2 = — e2 / 4πε0mrn
в выражение полной энергии, получим:
E = (m / 2) (e2 / 4πε0mrn) — (e2 / 4πε0rn)
Подставляя в эту формулу выражение для радиусов орбит, получим энергетические уровни электрона в атоме водорода (значения энергий стационарных состояний атома):
En = -(1 /(4πε0)2) me4 / 2h’2n2 = — (me4 / 8h2ε02) * (1 / n2), n = 1,2,3…
Энергия Еn электрона в атоме водорода зависит от главного квантового числа n, которое определяет энергетические уровни электрона в атоме водорода.
Основное энергетическое состояние атома (нормальное состояние атома) – это энергетический уровень при n = 1.
Значение энергии, соответствующее первому (низшему) энергетическому уровню в атоме водорода равно:
E1 = -(1 /(4πε0)2) me4 / 2h’2λ = -2,485 * 10-19 Дж = -13,53 эВ
В этом состоянии атом может находиться сколько угодно долго. Для того чтобы ионизировать атом водорода, ему нужно сообщить энергию 13,53 эВ, которая называется энергия ионизации.
Энергетические уровни при n > 1 – это возбуждённые энергетические состояния (возбуждённые состояния атома). Возбуждённое состояние атома является менее устойчивым, чем основное состояние. Время жизни атома в этом состоянии имеет порядок 10-8 секунд. За это время электрон успевает совершить около ста миллионов оборотов вокруг ядра.
При переходе электрона с удалённой от ядра стационарной k-орбиты на ближайшую n-ую орбиту атом излучает фотон, энергия которогоhvnk согласно второму постулату Бора определяется:
hvkn = Ek — En = -(1 / (4πε0)2) * (me4 / 2h’2) * [(1 / n2) — (1 / k2)] = (me4 / 8h2ε02) * [(1 / n2) — (1 / k2)]
Частота излучения атома водорода:
vkn = (1 / (4πε0)2) * (me4 / h’3) * [(1 / n2) — (1 / k2)] = R[(1 / n2) — (1 / k2)]
Где
R = (me4 / (4πε0)2) * 4πh’3) = (me4 / 8h3ε02) = 3,288 * 1015 c-1— постоянная Ридберга
Постоянная Ридберга определяется через постоянную Планка, массу и заряд электрона.
Длина волны излучения определяется соотношением:
1 / λnk = vnk / c = (me4 / 8ε02h3c) * [(1 / n2) — (1 / k2)] = Rc[(1 / n2) — (1 / k2)]
Где
Rc = R / c = 1,0974 * 107 м-1 — также постоянная Ридберга
с = 3*108 м/с – скорость света в вакууме.
Теоретическое значение R совпадает с экспериментальным значением, полученным из спектроскопических измерений.
Энергия обычно измеряется в электронвольтах (эВ). Электронвольт– это значение энергии, которую приобретает электрон, пройдя ускоряющую разность потенциалов в 1 В:
1 эВ = 1,6 * 10-19 Кл * 1В = 1,6 * 10-19 Дж
Содержание
- Энергия электрона. Откуда Электрон берет энергию,, чтобы вечно вращаться вокруг ядра?
- Заряд электрона. Опыты Милликена и Иоффе
- Энергия сродства к электрону
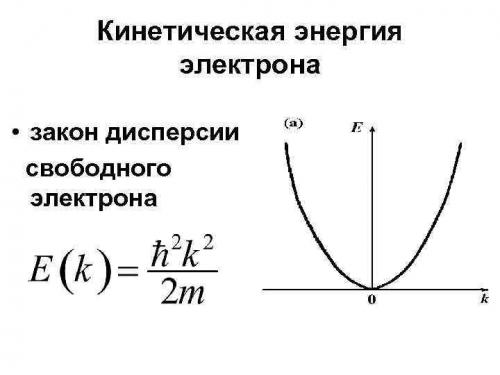
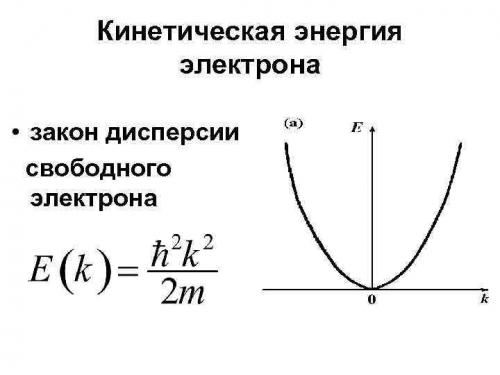
- Кинетическая энергия электрона •
- Почему Электрон теряет кинетическую энергию при излучении. Откуда электрон берет энергию, чтобы вечно вращаться вокруг ядра?
- Энергия альфа частицы. Энергия образования
- Масса электрона – мал золотник да дорог
Энергия электрона. Откуда Электрон берет энергию,, чтобы вечно вращаться вокруг ядра?
Ниоткуда. Она ему не нужна, поскольку он вокруг ядра не вращается.
Электрон, казалось бы, должен бесконечно вращаться вокруг ядра, как луна вокруг земли. Так было бы, не имей электрон заряда. Двигаясь по кругу с постоянной скоростью, он все же меняет скорость, поскольку меняется направление. Но заряженная частица, скорость которой непостоянна, излучает электромагнитные волны, то есть теряет энергию. Однако электрон почему-то не излучает. Дело в том, что он в описанной схеме выступает как частица, а на самом деле является одновременно и частицей, и волной. Волна же бывает бегущая и стоячая. Например, от камешка, упавшего в море, – бегущие, а если камешек упадет в таз с водой, то бегущая к стенкам волна сложится с той, что от них отразилась, и возникнет стоячая волна: горбы и впадины “Стоят” на месте. Нечто подобное происходит и в атоме, только стенки здесь две: одна – ядро, роль другой выполняет сила электрического притяжения между ядром и электроном, не позволяющая электрону улететь. Орбита электрона – место, где амплитуда “Электронной” стоячей волны максимальна. И оставаться на ней он может сколь угодно долго, поскольку здесь нет никакого изменения скорости, а значит, и излучения. Источник: журнал “Вокруг Света”.
Заряд электрона. Опыты Милликена и Иоффе
Американский ученый Р. Милликен экспериментально доказал то, что элементарный заряд существует. В своих опытах он измерял скорость движения капель масла в однородном электрическом поле, которое создавалось между двумя электрическими пластинами. Капля заряжалась при столкновении с ионом. Сравнивались скорости движения капли не имеющей заряда и этой же капли после столкновения с ионом (приобретшей заряд). Зная напряженность поля между пластинами, вычислялся заряд капли.
Опыты Милликена повторил А.Ф. Иоффе. Он использовал металлические пылинки вместо капель масла. Изменяя напряженность поля между пластинками, Иоффе добивался равенства силы тяжести и силы Кулона, пылинка при этом оставалась неподвижной. Пылинку освещали ультрафиолетом. Заряд ее при этом изменялся, для уравновешивания силы тяжести приходилось изменять напряженность поля. По полученным величинам напряженности ученый судил об отношении электрических зарядов пылинки.
В опытах Милликена и Иоффе было показано, что заряды пылинок и капель всегда изменялись скачком. Минимальное изменение заряда было равно:
Электрический заряд всякого заряженного тела равен целому числу и кратен заряду электрона. Сейчас существует мнение, что имеются элементарные частицы – кварки, которые обладают дробным зарядом ().
Энергия сродства к электрону
Материал из Википедии — свободной энциклопедии
Зависимость сродства к электрону атома от атомного номера элемента (экзоэффект указан со знаком минус, эндоэффект со знаком плюс)
Эне́ргией сродства́ а́тома к электро́ну , или просто его сродством к электрону (ε), называют энергию, выделяющуюся или поглощающуюся в процессе присоединения электрона к свободному атому в его основном состоянии с превращением его в отрицательный ион A−(сродство атома к электрону численно равно, но противоположно по знаку энергии ионизации соответствующего изолированного однозарядного аниона).
В отличие от ионизационного потенциала атома , имеющего всегда эндоэнергетическое значение, сродство атома к электрону описывается как экзоэнергетическими, так и эндоэнергетическими значениями.
| Элемент | ε | Элемент | ε | Элемент | ε |
|---|---|---|---|---|---|
| H | -0,75 | Na | -0,78 | K | -0,92 |
| He | 0,30 | Mg | 0,32 | Ca | 0,40 |
| Li | -0,58 | Al | -0,52 | Sc | 0,14 |
| Be | 0,19 | Si | -1,39 | Ti | -0,40 |
| B | -0,33 | P | -0,78 | V | -0,94 |
| C | -1,12 | S | -2,07 | Cr | -0,98 |
| N | 0,27 | Cl | -3,61 | Mn | 1,07 |
| О | -1,47 | Br | -3,36 | Fe | -0,58 |
| F | -3,45 | I | -3,06 | Co | -0,94 |
| Ne | 0,55 | Ni | -1,28 | ||
| Cu | -1,80 |
Сродство к электрону определяет окислительную способность частицы. Молекулы с большим сродством к электрону являются сильными окислителями. Наибольшим сродством к электрону обладают элементы 17 группы ( p -элементы VII группы). Наименьшее сродство к электрону у атомов с конфигурацией s2( Be , Mg , Zn ) и s2p6( Ne , Ar ) или с наполовину заполненными p – орбиталями ( N , P , As ):
Небольшие расхождения в цифрах между табл. 1 и табл. 2 обусловлены тем, что данные взяты из разных источников, а также погрешностью измерений.
Наибольшее значение сродства к электрону имеет гексафторид платины : 7,00±0,35 эВ.
Кинетическая энергия электрона •
Скачать презентацию Кинетическая энергия электрона •
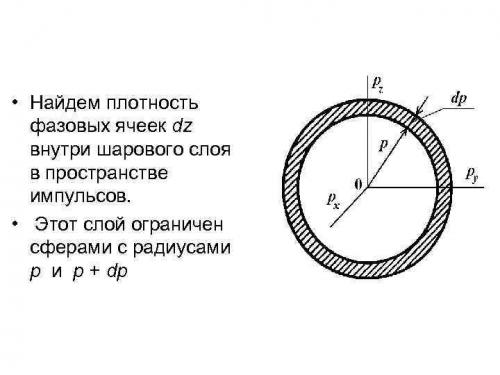
13 плотность состояний.ppt
- Количество слайдов: 8
Кинетическая энергия электрона • закон дисперсии свободного электрона
Соотношение неопределенностей Принцип неопределенности Гейзенберга : произведение неопределенностей двух канонически сопряженных величин не может быть меньше постоянной Планка Соотношение неопределенностей характеризует область пространственной локализации микрочастицы при заданном интервале проекций импульсов
Для направления x соотношение неопределенностей имеет вид : произведение неопределенностей проекций координаты dх и импульса dрх на ось x для любой микрочастицы больше или равно постоянной Планка
Для трех пространственных координат соотношение неопределенностей Их произведение дает Определим фазовую ячейку в шестимерном пространстве координат-импульсов, «разрешенную» частице, следующим условием
Плотность электронных состояний Число фазовых ячеек d. Z в объеме координатного пространства d. V и в объеме трехмерного пространства импульсов dpxdpydpz равно Плотность фазовых ячеек (в единичном объеме трехмерного пространства) в объеме трехмерного пространства импульсов dpxdpydpz равна
• Найдем плотность фазовых ячеек dz внутри шарового слоя в пространстве импульсов. • Этот слой ограничен сферами с радиусами р + dp
Объем шарового слоя равен К инетическая энергия частицы свободной частицы равна полной энергии Е , так как потенциальная энергия свободной частицы равна нулю.
Число фазовых ячеек, приходящихся на интервал энергии d. E С учетом 2 -х спиновых состояний электронов число фазовых ячеек в единичном интервале энергии равно плотность электронных состояний Зависимость плотности состояний от энергии E свободных электронов
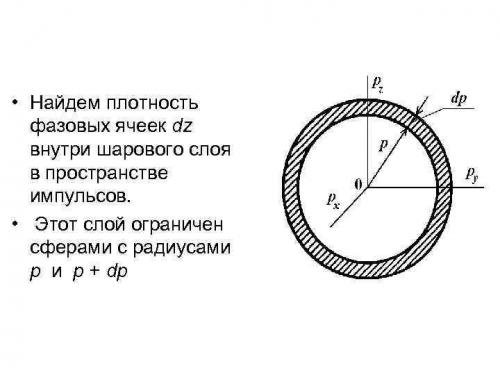
Почему Электрон теряет кинетическую энергию при излучении. Откуда электрон берет энергию, чтобы вечно вращаться вокруг ядра?
ПОДЕЛИТЬСЯ
Ниоткуда. Она ему не нужна, поскольку он вокруг ядра не вращается
Электрон, казалось бы, должен бесконечно вращаться вокруг ядра, как Луна вокруг Земли. Так было бы, не имей электрон заряда. Двигаясь по кругу с постоянной скоростью, он все же меняет скорость, поскольку меняется направление. Но заряженная частица, скорость которой непостоянна, излучает электромагнитные волны, то есть теряет энергию. Однако электрон почему-то не излучает. Дело в том, что он в описанной схеме выступает как частица, а на самом деле является одновременно и частицей, и волной. Волна же бывает бегущая и стоячая. Например, от камешка, упавшего в море, — бегущие, а если камешек упадет в таз с водой, то бегущая к стенкам волна сложится с той, что от них отразилась, и возникнет стоячая волна: горбы и впадины «стоят» на месте. Нечто подобное происходит и в атоме, только стенки здесь две: одна — ядро, роль другой выполняет сила электрического притяжения между ядром и электроном, не позволяющая электрону улететь. Орбита электрона — место, где амплитуда «электронной» стоячей волны максимальна. И оставаться на ней он может сколь угодно долго, поскольку здесь нет никакого изменения скорости, а значит, и излучения.
Энергия альфа частицы. Энергия образования
Чтобы рассчитать энергию образования альфа-частицы, следует воспользоваться знаменитым уравнением Эйнштейна, которое связывает массу и энергию через одну из фундаментальных постоянных нашей Вселенной – скорость света. Это уравнение имеет вид: E = mc2, где E – энергия, m – масса, c – скорость света в вакууме.
Зная, что при образовании альфа-частицы масса ее компонентов уменьшается на 0,015 * 10-27кг, а также зная, что скорость света составляет 3 * 108м/с, получаем энергию, которая выделяется во время этого процесса. Она равна E = 0,015 * 10-27* 9 * 1016= 1,35 * 10-12Дж. В физике элементарных частиц принято энергии записывать в электрон-вольтах (эВ). Один электрон-вольт равен 1,602177 * 10−19Дж. Тогда энергия образования альфа-частицы равна 8,426 * 106эВ, или 8,426 МэВ (мегаэлектрон-вольт).
Чтобы понять, насколько велика эта энергия, можно провести простой расчет. Представим, что вся энергия образования альфа-частицы переводится на ее ускорение. Пользуясь уравнением Лоренца для нерелятивистских скоростей, то есть полагая, что кинетическая энергия-альфа частицы равна mv2/2, где v – скорость ее движения, получаем, что этой энергии образования будет достаточно, чтобы разогнать альфа-частицу до скорости 2 * 107м/c, что составляет 6,7 % от скорости света в вакууме. Отметим, что задавать вопрос о том, на сколько увеличится масса альфа-частицы при таких скоростях, не имеет смысла, поскольку увеличением ее массы можно пренебречь, так как она составит всего 0,015/6,68 * 100 = 0,2 %.
Масса электрона – мал золотник да дорог
Если навскидку попросить 100 человек назвать хотя бы три известные элементарные частицы, то, возможно, не все назовут все три, но никто не забудет назвать чемпиона по популярности – электрон. Маленький, самый легкий среди несущих заряд частиц, вездесущий и…, к сожалению, «отрицательный», он входит в состав любого вещества на Земле и уже этим заслуживает особое к себе отношение. Название частицы возникло еще в древней Греции от греческого слова «янтарь» – материал, который любили древние за его способность притягивать мелкие предметы. Затем, когда исследования электричества получили больший размах, термин «электрон» стал означать неделимую, а значит, и наименьшую единицу заряда.
Вечную жизнь электрону, как неотъемлемой частичке вещества, подарила группа физиков, руководимая Дж. Дж.Томсоном. В 1897 г. они, исследуя катодные лучи, определили, как относится масса электрона к его заряду, и установили, что это отношение не зависит от материала катода. Следующий шаг в познании природы электрона сделал Беккерель в 1900 г. В его эксперименте было доказано, что бета-лучи радия также отклоняются в электрическом поле, и у них отношение массы к заряду одинаковое с катодными лучами. Это стало неоспоримым доказательством того, что электрон – это «самостоятельный кусочек» атома любого вещества. А потом, в 1909 г., Роберт Милликен в опыте с капельками масла, которые падали в электрическом поле, сумел измерить электрическую силу, уравновешивающую силу тяжести. Тогда же стала известной величина элементарного, т.е. наименьшего, заряда:
eo = – 1,602176487(49) * 10-19 Кл.
Этого стало достаточно, чтоб была вычислена масса электрона:
me = 9,10938215(15) * 10-31кг.
Казалось бы, вот теперь порядок, все позади, но это было только начало длинного пути познания природы электрона.
Долгое время тупиком физики была еще не доказанная, но все более заявляющая о себе двуликая сущность электрона: его квантово-механические свойства указывали на частицу, а в экспериментах по интерференции электронных пучков на параллельных щелях проявлялась волновая природа. Момент истины настал в 1924 г., когда сначала Луи де Бройль наделил все материальное, и электрон тоже, волнами, названными его именем, а через 3 года Паули завершил формирование исходных понятий квантовой механики, описывающих квантовую природу частиц. Затем наступил черед Эрвина Шредингера и Поля Дирака – дополняя друг друга, они нашли уравнения для описания сущности электрона, в которых масса электрона и постоянная Планка, квантовые величины, нашли свое отражение через волновые характеристики – частоту и длину волны.
Безусловно, такое двуличие элементарной частицы имело далеко идущие последствия. Со временем стало понятно, что характеристики свободного электрона вне вещества (как пример – катодные лучи) – это совсем не то же самое, что у электрона в виде электрического тока в кристалле. Для свободного электрона его масса известна как «масса покоя электрона». Физическая природа различия масс электрона в разных условиях вытекает из того факта, что его энергия зависит от насыщения магнитным полем пространства, в котором он движется. Более глубокие «разборки» показывают, что величина магнитного поля движущихся в проводнике электронов, точнее, протекания тока в веществе, зависит не от величины заряда носителей тока, а от их массы. Но, с другой стороны, удельная энергия магнитного поля равна плотности кинетической энергии движущихся зарядов, а рост этой энергии фактически эквивалентен увеличенной массе носителей заряда, которую назвали «эффективная масса электрона». Аналитически было определено, что она больше массы свободного электрона в a/2λ раз, где a – расстояние между плоскостями, ограничивающими проводник, λ – глубина скин-слоя магнитного поля.
В физике элементарных частиц масса электрона является одной из опорных констант. Биография электрона не закончилась – всегда актуальны и востребованы исследования, где он выступает непременным участником. Уже давно стало ясно, что хоть и маленький, элементарный, а Вселенной без него – ни шагу.
Нужно найти кинетическую энергию электрона и перевести ее в эВ
Знаток
(401),
закрыт
9 лет назад
Валентина Вавилова(Серкова)
Гений
(62183)
9 лет назад
Всё верно у тебя, кинетическая энергия только численно равна напряжению, но это две разные физические величины. ( разве не бывает скорость = 2м/c, и пройденный путь =2м, мы же не говорим, что они равны, просто числа одинаковые, вот и всё).
JULIANDCЗнаток (401)
9 лет назад
хорошо численно они равны, как быть с единицами измерения? не можем же просто поделив и умножив на одно и тоже (e) получить разные величины, это должно как то объясняться, значит формула не верная, т. к.
U = S(м) / t(с) и равно мс и если U*tt = все также будут мс и ничто иное. непонятно.
