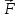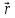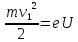5
18-Jul-19
Лекция
№ 6
Движение
электрона в электрическом поле
Электронная
оптика занимается задачами
-
формирования,
-
фокусировки
-
отклонения
электронных
пучков с помощью
-
электрических
и -
магнитных
полей.
Ее
физической основой является аналогия
между
-
законами
распространения света
и -
движением
заряженных частиц,
в том числе и электронов,
в
электрических и магнитных полях.
Эта
оптико-механическая аналогия позволяет
подойти к задаче о траектории движения
электрона
-
как
c
механической, корпускулярной,
точки зрения, когда электрон рассматривается
как частица, -
так
и с оптической, волновой,
позиции, когда учитываются волновые
свойства электрона.
В
первом
случае (корпускулярный
подход)
задача нахождения траектории электрона
решается на основе использования второго
закона Ньютона:



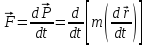
-
где
—
сила, действующая со стороны поля на
электрон; -
—
скорость электрона; -
—радиус-вектор
электрона, характеризующий его положение
в пространстве в момент времени t
относительно
некоторого начала координат..
Если
сила
известна,
то можно, решив уравнение (3), найти
зависимость радиуса-вектора
от
времени и тем самым установить траекторию
движения электрона. Однако точное
интегрирование этого уравнения возможно
лишь для случая весьма простых полей,
в частности, однородных электрических
и магнитных. В более сложных случаях
приходится прибегать к приближенным
методам решения этого уравнения.
При
волновом
подходе к задаче движения электрона
используется аналогия с принципам
Ферма в
оптике, утверждающем, что из всех
возможных траекторий между двумя точками
А
и
В
световой
луч распространяется по той, которая
имеет наименьшую оптическую длину, так
что

где:
n
— показатель преломления;
dl.—
элемент траектории светового луча.
Как
в световой, так и в электронной оптике
из принципа Ферма следует основной
закон геометрической оптики — закон
преломления.
-
Электрическое
поле (в отличие от магнитного) вызывает
изменение величины
скорости электрона (включая
ее направление). -
Магнитное
поле приводит только к изменению
направления
скорости электрона.
Для
стационарного поля сумма потенциальной
и кинетической энергии движущегося в
этом поле электрона является величиной
постоянной
(5)
Если
то
Потенциальная
энергия электрона в электростатическом
поле в точке, характеризуемой потенциалом
φ,
равна Епот
= – eφ
Выберем
на траектории электрона две точки, из
которых одна произвольная, а вторая
лежит на катоде, эмиттирующем электроны.
У
электрона на
поверхности
катода (x=0)
энергия слагается из
-
потенциальной
-еφ0
и -
кинетической
составляющих.
У
электрона, находящегося на
расстоянии
X
от катода энергия также слагается из
потенциальной
-еφ1
и кинетической
составляющих.
Тогда
на основании формулы (2) можно написать,
что
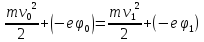
затем
(7)
Примем
во внимание, что на катоде скорость
электрона
значительно
меньше скорости

а потому может быть приравнена нулю,
как и потенциал φ0
на поверхности катода также равен нулю.
Тогда

Т.е.
φ1=
U,
и тогда
(8)
где
U
—
разность потенциалов, пройденная
электроном на траектории своего движения.
Поскольку,
проходя разность потенциалов U,
электрон
приобретает скорость V1,
т.
е. ускоряется,
величина U
носит
название ускоряющего напряжения.
Если
U<
0,
то при движении по траектории электрон
будет терять свою скорость и U
будет
являться напряжением замедляющим.
Уравнение
(3) дает возможность выражать энергию
электрона и его скорость через разность
потенциалов
U,
которую
должен пройти первоначально покоившийся
электрон, чтобы приобрести скорость V
или
соответствующую ей кинетическую энергию

Единица
измерения кинетической энергии электрона:
1
электронвольт = 1,6•10-12
эрг = 1,6•10-19
дж
/var/www/studfiles2/data/www/download/2706/299/Qis9IxpslN.CR3t
Соседние файлы в папке Новая папка
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В первом приближении можно считать, что электрон в атоме водорода движется по круговой орбите с линейной скоростью v. Найти угловую скорость ω вращения электрона вокруг ядра и его нормальное ускорение аn.
Определить долю свободных электронов в металле при температуре Т = 0 К, энергии ε которых заключены в интервале значений от 1/2εmax до εmax.
Каково значение энергии Ферми εF у электронов проводимости двухвалентной меди? Выразить энергию Ферми в джоулях и электрон-вольтах.
Вычислить по теории Бора радиус r2 второй стационарной орбиты и скорость v2 электрона на этой орбите для атома водорода.
Вычислить по теории Бора период Т вращения электрона в атоме водорода, находящегося в возбужденном состоянии, определяемом главным квантовым числом n = 2.
Определить изменение энергии ΔE электрона в атоме водорода при излучении атомом фотона с частотой ν = 6,28×1014 Гц.
Во сколько раз изменится период Т вращения электрона в атоме водорода, если при переходе в невозбужденное состояние атом излучил фотон с длиной волны λ = 97,5 нм?
На сколько изменилась кинетическая энергия электрона в атоме водорода при излучении атомом фотона с длиной волны λ = 435 нм?
В каких пределах Δλ должна лежать длина волн монохроматического света, чтобы при возбуждении атомов водорода квантами этого света радиус орбиты электрона увеличился в 16 раз?
Электрон в атоме водорода находится на третьем энергетическом уровне. Определить кинетическую Ek, потенциальную Ep и полную Е энергию электрона. Ответ выразить в электрон-вольтах.
Определить энергию ΔE, которую необходимо дополнительно сообщить электрону, чтобы его дебройлевская длина волны уменьшилась от λ1 = 0,2 нм до λ2 = 0,1 нм.
Параллельный пучок моноэнергетических электронов падает нормально на диафрагму в виде узкой прямоугольной щели, ширина которой а = 0,06 мм.
При каких значениях кинетической энергии Ek электрона ошибка в определении дебройлевской длины волны λ, по нерелятивистской формуле не превышает 10%?
Из катодной трубки на диафрагму с узкой прямоугольной щелью нормально к плоскости диафрагмы направлен поток моноэнергетических электронов.
Электрон обладает кинетической энергией Ek = 1,02 МэВ. Во сколько раз изменится длина волны де Бройля, если кинетическая энергия Ek электрона уменьшится вдвое?
Кинетическая энергия Ek электрона равна удвоенному значению его энергии покоя (2m0с ). Вычислить длину волны λ, де Бройля для такого электрона.
Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию электрона, движущегося внутри сферы радиусом R = 0,05 нм.
Используя соотношение неопределенностей, оценить наименьшие ошибки ΔV в определении скорости электрона и протона, если координаты центра масс этих частиц могут быть установлены с неопределенностью 1 мкм.
Используя соотношение неопределенностей, оценить ширину L одномерного потенциального ящика, в котором минимальная энергия электрона T = 10 эВ.
Для приближенной оценки минимальной энергии электрона в атоме водорода можно предположить, что неопределенность Δr радиуса r электронной орбиты и неопределенность Δp импульса p электрона на такой орбите соответственно связаны следующим обра
Моноэнергетический пучок электронов высвечивает в центре экрана электронно-лучевой трубки пятно радиусом r = 10-3 см.
Для приближенной оценки минимальной энергии электрона в атоме водорода можно предположить, что неопределенность Δr радиуса r электронной орбиты и неопределенность Δр импульса p электрона на такой орбите соответственно связаны следующим обр
Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l = 0,1 нм. Определить в электрон-вольтах наименьшую разность энергетических уровней электрона.
Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид ψ(r) = Ae–r/a0, где А — некоторая постоянная; а
Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид ψ(r) = Ae–r/a0, где А — некоторая постоянная; а
Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной L. В каких точках в интервале 0 < x < L плотности вероятности нахождения электрона на втором и третьем энергетических уровнях одинаковы?
Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид ψ(r) = Ae–r/a0, где А — некоторая постоянная; а
Определить отношение релятивистского импульса P электрона с кинетической энергией Т =1,53 МэВ к комптоновскому импульсу m0с электрона.
Скорость электрона V = 0,8 с (где с — скорость света в вакууме). Зная энергию покоя электрона в мегаэлектрон-вольтах, определить в тех же единицах кинетическую энергию Ek электрона.
Во сколько раз релятивистская масса электрона, обладающего кинетической энергией Т = 1,53 МэВ, больше массы покоя m0?
Какова должна быть длина волны γ-излучения, падающего на платиновую пластину, чтобы максимальная скорость фотоэлектронов была Vmax = 3 Мм/с?
На металлическую пластину направлен пучок ультрафиолетового излучения (λ = 0,25 мкм). Фототок прекращается при минимальной задерживающей разности потенциалов U = 0,96 В. Определить работу выхода А электронов из металла.
На поверхность металла падает монохроматический свет с длиной волны λ = 0,1 мкм. Красная граница фотоэффекта λ0 = 0,3 мкм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии?
Фотон при эффекте Комптона на свободном электроне был рассеян на угол φ = π/2. Определить импульс Pe (в МэВ/с), приобретенный электроном, если энергия фотона до рассеяния была εф = 1,02 МэВ.
Рентгеновское излучение (λ = 1 нм) рассеивается электронами, которые можно считать практически свободными. Определить максимальную длину волны λmax рентгеновского излучения в рассеянном пучке.
Фотон с длиной волны λ1 = 15 пм рассеялся на свободном электроне. Длина волны рассеянного фотона λ2 = 16 пм. Определить угол φ рассеяния.
Электрон в атоме водорода движется вокруг ядра (протона) по окружности радиусом (R = 53) пм. Определить магнитный момент ({P_m}) эквивалентного кругового тока.
Электрон прошел ускоряющую разность потенциалов (U = 800) В и, влетев в однородное магнитное поле (B = 47) мТл, стал двигаться по винтовой линии с шагом (h = 6) см. Определить радиус (R) винтовой линии.
Электрон влетел в однородное магнитное поле ((B = 200) мТл) перпендикулярно линиям магнитной индукции. Определить силу эквивалентного кругового тока (I), создаваемого движением электрона в магнитном поле.
Электрон, пройдя ускоряющую разность потенциалов (U = 1,2) кВ, попал в скрещенные под прямым углом однородные магнитное и электрическое поля. Определить напряженность (E) электрического поля, если магнитная индукция (B) поля равна 6 мТл.
Однородные магнитное ((B = 2,5) мТл) и электрическое ((E = 10) кВ/м) поля скрещены под прямым углом. Электрон, скорость (v) которого равна (4 cdot {10^6}) м/с, влетает и эти поля так, что силы, действующие на него со стороны магнитного и электрического полей, сонаправлены.
Магнитное ((B = 2) мТл) и электрическое ((E = 1,6) кВ/м) поля сонаправлены. Перпендикулярно векторам (B) и (E) влетает электрон со скоростью (v = 0,8) Мм/с. Определить ускорение (a) электрона.
Электрон, обладавший кинетической энергией (T = 10) эВ, влетел в однородное электрическое поле в направлении силовых линий поля. Какой скоростью будет обладать электрон, пройдя в этом поле разность потенциалов (U = 8) В?
Электрон с энергией (T = 400) эВ (в бесконечности) движется вдоль силовой линии по направлению к поверхности металлической заряженной сферы радиусом (R = 10) см. Определить минимальное расстояние, на которое приблизится электрон к поверхности сферы, если заряд ее (Q = – 10) нКл.
Электрон, пройдя в плоском конденсаторе путь от одной пластины до другой, приобрел скорость (V = {10^5}) м/с. Расстояние между пластинами (d = 8) мм. Найти: 1) разность потенциалов (U) между пластинами; 2) поверхностную плотность заряда (sigma ) на пластинах.
Пылинка массой (m = 5) нг, несущая на себе (N = 10) электронов, прошла в вакууме ускоряющую разность потенциалов (U = 1) MB. Какова кинетическая энергия (T) пылинки? Какую скорость (v) приобрела пылинка?
В однородное электрическое поле напряженностью (E = 200) В/м влетает (вдоль силовой линии) электрон со скоростью ({v_0} = 2) Мм/с. Определить расстояние (L), которое пройдет электрон до точки, в которой его скорость будет равна половине начальной.
Электрическое поле создано бесконечной заряженной прямой линией с равномерно распределенным зарядом ((tau = 10) нКл/м). Определить кинетическую энергию ({T_2}) электрона в точке 2, если в точке 1 его кинетическая энергия ({T_1} = 200) эВ.
Электрон движется вдоль силовой линии однородного электрического поля. В некоторой точке поля с потенциалом ({varphi _1} = 100) В электрон имел скорость ({V_1} = 6) Мм/с. Определить потенциал ({varphi _2}) точки поля, дойдя до которой электрон потеряет половину своей скорости.
В электронных приборах происходит движение электронов в электрическом поле в вакууме.

Рис. 13-1. Электрон в ускоряющем электрическом поле
Допустим, что электрон, покинувший отрицательный электрод — катод, с достаточно малой начальной скоростью 

направление которой противоположно направлению поля, так как заряд электрона отрицателен.
Под действием этой силы электрон получает ускорение, пропорциональное величине силы и обратно пропорциональное массе тела,

где 



Отношение заряда электрона к его массе

В данном случае для электрона электрическое поле будет ускоряющим, так как направление начальной скорости 

Двигаясь равноускоренно, электрон, пройдя путь d, достигнет положительного электрода (анода) со скоростью v и будет обладать при этом кинетической энергией

Эту энергию электрон приобрел на пути d в результате работы, совершенной силами поля.
Так как эта работа

то, следовательно, энергия электрона

т. е. работе сил поля на пути электрона с разностью потенциалов 
Приняв заряд электрона за единицу при разности потенциалов U = 1 В, поручим единицу энергии электрона 1 электронвольт (эВ).
Так как заряд электрона равен 

Из (13-5) определим скорость электрона в произвольной точке ускоряющего поля

Следовательно, скорость электрона в ускоряющем поле зависит от разности потенциалов между конечной и начальной точками пути электрона. Так. например, если электрон покинул катод лампы с малой скоростью 

Определим время пролета электрона от катода до аиода, если d — расстояние между ними.
Средняя скорость равноускоренного движения 



Рассмотрим движение электрона в тормозящем поле. Допустим, что электрон вылетел с начальной скоростью 

Рис. 13-2. Электрон в тормозящем электрическом поле.

Рис. 13-3. Электрон в поперечном электрическом поле.
Естественно, поле в этом случае называют тормозящим.
Кинетическая энергия, которой обладал электрон в начальный момент, 

Если начальная энергия электрона 


Рассмотрим движение электрона в электрическом поле в направлении, перпендикулярном направлению поля. Допустим, что электрон, двигаясь в направлении, перпендикулярном электрическому полю, попадет в него со скоростью 

 —
—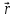 —радиус-вектор
—радиус-вектор