У этого термина существуют и другие значения, см. Ферми (значения).
Энергия (уровень) Фе́рми (
Для нерелятивистских невзаимодействующих частиц со спином 1/2 в трёхмерном пространстве
Название дано в честь итальянского физика Энрико Ферми. Здесь 


Фермионы — частицы с полуцелым спином, обычно 1/2, такие, как электроны — подчиняются принципу запрета Паули, согласно которому две одинаковые частицы, образуя квантово-механическую систему (например, атом), не могут принимать одно и то же квантовое состояние. Следовательно, фермионы подчиняются статистике Ферми — Дирака. Основное состояние невзаимодействующих фермионов строится начиная с пустой системы и постепенного добавления частиц по одной, последовательно заполняя состояния в порядке возрастания их энергии (например, заполнение электронами электронных орбиталей атома). Когда необходимое число частиц достигнуто, энергия Ферми равна энергии самого высокого заполненного состояния (или самого низкого незанятого состояния: в случае макроскопической системы различие неважно). Поэтому энергию Ферми называют также уровнем Фе́рми. Частицы с энергией, равной энергии Ферми, двигаются со скоростью, называемой скоростью Фе́рми.
В свободном электронном газе (квантово-механическая версия идеального газа фермионов) квантовые состояния могут быть помечены согласно их импульсу. Нечто подобное можно сделать для периодических систем типа электронов, движущихся в атомной решётке металла, используя так называемый квазиимпульс (Частица в периодическом потенциале). В любом случае состояния с энергией Ферми расположены на поверхности в пространстве импульсов, известной как поверхность Ферми. Для свободного электронного газа, поверхность Ферми — поверхность сферы; для периодических систем она вообще имеет искаженную форму. Объём, заключённый под поверхностью Ферми, определяет число электронов в системе, и её топология непосредственно связана с транспортными свойствами металлов, например, электрической проводимостью. Поверхности Ферми большинства металлов хорошо изучены экспериментально и теоретически.
Уровень Ферми при ненулевых температурах[править | править код]
Для важного случая электронов в металле при всех разумных температурах 




Энергия Ферми свободного ферми-газа связана с химическим потенциалом уравнением
Следовательно, химический потенциал приблизительно равен энергии Ферми при температурах намного меньше характерной температуры Ферми 

При температуре 







В качестве уровня Ферми при 
Энергия, температура и скорость Ферми[править | править код]
| Элемент | Энергия Ферми, эВ | Температура Ферми, ×10 000 K | Скорость Ферми, ×1000 км/с |
|---|---|---|---|
| Li | 4,74 | 5,51 | 1,29 |
| Na | 3,24 | 3,77 | 1,07 |
| K | 2,12 | 2,46 | 0,86 |
| Rb | 1,85 | 2,15 | 0,81 |
| Cs | 1,59 | 1,84 | 0,75 |
| Cu | 7,00 | 8,16 | 1,57 |
| Ag | 5,49 | 6,38 | 1,39 |
| Au | 5,53 | 6,42 | 1,40 |
| Be | 14,3 | 16,6 | 2,25 |
| Mg | 7,08 | 8,23 | 1,58 |
| Ca | 4,69 | 5,44 | 1,28 |
| Sr | 3,93 | 4,57 | 1,18 |
| Ba | 3,64 | 4,23 | 1,13 |
| Nb | 5,32 | 6,18 | 1,37 |
| Fe | 11,1 | 13,0 | 1,98 |
| Mn | 10,9 | 12,7 | 1,96 |
| Zn | 9,47 | 11,0 | 1,83 |
| Cd | 7,47 | 8,68 | 1,62 |
| Hg | 7,13 | 8,29 | 1,58 |
| Al | 11,7 | 13,6 | 2,03 |
| Ga | 10,4 | 12,1 | 1,92 |
| In | 8,63 | 10,0 | 1,74 |
| Tl | 8,15 | 9,46 | 1,69 |
| Sn | 10,2 | 11,8 | 1,90 |
| Pb | 9,47 | 11,0 | 1,83 |
| Bi | 9,90 | 11,5 | 1,87 |
| Sb | 10,9 | 12,7 | 1,96 |
| Ni | 11,67 | 2,04 | |
| Cr | 6,92 | 1,56 |
Связь энергии Ферми и концентрации электронов проводимости[править | править код]
Концентрация электронов проводимости в вырожденных полупроводниках связана с расстоянием от края частично заполненной энергетической зоны до уровня Ферми. Эту положительную величину иногда тоже называют энергией Ферми, по аналогии с энергией Ферми свободного электронного газа, которая, как известно, положительна.
В металлах обычно имеется несколько частично заполненных энергетических зон, поэтому указать точный вид зависимости концентрации свободных носителей заряда от положения уровня Ферми не представляется возможным.
См. также[править | править код]
- Квазиуровень Ферми
Примечания[править | править код]
- ↑ 1 2 Н.Ашкрофт, Н.Мермин. ФИЗИКА ТВЕРДОГО ТЕЛА. Том 1. — Москва: Мир, 1979. — 458 с.
Литература[править | править код]
- Гусев В. Г., Гусев Ю. М. Электроника. — М.: Высшая школа, 1991. — С. 53. — ISBN 5-06-000681-6.
-
Энергия Ферми и концентрация электронов в металле
Электронный газ металла, находящийся
в основном состоянии при абсолютном
нуле, заполняет в
–
пространстве все состояния внутри
некоторой сферы, которая называется
поверхностью Ферми. Энергия, соответствующая
этой поверхности, называется энергией
Ферми и представляет максимальную
энергию, что могут иметь электроны при
абсолютном нуле температур. Таким
образом, поверхность Ферми отделяет в
–
пространстве занятые состояния от
свободных.
Определим величину энергии Ферми
через
концентрацию электронов
Для этого проинтегрируем (4.76) по всем
возможными значениями энергии и учтем,
что при
функция
равняется единице для всех
и нулю для всех
(4.78)
Отсюда
энергия Ферми при
равна
(4.79)
Для отличной от абсолютного нуля
температуры энергия Ферми будет являться
функцией температуры
.
(4.80)
Поскольку в металлах при любой температуре,
то положение уровня Ферми в металлах
определяется лишь концентрацией
свободных электронов и практически не
изменяется с температурой.
Скорость электронов на поверхности
Ферми и температура Ферми определяются
через энергию Ферми
и
.
(4.81)
Оценим величину энергии Ферми для
типичного металла, считая концентрацию
электронов
м-3,
эВ.
Среднюю энергию электронов можно
определить через энергию Ферми
(4.82)
Следовательно, средняя энергия электронов
по порядку величины совпадает с энергией
Ферми. Такой энергией молекулы
классического газа обладали бы при
температуре в несколько десятков тысяч
градусов. Это свидетельствует о том,
что электронный газ в металлах находится
в особом, вырожденном состоянии. Его
энергия практически не зависит от
температуры.
В том случае, когда фермиевская функция
распределения переходит в максвелловскую,
вырождение с электронного газа снимается.
Это возможно при выполнении условия
(4.83)
Выразим это условие через параметры
электронного газа. Для этого проинтегрируем
(4.76) с учетом (4.83)
Отсюда условие снятия вырождения с
электронного газа может быть представлено
в виде
(4.84)
Обратное неравенство означает, что
электронный газ находится в вырожденном
состоянии.
Если приравнять левую часть неравенства
(4.84) единице, можно определить температуру
снятия вырождения:
(4.85)
Оценивая величину этой температуры для
концентрации электронов
м-3,
получим
К.
Таким образом, электронный газ в металлах
всегда находится в вырожденном состоянии.
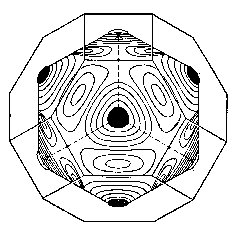
В заключение заметим, что поверхность
Ферми является сферической только в
приближении свободных электронов. Для
реальных металлов, когда закон дисперсии
носит сложный характер, вид поверхности
Ферми может быть весьма экзотическим
(рис. 4.18).
|
|
|
|
Рис.4.18. Поверхность Ферми |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
08.05.20151.69 Mб584.doc
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Энергия Ферми
- В металле по энергиям. Уровень и энергия Ферми. Вырождение электронного газа в металлах
- Энергия Ферми — Fermi energy
- СОДЕРЖАНИЕ
- Контекст
- Формула и типовые значения
- Металлы
- Белые карлики
- Связанные количества
Энергия Ферми



Вырожденный электронный газ в металле.
Распределение электронов по различным квантовым состояниям подчиняется принципу Паули, согласно которому в одном состоянии не может быть двух одинаковых (с одинаковым набором четырех квантовых чисел) электронов, они должны отличаться какой-то характеристикой, например направлением спина. Следовательно, по квантовой теории, электроны в металле не могут располагаться на самом низшем энергетическом уровне даже при 0 К. Принцип Паули вынуждает электроны взбираться вверх «по энергетической лестнице».
Электроны проводимости в металле можно рассматривать как идеальный газ, подчиняющийся распределению Ферми-Дирака. Если μ – химический потенциал электронного газа при T = 0 К, то, среднее число 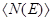
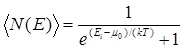
Для фермионов (электроны являются фермионами) среднее число частиц в квантовом состоянии и вероятность заселенности квантового состояния совпадают, так как квантовое состояние либо может быть не заселено, либо в нем будет находиться одна частица. Это означает, что для фермионов 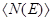
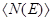
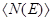
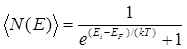
Наивысший энергетический уровень, занятый электронами, называется уровнем Ферми.Уровню Ферми соответствует энергия Ферми ЕF:, которую имеют электроны на этом уровне. Уровень Ферми, очевидно, будет тем выше, чем больше плотность электронного газа. Работу выхода электрона из металла нужно отсчитывать не от дна «потенциальной ямы», как это делалось в классической теории, а от уровня Ферми, т. с. от верхнего из занятых электронами энергетических уровней.
Для металлов при не слишком высоких температурах выполняется неравенство kT 4 К, т.е. для всех температур, при которых металл может существовать в твердом состоянии, электронный газ в металле вырожден.
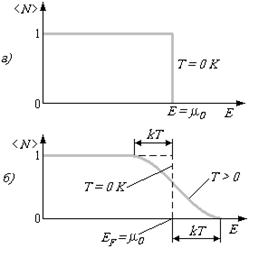
При температурах, отличных от 0 К, функция распределения Ферми-Дирака (2) плавно изменяется от 1 до 0 в узкой области (порядка kT ) в окрестности ЕF (рис. 15, б). (Здесь же для сравнения пунктиром приведена функция распределения при Т = 0 К.) Это объясняется тем, что при T > 0 небольшое число электронов с энергией, близкой к ЕF, возбуждается за счет теплового движения и их энергия становится больше ЕF. Вблизи границы Ферми при Е ЕF. — больше нуля. В тепловом движении участвует лишь небольшое число электронов, например при комнатной температуре Т ≈ 300 К и температуре вырождения T = 3 10 4 К, — это 10 -5 от общего числа электронов.
Если (Е — ЕF) >> kТ («хвост» функции распределения), то единицей в знаменателе (2) можно пренебречь по сравнению с экспонентой и тогда распределение Ферми — Дирака переходит в распределение Максвелла — Больцмана.
Источник
Свободные электроны в металле можно рассматривать как своеобразный электронный газ. Первая попытка описать свойства металлов была предпринята Друде и Лоренцем в классической электронной теории металлов. Согласно этой теории электронный газ ведет себя подобно электронному газу, состоящему из молекул, и поэтому должен подчиняться статистике Максвелла-Больцмана. Но эта теория не смогла объяснить ряд явлений. Так, например, из опыта известно, что молярные теплоемкости всех твердых тел (и металлов, и диэлектриков) приблизительно одинаковы и равны 3R (закон Дюлонга и Пти). Отсюда следует, что теплоемкость электронного газа в металлах настолько мала, что ее вклад в общую теплоемкость не обнаруживается на опыте. По классической же теории теплоемкость электронного газа должна быть равна 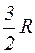
C = 3R + 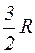
Другим существенным затруднением классической теории является невозможность объяснения температурной зависимости сопротивления металлов. Опытным путем установлено, что удельное сопротивление практически всех металлов в достаточно широком температурном интервале линейно зависит от температуры
где r- удельное сопротивление при температуре t, r — удельное сопротивление при температуре 0°C, a — температурный коэффициент сопротивления при температуре 0°C.
Из классической же теории следует, что удельное сопротивление должно быть пропорционально корню квадратному из температуры.
Дальнейшее развитие физической науки привело к созданию квантовой механики и квантовой теории металлов, учитывающих волновые свойства электронов. Согласно квантовым представлениям электронный газ в металле подчиняется принципу Паули и описывается квантовой статистикой Ферми – Дирака
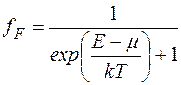
где fF — функция распределения Ферми-Дирака, характеризующая вероятность заполнения квантового состояния (уровня) с энергией Е, и равнаясредней степени заселенности электронами квантового состояния, соответствующего энергии Е, m — химический потенциал электронного газа. При абсолютном нуле температуры (Т=0 К) химический потенциал называют также энергией Ферми и обозначают EF.
Найдем вид функции распределения fF при Т=0 К.
Рассмотрим состояния электронов с энергией E EF показатель экспоненты в выражении (2.4) положителен;
при T → 0 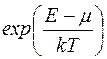
Из этого рассмотрения следует, что при Т=0 функция распределения fF принимает значения

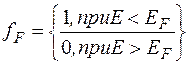

Уровни, энергия которых выше EF, остаются совершенно свободными (вероятность их заполнения равна 0). Следовательно, энергия Ферми EF представляет собой максимальную энергию, которую могут иметь электроны при абсолютном нуле температуры. Эта энергия не является тепловой (kТ=0), она имеет квантовую природу, обусловленную, в частности, принципом Паули, и зависит от концентрации свободных электронов в металле. Расчет дает для энергии Ферми следующее выражение
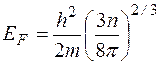
Здесь h — постоянная Планка; n — концентрация электронов.
Наивысший энергетический уровень, занятый электронами при Т=0, называют уровнем Ферми. Уровень Ферми будет тем выше, чем больше концентрация n электронов. Как показывает расчет, средняя энергия 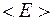
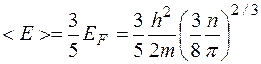
В таблице 3.1 приведены значения энергии Ферми для некоторых металлов.
Источник
Энергия Ферми — Fermi energy
Энергия Ферми — это понятие в квантовой механике, обычно относящееся к разнице энергий между самым высоким и самым низким занятыми одночастичными состояниями в квантовой системе невзаимодействующих фермионов при температуре абсолютного нуля . В ферми-газе считается, что самое низкое заполненное состояние имеет нулевую кинетическую энергию, тогда как в металле нижнее заполненное состояние обычно означает дно зоны проводимости .
Термин «энергия Ферми» часто используется для обозначения другого, но тесно связанного с ним понятия, уровня Ферми (также называемого электрохимическим потенциалом ). Есть несколько ключевых различий между уровнем Ферми и энергией Ферми, по крайней мере, в том виде, в котором они используются в этой статье:
- Энергия Ферми определяется только при абсолютном нуле, в то время как уровень Ферми определяется для любой температуры.
- Энергия Ферми — это разность энергий (обычно соответствующая кинетической энергии ), тогда как уровень Ферми — это уровень полной энергии, включающий кинетическую энергию и потенциальную энергию.
- Энергия Ферми может быть определена только для невзаимодействующих фермионов (где потенциальная энергия или край зоны является статической, хорошо определенной величиной), тогда как уровень Ферми остается хорошо определенным даже в сложных взаимодействующих системах при термодинамическом равновесии.
Поскольку уровень Ферми в металле при абсолютном нуле является энергией наивысшего занятого одночастичного состояния, тогда энергия Ферми в металле представляет собой разность энергий между уровнем Ферми и нижним занятым одночастичным состоянием при нулевой температуре.
СОДЕРЖАНИЕ
Контекст
В квантовой механике группа частиц, известных как фермионы (например, электроны , протоны и нейтроны ), подчиняется принципу исключения Паули . Это означает, что два фермиона не могут находиться в одном и том же квантовом состоянии . Поскольку идеализированный невзаимодействующий ферми-газ можно анализировать с точки зрения одночастичных стационарных состояний , мы можем, таким образом, сказать, что два фермиона не могут находиться в одном и том же стационарном состоянии. Эти стационарные состояния обычно различаются по энергии. Чтобы найти основное состояние всей системы, мы начинаем с пустой системы и добавляем частицы по одной, последовательно заполняя незанятые стационарные состояния с наименьшей энергией. Когда все частицы помещены внутрь, энергия Ферми является кинетической энергией самого высокого занятого состояния.
Как следствие, даже если мы извлекли всю возможную энергию из ферми-газа, охладив его до температуры, близкой к абсолютному нулю , фермионы все еще движутся с высокой скоростью. Самые быстрые из них движутся со скоростью, соответствующей кинетической энергии, равной энергии Ферми. Эта скорость известна как скорость Ферми . Только когда температура превышает соответствующую температуру Ферми , электроны начинают двигаться значительно быстрее, чем при абсолютном нуле.
Энергия Ферми — важное понятие в физике твердого тела металлов и сверхпроводников . Это также очень важная величина в физике квантовых жидкостей, таких как низкотемпературный гелий (как нормальный, так и сверхтекучий 3 He), и очень важна для ядерной физики и для понимания устойчивости белых карликов к гравитационному коллапсу .
Формула и типовые значения
Энергия Ферми для невзаимодействующего ансамбля идентичных фермионов со спином 1/2 в трехмерной ( нерелятивистской ) системе определяется выражением
E F знак равно ℏ 2 2 м 0 ( 3 π 2 N V ) 2 / 3 , < displaystyle E _ < text > = < frac < hbar ^ <2>> <2m_ <0>>> left ( < frac <3 pi ^ <2>N> > right) ^ <2>,>
где N — количество частиц, m — масса покоя каждого фермиона, V — объем системы и приведенная постоянная Планка . ℏ < displaystyle hbar>
Металлы
В рамках модели свободных электронов электроны в металле можно рассматривать как ферми-газ. Плотность электронов проводимости в металлах составляет примерно от 10 28 до 10 29 электронов / м 3 , что также является типичной плотностью атомов в обычном твердом веществе. Эта числовая плотность дает энергию Ферми порядка от 2 до 10 электронвольт . N / V < Displaystyle N / V>
Белые карлики
Звезды, известные как белые карлики, имеют массу, сравнимую с массой нашего Солнца , но имеют примерно одну сотую его радиуса. Высокая плотность означает, что электроны больше не связаны с отдельными ядрами и вместо этого образуют вырожденный электронный газ. Их энергия Ферми составляет около 0,3 МэВ.
Другой типичный пример — это нуклоны в ядре атома. Радиус ядра допускает отклонения, так что типичное значение для энергии Ферми обычно дается как 38 МэВ .
Связанные количества
Используя это определение энергии Ферми, приведенное выше, могут быть полезны различные связанные величины.
Температура Ферми определяется как
Т F знак равно E F k B , < displaystyle T _ < text > = < frac >> >>>,>
где — постоянная Больцмана , а энергия Ферми. Температуру Ферми можно рассматривать как температуру, при которой тепловые эффекты сравнимы с квантовыми эффектами, связанными со статистикой Ферми. Температура Ферми для металла на пару порядков выше комнатной. k B < displaystyle k _ < text >> 
Другие величины, определяемые в этом контексте, — это импульс Ферми
п F знак равно 2 м 0 E F < displaystyle p _ < text > = < sqrt <2m_ <0>E _ < text >>>>
и скорость Ферми
v F знак равно п F м 0 . < displaystyle v _ < text > = < frac
>> >>.>
Импульс Ферми также можно описать как
п F знак равно ℏ k F , < displaystyle p _ < text > = hbar k _ < text >,>
где , называемый волновым вектором Ферми , — радиус сферы Ферми. k F < displaystyle k _ < text >>
Эти величины могут не быть четко определены в случаях , когда поверхность Ферми несферична.
Источник
From Wikipedia, the free encyclopedia
The Fermi energy is a concept in quantum mechanics usually referring to the energy difference between the highest and lowest occupied single-particle states in a quantum system of non-interacting fermions at absolute zero temperature.
In a Fermi gas, the lowest occupied state is taken to have zero kinetic energy, whereas in a metal, the lowest occupied state is typically taken to mean the bottom of the conduction band.
The term “Fermi energy” is often used to refer to a different yet closely related concept, the Fermi level (also called electrochemical potential).[note 1]
There are a few key differences between the Fermi level and Fermi energy, at least as they are used in this article:
- The Fermi energy is only defined at absolute zero, while the Fermi level is defined for any temperature.
- The Fermi energy is an energy difference (usually corresponding to a kinetic energy), whereas the Fermi level is a total energy level including kinetic energy and potential energy.
- The Fermi energy can only be defined for non-interacting fermions (where the potential energy or band edge is a static, well defined quantity), whereas the Fermi level remains well defined even in complex interacting systems, at thermodynamic equilibrium.
Since the Fermi level in a metal at absolute zero is the energy of the highest occupied single particle state,
then the Fermi energy in a metal is the energy difference between the Fermi level and lowest occupied single-particle state, at zero-temperature.
Context[edit]
In quantum mechanics, a group of particles known as fermions (for example, electrons, protons and neutrons) obey the Pauli exclusion principle. This states that two fermions cannot occupy the same quantum state. Since an idealized non-interacting Fermi gas can be analyzed in terms of single-particle stationary states, we can thus say that two fermions cannot occupy the same stationary state. These stationary states will typically be distinct in energy. To find the ground state of the whole system, we start with an empty system, and add particles one at a time, consecutively filling up the unoccupied stationary states with the lowest energy. When all the particles have been put in, the Fermi energy is the kinetic energy of the highest occupied state.
As a consequence, even if we have extracted all possible energy from a Fermi gas by cooling it to near absolute zero temperature, the fermions are still moving around at a high speed. The fastest ones are moving at a velocity corresponding to a kinetic energy equal to the Fermi energy. This speed is known as the Fermi velocity. Only when the temperature exceeds the related Fermi temperature, do the particles begin to move significantly faster than at absolute zero.
The Fermi energy is an important concept in the solid state physics of metals and superconductors. It is also a very important quantity in the physics of quantum liquids like low temperature helium (both normal and superfluid 3He), and it is quite important to nuclear physics and to understanding the stability of white dwarf stars against gravitational collapse.
Formula and typical values[edit]
The Fermi energy for a non-interacting ensemble of identical spin-1⁄2 fermions in a three-dimensional (non-relativistic) system is given by[1]
where N is the number of particles, m0 the rest mass of each fermion, V the volume of the system, and 
Metals[edit]
Under the free electron model, the electrons in a metal can be considered to form a Fermi gas. The number density 
White dwarfs[edit]
Stars known as white dwarfs have mass comparable to the Sun, but have about a hundredth of its radius. The high densities mean that the electrons are no longer bound to single nuclei and instead form a degenerate electron gas. Their Fermi energy is about 0.3 MeV.
Nucleus[edit]
Another typical example is that of the nucleons in the nucleus of an atom. The radius of the nucleus admits deviations, so a typical value for the Fermi energy is usually given as 38 MeV.
[edit]
Using this definition of above for the Fermi energy, various related quantities can be useful.
The Fermi temperature is defined as
where 

Other quantities defined in this context are Fermi momentum
and Fermi velocity
These quantities are respectively the momentum and group velocity of a fermion at the Fermi surface.
The Fermi momentum can also be described as
where 
These quantities may not be well-defined in cases where the Fermi surface is non-spherical.
See also[edit]
- Fermi–Dirac statistics: the distribution of electrons over stationary states for non-interacting fermions at non-zero temperature.
- Fermi level
- Quasi Fermi level
Notes[edit]
- ^ The use of the term “Fermi energy” as synonymous with Fermi level (a.k.a. electrochemical potential) is widespread in semiconductor physics. For example: Electronics (fundamentals And Applications) by D. Chattopadhyay, Semiconductor Physics and Applications by Balkanski and Wallis.
References[edit]
- ^ Kittel, Charles (1986). “Ch. 6: Free electron gas”. Introduction to Solid State Physics. Wiley.
- ^ Nave, Rod. “Fermi Energies, Fermi Temperatures, and Fermi Velocities”. HyperPhysics. Retrieved 2018-03-21.
- ^ Torre, Charles (2015-04-21). “PHYS 3700: Introduction to Quantum Statistical Thermodynamics” (PDF). Utah State University. Retrieved 2018-03-21.
- ^ Ashcroft, Neil W.; Mermin, N. David (1976). Solid State Physics. Holt, Rinehart and Winston. ISBN 978-0-03-083993-1.
Further reading[edit]
- Kroemer, Herbert; Kittel, Charles (1980). Thermal Physics (2nd ed.). W. H. Freeman Company. ISBN 978-0-7167-1088-2.
EF – параметр распределения, называемый энергией или уровнем Ферми (см. дальше).
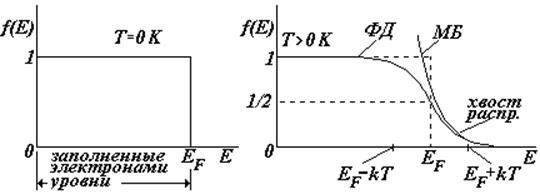
На рисунках показаны графики функции ФД, их часто называют распределением электронов по энергиям. При температуре Т = 0 К вероятность того, что электрон имеет какое-либо значение энергии в пределах 0 ¸ EF равна единице; вероятность обнаружить электрон с энергией > EF равна нулю.
При температуре
Т > 0 К электроны за счет энергии теплового движения «покидают» свои уровни и переходят на более высокие.
Для металлов уровень Ферми (энергия Ферми) определяется следующим образом. (для полупроводников – см. дальше)
1)При Т = 0 К — это уровень энергии, отделяющий заполненные электронами
уровни от незаполненных или это максимальная энергия
электронов при Т = 0 К
2) При Т > 0 К — это энергетический уровень, который занимает электрон с
вероятностью, равной 1/2.
При высоких температурах или малых концентрациях электронов распределение ФД переходит в классическое распределение МБ. Действительно, при Е-ЕF >> кТ можно пренебречь единицей в знаменателе распределения ФД, тогда получим:
Иначе говоря, на хвосте распределения (см. рис.) можно использовать классическую формулу.
|
|
Энергия Ферми при Т = 0 К, не зависит от числа электронов в образце и его объема, а определяется только концентрацией электронов n=N / V .Для одновалентных атомов характерны величины EoF @ 100 кТ @ 2,5 эВ |
|
|
Для металлов энергия Ферми очень слабо зависит от температуры (kT / EoF @ 0,01 при комнатных температурах) |
|
|
средняя энергия электронов в зоне проводимости (см. дальше ) связана с энергией Ферми указанным образом |
Зная энергию Ферми EoF можно оценить скорость vF фермиевских электронов и их температуру ТF. Следует иметь в виду, что это не температура вещества, а температура воображаемого облака электронов, средняя скорость движения которых равна vF .
|
Þ vF |
Þ ТF. |
|
элемент |
EoF (эВ) |
ТF., К |
vF, 106 м/с |
|
калий |
2,1 |
25000 |
0,85 |
|
медь |
7,0 |
82000 |
1,6 |
|
золото |
5,5 |
64000 |
1,4 |
ЭЛЕМЕНТЫ ЗОННОЙ ТЕОРИИ ТВЕРДЫХ ТЕЛ.
Зонная теория – это один из разделов квантовой механики твердых тел – теория валентных электронов в периодическом поле кристаллической решетки.
Аналитически решить уравнение Шрёдингера для электрона, движущегося внутри металла, т. е. в поле, создаваемом множеством заряженных ионов решетки, невозможно. Для решения применяют различные приближенные методы.
Образование энергетических зон в кристаллах.

На рисунке показано символически, как можно представить себе образование зон. Здесь r – расстояние между атомами. При сближении атомов до некоторого расстояния r0 образуется кристалл, и, соответственно, энергетические зоны. В некоторых случаях зоны могут перекрываться, образуя более широкую зону. Чем дальше электрон от ядра, тем шире зона. Верхние зоны имеют ширину 1 эВ и более, нижние – несколько сотых эВ.

Уровни в зоне распределяются неравномерно, в середине зоны они располагаются гуще. Для характеристики распределения уровней пользуются понятием плотности уровней. Если на интервал энергий dE приходится dZ уровней, то
|
|
плотность энергетических уровней в зоне — по смыслу – это число уровней, приходящихся на единичный интервал энергий. |
|
|
Приближенная формула для зависимости плотности уровней от энергии; С = const для данного объема V тела, m— масса электрона |
Проводники, полупроводники и диэлектрики.
Теоретически количество разрешенных зон бесконечно, а число электронов в данном теле хотя и очень велико, но имеет конечное значение. Поэтому не все зоны заполняются электронами. При температуре Т = 0 К заполнены полностью все зоны с наименьшей энергией, все остальные – пустые. Разрешенные зоны принято изображать прямоугольниками. Т. к. уровней в зоне огромное количество, целесообразно заполненную зону полностью или частично заштриховывать, а незаполненную — оставить пустой. Заполненная зона, граничащая с незаполненной, называется валентной, зона выше валентной называется зоной проводимости
Электрические свойства различных веществ — проводников (металлов), собственных полупроводников, диэлектриков и примесных полупроводников — с позиций зонной теории можно объяснить различной заполненностью зон электронами и шириной запрещенной зоны DЕ. И у металлов и у диэлектриков имеется множество свободных электронов, но у них разные энергетические возможности. Основное, что следует понять, что электрон только тогда «принимает», сообщаемую ему энергию, когда он при этом имеет возможность перейти на более высокий свободный энергетический уровень.

![mu =E_{F}left[1-{frac {pi ^{2}}{12}}left({frac {kT}{E_{F}}}right)^{2}+{frac {pi ^{4}}{80}}left({frac {kT}{E_{F}}}right)^{4}+ldots right],](https://wikimedia.org/api/rest_v1/media/math/render/svg/7de225de97f37b3abc39e0affc41ad4a56d6b54b)

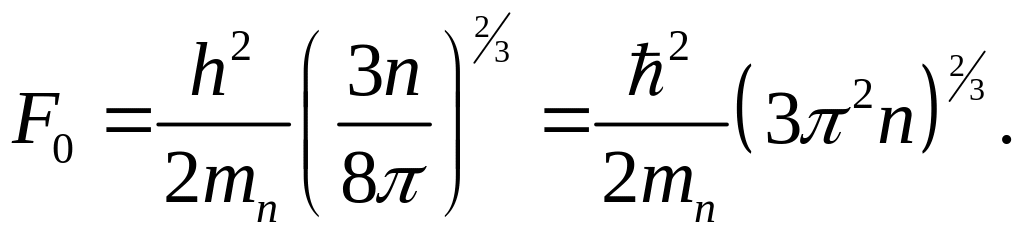
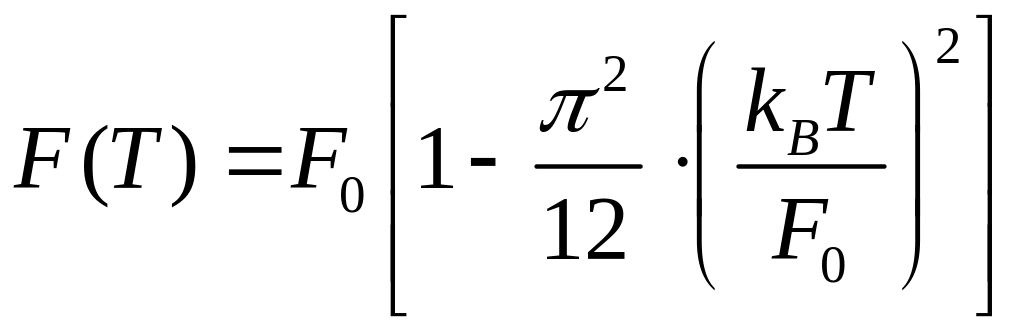
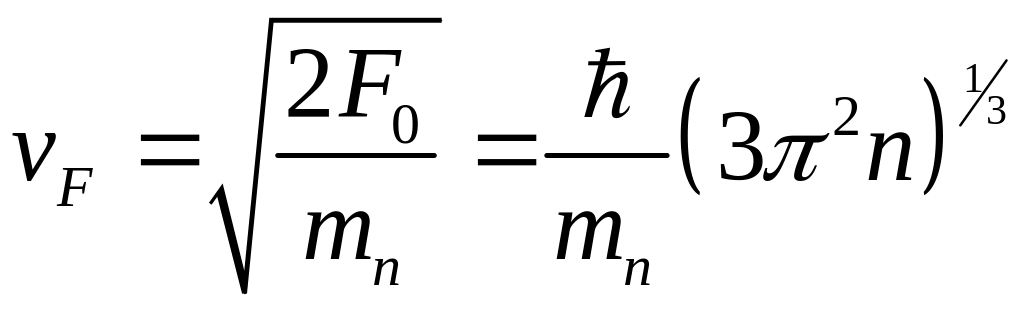






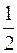





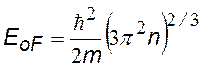



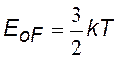
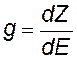 (1/эВ)
(1/эВ)
