Как найти энергию физика формулы

Содержание:

Работа, мощность и энергия:

Мы часто слышим от друзей: «Я сегодня выполнил большую работу: выучил наизусть стихотворение и решил пять задач по математике». Но с точки зрения физики никакой работы не совершено, даже если выучить наизусть целую поэму. Что же такое работа в физике?

В физике работа оценивает то, что вызвала сила, действуя на движущееся тело. Покажем это на примерах. Рассмотрите внимательно рисунок 216. Что общего в результатах действия силы тяжести на мяч (рис. 216, а), силы давления газа на пулю в пистолете (рис. 216, б) и силы упругости сжатой пружины на шарик (рис. 216, в) после пережигания нити? Все перечисленные силы вызывают разгон тел (мяча, пули, шарика), т. е. увеличение скорости движения.

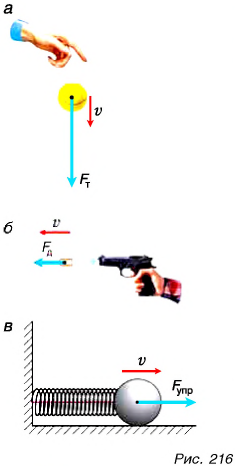
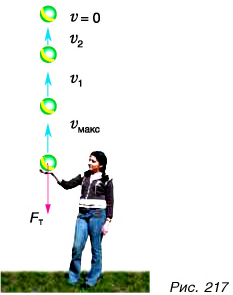
Л может ли сила, действующая на движущееся тело, уменьшать его скорость? Подбросьте мяч и наблюдайте за его движением вверх (рис. 217). Теперь сила тяжести уменьшает скорость его движения. Во всех случаях, когда сила изменяет скорость движения (увеличивает или уменьшает), говорят, что сила совершает механическую работу.

Механическая работа является физической величиной. Ее значение можно рассчитать. Рассмотрим самый простой случай: направление силы совпадает с направлением движения. Например, идет разгон спортивных саней (рис. 218). Изменение скорости саней, а значит, и работа по их разгону зависят от значения действующей силы (силы спортсменов, разгоняющих сани) и от пройденного санями пути. Чем больше сила и путь, тем большая совершается работа. Этот вывод справедлив для всех движущихся под действием силы тел.

Таким образом, механическая работа — физическая величина, пропорциональная действующей на тело силе и пройденному пути.

Обозначим работу буквой А. Тогда, если направление силы совпадает с направлением движения тела,

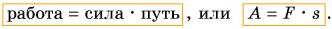
Единицей работы в СИ является 1 джоуль (1 Дж). Названа она в честь известного английского физика Дж. П. Джоуля. Один джоуль — это работа, совершаемая силой 1 Н на пути 1 м.

1 джоуль = 1 ньютон • 1 метр.

Для измерения большой работы используют кратные джоулю единицы:

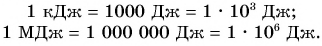
В случае малой работы применяются дольные единицы:

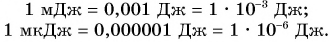
Из формулы работы следует, что если есть силы, но нет движения, то нет и работы. Например, сила тяжести, действующая на лежащий на столе мяч (рис. 219, а), работы не совершает, а в случае падающего мяча (рис. 219, б) — совершает.

Сила не всегда увеличивает скорость движения тела. Так, при движении мяча вверх (см. рис. 217) сила тяжести замедляет его движение. Аналогично при скольжении шайбы по льду сила трения уменьшает скорость движения шайбы. Работу силы (тяжести, трения) в подобных случаях считают отрицательной.

Но положительная и отрицательная работы могут совершаться одновременно и даже быть равными по абсолютной величине. В этом случае скорость движения постоянна. Например, электропоезд на данном участке пути движется равномерно. Это значит, что равнодействующая сил (тяги двигателя и сопротивления движению) равна нулю. По и сила тяги, и сила сопротивления совершают работу. Только работа силы тяги 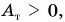 а силы сопротивления 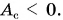Сумма же их равна 0, т. е.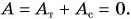

Главные выводы:

1. Механическая работа характеризует результат действия силы на движущееся тело и пропорциональна действующей на тело силе и пройденному телом пути.
2. Силы, ускоряющие движение тела; совершают положительную работу.
3. Силы, замедляющие движение тела, совершают отрицательную работу.
4. Единица работы в СИ — 1 джоуль (1 Дж).

Пример решения задачи:

Подъемный кран равномерно поднимает с земли бетонную плиту массой m = 500 кг на один из этажей строящегося дома. Сила упругости троса при этом совершает работу А = 100 кДж. Определите, на какой этаж была поднята плита, если высота одного этажа 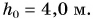Чему равна работа равнодействующей сил, приложенных к плите? Коэффициент  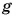примите равным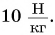 

Дано:

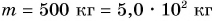
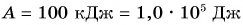
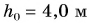
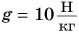
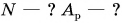
Решение:

При равномерном подъеме сила упругости троса равна силе тяжести, действующей на плиту: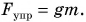 

Работа силы упругости 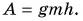 Высота подъема  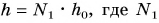– число этажей. Тогда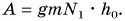 

Отсюда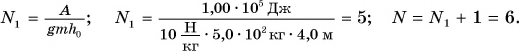  

Так как движение плиты равномерное, то равнодействующая сил, приложенных к ней, 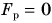 и работа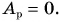 

Ответ: плита поднята на 6-й этаж; работа равнодействующей сил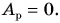 

Полезная и совершённая работа

Оценивая работу машины, механизма и др., говорят об их коэффициенте полезного действия (КПД). Но что такое КПД? Что означают слова «полезного действия»? А что такое неполезное действие?

Рассмотрим ситуацию: идет уборка картофеля на поле. Фермер поднимает картофель в ведре в кузов автомашины (рис. 221), выгружает, а ведро опускает на землю. Механическую работу совершает мускульная сила фермера, поднявшего ведро массой, например, 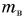 = 2,0 кг и картофель массой m = 10,0 кг на высоту h = 1,5 м. Какая работа здесь является полезной?

Цель фермера — погрузить в кузов картофель. Исходя из этого, полезной работой является работа по подъему картофеля: 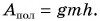А вот работа но подъему самого ведра не является полезной: 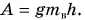Вся же совершенная (полная работа) равна:

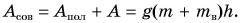
Какую долю составляет полезная работа от совершенной?

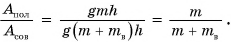
Обозначим отношение 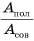 буквой  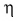(эта) и назовем коэффициентом полезного действия (КПД). Тогда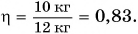

КПД, как правило, выражают в процентах. 

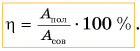
Таким образом, КПД (эффективность работы) в данном случае равен 83 %.

Рассмотрим еще один пример. Дети разгоняют санки, действуя силой F в направлении их движения (рис. 222). Совершенная (полная) работа здесь 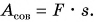Цель детей — увеличить скорость движения санок. Но на санки действует еще сила трения скольжения  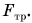Она тормозит движение санок. Значит, работа детей по преодолению силы трения не является полезной:

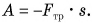
Полезной же работой была

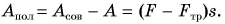
Тогда доля полезной работы (КПД)

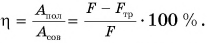
Физическая величина, равная отношению полезной работы к совершенной (полной), называется коэффициентом полезного действия.

А могут ли механизм, машина, человек работать так, чтобы КПД = 100 %, т. е. чтобы вся совершенная работа была полезной?

Ученые неоднократно пытались создать такую машину (рис. 223), но все попытки оказались безуспешными. (Самостоятельно познакомьтесь в Интернете или справочной литературе с информацией о вечном двигателе.) В работе любой машины, механизма всегда есть неполезная работа, идущая на преодоление трения, сопротивления. А значит, КПД всегда меньше 100 %. А вот сделать неполезную работу минимальной означает повысить КПД.

Главные выводы:

1. Совершенная (т. е. полная) механическая работа всегда больше полезной.
2. КПД показывает, какую долю составляет полезная работа от всей совершенной.
3. Чем больше полезная работа, тем выше КПД.
4. КПД всегда меньше 100 %.

Пример решения задачи:

При подъеме картофеля из хранилища глубиной h = 3,6 м подъемным устройством с КПД 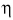 = 90 % совершена работа  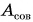= 40 кДж. Сколько мешков картофеля массой  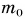= 40 кг каждый было поднято из хранилища? Примите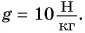

Дано:

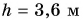
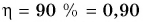
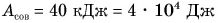
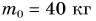
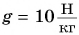
Решение:

Зная совершенную работу и КПД, можно найти полезную работу по подъему мешков картофеля:

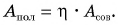
Полезная работа – это работа подъемного устройства по преодолению силы тяжести, действующей на картофель:

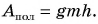
Масса 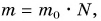 где N – число мешков картофеля. Тогда  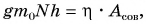откуда

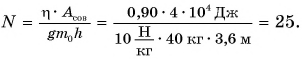
Ответ: N = 25 мешков.

Мощность и единицы мощности

Приобретая автомобиль (рис. 226), газонокосилку, микроволновую печь (рис. 227) и др., человек интересуется их мощностью. Именно мощность является паспортной характеристикой машин и механизмов. Что же такое мощность? Почему так важно ее знать?

Рассмотрим пример. Человек лопатой копает яму для погреба в течение нескольких дней. Такую же яму экскаватор (рис. 228) выкопает за несколько минут. Работа выполняется одинаковая. Одинаковая масса грунта поднимается на одну и ту же высоту. Но быстрота совершения работы человеком и экскаватором разная. За единицу времени экскаватор выполняет во много раз большую работу, чем человек. Для описания быстроты совершения работы вводится мощность.

Физическая величина, равная отношению работы к промежутку времени, за который эта работа совершена, называется мощностью. Обозначается мощность буквой Р.

За единицу мощности в СИ принимается мощность, при которой действующая на тело сила за время t = 1 с совершает работу А = 1 Дж. Эта единица мощности называется ватт (Вт) в честь английского изобретателя Дж. Уатта. Для измерения больших мощностей используют кратные единицы: гектоватт (гВт), киловатт (кВт), мегаватт (МВт). Обратите внимание:

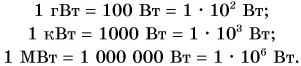
Для малых мощностей употребляются дольные единицы — милливатт (мВт), микроватт (мкВт): 

В быту часто необдуманно единицу мощности киловатт принимают за единицу работы. Но работа 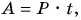из чего следует, что единицей работы может быть только киловатт-час (кВт • ч), но не киловатт (кВт). Выразим мощность через другие единицы — силу и скорость. Мощность 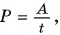но работа 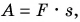путь 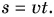Тогда

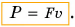
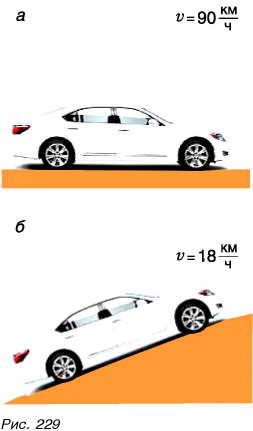
Мощность пропорциональна силе, совершающей работу, и скорости движения. Тогда при постоянной мощности чем меньше скорость, тем больше сила. Вот почему водитель, трогаясь с места или поднимаясь в гору (рис. 229), когда требуется большая сила, едет на малой скорости. Тем самым он увеличивает силу тяги двигателя автомобиля.

Главные выводы

1. Мощность — физическая величина, характеризующая быстроту совершения работы.
2. Единицей мощности в СИ является 1 ватт.
3. Одинаковую мощность можно получить либо при большой скорости и небольшой силе, либо при малой скорости и большой силе.

Для любознательных

В автомобилестроении по традиции используют старинную единицу мощности — лошадиную силу (л. с.). С помощью рисунка сформулируйте самостоятельно определение мощности в 1 лошадиную силу.

Запишем связь 1 л. с. и ватта: 1 л. с. = 736 Вт.

В этих внесистемных единицах мощность первого белорусского трактора МТЗ-2 (1953 г.) была равна 37 л. с. Освоенный в 2010 г. трактор «Беларус-3023» имеет двигатель мощностью 300 л. с. Переведите эти знамения мощности в единицы СИ самостоятельно и сравните их.

Пример решения задачи:

На уроке физкультуры мальчик массой m = 40 кг поднялся по канату на высоту h = 5,0 м за промежуток времени t = 10 с. Определите среднюю мощность, развиваемую мальчиком при подъеме. Коэффициент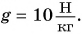

Дано:

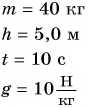
Решение:

При подъеме по канату работа мускульной силы рук идет на преодоление силы тяжести.

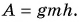
Тогда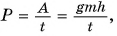 

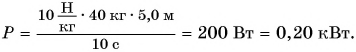
Ответ: P = 0, 20 кВт.

Кинетическая энергия

Энергия — одно из наиболее важных и сложных понятий. Причем не только в физике, но и в других науках. А что же такое кинетическая энергия?

Рассмотрим два примера. Шайба, попадая в сетку ворот (рис. 230), прогибает ее. Молот для забивания свай (рис. 231), падая на сваю, загоняет ее в землю на некоторую глубину. Чтобы сильнее прогнуть сетку или глубже забить сваю, шайба и молот должны иметь большую скорость. И шайба, и молот совершили работу. При этом скорость их движения изменилась (уменьшилась до нуля). Совершенные ими работы были разными, даже если предположить, что скорости движения были одинаковыми. Но массы молота и шайбы не равны.

Если тело способно совершить работу, то оно обладает энергией. В физике энергию движущегося тела называют кинетической (от греч. kinetikos — приводящий в движение). Кинетическая энергия обозначается буквой К (или 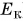) и измеряется в СИ в тех же единицах, что и работа, т. е. в джоулях.

Большая кинетическая энергия движущихся тел — камня, автомобиля, железнодорожного состава (рис. 232), метеорита и др. — означает, во-первых, что при разгоне их до данной скорости разгоняющей силой была совершена большая работа и, во-вторых, при их остановке тормозящей силой будет совершена такая же большая работа.

Из примеров следует, что кинетическая энергия зависит от массы тела и скорости его движения. Какой является эта зависимость?

Опыты показывают, что кинетическая энергия прямо пропорциональна массе тела и квадрату скорости его движения:

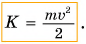
Увеличение скорости движения тела, например в 4 раза, приводит к возрастанию кинети- Обратите внимание! ческой энергии в 16 раз. Об этом должны всегда помнить водители и пешеходы.

Главные выводы:

1. Кинетическая энергия выражает способность движущихся тел совершать работу.
2. Кинетическая энергия, как и работа, измеряется в джоулях.
3. Кинетическая энергия тела зависит от его массы и скорости.
4. Изменить (увеличить или уменьшить) кинетическую энергию тела можно только путем совершения работы (положительной или отрицательной).

Пример решения задачи:

Скорость движения груженого автомобиля массой m = 4,0 т увеличилась от 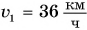до 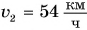 на пути s = 25 м. Определите силу тяги двигателя автомобиля и работу, которую совершила эта сила. Сопротивление движению не учитывать.

Дано:

Решение:

Чтобы увеличить кинетическую энергию от 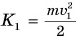 до 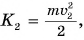 сила тяги должна была совершить работу:

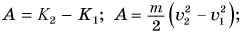
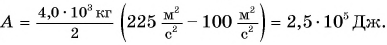
Но работа 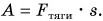 Отсюда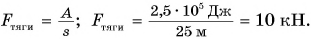 

Ответ: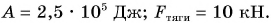 

Потенциальная энергия

При разгоне любого тела (санок, автомобиля и др.) у него возникает способность совершить механическую работу — у движущегося тела появляется кинетическая энергия. А если тело неподвижно? Обладает ли оно способностью совершить работу?

Проведем два опыта. В первом поднимем и укрепим на нити над ящиком с песком гирю (рис. 235, а). Во втором между упором и шариком поместим предварительно сжатую и связанную ниткой пружину (рис. 235, б). Оба тела (гиря и пружина) неподвижны 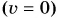 и не обладают кинетической энергией. Но и у гири, и у пружины есть возможность совершить работу. Для этого достаточно в обоих случаях пережечь нить. В физике говорят, что тела (поднятая гиря, взаимодействующая с Землей, и сжатая пружина) обладают потенциальной энергией (от лат. potentia — скрытая способность). Потенциальную энергию в СИ измеряют в тех же единицах, что и работу, — в джоулях.

Важно понимать, что потенциальная энергия не появляется сама по себе. В этих опытах гиря была поднята над столом, пружина была сжата какой-то силой. Значит, чтобы тело запасло потенциальную энергию, необходимо совершить работу. Чем сильнее будет сжата пружина, чем выше будет поднято тело, тем больше у них будет запас потенциальной энергии. Тела, представленные на рисунке 236, уже обладают потенциальной энергией. У трамплина она вызвана прогибом (деформацией) доски, у мышеловки — закручиванием пружины, у лука — изменением расположения древка и тетивы. Из этих и других примеров следует, что потенциальная энергия — это энергия, обусловленная взаимным расположением взаимодействующих тел или частей тела (гири и Земли, стрелы и тетивы, звеньев пружины). Обозначается потенциальная энергия буквой П (или ).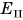

Именно благодаря потенциальной энергии сжатой (закрученной) пружины работают механические часы, реле времени микроволновых печей, стиральных машин, движутся некоторые детские игрушки. Потенциальная энергия поднятой с помощью плотины воды заставляет работать гидроэлектростанции (рис. 237).

Главные выводы:

1. Неподвижные взаимодействующие тела (система тел) могут обладать способностью совершать механическую работу, а значит, потенциальной энергией.
2. Значение потенциальной энергии зависит от взаимного расположения взаимодействующих тел (частей тела).
3. Потенциальная энергия изменяется только при совершении работы.

Расчет потенциальной энергии

Кинетическая энергия тела, зависящая от его массы и скорости, выражается формулой 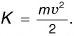Данная формула справедлива и для планеты Земля, мчащейся со скоростью 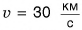по орбите вокруг Солнца, и для невидимого нашему глазу атома. Существует ли единая формула для расчета потенциальной энергии?

Рассмотрим отдельно два случая: потенциальную энергию притяжения поднятого над поверхностью Земли тела и потенциальную энергию деформированного тела.

В первом случае формулу для расчета потенциальной энергии легко вывести. Если тело массой m поднято относительно поверхности Земли на высоту h (рис. 238), то при его падении сила тяжести 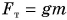может совершить работу:

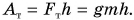
Это и есть потенциальная энергия поднятого тела:

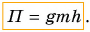
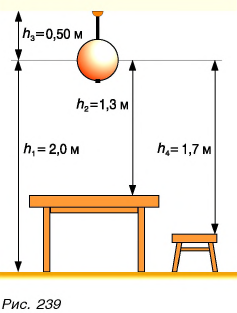
Значение потенциальной энергии относительно. Так, относительно пола потенциальная энергия светильника (рис. 239) массой m = 1,0 кг, центр тяжести которого расположен на высоте 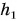 от пола, равна:

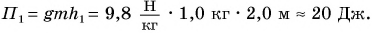
Относительно потолка 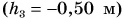 она равна:

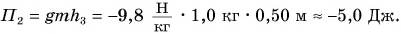
Поэтому, приводя значение потенциальной энергии, необходимо указывать уровень, относительно которого она задана, — нулевой уровень потенциальной энергии (это может быть, к примеру, поверхность пола, потолка, стола и т. д.).

Гораздо сложнее дело обстоит с расчетом потенциальной энергии деформированного тела. Мы можем растянуть или сжать пружину, изогнуть или закрутить ее (рис. 240). Потенциальная энергия у пружины будет в каждом из этих случаев. И чем больше упругая деформация, тем больше потенциальная энергия пружины. В данном примере расчет потенциальной энергии придется вести по различным формулам. Более детально с этим вы будете знакомиться в 9-м классе.

Главные выводы:

1. Потенциальная энергия притяжения тела к Земле зависит от массы тела и высоты его подъема над нулевым уровнем энергии.
2. Значение потенциальной энергии тела зависит от выбора нулевого уровня энергии.
3. Потенциальная энергия деформированного тела зависит от величины деформации.

Пример решения задачи:

Парафиновый однородный кубик с длиной ребра а = 10 см лежит на столе на высоте 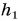 = 0,80 м от пола. Определите потенциальную энергию кубика относительно поверхностей: а) пола; б) стола. Какую работу нужно совершить, чтобы поднять кубик с пола на стол? Коэффициент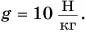 

Дано:

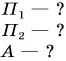
Решение:

Потенциальная энергия кубика относительно поверхности пола (рис. 241) определяется положением его центра (точки O):

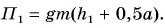
Масса кубика 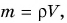 объем 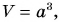 тогда:

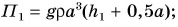
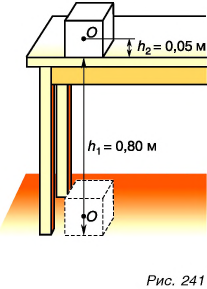
Потенциальная энергия кубика относительно поверхности стола:

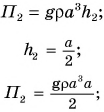
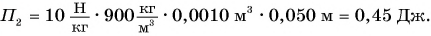
Работа по подъему кубика на высоту 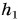 равна изменению его потенциальной энергии. Получаем:

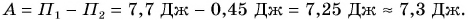
Ответ: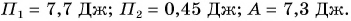 

Закон сохранения механической энергии

Кинетическая и потенциальная энергии — это два вида механической энергии. Связаны ли они друг с другом? И если да, то в чем выражается эта связь?

Проследим за движением брошенного вверх металлического шарика (рис. 243). В нижней точке траектории сила действия руки на шарик сообщает ему кинетическую энергию. Шарик движется вверх. Скорость его движения, а значит, и кинетическая энергия уменьшаются. Но исчезает ли кинетическая энергия бесследно? Поднимаясь выше, шарик приобретает все большую потенциальную энергию (вспомните: ). В верхней точке скорость и кинетическая энергия шарика равны нулю, а потенциальная максимальна. Значит, в рассмотренном примере происходит превращение энергии из одного вида (кинетической) в другой (потенциальную). При возвращении шарика обратно снова будет идти превращение энергии: с уменьшением высоты (и потенциальной энергии) увеличивается скорость движения шарика (и кинетическая энергия).

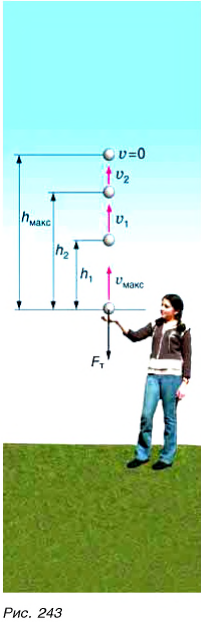
Если сопротивление воздуха мало (и им можно пренебречь), брошенный вверх шарик возвращается назад практически с такой же, как в момент бросания, скоростью и кинетической энергией.

А каким будет значение механической энергии шарика в промежуточных точках? Например, на высоте  (рис. 243)? При подъеме шарика на высоту  его кинетическая энергия уменьшилась, но при этом появилась потенциальная энергия. А чему равна их сумма, т. е. полная механическая энергия? Данный и подобные опыты и расчеты показывают, что если сил сопротивления нет, то полная механическая энергия тела (системы тел), равная сумме кинетической и потенциальной энергий 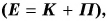сохраняется. Данное утверждение о постоянстве механической энергии в физике называют законом сохранения механической энергии.

Если силами трения или сопротивления движению нельзя пренебречь, этот закон не выполняется. Заменим в опыте металлический шарик на пенопластовый брусок такой же массы (рис. 244). Мы увидим, что даже при большей, чем у металлического шарика, начальной скорости он не поднимется на такую же высоту и вернется назад с заметно меньшей скоростью. Убывает кинетическая энергия движущейся по горизонтальной поверхности льда шайбы, но потенциальная энергия взамен не появляется. За счет кинетической энергии шайбы совершается работа против сил трения.

В заключение заметим, что явление превращения энергии из одного вида в другой человек научился использовать в практических целях. Энергия падающей воды приводит в действие водяные мельницы и гидроэлектростанции. В Республике Беларусь успешно реализуется государственная программа использования энергии рек. Важная роль в ней отводится таким рекам, как Неман и Западная Двина. Па Немане работает Гродненская ГЭС мощностью 17 МВт. Установленная мощность Витебской ГЭС на Западной Двине — 40 МВт.

Кинетическую энергию ветра человек с давних времен начал использовать с помощью паруса (рис. 245), затем стал применять в ветряных мельницах. В последние годы в нашей стране начато сооружение ветроэлектростанций (рис. 246). Они уникальны тем, что не оказывают вредного воздействия на окружающую среду. Во многих странах успешно используют энергию приливов и отливов вод морей и океанов. Там созданы приливные электростанции.

Главные выводы:

1. Кинетическая и потенциальная энергии взаимо-превращаемы.
2. При отсутствии сил трения и сопротивления движению полная механическая энергия тела (системы тел) сохраняется.
3. Закон сохранения механической энергии не выполняется, если силами трения (сопротивления) нельзя пренебречь.

• Заказать решение задач по физике

Пример решения задачи:

Камень бросили вертикально вверх со скоростью 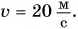На какой высоте от точки бросания кинетическая энергия камня будет в 4 раза меньше его потенциальной энергии? Сопротивлением движению камня пренебречь. Коэффициент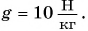

Дано:

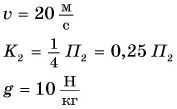
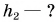
Решение:

За нулевой уровень потенциальной энергии примем уровень O – O, проходящий через точку бросания камня (рис. 247). Значит, 

Полная механическая энергия камня в точке бросания 1:

 

Полная механическая энергия камня в точке 2:

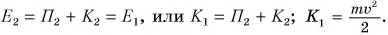
По условию 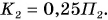Значит,

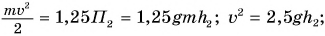
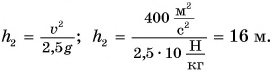
Ответ: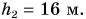 

Энергия и работа

Энергия – эта количественная мера различных форм движения и взаимодействия (по гречески слово «энергия» означает действие). Энергия в зависимости от вида движения в природе проявляется по-разному. Например, механическая, тепловая, электромагнитная, ядерная энергия и другие. В результате взаимодействия энергия одного вида превращается в энергию другого вида. Однако во всех этих процессах энергия, переданная от одного тела второму (независимо от ее вида), будет равна энергии, полученной вторым телом от первого.

Как известно из второго закона Ньютона, чтобы изменить механическое движение тела на него должны подействовать другие тела. Иначе говоря, среди этих тел происходит обмен энергиями. Для описания такого обмена энергии в механике введено понятие механическая работа, которую принято обозначать буквой .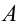

Механическая работа. Величина, равная скалярному произведению силы на перемещение в направлении действия силы, называется механической работой, т.е. 

Здесь: 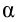– угол между силой  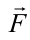и перемещением 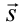s (рисунок 3.1). 
Если учитывать, что 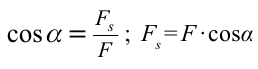, то уравнение (3.1) примет вид:

Здесь 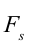– проекция силы в направлении смещения.
Основываясь на выражении (3.2), можно сделать следующий вывод:
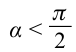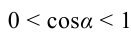если , то – работа силы положительна, направление силы и смещение совпадают;
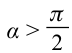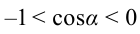если , то – работа силы отрицательная, направления силы и смещения противоположны;
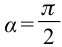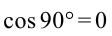если , то – работа, выполненная силой, равна нулю, направление силы будет перпендикулярным к направлению смещения.
Работа считается аддитивной (аддитив – по-латински означает суммарный) величиной (в физике аддитивность величины означает, что величина, относящаяся к системе в целом, равна сумме величины, относящихся к ее составным частям).
Если на тело действует несколько сил, то будет:

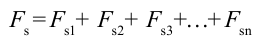
тогда полная работа равна работе, выполненной равнодействующей сил.

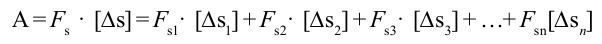
или

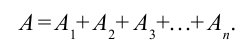
Единица работы. Единица измерения работы в системе СИ – Джоуль (Дж):

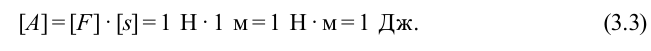
В качестве единицы работы в СИ принята работа выполненная силой 1Н при смещении тела на 1 м.
Работа силы тяжести. На поверхности Земли на тело действует сила тяжести со стороны Земли, равная 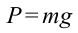. При перемещении тела из точки 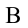на высоте 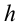от поверхности Земли в точку 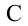на высоте 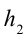от поверхности Земли, смещение тела равно: 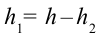(рис. 3.2).

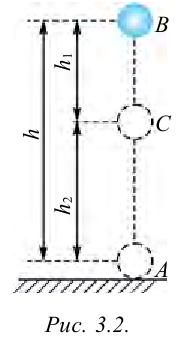
Здесь выполненная силой тяжести работа выражается следующей формулой:

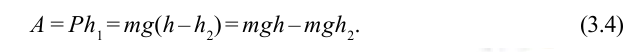
Здесь: 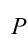– вес тела, 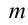– его масса, 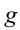– ускорение свободного падения, 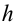– расстояние между уровням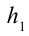и и 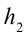 по вертикали.
Работа, выполненная силой тяжести, не зависит от формы пути, зависит только от высоты спуска. Поэтому работа, выполненная под действием силы тяжести, зависит не от формы  траектории, а от начального и конечного состояний. Такая сила называются потенциальной или консервативной. Поле такой силы называется потенциальным полем.

При движении тела вниз из-за соответствия направления силы тяжести и смещения выполненная работа будет положительной, при движении вверх из-за противоположности направлений работа будет отрицательной. Поэтому в случае, когда тело под воздействием силы тяжести смещено и вернулось обратно, выполненная общая работа равняется нулю.

Полной механической энергией системы называется сумма кинетической и потенциальной энергии системы. Например, полная механическая энергия тела массой 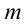, двигающегося со скоростью  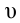относительно Земли на высоте 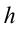от поверхности Земли:

Полная механическая энергия системы остается неизменной с течением времени:
 

Возможны лишь превращения потенциальной энергии и кинетическую и обратно. Выражение (3.5) представляет собой закон сохранения механической энергии.

Проведенные многочисленные эксперименты, теоретические выводы подтвердили строгое соблюдение закона сохранения энергии. 
В природе постоянно происходят превращения одного вида энергии в другой (например, механическая энергия переходит в тепловую энергию). Поэтому этот закон также называют законом сохранения и превращения энергии. Этот закон является основным законом природы и действителен не только для макроскопических, но и микроскопических систем.

Энергия никогда не исчезает, ниоткуда не появляется, она может только преобразовываться из одного вида в другой. 

В закрытых системах полная энергия сохраняется.

Например, потенциальная энергия тела, падающего с высоты 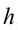, зависит от его веса и абсолютно не зависит от времени проведения экспериментов.
Коэффициент полезного действия. Введена величина, показывающая, какая часть израсходованной энергии машин и двигателей превращается в полезную работу.

Отношение полезной работы к полной работе называется коэффициентом полезного действия (КПД) и обозначается буквой .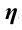 
Если полезную работу обозначить 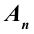, полную работу 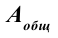, тогда формулу КПД можно записать в виде:

КПД не может быть больше единицы (100%). В машинах и двигателях в результате работы силы трения часть полной энергии расходуется и поэтому КПД всегда меньше единицы.

Рассмотрим наклонную плоскость и выполненную работу при подъеме тела вверх. По «золотому правилу» механики, во сколько раз выигрываем в силе, во столько раз проиграем в расстоянии. Но из-за увеличения расстояния смещения не меняется выполненная работа.

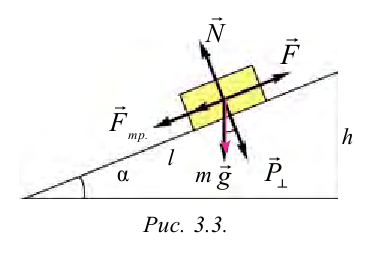
Рассмотрим груз с весом 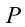на наклонной плоскости длиной 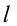, высотой  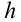(рис. 3.3). Здесь на тело действует сила трения 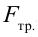, параллельная наклонной поверхности тянущая вверх сила 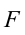, перпендикулярно направленная к наклонной плоскости 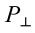и противоположно направленная перпендикулярно к поверхности сила 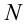(реактивная сила поверхности).
Если не учитывать силу трения, получим уравнение:

Однако с учетом силы трения,

Тогда 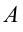пишется в следующем виде:

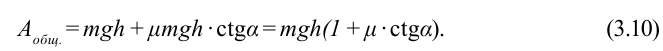
Коэффициент полезного действия:

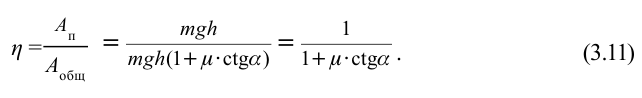
Сила притяжения, действующая на груз, равна:
 

Энергия – важнейшее понятие и термин в механике. Что такое энергия, и что она значит? Существует множество определений, и вот одно из них.

Что такое энергия?

Энергия в физике – это способность тела совершать работу. 

Кинетическая энергия

Что такое кинетическая энергия?

Рассмотрим тело, которое двигалось под действием каких-то сил, изменило свою скорость с v1→ до v2→. В этом случае силы, действующие на тело, совершили определенную работу A. 

Работа всех сил, действующих на тело, равна работе равнодействующей силы. 

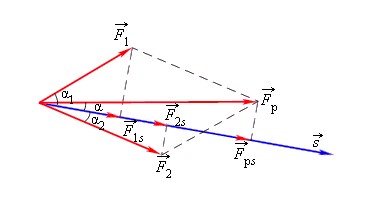
Fр→=F1→+F2→

A=F1·s·cosα1+F2·s·cosα2=Fрcosα.

Как находить связь между изменением скорости тела и работой, совершенной действующими на тело силами. Для простоты будем считать, что на тело действует одна сила F→, направленная вдоль прямой линии. Под действием этой силы тело движется равноускоренно и прямолинейно. В этом случае векторы F→, v→, a→, s→ совпадают по направлению и их можно рассматривать как алгебраические величины. 

Работа силы F→ равна A=Fs. Перемещение тела выражается формулой s=v22-v122a. Отсюда:

A=Fs=F·v22-v122a=ma·v22-v122a

A=mv22-mv122=mv222-mv122.

Если вычислять, то работа, совершенная силой, пропорционально изменению квадрата скорости тела. 

Теорема о кинетической энергии

Вновь будем работать с рассмотренным примером и сформулируем теорему о кинетической энергии тела.

Таким образом, кинетическая энергия тела массы m, движущегося со скоростью v→, будет измеряться (при измерении) и равна работе, которую сила должна совершить, чтобы разогнать тело до этой скорости.

A=mv22=EK.

Чтобы остановить тело, нужно совершить работу 

A=-mv22=-EK

Потенциальная энергия

Что будет означать или обозначать кинетическая энергия?

Кинетическая энергия – это энергия движения. Наряду с кинетической энергией есть еще такой вид энергии как потенциальная энергия, то есть энергия взаимодействия тел, которая будет вычисляться и зависеть от их положения. Кинетическая и потенциальная энергии рассматриваются параллельно.

Формула потенциальной энергии:

E пот = m * g * h

Например, тело поднято над поверхностью земли. Чем выше оно поднято, тем больше будет потенциал-я энергия. Когда тело движется и падает вниз под действием силы тяжести (притяжения), эта сила совершает работу. Причем работа силы тяжести определяется только вертикальным перемещением тела и не зависит от траектории.

Вообще о потенциально энергии можно говорить только в контексте тех сил, работа которых не зависит от формы траектории тела. Такие силы называются консервативными.

Примеры консервативных сил: сила тяжести, сила упругости.

Когда тело движется вертикально вверх, сила тяжести совершает отрицательную работу. 

Рассмотрим вычисление на примере, когда шар переместился из точки с высотой h1 в точку с высотой h2. 

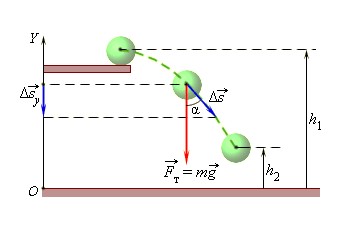
При этом сила тяжести совершила работу, равную 

A=-mg(h2-h1)=-(mgh2-mgh1).

Эта работа равна изменению величины mgh, взятому с противоположным знаком. 

Величина ЕП=mgh – потенциальна энергия в поле силы тяжести. На нулевом уровне (на земле) потенциальную энергию тела можно не рассчитывать: она равна нулю.

Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.

A=-(EП2-EП1).

Ясно, что потенциальная энергия зависит от выбора нулевого уровня (начала координат оси OY). Подчеркнем, что физический смысл имеет изменение потенциальной энергии при перемещении тел друг относительно друга. При любом выборе нулевого уровня изменение потенциальной энергии будет одинаковым.

При расчете движения тел в поле гравитации Земли, но на значительных расстояниях от нее, во внимание нужно принимать закон всемирного тяготения (зависимость силы тяготения от расстояния до цента Земли). Приведем формулу, выражающую зависимость потенциальной энергии тела.

EП=-GmMr.

Здесь G – гравитационная постоянная, M – масса Земли.

Потенциальная энергия пружины

Представим, что в первом случае мы взяли пружину и удлинили ее на величину x. Во втором случае мы сначала удлинили пружину на 2x, а затем уменьшили на x. В обоих случаях пружина оказалась растянута на x, но это было сделано разными способами. 

При этом работа силы упругости при изменении длины пружины на x в обоих случаях была одинакова и равна

Aупр=-A=-kx22.

Величина Eупр=kx22 называется потенциальной энергией сжатой пружины. Она равна работе силы упругости при переходе из данного состояния тела в состояние с нулевой деформацией.

Если перед вами часто поднимается вопрос определения и характеристики энергии, как явления, вам стоит подумать о сохранении описанной выше информации.

Энергия — что это в физике, как понять на какую энергию задача, что такое закон сохранения энергии, кинетическая энергия, мощность, потенциальная энергия и формула мощности, формула работы все это мы с вами сейчас изучим. Это базовые понятия физики, которые разберем подробно.

Что такое энергия в физике

Энергия — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие.

В механике есть два вида энергии: кинетическая энергия и потенциальная энергия. Их сумма называется полной механической энергией.

Энергия и работа

Энергия является мерой способности физической системы совершить работу, поэтому количественно энергия и работа выражаются в одних единицах (джоулях, [Дж]).

Механическая работа численно равна изменению механической энергии. Эту связь работы и энергии мы легко можем почувствовать на себе: например, если провести день очень активно, то к вечеру никаких сил и энергии не останется.

В механике принято считать, что работу по перемещению тела из одного положения в другое совершает сила. Работу силы можно вычислить по формуле:

A=F∙s∙cosα,

где F — сила, совершающая работу, [H];

S — перемещение тела, [м];

α — угол между направлением силы и направлением перемещения.

Если угол α острый, то работа силы положительна, если прямой, то работа равна нулю, если тупой, то работа отрицательна.

Кинетическая энергия

Кинетическая энергия — это энергия движения тела. Кинетическая энергия зависит только от скорости и от массы тела, и определяется формулой:

.

где m — масса тела, [кг],

v — скорость тела, [м/с].

Если тело покоится, его кинетическая энергия равна нулю.

Движущееся тело обладает способностью совершить работу. Например, шар для боулинга способен сбить все 10 кеглей.

Потенциальная энергия

Потенциальная энергия — это энергия взаимодействия тел или частей тела между собой или с внешними полями. Основной физический смысл имеет не само потенциальной энергии, а её изменение. Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Любая физическая система стремится к состоянию с наименьшей потенциальной энергией.

Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его. Такие силы называются консервативными (потенциальными).

Например, работа силы тяжести не зависит от траектории перемещения тела и равна mgh.

Закон сохранения энергии

Энергия замкнутой физической системы сохраняется. Замкнутой называется система, в которой действуют только консервативные силы.

Закон сохранения механической энергии

Общая сумма потенциальной и кинетической энергии тела остается неизменной, если действуют только силы упругости и тяготения, а сила трения отсутствует.

E_кин+E_пот=const

Потенциальная энергия в поле силы тяжести выражается формулой:

E_пот=mgh

где m — масса тела, [кг],

g — ускорение свободного падения, [Н/кг] или [м/c2].

h — высота положения тела над поверхностью, [м].

За нулевое положение тела может быть принято любое удобное нам положение в зависимости от условий, проводимых опыта и измерений. Это может быть поверхность пола, стола, Земли и так далее.

Закон сохранения энергии для математического маятника

Закон сохранения энергии в поле силы тяжести хорошо иллюстрируется движением математического маятника.

В положении 1 и 3 шарик находится в состоянии покоя на высоте h, его кинетическая энергия равна нулю, а потенциальная равна mgh. При переходе из положения 1 в положение 2 высота и потенциальная энергия уменьшаются, но зато скорость и кинетическая энергия увеличиваются, и в положении 2 кинетическая энергия максимальна и равна mv2/2, а потенциальная энергия минимальна и равна нулю.

Таким образом,

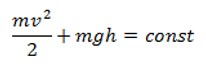
Поднятый над землей груз работы не совершает, но может совершить, если начнет падать вниз. Например, потенциальная энергия падающей воды может превратиться в механическую энергию жернова.

Потенциальная энергия пружины

Потенциальная энергия  характеризует взаимодействие между собой частей тела и приближённо выражается формулой:

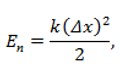
где k — жёсткость деформированного тела, [Н/м],

Δx — смещение от положения равновесия.

Потенциальная энергия пружины равна нулю, когда пружина не растянута.

Сжатая пружина, распрямляясь, может совершить работу, например, поднять вверх небольшой груз.

Внутренняя энергия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекул. Внутреннюю энергию тела нельзя измерить напрямую.

Предыдущий урок: Физика для чайников. Урок 10. Вывод закон сохранения импульса

Итак, вот постепенно мы добрались и до понятия энергии. Надо сказать, что энергия – это весьма интересная штука. Вот такое определение дает на википедия: «Энергия — действие, деятельность, сила, мощь) — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие». Согласитесь, не очень понятно. Еще более странно, что существует какой-то закон сохранения энергии, согласно которому, энергия не исчезает бесследно и не появился из ниоткуда. По научному он звучит так: «Закон сохранения энергии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени».

На самом деле, этот сохранения энергии выполнялся только для замкнутой системы. Этот как закон сохранения импульса (см. прошлый урок), выводиться аналогично.

Энергия бывают многих разных видов. Разберем некоторые из них.

Кинетическая энергия. Это энергия движущегося тела. Она пропорциональна массе и квадрату скорости, и именно:

В этой формуле E – это энергия, m – масса тела, v – его скорость.

Почему формула именно такая? Дело в том, что кинетическая энергия – эта работа, которую совершит сила, перемещая тело заданной массы на заданное расстояние. Эта работа измеряется в Н*м (Ньютонах на метр). Другое название данной единицы – Джоуль (Дж). Но как связаны расстояние, сила, масса и скорость? Согласно второму закону Ньютона, силы равна произведению массы на ускорение. А пройдённое расстояние равноускоренного тела вычисляется по формуле:

Помните в уроке Физика для чайников. Урок 4. Прямолинейное движение я говорил, что это важная формула? Не правда, ли, формула кинетической энергии похожа на нее? Напомню, что здесь S – пройденное расстояние, a – ускорение, t – время.

А теперь в определении энергии как силы на единицу длины и выполним подстановку:

Здесь F – это сила, v/t – это ускорение (изменение скорости за единицу времени).

Потенциальная энергия. Предположим, Сизиф поднял камень, массой 1 тонна на высоту 1 километр. Когда он толкал камень в гору, он совершал работу. Тратил энергию. Но камень остался неподвижный. Вопрос: куда делась эта энергия? По закону сохранения энергии она же не могла бесследно исчезнуть? И она не исчезла. А превратилась в потенциальную энергию. Чем равна потенциальная энергия? А она равна работе силы тяжести (точнее, работе против силы тяжести):

где h – высота, на которую поднято тело, g – ускорение свободного падения, примерно 9.8 м/с^2, ну а m – масса тела.

В нашем примере Сизиф поднял камень массой 1 тонну на высотку 1 километр, значит, его потенциальная энергия равна

Если камень вдруг скатиться с горы, то его потенциальная энергия превратиться в кинетическую, и горе тому, кого он сшибет.

Тепловая энергия. До сих пор мы рассматривали идеальные случаи (сферического коня в вакууме, так сказать). Но в реальном мире существует сила трения. Вот едет автомобиль, за счет работы двигателя к нему приложена сила, которая двигает его вперед. Но почему при этом скорость автомобиля остается после разгона одинаковой? Почему автомобиль не может разгонятся вечно? Все дело в том, что на него действует сила трения. С одной стороны, работа двигателя толкает автомобиль вперед, с другой стороны тормозит сила терния. Они друг друга уравновешивают, и потому, согласно первому закону Ньютона, автомобиль продолжает движение с одной и той же скоростью.

Но тут получается, что сила, с которой двигатель двигает автомобиль, совершает работу, с затратой энергии. А куда девается эта энергия? Она уходит в тепловую энергию. Если вы будете интенсивно тереть друг о друга две деревяшки, то они нагреться. И могут даже загореться. В древние времена именно так и добывали огонь.

Существует и обратное преобразование: тепловая энергия в кинетическую. Например, нагретый пар толкает поршень, который вращает колесо (паровой двигатель).

Другие виды энергии. Кроме кинетической, тепловой и потенциальной, существует еще множество других видов энергии. Например, электрическая, химическая, ядерная. Вообще, парадоксально, но факт, материя может превращаться в энергию и энергия в материю. Это зафиксировано в знаменитой формуле Эйнштейна:

Здесь m – масса, c – скорость света, примерно 300 миллионов метров в секунду (300 тыс. км/с). Но в расчета используются именно метры в секунду. Это значит, что в одном килограмме вещества запасено 9*10^16 (90 тыс. триллионов) Джоулей энергии. Для сравнения, энергия взрыва атомной бомбы порядка 2 *10^14 Дж, почти в четыреста раз меньше.

Подытожим. Мы познакомились с понятием энергии. Возможно, вы все еще не совсем поняли, что это такое. Не страшно, даже сами физики толком не знают, а что же такое энергия. Поэтому, просто примите как факт, что энергия – это такая неведомая фигня, которая описывается формулами и которая подчиняется закону сохранения энергии. Но если сказать простыми словами, очень утрированно, то энергия – это способность совершать полезную работу. И еще, немаловажно: халявной энергии не бывает и вечный двигатель невозможен.

В будущих уроках (когда мы будем изучать термодинамику), вы познакомитесь с энергией поближе.

Следующий урок: Физика для чайников. Урок 12. Термодинамика

Если вам была полезна статья, то вы всегда можете Отблагодарить автора

Механическая работа. Единицы работы.

В обыденной жизни под понятием «работа» мы понимаем всё.

В физике понятие работа несколько иное. Это определенная физическая величина, а значит, ее можно измерить. В физике изучается прежде всего механическая работа.

Рассмотрим примеры механической работы.

Поезд движется под действием силы тяги электровоза, при этом совершается механическая работа. При выстреле из ружья сила давления пороховых газов совершает работу — перемещает пулю вдоль ствола, скорость пули при этом увеличивается.

Из этих примеров видно, что механическая работа совершается, когда тело движется под действием силы. Механическая работа совершается и в том случае, когда сила, действуя на тело (например, сила трения), уменьшает скорость его движения.

Желая передвинуть шкаф, мы с силой на него надавливаем, но если он при этом в движение не приходит, то механической работы мы не совершаем. Можно представить себе случай, когда тело движется без участия сил (по инерции), в этом случае механическая работа также не совершается.

Итак, механическая работа совершается, только когда на тело действует сила, и оно движется.

Нетрудно понять, что чем большая сила действует на тело и чем длиннее путь, который проходит тело под действием этой силы, тем большая совершается работа.

Механическая работа прямо пропорциональна приложенной силе и прямо пропорциональна пройденному пути.

Поэтому, условились измерять механическую работу произведением силы на путь, пройденный по этому направлению этой силы:

работа = сила × путь

или

A = Fs,

где А — работа, F — сила и s — пройденный путь.

За единицу работы принимается работа, совершаемая силой в 1Н, на пути, равном 1 м.

Единица работы — джоуль (Дж) названа в честь английского ученого Джоуля. Таким образом,

1 Дж = 1Н · м.

Используется также килоджоули (кДж) .

1 кДж = 1000 Дж.

Формула А = Fs применима в том случае, когда сила F постоянна и совпадает с направлением движения тела.

Если направление силы совпадает с направлением движения тела, то данная сила совершает положительную работу.

Если же движение тела происходит в направлении, противоположном направлению приложенной силы, например, силы трения скольжения, то данная сила совершает отрицательную работу.

A = -Fs.

Если направление силы, действующей на тело, перпендикулярно направлению движения, то эта сила работы не совершает, работа равна нулю:

A = 0.

В дальнейшем, говоря о механической работе, мы будем кратко называть ее одним словом — работа.

Пример. Вычислите работу, совершаемую при подъеме гранитной плиты объемом 0,5 м3 на высоту 20 м. Плотность гранита 2500 кг/м³.

Запишем условие задачи, и решим ее.

Дано:

V = 0,5 м³

ρ = 2500 кг/м³

h = 20 м

Решение:

A = Fs,

где F -сила, которую нужно приложить, чтобы равномерно поднимать плиту вверх. Эта сила по модулю равна силе тяж Fтяж, действующей на плиту, то есть F = Fтяж. А силу тяжести можно определить по массе плиты: Fтяж = gm. Массу плиты вычислим, зная ее объем и плотность гранита: m = ρV; s = h, то есть путь равен высоте подъема.

Итак, m = 2500 кг/м3 · 0,5 м3 = 1250 кг.

F = 9,8 Н/кг · 1250 кг ≈ 12 250 Н.

A = 12 250 Н · 20 м = 245 000 Дж = 245 кДж.

А — ?

Ответ: А =245 кДж.

Рычаги. Мощность. Энергия

На совершение одной и той же работы различным двигателям требуется разное время. Например, подъемный кран на стройке за несколько минут поднимает на верхний этаж здания сотни кирпичей. Если бы эти кирпичи перетаскивал рабочий, то ему для этого потребовалось бы несколько часов. Другой пример. Гектар земли лошадь может вспахать за 10-12 ч, трактор же с многолемешным плугом (лемех — часть плуга, подрезающая пласт земли снизу и передающая его на отвал; многолемешный — много лемехов), эту работу выполнит на 40-50 мин.

Ясно, что подъемный кран ту же работу совершает быстрее, чем рабочий, а трактор — быстрее чем лошадь. Быстроту выполнения работы характеризуют особой величиной, называемой мощностью.

Мощность равна отношению работы ко времени, за которое она была совершена.

Чтобы вычислить мощность, надо работу разделить на время, в течение которого совершена эта работа.
мощность = работа/время.

или

N = A/t,

где N — мощность, A — работа, t — время выполненной работы.

Мощность — величина постоянная, когда за каждую секунду совершается одинаковая работа, в других случаях отношение A/t определяет среднюю мощность:

Nср = A/t .
За единицу мощности приняли такую мощность, при которой в 1 с совершается работа в Дж.

Эта единица называется ваттом (Вт) в честь еще одного английского ученого Уатта.

Итак,

1 ватт = 1 джоуль/ 1 секунда, или 1 Вт = 1 Дж/с .

Ватт (джоуль в секунду) — Вт (1 Дж/с).

В технике широко используется более крупные единицы мощности — киловатт (кВт), мегаватт (МВт) .

1 МВт = 1 000 000 Вт

1 кВт = 1000 Вт

1 мВт = 0,001 Вт

1 Вт = 0,000001 МВт

1 Вт = 0,001 кВт

1 Вт = 1000 мВт

Пример. Найти мощность потока воды, протекающей через плотину, если высота падения воды 25 м, а расход ее — 120 м3 в минуту.

Запишем условие задачи и решим ее.

Дано:

h = 25 м

V = 120 м3

ρ = 1000 кг/м3

t = 60 c

g = 9,8 м/с2

Решение:

Масса падающей воды: m = ρV,

m = 1000 кг/м3 · 120 м3 = 120 000 кг (12 · 104 кг).

Сила тяжести, действующая на воду:

F = gm,

F = 9.8 м/с2 · 120 000 кг ≈ 1 200 000 Н (12 · 105 Н)

Работа, совершаемая потоком в минуту:

A = Fh,

А — 1 200 000 Н · 25 м = 30 000 000 Дж (3 · 107 Дж).

Мощность потока: N = A/t,

N = 30 000 000 Дж / 60 с = 500 000 Вт = 0,5 МВт.

N — ?

Ответ: N = 0.5 МВт.

Различные двигатели имеют мощности от сотых и десятых долей киловатта (двигатель электрической бритвы, швейной машины) до сотен тысяч киловатт (водяные и паровые турбины).

Таблица 5.

Мощность некоторых двигателей, кВт.

Вид транспортного средства	Мощность двигателя	Вид транспортного средства	Мощность двигателя
Автомобиль «Волга — 3102»	70	Ракета-носитель космического корабля
Самолет Ан-2	740
Дизель тепловоза ТЭ10Л	2200	«Восток»	15 000 000
Вертолет Ми — 8	2×1100	«Энергия»	125 000 000

На каждом двигателе имеется табличка (паспорт двигателя), на которой указаны некоторые данные о двигателе, в том числе и его мощность.

Мощность человека при нормальный условиях работы в среднем равна 70-80 Вт. Совершая прыжки, взбегая по лестнице, человек может развивать мощность до 730 Вт, а в отдельных случаях и еще бóльшую.

Зная мощность двигателя, можно рассчитать работу, совершаемую этим двигателем в течение какого-нибудь промежутка времени.

Из формулы N = A/t следует, что

A = Nt.

Чтобы вычислить работу, необходимо мощность умножить на время, в течение которого совершалась эта работа.

Пример. Двигатель комнатного вентилятора имеет мощность 35 Вт. Какую работу он совершает за 10 мин?

Запишем условие задачи и решим ее.

Дано:

N = 35 Вт

t = 10 мин

A = ?

Си 600 с.

Решение:

A = Nt,

A = 35 Вт * 600с = 21 000 Вт* с = 21 000 Дж = 21 кДж.

Ответ A = 21 кДж.

Простые механизмы.

С незапамятных времен человек использует для совершения механической работы различные приспособления.

Каждому известно, что тяжелый предмет (камень, шкаф, станок), который невозможно сдвинуть руками, можно сдвинуть с помощью достаточно длинной палки — рычага.

На данный момент считается, что с помощью рычагов три тысячи лет назад при строительстве пирамид в Древнем Египте передвигали и поднимали на большую высоту тяжелые каменные плиты.

Во многих случаях, вместо того, чтобы поднимать тяжелый груз на некоторую высоту, его можно вкатывать или втаскивать на ту же высоту по наклонной плоскости или поднимать с помощью блоков.

Приспособления, служащие для преобразования силы, называются механизмами.

К простым механизмам относятся: рычаги и его разновидности — блок, ворот; наклонная плоскость и ее разновидности — клин, винт. В большинстве случаев простые механизмы применяют для того, чтобы получить выигрыш в силе, то есть увеличить силу, действующую на тело, в несколько раз.

Простые механизмы имеются и в бытовых, и во всех сложных заводских и фабричных машинах, которые режут, скручивают и штампуют большие листы стали или вытягивают тончайшие нити, из которых делаются потом ткани. Эти же механизмы можно обнаружить и в современных сложных автоматах, печатных и счетных машинах.

Рычаг. Равновесие сил на рычаге.

Рассмотрим самый простой и распространенный механизм — рычаг.

Рычаг представляет собой твердое тело, которое может вращаться вокруг неподвижной опоры.

На рисунках показано, как рабочий для поднятия груза в качестве рычага, использует лом. В первом случае рабочий с силой F нажимает на конец лома B, во втором — приподнимает конец B.

Рабочему нужно преодолеть вес груза P — силу, направленную вертикально вниз. Он поворачивает для этого лом вокруг оси, проходящей через единственную неподвижную точку лома — точку его опоры О. Сила F, с которой рабочий действует на рычаг, меньше силы P, таким образом, рабочий получает выигрыш в силе. При помощи рычага можно поднять такой тяжелый груз, который своими силами поднять нельзя.

На рисунке изображен рычаг, ось вращения которого О (точка опоры) расположена между точками приложения сил А и В. На другом рисунке показана схема этого рычага. Обе силы F1 и F2, действующие на рычаг, направлены в одну сторону.

Кратчайшее расстояние между точкой опоры и прямой, вдоль которой действует на рычаг сила, называется плечом силы.

Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы.

Длина этого перпендикуляра и будет плечом данной силы. На рисунке показано, что ОА — плечо силы F1; ОВ — плечо силы F2 . Силы, действующие на рычаг могут повернуть его вокруг оси в двух направлениях: по ходу или против хода часовой стрелки. Так, сила F1 вращает рычаг по ходу часовой стрелки, а сила F2 вращает его против часовой стрелки.

Условие, при котором рычаг находится в равновесии под действием приложенных к нему сил, можно установить на опыте. При этом надо помнить, что результат действия силы, зависит не только от ее числового значения (модуля), но и от того, в какой точке она приложена к телу, или как направлена.

К рычагу (см рис.) по обе стороны от точки опоры подвешиваются различные грузы так, что каждый раз рычаг оставался в равновесии. Действующие на рычаг силы, равны весам этих грузов. Для каждого случая измеряются модули сил и их плечи. Из опыта изображенного на рисунке 154, видно, что сила 2 Н уравновешивает силу 4 Н. При этом, как видно из рисунка, плечо меньшей силы в 2 раза больше плеча большей силой.

На основании таких опытов было установлено условие (правило) равновесия рычага.

Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил.

Это правило можно записать в виде формулы:

F1/F2 = l2/l1,

где F1 и F2– силы, действующие на рычаг, l1 и l2, — плечи этих сил (см. рис.).

Правило равновесия рычага было установлено Архимедом около 287—212 гг. до н. э. (но ведь в прошлом параграфе говорилось, что рычаги использовались египтянами? Или тут важную роль играет слово «установлено»?)

Из этого правила следует, что меньшей силой можно уравновесить при помощи рычага бóльшую силу. Пусть одно плечо рычага в 3 раза больше другого (см рис.). Тогда, прикладывая в точке В силу, например, в 400 Н, можно поднять камень весом 1200 Н. Что0бы поднять еще более тяжелый груз, нужно увеличить длину плеча рычага, на которое действует рабочий.

Пример. С помощью рычага рабочий поднимает плиту массой 240 кг (см рис. 149). Какую силу прикладывает он к большему плечу рычага, равному 2,4 м, если меньшее плечо равно 0,6 м?

Запишем условие задачи, и решим ее.

Дано:

m = 240 кг

g =9,8 Н/кг

l1 = 2,4 м

l2 =0,6 м

Решение:

По правилу равновесия рычага F1/F2 = l2/l1, откуда F1 = F2 l2/l1, где F2 = Р — вес камня. Вес камня asd = gm, F = 9,8 Н · 240 кг ≈ 2400 Н

Тогда, F1 = 2400 Н · 0,6/2,4 = 600 Н.

F — ?

Ответ : F1 = 600 Н.

В нашем примере рабочий преодолевает силу 2400 Н, прикладывая к рычагу силу 600 Н. Но при этом плечо, на которое действует рабочий, в 4 раза длиннее того, на которое действует вес камня (l1 : l2 = 2,4 м : 0,6 м = 4).

Применяя правило рычага, можно меньшей силой уравновесить бóльшую силу. При этом плечо меньшей силы должно быть длиннее плеча большей силы.

Момент силы.

Вам уже известно правило равновесия рычага:

F1 / F2 = l2 / l1,

Пользуясь свойством пропорции (произведение ее крайних членов, равно произведению ее средних членов), запишем его в таком виде:

F1l1 = F2l2 .

В левой части равенства стоит произведение силы F1 на ее плечо l1, а в правой — произведение силы F2 на ее плечо l2 .

Произведение модуля силы, вращающей тело, на ее плечо называется моментом силы; он обозначается буквой М. Значит,

M = Fl.

Рычаг находится в равновесии под действием двух сил, если момент силы, вращающий его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки.

Это правило, называемое правилом моментов, можно записать в виде формулы:

М1 = М2

Действительно, в рассмотренном нами опыте, (§ 56) действующие силы были равны 2 Н и 4 Н, их плечи соответственно составляли 4 и 2 давления рычага, то есть моменты этих сил одинаковы при равновесии рычага.

Момент силы, как и всякая физическая величина, может быть измерена. За единицу момента силы принимается момент силы в 1 Н, плечо которой ровно 1 м.

Эта единица называется ньютон-метр (Н · м).

Момент силы характеризует действие силы, и показывает, что оно зависит одновременно и от модуля силы, и от ее плеча. Действительно, мы уже знаем, например, что действие силы на дверь зависит и от модуля силы, и от того, где приложена сила. Дверь тем легче повернуть, чем дальше от оси вращения приложена действующая на нее сила. Гайку, лучше отвернуть длинным гаечным ключом, чем коротким. Ведро тем легче поднять из колодца, чем длиннее ручка вóрота, и т. д.

Рычаги в технике, быту и природе.

Правило рычага (или правило моментов) лежит в основе действия различного рода инструментов и устройств, применяемых в технике и быту там, где требуется выигрыш в силе или в пути.

Выигрыш в силе мы имеем при работе с ножницами. Ножницы — это рычаг (рис), ось вращения которого, происходит через винт, соединяющий обе половины ножниц. Действующей силой F1 является мускульная сила руки человека, сжимающего ножницы. Противодействующей силой F2 — сила сопротивления такого материала, который режут ножницами. В зависимости от назначения ножниц их устройство бывает различным. Конторские ножницы, предназначенные для резки бумаги, имеют длинные лезвия и почти такой же длины ручки. Для резки бумаги не требуется большой силы, а длинным лезвием удобнее резать по прямой линии. Ножницы для резки листового металла (рис.) имеют ручки гораздо длиннее лезвий, так как сила сопротивления металла велика и для ее уравновешивания плечо действующей силы приходится значительно увеличивать. Еще больше разница между длиной ручек и расстоянии режущей части и оси вращения в кусачках (рис.), предназначенных для перекусывания проволоки.

Рычаги различного вида имеются у многих машин. Ручка швейной машины, педали или ручной тормоз велосипеда, педали автомобиля и трактора, клавиши пианино — все это примеры рычагов, используемых в данных машинах и инструментах.

Примеры применения рычагов — это рукоятки тисков и верстаков, рычаг сверлильного станка и т. д.

На принципе рычага основано действие и рычажных весов (рис.). Учебные весы, изображенные на рисунке 48 (с. 42), действуют как равноплечий рычаг. В десятичных весах плечо, к которому подвешена чашка с гирями, в 10 раз длиннее плеча, несущего груз. Это значительно упрощает взвешивание больших грузов. Взвешивая груз на десятичных весах, следует умножить массу гирь на 10.

Устройство весов для взвешивания грузовых вагонов автомобилей также основано на правиле рычага.

Рычаги встречаются также в разных частях тела животных и человека. Это, например, руки, ноги, челюсти. Много рычагов можно найти в теле насекомых (прочитав книгу про насекомых и строение их тела), птиц, в строении растений.

Применение закона равновесия рычага к блоку.

Блок представляет собой колесо с желобом, укрепленное в обойме. По желобу блока пропускается веревка, трос или цепь.

Неподвижным блоком называется такой блок, ось которого закреплена, и при подъеме грузов не поднимается и не опускается (рис).

Неподвижный блок можно рассматривать как равноплечий рычаг, у которого плечи сил равны радиусу колеса (рис): ОА = ОВ = r. Такой блок не дает выигрыша в силе. (F1 = F2), но позволяет менять направление действие силы.
Подвижный блок — это блок. ось которого поднимается и опускается вместе с грузом (рис.). На рисунке показан соответствующий ему рычаг: О — точка опоры рычага, ОА — плечо силы Р и ОВ — плечо силы F. Так как плечо ОВ в 2 раза больше плеча ОА, то сила F в 2 раза меньше силы Р:

F = P/2 .

Таким образом, подвижный блок дает выигрыш в силе в 2 раза.

Это можно доказать и пользуясь понятием момента силы. При равновесии блока моменты сил F и Р равны друг другу. Но плечо силы F в 2 раза больше плеча силы Р, а, значит, сама сила F в 2 раза меньше силы Р.

Обычно на практике применяют комбинацию неподвижного блока с подвижным (рис.). Неподвижный блок применяется только для удобства. Он не дает выигрыша в силе, но изменяет направление действия силы. Например, позволяет поднимать груз, стоя на земле. Это пригождается многим людям или рабочим. Тем не менее, он даёт выигрыш в силе в 2 раза больше обычного!

Равенство работ при использовании простых механизмов. «Золотое правило» механики.

Рассмотренные нами простые механизмы применяются при совершении работы в тех случаях, когда надо действием одной силы уравновесить другую силу.

Естественно, возникает вопрос: давая выигрыш в силе или пути, не дают ли простые механизмы выигрыша в работе? Ответ на поставленный вопрос можно получить из опыта.

Уравновесив на рычаге две какие-нибудь разные по модулю силы F1 и F2 (рис.), приводим рычаг в движение. При этом оказывается, что за одно и то же время точка приложения меньшей силы F2 проходит больший путь s2 , а точка приложения большей силы F1 — меньший путь s1. Измерив эти пути и модули сил, находим, что пути, пройденные точками приложения сил на рычаге, обратно пропорциональны силам:

s1 / s2 = F2 / F1.

Таким образом, действуя на длинное плечо рычага, мы выигрываем в силе, но при этом во столько же раз проигрываем в пути.

Произведение силы F на путь s есть работа. Наши опыты показывают, что работы, совершаемые силами, приложенными к рычагу, равны друг другу:

F1 s1 = F2 s2, то есть А1 = А2.

Итак, при использовании рычага выигрыша в работе не получится.

Пользуясь рычагом, мы можем выиграть или в силе, или в расстоянии. Действуя же силой на короткое плечо рычага, мы выигрываем в расстоянии, но во столько же раз проигрываем в силе.

Существует легенда, что Архимед, восхищенный открытием правила рычага, воскликнул: «Дайте мне точку опоры, и я переверну Землю!».

Конечно, Архимед не мог бы справиться с такой задачей, если бы даже ему и дали бы точку опоры (которая должна была бы быть вне Земли) и рычаг нужной длины.

Для подъема земли всего на 1 см длинное плечо рычага должно было бы описать дугу огромной длины. Для перемещения длинного конца рычага по этому пути, например, со скоростью 1 м/с, потребовались бы миллионы лет!

Не дает выигрыша в работе и неподвижный блок, в чем легко убедиться на опыте (см. рис.). Пути, проходимые точками приложения сил F и F, одинаковы, одинаковы и силы, а значит, одинаковы и работы.

Можно измерить и сравнить между собой работы, совершаемые с помощью подвижного блока. Чтобы при помощи подвижного блока поднять груз на высоту h, необходимо конец веревки, к которому прикреплен динамометр, как показывает опыт (рис.), переместить на высоту 2h.

Таким образом, получая выигрыш в силе в 2 раза, проигрывают в 2 раза в пути, следовательно, и подвижный блок, на дает выигрыша в работе.

Многовековая практика показала, что ни один из механизмов не дает выигрыш в работе. Применяют же различные механизмы для того, чтобы в зависимости от условий работы выиграть в силе или в пути.

Уже древним ученым было известно правило, применимое ко всем механизмом: во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии. Это правило назвали «золотым правилом» механики.

Коэффициент полезного действия механизма.

Рассматривая устройство и действие рычага, мы не учитывали трение, а также вес рычага. в этих идеальных условиях работа, совершенная приложенной силой (эту работу мы будем называть полной), равна полезной работе по подъему грузов или преодоления какого — либо сопротивления.

На практике совершенная с помощью механизма полная работа всегда несколько больше полезной работы.

Часть работы совершается против силы трения в механизме и по перемещению его отдельных частей. Так, применяя подвижный блок, приходится дополнительно совершать работу по подъему самого блока, веревки и по определению силы трения в оси блока.

Какой мы механизм мы не взяли, полезная работа, совершенная с его помощью, всегда составляет лишь часть полной работы. Значит, обозначив полезную работу буквой Ап, полную(затраченную) работу буквой Аз, можно записать:

Ап < Аз или Ап / Аз < 1.

Отношение полезной работы к полной работе называется коэффициентом полезного действия механизма.

Сокращенно коэффициент полезного действия обозначается КПД.

КПД = Ап / Аз.

КПД обычно выражается в процентах и обозначается греческой буквой η, читается он как «эта»:

η = Ап / Аз · 100 %.

Пример: На коротком плече рычага подвешен груз массой 100 кг. Для его подъема к длинному плечу приложена сила 250 Н. Груз подняли на высоту h1 = 0,08 м, при этом точка приложения движущей силы опустилась на высоту h2 = 0,4 м. Найти КПД рычага.

Запишем условие задачи и решим ее.

Дано:

m = 240

g = 9,8 Н/кг

F = 250 Н

h1 = 0.08 м

h2 =0,04 м

Решение:

η = Ап / Аз · 100 %.

Полная (затраченная) работа Аз = Fh2.

Полезная работа Ап = Рh1

Р = gm.

Р = 9,8 · 100 кг ≈ 1000 Н.

Ап = 1000 Н · 0,08 = 80 Дж.

Аз = 250 Н · 0,4 м = 100 Дж.

η = 80 Дж/100 Дж · 100 % = 80 %.

η — ?

Ответ : η = 80 %.

Но «золотое правило» выполняется и в этом случае. Часть полезной работы — 20 % ее-расходуется на преодоление трения в оси рычага и сопротивления воздуха, а также на движение самого рычага.

КПД любого механизма всегда меньше 100 %. Конструируя механизмы, люди стремятся увеличить их КПД. Для этого уменьшаются трение в осях механизмов и их вес.

Энергия.

На заводах и фабриках, станки и машины приводятся в движения с помощью электродвигателей, которые расходуют при этом электрическую энергию (отсюда и название).

Автомобили и самолеты тепловозы и теплоходы, работают, расходуя энергию сгорающего топлива, гидротурбины — энергию падающей с высоты воды. Да и сами мы, чтобы жить, учиться и работать, возобновляем свой запас энергии при помощи пищи, которую мы едим.

Слово «энергия» употребляется нередко и в быту. Так, например, людей, которые могут быстро выполнять большую работу, мы называем энергичными, обладающими большой энергией. Что же такое энергия? Чтобы ответить на этот вопрос, рассмотрим примеры.

Сжатая пружина (рис), распрямляясь, совершить работу, поднять на высоту груз, или заставить двигаться тележку.

Поднятый над землей неподвижный груз не совершает работы, но если этот груз упадет, он может совершить работу (например, может забить в землю сваю).

Способностью совершить работу обладает и всякое движущееся тело. Так, скатившийся с наклонной плоскости стальной шарик А (рис), ударившись о деревянный брусок В, передвигает его на некоторое расстояние. При этом совершается работа.

Если тело или несколько взаимодействующих между собой тел (система тел) могут совершить работу, говорится, что они обладают энергией.

Энергия — физическая величина, показывающая, какую работу может совершить тело (или несколько тел). Энергия выражается в системе СИ в тех же единицах, что и работу, то есть в джоулях.

Чем большую работу может совершить тело, тем большей энергией оно обладает.

При совершении работы энергия тел изменяется. Совершенная работа равна изменению энергии.

Потенциальная и кинетическая энергия.

Потенциальной (от лат. потенция — возможность) энергией называется энергия, которая определяется взаимным положением взаимодействующих тел и частей одного и того же тела.

Потенциальной энергией, например, обладает тело, поднятое относительно поверхности Земли, потому что энергия зависит от взаимного положения его и Земли. и их взаимного притяжения. Если считать потенциальную энергию тела, лежащего на Земле, равной нулю, то потенциальная энергия тела, поднятого на некоторую высоту, определится работой, которую совершит сила тяжести при падении тела на Землю. Обозначим потенциальную энергию тела Еп, поскольку Е = А , а работа, как мы знаем, равна произведению силы на путь, то

А = Fh,

где F — сила тяжести.

Значит, и потенциальная энергия Еп равна:

Е = Fh, или Е = gmh,

где g — ускорение свободного падения, m — масса тела, h — высота, на которую поднято тело.

Огромной потенциальной энергией обладает вода в реках, удерживаемая плотинами. Падая вниз, вода совершает работу, приводя в движение мощные турбины электростанций.

Потенциальную энергию молота копра (рис.) используют в строительстве для совершению работы по забиванию свай.

Открывая дверь с пружиной, совершается работа по растяжению (или сжатию) пружины. За счет приобретенной энергии пружина, сокращаясь (или распрямляясь), совершает работу, закрывая дверь.

Энергию сжатых и раскрученных пружин используют, например, в ручных часах, разнообразных заводных игрушках и пр.

Потенциальной энергией обладает всякое упругое деформированное тело. Потенциальную энергию сжатого газа используют в работе тепловых двигателей, в отбойных молотках, которые широко применяют в горной промышленности, при строительстве дорог, выемке твердого грунта и т. д.

Энергия, которой обладает тело вследствие своего движения, называется кинетической (от греч. кинема — движение) энергией.

Кинетическая энергия тела обозначается буквой Ек .

Движущаяся вода, приводя во вращение турбины гидроэлектростанций, расходует свою кинетическую энергию и совершает работу. Кинетической энергией обладает и движущийся воздух — ветер.

От чего зависит кинетическая энергия? Обратимся к опыту (см. рис.). Если скатывать шарик А с разных высот, то можно заметить, что чем с большей высоты скатывается шарик, тем больше его скорость и тем дальше он продвигает брусок, то есть совершает большую работу. Значит, кинетическая энергия тела зависит от его скорости.

За счет скорости большой кинетической энергией обладает летящая пуля.

Кинетическая энергия тела зависит и от его массы. Еще раз проделаем наш опыт, но будем скатывать с наклонной плоскости другой шарик — большей массы. Брусок В передвинется дальше, то есть будет совершена бóльшая работа. Значит, и кинетическая энергия второго шарика, больше, чем первого.

Чем больше масса тела и скорость, с которой он движется, тем больше его кинетическая энергия.

Для того чтобы определить кинетическую энергию тела, применяется формула:

Ек = mv² /2,

где m — масса тела, v — скорость движения тела.

Кинетическую энергию тел используют в технике. Удерживаемая плотиной вода обладает, как было уже сказано, большой потенциальной энергией. При падении с плотины вода движется и имеет такую же большую кинетическую энергию. Она приводит в движение турбину, соединенную с генератором электрического тока. За счет кинетической энергии воды вырабатывается электрическая энергия.

Энергия движущейся воды имеет большое значение в народном хозяйстве. Эту энергию используют с помощью мощных гидроэлектростанций.

Энергия падающей воды является экологически чистым источником энергии в отличие от энергии топлива.

Все тела в природе относительно условного нулевого значения обладают либо потенциальной, либо кинетической энергией, а иногда той и другой вместе. Например, летящий самолет обладает относительно Земли и кинетической и потенциальной энергией.

Мы познакомились с двумя видами механической энергии. Иные виды энергии (электрическая, внутренняя и др.) будут рассмотрены в других разделах курса физики.

Превращение одного вида механической энергии в другой.

В природе, технике и быту можно часто наблюдать превращение одного вида механической энергии в другой: потенциальную в кинетическую и кинетическую в потенциальную. Например, при падении воды с плотины ее потенциальная энергия превращается в кинетическую. В качающемся маятнике периодически эти виды энергии переходят друг в друга.

Явление превращения одного вида механической энергии в другой очень удобно наблюдать на приборе, изображенном на рисунке. Накручивая на ось нить, поднимают диск прибора. Диск, поднятый вверх, обладает некоторой потенциальной энергией. Если его отпустить, то он, вращаясь, начнет падать. По мере падения потенциальная энергия диска уменьшается, но вместе с тем возрастает его кинетическая энергия. В конце падения диск обладает таким запасом кинетической энергии, что может опять подняться почти до прежней высоты. (Часть энергии расходуется на работу против силы трения, поэтому диск не достигает первоначальной высоты.) Поднявшись вверх, диск снова падает, а затем снова поднимается. В этом опыте при движении диска вниз его потенциальная энергия превращается в кинетическую, а при движении вверх кинетическая превращается в потенциальную.

Превращение энергии из одного вида в другой происходит также при ударе двух каких-нибудь упругих тел, например резинового мяча о пол или стального шарика о стальную плиту.

Если поднять над стальной плитой стальной шарик (рис) и выпустить его из рук, он будет падать. По мере падения шарика его потенциальная энергия убывает, а кинетическая растет, так как увеличивается скорость движения шарика. При ударе шарика о плиту произойдет сжатие как шарика, так и плиты. Кинетическая энергия, которой шарик обладал, превратится в потенциальную энергию сжатой плиты и сжатого шарика. Затем благодаря действию упругих сил плита и шарик, примут свою первоначальную форму. Шарик отскочит от плиты, а их потенциальная энергия вновь превратится в кинетическую энергию шарика: шарик отскочит вверх со скоростью, почти равной скорости, которой обладал в момент удара о плиту. При подъеме вверх скорость шарика, а значит, и его кинетическая энергия уменьшаются, потенциальная энергия увеличивается. отскочив от плиты, шарик поднимается почти до той же высоты, с которой начал падать. В верхней точке подъема вся его кинетическая энергия вновь превратится в потенциальную.

Явления природы обычно сопровождается превращением одного вида энергии в другой.

Энергия может и передаваться от одного тела к другому. Так, например, при стрельбе из лука потенциальная энергия натянутой тетивы переходит в кинетическую энергию летящей стрелы.