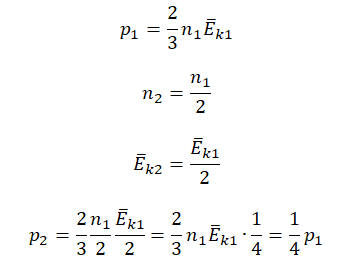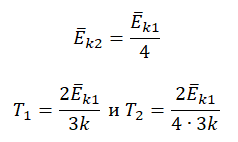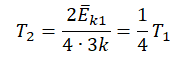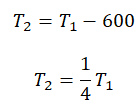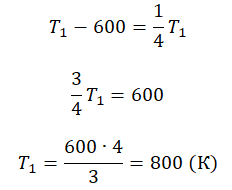Как найти энергию газа зная температуру

На этой странице вы можете рассчитать внутреннюю энергию идеального газа с помощью калькулятора онлайн или самостоятельно по формулам.

Формула внутренней энергии идеального газа через массу, молярную массу и температуру

Формула внутренней энергии идеального газа через давление и объем

Формула внутренней энергии идеального газа через количество вещества и температуру

Формула внутренней энергии идеального газа через степени свободы

Количество степеней свободы молекулы идеального газа

• для одноатомного газа (гелий, неон, аргон, криптон, ксенон, радон, оганесон и т. д.) i=3;
• для двухатомного газа (водород, азот, кислород, фтор, хлор и т. д.) i=5;
• для трехатомного газа i=6;
• для многоатомного (>3) газа i=6;

1. Внутренняя энергия газа

Из курса физики основной школы вы знаете, что сумму кинетической энергии хаотического движения частиц и потенциальной энергии их взаимодействия называют внутренней энергией.

Внутренняя энергия U данной массы одноатомного идеального газа равна произведению средней кинетической энергии 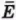одной молекулы на число молекул N:

U = 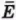N.

? 1. Объясните, почему внутренняя энергия U данной массы одноатомного идеального газа выражается формулой

Итак, внутренняя энергия идеального газа определяется только его абсолютной температурой и числом молекул в нем.

? 2. Объем одного моля газа при температуре 20 ºС и нормальном атмосферном давлении составляет 24 л.
а) Чему равна внутренняя энергия этого газа, если он одноатомный и его можно считать идеальным?
б) На какую высоту можно было бы забросить мяч массой 365 г, если бы можно было сообщить ему такую кинетическую энергию и пренебречь сопротивлением воздуха?

Выполнив это задание, вы сможете представить, как велика внутренняя энергия тела. Объясняется это тем, что скорость хаотического движения молекул в десятки и сотни раз превышает скорости движения окружающих нас тел. А кинетическая энергия пропорциональна квадрату скорости. Поэтому при увеличении скорости в 10 раз кинетическая энергия увеличивается в 100 раз, а при увеличении скорости в 100 раз кинетическая энергия увеличивается в 10 000 раз.

Внутреннюю энергию идеального одноатомного газа можно выразить также через его давление p и объем V.

? 3. Объясните, почему внутренняя энергия U данной массы одноатомного идеального газа выражается формулой

U = (3/2)pV.     (2)

Подсказка. Воспользуйтесь формулой (1) и уравнением состояния идеального газа.

? 4. Из формулы (1) следует, что внутренняя энергия одного моля газа зависит только от его абсолютной температуры и количества вещества (числа молекул). А из формулы (2) следует, что она зависит от давления и объема, но зато не зависит от количества вещества. Объясните, почему тут нет противоречия.

? 5. Ширина класса 5 м, длина 10 м, а высота – 4 м. Температура воздуха 20 ºС, давление равно нормальному атмосферному давлению.
а) Чему была бы равна внутренняя энергия газа, заполняющего класс, если бы он был одноатомным? (Воздух состоит в основном из двухатомных молекул. Как показывает расчет, выходящий за рамки нашего курса, внутренняя энергия двухатомного газа при тех же макроскопических параметрах в 5/3 раза больше, чем внутренняя энергия одноатомного газа.)
б) На какую высоту можно было бы поднять автомобиль массой 1 т, затратив такую энергию?
в) Есть ли в условии лишние данные?

Результаты выполнения этого задания раскроют, какая огромная энергия «окружает» каждого из нас! А ведь мы ее практически не замечаем, считая воздух «пустотой».

Большую внутреннюю энергию имеют, конечно, и другие тела. Например, внутренняя энергия литра кипятка больше внутренней энергии того же литра воды при комнатной температуре на величину, равную работе, которую надо совершить для того, чтобы поднять легковой автомобиль на двенадцать этажей!

При изучении тепловых явлений мы учитываем только кинетическую энергию хаотического движения молекул и потенциальную энергию их взаимодействия. А ведь есть еще и во много раз большая энергия взаимодействия частиц в атомных ядрах. Вы знаете о ней из курса физики основной школы. К ядерной физике мы вернемся в 11-м классе.

Соотношение между различными видами энергии, которыми обладает данное тело, схематически представлено на рисунке 42.1. Мы видим, что непосредственно наблюдаемая механическая энергия составляет лишь очень малую долю всей энергии тела. Соблюсти масштаб на этом рисунке невозможно, потому что тепловая внутренняя энергия в тысячи раз больше механической, а ядерная – в миллионы раз больше тепловой.

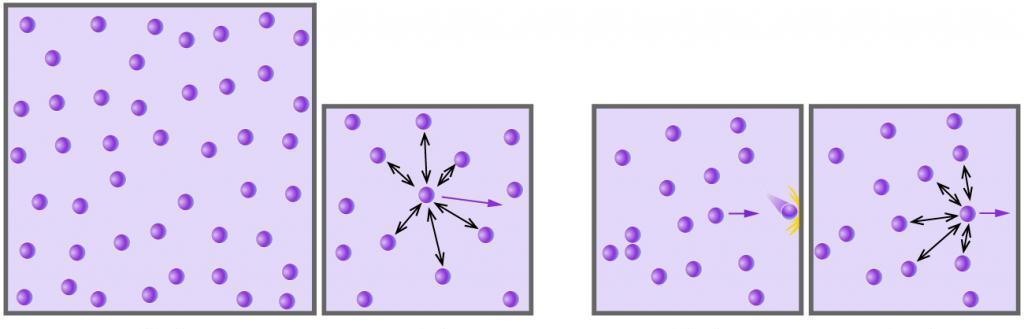
Два способа изменения внутренней энергии

Из курса физики основной школы вы знаете, что внутреннюю энергию тела можно изменить двумя способами:

• совершая работу над телом – например, сжимая газ (рис. 42.2, а);
• посредством теплопередачи, то есть без совершения работы, – например, при контакте с более горячим телом (рис. 42.2, б). (Теплопередачу называют иногда также теплообменом.)

Напомним, что меру изменения внутренней энергии при теплопередаче называют количеством теплоты и обозначают Q. Количество теплоты измеряют в джоулях.

Как мы знаем, внутренняя энергия данной массы идеального газа определяется только его температурой и числом молекул. Поэтому при постоянном числе молекул изменить внутреннюю энергию идеального газа можно только изменив его температуру.

Например, при сжатии газа в теплоизолированном сосуде газ нагревается вследствие того, что над ним производят работу. Нагревание газа может быть при атом весьма заметным.

Поставим опыт

Поместим кусочек сухой ваты в толстостенный прозрачный цилиндр и быстро (резким толчком) вдвинем в цилиндр поршень (рис. 42.3).

Воздух в цилиндре нагреется так сильно, что вата воспламенится.

Нагревание газа при сжатии используют в дизельных двигателях: при сжатии горючая смесь в цилиндре нагревается настолько, что воспламеняется без искры.

Газовый процесс, который происходит в теплоизолированном сосуде, то есть без теплопередачи, называют адиабатным. Адиабатным можно считать также процесс, когда тепло- передачей можно пренебречь: например, если процесс происходит за время, в течение которого не успевает произойти теплообмен с окружающей средой.

При адиабатном расширении газ охлаждается. По этой причине, например, образуются облака. Поднимающийся влажный воздух попадает в более разреженные слои атмосферы, расширяется и вследствие этого охлаждается. Как мы увидим далее, при охлаждении ниже определенной температуры (точки росы) содержащийся в воздухе водяной пар конденсируется: образуются капельки тумана, из которого и состоят облака.

Увеличить или уменьшить температуру газа можно, конечно, и посредством теплопередачи. Например, сосуд с газом можно поместить над огнем, в кипящую воду или в морозильную камеру.

? 6. Изменяется ли, н если да, то как внутренняя энергия данной массы идеального газа:
а) при изотермическом расширении? сжатии?
б) при изобарном расширении? сжатии?
в) при изохорном охлаждении? нагревании?
г) при адиабатном сжатии? расширении?

2. Первый закон термодинамики

Итак, внутренняя энергия газа U может изменяться как вследствие того, что ему сообщают количество теплоты Q, так и потому, что внешние силы совершают работу A над газом.

Согласно закону сохранения энергии

изменение внутренней энергии газа ∆U равно сумме количества теплоты Q, переданного газу, и работы A, совершенной над газом:

∆U = Q + A.     (3)

Закон сохранения энергии применительно к тепловым явлениям называют первым законом термодинамики. (Термодинамикой называют раздел физики, изучающий общие законы тепловых явлений.)

Как Q, так и A могут быть положительными, отрицательными или равными нулю. Если газ сжимают, то A > 0, а если он расширяется, то A < 0. Если объем газа не изменяется, то A = 0. Если газу передают некоторое количество теплоты, то Q > 0, а если газ отдает некоторое количество теплоты, то Q < 0.

В практических расчетах и при решении многих задач часто используют другую формулировку первого закона термодинамики. Дело в том, что при рассмотрении тепловых двигателей главный интерес представляет работа, совершенная самим газом (то есть силой давления, действующей со стороны газа на поршень; при расширении газа работа газа положительна).

Обозначим работу газа A_г. Она связана с работой A, совершенной внешними силами над газом, соотношением

A_г = –A.

При сжатии газа A > 0, A_г < 0; а при расширении газа A < 0, A_г > 0.

Используя понятие работы газа, первый закон термодинамики формулируют так:

количество теплоты, переданное газу, равно сумме изменения внутренней энергии газа и работы, совершенной газом:

Q = ∆U + A_г.     (4)

Чтобы использовать соотношения (3) и (4) на практике, надо уметь находить выражения для изменения внутренней энергии газа и работы газа (или работы внешних сил).

Как найти изменение внутренней энергии газа?

Для одноатомного идеального газа внутренняя энергия выражается формулой (1), поэтому для изменения ∆U внутренней энергии получаем:

∆U = (3/2)νR∆T.     (5)

Здесь ∆T = T₂ – T₁, ∆U = U₂ – U₁, а индексами 1 и 2 обозначены соответственно начальное и конечное состояния газа.

? 7. Начальная температура пяти молей гелия 100 ºС. Газ нагрели на 50 ºС.
а) Насколько увеличилась внутренняя энергия газа?
б) Есть ли в условии лишние данные?

Изменение внутренней энергии одноатомного идеального газа можно найти и с помощью формулы (2):

∆U = (3/2)∆(pV).     (6)

Здесь ∆(pV) – изменение произведения давления на объем. Например, при переходе газа из состояния 1 в состояние 2

∆(pV) = p₂V₂ – p₁V₁.     (7)

? 8. Чему равно изменение внутренней энергии одного моля одноатомного идеального газа:
а) при изобарном расширении, если давление газа равно p₀, а объем газа увеличился от V₀ до 3V₀?
б) при изохорном охлаждении, если объем газа равен V₀, а давление газа уменьшилось от p₀ до 0,5p₀?
в) в процессе, в котором начальные давление и объем газа равны p₀ и V₀, а конечные равны 2p₀ и 3V₀?
Есть ли в условии лишние данные?

Важным достоинством формулы (6) является то, что в нее не входят ни количество вещества в газе, ни его масса. Поэтому, например, если давление и объем газа остались неизменными, то не изменилась и внутренняя энергия газа, хотя при этом могла измениться его масса. Рассмотрим пример, в котором речь идет о воздухе, который состоит в основном из двух- атомных молекул. Их средняя кинетическая энергия при заданной температуре больше, чем у одноатомных молекул (двухатомные молекулы обладают еще кинетической энергией вращательного движения). Однако для выполнения следующего задания то, что воздух состоит из двухатомных молекул, несущественно.

? 9. До включения отопления температура воздуха в комнате объемом 60 м³ была равна 15 ºС. После включения отопления воздух нагрелся до 20 ºС. Давление воздуха постоянно и равно 10⁵ Па.
а) На сколько процентов увеличилась средняя кинетическая энергия молекул в воздухе?
б) Как изменилась внутренняя энергия воздуха в комнате?
в) На сколько процентов изменилась концентрация молекул воздуха?
г) Насколько изменилась масса воздуха в комнате?

Как найти совершенную газом работу?

Рассмотрим сначала изобарное расширение газа в цилиндре под поршнем (рис. 42.4). Газ давит на поршень с силой F = pS, где p – давление газа, S – площадь поршня.

Если поршень переместился на ∆x, то совершенная газом работа A_г = F * ∆x = pS * ∆x. Так как S * ∆x = ∆V, получаем, что при изобарном расшинерии работа газа выражается формулой

A_г = p * ∆V.     (8)

? 10. Используя рисунок 42.5, объясните, почему работа газа численно равна площади фигуры под графиком зависимости p(V).

Это свойство графика зависимости p(V) сохраняется и тогда, когда давление газа изменяется.

Пусть, например, график зависимости p(V) имеет вид, изображенный на рисунке 42.6. Процесс расширения газа мысленно разобьем на большое число этапов, в каждом из которых объем газа изменяется настолько мало, что его давление можно считать практически постоянным. Поскольку для каждого этапа работа газа численно равна площади под соответствующим участком графика, то и вся работа, совершенная газом при расширении, равна площади под всем графиком p(V).

? 11. Один моль идеального газа можно перевести из состояния 1 в состояние 2 многими способами. Рассмотрим процессы, которым соответствуют графики а и б (рис. 42.7).
а) В каком случае совершенная газом работа больше? Во сколько раз больше?
б) В каком случае изменение внутренней энергии газа больше? Во сколько раз больше?
в) В каком случае переданное газу количество теплоты больше? Во сколько раз больше?

На примере этого задания вы могли заметить, что изменение ∆U внутренней энергии данной массы идеального газа определяется только начальным и конечным состоянием газа.

Обусловлено это тем, что каждому состоянию данной массы газа (с определенными значениями p, V и T) соответствует одно определенное значение внутренней энергии, которое можно найти либо по формуле (1), либо по формуле (2).

А вот работа, совершенная газом при переходе из начального состояния в конечное, зависит от характера процесса, которым газ был переведен из начального состояния в конечное.

Действительно, работа газа численно равна площади под графиком зависимости p(V). А эта площадь зависит от того, какой вид имела функция p(V).

Если газ не расширяется, а сжимается (рис. 42.8), то внешние силы производят работу над газом. В таком случае говорят также, что газ производит отрицательную работу. Она численно равна взятой со знаком минус площади S под графиком зависимости p(V).

На том, что работа газа зависит от вида зависимости p(V), а не только от начального и конечного состояния, основан принцип действия тепловых двигателей (в следующем параграфе мы рассмотрим их подробнее).

В тепловых двигателях газ расширяется при высокой температуре. При атом давление газа велико, поэтому он совершает большую работу. А сжимают газ при более низкой температуре, когда давление газа меньше. Поэтому для того, чтобы вернуть газ в начальное состояние, внешние силы должны совершить меньшую работу.

Рассмотрим пример.

? 12. Газ совершает циклический процесс: переходит из состояния 1 в состояние 2 (рис. 42.9), а потом возвращается в состояние 1. При этом объем газа не должен быть меньше начального и больше конечного.

а) Какую максимально возможную работу может совершить газ при переходе 1–2, если давление газа не должно превышать 3p₀?
б) Какую минимально возможную работу должны совершить внешние силы при переходе 2–1, если давление газа не должно быть меньше p₀?
в) Насколько в этом случае работа газа при циклическом процессе больше работы внешних сил?

Применение первого закона термодинамики к изопроцессам и адиабатному процессу

? 13. Используя первый закон термодинамики, а также выражения для внутренней энергии и работы газа, объясните, почему:
а) при изохорном процессе A_г = 0, Q = ∆U, то есть сообщенное газу количество теплоты (напомним, что оно может быть как положительным, так и отрицательным) равно изменению внутренней энергии газа;
б) при изотермическом процессе ∆U = 0, Q = A_г, то есть сообщенное газу количество теплоты равно работе газа;
в) при изобарном процессе A_г ≠ 0, ∆U ≠ 0;
г) при адиабатном процессе Q = 0, A_г = –∆U, то есть при расширении газ совершает работу за счет уменьшения внутренней энергии, а при сжатии газа его внутренняя энергия увеличивается за счет работы внешних сил.
Подсказка. Если давление не изменяется, то ∆(pV) = p∆V.

Дополнительные вопросы и задания

14. На рисунках 42.10, а, б, в изображены графики трех процессов с данной массой одноатомного идеального газа. Чему равно изменение внутренней энергии газа для каждого из этих процессов при переходе 1–2?

15. При изобарном расширении данной массы одноатомного идеального газа его температура возросла от 0 ºС до 100 ºС. При этом газу было передано количество теплоты, равное 5 кДж.
а) Насколько изменилась внутренняя энергия газа?
б) Чему равно количество вещества в сосуде с газом?

Как найти внутреннюю энергию газа

Поскольку внутренняя энергия газа является суммой всех кинетических энергий его молекул, то измерить ее непосредственно, не представляется возможным. Поэтому для ее расчета воспользуйтесь специальными формулами, которые выражают эту величину через такие макроскопические параметры как температура, объем и давление.

Вам понадобится

• Термометр, манометр, герметичный баллон, весы

Инструкция

Рассчитать внутреннюю энергию газа достоверно можно только тогда, когда его состояние близко к идеальному. Тогда можно пренебречь потенциальной энергией взаимодействия его молекул. Практически все газы при комнатной температуре имеют свойства, схожие с идеальным газом.

Сначала определите химическую формулу газа, внутренняя энергия которого вычисляется. Измерьте массу газа с помощью весов в граммах. Для этого взвесьте сначала пустой баллон, а затем заполненный газом, разность их масс будет равна массе газа. С помощью таблицы Менделеева найдите его молярную массу в граммах на моль.
С помощью термометра измерьте температуру газа. Если шкала термометра проградуирована в градусах Цельсия, переведите ее в Кельвины. Для этого к полученному значению прибавьте 273.
Рассчитайте внутреннюю энергию газа. Для этого массу газа поделите на молярную массу. Получившийся результат умножьте на значение температуры и число 8,31 (универсальную газовую постоянную), затем умножьте на число степеней вольности молекулы газа и поделите на 2 (U=m/M•(R•T)•i/2). Количество степеней вольности для одноатомного газа составляет 3, для двухатомной молекулы 5, а для многоатомной молекулы 6. Это связанно с особенностями движения каждой из молекул.

Если нет возможности измерить температуру газа, но и известны его объем и давление, рассчитайте его внутреннюю энергию через эти величины. Для этого измерьте массу газа, его молярную массу и узнайте химическую формулу. Выразите объем в м³, а давление в Паскалях. Рассчитайте внутреннюю энергию газа, перемножив число степеней вольности молекулы газа, значения его массы, давления и объема, а результат поделите на 2 и значение молярной массы газа (U = i•m•P•V/(2•M)).
В общем случае изменение внутренней энергии газа равно разности полученной им извне теплоты и выполненной работы ΔU=Q-A.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Определение

Идеальный газ — газ, удовлетворяющий трем условиям:

• Молекулы — материальные точки.
• Потенциальная энергия взаимодействия молекул пренебрежительно мала.
• Столкновения между молекулами являются абсолютно упругими.

Реальный газ с малой плотностью можно считать идеальным газом.

Измерение температуры

Температуру можно измерять по шкале Цельсия и шкале Кельвина. По шкале Цельсия за нуль принимается температура, при которой происходит плавление льда. По шкале Кельвина за нуль принимается абсолютный нуль — температура, при котором давление идеального газа равно нулю, и его объем тоже равен нулю.

Обозначение температуры

1. По шкале Цельсия — t. Единица измерения — 1 градус Цельсия (1 ^oC).
2. По шкале Кельвина — T. Единица измерения — 1 Кельвин (1 К).

Цена деления обеих шкал составляет 1 градус. Поэтому изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах:

∆t = ∆T

При решении задач в МКТ используют значения температуры по шкале Кельвина. Если в условиях задачи температура задается в градусах Цельсия, нужно их перевести в Кельвины. Это можно сделать по формуле:

T = t + 273

Если особо важна точность, следует использовать более точную формулу:

T = t + 273,15

Пример №1. Температура воды равна ^oC. Определить температуру воды в Кельвинах.

T = t + 273 = 2 + 273 = 275 (К)

Основное уравнение МКТ идеального газа

Давление идеального газа обусловлено беспорядочным движением молекул, которые сталкиваются друг с другом и со стенками сосуда. Основное уравнение МКТ идеального газа связывает давление и другие макропараметры (объем, температуру и массу) с микропараметрами (массой молекул, скоростью молекул и кинетической энергией).

Основное уравнение МКТ

Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

p=23n−Ek

p — давление идеального газа, n — концентрация молекул газа, −Ek — средняя кинетическая энергия поступательного движения молекул.

Выражая физические величины друг через друга, можно получить следующие способы записи основного уравнения МКТ идеального газа:

p=13m0n−v2	m0— масса одной молекулы газа; n — концентрация молекул газа; −v2 — среднее значение квадрата скорости молекул газа. Среднее значение квадрата скорости не следует путать со среднеквадратичной скоростью v, которая равна корню из среднего значения квадрата скорости: v=√−v2
p=13ρ−v2	ρ — плотность газа
p=nkT	k — постоянная Больцмана (k = 1,38∙10–3 Дж/кг) T — температура газа по шкале Кельвина

Пример №2. Во сколько раз уменьшится давление идеального одноатомного газа, если среднюю кинетическую энергию теплового движения молекул и концентрацию уменьшить в 2 раза?

Согласно основному уравнению МКТ идеального газа, давление прямо пропорционально произведению средней кинетической энергии теплового движения молекул и концентрации его молекул. Следовательно, если каждая из этих величин уменьшится в 2 раза, то давление уменьшится в 4 раза:

Следствия из основного уравнения МКТ идеального газа

Через основное уравнение МКТ идеального газа можно выразить скорость движения молекул (частиц газа):

v=√3kTm0=√3RTM

R — универсальная газовая постоянная, равная произведения постоянной Авогадро на постоянную Больцмана:

R=NAk=8,31 Дж/К·моль

Температура — мера кинетической энергии молекул идеального газа:

−Ek=32kT

T=2−Ek3k

Полная энергия поступательного движения молекул газа определяется формулой:

E=N−Ek

Пример №3. При уменьшении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул неона уменьшилась в 4 раза. Какова начальная температура газа?

Запишем формулу, связывающую температуру со средней кинетической энергией теплового движения молекул, для обоих случаев, с учетом что:

Следовательно:

Составим систему уравнений:

Отсюда:

Задание EF19012

На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.

---

Алгоритм решения

1.Указать, в каких координатах построен график.

2.На основании основного уравнения МКТ идеального газа и уравнения Менделеева — Клапейрона выяснить, как меняются указанные физические величины во время процессов 1–2 и 2–3.

Решение

График построен в координатах (V;E_k). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:

T=2−Ek3

Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.

Запишем уравнение Менделеева — Клапейрона:

pV=νRT

Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:

νR=p1V1T1=p2V2T2

Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.

Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.

Ответ:

• Участок 1–2 — изобарный процесс. Температура увеличивается, давление постоянно.

• Участок 2–3 — изотермический процесс. Температура постоянно, давление увеличивается.

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17560

Первоначальное давление газа в сосуде равнялось р₁. Увеличив объём сосуда, концентрацию молекул газа уменьшили в 3 раза, и одновременно в 2 раза увеличили среднюю энергию хаотичного движения молекул газа. В результате этого давление р₂ газа в сосуде стало равным

Ответ:

а) 13p1

б) 2p1

в) 23p1

г) 43p1

---

Алгоритм решения

1.Записать исходные данные.

2.Записать основное уравнение МКТ идеального газа.

3.Составить уравнения для состояний 1 и 2.

4.Выразить искомую величину.

Решение

Исходные данные:

• Начальное давление: p₀.

• Начальная концентрация молекул: n₁ = 3n.

• Конечная концентрация молекул: n₂ = n.

• Начальная средняя энергия хаотичного движения молекул: E_k1 = E_k.

• Конечная средняя энергия хаотичного движения молекул: E_k2 = 2E_k.

Основное уравнение МКТ:

p=23n−Ek

Составим уравнения для начального и конечного состояний:

p1=23n1−Ek1=233n−Ek=2n−Ek

p2=23n2−Ek2=23n2−Ek=43n−Ek

Отсюда:

n−Ek=p12=3p24

p2=4p16=23p1

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18416

Цилиндрический сосуд разделён неподвижной теплоизолирующей перегородкой. В одной части сосуда находится кислород, в другой – водород, концентрации газов одинаковы. Давление кислорода в 2 раза больше давления водорода. Чему равно отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода?

---

Алгоритм решения

1.Записать исходные данные.

2.Записать основное уравнение МКТ идеального газа.

3.Составить уравнения для обоих газов.

4.Найти отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода.

Решение

Анализируя условия задачи, можно выделить следующие данные:

• Концентрации кислорода и водорода в сосуде равны. Следовательно, n₁ = n₂ = n.

• Давление кислорода вдвое выше давления водорода. Следовательно, p₁ = 2p, а p₂ = p.

Запишем основное уравнение идеального газа:

p=23n−Ek

Применим его для обоих газов и получим:

p1=23n1−Ek1 или 2p=23n−Ek1 

p2=23n2−Ek2 или p=23n−Ek2 

Выразим среднюю кинетическую энергию молекул газа из каждого уравнения:

−Ek1=3pn

−Ek2=3p2n

Поделим уравнения друг на друга и получим:

−Ek1−Ek2=3pn·2n3p=2

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18824

В одном сосуде находится аргон, а в другом – неон. Средние кинетические энергии теплового движения молекул газов одинаковы. Давление аргона в 2 раза больше давления неона. Чему равно отношение концентрации молекул аргона к концентрации молекул неона?

---

Алгоритм решения

1.Записать исходные данные.

2.Записать основное уравнение МКТ идеального газа.

3.Составить уравнения для обоих газов.

4.Найти отношение концентрации молекул аргона к концентрации молекул неона.

Решение

Анализируя условия задачи, можно выделить следующие данные:

• Средние кинетические энергии теплового движения молекул газов одинаковы. Следовательно, −Ek1=−Ek2=−Ek.

• Давление аргона в 2 раза больше давления неона. Следовательно, p₁ = 2p, а p₂ = p.

Запишем основное уравнение идеального газа:

p=23n−Ek

Применим его для обоих газов и получим:

p1=23n1−Ek1 или 2p=23n1−Ek 

p2=23n2−Ek2 или p=23n2−Ek 

Выразим концентрации молекул газа из каждого уравнения:

n1=3p−Ek

n2=3p2−Ek

Поделим уравнения друг на друга и получим:

n1n2=3p−Ek·2−Ek3p=2

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 10.8k

Изучая поведение газов в физике, часто возникают задачи на определение запасенной в них энергии, которую теоретически можно использовать для совершения некоторой полезной работы. В данной статье рассмотрим вопрос, по каким формулам внутренняя энергия идеального газа может быть рассчитана.

Понятие о газе идеальном

Четкое понимание концепции идеального газа важно при решении задач с системами, находящимися в этом агрегатном состоянии. Любой газ принимает форму и объем сосуда, в который его помещают, однако, не всякий газ является идеальным. Например, воздух можно считать смесью идеальных газов, в то же время водяной пар не является таковым. В чем же заключается принципиальная разница между реальными газами и их идеальной моделью?

Вам будет интересно:«Заклание» – это про необходимую жертву

Ответом на поставленный вопрос будут две следующие особенности:

• соотношение между кинетической и потенциальной энергией молекул и атомов, составляющих газ;
• соотношение между линейными размерами частиц газа и средним расстоянием между ними.

Газ считается идеальным только в том случае, когда средняя кинетическая энергия его частиц несоизмеримо больше энергии связи между ними. Разница между этими энергиями такова, что можно считать, что взаимодействие между частицами полностью отсутствует. Также для идеального газа характерно отсутствие размеров у его частиц, вернее эти размеры можно не учитывать, поскольку они намного меньше средних межчастичных расстояний.

Вам будет интересно:Московская лингвистическая школа: общая характеристика, основатель, представители

Хорошими эмпирическими критериями, позволяющими определить идеальность газовой системы, являются такие ее термодинамические характеристики, как температура и давление. Если первая больше 300 К, и второе меньше 1 атмосферы, то любой газ может полагаться идеальным.

Что это внутренняя энергия газа?

Прежде чем записать формулу внутренней энергии газа идеального, необходимо познакомится с этой характеристикой ближе.

В термодинамике внутреннюю энергию, как правило, обозначают латинской буквой U. Определяется в общем случае она по следующей формуле:

U = H – P*V

Где H – энтальпия системы, P и V – давление и объем.

По своему физическому смыслу внутренняя энергия состоит из двух составляющих: кинетической и потенциальной. Первая связана с различного рода движением частиц системы, а вторая – с силовым взаимодействием между ними. Если применить это определение к концепции газа идеального, у которого отсутствует потенциальная энергия, то величина U при любом состоянии системы будет точно равна его кинетической энергии, то есть:

U = Ek.

Вывод формулы внутренней энергии

Выше мы установили, что для ее определения у системы с идеальным газом необходимо рассчитать его кинетическую энергию. Из курса общей физики известно, что энергия частицы массой m, которая поступательно движется в некотором направлении со скоростью v, определяется по формуле:

Ek1 = m*v2/2.

Ее также можно применить для газовых частиц (атомов и молекул), однако, необходимо сделать некоторые замечания.

Во-первых, под скоростью v следует понимать некоторую среднюю величину. Дело в том, что газовые частицы движутся с разными скоростями согласно распределению Максвелла-Больцмана. Последнее позволяет определить среднюю скорость, которая с течением времени не изменяется, если отсутствуют внешние воздействия на систему.

Во-вторых, формула для Ek1 предполагает энергию на одну степень свободы. Газовые частицы могут двигаться во всех трех направлениях, а также вращаться в зависимости от их строения. Чтобы учесть величину степени свободы z, следует ее умножить на Ek1, то есть:

Ek1z = z/2*m*v2.

Кинетическая энергия всей системы Ek в N раз больше, чем Ek1z, где N – общее число газовых частиц. Тогда для U получаем:

U = z/2*N*m*v2.

Согласно этой формуле, изменение внутренней энергии газа возможно только в том случае, если поменять число частиц N в системе, либо их среднюю скорость v.

Внутренняя энергия и температура

Применяя положения молекулярно-кинетической теории идеального газа, можно получить следующую формулу связи между средней кинетической энергией одной частицы и абсолютной температурой:

m*v2/2 = 1/2*kB*T.

Здесь kB – постоянная Больцмана. Подставляя это равенство в формулу для U, полученную в пункте выше, приходим к следующему выражению:

U = z/2*N*kB*T.

Данное выражение можно переписать через количество вещества n и газовую постоянную R в следующем виде:

U = z/2*n*R *T.

В соответствии с этой формулой, изменение внутренней энергии газа возможно, если поменять его температуру. Величины U и T зависят друг от друга линейно, то есть график функции U(T) представляет собой прямую линию.

Как строение газовой частицы влияет на внутреннюю энергию системы?

Под строением частицы газа (молекулы) имеется в виду количество атомов, которое ее составляет. Оно играет определяющую роль при подстановке соответствующей степени свободы z в формулу для U. Если газ является одноатомным, формула внутренней энергии газа принимает такой вид:

U = 3/2*n*R*T.

Откуда взялась величина z=3? Ее появление связано всего с тремя степенями свободы, которыми обладает атом, поскольку он может двигаться только в одном из трех пространственных направлений.

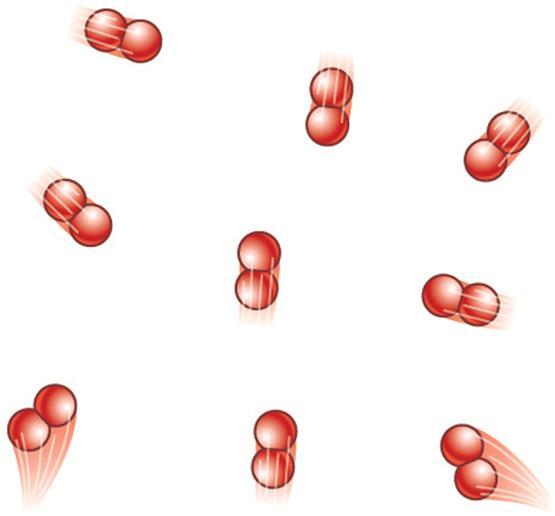
Если рассматривается двухатомная молекула газа, то внутреннюю энергию следует вычислять по такой формуле:

U = 5/2*n*R*T.

Как видим, двухатомная молекула уже имеет 5 степеней свободы, 3 из которых являются поступательными и 2 вращательными (в соответствии с геометрией молекулы, она может вращаться вокруг двух взаимно перпендикулярных осей).

Наконец, если газ является трех- и более атомным, то справедливо следующее выражение для U:

U = 3*n*R*T.

Сложные молекулы имеют 3 поступательных и 3 вращательных степени свободы.

Пример задачи

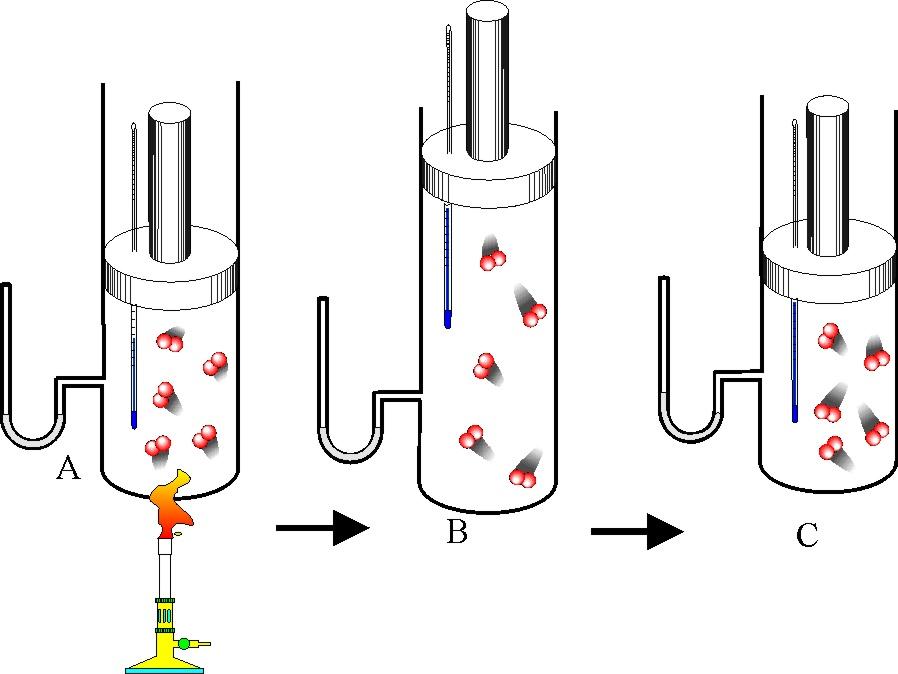
Под поршнем находится одноатомный газ при давлении 1 атмосфера. В результате нагрева газ расширился так, что его объем увеличился от 2-х литров до 3-х. Как при этом изменилась внутренняя энергия газовой системы, если процесс расширения был изобарным.

Чтобы решить эту задачу, недостаточно приведенных в статье формул. Необходимо вспомнить об уравнении состояния идеального газа. Оно имеет вид, представленный ниже.

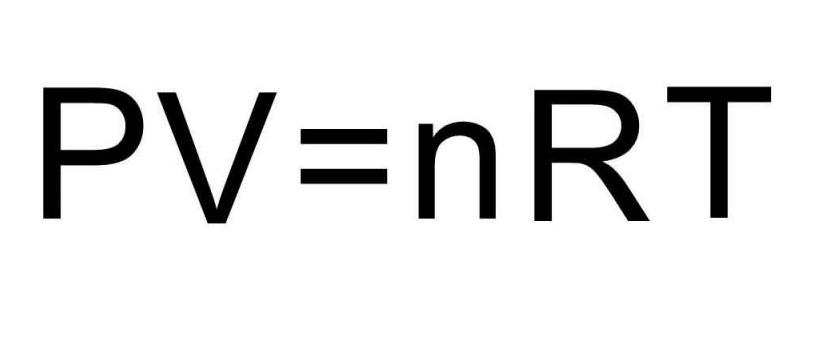
Поскольку поршень закрывает цилиндр с газом, то в процессе расширения количество вещества n остается постоянным. Во время изобарного процесса температура изменяется прямо пропорционально объему системы (закон Шарля). Это означает, что формула выше запишется так:

P*ΔV = n*R*ΔT.

Тогда выражение для внутренней энергии одноатомного газа примет форму:

ΔU = 3/2*P*ΔV.

Подставляя в это равенство значения давления и изменения объема в единицах СИ, получаем ответ: ΔU ≈ 152 Дж.