Как найти энергию гиббса химической реакции

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 сентября 2020 года; проверки требуют 23 правки.

Свобо́дная эне́ргия Ги́ббса (или просто эне́ргия Ги́ббса, или потенциа́л Ги́ббса, или изобарно-изотермический потенциал, или термодинами́ческий потенциа́л в узком смысле) — это величина, изменение которой в ходе химической реакции равно изменению внутренней энергии системы. Энергия Гиббса показывает, какая часть от полной внутренней энергии системы может быть использована для химических превращений или получена в их результате в заданных условиях и позволяет установить принципиальную возможность протекания химической реакции в заданных условиях. Математически это термодинамический потенциал следующего вида:

Энергию Гиббса можно понимать как полную потенциальную химическую энергию системы (кристалла, жидкости и т. д.)

Понятие энергии Гиббса широко используется в термодинамике и химии.

Самопроизвольное протекание изобарно-изотермического процесса определяется двумя факторами: энтальпийным, связанным с уменьшением энтальпии системы (), и энтропийным , обусловленным увеличением беспорядка в системе вследствие роста её энтропии. Разность этих термодинамических факторов является функцией состояния системы, называемой изобарно-изотермическим потенциалом или свободной энергией Гиббса (, кДж)

Определение[править | править код]

Классическим определением энергии Гиббса является выражение

где  — внутренняя энергия,  — давление среды,  — объём,  — абсолютная температура среды,  — энтропия.

Дифференциал энергии Гиббса для системы с постоянным числом частиц, выраженный в собственных переменных — через давление и температуру :

Для системы с переменным числом частиц этот дифференциал записывается так:

Здесь  — химический потенциал, который можно определить как энергию, которую необходимо затратить, чтобы добавить в систему ещё одну частицу.

Связь с термодинамической устойчивостью системы[править | править код]

Покажем, что минимум потенциала Гиббса соответствует устойчивому равновесию термодинамической системы с фиксированными температурой, давлением и числом частиц.

Запишем обобщённое уравнение первого и второго начал термодинамики:

При

Таким образом в системе при постоянных температуре и давлении энергия Гиббса достигает минимального значения.

Применение в химии[править | править код]

Связь с химическим потенциалом[править | править код]

Используя свойства экстенсивности термодинамических потенциалов, математическим следствием которых является соотношение Гиббса-Дюгема, можно показать, что химический потенциал для системы с одним типом частиц есть отношение энергии Гиббса к числу молей вещества n в системе:

Если система состоит из частиц нескольких сортов с числом молей частиц каждого сорта, то соотношения Гиббса-Дюгема приводят к выражению

Химический потенциал применяется при анализе систем с переменным числом частиц, а также при изучении фазовых переходов. Так, исходя из соотношений Гиббса — Дюгема и из условий равенства химических потенциалов находящихся в равновесии друг с другом фаз, можно получить уравнение Клапейрона — Клаузиуса, определяющее линию сосуществования двух фаз в координатах через термодинамические параметры (удельные объёмы) фаз и теплоту перехода между фазами.^[1]

Энергия Гиббса и направление протекания реакции[править | править код]

В химических процессах одновременно действуют два противоположных фактора — энтропийный () и энтальпийный (). Суммарный эффект этих противоположных факторов в процессах, протекающих при постоянном давлении и температуре, определяет изменение энергии Гиббса () согласно
уравнению Гиббса — Гельмгольца :

Из этого выражения следует, что , то есть некоторое количество теплоты расходуется на увеличение энтропии (), эта часть энергии потеряна для совершения полезной работы (рассеивается в окружающую среду в виде тепла), её часто называют связанной энергией. Другая часть теплоты () может быть использована для совершения работы, поэтому энергию Гиббса часто называют также свободной энергией.

Характер изменения энергии Гиббса позволяет судить о принципиальной возможности осуществления процесса.

	процесс может протекать — самопроизвольный процесс,
	система находится в состоянии химического равновесия.
	процесс протекать не может — несамопроизвольный процесс

Иными словами, если энергия Гиббса в исходном состоянии системы больше, чем в конечном, то процесс принципиально может протекать, если наоборот — то не может. Речь идёт исключительно о принципиальной возможности протекания реакции. В реальных же условиях реакция может не начинаться и при соблюдении неравенства (по кинетическим причинам).

Изотерма Вант-Гоффа[править | править код]

Изотерма Вант-Гоффа — соотношение, связывающее изменение свободной энергии Гиббса в ходе химической реакции с её константой равновесия :

где  — равновесная константа (безразмерная величина).

 — коэффициент реакции

Вообще говоря, любая реакция может быть рассмотрена как обратимая (даже если на практике она таковой не является). При этом константа равновесия определяется как

где  — константа скорости прямой реакции,  — константа скорости обратной реакции.

Историческая справка[править | править код]

Энергия Гиббса названа в честь одного из основателей термодинамики, Джозайи Уилларда Гиббса.

Примечания[править | править код]

Литература[править | править код]

• Ахметов Н. С. Актуальные вопросы курса неорганической химии. — М.: Просвещение, 1991. — 495 с. — ISBN 5-09-002630-0.
• Базаров И. П. Термодинамика. — М.: Высшая школа, 1991. — 376 с. — ISBN 5-06-000626-3.
• Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. — Издание 3-е, доп. — М.: Наука, 1976. — 584 с. — («Теоретическая физика», том V).

См. также[править | править код]

• Термодинамический потенциал
• Свободная энергия Гельмгольца

Биохимические
реакции обычно происходят при изобарно-
изотермических условиях. В этих условиях
энергетическое состояние системы
характеризуется энтальпией, а мерой
неупорядоченности системы будет
произведение температуры и энтропии.
Функцией, учитывающей обе эти характеристики
и противоположность в тенденции их
изменения при самопроизвольных процессах,
является свободная
энергия Гиббса.

Энергия
Гиббса (или изобарно – изотермический
потенциал) является обобщенной функцией
состояния системы, учитывающей энергетику
и неупорядоченность системы при изобарно
– изотермических условиях.

Названа она в честь одного из основателей
химической термодинамики, американского
ученого Джозайи Уилларда Гиббса (1839 –
1903).

Изменение
энергии Гиббса для биохимических
процессов в условиях, отличных от
стандартных, можно рассчитать на основе
экспериментальных значений ∆Н и ∆S
для этих процессов по уравнению:

∆G
=∆Н – Т∆S,

где
∆Н – характеризует полное изменение
энергии системы при p,T
= const и отражает стремление
системы к минимуму энергии (энтальпийный
фактор);

Т∆S
– характеризует ту часть энергии,
которую нельзя превратить в работу, и
отражает стремление системы к максимуму
неупорядоченности (энтропийный фактор);

∆G – характеризует ту часть энергии,
которую можно перевести в работу, и
является термодинамическим критерием
самопроизвольного протекания любых
процессов при p,T=const.

Если в уравнение для расчета свободной
энергии Гиббса ввести значение ∆Н°_р.и ∆S°_р., найденные
с использованием следствия из закона
Гесса, то мы получаем формулу для расчета
∆G реакции, протекающей в стандартных
условиях:

∆G°_p.f=∑ν_j∆G°_j
– ∑ν_i∆G°_i

где ∆G°_j, ∆G°_i– значения энергии Гиббса продуктов
реакции и исходных веществ, ν_j,ν_i
– соответствующие стехиометрические
коэффициенты в уравнении химической
реакции.

В термодинамических расчетах используют
значения энергии Гиббса, измеренные
при стандартных условиях (∆G°, кДж/моль).
Данные величины приведены в справочниках
термодинамических величин. Для простых
веществ в термодинамически устойчивой
форме стандартная энергия Гиббса их
образования принята равной нулю.

Таблица 12.

Значение ∆G°_f
298некоторых соединений.

Молекулярная формула	∆G°f 298, кДж/моль	Молекулярная формула	∆G°f 298, кДж/моль
О2 (г)	0	HF(г)	-275.41
НCl(г)	-95.3	HI(г)	1.58
H2O(ж)	-228.61	CH4 (г)	-50.85
CO2(г)	-394.37	C6H6(ж)	124.38
CO(г)	-137.15	NO2 (г)	52.29
NO(г)	87.58	NH3 (г)	-16.48
HCN(г)	121.58	NaСl(кр.)	-384.13

Рассчитав ∆G химической реакции, можно
не производя экспериментов, дать ответ
о принципиальной (термодинамической)
возможности (или невозможности) ее
протекания:

∆G<0 – реакция протекает самопроизвольно;

∆G=0 – реакция находится в состоянии
равновесия;

∆G>0 – несамопроизвольная реакция
(самопроизвольна обратная реакция).

Знак ∆G, а значит, и самопроизвольность
реакции зависит от величины соотношения
∆Н и Т∆S. Самопроизвольное осуществление
реакции (∆G<0) возможно в следующих
случаях:

1. ∆Н<0 (экзотермический процесс) и в то
   же время |∆Н |>| Т∆S |, т.е. при
   экзотермических процессах знаки ∆Н
   и ∆G совпадают, что означает возможность
   протекания процесса независимо от
   знака ∆S;

2. ∆Н>0 (эндотермический процесс) и |∆Н
   |<| Т∆S |, тогда возрастание энтальпии
   компенсируется значительно большим
   ростом энтропийного фактора, что
   осуществимо при высоких температурах
   или при реакциях с участием газовой
   фазы, когда наблюдается значительное
   увеличение энтропии. Этим и объясняется
   возможность протекания эндотермических
   реакций, что не согласуется с принципом
   Бертло о самопроизвольности только
   экзотермических реакций. Судить о
   направлении процесса по знаку изменения
   энтальпии в соответствии с этим признаком
   можно лишь: а) при низких температурах
   (при Т→0, Т∆S→0, и Т∆S<< ∆Н), когда
   знаки изменения свободной энергии и
   энтальпии совпадают; б) в конденсированных
   системах, в которых в процессе
   взаимодействия энтропия меняется
   незначительно, (беспорядок не может
   существенно возрасти, если, например,
   одно кристаллическое вещество
   превращается в другое кристаллическое
   вещество). Поэтому при низких температурах
   и в конденсированных системах возможно
   лишь протекание экзотермических реакций
   (∆G<0, когда ∆Н<0).

Возможность протекания реакции в
зависимости от знака ∆Н и ∆S и температуры
суммарно можно выразить в таблице:

Таблица 13.

Знак ∆Н	Знак ∆S	Знак ∆G	Самопроизвольность реакции	Пример
–	+	Всегда «-»	Самопроизвольна при любых температурах	2О3 (г)→ 3О2 (г)
+	–	Всегда «+»	Несамопроизвольна при любых температурах	3О2 (г)→2О3 (г)
–	–	«-» при низких температурах «+» при высоких температурах	Самопроизвольна при низких температурах, несамопроизвольна при высоких температурах	2Н2 (г)+О2 (г)→ →2Н2О(г)
+	+	«+» при низких температурах, «-» при высоких температурах	Несамопроизвольна при низких температурах, самопроизвольна при высоких температурах	2Н2О(г)→ →2Н2 (г)+О2 (г)

Второй
закон термодинамики для любых систем
формулируется следующим образом:

В
системе при постоянной температуре и
давлении самопроизвольно могут
совершаться только такие процессы, в
результате которых энергия Гиббса
уменьшается, т.е. ΔG_кон
>
ΔG_нач,
или ΔG
< 0.

Для закрытых термодинамических систем
наряду со свободной энергией Гиббса ∆G(изобарно-изотермический потенциал) в
изохорных условиях (V=const) применяют функцию
состояния системыэнергию Гельмгольца
(F) (изохорно
– изотермический потенциал).
В химии энергия Гиббса имеет более
широкое применение, чем энергия
Гельмгольца, так как химические процессы
чаще протекают при постоянном давлении,
а не при постоянном объеме.

Энергия Гельмгольца находится по
формуле:

F=U–T∙S,
гдеU- внутренняя энергия
системы

Энергия Гельмгольца характеризует
работоспособность системы, т.е. определяет
ту часть энергии, которая в
изохорно-изотермическом процессе
превращается в работу.

Энергию Гиббса можно выразить через
энергию Гельмгольца следующим образом:

G=U+pV–TS=F+pV

Оба рассмотренных термодинамических
потенциала являются функциями состояния,
зависят от природы веществ – участников
реакции, их массы и температуры. Кроме
того, энергия Гиббса зависит от давления,
а энергия Гельмгольца – от объема
системы. Абсолютные значения
термодинамических потенциалов неизвестны,
а для расчетов пользуются обычно
изменениями потенциалов (∆Gи ∆F).

Соседние файлы в предмете Химия

• #
• #

Материалы из методички: Сборник задач по теоретическим основам химии для студентов заочно-дистанционного отделения / Барботина Н.Н., К.К. Власенко, Щербаков В.В. – М.: РХТУ им. Д.И. Менделеева, 2007. -155 с.

Понятие энтропии

Абсолютная энтропия веществ и изменение энтропии в процессах

Стандартная энтропия

Стандартная энтропия образования

Энергия Гиббса

Стандартная энергия Гиббса образования

Энтальпийный, энтропийный фактор и направление процесса

Примеры решения задач

Задачи для самостоятельного решения

Понятие энтропии

Энтропия S – функция состояния системы. Энтропия характеризует меру неупорядоченности (хаотичности) состояния системы. Единицами измерения энтропии являются Дж/(моль·К).

Абсолютная энтропия веществ и изменение энтропии в процессах

При абсолютном нуле температур (Т = 0 К) энтропия идеального кристалла любого чистого простого вещества или соединения равна нулю. Равенство нулю S при 0 К позволяет вычислить абсолютные величины энтропий веществ на основе экспериментальных данных о температурной зависимости теплоемкости.

Изменение энтропии в процессе выражается уравнением:

ΔS = S_(прод.) – S_(исх.)

где S_(прод.) и S_(исх.) – соответственно абсолютные энтропии продуктов реакции и исходных веществ.

На качественном уровне знак S реакции можно оценить по изменению объема системы ΔV в результате процесса. Знак ΔV определяется по изменению количества вещества газообразных реагентов Δn_г. Так, для реакции

CaCO₃(к) = CaO(к) + CO₂(г)

(Δn_г = 1) ΔV > 0, значит, ΔS > 0.

Для реакции:

С(графит) + 2Н₂(г) = СН₄(г)

(Δn_г = -1) ΔV < 0, следовательно и ΔS < 0.

Стандартная энтропия

Величины энтропии принято относить к стандартному состоянию. Чаще всего значения S рассматриваются при Р = 101,325 кПа (1 атм) и температуре Т = 298,15 К (25^оС). Энтропия в этом случае обозначается S^о₂₉₈ и называется стандартной энтропией при Т = 298,15 К. Следует подчеркнуть, что энтропия вещества S (S^о) увеличивается при повышении температуры.

Стандартная энтропия образования

Стандартная энтропия образования ΔS^о_f,298 (или ΔS^о_обр,298) – это изменение энтропии в процессе образования данного вещества (обычно 1 моль), находящегося в стандартном состоянии, из простых веществ, также находящихся в стандартном состоянии.

Энергия Гиббса

Энергия Гиббса G – функция состояния системы. Энергия Гиббса равна:

G = Н – ТS.

Абсолютное значение энергии Гиббса определить невозможно, однако можно вычислить изменение δG в результате протекания процесса.

Критерий самопроизвольного протекания процесса: в системах, находящихся при Р, Т = const, самопроизвольно могут протекать только процессы, сопровождающиеся уменьшением энергии Гиббса (ΔG < 0). При достижении равновесия в системе ΔG = 0.

Стандартная энергия Гиббса образования

Стандартная энергия Гиббса образования δG^о_f,298 (или δG^о_обр,298) – это изменение энергии Гиббса в процессе образования данного вещества (обычно 1 моль), находящегося в стандартном состоянии, из простых веществ, также находящихся в стандартном состоянии, причем простые вещества пристутствуют в наиболее термодинамически устойчивых состояниях при данной температуре.

Для простых веществ, находящихся в термодинамически наиболее устойчивой форме, δG^о_f,298 = 0.

Энтальпийный, энтропийный фактор и направление процесса

Проанализируем уравнение ΔG^о_Т = ΔН^о_Т — ΔТS^о_Т. При низких температурах ТΔS^о_Т мало. Поэтому знак ΔG^о_Т определяется в основном значением ΔН^о_Т (энтальпийный фактор). При высоких температурах ТΔS^о_Т – большая величина, знак Δ G^о_Т определяется и энтропийным фактором. В зависимости от соотношения энтальпийного (ΔН^о_Т) и энтропийного (ТΔS^о_Т) факторов существует четыре варианта процессов.

• • 1. Если ΔН^о_Т < 0, ΔS^о_Т > 0, то ΔG^о_Т < 0 всегда (процесс может протекать самопроизвольно при любой температуре).
    2. Если ΔН^о_Т > 0, ΔS^о_Т < 0, то ΔG^о_Т > 0 всегда (процесс не протекает ни при какой температуре).
    3. Если ΔН^о_Т < 0, ΔS^о_Т < 0, то ΔG^о_Т < 0 при Т < ΔН^о/ΔS^о (процесс идет при низкой температуре за счет энтальпийного фактора).
    4. Если ΔН^о_Т > 0, ΔS^о_Т > 0, то ΔG^о_Т < 0 при Т > ΔН^о/ ΔS^о (процесс идет при высокой температуре за счет энтропийного фактора).

Примеры решения задач

Задача 1. Используя термодинамические справочные данные, вычислить при 298,15 К изменение энтропии в реакции:

4NH_3(г) + 5O_2(г) = 4NО_(г) + 6H₂O_(ж)

Объяснить знак и величину ΔS^о.

Решение. Значения стандартных энтропий исходных веществ и продуктов реакции приведены ниже:

Вещество	NH3(г)	O2(г)	NО(г)	H2O(ж)
Sо298, Дж/(моль·К)	192,66	205,04	210,64	69,95

ΔS^о_х.р.,298 = 4S^о₂₉₈(NО_(г) ) + 6S^о₂₉₈(H₂O_(ж)) — 4S^о₂₉₈(NH_3(г)) — 5S^о₂₉₈(O_2(г)) = 4× 210,64 + 6× 69,95 — 4× 192,66 — 5× 205,04 = — 533,58 Дж/К

В данной реакции ΔV < 0 (Δn_г = — 5), следовательно и ΔS^o_х.р.,298 < 0, что и подтверждено расчетом.

Задача 2. Используя справочные термодинамические данные, рассчитать стандартную энтропию образования NH₄NO_3(к). Отличается ли стандартная энтропия образования NH₄NO_3(к) от стандартной энтропии этого соединения?

Решение. Стандартной энтропии образования NH₄NO₃ отвечает изменение энтропии в процессе:

N_(г) + 2H_2(г) + 3/2O_2(г) = NH₄NO_3(к); δS^о_f,298(NH₄NO_3(к)) = ?

Значения стандартных энтропий исходных веществ и продуктов реакции приведены ниже:

Вещество	N2(г)	H2(г)	O2(г)	NH4NO3(к)
Sо298, Дж/(моль·К)	191,50	130,52	205,04	151,04

ΔS^о_х.р.,298 = ΔS^о_f,298(NH₄NO_3(к)) = S^о₂₉₈(NH₄NO_3(к)) — S^о₂₉₈(N_2(г)) — 2S^о₂₉₈(H_2(г)) – 3/2S^о₂₉₈(O_2(г)) = 151,04–191,50 —— 2× 130,52–3/2× 205,04 = — 609,06 Дж/(моль·К).

Стандартная энтропия образования NH₄NO₃(к), равная — 609,06 Дж/(моль·К), отличается от стандартной энтропии нитрата аммония S^о₂₉₈(NH₄NO_3(к)) = +151,04 Дж/(моль·К) и по величине, и по знаку. Следует помнить, что стандартные энтропии веществ S^о₂₉₈ всегда больше нуля, в то время как величины ΔS⁰_f,298, как правило, знакопеременны.

Задача 3. Изменение энергии Гиббса реакции:

2Н_2(г) + О_2(г) = 2 Н₂О_(ж)

равно δG^о₂₉₈= –474,46 кДж. Не проводя термодинамические расчеты, определить, за счет какого фактора (энтальпийного или энтропийного) протекает эта реакция при 298 К и как будет влиять повышение температуры на протекание этой реакции.

Решение. Поскольку протекание рассматриваемой реакции сопровождается существенным уменьшением объема (из 67,2 л (н.у.) исходных веществ образуется 36 мл жидкой воды), изменение энтропии реакции ΔS^о<0. Поскольку ΔG^о₂₉₈ реакции меньше нуля, то она может протекать при температуре 298 К только за счет энтальпийного фактора. Повышение температуры уменьшает равновесный выход воды, поскольку ТΔS^о<0.

Задача 4. Используя справочные термодинамические данные, определить может ли при 298,15 К самопроизвольно протекать реакция:

С₄Н_10(г) = 2С₂Н_4(г) + Н_2(г)

Если реакция не будет самопроизвольно протекать при 298,15 К, оценить возможность ее протекания при более высоких температурах.

Решение. Значения стандартных энергий Гиббса и энтропий исходных веществ и продуктов реакции приведены ниже:

Вещество	С4Н10(г)	С2Н4(г)	Н2(г)
ΔGоf,298× , кДж/моль	— 17,19	68,14	0
Sо298, Дж/(моль·К)	310,12	219,45	130,52

ΔG^о_х.р.,298 = 2ΔG^о_f,298(С₂Н_4(г)) + ΔG^о_f,298(Н_2(г)) — ΔG^о_f,298(С₄Н_10(г)) = 2× 68,14 + 17,19 = 153,47 кДж.

ΔG^о_х.р.,298 > 0, следовательно, при Т = 298,15 К реакция самопроизвольно протекать не будет.

ΔS^о_х.р.,298 = 2S^о₂₉₈(С₂Н_4(г)) + S^о₂₉₈(Н_2(г)) — S^о₂₉₈(С₄Н_10(г)) = 2× 219,45 + 130,52 – 310,12 = +259,30 Дж/К.

Поскольку ΔS^о_х.р.,298 > 0, то при температуре Т>ΔН^о/ΔS^о величина ΔG^о_х.р.,298 станет величиной отрицательной и процесс сможет протекать самопроизвольно.

Задача 5. Пользуясь справочными данными по ΔG^о_f,298 и S^о₂₉₈, определите ΔH^о₂₉₈ реакции:

N₂O_(г) + 3H_2(г) = N₂H_4(г) + H₂O_(ж)

Решение. Значения стандартных энергий Гиббса и энтропий исходных веществ и продуктов реакции приведены ниже:

Вещество	N2O(г)	H2(г)	N2H4(г)	H2O(ж)
ΔGоf,298, кДж/моль	104,12	0	159,10	-237,23
Sо298, Дж/(моль·К)	219,83	130,52	238,50	69,95

ΔG^о_х.р.,298 = ΔG^о_f,298(N₂H₄(г)) + ΔG^о_f,298(H₂O(ж)) – ΔG^о_f,298(N₂O(г)) – 3ΔG^о_f,298(H₂(г)) = 159,10 + (–237,23) – 104,12 – 0 = –182,25 кДж.

ΔS^о_х.р.,298 = S^о₂₉₈(N₂H₄(г)) + S^о₂₉₈(H₂O(ж)) – S^о₂₉₈(N₂O(г)) — 3S^о₂₉₈(H₂(г)) = 238,50 + 69,95 – 219,83 –3× 130,52 = –302,94 Дж/К.

ΔG^о₂₉₈ = ΔН^о₂₉₈ – ТΔS^о₂₉₈. Подставляя в это уравнение величины ΔН^о₂₉₈ и ТΔS^о₂₉₈, получаем:

ΔН^о₂₉₈ = –182,25× 10³ + 298·(–302,94) = –272526,12 Дж = – 272,53 кДж.

Следует подчеркнуть, что поскольку ΔS^о₂₉₈ выражена в Дж/(моль× К), то при проведении расчетов ΔG⁰₂₉₈ необходимо также выразить в Дж или величину ΔS⁰₂₉₈ представить в кДж/(мольK).

Задачи для самостоятельного решения

1. Используя справочные данные, определите стандартную энтропию образования ΔS^о_f,298 NaHCO_3(к).

2. Выберите процесс, изменение энергии Гиббса которого соответствует стандартной энергии Гиббса образования NO_2(г):

а) NO_(г) + 1/2O_2(г) = NO_2(г);

б) N_2(г) + 2O_2(г) = 2NO_2(г);

в) 1/2N_2(г) + O_2(г) = NO_2(г);

г) N_(г) + O_2(г) = NO_2(г).

3. Используя справочные данные, вычислите при 298,15 К изменение энтропии в реакции:

2NH₄NO_3(к) = 2N_2(г) + 4H₂O_(г) + О_2(г).

Объясните знак и величину  ΔSº реакции.

• .

δSох.р.,298 =1040,84 Дж/К. В данной реакции δV > 0 (D nг = 7), следовательно и δSох.р.,298 > 0, что и подтверждено расчетом.

4. Используя справочные данные, определите принципиальную возможность протекания реакции при 298,15 К:

NiO_(к) + C_{(графит)} = Ni_(к) + CO_(г)

Если реакция не будет самопроизвольно протекать при 298,15 К, оценить возможность ее протекания при более высоких температурах.

ΔGох.р.,298 = 74,45 кДж > 0, следовательно, при Т = 298,15 К реакция самопроизвольно протекать не будет. Поскольку ΔSох.р.,298 = 183,69 Дж/К, то есть больше нуля, то при достаточно высоких температурах ΔGох.р.,298 изменит знак на обратный.

5. Рассчитайте стандартную энергию Гиббса образования ΔG^о_f,298 C₂H₅OH_(ж), используя справочные данные о величинах ΔН^о_f,298 и S^о₂₉₈.

6. Используя справочные данные, определите стандартную энтропию образования ΔS^о_f,298 K₂Cr₂O_7(к).

7. На основе расчетов термодинамических величин покажите, чем эффективнее восстанавливать при 298 К Cr₂O_3(к) до металла — алюминием или магнием:

1) Cr₂O_3(к) + 3Mg_(к) = 3MgO_(к) + 2Cr_(к); ΔG^о₁;
2) Cr₂O_3(к) + 2Al_(к) = Al₂O_3(к) + 2Cr_(к); ΔG^о₂.

ΔGо1=-648,9 кДж; ΔGо2=-523,3 кДж. Таким образом, самопроизвольно протекают два процесса. Так как значение ΔGо1 более отрицательное, то эффективнее при 298 К будет протекать процесс восстановления магнием.

8. Используя справочными данными по величинам S^о₂₉₈, определите возможность самопроизвольного протекания в изолированной системе при 298 К процесса:

KClO_3(к) = KCl_(к) + 3/2O_2(к)

ΔSо298=247,1 Дж/К. ΔSо298 больше 0, следовательно данный процесс будет протекать самопроизвольно в изолированной системе при 298 К.

9. Используя справочные данные, вычислите при 298 К изменение энтропии в процессе:

Н_2(г) + 1/2О_2(г) = Н₂О_(г)

10. На основе справочных данных оценить температуру восстановления WO_3(к) водородом:

WO_3(к) + 3H_2(г) = W_(к) + 3H₂O_(г).

Расчет энергии Гиббса и энтропии химической реакции

Вычисление энергии Гиббса

Задание 101. 
Вычислите  для следующих реакций:

а) 2NaF _(к) + Cl_{2 (г)} = 2NaCl _(к) + F₂ 
б) PbO_{2 (к)} + 2Zn _(к) = Pb _(к) + 2ZnO _(к)
Можно ли получить фтор по реакции (а) и восстановить РbO₂ цинком по реакции (б). Ответ: +313,94 кДж; -4 17,4 кДж.
Решение: 
Реакция имеет вид:

2NaF _(к) + Cl_{2 (г)} = 2NaCl _(к) + F₂

Для вычисления энергии Гиббса прямой реакции используются значения   соответствующих веществ, приведённых в специальных таблицах. Зная, что  есть функция состояния и, что   для простых веществ, находящихся в устойчивом при стандартных условиях агрегатных состояниях, равны нулю, находим  , получим:

  = 2 (NaCl) – 2(NaF) = 2(-384,03) – 2(-54!,0) = +313,94 кДж.

То, что  > 0, указывает на невозможность протекания прямой реакции при Т = 298 К и давлении взятых газов равном 1,01325 Па (760 мм. рт. ст. = 1 атм). 

б) Реакция имеет вид:

PbO_{2 (к)} + 2Zn _(к) = Pb _(к) + 2ZnO _(к)

Находим   реакции, получим:

 = 2(ZnO) – (PbO₂) = 2(-318,2) – (-219,0) = -417,4 кДж.

То, что  < 0, указывает на возможность протекания прямой реакции при Т = 298 К и давлении взятых газов равном 1,01325 Па (760 мм. рт. ст. = 1 атм).

Ответ: +313,94 кДж; -4 17,4 кДж.

---

Равновесие системы 

Задание 102. 
При какой температуре наступит равновесие системы
4НСI _(г) + 0_{2 (г)} = 2Н₂О _(г) + 2С1_{2 (г)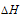};   = -114,42 кДж?
Хлор или кислород в этой системе является более сильным окислителем и при какой температуре? Ответ: 891 К.
Решение:
Уравнение реакции имеет вид:

4НСI _(г) + O_{2 (г)} = 2Н₂О _(г) + 2С1_{2 (г)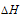};   = -114,42 кДж?

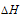 < 0, значит, реакция экзотермическая, идёт с выделением теплоты.
Находим 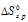 из соотношения:

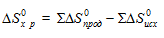
Для данной реакции:

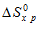  = 2(Н₂О) + 2 (Cl₂) – (4 (HCl) +  (O²);
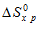  = 2(188,72) + 2(222,95) –[ 4(186,69) + 205,03] = 128,41 Дж/моль . К.

Зная 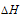   и 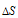, и, то, что   = 0 можно вычислить температуру, при которой наступит равновесие системы, получим:

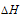  =   – Т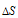

При   = 0 получим равенство:

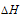  = Т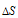

Тогда

Т = 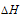/  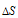= 114,42/(128,41 . 10-3) = 891 K.

Находим энергии Гиббса реакции:

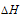  =   – Т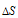 = -114,42 – 298(-0б12841) = -76б15 кДж.

Так как   < 0, то реакция при стандартных условиях возможна, т.е. будет идти окисление хлора и при данных условиях (Т = 298) кислород является более сильным окислителем до температуры 891 К, т. е. до тех пор пока не наступит состояние равновесия системы, а выше 891 К более сильным окислителем станет кислород.

Ответ: 891 К.

---

Задание 103.
Восстановление Fe₃O₄ оксидом углерода идет по уравнению
Fe₃O_{4 (к)} + СО _(г) = 3ЕеО _(к) + СO_{2 (г)}
Вычислите   и сделайте вывод о возможности самопроизвольного протекания этой реакции при стандартных условиях, Чему равно 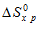  в этом процессе? Ответ. +24,19 кДж; + 31,34 Дж/(моль ^. К).
Решение:
Реакция имеет вид:

Fe₃O_{4 (к)} + СО _(г) = 3ЕеО _(к) + СO_{2 (г)}

Для вычисления энергии Гиббса прямой реакции используются значения   соответствующих веществ, приведённых в специальных таблицах. Зная, что   есть функция состояния и, что   для простых веществ, находящихся в устойчивом при стандартных условиях агрегатных состояниях, равны нулю, находим  , получим:

 = 3 (FeO) +  (CO₂) – [ (Fe₃O₄) +  (CO)]; 
  = 3(-244,3) + (-394,38) – [(-1014,2) + (-137,27) = +24,19 кДж.

То, что  > 0, указывает на невозможность протекания прямой реакции при Т = 298 К и давлении взятых газов равном 1,01325 Па (760 мм. рт. ст. = 1 атм).

Находим 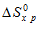 из соотношения:

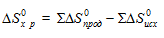
Для данной реакции:

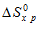  =  FeО) +  (CO₂) – [(Fe₃O₄) + )))э (CO)];

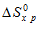  = (3 . 54,0 + 213,65) – (146,4 + 197,91) = +31,34 Дж/моль ^. К.

Ответ. +24,19 кДж; + 31,34 Дж/(моль . К).

---

Энтропия системы

Задание 104.
Реакция горения ацетилена идет по уравнению
С₂Н_{2 (г)} + 5/2О_{2 (г)} = 2СО_{2 (г)} + Н₂О _(ж)
Вычислите   и 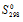 . Объясните уменьшение энтропии в результате этой реакции. Ответ: -1235,15 кДж; -216,15 Дж/(моль ^. К).
Решение:
Реакция имеет вид:

С₂Н_{2 (г)} + 5/2О_{2 (г)} = 2СО_{2 (г)} + Н₂О _(ж)

Для вычисления энергии Гиббса прямой реакции используются значения   соответствующих веществ, приведённых в специальных таблицах. Зная, что   есть функция состояния и, что  для простых веществ, находящихся в устойчивом при стандартных условиях агрегатных состояниях, равны нулю, находим  , получим:

   = 2 (CO₂) +  (Н₂O)  – [(С₂Н₂) + 5/2(O₂)];
  = 2(-394,38) + (-237,19) – [(209,20) = -1235,15 кДж.

Энтропия (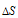) является функцией состояния, т. е. её изменение зависит только от начального (S₁) и конечного (S₂) состояний и, не зависит от пути процесса:

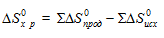
Значения   находим из специальных таблиц.
Для данной реакции:

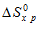  = 2S⁰(СО₂) +  S⁰(Н₂О) – [( S⁰(С₂Н₂) + 5/2 S^o(O₂);
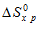 = (2 . 213,65 + 69,94) – (200,82 + 5/2 .205,03) = -216,15 Дж/моль ^. К.

Уменьшение энтропии объясняется тем, что система в результате реакции переходит в более устойчивое состояние, так как из 3,5 объёмов газообразных веществ происходит образование 2 объёмов газообразных веществ и образуется 1 моль жидкого вещества, т. е. объём системы уменьшается, и агрегатное состояние вещества упорядочивается,   < 0.

Ответ: -1235,15 кДж; -216,15 Дж/(моль ^. К).

---

Задание 105.
Уменьшается или увеличивается энтропии при переходах: а) воды в пар; б) графита в алмаз? Почему? Вычислите 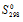для каждого превращения. Сделайте вывод о количественном изменении энтропии при фазовых и аллотропических превращениях. Ответ: а) 118,78 Дж(моль . К); 6) -3,25 Дж/(моль . К).
Решение:
Энтропия является свойством вещества, пропорциональным его количеству. Она обладает аддитивными свойствами, т. е. при соприкосновении систем суммируется. Энтропия отражает движение частиц вещества и является мерой неупорядоченности системы. Она возрастает с увеличением движения частиц (при нагревании, испарении, плавлении, расширении газа, при ослаблении или разрыве связей между атомами и т.п.), 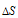  > 0 Процессы, связанные с упорядоченностью системы (конденсация, кристаллизация, сжатие, упорядочение связей, полимеризация и т.п.)  ведут к уменьшению энтропии,  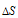< 0.
а) Изменение значений энтропии при переходе  воды в пар. 
При переходе воды в пар энтропия будет возрастать, потому что  при испарении воды происходит увеличение движения молекул, т. е. система переходит в менее устойчивое состояние, из жидкого в газообразное, 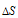 > 0.
Уравнение реакции имеет вид:

Н₂О (ж) → Н₂О (г);

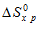  =  [Н₂О] (г) –   [Н₂О] (ж);
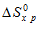 = 188,72 – 69,94 = +118,78 Дж/моль ^. К.

 б) Изменение значений энтропии при переходе. При переходе графита в алмаз образуются более прочные связи между атомами углерода в алмазе, чем в графите, т. е. происходит процесс с упорядоченностью системы, упрочнение связей, что ведёт к уменьшению энтропии, 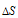  < 0.
 Уравнение реакции имеет вид:

С _{(графит)} → С _{(алмаз);}
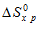  = S⁰ С (алмаз) –   S⁰С (графит);
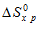  = 2,44 – 5,69 = -3,25 Дж/моль . К.

Значения 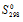  взяты из специальных таблиц.

Ответ: а) 118,78 Дж(моль . К); 6) -3,25 Дж/(моль . К).

---

Определение энергии Гиббса реакции 

Задание 106.
Чем можно объяснить, что при стандартных условиях невозможна экзотермическая реакция
Н_{2 (г)} + СО_{2 (г)} = СО _(г) + Н₂О _(ж); 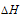  = -2,85 кДж.
Зная тепловой эффект реакции и абсолютные стандартные энтропии соответствующих веществ, определите  этой реакции. Ответ: +19,91 кДж.
Решение:

Уравнение реакции имеет вид:

Н_{2 (г)} + СО_{2 (г)} = СО _(г) + Н₂О _(ж); 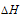  = -2,85 кДж.

Значения   находим из специальных таблиц.

Для данной реакции:

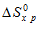  =  S⁰(СО) + S⁰ (Н₂О) – [( S⁰(Н₂) +  (S⁰СO₂)];
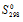  = (197,91 + 69,94) – (130,59 + 213,65) = -76,39 Дж/моль . К.

Теперь вычислим   реакции из уравнения Гиббса:

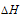  =   – Т;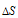
  = -2,85 – 298(-76,39) = +19,91 кДж.

То, что  > 0, указывает на невозможность протекания прямой реакции при Т = 298 К и давлении взятых газов равном 1,01325 Па (760 мм. рт. ст. = 1 атм).

Ответ: +19,91 кДж.

---

Задание 107.
Прямая или обратная реакция будет протекать при стандартных условиях в системе
2NO _(г) + O_{2 (г)} = 2NO_{2 (г)}
Ответ мотивируйте, вычислив  прямой реакции. Ответ: -69,70 кДж.
Решение:
Уравнение процесса:

2NO _(г) + O_{2 (г)} = 2NO_{2 (г)}

Для вычисления энергии Гиббса прямой реакции используются значения   соответствующих веществ, приведённых в специальных таблицах. Зная, что   есть функция состояния и, что   для простых веществ, находящихся в устойчивом при стандартных условиях агрегатных состояниях, равны нулю, находим  , получим:

 = 2(NO₂) – 2Г(NO) = 2 ^. 51,84 – 2  ^.  86,69  = -69,70 кДж.

То, что  < 0, указывает на возможность протекания прямой реакции при Т = 298 К и давлении взятых газов равном 1,01325 Па (760 мм. рт. ст. = 1 атм.), обратная реакция не протекает при н. у..

Ответ: -69,70 кДж.

---

Здесь вы найдете примеры задач на вычисление таких термодинамических параметров как энтальпия, энтропия, энергия Гиббса. Определение возможности самопроизвольного протекания процесса, а также составление термохимических уравнений.

Задачи к разделу Основы термодинамики с решениями

Задача 1. Рассчитайте стандартную энтальпию и стандартную энтропию химической реакции. Определите в каком направлении при 298 °К  (прямом или обратном) будет протекать реакция. Рассчитайте температуру, при которой равновероятны оба направления реакции.
Fe₂O_{3 (к)} + 3H₂ = 2Fe_(к) + 3H₂O_(г)

Показать решение »

Задача 2. Вычислите энергию Гиббса и определите возможность протекания реакции при температурах 1000 и 3000 К.

	Cr2O3 (т) + 3C (т) = 2Cr (т) + 3CO (г)
ΔH298, кДж/моль	— 1141	0	0	— 110,6
ΔS298, Дж/(моль×К)	81,2	5,7	23,6	197,7

Задача 3. Определите тепловой эффект сгорания жидкого CS₂(ж) до образования газообразных СО₂ и SO_2. Сколько молей CS₂ вступят в реакцию, если выделится 700 кДж тепла?

Задача 4. Вычислите тепловой эффект реакции восстановления оксида железа (II) водородом, исходя из следующих термохимических уравнений:
1. FeO (к) + CO (г) = Fe (к) + CО₂ (г);          ΔH₁ = -18,20 кДж;
2. СO (г) + 1/2O₂ (г) = СO₂ (г)                         ΔН₂ = -283,0 кДж;
3. H₂ (г) + ½ O₂ (г) = H₂O (г)                         ΔН₃ = -241,83 кДж.

Задача 5. Реакция горения бензола выражается термохимическим уравнением:
С₆Н_6(ж) + 7½ О_2(г) = 6СО_2(г) + 3Н₂О_(г) – 3135,6 кДж.
Вычислите теплоту образования жидкого бензола. Определите теплотворную способность жидкого бензола при условии, что стандартные условия совпадают с нормальными.

Задача 6. Реакция окисления этилового спирта выражается уравнением:
С₂Н₅ОН_(ж) + 3,0 О_2(г) = 2СО_2(г) + 3Н₂О_(ж).
Определить теплоту образования С₂Н₅ОН_(ж), зная ΔН х.р. = — 1366,87 кДж. Напишите термохимическое уравнение. Определите мольную теплоту парообразования С₂Н₅ОН_(ж) → С₂Н₅ОН_(г), если известна теплота образования С₂Н₅ОН_(г), равная  –235,31 кДж·моль^-1.

Задача 7. Чем можно объяснить, что при стандартных условиях, невозможна экзотермическая реакция:
СО_{2 (г)}+Н_{2 (г)} ↔ СО _(г)+Н₂О _(ж)?
Рассчитайте ΔG данной реакции. При каких температурах данная реакция становится самопроизвольной?

Задача 8. Рассчитав на основании табличных данных ΔG и ΔS, определите тепловой эффект реакции:
2 NO _(г) + Cl_{2 (г)} ↔  2 NOCl_(г).

Задача 9. С чем  будет более интенсивно взаимодействовать газообразный хлористый водород (в расчете на 1 моль): с алюминием или с оловом? Ответ дайте, рассчитав ΔG⁰ обеих реакций. Продуктами реакций являются твердая соль и газообразный водород.

Задача 10. Не прибегая к вычислениям, определите, какие знаки (>0, <0, ≅0) имеют ΔG, ΔH и ΔS для протекающей в прямом направлении реакции:
4 НBr _(г) +  O_2(г) ↔ 2 H₂O_(г) + 2 Br_2(г)
Как повлияет повышение температуры на направленность химической реакции?