Энергия плоского воздушного конденсатора 2 · 10−7 Дж. Определите энергию конденсатора после заполнения его диэлектриком с диэлектрической проницаемостью 
если конденсатор отключен от источника питания.
Спрятать решение
Решение.
При отключении конденсатора от источника тока его заряд не изменится. Тогда используем формулу энергии конденсатора 
После заполнения конденсатора диэлектриком его емкость увеличится в 2 раза. Поэтому энергия уменьшится в 2 раза и станет равной 10-7 Дж.
Ответ: 10−7 Дж.
Источник: Кирик Л. А. Самостоятельные и контрольные работы для 10 класса, Х.: «Гимназия», 2002 (№ 1 (дост.) стр. 105)
Что будет если конденсатор отключить от источника напряжения
Плоский конденсатор отключили от источника тока, а затем уменьшили расстояние между его пластинами. Как изменили при этом заряд на обкладках конденсатора, электроемкость конденсатора и напряжение на его обкладках? (Краевыми эффектами пренебречь, считая пластины конденсатора большими. Диэлектрическую проницаемость воздуха принять равной 1.)
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Заряд конденсатора | Электроёмкость | Напряжение на обкладках |
Поскольку конденсатор отключен от источника, при изменении расстояния между пластинами заряд конденсатора никак не изменяется. Электроемкость плоского конденсатора обратно пропорциональна расстоянию между пластинами: 
Следовательно, уменьшение расстояния между обкладками конденсатора приводит к увеличению его электроемкости. Наконец, напряжение на обкладках связано с зарядом конденсатора и его емкостью соотношением 
Таким образом, напряжение уменьшается.
Источник
Что будет если конденсатор отключить от источника напряжения
Плоский конденсатор отключили от источника тока, а затем уменьшили расстояние между его пластинами. Как изменили при этом заряд на обкладках конденсатора, электроемкость конденсатора и напряжение на его обкладках? (Краевыми эффектами пренебречь, считая пластины конденсатора большими. Диэлектрическую проницаемость воздуха принять равной 1.)
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Заряд конденсатора | Электроёмкость | Напряжение на обкладках |
Поскольку конденсатор отключен от источника, при изменении расстояния между пластинами заряд конденсатора никак не изменяется. Электроемкость плоского конденсатора обратно пропорциональна расстоянию между пластинами: Следовательно, уменьшение расстояния между обкладками конденсатора приводит к увеличению его электроемкости. Наконец, напряжение на обкладках связано с зарядом конденсатора и его емкостью соотношением Таким образом, напряжение уменьшается.
Источник
Действия с конденсатором
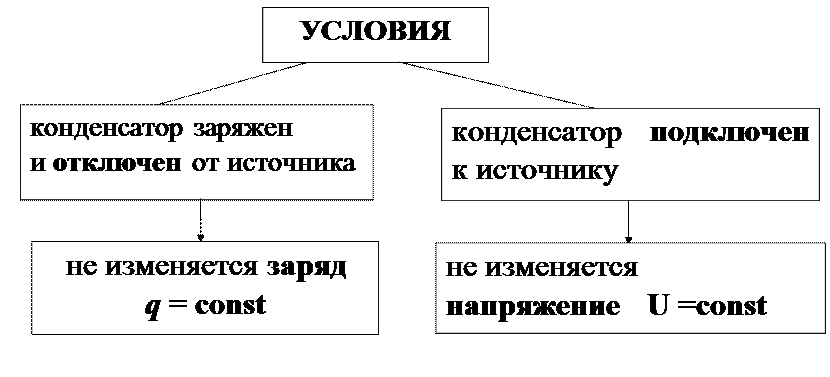
9. Емкость плоского конденсатора С1 = 10 -10 Ф. Диэлектрик – фарфор. Конденсатор зарядили до разности потенциалов U1 = 600 В и отключили от источника. Какую работу необходимо совершить, чтобы вынуть диэлектрик из конденсатора? Трением пренебречь.
Если конденсатор отключили от источника, то напряжение уменьшается, но остается q = const.Энергия конденсатора: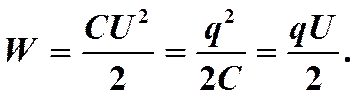 
Т.к. q=const, то необходимо использовать формулу 
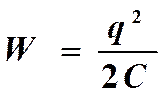. Авнеш. = W2 – W1
. 
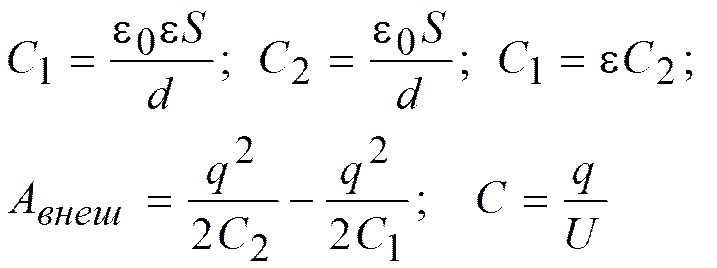
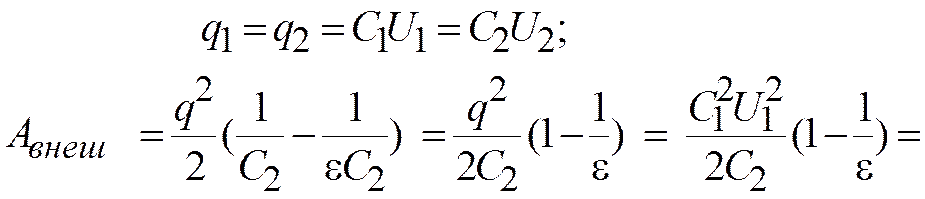
Если конденсатор остается подключенным к источнику, то q ≠ const, а
U = const = q1/C1 = q2/C2и W = ½ (CU 2 ).
10.Плоский конденсатор электроемкостью 4нФ подсоединен к источнику напряжения 10 В. Затем, не отключая конденсатор от источника, расстояние между его обкладками увеличили в 2 раза.
1) Найти, во сколько раз изменились следующие величины: а) электроемкость конденсатора, б) заряд на его обкладках, в) напряжение на конденсаторе, г) поверхностная плотность заряда, д) напряженность электростатического поля, е) поток Е через пластину конденсатора,
ж) электрическая индукция D, з) плотность энергии электрического поля в конденсаторе,
и) энергия конденсатора.
2) Рассчитать работу, затраченную на изменение расстояния между обкладками.
3) Найти заряд, прошедший через источник.
1) а)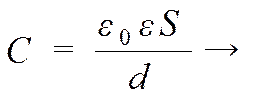 
если С1 = 4 нФ, то
в) Т.к. конденсатор от источника не отключается, то U2 = U1 = U =10 B, но изменяется заряд:
г)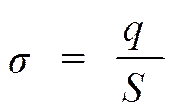 
→ σ2 / σ1 = ½. д) 
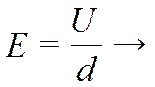Е2 / Е1 = ½.
е)NE = ES , NE2 / NE1 = ½. ж)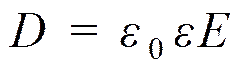 
→ D2 /D1 = ½.
и)Когда U = const, то W = ½CU 2 ,
2) Работа внешних сил, затраченная на изменение расстояние между обкладками, рассчитывается как изменение энергии конденсатора:
3) Найдем заряд, прошедший через источник:
Источник
Что будет если конденсатор отключить от источника напряжения
Плоский конденсатор отключили от источника тока, а затем уменьшили расстояние между его пластинами. Как изменили при этом заряд на обкладках конденсатора, электроемкость конденсатора и напряжение на его обкладках? (Краевыми эффектами пренебречь, считая пластины конденсатора большими. Диэлектрическую проницаемость воздуха принять равной 1.)
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Заряд конденсатора | Электроёмкость | Напряжение на обкладках |
Поскольку конденсатор отключен от источника, при изменении расстояния между пластинами заряд конденсатора никак не изменяется. Электроемкость плоского конденсатора обратно пропорциональна расстоянию между пластинами: Следовательно, уменьшение расстояния между обкладками конденсатора приводит к увеличению его электроемкости. Наконец, напряжение на обкладках связано с зарядом конденсатора и его емкостью соотношением Таким образом, напряжение уменьшается.
Источник
№ 765. Во сколько раз изменится энергия поля заряженного конденсатора, если пространство между пластинами конденсатора заполнить маслом? Рассмотреть случаи: а) конденсатор отключен от источника напряжения; б) конденсатор остается присоединенным к источник
№ 765. Во сколько раз изменится энергия поля заряженного конденсатора, если пространство между пластинами конденсатора заполнить маслом? Рассмотреть случаи: а) конденсатор отключен от источника напряжения; б) конденсатор остается присоединенным к источнику постоянного напряжения. Ответ объяснить, пользуясь законом сохранения энергии.
а) Конденсатор отключен от источника напряжения.
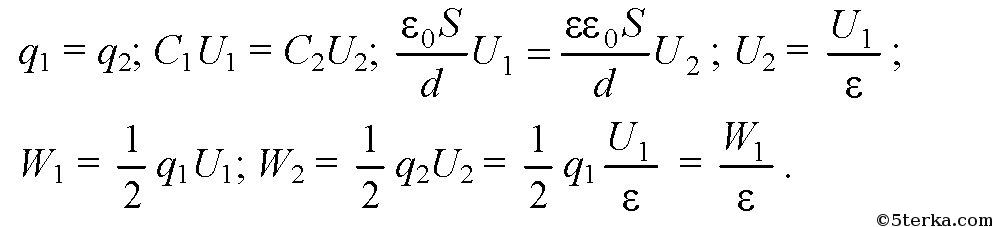
Таким образом, энергия поля заряженного конденсатора после заполнения пространства между его пластинами маслом уменьшится в ε = 2,5 раза за счет того, что часть энергии расходуется на поляризацию диэлектрика.
б) Конденсатор остается присоединенным к источнику постоянного напряжения.
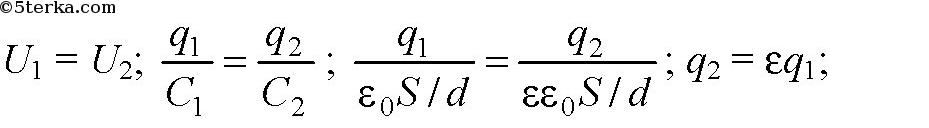
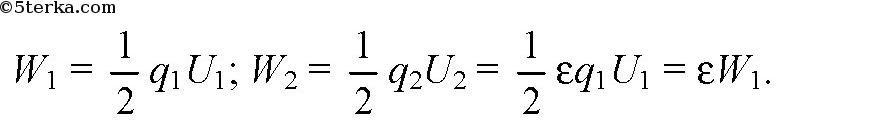
Таким образом, энергия поля конденсатора увеличится в ε = 2,5 раза. Энергия пополняется за счет источника напряжения.
Решебник по физике за 10, 11 класс (А.П. Рымкевич, 2001 год),
задача №765
к главе «ЭЛЕКТРОДИНАМИКА. ГЛАВА VII. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ. 35. Электроемкость конденсатора. Энергия заряженного конденсатора. Энергия электрического поля».
Источник
Задача 8
Между обкладками плоского воздушного конденсатора, имеющими площадь S = 1800 см 2 и напряжение U0 = 1 кВ, расстояние l составляет 0,5 см. Определить напряженность электрического поля и заряд конденсатора. Как изменятся эти величины, если конденсатор отключить от источника напряжения, а пространство между обкладками заполнить парафином (ε=2)?
Напряженность электрического поля плоского конденсатора определяется отношением напряжения к расстоянию между обкладками:
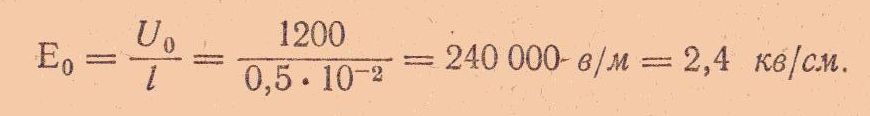
Для определения заряда найдем емкость конденсатора по формуле:
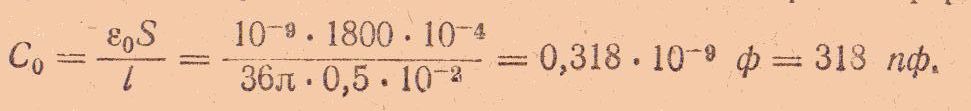
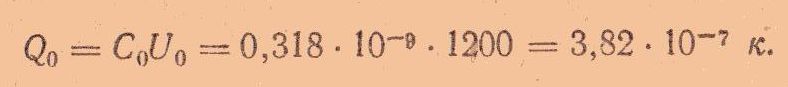
После отключения конденсатора от источника напряжения заряд Q сохраняется неизменным и в том случае, если воздух, как диэлектрик между пластинами, заменить парафином. При этом предполагается, что утечки заряда нет.
Емкость конденсатора с парафином будет уже другой, так как в формулу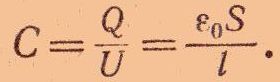 
вместо ε0 должна быть подставлена величина εа = ε0ε
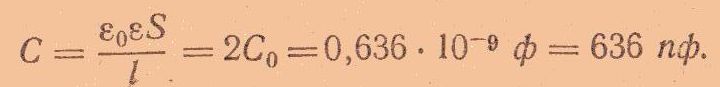
При этом же заряде Q0 и увеличении емкости напряжение между обкладками уменьшиться: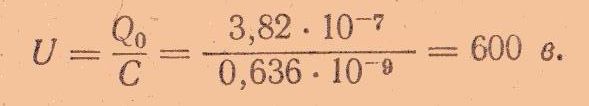
Напряженность поля также уменьшится:
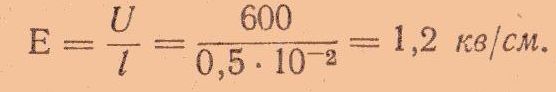
Вывод. При замене диэлектрика заряд конденсатора, отключенного от источника напряжения, сохраняется неизменным; напряжение между обкладками и напряженность поля изменяются обратно пропорционально относительной диэлектрической проницаемости.
Решим эту задачу при условии, что конденсатор остается подключенным к источнику напряжения.
Если конденсатор после замены диэлектрика остается подключенным к источнику напряжения, то напряженность поля при любом диэлектрике остается неизменной (геометрические размеры конденсатора также не изменялись):
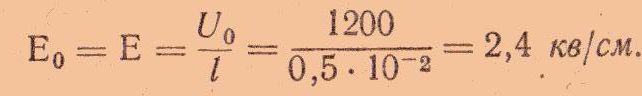
Изменение емкости конденсатора (в данном случае увеличение в два раза) приведет к увеличению заряда в два раза:
Источник
Подробнее о процессах зарядки и разрядки конденсатора
Основной характеристикой конденсатора является его электрическая ёмкость С .
Под ёмкостью конденсатора понимается его способность накопить на своих обкладках и удержать на них электрический заряд.
Чем больший электрический заряд соберёт на себе конденсатор, тем больший заряд при разряде он отдаст во внешнюю электрическую цепь.
Ёмкость плоского конденсатора тем больше, чем больше площадь его пластин, чем меньше расстояние между ними и чем больше диэлектрическая проницаемость диэлектрика между его обкладками (объяснение дано в Занятии 53 ):
На практике конденсатор заряжают, присоединив его обкладки к полюсам источника постоянного напряжения.
Как происходит процесс зарядки конденсатора?
До зарядки каждая обкладка конденсатора имела одинаково е количество положительных и отрицательных зарядов, то есть не была заряжена.
Чтобы зарядить конденсатор надо, чтобы какое-то количество свободных электронов перешло с одной обкладки на другую. Поэтому обкладки и получают одинаковые по модулю, но противоположные по знаку заряды.
Эту роль выполняет источник постоянного напряжения.
Обкладка конденсатора, соединённая с положительным полюсом источника напряжения, получает заряд
а обкладка соединённая с отрицательным полюсом источника получает такой же по модулю отрицательный заряд
Источни к перемещает свободные электроны по внешней цепи (по проводам).
Это направленное движение электронов в проводах от «минуса» источника к «плюсу» есть электрический ток .
Этот ток называется «зарядным током» (заряжает конденсатор). Продолжительность зарядки конденсатора зависит от его ёмкости и внутреннего сопротивления источника напряжения.
Зарядный ток протекает (конденсатор заряжается) до тех пор , пока напряжение на конденсаторе (разность потенциалов между его обкладками) не станет равной ЭДС (электродвижущей силе) источника.
С увеличением напряжения на конденсаторе зарядный ток уменьшается.
При полной зарядке конденсатора (при равенстве напряжения и ЭДС источника) зарядный ток становится равным нулю, и дальше напряжение на конденсаторе остаётся постоянным.
Величина заряда на обкладке равна произведению ёмкости конденсатора на напряжение между его обкладками:
Если заряженный конденсатор отключить от источника и присоединить его к внешней цепи, то конденсатор станет разряжаться .
Электроны по проводам , отталкиваясь от отрицательно заряженной обкладки, станут двигаться к положительно заряженной обкладке конденсатора — по внешней цепи потечёт » разрядный ток».
Если во внешней цепи есть электрическая лампочка, то на короткое время будет наблюдаться вспышка света, что указывает на разрядный ток.
Процесс разрядки конденсатора идёт до тех пор, пока потенциалы обкладок не сравняются (пока напряжение между обкладками не станет равным нулю).
Про работу источника постоянного напряжения (или тока) будет идти речь далее в теме «Постоянный ток».
Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Сообщите друзьям о существовании этого канала.
Предыдущая запись : Нахождение заряда и напряжения на каждом конденсаторе при их последовательном соединении.
Следующая запись: Последовательное и параллельное соединения конденсаторов.
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Источник
Содержание
- Что происходит при отключении конденсатора от источника тока
- 4. Конденсатор в цепи переменного тока
- Действия с конденсатором
- 35. Электродинамика Читать 0 мин.
- 35.441. Цепи
Что происходит при отключении конденсатора от источника тока
Плоский конденсатор отключили от источника тока, а затем уменьшили расстояние между его пластинами. Как изменили при этом заряд на обкладках конденсатора, электроемкость конденсатора и напряжение на его обкладках? (Краевыми эффектами пренебречь, считая пластины конденсатора большими. Диэлектрическую проницаемость воздуха принять равной 1.)
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Заряд конденсатора | Электроёмкость | Напряжение на обкладках |
Поскольку конденсатор отключен от источника, при изменении расстояния между пластинами заряд конденсатора никак не изменяется. Электроемкость плоского конденсатора обратно пропорциональна расстоянию между пластинами: Следовательно, уменьшение расстояния между обкладками конденсатора приводит к увеличению его электроемкости. Наконец, напряжение на обкладках связано с зарядом конденсатора и его емкостью соотношением Таким образом, напряжение уменьшается.
Источник
4. Конденсатор в цепи переменного тока
Рассмотрим процессы, протекающие в электрической цепи переменного тока с конденсатором. Если подключить конденсатор к источнику постоянного тока, то в цепи возникнет кратковременный импульс тока, который зарядит конденсатор до напряжения источника, а затем ток прекратится. Если заряженный конденсатор отключить от источника постоянного тока и соединить его обкладки с выводами лампы накаливания, то конденсатор будет разряжаться, при этом наблюдается кратковременная вспышка лампы.
При включении конденсатора в цепь переменного тока процесс его зарядки длится четверть периода. После достижения амплитудного значения напряжение между обкладками конденсатора уменьшается и конденсатор в течение четверти периода разряжается. В следующую четверть периода конденсатор вновь заряжается, но полярность напряжения на его обкладках изменяется на противоположную и т.д. Процессы зарядки и разрядки конденсатора чередуются с периодом, равным периоду колебаний приложенного переменного напряжения.
Как и в цепи постоянного тока, через диэлектрик, разделяющий обкладки конденсатора, электрические заряды не проходят. Но в результате периодически повторяющихся процессов зарядки и разрядки конденсатора по проводам, соединенным с его выводами, течет переменный ток. Лампа накаливания, включенная последовательно с конденсатором в цепь переменного тока (рис. 6), кажется горящей непрерывно, так как человеческий глаз при высокой частоте колебаний силы тока не замечает периодического ослабления свечения нити лампы.
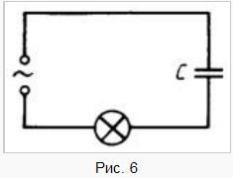
Установим связь между амплитудой колебаний напряжения на обкладках конденсатора и амплитудой колебаний силы тока. При изменениях напряжения на обкладках конденсатора по гармоническому закону
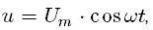
заряд на его обкладках изменяется по закону:
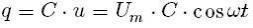
Электрический ток в цепи возникает в результате изменения заряда конденсатора: i = q’. Поэтому колебания силы тока в цепи происходят по закону:
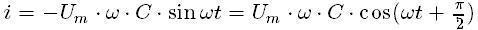
Следовательно, колебания напряжения на обкладках конденсатора в цепи переменного тока отстают по фазе от колебаний силы тока на р/2 или колебания силы тока опережают по фазе колебания напряжения на р/2 (рис. 7). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того как напряжение достигает максимума, сила тока становится равной нулю и т.д.
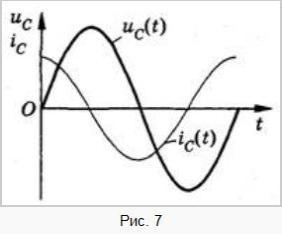
Произведение Um⋅щ⋅C является амплитудой колебаний силы тока:
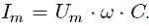
Отношение амплитуды колебаний напряжения на конденсаторе к амплитуде колебаний силы тока называют емкостным сопротивлением конденсатора (обозначается ХC):
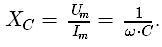
Связь между амплитудным значением силы тока и амплитудным значением напряжения по форме совпадает с выражением закона Ома для участка цепи постоянного тока, в котором вместо электрического сопротивления фигурирует емкостное сопротивление конденсатора:
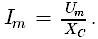
Емкостное сопротивление конденсатора, как и индуктивное сопротивление катушки, не является постоянной величиной. Оно обратно пропорционально частоте переменного тока. Поэтому амплитуда колебаний силы тока в цепи конденсатора при постоянной амплитуде колебаний напряжения на конденсаторе возрастает прямо пропорционально частоте.
Источник
Действия с конденсатором
9. Емкость плоского конденсатора С1 = 10 -10 Ф. Диэлектрик – фарфор. Конденсатор зарядили до разности потенциалов U1 = 600 В и отключили от источника. Какую работу необходимо совершить, чтобы вынуть диэлектрик из конденсатора? Трением пренебречь.
Если конденсатор отключили от источника, то напряжение уменьшается, но остается q = const.Энергия конденсатора: 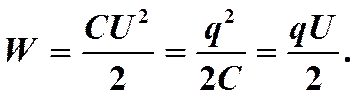Т.к. q=const, то необходимо использовать формулу 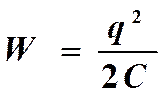. Авнеш. = W2 – W1
.
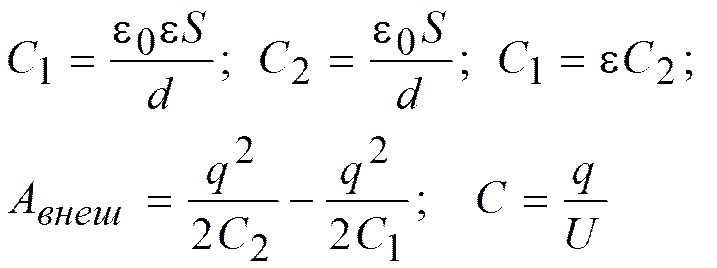
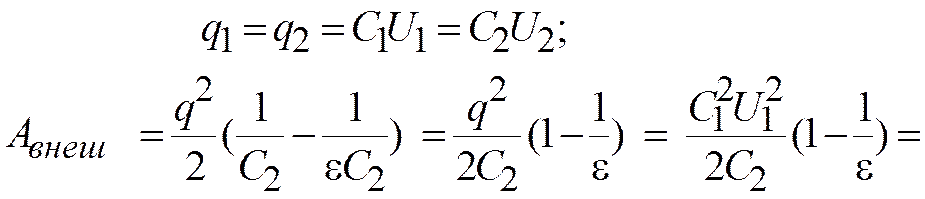
Если конденсатор остается подключенным к источнику, то q ≠ const, а
U = const = q1/C1 = q2/C2и W = ½ (CU 2 ).
10.Плоский конденсатор электроемкостью 4нФ подсоединен к источнику напряжения 10 В. Затем, не отключая конденсатор от источника, расстояние между его обкладками увеличили в 2 раза.
1) Найти, во сколько раз изменились следующие величины: а) электроемкость конденсатора, б) заряд на его обкладках, в) напряжение на конденсаторе, г) поверхностная плотность заряда, д) напряженность электростатического поля, е) поток Е через пластину конденсатора,
ж) электрическая индукция D, з) плотность энергии электрического поля в конденсаторе,
и) энергия конденсатора.
2) Рассчитать работу, затраченную на изменение расстояния между обкладками.
3) Найти заряд, прошедший через источник.
1) а) 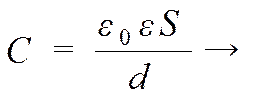если С1 = 4 нФ, то
в) Т.к. конденсатор от источника не отключается, то U2 = U1 = U =10 B, но изменяется заряд:
г) 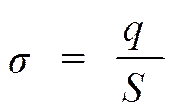→ σ2 / σ1 = ½. д) 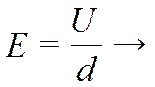Е2 / Е1 = ½.
е)NE = ES , NE2 / NE1 = ½. ж) 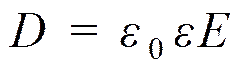→ D2 /D1 = ½.
и)Когда U = const, то W = ½CU 2 ,
2) Работа внешних сил, затраченная на изменение расстояние между обкладками, рассчитывается как изменение энергии конденсатора:
3) Найдем заряд, прошедший через источник:
Источник
35. Электродинамика 
Читать 0 мин.
Читать 0 мин.35.441. Цепи
Через конденсатор постоянный ток не течёт.
Напряжение на параллельных участках цепи одинаково.
В системе отключенных конденсаторов заряд всегда остаётся постоянным. Напряжение и ёмкость может меняться.
Выделившееся количество теплоты равно разности начальной и конечной энергии:
Eн ― начальная энергия системы [Дж];
Ек ― конечная энергия системы [Дж].
Начальные и конечные энергии определяются энергиями конденсаторов и катушек индуктивности входящих в цепь.
После установления равновесия, напряжение есть только на конденсаторах, не подключенных параллельно к резисторам.
Конденсатор в цепи постоянного тока
Плоский конденсатор представляет собой пластинки, на которых может скапливаться заряд. Между пластинками находится пространство, заполненное диэлектриком (или воздухом в роли диэлектрика). Поскольку диэлектрики ― вещества, плохо проводящие ток, от одной пластины конденсатора через слой диэлектрика на другую пластину заряд перейти не может, а значит, через конденсатор ток не проходит. Если на участке цепи находится такой конденсатор ― этот участок «заблокирован», тока в нем нет.
Если на участке цепи находится конденсатор не заряженный, или заряженный частично, а цепь подключают к источнику тока ― на обкладках конденсатора начинает скапливаться заряд. Это означает, что на этом участке цепи до конденсатора есть ток ― до тех пор, пока конденсатор не заряжен полностью.
Если цепь от источника тока отключить, и в ней есть заряженный конденсатор ― конденсатор начинает разряжаться. Заряды с одной обкладки конденсатора пытаются перейти на другую, по «длинному пути» ― через всю цепь, создавая, таким образом, ток. Ток в такой цепи будет до тех пор, пока конденсатор не разрядится.
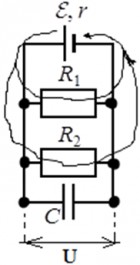
Пример: Пусть в цепи есть два резистора с сопротивлениями R1 и R2, источник ЭДС ε, и конденсатор емкостью C:
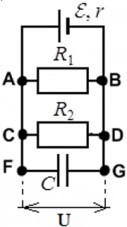
Конденсатор C полностью заряжен. В этом случае токи в цепи не проходят через участок цепи FG ― его словно нет в цепи, и в расчетах параметров цепи он не учитывается. Ток считается выходящим из положительно заряженной клеммы источника ЭДС (тонкая и длинная) к входящим в отрицательно заряженную клемму (жирная короткая черта):
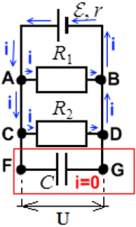
Конденсатор разряжен или заряжен не док конца. В этом случае конденсатор только заряжается, и ток в цепи через точку F проходит — вплоть до обкладки конденсатора – но дальше, в точку G ток не проходит.
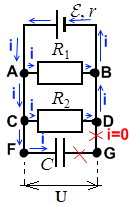
Конденсатор заряжен, но от источника ЭДС цепь отключена. В этом случае ток идет через всю цепь ― пока конденсатор может служить источником зарядов и пока полностью не разрядится. Когда конденсатор разрядится ― ток в цепи прекратится.
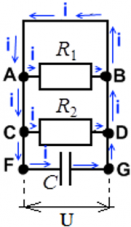
Напряжения на всех параллельных участках цепи равны ― это основное свойство параллельного подключения. Вне зависимости от того, находится на ветви резистор, или конденсатор. Таким образом, во всех случаях для примера выше, напряжение на конденсаторе C равно напряжению на резисторе R1, и равно напряжению на резисторе R2. Благодаря этому свойству, зная, например, энергию, скопившуюся на заряженном конденсаторе, или его заряд, можно вычислить напряжение на резисторах.
Заряженный конденсатор, отключенный от цепи. У заряженного конденсатора на обкладках находится определенное количество заряда. Если конденсатор отключить от цепи ― заряду некуда переместиться, и он остается на конденсаторе неизменным. Получить дополнительный заряд, если он заряжен не до конца, конденсатору тоже неоткуда. Заряд конденсатора, отключенного от цепи, постоянен.
Электроемкость конденсатора ― это его физико-геометрическая характеристика, показывающая, как много заряда он может скопить. Электроемкость конденсатор не зависит ни от заряда на его обкладках, ни от напряжения в цепи.
Электроемкость конденсатора равна C = $frac <varphi_2 – varphi_1>= frac
$ , где
C ― электроемкость конденсатора, [Ф];
(φ2 – φ1) ― разность потенциалов на обкладках конденсатора, [В];
U ― напряжение на обкладках конденсатора [В].
Электроемкость плоского конденсатора зависит от размеров его пластин, расстояния между ними, а также типа диэлектрика, который заполняет пространство между пластинами.
Электроемкость плоского конденсатора равна C = $frac<varepsilonvarepsilon_0 S>$ , где
C ― ёмкость конденсатора [Ф];
ε ― диэлектрическая проницаемость;
ε0 ― электрическая постоянная;
S ― площадь обкладок конденсатора [м2];
d ― расстояние между обкладками [м].
В электрической цепи за счет сопротивления, которое преодолевают движущиеся в материале заряды, выделяется тепло. Количество теплоты, которая выделяется в цепи, равно разности начальной и конечной энергии всей системы Q = Eн – Eк¸ где
Eн ― начальная энергия системы [Дж];
Eк ― конечная энергия системы [Дж].
В цепи энергия скапливается на конденсаторах (энергия электрического поля) и на катушках индуктивности (энергия магнитного поля). Поэтому энергия электромагнитных сил в цепи в любой момент равна сумме энергий на конденсаторах и на катушках, которые входят в цепь.
Энергия электрического поля заряженного конденсатора равна We = $frac <2>= frac <2>= frac<2c>$ , где
We ― энергия электрического поля конденсатора, [Дж];
C ― электроемкость конденсатора, [Ф];
U ― напряжение на обкладках конденсатора, [В];
q ― заряд на обкладках конденсатора, [Кл].
Энергия магнитного поля катушки индуктивности равна E = $frac<2>$ , где
E ― энергия магнитного поля катушки [Дж];
L ― индуктивность катушки [Гн];
I ― сила тока в катушке [А].
Состояние равновесия и зарядка конденсаторов
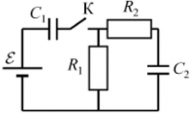
Пример 1: в цепи, изображенной на рисунке, есть ЭДС и резисторы с сопротивлениями R1 и R2, оба конденсатора емкостями C1 и C2 разряжены.
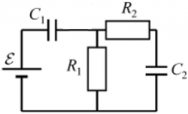
Ток от источника ЭДС до конденсатора C1 будет идти до тех пор, пока конденсатор C1 не будет полностью заряжен. При этом от конденсатора C1 дальше заряды не проходят ― ни на резисторы R1 и R2, ни на конденсаторC2. Как только конденсатор C1 полностью заряжается, в системе наступает состояние равновесия ― напряжение на конденсаторе становится равным ЭДС, весь возможный заряд конденсатор принял. Поскольку ток через него не прошел до конденсатора C2 ― этот конденсатор так и остался незаряженным. Напряжение есть лишь на конденсаторе C1, а на конденсаторе C2напряжение равно нулю. Зарядка конденсатораC1:
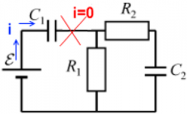
После того, как конденсатор C1 заряжен, ток в цепи прекращается.
Пример 2: в цепи, изображенной на рисунке, есть ЭДС и резисторы с сопротивлениями R1 и R2, все три конденсатора емкостями C1, C2 и C3 разряжены.
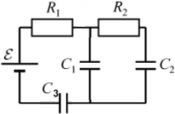
Ток, выходя из источника ЭДС, разделяется на два тока ― один питает подзарядку конденсатораC1, а другой ― конденсатораC2. Состояние равновесия наступает, когда оба конденсатора полностью заряжены ― в цепи ток больше не проходит. Но так как ток дальше конденсаторов не проходит ― конденсатор C3 не получает заряд, и остается разряженным. Напряжение на конденсаторе C3 равно нулю.
Зарядка конденсаторов C1 иC2:
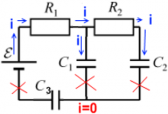
После того, как конденсаторыC1 и C2 заряжены, ток в цепи прекращается.
Источник
Энергия поля конденсатора
При решении задач, связанных с определением энергии поля, важно помнить, что при отключении конденсатора от источника питания он сохраняет заряд, а если конденсатор остается подключенным к источнику, то напряжение будет постоянно.
Задача 1. Расстояние между пластинами плоского конденсатора уменьшили в 2 раза. Во сколько раз изменятся: заряд на пластинах, напряжение между пластинами, напряженность поля между пластинами и энергия конденсатора. Рассмотреть два случая: а) конденсатор отключен от источника напряжения; б) конденсатор остается присоединенным к источнику постоянного напряжения.
а) Если конденсатор отключен от питания, то он сохраняет заряд. Следовательно, в этом случае заряд не изменится. Емкость же вырастет вдвое, так как
Энергия
уменьшится вдвое (ведь емкость выросла).
Напряженность поля зависит только от заряда и поэтому тоже не изменится.
б) Если конденсатор подключен к источнику питания, то , и
– энергия увеличится вдвое. Так как емкость выросла вдвое, следовательно, вдвое вырос и заряд конденсатора. А это значит, что и напряженность поля также вдвое увеличится.
Задача 2.
Заряженный конденсатор подключили параллельно к такому же, незаряженному. Во сколько раз изменилась энергия поля первого конденсатора?
При параллельном подключении заряд поделится между двумя конденсаторами поровну. Поэтому, так как
То энергия изменится в 4 раза:
Задача 3.
Плотность энергии заряженного конденсатора Дж/м. С какой силой взаимодействуют обкладки конденсатора, если их площадь м?
Сила взаимодействия пластин:
Ответ: 3 Дж
Задача 4.
Определить энергию заряженного плоского конденсатора с твердым диэлектриком по следующим данным: объем диэлектрика м, относительная диэлектрическая проницаемость , напряженность поля в диэлектрике В/м.
Ответ: мДж.
Задача 5.
Определить энергию, перешедшую в тепло при соединении конденсаторов одноименно заряженными обкладками. Емкость первого конденсатора мкФ, второго мкФ. Напряжение на первом конденсаторе до соединения В, а на втором – В.
Энергия первого конденсатора:
Второго:
А после соединения заряд перераспределится и поэтому энергия системы будет равна
Где . Заряд первого конденсатора
Заряд второго
Заряд обоих конденсаторов
Тогда энергия системы равна
Таким образом, выделившееся тепло равно
Ответ: 0,5 мДж
Энергия конденсатора
Господа, всем приветище! Сегодня речь пойдет про энергию конденсаторов. Внимание, сейчас будет спойлер: конденсатор может накапливать в себе энергию. Причем иногда очень большую. Что? Это не спойлер, это и так было всем очевидно? Здорово если так! Тогда поехали в этом более подробно разбираться!
В прошлой статье мы пришли к выводу, что заряженный конденсатор, отсоединенный от источника напряжения, может сам в течении некоторого времени (пока не разрядится) давать некоторый ток. Например, через какой-то резистор. По закону Джоуля-Ленца если через резистор течет ток, то на нем выделяется тепло. Тепло – значит, энергия. И берется эта самая энергия из конденсатора – больше, собственно, неоткуда. Значит, в конденсаторе может хранится некоторая энергия. Итак, физика процессов более-менее понятна, поэтому теперь давайте поговорим, как это все описать математически. Потому что одно дело все описать на словах – это круто, замечательно, это должно быть, но в жизни часто надо что-то рассчитать и тут уже обычных слов не достаточно.
Для начала давайте вспомним определение работы из механики. Работа A силы F это произведение этой самой силы F на вектор перемещения s.
Полагаю, что механику вы изучали когда-то и это знаете 
. Страшные значки векторов нужны только в случае, если направление силы не совпадает с перемещением: вроде случая, когда сила тянет строго прямо, а перемещение идет под каким-то углом к силе. Такое бывает, например, когда груз перемещается по наклонной плоскости. Если же направление силы и перемещения совпадают, то можно смело отбросить вектора и просто перемножать силу на длину пути, получая таким образом работу:
Вспомним теперь статью про закон Кулона. Мы там получили замечательную формулу, которую сейчас самое время вспомнить:
То есть, если у нас есть электрическое поле с напряженностью Е и мы в него помещаем некоторый заряд q, то на этот заряд будет действовать сила F, которую можно рассчитать по этой формуле.
Нам никто не мешает подставить эту формулу в чуть выше написанную формулу для работы. И таким образом найти работу, которую совершает поле при перемещении в нем заряда q на расстояние s. Будем полагать, что мы перемещаем наш заряд q точно по направлению силовых линий поля. Это позволяет использовать формулу работы без векторов:
Теперь, господа, внимание. Напоминаю одну важную штуку из той же механики. Есть такой особый класс сил, которые называются потенциальные. Если говорить упрощенным языком, то для них верно утверждение, что если эта сила на каком-то отрезке пути совершила работу А, то это значит, что в начале этого пути у тела, над которым совершалась работа, энергия была на это самое А больше, чем в конце. То есть на сколько поработали, на столько и изменилась потенциальная энергия. Работа потенциальных сил не зависит от траектрии и определяется только начальной и конечной точкой. А на замнкнутом пути она вообще равна нулю. Как раз-таки сила электрического поля относится к этому классу сил.
Вот мы помещаем наш зарядик q в поле. Он под действием этого поля перемещается на некоторое расстояние от точки С до точки D. Пусть для определенности в точке D энергия заряда будет равна 0. При этом перемещении поле совершает работу А. Из этого следует, что в начале пути (в точке C) наш зарядик обладал некоторой энергией W=A. То есть, мы можем записать
Теперь самое время рисовать картинки. Взглянем на рисунок 1. Это немного упрощенная иллюстрация физики процессов плоского конденсатора. Более полное мы рассматривали это в прошлый раз.
Рисунок 1 – Плоский конденсатор
Давайте теперь чуть-чуть искривим свое сознание и глянем на наш конденсатор по-другому, чем раньше. Давайте предположим, что у нас за основу взята, например, синяя пластина. Она создает некоторое поле с некоторой напряженностью. Безусловно, и красная пластина тоже создает поле, но в данный момент это не интересно. Давайте смотреть на красную пластину, как на некоторый заряд +q, расположенный в поле синей пластины. И сейчас мы попробуем применить все вышеописанное к красной пластине как будто это и не пластина вовсе, а просто некоторый заряд +q. Вот так вот хитро. Почему, собственно, нет? Возможно, вы скажите – как же так, раньше мы везде исходили из того, что заряды у нас точечные, а тут – целая большая пластина. Она как-то на точку не совсем тянет. Спокойствие, господа. Никто нам не мешает разбить красную пластину на огромную кучу маленьких частичек, каждую из которых можно считать точечным зарядом Δq. Тогда уже можно без проблем применять все вышеописанное. И если мы выполним все расчеты сил, напряженностей, энергий и прочего для вот таких вот отдельных Δq и потом сложим результаты между собой, то получится, что мы зря так переусердствовали – результат будет ровно таким же, как если бы мы просто при расчетах брали заряд +q. Кто хочет – может проверить, я только за . Однако мы будем сразу работать по упрощенной схеме. Хотелось бы только отметить, что это верно для случая, когда поле у нас однородно и заряды по всем пластинам распределены равномерно. В действительности это не всегда так, однако такое упрощение позволяет существенно облегчить все расчеты и избежать всяких градиентов и интегралов без существенного вреда для практики.
Итак, вернемся к рисунку 1. На нем показано, что между обкладками конденсатора существует поле с некоторой напряженностью Е. Но мы договорились сейчас разделить роли обкладок – синяя у нас источник поля, а красная – заряд в поле. Какое же поле создает одна синяя обкладка отдельно от красной? Какова его напряженность? Очевидно, что она в два раза меньше общей напряженности. Почема это так? Да потому, что если забыть про нашу абстракцию (типа красная пластина – и не пластина вовсе, а просто заряд), то в результирующую напряженность Е вносят одинаковый вклад обе обкладки – и красная, и синяя: каждая по Е/2. В результате суммы этих Е/2 как раз и получается та самая Е, которая у нас на картинке. Таким образом (отбрасывая вектора), можно записать
Теперь посчитаем, если можно так выразиться, потенциальную энергию красной обкладки в поле синей обкладки. Заряд мы знаем, напряженность мы знаем, расстояние между обкладками тоже знаем. Поэтому смело записываем
Идем дальше. На деле же никто не мешает поменять местами красную и синюю обкладки. Давайте рассуждать наоборот. Будем рассматривать теперь красную обкладку как источник поля, а синюю – как некоторый заряд –q в этом поле. Думаю, даже без проведения расчета будет очевидно, что результат будет точно такой же. То есть энергия красной пластины в поле синей пластины равна энергии синей пластины в поле красной пластины. И, как вы возможно уже догадались, это и есть энергия конденсатора. Да, вот по этой самой формуле можно произвести расчет энергии заряженного конденсатора:
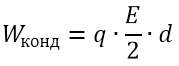
Слышу, как мне уже кричат: стоп, стоп, опять ты втираешь мне какую-то дичь! Ну ладно, расстояние между пластинами я еще как-то смогу измерить. Но меня почему-то опять заставляют считать заряд, что не понятно как сделать, да еще и напряженность надо знать, а чем я ее померяю?! Мультиметр вроде как не умеет это делать! Все верно, господа, сейчас мы займемся преобразованиями, которые позволят вам измерить энергию конденсатора всего лишь с применением обыкновенного мультиметра.
Давайте сперва избавимся от напряженности. Для этого вспомним замечательную формулу, которая связывает напряженность с напряжение:
Да, напряжение между двумя точками в поле равно произведению напряженности этого поля на расстояние между этими двумя точками. Итак, подставляя это полезнейшее выражение в формулу для энергии, получаем
Уже легче, напряженность ушла. Но остался еще заряд, который не понятно как мерить. Что бы от него избавиться, давайте вспомним формулу емкости конденсатора из предыдущей статьи:
Да, для тех, кто забыл, напоминаю, что емкость определяется как отношение этого злополучного заряда, накопленного конденсатором, к напряжению на конденсаторе. Давайте из этой формулы выразим заряд q и подставим его в формулу энергии конденсатора. Получаем
Вот это уже дельная формула, для энергии заряженного конденсатора! Если нам нужно узнать, какая энергия запасена в конденсаторе с емкостью С, заряженного до напряжения U, мы вполне можем это сделать по вот этой вот формуле. Емкость С обычно пишется на самом конденсаторе или на его упаковке, а напряжение всегда можно измерить мультиметром. Из формулы видно, что энергии в конденсаторе тем больше, чем больше емкость самого конденсатора и напряжение на нем. Причем энергия растет прямо пропорционально квадрату напряжения. Это важно помнить. Увеличение напряжения гораздо быстрее приведет к росту энергии, запасенной в конденсаторе, чем увеличение его емкости.
Для особых любителей зарядов можно из формулы определения емкости выразить не заряд, а напряжение и подставить его в формулу для энергии конденсатора. Таким образом, получаем еще одну формулу энергии
Используется эта формула довольно редко, а на практике вообще не припомню, что б по ней что-то считал, но раз она есть, то путь тут тоже будет для полноты картины. Самая ходовая формула – это средняя.
Давайте для интереса произведем некоторые расчеты. Пусть у нас есть вот такой вот конденсатор
Рисунок 2 – Конденсатор
И давайте мы его зарядим до напряжения, скажем, 8000 В. Какая энергия будет запасена в таком конденсаторе? Как мы видим из фотографии, емкость данного конденсатора составляет 130 мкФ. Теперь легко выполнить расчет энергии:
Много это или мало? Безусловно, не мало! Даже очень не мало! Скажем так, разрешенная энергия электрошокеров составляет какие-то там смешные единицы джоулей, а тут их тысячи! Принимая во внимание высокое напряжение (8кВ) можно смело утверждать, что для человека контакт с таким заряженным конденсатором скорее всего закончится очень и очень печально. Следует соблюдать особую осторожность при больших напряжениях и энергиях! У нас был случай, когда произошло короткое замыкание нескольких таких вот конденсаторов, соединенных параллельно и заряженных до нескольких киловольт. Господа, это было зрелище не для слабонервных! Бабахнуло так, что у меня потом в ушах пол дня звенело! А на стенах лаборатории осела медь от расплавленных проводов! Спешу успокоить, никто не пострадал, но это стало хорошим поводом дополнительно подумать над способами отвода такой гигантской энергии в случае нештатных ситуаций.
Кроме того, господа, важно всегда помнить, что конденсаторы блоков питания приборов тоже не могут мгновенно разрядиться после отключения прибора от сети, хотя там, безусловно, должно быть какие-то цепи, предназначенные для их разряда. Но должны быть, это не значит, что они там точно есть 
. Поэтому в любом случае после отключения любого прибора от сети, прежде чем лезть к нему внутрь, лучше подождать пару минут для разряда всех кондеров. И потом, после снятия крышки, прежде чем лапками хвататься за все подряд, следует сначала померить напряжение на силовых накопительных конденсаторах и при необходимости выполнить их принудительный разряд каким-нибудь резистором. Можно, конечно, просто отверткой замкнуть их выводы, если емкости не слишком большие, но такое делать крайне не рекомендуется!
Итак, господа, сегодня мы познакомились с различными методами расчета энергии, запасенной в конденсаторе, а также обсудили, как эти расчеты можно выполнять на практике. На этом потихоньку закругляемся. Всем вам удачи, и до новых встреч!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
