Энергия конденсатора .
Конденсатор это устройство, способное накапливать электрический заряд.
Энергия заряженного конденсатора:
(W=dfrac{q^2}{2C} )
(q ) – заряд конденсатора
(C )- емкость конденсатора
Заряд, емкость и напряжение на конденсаторе связаны следующим соотношением:
( q=CU )
Подставим в его в числитель дроби:
(W=dfrac{q^2}{2C} = dfrac{C^2U^2}{2C}=dfrac{CU^2}{2} )
Значит энергию конденсатора можно вычислить по формуле:
( W= dfrac{CU^2}{2} )
На этой схеме конденсатор подключен к источнику питания(батарейке):
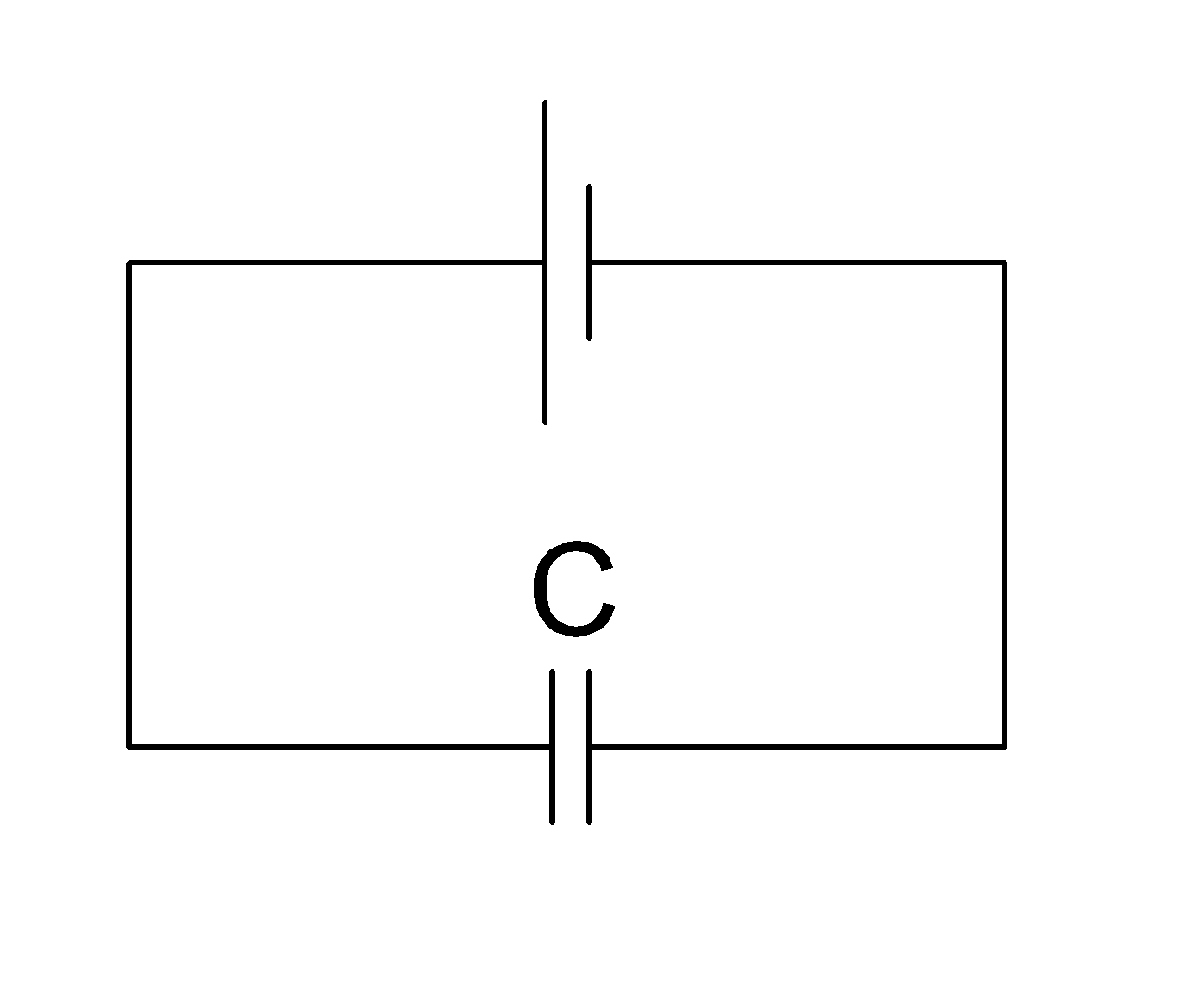
Задача 1.
Найти энергию
конденсатора, если его заряд (q=0,01 Кл ), а
емкость (C=0,0001 Ф . )
Показать ответ
Показать решение
Видеорешение
Задача 2.
Какова энергия конденсатора емкостью ( C=0,4 мкФ ), если его заряд ( q=800 мкКл . )
Показать ответ
Показать решение
Видеорешение
Задача 3.
Какова энергия конденсатора емкостью ( C=0,5 нФ ), если его заряд ( q=2 мкКл . )
Показать ответ
Показать решение
Видеорешение
Задача 4.
Энергия конденсатора емкостью ( C=64 мкФ ), равна 0,5 Джоуля.
Найдите заряд этого конденсатора .
Показать ответ
Показать решение
Видеорешение
Задача 5.
Энергия конденсатора емкостью ( C=500 пкФ ), равна 10 микроджоулей.
Найдите заряд этого конденсатора .
Дать ответ в микрокулонах.
Показать ответ
Показать решение
Видеорешение
Задача 6.
Энергия заряженного конденсатора (E=10^{-9} Дж ), а его емкость ( C=98 нФ . )
Найдите заряд этого конденсатора .
Дать ответ в нанокулонах.
Показать ответ
Показать решение
Видеорешение
Задача 7.
Напряжение на контактах конденсатора составляет 250 Вольт.
Какова энергия этого конденсатора, если его емкость (C=80 мкФ ? )
Показать ответ
Показать решение
Видеорешение
Задача 8.
Конденсатор, емкостью (C=5 мкФ ), подключен к источнику тока с напряжением (U= 12 В . )
Найдите энергию этого конденсатора .
Дать ответ в микроджоулях.
Показать ответ
Показать решение
Видеорешение
Электрическая
ёмкость —
характеристика проводника, мера его
способности накапливать электрический
заряд.
В теории электрических цепей ёмкостью
называют взаимную ёмкость между двумя
проводниками; параметр ёмкостного
элемента электрической схемы,
представленного в виде двухполюсника.
Такая ёмкость определяется как отношение
величины электрического заряда к разности
потенциалов между
этими проводниками.
В системе СИ ёмкость
измеряется в фарадах.
В системе СГС в сантиметрах.
Для одиночного
проводника ёмкость равна отношению
заряда проводника к его потенциалу в
предположении, что все другие
проводники бесконечно удалены
и что потенциал бесконечно удалённой
точки принят равным нулю. В математической
форме данное определение имеет вид
![]() где
где ![]() — заряд,
— заряд, ![]() —
—
потенциал проводника.
Ёмкость определяется
геометрическими размерами и формой
проводника и электрическими свойствами
окружающей среды (еёдиэлектрической
проницаемостью)
и не зависит от материала проводника.
К примеру, ёмкость проводящего шара
радиуса R равна
(в системе СИ):
![]()
Понятие ёмкости
также относится к системе проводников,
в частности, к системе двух проводников,
разделённых диэлектриком —конденсатору.
В этом случае взаимная
ёмкость этих
проводников (обкладок конденсатора)
будет равна отношению заряда, накопленного
конденсатором, к разности потенциалов
между обкладками. Для плоского конденсатора
ёмкость равна:
![]()
где S —
площадь одной обкладки (подразумевается,
что они равны), d —
расстояние между обкладками, ε — относительная
диэлектрическая проницаемость среды
между обкладками, ε0 =
8.854·10−12 Ф/м
— электрическая
постоянная.
Конденса́тор (от лат. condensare —
«уплотнять», «сгущать») — двухполюсник с
определённым значением ёмкости и
малой омической проводимостью;
устройство для накопления заряда и
энергии электрического поля. Конденсатор
является пассивным электронным
компонентом. Обычно состоит из двух
электродов в форме пластин
(называемых обкладками),
разделённыхдиэлектриком,
толщина которого мала по сравнению с
размерами обкладок.
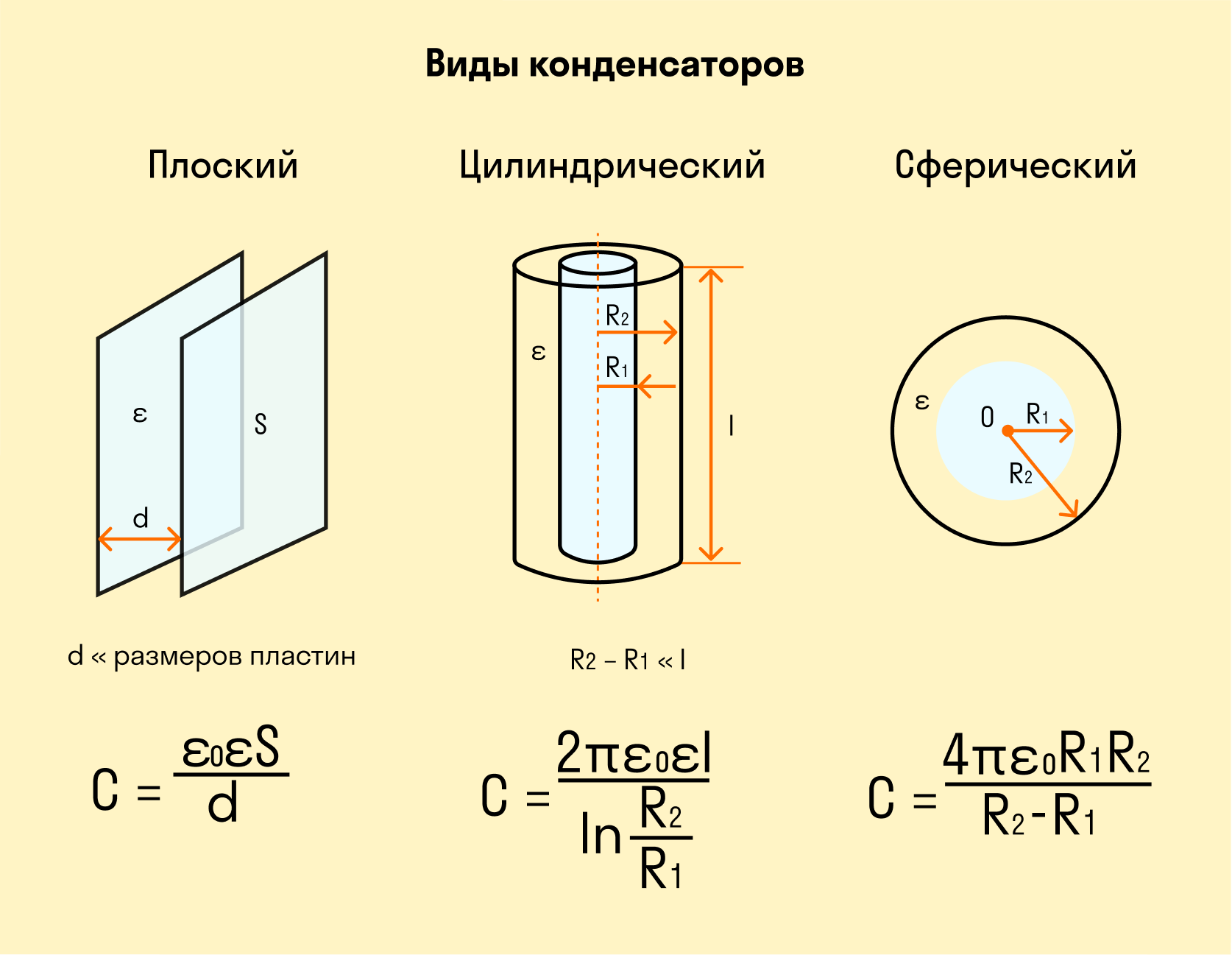
Виды конденсаторов:
1.
по виду диэлектрика: воздушные, слюдяные,
керамические, электролитические
2. по
форме обкладок: плоские, сферические.
3.
по величине емкости: постоянные,
переменные (подстроечные).
Электроемкость
плоского конденсатора
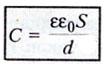
где
S – площадь пластины (обкладки) конденсатора
d
– расстояние между пластинами
eо –
электрическая постоянная
e –
диэлектрическая проницаемость диэлектрика
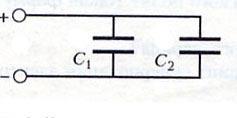
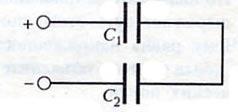
Включение
конденсаторов в электрическую цепь
параллельное
последовательное
ЭНЕРГИЯ ЗАРЯЖЕННОГО
КОНДЕНСАТОРА
Конденсатор – это
система заряженных тел и обладает
энергией.
Энергия любого конденсатора:
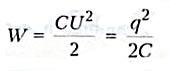 где
где
С – емкость конденсатора
q – заряд
конденсатора
U – напряжение на обкладках
конденсатора
Энергия конденсатора
равна работе, которую совершит
электрическое поле при сближении пластин
конденсатора вплотную,
или равна
работе по разделению положительных и
отрицательных зарядов , необходимой
при зарядке конденсатора.
ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО
ПОЛЯ КОНДЕНСАТОРА
Энергия конденсатора
приблизительно равна квадрату
напряженности эл. поля внутри
конденсатора.
Плотность энергии эл.
поля конденсатора:
![]()
13.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как рассчитать энергию заряженного конденсатора
Содержание:
-
Что такое энергия заряженного конденсатора
- Где сосредоточена, в каких единицах измеряется
-
Чему равна энергия заряженного конденсатора
- По какой формуле можно найти
- Применение конденсаторов
Что такое энергия заряженного конденсатора
Конденсатор состоит из двух проводников, разделенных слоем диэлектрика.
Простейший конденсатор — две металлические пластины-обкладки, расположенные параллельно, с тонкой прослойкой воздуха между ними. Когда заряды пластин противоположны по знаку, электрическое поле оказывается сосредоточено внутри конденсатора и почти не взаимодействует с внешним миром, что позволяет накапливать на пластинах заряд. Для описания работы, которую нужно затратить, чтобы разделить положительные и отрицательные заряды и полностью зарядить конденсатор, вводится понятие энергии.
Энергия заряженного конденсатора равна работе внешних сил, затраченной, чтобы зарядить его.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Где сосредоточена, в каких единицах измеряется
Вся энергия конденсатора сосредоточена в электрическом поле его пластин. Единица измерения СИ — джоуль.
Чему равна энергия заряженного конденсатора
Согласно закону сохранения энергии, энергия заряженного конденсатора равна работе, которую совершит электрическое поле при сближении пластин вплотную.
По какой формуле можно найти
Основная характеристика поля, напряженность, создаваемая одной из пластин, равна половине напряженности поля во всем конденсаторе. Заряд q, распределенный по поверхности одной пластины, находится в однородном электрическом поле другой. Потенциальную энергию заряда можно найти по формуле:
(W_п;=;qfrac E2d)
где Е — напряженность поля во всем конденсаторе, а d — расстояние между пластинами.
В этой формуле могут использоваться другие известные величины, например, разность потенциалов между пластинами, обозначаемая буквой U. Чтобы вычислить ее, нужно умножить напряженность поля Е на расстояние между пластинами d. Тогда формула для вычисления энергии будет иметь вид:
(W_п;=;frac{qU}2)
Электроемкость изолированного проводника С равна отношению изменения заряда q к изменению потенциала проводника (varphi). Ее можно найти по формуле:
(С;=;frac qU)
Таким образом, для решения задач можно использовать три выражения:
(W_п;=;frac{qU}2;=;frac{q^2}{2C};=;frac{CU^2}2)
Эти формулы справедливы для любого конденсатора, не только для плоского. Если малыми порциями (-triangle q) переносить отрицательный заряд с одной пластины на другую, поле внутри конденсатора будет совершать работу. Если порции заряда малы, для простоты расчетов можно предположить, что напряжение между пластинами не меняется. Тогда работа:
(triangle А = -triangle qU;=;-frac1Cqtriangle q)
(triangle W_п;=;frac1Cqtriangle q)
Построив график зависимости (;frac qC) от (q), мы видим, что приращение энергии численно равно площади прямоугольника (abcd) со сторонами (;frac qCtriangle q). Полное изменение энергии (W_п )будет равняться площади треугольника OBD.
Следовательно, (W_{п;}=;frac{OD;times;DB}2;=;frac{q^2}{2C}).
Применение конденсаторов
Емкость конденсатора не слишком велика, но энергия при разрядке отдается почти мгновенно. Свойство конденсаторов быстро выдавать импульс большой мощности находит применение в лампах-вспышках для фотографирования, электромагнитных ускорителях, импульсных лазерах.Примером может служить генератор Ван де Граафа, позволяющий создавать в лабораторных условиях напряжение в миллионы вольт, чтобы моделировать разряды молний. Также конденсаторы используют в радиотехнике.
Существует тип компьютерных клавиатур, целиком состоящий из конденсаторов под каждой клавишей, при нажатии которой его пластины сближаются. Электронная схема, к которой они подсоединены, распознает, какую клавишу нажали, и передает эту информацию дальше.
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Что такое конденсатор
Конструкция простейшего устройства этой категории состоит их двух проводящих пластин с диэлектриком в промежутке. Подключением такого устройства к источнику постоянного тока накапливают на рабочих элементах положительные и отрицательные заряды. После разрыва цепи питания энергетический потенциал сохраняется.
Характеристики конденсатора
Основной характеристикой данного элемента является емкость, или С. Она определяет способность устройства собирать электрический заряд, зависит от геометрической конфигурации крышек и от электрической проницаемости диэлектрика между крышками.
Важно! Емкость зависит от типа используемого диэлектрика, а также от геометрических размеров элемента.
Для того, чтобы описать принцип работы устройства формулой, необходимо понять, что это постоянная пропорциональность в уравнении, представляющая собой взаимную зависимость накопленного заряда q от площади пластинок и от разности потенциалов V между ними.
Мощность выражается в единицах, называемых фарадами F. Но на практике используются и более мелкие единицы, такие как микрофарады и пикофарады.

Внешний вид устройств
Таким образом, если напряжение U приложено к конденсатору, электрический заряд накапливается на крышках детали. Значение накопленного заряда на каждой пластинке одинаково, они отличаются только знаком. Этот процесс накопления электрического показателя на называется зарядкой.
Другим параметром детали является номинальное напряжение, а именно, его максимальное значение, которое может подаваться на конденсатор. При подключении более высокого напряжения возникает пробой диэлектрика. Это приводит к короткому замыканию элемента. Каким будет номинальное значение напряжения, зависит от типа диэлектрика и его толщины.
Важно! Чем толще диэлектрик, тем выше номинальное напряжение, которое он выдерживает.
Условные обозначения
Ещё одним параметром является ток утечки -значение проводящего показателя, возникающее при подаче постоянного напряжения на концы элемента.
Виды конденсаторов
Энергия конденсатора
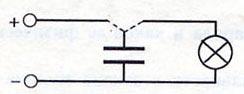
У конденсатора, как и у любой системы заряженных тел, есть энергия. Чтобы зарядить конденсатор, необходимо совершить работу по разделению отрицательных и положительных зарядов. По закону сохранения энергии эта работа будет как раз равна энергии конденсатора.
Доказать, что заряженный конденсатор обладает энергией, несложно. Для этого понадобится электрическая цепь, содержащая в себе лампу накаливания и конденсатор. При разрядке конденсатора вспыхнет лампа — это будет означать, что энергия конденсатора превратилась в тепло и энергию света.
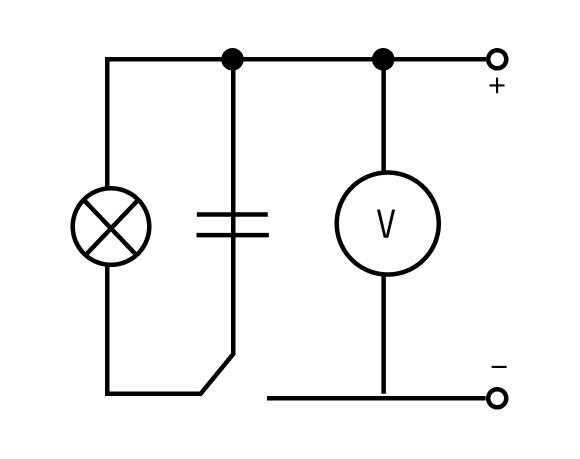
Чтобы вывести формулу энергии плоского конденсатора, нам понадобится формула энергии электростатического поля.
Wp = qEd
Wp — энергия электростатического поля [Дж]
q — электрический заряд [Кл]
E — напряженность электрического поля [В/м]
d — расстояние от заряда [м]
В случае с конденсатором d будет представлять собой расстояние между пластинами.
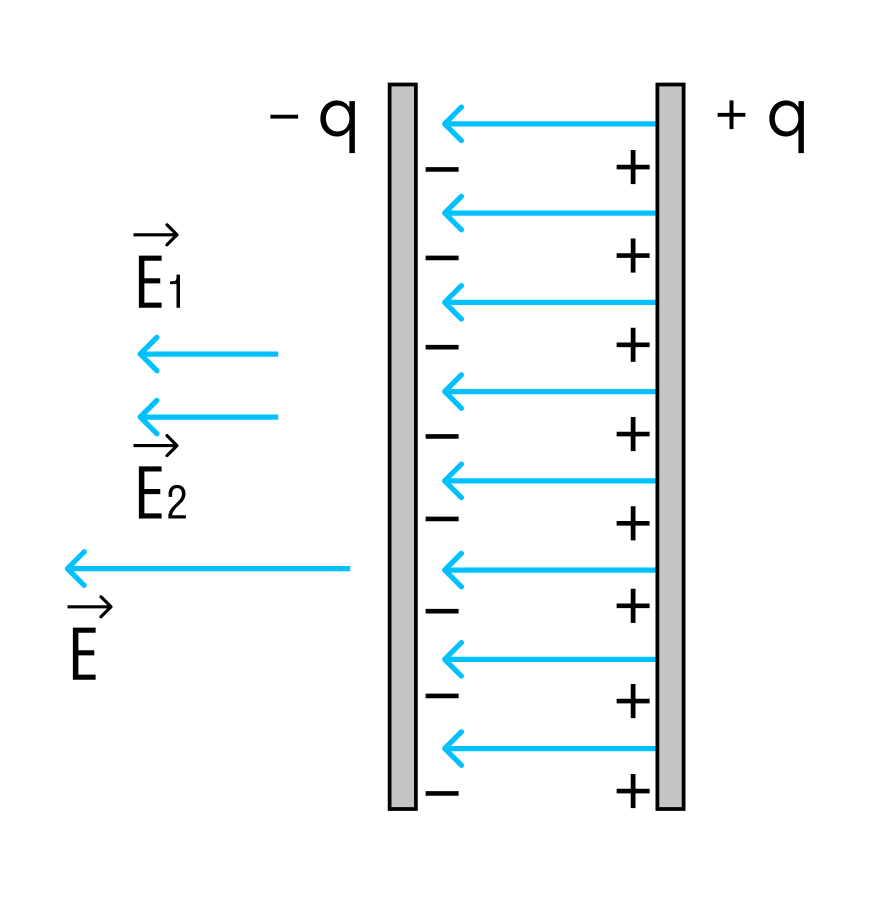
Заряд на пластинах конденсатора равен по модулю, поэтому можно рассматривать напряженность поля, создаваемую только одной из пластин.
Напряженность поля одной пластины равна Е/2, где Е — напряженность поля в конденсаторе.
В однородном поле одной пластины находится заряд q, распределенный по поверхности другой пластины.
Тогда энергия конденсатора равна:
Wp = qEd/2
Разность потенциалов между обкладками конденсатора можно представить, как произведение напряженности на расстояние:
U = Ed
Поэтому:
Wp = qU/2
Эта энергия равна работе, которую совершит электрическое поле при сближении пластин.
Заменив в формуле разность потенциалов или заряд с помощью выражения для электроемкости конденсатора C = q/U, получим три различных формулы энергии конденсатора:
Wp = qU/2
Wp — энергия электростатического поля [Дж]
q — электрический заряд [Кл]
U — напряжение на конденсаторе [В]
Wp = q2/2C
Wp — энергия электростатического поля [Дж]
q — электрический заряд [Кл]
C — электроемкость конденсатора [Ф]
Wp = CU2/2
Wp — энергия электростатического поля [Дж]
C — электроемкость конденсатора [Ф]
U — напряжение на конденсаторе [В]
Эти формулы справедливы для любого конденсатора.
Определение энергии конденсатора
Электроемкость плоского конденсатора
Чтобы выяснить, от чего будут зависеть накопительные характеристики, можно применить две методики. Первая – это определение работы, которая выполняется для распределения зарядов на обкладках. Подразумевается, что для этого понадобится затратить определенную энергию. Во втором варианте пользуются притяжением разноименных зарядов. Для перемещения пластин до прямого контакта нужно выполнить соответствующую работу.
Энергия заряженного конденсатора
Существует еще одна эквивалентная запись заряженного конденсатора при использовании соотношения Q=CU:
We=Q22C=CU22=QU2.
Электрическая энергия We рассматривается как потенциальная. Формулы для We аналогичны формулам потенциальной энергии Ep деформированной пружины, а именно:
Ep=kx22=F22k=Fx2, где k является жесткостью пружины, х – деформацией, F=kx – внешней силой.
Современные представления электрической энергии говорят о том, что она сосредоточена между пластинами конденсатора. В связи с этим и получила название энергии электрического поля. Это объяснимо с помощью иллюстрирования заряженного плоского конденсатора.
Плоский конденсатор.
Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин:
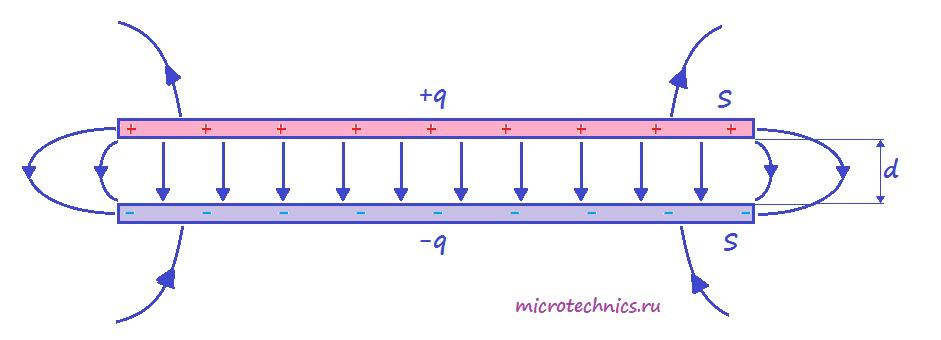
Такое устройство называется плоским конденсатором, а пластины — обкладками конденсатора. Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).
А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит.
Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора:
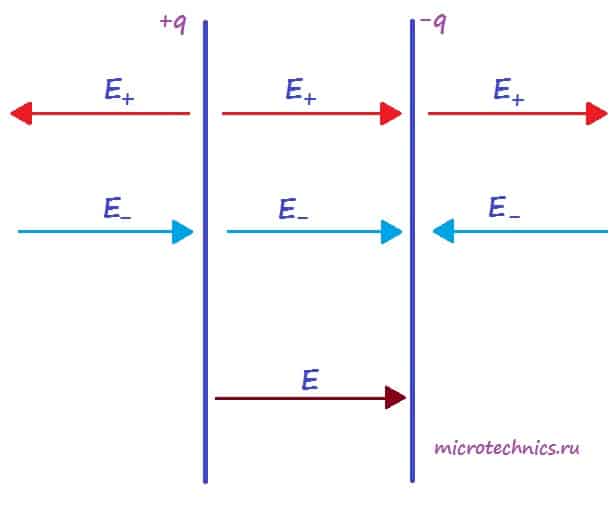
Каждая из обкладок конденсатора в отдельности создает электрическое поле:
- положительно заряженная пластина (+q) создает поле, напряженность которого равна E_{+}
- отрицательно заряженная пластина (-q) создает поле, напряженность которого равна E_{-}
Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом:
E = frac{sigma}{2varepsilon_0thinspacevarepsilon}
Здесь sigma— это поверхностная плотность заряда: sigma = frac{q}{S}, а varepsilon — диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой:
E_+ = E_- = frac{q}{2varepsilon_0thinspacevarepsilon S}
Но направления векторов разные — внутри конденсатора вектора направлены в одну сторону, а вне — в противоположные. Таким образом, внутри обкладок результирующее поле определяется следующим образом:
E = E_+ + E_- = frac{q}{2varepsilon_0thinspacevarepsilon S} + frac{q}{2varepsilon_0thinspacevarepsilon S} = frac{q}{varepsilon_0thinspacevarepsilon S}
А какая же будет величина напряженности вне конденсатора? А все просто — слева и справа от обкладок поля пластин компенсируют друг друга и результирующая напряженность равна 0
Процессы зарядки и разрядки конденсаторов.
С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:
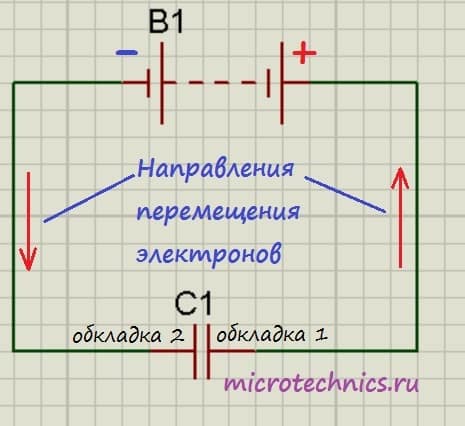
Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить?
Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника. Из-за этого на обкладке возникнет недостаток отрицательно заряженных частиц, и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора. В результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной. Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов. Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока. После этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.
При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:
В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Вот так и происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию.
Из истории
Первым конденсатором считается лейденская банка. Её разработали независимо сразу двое учёных:
- Эвальд Георг фон Клейст (11 октября 1745 года).
- Питер ван Мушенбрук (1745 – 1746 годы).
Двумя десятилетиями позже на свет появился электрофорус (1762 год), рассматриваемый как первый плоский конденсатор. Тогда не существовало терминов, вопросы накопления заряда мало интересовали. Учёные пока что развлекались получением статического заряда. К примеру, ван Мушенбрук испытывал лейденскую банку на слишком смелых студентах, когда сам оказался однажды полупарализован электрическим зарядом.
Наука не шла вперёд, хотя светила, включая Бенджамина Франклина, вовсю толкали паровоз. Современный этап развития физики начался с Алессандро Вольта. Учёный оказался привлечён конструкцией электрофоруса и заинтригован. Натёртая резина могла сколь угодно долго заряжать металлическую пластину. В то время предполагалось, что электричество переносится флюидами атмосферы, и Вольта считал аналогично. Узрев, что электрофорус способен запасать заряд, учёный решил посчитать и количество.
Концепция Вольты
Как свидетельствуют записки учёного, уже в 1778 году он получил представление о разнице потенциалов, которые называл tension – напряжение. С 1775 года Вольта придерживается концепции электрической ёмкости – capacita, выдвинутой его учителем Беккарией. Вольта уже знает, что электрофорус способен накопить заряд, называет прибор конденсатором, и решает подтвердить теорию практикой. Иначе – найти взаимосвязь напряжения, ёмкости и объёмом (quantita) заряда.
Вольта начал с лейденской банки. Он заряжал её от статического генератора и пробовал определить энергию конденсатора тремя путями:
- Наблюдал получаемую искру электрической дуги от различной конструкции лейденских банок, заряженных одинаковым напряжением.
- Измерял количество произведённой электростатическими генераторами трения работу, пока показания электрометра не росли до определённого уровня.
- Разряжал лейденские банки на открытом воздухе и пытался сравнить производимый ими электрический шок по истечении времени.
Все перечисленное привело исследователя к странным выводам, что высокие лейденские банки более вместительные (при одинаковых площадях обкладок и прочих равных условиях). Вероятно, это связано со скоростью разряда их дуги на воздухе вследствие различий в кривизне поверхностей. Силу разряда Вольта увязывал с электрическим током: чем быстрее течёт флюид, тем более жаркий (по ощущениям) эффект. В результате, Вольта счёл, что разница потенциалов единственная определяет процесс возникновения удара. Он решил, что напряжение допустимо измерить двумя путями:
- Через количество оборотов генератора статического заряда.
- Сравнивая силу электрического удара при разряде лейденской банки.
Вольта нашёл, что заряжая пустую лейденскую банку от полной, шок получается вдвое слабее. Постепенно (1782 год) Вольта пришёл к выводу, что вышеуказанные величины соотносятся между собой: tension x capacity ~ load, в современном мире выглядит как U C = q или C = q / U.
Вольта заключил, что ёмкость больше там, где при меньшем напряжении вмещается больше заряда. Последовало заключение, что количество накопленного флюида прямо пропорционально площади обкладок плоского конденсатора. Что согласуется с современными формулами. Вольта обобщил знания на случай произвольного проводника (экспериментировал со стержнями лейденских банок). Изменяя расстояние между обкладками, установил:
С ~ S / d.
Что фактически стало выражением ёмкости плоского конденсатора. Вольта объяснил зависимость наличием некоего сопротивления (resistance) между обкладками, подразумевая воздух. Изменяя дистанцию, удаётся варьировать этот параметр в обе стороны. Это слегка не согласуется с современными концепциями, но Вольта помог Георгу Ому 40 лет спустя вывести зависимость между током и напряжением.
Фактически измерения проделывались на основе работы поля, проявлявшейся лишь вследствие заряда конденсатора. Очевидно, что указанная величина равна энергии – одной из первых физических характеристики, использованных для вывода аналитических выражений.
Единицы измерения
Энергию и работу принято измерять в джоулях, электрическое напряжение и потенциал – в вольтах.
Вольтом называется разница потенциалов, при перемещении единичного положительного заряда между которыми совершается работа в 1 джоуль.
Мера энергии заряженного конденсатора
При расчёте фильтров цепей питания и прочих электрических фильтров встаёт задача определения номиналов. Кажется, достаточно взять формулу частоты резонансного контура, но простота обманчива. Легко убедиться, что одинаковому ответу соответствует множество значений. Которое выбрать?
Чем больше мощность источника, питания прибора, тем большая энергия здесь проходит в единицу времени. Для конденсатора она зависит от квадрата напряжения и ёмкости, для дросселя – от величины электрического тока и индуктивности. Узнав период единственного колебания, эту цифру легко привязать к мощности, как выполняемой работе в единицу времени.
В результате инженер сумеет сказать приблизительно, какого размера ёмкость требуется в конкретном случае. Расчёт ведётся изначально по энергии заряженного конденсатора.
Аналогичное происходит в любой цепи. Конденсаторы служат для фильтрации и гальванической развязки, обязаны легко пропускать нужную частоту и оставаться ёмкими, чтобы не стать бутылочным горлышком в системе.
Калькулятор расчета запасаемой энергии в конденсаторе
| Напряжение (V): | В |
| Емкость (C): | мкФ |
| Сопротивление (R): | Ом |
| T (RC): | секунд |
| E: | Джоулей |
Величина энергии
Как будет вычисляться накопленный энергетический потенциал, разобраться можно с помощью показанного на снимке блока фотовспышки. Следует напомнить о том, что для увеличения емкости применяют параллельное соединение (Cобщ = C1 + C2 +…+ Cn). При последовательном варианте пропорциональная зависимость обратная (1/Cобщ = 1/C1 + 1/C2 +…+ 1/Cn).
Расчет:
- 2 емкости по 400 мкФ (Cобщ = C1 + C2 = 400 + 400 = 800 мкФ);
- источник питания будет заряжать элемент напряжением 300 В;
- энергия конденсатора W = ½ *C * U2 = ½ * 800 * 10-6 * 300 = 0,12 джоуля.
Использование конденсаторов
Подученное соотношение величин характерно для всех типов конденсаторов. Его используют для того, чтобы определить накопленную энергию при подключении к источнику питания. Измерить напряжение на выводах можно с помощью мультиметра. Кроме емкости, на корпусе конденсатора указывают другие важные параметры:
- рабочий ток;
- номинальное напряжение;
- диэлектрический материал;
- тип элемента.
К сведению. На миниатюрных деталях места для размещения всех данных недостаточно. Применяют систему сокращенных кодировок. Необходимые сведения уточняют в сопроводительной документации либо на официальном сайте производителя.
В следующем перечне приведены примеры электротехнических схем и устройств, которые создают с применением конденсаторов:
- частотный (сглаживающий) фильтр;
- колебательный контур;
- накопитель энергии для формирования мощного импульса (лазер, фотовспышка);
- ограничитель силы тока (компенсатор подключаемой реактивной нагрузки);
- измерение перемещений (изменение емкости при сближении/ отдалении обкладок).
Для автоматизированного расчета типовой схемы можно использовать специализированный калькулятор онлайн. Следующий пример демонстрирует расчет корректного подключения электродвигателя:
- соединение обмоток – треугольник;
- мощность потребления – 1 200 Вт;
- напряжения сети – 220 В;
- cos ϕ – 0,9;
- КПД – 85%;
- емкость рабочего (пускового) конденсатора – 52 (130) мкФ.
Как рассчитать емкость конденсатора
Расчеты, производимые с помощью онлайн калькулятора, позволяют вычислить емкость конденсатора в течение нескольких секунд. Кроме этого параметра, можно определить показатели заряда, мощности, тока, энергии и прочих качеств конденсатора, необходимых в конкретном устройстве.
Наиболее часто встречаются электролитические конденсаторы, применяемые в схеме асинхронного электродвигателя. Конструкции этих устройств могут быть полярными или неполярными. В первом случае отмечается более высокая емкость, поэтому перед подключением конденсатора к двигателю, необходимо в обязательном порядке выполнить расчеты. С помощью проводимых вычислений устанавливается необходимая емкость, соответствующая конкретному двигателю.
Особое значение придается дополнительным расчетам при эксплуатации трехфазных электродвигателей. В обычном режиме конденсатор функционирует нормально, однако при включении в однофазную сеть, его емкость заметно снижается. Это приводит к увеличению частоты вращения вала. Предварительные расчеты и правильное подключение позволяют избежать подобных ситуаций.

При запуске асинхронного двигателя, работающего от напряжения 220 вольт, требуется конденсатор с высокой емкостью. В связи с этим, невозможно обойтись без проведения расчетов с помощью онлайн калькулятора. Проведение расчетов полностью зависит от способа соединения обмоток электродвигателя. Данное соединение может быть выполнено двумя способами – звездой и треугольником. В первом случае применяется формула Ср=2800хI/U, а для второго случая используется немного измененная формула Ср=4800хI/U.
Следует учитывать, что в цепочке соединенных конденсаторов емкость пускового устройства должна быть примерно в три раза выше, чем в рабочем приборе. Для расчета применяется формула Сп=2.5хСр, в которой Сп и Ср являются соответственно пусковым и рабочим конденсатором.
Следующая
РазноеЧто такое активная мощность?
