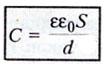Как найти энергию конденсатора в момент времени - Сайт, где вы сможете решить свои вопросы

Конденсатор. Энергия электрического поля

Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.
Ёмкость уединённого проводника
Ёмкость плоского конденсатора
Энергия заряженного конденсатора
Энергия электрического поля

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.

Предыдущие две статьи были посвящены отдельному рассмотрению того, каким образом ведут себя в электрическом поле проводники и каким образом — диэлектрики. Сейчас нам понадобится объединить эти знания. Дело в том, что большое практическое значение имеет совместное использование проводников и диэлектриков в специальных устройствах — конденсаторах.

Но прежде введём понятие электрической ёмкости.

к оглавлению ▴

Ёмкость уединённого проводника

Предположим, что заряженный проводник расположен настолько далеко от всех остальных тел, что взаимодействие зарядов проводника с окружающими телами можно не принимать во внимание. В таком случае проводник называется уединённым.

Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение varphi , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду. Коэффициент пропорциональности принято обозначать 1/C , так что

$varphi = frac{displaystyle q}{displaystyle C vphantom{1^a}}.$

Величина называется электрической ёмкостью проводника и равна отношению заряда проводника к его потенциалу:

$C = frac{displaystyle q}{displaystyle varphi }.$ (1)

Например, потенциал уединённого шара в вакууме равен:

$varphi = frac{displaystyle kq}{displaystyle R vphantom{1^a}}=frac{displaystyle q}{displaystyle 4 pi varepsilon_0R vphantom{1^a}},$

где — заряд шара, — его радиус. Отсюда ёмкость шара:

(2)

Если шар окружён средой-диэлектриком с диэлектрической проницаемостью , то его потенциал уменьшается в раз:

$varphi = frac{displaystyle q}{displaystyle 4 pi varepsilon_0 varepsilon R vphantom{1^a}}.$

Соответственно, ёмкость шара в раз увеличивается:

(3)

Увеличение ёмкости при наличии диэлектрика — важнейший факт. Мы ещё встретимся с ним при рассмотрении конденсаторов.

Из формул (2) и (3) мы видим, что ёмкость шара зависит только от его радиуса и диэлектрической проницаемости окружающей среды. То же самое будет и в общем случае: ёмкость уединённого проводника не зависит от его заряда; она определяется лишь размерами и формой проводника, а также диэлектрической проницаемостью среды, окружающей проводник. От вещества проводника ёмкость также не зависит.

В чём смысл понятия ёмкости? Ёмкость показывает, какой заряд нужно сообщить проводнику, чтобы увеличить его потенциал на В. Чем больше ёмкость — тем, соответственно, больший заряд требуется поместить для этого на проводник.

Единицей измерения ёмкости служит фарад (Ф). Из определения ёмкости (1) видно, что Ф = Кл/В.

Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным 6400 км.

$C = 4 pi varepsilon_0 R approx 4 cdot 3,14 cdot 8,85 cdot 10^{-12} cdot 6400 cdot 10^3 approx 712$ мкФ.

Как видите, Ф — это очень большая ёмкость.

Единица измерения ёмкости полезна ещё и тем, что позволяет сильно сэкономить на обозначении размерности диэлектрической постоянной . В самом деле, выразим из формулы (2):

$varepsilon_0 = frac{displaystyle C} {displaystyle 4 pi R vphantom{1^a}}.$

Следовательно, диэлектрическая постоянная может измеряться в Ф/м:

$varepsilon_0 = 8,85 cdot 10^{-12}$ Ф.

Так легче запомнить, не правда ли?

к оглавлению ▴

Ёмкость плоского конденсатора

Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.

Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости — но на сей раз о ёмкости этой системы проводников.

Наиболее простым и важным примером такой системы является плоский конденсатор. Он состоит из двух параллельных металлических пластин (называемых обкладками), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров.

Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух

Пусть заряды обкладок равны и . Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина — заряд положительной обкладки — называется зарядом конденсатора.

Пусть — площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.

Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости:

$E_+ = E_-=frac{displaystyle sigma }{displaystyle 2 varepsilon_0 vphantom{1^a}}.$

Здесь E_+ — напряжённость поля положительной обкладки, E_- — напряженность поля отрицательной обкладки, sigma — поверхностная плотность зарядов на обкладке:

$sigma =frac{displaystyle q}{displaystyle S vphantom{1^a}}.$

На рис. 1 (слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора.

Рис. 1. Электрическое поле плоского конденсатора

Согласно принципу суперпозиции, для результирующего поля vec{E} имеем:

$vec{E} = vec{E}_+ + vec{E}_-$

Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга):

Внутри конденсатора поле удваивается:

$E = E_+ + E_-= frac{displaystyle sigma }{displaystyle varepsilon_0},$

или

$E = frac{displaystyle q}{displaystyle varepsilon_0 S vphantom{1^a}}.$ (4)

Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак:

Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4). Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.

Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты: поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.

Пусть расстояние между обкладками конденсатора равно . Поскольку поле внутри конденсатора является однородным, разность потенциалов между обкладками равна произведению на (вспомните связь напряжения и напряжённости в однородном поле!):

$U=Ed=frac{displaystyle qd}{displaystyle varepsilon_0 S vphantom{1^a}}.$ (5)

Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками:

$C=frac{displaystyle q}{displaystyle U vphantom{1^a}}.$ (6)

Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на В. Формула (6), таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.

Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора:

$C=frac{displaystyle varepsilon_0 S}{displaystyle d vphantom{1^a}}.$ (7)

Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними.
Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Как изменится ёмкость конденсатора?

Напряжённость поля внутри конденсатора уменьшится в раз, так что вместо формулы (4) теперь имеем:

$E=frac{displaystyle q}{displaystyle varepsilon_0 varepsilon S vphantom{1^a}}.$ (8)

Соответственно, напряжение на конденсаторе:

$U=Ed=frac{displaystyle qd}{displaystyle varepsilon_0 varepsilon S vphantom{1^a}}.$ (9)

Отсюда ёмкость плоского конденсатора с диэлектриком:

$C=frac{displaystyle varepsilon_0 varepsilon S}{displaystyle d vphantom{1^a}}.$ (10)

Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор.

Важное следствие формулы (10): заполнение конденсатора диэлектриком увеличивает его ёмкость.

к оглавлению ▴

Энергия заряженного конденсатора

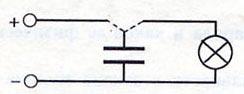
Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится.

Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке. Нетрудно понять, что этой энергией является потенциальная энергия взаимодействия обкладок конденсатора — ведь обкладки, будучи заряжены разноимённо, притягиваются друг к другу.

Мы сейчас вычислим эту энергию, а затем увидим, что существует и более глубокое понимание происхождения энергии заряженного конденсатора.

Начнём с плоского воздушного конденсатора. Ответим на такой вопрос: какова сила притяжения его обкладок друг к другу? Величины используем те же: заряд конденсатора , площадь обкладок .

Возьмём на второй обкладке настолько маленькую площадку, что заряд q_0 этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой

где E_1 — напряжённость поля первой обкладки:

$E_1=frac{displaystyle sigma }{displaystyle 2 varepsilon _0 vphantom{1^a}}=frac{displaystyle q}{displaystyle 2varepsilon_0 S vphantom{1^a}}.$

Следовательно,

$F_0=frac{displaystyle q_0q}{displaystyle 2 varepsilon_0 S vphantom{1^a}}.$

Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам).

Результирующая сила притяжения второй обкладки к первой складывается из всех этих сил F_0 , с которыми притягиваются к первой обкладке всевозможные маленькие заряды q_0 второй обкладки. При этом суммировании постоянный множитель вынесется за скобку, а в скобке просуммируются все q_0 и дадут . В результате получим:

$F=frac{displaystyle q^2}{displaystyle 2 varepsilon_0 S vphantom{1^a}}.$ (11)

Предположим теперь, что расстояние между обкладками изменилось от начальной величины d_1 до конечной величины d_2 . Сила притяжения пластин совершает при этом работу:

Знак правильный: если пластины сближаются , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины , то работа силы притяжения получается отрицательной, как и должно быть.

С учётом формул (11) и (7) имеем:

$A=frac{displaystyle q^2}{displaystyle 2 varepsilon_0 S vphantom{1^a}}left ( d_1-d_2 right )=frac{displaystyle q^2d_1}{displaystyle 2varepsilon_0 S vphantom{1^a}}-frac{displaystyle q^2d_2}{displaystyle 2varepsilon_0 S vphantom{1^a}}=frac{displaystyle q^2}{displaystyle 2C_1 vphantom{1^a}}-frac{displaystyle q^2}{displaystyle 2C_2 vphantom{1^a}}=W_1-W_2,$

где
$W_1=frac{displaystyle q^2}{displaystyle 2C_1 vphantom{1^a}},$
$W_2=frac{displaystyle q^2}{displaystyle 2C_2 vphantom{1^a}}$

Это можно переписать следующим образом:

где

$W=frac{displaystyle q^2}{displaystyle 2C vphantom{1^a}}.$ (12)

Работа потенциальной силы притяжения обкладок оказалась равна изменению со знаком минус величины . Это как раз и означает, что — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора.

Используя соотношение q = CU , из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):

$W=frac{displaystyle qU}{displaystyle 2 vphantom{1^a}},$ (13)

$W=frac{displaystyle CU^2}{displaystyle 2 vphantom{1^a}}.$ (14)

Особенно полезными являются формулы (12) и (14).

Допустим теперь, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью . Сила притяжения обкладок уменьшится в раз, и вместо (11) получим:

$F=frac{displaystyle q^2}{displaystyle 2 varepsilon_0 varepsilon S vphantom{1^a}}.$

При вычислении работы силы , как нетрудно видеть, величина войдёт в ёмкость , и формулы (12) — (14) останутся неизменными. Ёмкость конденсатора в них теперь будет выражаться по формуле (10).

Итак, формулы (12) — (14) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.

к оглавлению ▴

Энергия электрического поля

Мы обещали, что после вычисления энергии конденсатора дадим более глубокое истолкование происхождения этой энергии. Что ж, приступим.

Рассмотрим воздушный конденсатор и преобразуем формулу (14) для его энергии:

$W=frac{displaystyle CU^2}{displaystyle 2 vphantom{1^a}}=frac{displaystyle varepsilon_0 S}{displaystyle d vphantom{1^a}} cdot frac{displaystyle (Ed)^2}{displaystyle 2 vphantom{1^a}}=frac{displaystyle varepsilon_0 E^2}{displaystyle 2 vphantom{1^a}}Sd.$

Но Sd = V — объём конденсатора. Получаем:

$W=frac{displaystyle varepsilon_0 E^2}{displaystyle 2 vphantom{1^a}}V.$ (15)

Посмотрите внимательно на эту формулу. Она уже не содержит ничего, что являлось бы специфическим для конденсатора! Мы видим энергию электрического поля , сосредоточенного в некотором объёме .

Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.

Итак, электрическое поле само по себе обладает энергией. Ничего удивительного для нас тут нет. Радиоволны, солнечный свет — это примеры распространения энергии, переносимой в пространстве электромагнитными волнами.

Величина — энергия единицы объёма поля — называется объёмной плотностью энергии. Из формулы (15) получим:

$omega =frac{displaystyle varepsilon_0 E^2}{displaystyle 2 vphantom{1^a}}.$ (16)

В этой формуле не осталось вообще никаких геометрических величин. Она даёт максимально чистую связь энергии электрического поля и его напряжённости.

Если конденсатор заполнен диэлектриком, то его ёмкость увеличивается в раз, и вместо формул (15) и (16) будем иметь:

$W =frac{displaystyle varepsilon_0 varepsilon E^2}{displaystyle 2 vphantom{1^a}}V.$ (17)

$omega =frac{displaystyle varepsilon_0 varepsilon E^2}{displaystyle 2 vphantom{1^a}}.$ (18)

Как видим, энергия электрического поля зависит ещё и от диэлектрической проницаемости среды, в которой поле находится.
Замечательно, что полученные формулы для энергии и плотности энергии выходят далеко за пределы электростатики: они справедливы не только для электростатического поля, но и для электрических полей, меняющихся во времени.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Конденсатор. Энергия электрического поля» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Конденсаторы часто применяются в электрических схемах, помогая трансформировать электросигнал под определенные характеристики. Используя их основное свойство — накапливать электрический заряд, можно регулировать прохождение тока по цепи, убирать нежелательные пульсации напряжения или повысить энергоэффективность сети. При решении подобных задач в расчет берутся конкретные параметры того или иного электронакопителя, а также общие процессы, связанные с зарядом и разрядом конденсаторов.

Заряд конденсатора
Процессы зарядки и разрядки конденсаторов
Емкость и энергия конденсатора
Как зарядить конденсатор
Время, необходимое для зарядки конденсатора
Заряд конденсатора: формула
Время разряда конденсатора

Заряд конденсатора

Устройство обычного конденсатора состоит из двух пластин (обкладок), подключаемых к выходам цепи, и диэлектрика между ними. При этом величина заряда, накаливаемого конденсатором, зависит от его емкостной характеристики основных параметров: площади обкладок, толщины и диэлектрических свойств прокладочного материала.

Емкость конденсатора определяется по формуле:

C = S • ε • ε0 / d,

где S – площадь обкладок, ε — диэлектрическая проницаемость прокладки, ε0 — диэлектрическая постоянная (8,85•10-12 Ф/м), d – расстояние между пластинами.

Конденсируемый же заряд равняется произведению емкости конденсатора на напряжение в цепи: q = С × U.

Процессы зарядки и разрядки конденсаторов

При включении конденсатора в цепь через него начинает проходить ток. С движением электронов по проводнику на одной обкладке устройства скапливается отрицательный заряд, а на другой (при недостатке электронов) — положительный. Между пластинами образуется индуктивное поле, создающее разность потенциалов определенного значения. В проводниках постоянного тока накопление заряда идет до тех пор, пока уровень напряжения на обкладках не сравняется с номинальным напряжением элемента питания, после чего течение электротока останавливается.

Когда цепь размыкается и на конденсатор не подается напряжение, он может сохранять заряд на протяжение определенного времени, а затем с исчезновением электрического поля между пластинами заряд начнет перетекать в проводник. Процесс разряда конденсатора характеризуется переходом электронов с одной обкладки на другую. Конденсатор разряжается полностью, когда количество свободных электронов на обеих пластинах сравнивается. При этом все электродинамические процессы в цепи прекращаются.

Емкость и энергия конденсатора

Конденсатор, как и всякий объект, получающий электрический заряд, обладает энергией. Для его зарядки требуется определенная работа, которая идет на разделение заряженных частиц — именно она считается энергией конденсаторного устройства. Ее можно увидеть, если заряженный конденсатор присоединить, например, к светодиоду. Накопитель отдаст заряд лампочке, и она на некоторое время загорится, тем самым энергия перейдет в свет и тепло.

Для определения энергии конденсатора в расчет берут количество заряда, толщину диэлектрика и напряженность электрического поля. Последняя является векторной величиной и представляет собой силу, действующую на точечный заряд.

Поскольку заряды на обкладках равны между собой по модулю, во внимание принимается только значение напряженности одной из них, а значит, эта величина делится пополам — Е/2. Общая же энергия определяется по формуле:

Wp = qEd/2.

Произведение напряженности на расстояние между пластинами само себе представляет разность потенциалов или напряжение — U = E × d. Таким образом, энергию можно выразить через заряд и напряжение на конденсаторе. Формула будет иметь следующий вид:

Wp = qU/2.

Учитывая, что заряд и напряжение находятся в зависимости от емкости конденсатора, можно вывести еще пару формул энергии:

Wp = q2/2C

Wp = CU2/2

Как зарядить конденсатор

Для зарядки конденсатора требуется генератор электротока. Возникающие при этом процессы удобнее разобрать на примере простой цепи, включающей в себя конденсатор (С) и резистор (R).

Зарядка конденсатора от источника постоянной ЭДС

В соответствии с законом Ома разность потенциалов, возникающая на резисторе и конденсаторе, суммарно равна электродвижущей силе генератора тока. Математически это можно представить следующими формулами:

UC = q/C – напряжение конденсатора;

UR = IR – напряжение резистора;

ε = UC + UR – ЭДС источника.

Для пояснения зарядного процесса определим равенство

IR = ε – q / C.

Эта формула представляет динамические изменения заряда силы тока. Более конкретно это может быть выражено уравнением:

I = dq / dt.

Изменение заряда во времени можно подставить к сопротивлению. Соответственно, получаем

R • dq / dt = ε – q / C.

В строгом смысле это уравнение предписывает бесконечное время зарядки конденсаторного устройства. Однако этим можно пренебречь, если учесть, что заряд фактически дискретен и может быть подвержен случайным изменением и флуктуациям. Таким образом, в данном выражении имеются в виду усредненная динамика зарядного процесса. На его основании можно записать изменение ЭДС и составляющих напряжений обоих элементов цепи:

dε = d(IR) + d(q/C).

Фактически ЭДС генератора не меняется во времени, а значит, dε = 0, а емкость конденсатора и сопротивление обладают постоянными значениями, поэтому их можно обозначить без d:

R • dI = — 1/C • dq.

Поделив данное уравнение на временной период, за который заряжается конденсатор, можно вывести выражение, учитывающее корреляцию между динамикой заряда и силой тока:

dI / dt = –I/RC.

Это уравнение означает отношение скорости, с которой уменьшается сила тока к ее фактическому значению.

В начале процесса заряда конденсатора значение q равняется нулю. В этот момент при наибольшей разнице напряжений источника питания и электронакопителя сила тока имеет максимальное значение. По мере увеличения заряда значение I постепенно падает. Когда конденсатор заряжается полностью, его напряжение сравнивается с ЭДС генератора, а сила тока принимает значение 0. Соответственно, электродинамический процесс прекращается.

Дополнительно можно рассмотреть, как в процессе зарядки трансформируется энергия. Вполне очевидно, что генератор тока является причиной возникновения электротока в цепи и, следовательно, заряда электронакопителя.

В этом усматривается некое противоречие: когда конденсатор получает от генератора тока заряд q, это значит, что ЭДС выполнила работу равную заряду (А = qe), однако энергия самого накопителя определяется по формуле W = q2 / 2C = qε / 2, что составляет только половину от работы, произведенной источником питания. Этот парадокс объясняется самим фактом прохождения тока по электроцепи, которое сопровождается выделением тепловой энергии на резисторе, то есть определенное количество энергопотери приходится на тепло.

Дифференциальные расчеты для малых отрезков времени процесса зарядки показывают, что энергия от генератора, действительно, разделяется на электрическую, идущую на заряд конденсаторного устройства, и тепловую. При этом сопротивление цепи само по себе никак не влияет на количество выделяемой теплоты, которое равняется энергии конденсатора.

Заряд конденсатора, ток

При подключении конденсатора к источнику тока в начале зарядки заряд на пластинах практически отсутствует. Максимальное значение I в этой ситуации объясняется минимальным сопротивлением. С увеличением заряженных частиц, возрастает сопротивление индуктивного поля, которое препятствует прохождению тока по проводнику.

Период времени, за начальную точку которого берут момент наибольшей силы тока, а за конечную полное прекращение движения заряженных частиц, носит название переходного периода зарядки конденсатора.

Начальный момент зарядки конденсатора характеризуется нулевым напряжением между его пластинами. Показатель U начинает возрастать с появлением на обкладках разноименно заряженных частиц. Большая сила тока в начале процесса обусловливает большую скорость увеличения напряжения. По мере ее падения рост напряжения замедляется, достигнув максимального значения при полной зарядке электронакопителя.

График увеличения напряжения имеет вид параболы, будучи противоположным графику снижения силы тока.

Математически динамическую взаимозависимость тока, напряжения и емкости конденсатора можно выразить следующим образом:

I = С • dV / dt.

Время, необходимое для зарядки конденсатора

Время зарядки конденсатора определяется его емкостью, электродвижущей силой генератора тока, напряжением и сопротивлением в цепи.

Заряд конденсатора описывается как экспоненциальный процесс. Чтобы оценить его время, принимается, что значение заряда увеличивается равномерно, при этом скорость заряда приравнивается к силе тока в начале процесса. Отсюда следует уравнение постоянной времени:

τ = q / I0 = RC.

Зависимость динамики напряжения от длительности зарядки определяется по следующей формуле:

U(t) = UC • (1 – e-t/τ).

Значение высчитывается с привлечением основания натурального логарифма (е), которое относится к функции экспоненты и равняется приблизительно 2,718. При этом UC обозначает напряжение ЭДС источника.

Процент заряда по постоянной времени τ определяется в соответствии с формулой:

(1 — 1/еτ) • 100%.

Таким образом, конденсатор достигает почти полной зарядки за 5 τ.

• 1 τ — 63,2%;

• 2 τ — 86,5%

• 3 τ — 95,1%

• 4 τ — 98,2%

• 5 τ — 99,3%

Учитывая экспоненциальный характер увеличения напряжения конденсатора, можно сказать, что время его зарядки до уровня ЭДС генератора длится бесконечно долго.

Заряд конденсатора: формула

Конденсатор заряжается довольно быстро. Обычно для этого достаточно нескольких миллисекунд. Равенство напряжения электродвижущей силы источника питания и электронакопителя определяет максимальный заряд конденсатора. Формула заряда может быть определена с учетом общих параметров конденсатора:

q = Uεε0S/d.

Также можно принять во внимание конструкционные особенности конденсатора. Так, для цилиндрического накопителя заряд равняется:

q = U2πεε0l/ln(r2/r1),

где l – высота цилиндров, r2 – радиус наружной пластины, r1 — радиус внутренней пластины.

Время разряда конденсатора

Если конденсатор переключить на нагрузку резистора, он сам станет источником питания и будет отдавать заряд в цепь. Движение тока при этом начинается от пластины с отрицательным зарядом на положительно заряженную пластину и далее по контуру. Напряжение в начальный момент будет такое же как и после полной зарядки накопителя. В соответствии с законом Ома можно определить и первоначальную силу тока:

IC = UC / R.

Отдавая заряд, конденсатор будет терять напряжение. Соответственно будет уменьшаться и сила тока. Снижение обоих показателей идет по экспоненциальной кривой с замедлением скорости падения. Это значит, что динамику разрядки конденсатора можно описать, как и в случае зарядки, при помощи постоянной времени τ.

Изменение основных электрических показателей при заряде и разряде конденсатора играют ключевую роль в электротехнике и радиоэлектронике. Эта функциональность в полной мере проявляется в цепях переменного тока, где оба процесса сменяют друг друга с определенной периодичностью. На частотно-зависимых качествах электронакопителей основан принцип действия таких электроустановок, как колебательные контуры, реле времени, цепи обратной связи, частотные фильтры и другие.

Понравилась статья? Расскажите друзьям:

Оцените статью, для нас это очень важно:

Проголосовавших: 3 чел.
Средний рейтинг: 5 из 5.

Источник

Электрическая
ёмкость —
характеристика проводника, мера его
способности накапливать электрический
заряд.
В теории электрических цепей ёмкостью
называют взаимную ёмкость между двумя
проводниками; параметр ёмкостного
элемента электрической схемы,
представленного в виде двухполюсника.
Такая ёмкость определяется как отношение
величины электрического заряда к разности
потенциалов между
этими проводниками.

В системе СИ ёмкость
измеряется в фарадах.
В системе СГС в сантиметрах.

Для одиночного
проводника ёмкость равна отношению
заряда проводника к его потенциалу в
предположении, что все другие
проводники бесконечно удалены
и что потенциал бесконечно удалённой
точки принят равным нулю. В математической
форме данное определение имеет вид

где — заряд, —
потенциал проводника.

Ёмкость определяется
геометрическими размерами и формой
проводника и электрическими свойствами
окружающей среды (еёдиэлектрической
проницаемостью)
и не зависит от материала проводника.
К примеру, ёмкость проводящего шара
радиуса R равна
(в системе СИ):

Понятие ёмкости
также относится к системе проводников,
в частности, к системе двух проводников,
разделённых диэлектриком —конденсатору.
В этом случае взаимная
ёмкость этих
проводников (обкладок конденсатора)
будет равна отношению заряда, накопленного
конденсатором, к разности потенциалов
между обкладками. Для плоского конденсатора
ёмкость равна:

где S —
площадь одной обкладки (подразумевается,
что они равны), d —
расстояние между обкладками, ε — относительная
диэлектрическая проницаемость среды
между обкладками, ε₀ =
8.854·10⁻¹² Ф/м
— электрическая
постоянная.

Конденса́тор (от лат. condensare —
«уплотнять», «сгущать») — двухполюсник с
определённым значением ёмкости и
малой омической проводимостью;
устройство для накопления заряда и
энергии электрического поля. Конденсатор
является пассивным электронным
компонентом. Обычно состоит из двух
электродов в форме пластин
(называемых обкладками),
разделённыхдиэлектриком,
толщина которого мала по сравнению с
размерами обкладок.

Виды конденсаторов:
1.
по виду диэлектрика: воздушные, слюдяные,
керамические, электролитические
2. по
форме обкладок: плоские, сферические.
3.
по величине емкости: постоянные,
переменные (подстроечные).

Электроемкость
плоского конденсатора

где
S – площадь пластины (обкладки) конденсатора
d
– расстояние между пластинами
eо –
электрическая постоянная
e –
диэлектрическая проницаемость диэлектрика

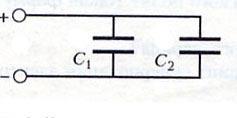
Включение
конденсаторов в электрическую цепь

параллельное

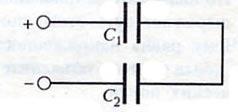
последовательное

ЭНЕРГИЯ ЗАРЯЖЕННОГО
КОНДЕНСАТОРА

Конденсатор – это
система заряженных тел и обладает
энергией.
Энергия любого конденсатора:

где
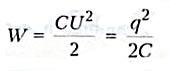
С – емкость конденсатора
q – заряд
конденсатора
U – напряжение на обкладках
конденсатора
Энергия конденсатора
равна работе, которую совершит
электрическое поле при сближении пластин
конденсатора вплотную,
или равна
работе по разделению положительных и
отрицательных зарядов , необходимой
при зарядке конденсатора.

ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО
ПОЛЯ КОНДЕНСАТОРА

Энергия конденсатора
приблизительно равна квадрату
напряженности эл. поля внутри
конденсатора.
Плотность энергии эл.
поля конденсатора:

13.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Содержание

1 Колебательный контур
- 1.1 Энергии контура
- 1.2 Процессы в колебательном контуре
- 1.3 Свободные электромагнитные колебания
  - 1.3.1 *Вывод формулы Томсона
2 Литература

Колебательный контур

Электромагнитные колебания – это периодические изменения со временем электрических и магнитных величин в электрической цепи.

Свободными называются такие колебания, которые возникают в замкнутой системе вследствие отклонения этой системы от состояния устойчивого равновесия.

При колебаниях происходит непрерывный процесс превращения энергии системы из одной формы в другую. В случае колебаний электромагнитного поля обмен может идти только между электрической и магнитной составляющей этого поля. Простейшей системой, где может происходить этот процесс, является колебательный контур.

Идеальный колебательный контур (LC-контур) — электрическая цепь, состоящая из катушки индуктивностью L и конденсатора емкостью C.

В отличие от реального колебательного контура, который обладает электрическим сопротивлением R, электрическое сопротивление идеального контура всегда равна нулю. Следовательно, идеальный колебательный контур является упрощенной моделью реального контура.

На рисунке 1 изображена схема идеального колебательного контура.

Энергии контура

Полная энергия колебательного контура

(W=W_{e} + W_{m}, ; ; ; W_{e} =dfrac{Ccdot u^{2} }{2} = dfrac{q^{2} }{2C}, ; ; ; W_{m} =dfrac{Lcdot i^{2}}{2},)

где W_e — энергия электрического поля колебательного контура в данный момент времени, С — электроемкость конденсатора, u — значение напряжения на конденсаторе в данный момент времени, q — значение заряда конденсатора в данный момент времени, W_m — энергия магнитного поля колебательного контура в данный момент времени, L — индуктивность катушки, i —значение силы тока в катушке в данный момент времени.

Процессы в колебательном контуре

Рассмотрим процессы, которые возникают в колебательном контуре.

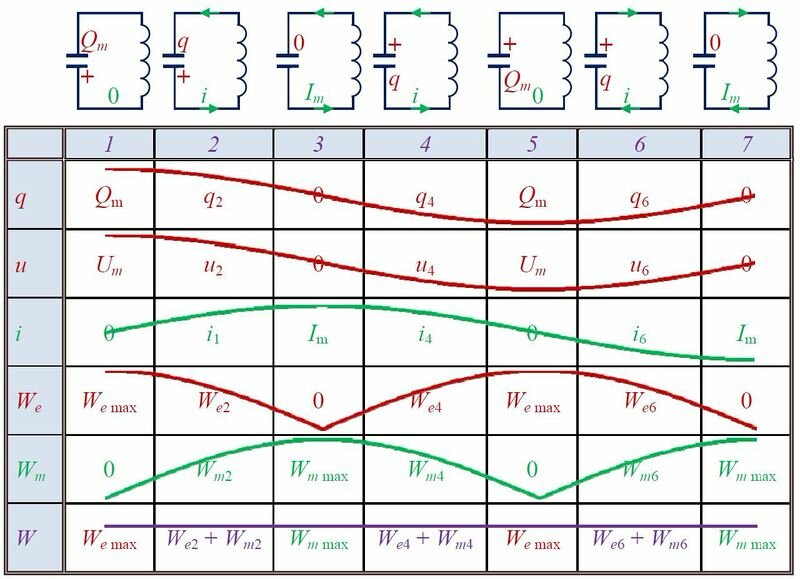
Для выведения контура из положения равновесия зарядим конденсатор так, что на его обкладках будет заряд Q_m (рис. 2, положение 1). С учетом уравнения (U_{m}=dfrac{Q_{m}}{C}) находим значение напряжения на конденсаторе. Тока в цепи в этом момент времени нет, т.е. i = 0.

После замыкания ключа под действием электрического поля конденсатора в цепи появится электрический ток, сила тока i которого будет увеличиваться с течением времени. Конденсатор в это время начнет разряжаться, т.к. электроны, создающие ток, (Напоминаю, что за направление тока принято направление движения положительных зарядов) уходят с отрицательной обкладки конденсатора и приходят на положительную (см. рис. 2, положение 2). Вместе с зарядом q будет уменьшаться и напряжение u (left(u = dfrac{q}{C} right).) При увеличении силы тока через катушку возникнет ЭДС самоиндукции, препятствующая изменению силы тока. Вследствие этого, сила тока в колебательном контуре будет возрастать от нуля до некоторого максимального значения не мгновенно, а в течение некоторого промежутка времени, определяемого индуктивностью катушки.

Заряд конденсатора q уменьшается и в некоторый момент времени становится равным нулю (q = 0, u = 0), сила тока в катушке достигнет некоторого значения I_m (см. рис. 2, положение 3).

Без электрического поля конденсатора (и сопротивления) электроны, создающие ток, продолжают свое движение по инерции. При этом электроны, приходящие на нейтральную обкладку конденсатора, сообщают ей отрицательный заряд, электроны, уходящие с нейтральной обкладки, сообщают ей положительный заряд. На конденсаторе начинает появляться заряд q (и напряжение u), но противоположного знака, т.е. конденсатор перезаряжается. Теперь новое электрическое поле конденсатора препятствует движению электронов, поэтому сила тока i начинает убывать (см. рис. 2, положение 4). Опять же это происходит не мгновенно, поскольку теперь ЭДС самоиндукции стремится скомпенсировать уменьшение тока и «поддерживает» его. А значение силы тока I_m (в положении 3) оказывается максимальным значением силы тока в контуре.

Далее сила тока становится равной нулю, а заряд конденсатора достигнет максимального значения Q_m (U_m) (см. рис. 2, положение 5).

И снова под действием электрического поля конденсатора в цепи появится электрический ток, но направленный в противоположную сторону, сила тока i которого будет увеличиваться с течением времени. А конденсатор в это время будет разряжаться (см. рис. 2, положение 6)до нуля (см. рис. 2, положение 7). И так далее.

Так как заряд на конденсаторе q (и напряжение u) определяет его энергию электрического поля W_e (left(W_{e}=dfrac{q^{2}}{2C}=dfrac{C cdot u^{2}}{2} right),) а сила тока в катушке i — энергию магнитного поля Wm (left(W_{m}=dfrac{L cdot i^{2}}{2} right),) то вместе с изменениями заряда, напряжения и силы тока, будут изменяться и энергии.

Обозначения в таблице:

(W_{e, max } =dfrac{Q_{m}^{2} }{2C} =dfrac{Ccdot U_{m}^{2} }{2}, ; ; ; W_{e, 2} =dfrac{q_{2}^{2} }{2C} =dfrac{Ccdot u_{2}^{2} }{2}, ; ; ; W_{e, 4} =dfrac{q_{4}^{2} }{2C} =dfrac{Ccdot u_{4}^{2} }{2}, ; ; ; W_{e, 6} =dfrac{q_{6}^{2} }{2C} =dfrac{Ccdot u_{6}^{2} }{2},)

(W_{m; max } =dfrac{Lcdot I_{m}^{2} }{2}, ; ; ; W_{m2} =dfrac{Lcdot i_{2}^{2} }{2}, ; ; ; W_{m4} =dfrac{Lcdot i_{4}^{2} }{2}, ; ; ; W_{m6} =dfrac{Lcdot i_{6}^{2} }{2}.)

Полная энергия идеального колебательного контура сохраняется с течением времени, поскольку в нем потерь энергии (нет сопротивления). Тогда

(W=W_{e, max } = W_{m, max } = W_{e2} + W_{m2} = W_{e4} +W_{m4} = …)

Свободные электромагнитные колебания

Таким образом, в идеальном LC-контуре будут происходить периодические изменения значений силы тока i, заряда q и напряжения u, причем полная энергия контура при этом будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.

Свободные электромагнитные колебания в контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без потребления энергии от внешних источников.

Таким образом, возникновение свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора и возникновением ЭДС самоиндукции в катушке, которая «обеспечивает» эту перезарядку. Заметим, что заряд конденсатора q и сила тока в катушке i достигают своих максимальных значений Q_m и I_m в различные моменты времени.

Свободные электромагнитные колебания в контуре происходят по гармоническому закону:

(q=Q_{m} cdot cos left(omega cdot t+varphi _{1} right), ; ; ; u=U_{m} cdot cos left(omega cdot t+varphi _{1} right), ; ; ; i=I_{m} cdot cos left(omega cdot t+varphi _{2} right).)

Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальному значению заряда данной обкладки), называется периодом свободных (собственных) электромагнитных колебаний в контуре.

Период свободных электромагнитных колебаний в LC-контуре определяется по формуле Томсона:

(T=2pi cdot sqrt{Lcdot C}, ;;; omega =dfrac{1}{sqrt{Lcdot C}}.)

Сточки зрения механической аналогии, идеальному колебательному контурусоответствует пружинный маятник без трения, а реальному — с трением. Вследствиедействия сил трения колебания пружинного маятника затухают с течением времени.

*Вывод формулы Томсона

Поскольку полная энергия идеального LC-контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство

(W=dfrac{Q_{m}^{2} }{2C} =dfrac{Lcdot I_{m}^{2} }{2} =dfrac{q^{2} }{2C} +dfrac{Lcdot i^{2} }{2} ={rm const}.)

Получим уравнение колебаний в LC-контуре, используя закон сохранения энергии. Продифференцировав выражение для его полной энергии по времени, с учетом того, что

(W’=0, ;;; q’=i, ;;; i’=q”,)

получаем уравнение, описывающее свободные колебания в идеальном контуре:

(left(dfrac{q^{2} }{2C} +dfrac{Lcdot i^{2} }{2} right)^{{‘} } =dfrac{q}{C} cdot q’+Lcdot icdot i’ = dfrac{q}{C} cdot q’+Lcdot q’cdot q”=0,)

(dfrac{q}{C} +Lcdot q”=0,; ; ; ; q”+dfrac{1}{Lcdot C} cdot q=0.)

Переписав его в виде:

(q”+omega ^{2} cdot q=0,)

замечаем, что это — уравнение гармонических колебаний с циклической частотой

(omega =dfrac{1}{sqrt{Lcdot C} }.)

Соответственно период рассматриваемых колебаний

(T=dfrac{2pi }{omega } =2pi cdot sqrt{Lcdot C}.)

Литература

Жилко, В.В. Физика: учеб. пособие для 11 класса общеобразоват. шк. с рус. яз. обучения / В.В. Жилко, Л.Г. Маркович. — Минск: Нар. Асвета, 2009. — С. 39-43.

Источник

Энергия заряженного конденсатора. Калькулятор онлайн для любых конденсаторов.

Онлайн калькулятор вычисления энергии электростатического поля заряженного конденсатора, позволит найти энергию заряженного конденсатора через напряжение, емкость и электрический заряд на одной из обкладок. Калькулятор произведет вычисление и даст подробное решение. Единицы измерения, могут включать любые приставки Си. Калькулятор автоматически переведет одни единицы в другие.

Калькулятор вычислит:
Энергию заряженного конденсатора через напряжение (разность потенциалов), до которого заряжен конденсатор и емкость.
Энергию заряженного конденсатора через напряжение (разность потенциалов), до которого заряжен конденсатор и электрический заряд на одной из обкладок
Энергию заряженного конденсатора через электрический заряд на одной из обкладок и емкость

Так же для вычисления энергии электростатического поля плоского, цилиндрического и сферического конденсаторов, можно воспользоваться
калькулятором вычисления энергии заряженного конденсатора для плоского, цилиндрического и сферического конденсаторов.

Энергия заряженного конденсатора через напряжение (разность потенциалов), до которого заряжен конденсатор и емкость

Энергия заряженного конденсатора через напряжение (разность потенциалов), до которого заряжен конденсатор и емкость определяется формулой, где

C – емкость конденсатора
U – напряжение (разность потенциалов), до которого заряжен конденсатор

Единицей измерения энергии является – Джоуль (Дж, J).

Электроемкость C =
Напряжение U =
Единица измерения энергии W

Энергия заряженного конденсатора через напряжение (разность потенциалов), до которого заряжен конденсатор и электрический заряд на одной из обкладок

Энергия заряженного конденсатора через напряжение (разность потенциалов), до которого заряжен конденсатор и электрический заряд на одной из обкладок определяется формулой, где

q – электрический заряд на одной из обкладок
U – напряжение (разность потенциалов), до которого заряжен конденсатор

Единицей измерения энергии является – Джоуль (Дж, J).

Заряд q =
Напряжение U =
Единица измерения энергии W

Энергия заряженного конденсатора через электрический заряд на одной из обкладок и емкость

Энергия заряженного конденсатора через электрический заряд на одной из обкладок и емкость определяется формулой, где

q – электрический заряд на одной из обкладок
C – емкость конденсатора

Единицей измерения энергии является – Джоуль (Дж, J).

Заряд q =
Электроемкость C =
Единица измерения энергии W

Вам могут также быть полезны следующие сервисы

Калькуляторы (физика)

Механика

Калькулятор вычисления скорости, времени и расстояния

Калькулятор вычисления ускорения, скорости и перемещения

Калькулятор вычисления времени движения

Калькулятор времени

Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения.

Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.

Импульс тела. Калькулятор вычисления импульса, массы и скорости

Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.

Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения

Оптика

Калькулятор отражения и преломления света

Электричество и магнетизм

Калькулятор Закона Ома

Калькулятор Закона Кулона

Калькулятор напряженности E электрического поля

Калькулятор нахождения точечного электрического заряда Q

Калькулятор нахождения силы F действующей на заряд q

Калькулятор вычисления расстояния r от заряда q

Калькулятор вычисления потенциальной энергии W заряда q

Калькулятор вычисления потенциала φ электростатического поля

Калькулятор вычисления электроемкости C проводника и сферы

Конденсаторы

Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе

Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе

Калькулятор вычисления энергии W заряженного конденсатора

Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов

Калькуляторы по астрономии

Вес тела на других планетах

Ускорение свободного падения на планетах Солнечной системы и их спутниках

Конвертеры величин

Конвертер единиц длины

Конвертер единиц скорости

Конвертер единиц ускорения

Цифры в текст

Калькуляторы (Теория чисел)

Калькулятор выражений

Калькулятор упрощения выражений

Калькулятор со скобками

Калькулятор уравнений

Калькулятор суммы

Калькулятор пределов функций

Калькулятор разложения числа на простые множители

Калькулятор НОД и НОК

Калькулятор НОД и НОК по алгоритму Евклида

Калькулятор НОД и НОК для любого количества чисел

Калькулятор делителей числа

Представление многозначных чисел в виде суммы разрядных слагаемых

Калькулятор деления числа в данном отношении

Калькулятор процентов

Калькулятор перевода числа с Е в десятичное

Калькулятор экспоненциальной записи чисел

Калькулятор нахождения факториала числа

Калькулятор нахождения логарифма числа

Калькулятор квадратных уравнений

Калькулятор остатка от деления

Калькулятор корней с решением

Калькулятор нахождения периода десятичной дроби

Калькулятор больших чисел

Калькулятор округления числа

Калькулятор свойств корней и степеней

Калькулятор комплексных чисел

Калькулятор среднего арифметического

Калькулятор арифметической прогрессии

Калькулятор геометрической прогрессии

Калькулятор модуля числа

Калькулятор абсолютной погрешности приближения

Калькулятор абсолютной погрешности

Калькулятор относительной погрешности

Дроби

Калькулятор интервальных повторений

Учим дроби наглядно

Калькулятор сокращения дробей

Калькулятор преобразования неправильной дроби в смешанную

Калькулятор преобразования смешанной дроби в неправильную

Калькулятор сложения, вычитания, умножения и деления дробей

Калькулятор возведения дроби в степень

Калькулятор перевода десятичной дроби в обыкновенную

Калькулятор перевода обыкновенной дроби в десятичную

Калькулятор сравнения дробей

Калькулятор приведения дробей к общему знаменателю

Калькуляторы (тригонометрия)

Калькулятор синуса угла

Калькулятор косинуса угла

Калькулятор тангенса угла

Калькулятор котангенса угла

Калькулятор секанса угла

Калькулятор косеканса угла

Калькулятор арксинуса угла

Калькулятор арккосинуса угла

Калькулятор арктангенса угла

Калькулятор арккотангенса угла

Калькулятор арксеканса угла

Калькулятор арккосеканса угла

Калькулятор нахождения наименьшего угла

Калькулятор определения вида угла

Калькулятор смежных углов

Калькуляторы систем счисления

Калькулятор перевода чисел из арабских в римские и из римских в арабские

Калькулятор перевода чисел в различные системы счисления

Калькулятор сложения, вычитания, умножения и деления двоичных чисел

Системы счисления теория

N₂ | Двоичная система счисления

N₃ | Троичная система счисления

N₄ | Четырехичная система счисления

N₅ | Пятеричная система счисления

N₆ | Шестеричная система счисления

N₇ | Семеричная система счисления

N₈ | Восьмеричная система счисления

N₉ | Девятеричная система счисления

N₁₁ | Одиннадцатиричная система счисления

N₁₂ | Двенадцатеричная система счисления

N₁₃ | Тринадцатеричная система счисления

N₁₄ | Четырнадцатеричная система счисления

N₁₅ | Пятнадцатеричная система счисления

N₁₆ | Шестнадцатеричная система счисления

N₁₇ | Семнадцатеричная система счисления

N₁₈ | Восемнадцатеричная система счисления

N₁₉ | Девятнадцатеричная система счисления

N₂₀ | Двадцатеричная система счисления

N₂₁ | Двадцатиодноричная система счисления

N₂₂ | Двадцатидвухричная система счисления

N₂₃ | Двадцатитрехричная система счисления

N₂₄ | Двадцатичетырехричная система счисления

N₂₅ | Двадцатипятеричная система счисления

N₂₆ | Двадцатишестеричная система счисления

N₂₇ | Двадцатисемеричная система счисления

N₂₈ | Двадцативосьмеричная система счисления

N₂₉ | Двадцатидевятиричная система счисления

N₃₀ | Тридцатиричная система счисления

N₃₁ | Тридцатиодноричная система счисления

N₃₂ | Тридцатидвухричная система счисления

N₃₃ | Тридцатитрехричная система счисления

N₃₄ | Тридцатичетырехричная система счисления

N₃₅ | Тридцатипятиричная система счисления

N₃₆ | Тридцатишестиричная система счисления

Калькуляторы площади геометрических фигур

Площадь квадрата

Площадь прямоугольника

КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ

Калькуляторы (Комбинаторика)

Калькулятор нахождения числа перестановок из n элементов

Калькулятор нахождения числа сочетаний из n элементов

Калькулятор нахождения числа размещений из n элементов

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка. Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами

Калькулятор скалярного произведения векторов через координаты

Калькулятор векторного произведения векторов через координаты

Калькулятор смешанного произведения векторов

Калькулятор умножения вектора на число

Калькулятор нахождения угла между векторами

Калькулятор проверки коллинеарности векторов

Калькулятор проверки компланарности векторов

Генератор Pdf с примерами

Тренажёры решения примеров

Тренажер по математике

Тренажёр таблицы умножения

Тренажер счета для дошкольников

Тренажер счета на внимательность для дошкольников

Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ.

Тренажер решения примеров с разными действиями

Тренажёры решения столбиком

Тренажёр сложения столбиком

Тренажёр вычитания столбиком

Тренажёр умножения столбиком

Тренажёр деления столбиком с остатком

Калькуляторы решения столбиком

Калькулятор сложения, вычитания, умножения и деления столбиком

Калькулятор деления столбиком с остатком

Генераторы

Генератор примеров по математике

Генератор случайных чисел

Генератор паролей

Источник

Конденсатор. Энергия электрического поля

Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.

Ёмкость уединённого проводника

Ёмкость плоского конденсатора

Энергия заряженного конденсатора

Энергия электрического поля

Заряд конденсатора

Процессы зарядки и разрядки конденсаторов

Емкость и энергия конденсатора

Как зарядить конденсатор

Зарядка конденсатора от источника постоянной ЭДС

Заряд конденсатора, ток

Время, необходимое для зарядки конденсатора

Заряд конденсатора: формула

Время разряда конденсатора

Содержание

Колебательный контур

Энергии контура

Процессы в колебательном контуре

Свободные электромагнитные колебания

*Вывод формулы Томсона

Литература

Энергия заряженного конденсатора. Калькулятор онлайн для любых конденсаторов.

Вам также может понравиться

Как найти коэффициент трения формула 7 класс

Как найти организацию в регистре сведений

Excel как найти процент от суммы

Добавить комментарий Отменить ответ