Как найти энергию магнитного поля длинного соленоида

Если
в контуре с индуктивностью L
течёт ток I,
то в момент размыкания цепи возникает
индукционный ток и им совершается
работа. Эта работа совершается за счёт
энергии исчезнувшего при размыкании
цепи магнитного поля. На основании
закона сохранения и превращения энергию
магнитного поля превращается главным
образом в энергию электрического поля,
за счёт которой происходит нагревание
проводников. Работа может быть определена
из соотношения

dA=ε_смIdt

Так
как
,
то

dA=-LIdI

Уменьшение
энергии магнитного поля равно работе
тока, поэтому

(16.18)

Формула
справедлива для любого контура и
показывает, что энергия магнитного поля
зависит от индуктивности контура и силы
тока, протекающего по нему.

Рассчитаем
энергию однородного магнитного поля
длинного соленоида, индуктивность
которого определяется по формуле L
= μμ₀n²V.
B
этом случае формула энергии примет вид

Учитывая,
что напряжённость поля внутри бесконечно
длинного соленоида Н=In,
получаем

(16.19)

Выразим
энергию через индукцию магнитного поля
B=
μμ₀H:

(16.20)

Или

(16.21)

Вследствие
того, что магнитное поле соленоида
однородно и локализовано внутри
соленоида, энергия распределена по
объёму соленоида с постоянной плотностью

(16.22)

Учитывая
последние три формулы, получаем

Учитывая
правило Ленца, можно заметить, что
явление самоиндукции аналогично
проявлению инертности тел в механике.
Так, вследствие инертности тело не
мгновенно приобретает определённую
скорость, а постепенно. Так же постепенно
происходит и его торможение. То же самое,
как мы видели, происходит и с силой тока
при самоиндукции. Эту аналогию можно
провести и дальше.

и

эти
уравнения эквивалентны.

т.е.
m
~L
, υ~I

Эквивалентны
и формулы

Примеры решения задач

Пример.
В магнитном поле, изменяющемся по закону
B=B₀cosωt
(B₀=5мТл,

ω=5с^-1),
помещён круговой проволочный виток
радиусом r=30см,
причём нормаль к витку образует с
направлением поля угол α=30º. Определите
ЭДС индукции, возникающую в витке в
момент времени t=10с.

Дано:
B=B₀cosωt;
B₀=5мТл=5∙10^-3
Тл;
ω=5с^-1;
r=30см=0,3
м;
α=30º; t=10 с.

Найти:
ε_i.

Решение:
Согласно
закону Фарадея,

,
(1)

Где
магнитный поток, сцепленный с витком
при произвольном его расположении
относительно магнитного поля.

Ф=BScosα.

По
условию задачи B=B₀cosωt,
а площадь кольца S=πr²,
поэтому

Ф=πr²
B₀cosωt∙cosα.
(2)

Подставив
выражение (2) в формулу (1) и продифференцировав,
получаем искомую ЭДС индукции в заданный
момент времени:

Ответ:
ε_i=4,69
мВ.

Пример
В
соленоиде длиной ℓ=50см и диаметром
d=6см
сила тока равномерно увеличивается на
0,3А за одну секунду. Определите число
витков соленоида, если сила индукционного
тока в кольце радиусом 3,1 см из медной
проволоки (ρ=17нОм∙м), надетом на катушку,
I_к=0,3
А.

Дано:
ℓ=50см=0,5
м; d=6см=0,06м;
;r_к=3,1см=3.1∙10^-2м;
ρ=17нОм∙м=17∙10^-9
Ом∙м; I_к=0,3
А.

Найти:
N.

Решение.
При изменении силы тока в соленоиде
возникает ЭДС самоиндукции

(1)

где
–
индуктивность соленоида. Подставив это
выражение в (1)

с
учётом

.

ЭДС
индукции, возникающая в одном кольце,
в N
раз меньше, чем найденное значение ЭДС
самоиндукции в соленоиде, состоящем из
N
витков, т.е.

.
(2)

Согласно
закону Ома, сила индукционного тока в
кольце

,
(3)

где
–
сопротивление кольца. Поскольку ℓ_к=πd,
а S_к=πr_к²,
выражение (3) примет вид

Подставив
в эту формулу выражение (2), найдём искомое
число витков соленоид

.

Ответ:
N=150

Пример
В
однородном магнитном поле подвижная
сторона (её длина ℓ=20см) прямоугольной
рамки (см. рисунок) перемещается
перпендикулярно линиям магнитной
индукции со скоростью υ=5 м/с. Определите
индукцию В магнитного поля, если
возникающая в рамке ЭДС индукции ε_i=0,2
В.

Дано:
ℓ=20см=0,2
м; υ=5 м/с; ε_i=0,2
В.

Найти:
B.

Решение.
При движении в магнитном поле подвижной
стороны рамки поток Ф вектора магнитной
индукции сквозь рамку возрастает, что,
согласно закону Фарадея,

,
(1)

приводит
к возникновению ЭДС индукции.

Поток
вектора магнитной индукции, сцепленный
с рамкой,

Ф=Bℓx.
(2)

Подставив
выражение (2) в формулу (1) и учитывая, что
B
и ℓ – величины постоянные, получаем

откуда
искомая индукция магнитного поля

Ответ:
В=0,2 Тл.

Пример
В
однородном магнитном поле с индукцией
В=0,2 Тл равномерно вращается катушка,
содержащая N=600
витков, с частотой n=6
с^-1.
Площадь
S
поперечного сечения катушка 100см².
Ось вращения перпендикулярна оси катушки
и направлению магнитного поля. Определите
максимальную ЭДС индукции вращающейся
катушки.

Дано:
В=0,2
Тл; N=600;
n=6
с^-1;
S=100см²=10^-2
м².

Найти:
(ε_i)_max.

Решение.
Согласно закону Фарадея,

где
Ф – полный магнитный поток, сцеплённый
со всеми витками катушки. При произвольном
расположении катушки относительно
магнитного поля

Ф=NBScosωt,
(1)

где
круговая частота ω=2πn.
Подставив ω в (1), получим

Ф=NBScos2πnt.

Тогда

ε_i=-NBS2πn(-sin2πnt)=2πnNBSsin2πnt,

ε_i=(
ε_i)_max
при
sin2πnt=1, поэтому

(ε_i)_max=2πnNBS

Ответ:
(ε_i)_max=45,2
В.

Пример
Однослойная
длинная катушка содержит N=300
витков, плотно прилегающих друг к другу.
Определите индуктивность катушки, если
диаметр проволоки d=0,7
мм (изоляция ничтожной толщины) и она
намотана на картонный цилиндр радиусом
r=1
см. .

Дано:
N=300;
d=0,7
мм=7∙10^-4
м; r=1
см=10^-2
м.

Найти:
L.

Решение.
Индуктивность катушки

(1)

где
Ф – полный магнитный поток, сцепленный
со всеми витками катушки; I
– сила тока в катушке.

Учитывая,
что полный магнитный поток

Ф=NBS

(N-число
витков катушки; В – магнитная индукция;
S
– площадь поперечного сечения катушки);
магнитная индукция в катушке без
сердечника

(μ₀
– магнитная постоянная; ℓ- длина
катушки), длина катушки

ℓ=Nd

(d-диаметр
проволоки; витки вплотную прилегают
друг к другу), площадь поперечного
сечения катушки

S=πr²,

Получим
осле подстановки записанных выражений
в формулу (1) искомую индуктивность
катушки:

Ответ:
L=1,69
мГн.

Пример
Первичная
обмотка понижающего трансформатора с
коэффициентом трансформации k=0,1
включена в сеть с источником переменного
напряжения с ЭДС ε₁=220
В. Пренебрегая потерями энергии в
первичной обмотке, определите напряжение
U₂
на зажимах вторичной обмотки, если её
сопротивление R₂=5
Ом и сила тока в ней I₂=2А.

Дано:
k=0,1;
ε₁=220
В; R₂=5
Ом; I₂=2А.

Найти:
U₂.

Решение.
В первичной обмотке под действием
переменной ЭДС ε₁
возникает переменный ток I₁,
создающий в сердечнике трансформатора
переменногый магнитный поток Ф, который
пронизывает вторичную обмотку. Согласно
закону Ома, для первичной обмотки

где
R₁
– сопротивление первичной обмотки.
Падение напряжения I₁R₁
при быстропеременных полях мало по
сравнению с ε₁
и ε₂.
Тогда можем записать:

(1)

ЭДС
взаимной индукции, возникающая во
вторичной обмотке,

(2)

Из
выражений (1) и (2) получаем

,

где
–
коэффициент трансформации, а знак «-»
показывает, что ЭДС в первичной и
вторичной обмотках противоположны по
фазе. Следовательно, ЭДС во вторичной
обмотке

ε₂=k
ε₂.

Напряжение
на зажимах вторичной обмотки

U₂=
ε₂-I₂R₂=
kε₁-I₂R₂.

Ответ:
U₂=12
В.

Пример
Соленоид
без сердечника с однослойной обмоткой
из проволоки диаметром d=0,4
мм имеет длину ℓ=0.5 м и поперечное сечение
S=60см².
За какое время при напряжении U=10
В и силе тока I=1,5
А в обмотке выделится количество теплоты,
равное энергии поля внутри соленоида?
Поле считать однородным.

Дано:
d=0,4
мм=0,4∙10^-4
м; ℓ=0,5 м; S=60см²=6∙10^-3
м²;
I=1,5А;
U=10В;
Q=W.

Найти:
t.

Решение.
При прохождении тока I
при напряжении U
в обмотке за время t
выделяется теплота

Q=IUt.
(1)

Энергия
поля внутри соленоида

(2)

где
(N
– общее число витков соленоида). Если
витки вплотную прилегают друг к другу,
то ℓ=Nd,
откуда
.
Подставив выражение для В иN
в
(2), получаем

.
(3)

Согласно
условию задачи, Q=W.
Приравняв выражение (1) и (3),найдём искомое
время:

Ответ:
t
=1,77 мс.

Пример
Катушка
без сердечника длиной ℓ=50 см содержит
N=200
витков. По катушке течёт ток I=1А.
Определите объёмную плотность энергии
магнитного поля внутри катушки..

Дано:
ℓ=50
см=0,5
м;
N=200; I=1 А.

Найти:
ω.

Решение.
Объёмная плотность энергии магнитного
поля (энергия единицы объёма)

,
(1)

где
–
энергия магнитного поля (L
– индуктивность катушки); V=Sℓ-
объём катушки (S
– площадь катушки; ℓ- длина катушки).

Магнитная
индукция поля внутри соленоида с
сердечником с магнитной проницаемостью
μ равна

.

Полный
магнитный поток, сцепленный со всеми
витками соленоида,

.

Учитывая,
что Ф=LI,
получаем формулу для индуктивности
соленоида:

(2)

Подставив
выражение (2) в формулу (1) с учётом того,
что
,
найдём искомую объёмную плотность
энергии магнитного поля внутри катушки:

Ответ:
ω=0,1
Дж/м³.

Магни?тное по?ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения, магнитная составляющая электромагнитного поля.

Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты). Энергия магнитного поля, создаваемого током в замкнутом контуре индуктивностью L, равна где I — сила тока в контуре.

Энергия магнитного поля катушки с индуктивностью L, создаваемого током I, равнаПроводник, по которому протекает электрический ток, всегда окружен магнитным полем, причем магнитное поле появляется и исчезает вместе с появлением и исчезновением тока. Магнитное поле, подобно электрическому, является носителем энергии. Естественно предположить, что энергия магнитного поля равна работе, которая затрачивается током на создание этого поля.

Рассмотрим контур индуктивностью L, по которому течет ток I. С данным контуром сцеплен магнитный поток (см. (126.1)) Ф = LI, причем при изменении тока на dI магнитный поток изменяется на dФ = LdI. Однако для изменения магнитного потока на величину dФ (см. § 121) необходимо совершить работу dА = IdФ = LIdI. Тогда работа по созданию магнитного потока Ф будет равнаСледовательно, энергия магнитного поля, связанного с контуром, (130.1)Исследование свойств переменных магнитных полей, в частности распространения электромагнитных волн, явилось доказательством того, что энергия магнитного поля локализована в пространстве. Это соответствует представлениям теории поля.

Энергию магнитного поля можно представить как функцию величин, характеризу­ющих это поле в окружающем пространстве. Для этого рассмотрим частный слу­чай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (130.1) выражение (126.2), получимТак как I = Bl/(m0mN) (см. (119.2)) и В = m0mH (см. (109.3)), то (130.2)где Sl = V — объем соленоида.

Магнитное поле соленоида однородно и сосредоточено внутри него, поэтому энергия (см. (130.2)) заключена в объеме соленоида и распределена в нем с постоянной объемной плотностью (130.3)Выражение (130.3) для объемной плотности энергии магнитного поля имеет вид, аналогичный формуле (95.8) для объемной плотности энергии электростатического поля, с той разницей, что электрические величины заменены в нем магнитными. Формула (130.3) выведена для однородного поля, но она справедлива и для неоднород­ных полей. Выражение (130.3) справедливо только для сред, для которых зависимость В от Н линейная, т.е. оно относится только к пара- и диамагнетикам.

Не нашли то, что искали? Воспользуйтесь поиском:

Определение 1

Самоиндукция – это значимый частный случай электромагнитной индукции, когда магнитный поток, изменяясь и вызывая ЭДС индукции, создается током в самом контуре.

В случае, когда ток рассматриваемого контура по каким-либо причинам изменен, то имеет место изменение и магнитного поля этого тока, а значит и собственного магнитного потока, проходящего через контур. В контуре создается ЭДС самоиндукции, создавая препятствие для изменений тока в контуре (по правилу Ленца).

Собственный магнитный поток

Φ

, который проходит через контур или катушку с током, является пропорциональным силе тока

I

: 

ΦLI

.

Определение 2

Коэффициент пропорциональности

L

в формуле

ΦLI

есть коэффициент самоиндукции или индуктивность катушки. Единица индуктивности в

СИ

носит название генри

Гн

. Индуктивность контура или катушки равна

Гн

, когда при силе постоянного тока

А

собственный поток составляет 

Вб

:

ГнВбА

.

Расчет индуктивности

Пример 1

Для наглядности произведем расчет индуктивности длинного соленоида, который имеет

N

витков, площадь сечения

S

и длину

l

. Соленоид – это цилиндрическая катушка индуктивности, у которой длина много больше диаметра. Магнитное поле соленоида задается формулой:

BμnI

,где I является обозначением тока в соленоиде, nNe указывает число витков на единицу длины соленоида.

Магнитный поток внутри катушки соленоида, проходящий через все N витков, составляет:

ΦBSNμnSl

Таким образом, индуктивность соленоида будет выражена формулой:

LμnSlμnV

,где VSl – объем соленоида, содержащий магнитное поле.

Результат, который мы получили, не берет в расчет краевых эффектов, а значит он является приближенно верным лишь для катушек достаточной длины. Когда соленоид заполнен веществом, имеющим магнитную проницаемость

μ

, при заданном токе

I

индукция магнитного поля будет возрастать по модулю в

μ

раз, а значит и индуктивность катушки с сердечником тоже получит увеличение в

μ

раз:

LμμLμμnV

.

Определение 3

ЭДС самоиндукции, которая возникает в катушке при постоянном значении индуктивности, в соответствии с законом Фарадея записывается в виде формулы: δиндδLΦtLIt.

ЭДС самоиндукции является прямо пропорциональной индуктивности катушки и скорости изменения силы тока в ней.

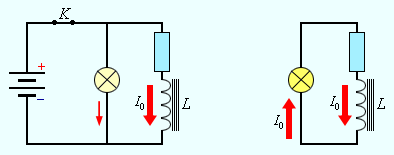
Магнитное поле выступает носителем энергии. Так же, как заряженный конденсатор обладает запасом электрической энергии, катушка, по виткам которой проходит ток, обладает запасом магнитной энергии. Включив электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, при размыкании ключа будем наблюдать короткую вспышку лампы (рис.

). Ток в цепи появится под влиянием ЭДС самоиндукции. Источником энергии, которая будет выделяться в этом процессе электрической цепью, будет служить магнитное поле катушки.

Рисунок 1211 Магнитная энергия катушки. В момент размыкания ключа K лампа ярко вспыхнет.

Закон сохранения энергии позволяет говорить, что вся энергия, составляющая запас катушки, будет выделена в виде джоулева тепла. Обозначим как

R

полное сопротивление цепи, тогда за время

Δt

будет выделено количество теплоты

ΔQIRΔt

.

Ток в цепи составляет: IδLRLRItВыражение для ΔQ можем записать так:

QLIIΦII

В данной записи ΔI0; значение тока в цепи постепенно снижается от изначального I0 до нуля. Полное количество теплоты, которое выделится в цепи, возможно получить, осуществив действие интегрирования в пределах от I0 до 0. Тогда получим:

QLI

[custom_ads_shortcode1]

Графический вывод формулы

Существует возможность получить записанную формулу, используя графический метод. Для этого отобразим на графике зависимость магнитного потока

ΦI

от тока

I

(рис.

). Полное количество выделившейся теплоты, которое равно изначальному запасу энергии магнитного поля, определится как площадь получившегося на рис.

треугольника:

Рисунок 1212 Вычисление энергии магнитного поля.

В итоге формула энергии

Wм

магнитного поля катушки с индуктивностью

L

, создаваемого током

I

, будет записана в виде формулы:

WмΦILIΦL

Используем выражение, которое мы получили, для энергии катушки к длинному соленоиду с магнитным сердечником. Применяя указанные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, получим запись:

WмμμnIVBμμV

В этой формуле V является объемом соленоида. Полученное выражение демонстрирует нам, что магнитная энергия имеет локализацию не в витках катушки, по которым проходит ток, а распределена по всему объему, в котором возникло магнитное поле.

Определение 4

Объёмная плотность магнитной энергии – это физическая величина, которая равна энергии магнитного поля в единице объема:

WмBμμ

.

В свое время Максвелл продемонстрировал, что указанная формула (в нашем случае выведенная для длинного соленоида) верна для любых магнитных полей. Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter.

Магнитное поле имеет энергию. Это можно показать экспериментальным путем. Например, рассмотрим процесс убывания силы тока в катушке, если от нее отключить источник тока.

[custom_ads_shortcode2]

Эмпирическое доказательство наличия энергии магнитного поля

Пусть до размыкания ключа (рис.1(a)) в катушке имеется ток $I$. Данный ток порождает магнитное поле. Если ключ разомкнут, то мы получаем последовательное соединение катушки и сопротивления (рис. 1(b)). Ток в катушке из-за процесса самоиндукции уменьшается постепенно. На сопротивлении при этом выделяется теплота. Но мы помним, что источник отключен, появляется вопрос об источнике энергии, которая тратится на тепло. Поскольку убывает ток и, соответственно, создаваемое им магнитное поле, то можно говорить об энергии тока или энергии магнитного поля, которое он создает. Рисунок 1. Энергия магнитного поля тока. Автор24 — интернет-биржа студенческих работЕсли магнитное поле создается постоянным током, то понять, где сосредоточена энергия невозможно, поскольку ток создает магнитное поле, а магнитные поля всегда сопровождаются токами.

Ничего непонятно?

Попробуй обратиться за помощью к преподавателямРассмотрим переменное магнитное поле в электромагнитной волне. В такой волне магнитные поля могут существовать при отсутствии токов. Известно, что электромагнитные волны переносят энергию, на этом основании сделаем вывод о том, что энергия заключена в магнитном поле. И так, энергия электрического тока локализована в магнитном поле, то есть в среде, которая окружает этот ток.

[custom_ads_shortcode3]

Вычисление энергии магнитного поля

По закону сохранения энергии имеем, что в эксперименте рис.1 (a-b), вся энергия магнитного поля в результате выделяется в виде Джоулева тепла на сопротивлении $R$. Уменьшение энергии магнитного поля можно найти как работу индукционного тока:

$-Delta E_{m}=A_{i}left( 1 right)$. Конечные величины силы тока, индукции магнитного поля и энергии равны нулю, обозначим начальное значение энергии магнитного поля как $E_m$, соответственно:

${-E}_{m}=A_{i}left( 2 right)$. Элементарную работу, совершаемую током, найдем как:

$dA_{i}=Ɛ_{i}Idt=-L, Ifrac{dI}{dt}dt=-L, IdIleft( 3 right),$где $dt$ – время совершения работы током индукции; $Ɛ_{i}=-L, frac{dI}{dt}$ – ЭДС самоиндукции. Возьмем интеграл от (3) учитывая, что ток изменяется от I до 0:

$E_{m}=-int {dA_{i}=Lintlimits_I^0 {IdI=frac{LI^{2}}{2}left( 4 right).}} $Выражение (4) является справедливым для всякого контура, она указывает на связь энергии магнитного поля, создаваемого током от силы тока и индуктивности контура. Сопоставим выражение (4) с выражением для кинетической энергии поступательного движения:

$E_{k}=frac{mv^{2}}{2}left( 5 right)$. Это сравнение показывает, что индуктивность контура связана с инерционностью контура. Нельзя остановить перемещающееся тело, без превращений энергии, так нет возможности остановить электрический ток без трансформации энергии.

[custom_ads_shortcode1]

Связь энергии магнитного поля и его основных характеристик

Рассмотрим энергию магнитного поля длинного соленоида. Пусть рассматриваемое нами поле можно считать однородным, и находится оно внутри соленоида. Тогда сила тока, текущая по соленоиду может быть выражена как: $I=frac{Hl}{N}left( 6 right)$,где $H$ – напряженность магнитного поля соленоида; $l$ – длина соленоида; $N$ – число витков соленоида. Для соленоида:

$L=mu mu_{0}n^{2}Sl, left( 7 right)$. где $μ$ – магнитная проницаемость сердечника соленоида; $S$ – площадь сечения соленоида; $n=frac{N}{l}$.

Принимая во внимание формулы (6) и (7) выражение (4) приведем к виду: $E_{m}=frac{mu mu_{0}N^{2}Sl}{2l^{2}}frac{H^{2}l^{2}}{N^{2}}=mu mu_{0}frac{H^{2}}{2}Sl=mu mu_{0}frac{H^{2}}{2}V, left( 8 right)$.

Часто в качестве энергетической характеристики магнитного поля используют такой параметр, как плотность энергии магнитного поля: $w=frac{E_{m}}{V}=mu mu_{0}frac{H^{2}}{2}left( 9 right)$.

Формула (9) применима для любого магнитного поля независимо от его происхождения, она показывает энергию магнитного поля в единице его объема. Для магнитоизотропной среды мы можем записать:

$vec{B}=mu mu_{0}vec{H}left( 10 right)$. Тогда уравнение (9) представим как:

$w=frac{BH}{2}left( 11 right)$. Если магнитное поле является неоднородным, то его разбивают на элементарные объемы ($dV$) (малые объемы в которых магнитное поле можно считать однородным). Энергию магнитного поля, которая заключена в этих объемах, считают равной:

$dE_{m}=wdVleft( 12 right)$. В таком случае суммарная энергия магнитного поля может быть найдена как:

$E_{m}=intlimits_V {wdVleft( 13 right),}$где интегрирование проводят по всему объему, который занимает магнитное поле.

[custom_ads_shortcode2]

Ограничения в применении формулы для вычисления плотности энергии магнитного поля

При получении формулы (9) считалось, что:

1. индуктивность контура, следовательно, магнитная проницаемость вещества не изменяются,
2. вся энергия источника тока переходит в энергию магнитного поля.

Эти условия справедливы точно, только для вакуума (при $mu$=1). При помещении контура с током в вещество, следует учитывать:

• Намагничивание вещества, что ведет к увеличению ее температуры.
• Объем и плотность вещества в магнитном поле способны меняться даже при неизменной температуре.

Данные нюансы указывают на то, что магнитная проницаемость вещества ($mu$), которая изменяется при изменении температуры и плотности среды не может быть неизменной при намагничивании. Кроме того, работа источника ЭДС не целиком переходит в энергию магнитного поля. Выше сказанное дает основание полагать, что в общем случае формула (2) не выражает в точности работу при намагничивании и выражение (9) не дает объемную плотность энергии магнитного поля в веществе. Допустим, что изменение объема вещества мало. Температура среды постоянна. Внешняя работа расходуется на рост энергии магнитного поля $E_m$ и на теплоотдачу $(Q)$, для поддержания постоянной температуры. Работа внешних сил, в нашем случае источника тока, которая совершается над телом при квазистатическом изотермическом процессе, будет равна приращению свободной энергии тела. Получается, что формула (9) отражает часть свободной энергии намагниченного вещества, которая связана с магнитным полем. Если количества теплоты ($Q$) в сравнении с энергией поля $E_m$ мало, тогда выполняется равенство (2).

Условие неизменности магнитной проницаемости вещества, означает, что справедлива линейная зависимость (10). Даная зависимость выполняется для вакуума. Ее можно применять для парамагнетиков и диамагнетиков. Но для ферромагнетиков связь между магнитной индукцией и напряженностью магнитного поля является сильно нелинейной даже при $T=const$, поэтому выражение (9) для этих веществ не применяется.

Пусть все рассматриваемое пространство заполняет однородный магнетик. В нем индукция магнитного поля, которое создают токи, изменяется в $mu $ раз в сравнении с индукцией в вакууме. Во столько же изменяются магнитные потоки $Ф$ и $dФ.$ Элементарная работа, выполняемая внешним источником против электродвижущей силы индукции, будет равна:

Допустим, что магнитное поле создается двумя контурами. Если $L_{11}$ – индуктивность первого контура, $L_{22}$ – индуктивность второго контура, то можно записать, что: Поток ${Phi }_{12}$, который пересекает контур (1), создаваемый током во втором контуре равен:

где $L_{12}$- постоянная, взаимная индуктивность первого и второго контуров. Для второго контура имеем: Из формул (2) – (4) следует, что если изменяются магнитные потоки в магнетике, то индукции контура и взаимные индукции увеличиваются в $mu $ раз. Это значит, что взаимные индукции контуров равны:

При этом магнитные потоки в магнитике могут быть выражены как:

Ничего непонятно? Попробуй обратиться за помощью к преподавателямгде $r_{21}=r_{12}$ – расстояния между элементами контуров с током $doverrightarrow{l_1}и doverrightarrow{l_2}$.

None Если магнитное поле образуется $N$ контурами, то его энергию можно вычислить как:

Рисунок 1. при $i=k$ коэффициент $L_{ik}$ называется индуктивностью контура ${rm I}$, при $ine k$, этот же коэффициент называют взаимной индуктивностью ${rm I}$-го и k-го контуров. Эти коэффициенты определяются формулами при $ine k$:

где $doverrightarrow{l_i},doverrightarrow{l_k}$ – элементы длины контуров ${rm I}$-го и $k$-го. $r_{ik}-$расстояние между ними. При этом $L_{ik}=L_{ki}$. В результате получается, что энергия магнитного поля токов, которые текут в неограниченном однородном магнетике, изменяется в $mu $ раз в сравнении с энергией этих же токов в вакууме.

[custom_ads_shortcode3]

Объемная плотность энергии магнитного поля

Магнитное поле, которое создают токи, распределено по всему пространству. Допустим, что магнитное поле создается одиночным контуром с током. Магнитная энергия поля в таком случае может быть представлена как: где поток магнитной индукции можно выразить как:

где $L$ контур тока, $S$ – поверхность, которая натянута на контур $L$, $overrightarrow{A} $- векторный потенциал, магнитного поля, которое создается током $I$. Замкнутый ток взаимодействует со своим магнитным полем. Каждый элемент тока $Idoverrightarrow{l}$ создает в пространстве собственное магнитное поле, с которым взаимодействуют другие элементы тока. Подставим (11) в формулу (10), получим:

Проведем переход от линейных токов к объемным токам с помощью соотношения: Из выражения (10) получим:

Используем известные формулы: Преобразуем выражение (12), получим:

По теореме Остроградского – Гаусса имеем:

В том случае, если точки рассматриваются в конечной области пространства, на больших расстояниях от этой области $Asim frac{1}{r}$, $Hsim frac{1}{r^2}$, то есть подынтегральное выражение убывает пропорционально $frac{1}{r^3}$. Поверхность при этом растет пропорционально $r^2$, получаем, что интеграл уменьшается $sim frac{1}{r}.$ Получается, что при $rto infty $, второй интеграл в выражении (15) равен нулю, тогда полная энергия выражается формулой:

Тогда, можно сказать, что объемная плотность энергии магнитного поля в пространстве равна:

[custom_ads_shortcode1]

Энергия магнетика во внешнем поле

Если имеется фиксированное распределение токов в пространстве, то энергия магнетика в магнитном поле равна: где $overrightarrow{J}$ – намагниченность магнетика, $overrightarrow{B_0}$ – магнитное поле в свободном пространстве.

Пример 1Задание: Вычислите магнитную проницаемость железа, если в поле с индукцией $B=1Тл$ плотность энергии магнитного поля в веществе $200 frac{Дж}{м^3}$. Решение: В качестве основания для решения задачи используем формулу [w_m=frac{1}{2}overrightarrow{H}overrightarrow{B}=frac{1}{2}frac{B^2}{mu {mu }_0} left(1.1right).] Из формулы (1.1) выразим магнитную проницаемость, получим:

[mu =frac{1}{2}frac{B^2}{w_m{mu }_0}left(1.2right).] Проведем вычисления:

[mu =frac{1}{2}cdot frac{1^2}{200cdot 1,26cdot {10}^{-6}}=2cdot {10}^3.] Ответ: $mu =2cdot {10}^3.$Пример 2Задание: Определите, как изменится объемная плотность энергии магнитного поля, если индукция магнитного поля тороида, который имеет ферромагнитный сердечник, увеличилась от $B_1=0,9 Тл до B_2=1,2 Тл$. Зависимость $B(H)$ представлена графиком на рис.2.

Рисунок 2. Решение: В качестве основания для решения задачи используем формулу [w_m=frac{1}{2}overrightarrow{H}overrightarrow{B}left(2.1right).] Запишем формулу (2.1) для двух состояний магнитного поля и найдем отношение $frac{w_{2m}}{w_{1m}}$:

None Следовательно, искомое отношение равно:

[frac{w_{2m}}{w_{1m}}=frac{1,2cdot 800}{1cdot 400}=2,4.] Ответ: $frac{w_{2m}}{w_{1m}}=2,4. $

Источники:

• studopedia.ru
• zaochnik.com
• spravochnick.ru
• spravochnick.ru

Продолжаем цикл статей о решении физических задач. Сегодня разберем несколько примеров на тему «Энергия магнитного поля».

Скучно решать задачи? Загляните на наш телеграм-канал, там много интересной и полезной информации для всех учащихся. А если хотите получить скидку на наши услуги, подписывайтесь на второй канал с приятными бонусами и акциями!

Энергия магнитного поля: задачи

Как решать физические задачи? Специально для новичков мы подготовили общую памятку, а также собрали вместе более 40 формул, которые обязательно пригодятся в учебе.

Кстати, в нашем блоге уже есть статья с задачами на  ЭДС самоиндукции и закон Фарадея. Всех интересующихся – милости просим.

Задача на энергию магнитного поля №1

Условие

Какова энергия магнитного поля соленоида, если по его обмотке индуктивностью L=0,2 Гн протекает ток I=10 А.

Решение

По определению, энергия магнитного поля равна:

W=LI22

Подставим значения, и вычислим:

W=0,2·1022=10 Дж

Ответ: 10 Дж.

Задача на энергию магнитного поля №2

Условие

Сила тока I в обмотке соленоида равна 1 А, а магнитный поток Ф через его поперечное сечение равен 0,1 мВб. Вычислить энергию магнитного поля соленоида, если он содержит N=1000 витков.

Решение

Для нахождения энергии магнитного поля будем использовать формуду из первой задачи. Очевидно, для вычисления нужно найти индуктивность. Выразим ее с помощью такой величины, как  потокосцепление – суммарный магнитный поток, сцепляющийся со всеми витками катушки:

ψ=LI=NФL=NФI

Подставим это выражение в формулу для энергии магнитного поля и высчислим ответ:

W=LI22=NФI2I·12=NФI2W=1000·0,1·10-3·12=0,05 Дж

Ответ: 0,05 Дж.

Задача на энергию магнитного поля №3

Условие

Плотность энергии w магнитного поля в железе равна 200 Дж/м3 при индукции поля B, равной 1 Тл. Какова магнитная проницаемость μ железа?

Решение

Запишем выражение для плотности энергии магнитного поля:

w= В22μ0μ

Выразим отсюда магнитную проницаемость и произведем вычисления:

μ=B22μ0w=122·1,26·10-6·200=2·103

Ответ: 2·103

Задача на энергию магнитного поля №4

Условие

Найти энергию магнитного поля соленоида, индуктивность которого 0,04 Гн, а магнитный поток через него составляет 0,5 Вб.

Решение

В данном случае для применения формулы W=LI22 не хватает величины I. Преобразуем данную формулу. Вспомним, что:

Ф=LII=ФL

Теперь первоначальную формулу для энергии магнитного поля можно записать в виде:

W=L2·Ф2L2=Ф22LW=0,522·0,04=3,125 Дж

Ответ: 3,125 Дж.

Задача на энергию магнитного поля №5

Условие

Какой должна быть сила тока в катушке с индуктивностью 0,8 Гн, чтобы энергия магнитного поля оказалась равной 2 Дж?

Решение

Запишем формулу для энергии магнитного поля и выразим из нее силу тока:

W=LI22I=2WL

Подставим значения из условия в формулу для силы тока и вычислим:

I=2·20,8=5=2,23 А

Ответ: 2,23 А.

Вопросы на тему «Энергия магнитного поля»

Вопрос 1. Что такое энергия магнитного поля?

Ответ. Магнитное поле обладает энергией. Эта физическая величина показывает, какую работу ток в проводнике (катушке индуктивности) затрачивает на создание данного магнитного поля. Энергия магнитного поля тока вычисляется по формуле:

W=LI22

Вопрос 2. Что такое объемная плотность энергии магнитного поля?

Ответ. Объемная плотность энергии магнитного поля определяет энергию поля в единице объема. Формула, выведенная Максвеллом для объемной плотности энергии магнитного поля соленоида:

w= B2μ0μ

Вопрос 3. От чего зависит энергия магнитного поля?

Ответ. Энергия магнитного поля прямо пропорциональна индуктивности.

Вопрос 4. Что такое индуктивность?

Ответ. Индуктивность – физическая величина, коэффициент пропорциональности между силой тока в контуре и магнитным потоком через контур, создаваемым данным током.

Индуктивность также называют коэффициентом самоиндукции, она характеризует магнитные свойства электрической цепи (контура, катушки и т.д.)

Вопрос 5. Как можно переписать формулу для энергии магнитного поля?

Ответ. Формула может быть записана в виде:

W=LI22=ФI2=Ф22L

Нужна помощь в решении задач или любых других заданий по учебе? Профессиональный сервис для студентов всегда готов поспособствовать с их решением.

Самоиндукция – это значимый частный случай электромагнитной индукции, когда магнитный поток, изменяясь и вызывая ЭДС индукции, создается током в самом контуре.

В случае, когда ток рассматриваемого контура по каким-либо причинам изменен, то имеет место изменение и магнитного поля этого тока, а значит и собственного магнитного потока, проходящего через контур. В контуре создается ЭДС самоиндукции, создавая препятствие для изменений тока в контуре (по правилу Ленца).

Собственный магнитный поток Φ, который проходит через контур или катушку с током, является пропорциональным силе тока I: Φ=LI.

Коэффициент пропорциональности L в формуле Φ=LI есть коэффициент самоиндукции или индуктивность катушки. Единица индуктивности в СИ носит название генри (Гн). Индуктивность контура или катушки равна 1 Гн, когда при силе постоянного тока 1 А собственный поток составляет 1 Вб: 1 Гн=1 Вб1 А.

Расчет индуктивности

ЭДС самоиндукции является прямо пропорциональной индуктивности катушки и скорости изменения силы тока в ней.

Магнитное поле выступает носителем энергии. Так же, как заряженный конденсатор обладает запасом электрической энергии, катушка, по виткам которой проходит ток, обладает запасом магнитной энергии. Включив электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, при размыкании ключа будем наблюдать короткую вспышку лампы (рис. 1.21.1). Ток в цепи появится под влиянием ЭДС самоиндукции. Источником энергии, которая будет выделяться в этом процессе электрической цепью, будет служить магнитное поле катушки.

Рисунок 1.21.1. Магнитная энергия катушки. В момент размыкания ключа K лампа ярко вспыхнет.

Закон сохранения энергии позволяет говорить, что вся энергия, составляющая запас катушки, будет выделена в виде джоулева тепла. Обозначим как R полное сопротивление цепи, тогда за время Δt будет выделено количество теплоты ΔQ=I2·R·Δt.

Ток в цепи составляет:

I=δLR=-LR∆I∆t

Выражение для ΔQ можем записать так:

∆Q=-L·I·∆I=-Φ(I)∆I

В данной записи ΔI < 0; значение тока в цепи постепенно снижается от изначального I0 до нуля. Полное количество теплоты, которое выделится в цепи, возможно получить, осуществив действие интегрирования в пределах от I0 до 0. Тогда получим:

Q=LI022

Графический вывод формулы

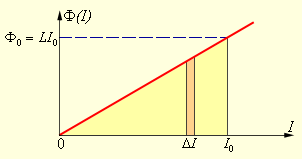
Существует возможность получить записанную формулу, используя графический метод. Для этого отобразим на графике зависимость магнитного потока Φ(I) от тока I (рис. 1.21.2). Полное количество выделившейся теплоты, которое равно изначальному запасу энергии магнитного поля, определится как площадь получившегося на рис. 1.21.2 треугольника:

Рисунок 1.21.2. Вычисление энергии магнитного поля.

В итоге формула энергии Wм магнитного поля катушки с индуктивностью L, создаваемого током I, будет записана в виде формулы:

Wм=ΦI2=LI22=Φ22L

Используем выражение, которое мы получили, для энергии катушки к длинному соленоиду с магнитным сердечником. Применяя указанные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, получим запись:

Wм=μ0·μ·n2·I22V=B22μ0·μV

В этой формуле V является объемом соленоида. Полученное выражение демонстрирует нам, что магнитная энергия имеет локализацию не в витках катушки, по которым проходит ток, а распределена по всему объему, в котором возникло магнитное поле.

Объёмная плотность магнитной энергии – это физическая величина, которая равна энергии магнитного поля в единице объема: Wм=B22μ·μ.

В свое время Максвелл продемонстрировал, что указанная формула (в нашем случае выведенная для длинного соленоида) верна для любых магнитных полей.