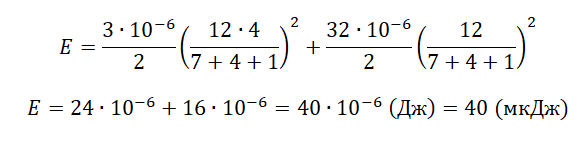Как найти энергию магнитного поля формулы - Сайт, где вы сможете решить свои вопросы

Магнитное поле, связанное с электрическим током, характеризуется определенной энергией.

Если через проводник или катушку проходит ток, то часть электроэнергии расходуется на преодоление сопротивления проводника и превращается в тепло, а часть образует магнитное поле, в котором накапливается некоторая часть энергии, превращается в потенциальную энергию.

Определение магнитной энергии

Магнитная энергия и электростатическая потенциальная энергия связаны уравнениями Максвелла. Потенциальная энергия магнитного момента mm в магнитном поле BB определяется как механическая работа магнитной силы (фактически магнитного момента) на повторное выравнивание вектора магнитного дипольного момента и равна:

E=−m⋅BE = – m cdot B

в то время как энергия, запасенная в катушке индуктивности (с индуктивностью LL) при прохождении через нее тока II, определяется как:

E=1/2LI2E = 1/2 LI^2

Это выражение лежит в основе сверхпроводящего накопления магнитной энергии.

Энергия также хранится в магнитном поле. Энергия на единицу объема в области пространства проницаемости μ0μ0, содержащей магнитное поле BB, равна:

U=B2/2μ0U = B^2/2μ_0

В более широком смысле, если мы предположим, что среда является парамагнитной или диамагнитной и существует линейное определяющее уравнение, связывающее BB, то можно показать, что магнитное поле хранит энергию

E=12∫HBdV,E=frac{1}{2}int{HBdV},

где интеграл оценивается по всей области, где существует магнитное поле.

Аналогично энергию магнитного поля тока можно определить также через работу тока против ЭДС самоиндукции, которая выполняется при замыкании цепи.

Сравнивая выражение энергии магнитного поля через индукцию и силу тока с формулой для определения кинетической энергии, делаем вывод, что индуктивность в электромагнитных явлениях играет такую же роль, как масса в механических явлениях, и является мерой инертности электрической цепи.

Энергия магнитного поля соленоида

Индуктивность контура

Физическая величина, определяемая удвоенной энергией магнитного поля, сформированного единичным током в этом контуре.

Определим энергию магнитного поля соленоида, индуктивность которого LL:

L=μμ0n02VL=mu {{mu }_{0}}n_{0}^{2}V

Wm=12μμ0n02I2V{{W}_{m}}=frac{1}{2}mu {{mu }_{0}}n_{0}^{2}{{I}^{2}}V.

Индукция магнитного поля внутри соленоида:

B=μμ0n0IB=mu {{mu }_{0}}{{n}_{0}}I

откуда

I=Bμμ0n0I=frac{B}{mu {{mu }_{0}}{{n}_{0}}}

Из данных формул получаем

Wm=12B2Vμμ0,{{W}_{m}}=frac{1}{2}frac{{{B}^{2}}V}{mu {{mu }_{0}}},

где VV –объем соленоида.

Поскольку поле соленоида однородно и почти полностью локализовано в его объеме, можно определить плотность энергии магнитного поля, то есть энергию, рассчитанную на единицу объема поля:

wm=WmV=12B2μμ0=BH2=μμ0H22{{w}_{m}}=frac{{{W}_{m}}}{V}=frac{1}{2}frac{{{B}^{2}}}{mu {{mu }_{0}}}=frac{BH}{2}=frac{mu {{mu }_{0}}{{H}^{2}}}{2}

Плотность энергии магнитного поля как характеристику поля относят к любой точке поля, в которых заданы векторы BB или HH.

Зная энергию магнитного поля, можно по теории относительности найти подходящую массу поля:

m=Wmc2m=frac{{{W}_{m}}}{{{c}^{2}}}

Итак, как электрическое, так и магнитное поля имеют не только энергию, но и массу. Эти поля так же материальны, как и вещества.

Тест по теме «Энергия магнитного поля»

Источник

Классическая электродинамика

Электричество · Магнетизм
Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал
Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Магнитная индукция
Электродинамика Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле
Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс
Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток
См. также: Портал:Физика

Магни́тное по́ле — поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения^[1]; магнитная составляющая электромагнитного поля^[2].

Магнитное поле может создаваться электрическим током или, в случае постоянных магнитов, магнитными моментами электронов в атомах (и моментами других частиц, что обычно проявляется в существенно меньшей степени).

Кроме этого, оно возникает в результате изменения во времени электрического поля.

Основной количественной характеристикой магнитного поля является вектор магнитной индукции (вектор индукции магнитного поля)^[3]. С математической точки зрения магнитное поле описывается векторным полем , заданным в каждой точке пространства в зависимости от времени .

Вместо магнитной индукции для описания магнитного поля можно использовать ещё одну фундаментальную величину, тесно с ней взаимосвязанную, — векторный потенциал ().

Нередко в литературе в качестве основной характеристики магнитного поля в вакууме (то есть в отсутствие вещества) выбирают не вектор магнитной индукции а вектор напряжённости магнитного поля , что формально можно сделать, так как в вакууме эти два вектора совпадают^[4]; однако в магнитной среде вектор не несёт уже того же физического смысла^[5], являясь важной, но всё же вспомогательной величиной. Поэтому, несмотря на формальную эквивалентность обоих подходов для вакуума, с систематической точки зрения следует считать основной характеристикой магнитного поля именно

Магнитное поле можно назвать особым видом материи^[6], посредством которого осуществляется взаимодействие между движущимися заряженными частицами или телами, обладающими магнитным моментом.

В специальной теории относительности магнитные поля являются необходимым следствием существования электрических полей. При переходе от одной ИСО к другой магнитные и электрические поля преобразуются совместно^[7].

Вместе магнитное и электрическое поля образуют электромагнитное поле, проявлениями которого являются, в частности, свет и все другие электромагнитные волны.

С точки зрения квантовой теории поля магнитное взаимодействие — как частный случай электромагнитного взаимодействия — переносится фундаментальным безмассовым бозоном — фотоном (частицей, которую можно представить как квантовое возбуждение электромагнитного поля), часто (например, во всех случаях статических полей) — виртуальным.

Источники и регистраторы поля[править | править код]

Магнитное поле создаётся (порождается) током заряженных частиц, или изменяющимся во времени электрическим полем, или собственными магнитными моментами частиц (последние для единообразия картины могут быть формальным образом сведены к электрическим токам).

Фудаментальным средством регистрации магнитного поля является плоская рамка с током, которая стремится расположиться так, чтобы её магнитный момент (нормаль к плоскости рамки) стал сонаправленным с детектируемым полем. Для практических количественных измерений существуют приборы, называемые тесламетрами.

Вычисление магнитного поля[править | править код]

В простых случаях магнитное поле ( или , — радиус-вектор) проводника с током, в том числе и для случая тока, распределённого произвольным образом по объёму, может быть найдено из закона Био — Савара — Лапласа или теоремы о циркуляции. Этот способ ограничивается случаем (приближением) магнитостатики, то есть случаем постоянных (если речь идёт о строгой применимости) или достаточно медленно меняющихся (если речь идёт о приближённом применении) магнитных и электрических полей.

В более сложных ситуациях магнитное поле ищется путём решения уравнений Максвелла — для полей или для потенциалов, в зависимости от того, какая величина выбрана для характеризации магнитного поля.

Применительно к магнитному полю (так же, как и к электрическому) обычно действует принцип суперпозиции: поле нескольких источников равно сумме полей, создаваемых источниками по отдельности. Исключением могут быть случаи присутствия ферромагнитных нелинейных сред (для электрических полей подобное исключение возникает при наличии сегнетоэлектриков).

Единицы измерения[править | править код]

Ниже приведены размерности основных величин, характеризующих магнитное поле.

Величина в системе единиц СИ измеряется в теслах (русское обозначение: Тл; международное: T), в системе СГС — в гауссах (русское обозначение: Гс; международное: G). Связь между ними выражается соотношениями: 1 Гс = 1·10⁻⁴ Тл и 1 Тл = 1·10⁴ Гс.

Векторное поле измеряется в амперах на метр (А/м) в системе СИ и в эрстедах (русское обозначение: Э; международное: Oe) в СГС. Связь между ними выражается соотношением: 1 эрстед = 1000/(4π) A/м ≈ 79,5774715459 А/м.

Векторный потенциал , ротор которого равен магнитной индукции, измеряется в Тл cdot м (в СИ) или Гс cdot см (в СГС). Связь: 1 Гс cdot см = 10⁻⁶ Тл cdot м, или 1 Тл cdot м = 10⁶ Гс cdot см.

Проявление магнитного поля[править | править код]

Магнитное поле проявляется в воздействии на магнитные моменты частиц и тел, на движущиеся заряженные частицы (или проводники с током).

Силовое воздействие на заряды и токи[править | править код]

Сила, действующая на движущуюся в магнитном поле электрически заряженную частицу, называется силой Лоренца, которая всегда направлена перпендикулярно к векторам v и B^[3]. Она пропорциональна заряду частицы q, составляющей скорости v, перпендикулярной направлению вектора магнитного поля B, и величине индукции магнитного поля B. В Международной системе единиц (СИ) сила Лоренца выражается так:

{displaystyle mathbf {F} =q[mathbf {v} ,mathbf {B} ]}

в системе единиц СГС:

${displaystyle mathbf {F} ={frac {q}{c}}[mathbf {v} ,mathbf {B} ]}$

где квадратными скобками обозначено векторное произведение.

Также (вследствие действия силы Лоренца на движущиеся по проводнику заряженные частицы) магнитное поле действует на проводник с током. Сила, действующая на проводник с током, называется силой Ампера. Эта сила складывается из сил, действующих на отдельные движущиеся внутри проводника заряды.

Взаимодействие двух магнитов[править | править код]

Одно из наиболее часто встречающихся в обычной жизни проявлений магнитного поля — взаимодействие двух магнитов: одинаковые полюса отталкиваются, противоположные притягиваются. Представляется заманчивым описать взаимодействие между магнитами как взаимодействие между двумя монополями, и с формальной точки зрения эта идея вполне реализуема и часто весьма удобна, а значит практически полезна (в расчётах); однако детальный анализ показывает, что на самом деле это не полностью правильное описание явления (наиболее очевидным вопросом, не получающим объяснения в рамках такой модели, является вопрос о том, почему монополи никогда не могут быть разделены, то есть почему эксперимент показывает, что никакое изолированное тело на самом деле не обладает магнитным зарядом; кроме того, слабостью модели является то, что она неприменима к магнитному полю, создаваемому макроскопическим током, а значит, если не рассматривать её как чисто формальный приём, приводит лишь к усложнению теории в фундаментальном смысле).

На магнитный диполь, помещённый в однородное поле, действует момент сил, стремящийся повернуть его так, чтобы магнитный момент диполя был сонаправлен с магнитным полем. При этом суммарная сила, действующая на магнит со стороны однородного магнитного поля, равна нулю. Сила, действующая на магнитный диполь с магнитным моментом m в случае неоднородного поля, выражается формулой^[8]^[9]:

{displaystyle mathbf {F} =left(mathbf {m} cdot nabla right)mathbf {B} }

Сила, действующая на магнит (не являющийся одиночным точечным диполем) со стороны неоднородного поля, может быть найдена суммированием всех сил (определяемых данной формулой), действующих на элементарные диполи, составляющие магнит.

Впрочем, возможен подход, сводящий взаимодействие магнитов к силе Ампера, а сама приведённая выше формула для силы, действующей на магнитный диполь, тоже может быть получена из выражения для силы Ампера.

Явление электромагнитной индукции[править | править код]

Если поток вектора магнитной индукции через замкнутый контур меняется во времени, в этом контуре возникает ЭДС электромагнитной индукции, порождаемая (в случае неподвижного контура) вихревым электрическим полем, возникающим вследствие изменения магнитного поля со временем (в случае неизменного со временем магнитного поля и изменения потока из-за движения контура-проводника такая ЭДС возникает посредством действия силы Лоренца).

В массивном проводнике, пронизываемом переменным магнитным потоком, возникают замкнутые (вихревые) электрические токи — так называемые токи Фуко́. Они являются индукционными токами, образующимися в проводящем теле либо вследствие изменения во времени магнитного поля, в котором оно находится, либо в результате движения тела в магнитном поле, приводящего к изменению магнитного потока через тело или любую его часть. Согласно правилу Ленца, магнитное поле токов Фуко направлено так, чтобы противодействовать изменению магнитного потока, индуцирующему эти токи^[10].

Математическое представление[править | править код]

Магнитное поле в макроскопическом описании представлено двумя различными векторными полями, обозначаемыми как H и B, а также векторным потенциалом A.

H называется напряжённостью магнитного поля; B называется магнитной индукцией. Термин магнитное поле применяется к обоим этим векторным полям (хотя исторически относился в первую очередь к H).

Магнитная индукция B является основной^[9]^[11]^[12] характеристикой магнитного поля, так как, во-первых, именно она определяет действующую на заряды силу, а во-вторых, векторы B и E на самом деле являются компонентами единого тензора электромагнитного поля. Аналогично, в единый тензор объединяются величины H и электрическая индукция D. В свою очередь, разделение электромагнитного поля на электрическое и магнитное является совершенно условным и зависящим от выбора системы отсчёта, поэтому вектора B и E должны рассматриваться совместно.

Впрочем, в вакууме (при отсутствии магнетиков), а значит и на фундаментальном микроскопическом уровне, H и B совпадают (в системе СИ с точностью до условного постоянного множителя, а в СГС — полностью), что позволяет в принципе авторам, особенно тем, кто не использует СИ, выбирать для фундаментального описания магнитного поля H или B произвольно, чем они нередко и пользуются (к тому же, следуя в этом традиции). Авторы же, пользующиеся системой СИ, систематически отдают и здесь в этом отношении предпочтение вектору B, хотя бы потому, что именно через него прямо выражается сила Лоренца.

Магнитные свойства веществ[править | править код]

С фундаментальной точки зрения, как это было указано выше, магнитное поле может создаваться (а значит — в контексте этого параграфа — и ослабляться или усиливаться) переменным электрическим полем, электрическими токами в виде потоков заряженных частиц или магнитными моментами частиц.

Наиболее общее соотношение, характеризующее поведение магнитного поля в веществе, представляет собой уравнение, связывающее и :

${displaystyle mathbf {B} =mu _{0}mu mathbf {H} }$

где $mu _{0}$ — магнитная постоянная, а — магнитная проницаемость среды в конкретной точне (часто является константой, но бывают и более сложные случаи, в том числе такие, когда зависит от ).

Конкретные микроскопические структуры и свойства различных веществ (а также их смесей, сплавов, агрегатных состояний, кристаллических модификаций и т. д.) приводят к тому, что на макроскопическом уровне они могут вести себя достаточно разнообразно под действием внешнего магнитного поля (в частности, ослабляя или усиливая его в разной степени).

В связи с этим вещества (и вообще среды) в отношении их магнитных свойств делятся на такие основные группы:

Антиферромагнетики — вещества, в которых установился антиферромагнитный порядок магнитных моментов атомов или ионов: магнитные моменты веществ направлены противоположно и равны по силе.
Диамагнетики — вещества, намагничивающиеся против направления внешнего магнитного поля.
Парамагнетики — вещества, которые намагничиваются во внешнем магнитном поле в направлении внешнего магнитного поля.
Ферромагнетики — вещества, в которых ниже определённой критической температуры (точки Кюри) устанавливается дальний ферромагнитный порядок магнитных моментов.
Ферримагнетики — материалы, у которых магнитные моменты вещества направлены противоположно и не равны по силе.
К перечисленным выше группам веществ в основном относятся обычные твёрдые или (к некоторым) жидкие вещества, а также газы. Существенно отличается взаимодействие с магнитным полем сверхпроводников и плазмы.

Энергия магнитного поля[править | править код]

Виды энергии:
	Механическая	Потенциальная Кинетическая
‹♦›	Внутренняя
	Электромагнитная	Электрическая Магнитная
	Химическая
	Ядерная
	Гравитационная
	Вакуума
Гипотетические:
	Тёмная
См. также: Закон сохранения энергии

Приращение плотности энергии магнитного поля равно

В линейном тензорном приближении магнитная проницаемость есть тензор (обозначим его ), и умножение вектора на неё есть тензорное (матричное) умножение:

${displaystyle mathbf {B} =mu _{0}{hat {mu }}mathbf {H} quad }$

или в компонентах^[13] $B_{i}=mu _{0}mu _{{ij}}H_{j}$

Плотность энергии в этом приближении равна

${displaystyle w={frac {mathbf {H} cdot mathbf {B} }{2}}={frac {mu _{0}mathbf {H} {hat {mu }}mathbf {H} }{2}}={frac {mu _{0}H_{i}mu _{ij}H_{j}}{2}}=}$

${displaystyle ={frac {mathbf {B} ({hat {mu }}^{-1})mathbf {B} }{2mu _{0}}}={frac {B_{i}({hat {mu }}^{-1})_{ij}B_{j}}{2mu _{0}}}}$

где $mu _{{ij}}$ — компоненты тензора магнитной проницаемости, ${hat mu }^{{-1}}$ — тензор, представимый матрицей, обратной матрице тензора проницаемости.

При выборе осей координат совпадающими с главными осями^[14] тензора магнитной проницаемости формулы в компонентах упрощаются:

$w={frac {mu _{0}mu _{{i}}(H_{i})^{2}}{2}}={frac {(B_{i})^{2}/mu _{{i}}}{2mu _{0}}}$

Здесь $mu _{{i}}$ — диагональные компоненты тензора магнитной проницаемости в его собственных осях (остальные компоненты в данных специальных координатах — и только в них! — равны нулю).

В изотропном линейном магнетике

$w={frac {HB}{2}}={frac {mu _{0}mu H^{2}}{2}}={frac {B^{2}}{2mu _{0}mu }}$

где — относительная магнитная проницаемость. В вакууме mu =1 и

$w={frac {mu _{0}H^{2}}{2}}={frac {B^{2}}{2mu _{0}}}={frac {epsilon _{0}c^{2}B^{2}}{2}}$

Энергию магнитного поля в катушке индуктивности можно найти по формуле

$W={frac {Phi I}{2}}={frac {LI^{2}}{2}}$

где Ф — магнитный поток, I — ток, L — индуктивность катушки или витка с током.

История развития представлений о магнитном поле[править | править код]

Один из первых рисунков магнитного поля (Рене Декарт, 1644)

Хотя магниты и магнетизм были известны с давних времён, изучение магнитного поля началось в 1269 году, когда французский учёный Пётр Перегрин (рыцарь Пьер из Мерикура) при помощи стальных игл разметил магнитное поле на поверхности сферического магнита и определил, что получающиеся линии магнитного поля пересекались в двух точках, которые он назвал «полюсами» (по аналогии с полюсами Земли). Почти три столетия спустя Уильям Гильберт Колчестер использовал труд Петра Перегрина и впервые определённо заявил, что сама Земля является магнитом. Работа Гилберта «De Magnete», опубликованная в 1600 году, заложила основы магнетизма как науки^[15].

В 1750 году Джон Мичелл заявил, что магнитные полюса притягиваются и отталкиваются в соответствии с законом обратных квадратов. Шарль-Огюстен де Кулон экспериментально проверил это утверждение в 1785 году и прямо заявил, что северный и южный полюс не могут быть разделены. Основываясь на этой силе, существующей между полюсами, Симеон Дени Пуассон создал первую успешную модель магнитного поля, которую он представил в 1824 году. В этой модели магнитное поле порождается магнитными полюсами, и магнетизм возникает из-за действия нескольких пар магнитных полюсов (диполей)^[15].

Работа Эрстеда, Der Geist in der Natur, 1854

Три открытия, совершённые в начале XIX века почти подряд, заставили пересмотреть эту модель. Во-первых, в 1819 году Ханс Кристиан Эрстед обнаружил, что электрический ток создаёт магнитное поле вокруг себя. Затем, в 1820 году, Андре-Мари Ампер показал, что параллельные провода, по которым идёт ток в одном и том же направлении, притягиваются друг к другу. Наконец, Жан-Батист Био и Феликс Савар в 1820 году открыли закон, названный законом Био-Савара-Лапласа, который правильно предсказывал магнитное поле вокруг любого провода, находящегося под напряжением^[15].

Расширив эти эксперименты, Ампер в 1825 году издал свою собственную успешную модель магнетизма. В ней он показал эквивалентность электрического тока и источника магнитного поля, создаваемого магнитами, и вместо диполей магнитных зарядов модели Пуассона предложил идею, что магнетизм связан с петлями постоянно текущего тока. Эта идея объясняла, почему «магнитный заряд» (отдельный полюс магнита) не может быть изолирован. Кроме того, Ампер вывел закон, названный его именем, который, как и закон Био-Савара-Лапласа, правильно описывал магнитное поле, создаваемое постоянным током; также была введена теорема о циркуляции магнитного поля. Кроме того, в этой работе Ампер ввёл термин «электродинамика» для описания взаимосвязи между электричеством и магнетизмом^[15].

В 1831 году Майкл Фарадей открыл электромагнитную индукцию, обнаружив, что переменное магнитное поле порождает электричество. Он создал определение этого явления, которое известно как закон электромагнитной индукции Фарадея. Позже Франц Эрнст Нейман доказал, что для движущегося проводника в магнитном поле индукция является следствием действия закона Ампера. При этом он ввёл векторный потенциал электромагнитного поля, который, как позднее было показано, был эквивалентен основному механизму, предложенному Фарадеем^[15].

В 1850 году лорд Кельвин, тогда известный как Уильям Томсон, обозначил различие между двумя типами магнитных полей как поля H и B. Первое было применимо к модели Пуассона, а второе — к модели индукции Ампера. Кроме того, он вывел, как H и B связаны друг с другом^[15].

Между 1861 и 1865 годами Джеймс Клерк Максвелл разработал и опубликовал уравнения Максвелла, которые объяснили и объединили электричество и магнетизм в классической физике. Первая подборка этих уравнений была опубликована в статье в 1861 году, озаглавленной «On Physical Lines of Force». Эти уравнения были признаны действительными, хотя и неполными. Максвелл улучшил эти уравнения в более поздней работе 1865 года «Динамическая теория электромагнитного поля» и определил, что свет представляет собой электромагнитные волны. Генрих Герц экспериментально подтвердил этот факт в 1887 году^[15].

Хотя выражение для подразумеваемой в законе Ампера силы магнитного поля, создаваемого движущимся электрическим зарядом, не было сформулировано в явном виде, в 1892 году Хендрик Лоренц вывел его из уравнений Максвелла. При этом классическая теория электродинамики была в основном завершена^[15].

Двадцатый век расширил взгляды на электродинамику благодаря появлению теории относительности и квантовой механики. Альберт Эйнштейн в статье 1905 года, где была обоснована специальная теория относительности, показал, что электрические и магнитные поля являются частью одного и того же явления, рассматриваемого в разных системах отсчёта. (См. Движущийся магнит и проблема проводника — мысленный эксперимент, который в конечном итоге помог Эйнштейну в разработке СТО). Наконец, в результате объединения квантовой механики с классической электродинамикой была создана квантовая электродинамика (КЭД)^[15].

См. также[править | править код]

Магнит
Магнитная плёнка-визуализатор
Магнитное поле звёзд
Магнитное поле планет
Магнитное поле Земли
Вращающееся магнитное поле
Магнитноротационная неустойчивость
Межпланетное магнитное поле
Магнитный монополь

Примечания[править | править код]

↑ БСЭ. 1973, «Советская энциклопедия»
↑ В частных случаях магнитное поле может существовать и в отсутствие электрического поля, но вообще говоря магнитное поле глубоко взаимосвязано с электрическим, как динамически (взаимное порождение переменными электрическим и магнитным полем друг друга), так и в том смысле, что при переходе в новую систему отсчёта магнитное и электрическое поле выражаются друг через друга, то есть вообще говоря не могут быть безусловно разделены.
↑ ¹ ² Яворский Б. М., Детлаф А. А. Справочник по физике: 2-е изд., перераб. — М.: Наука, Главная редакция физико-математической литературы, 1985, — 512 с.
↑ Точно совпадают в системе единиц СГС, в СИ — отличаются постоянным коэффициентом, что, конечно, не меняет факта их практического физического тождества.
↑ Самым важным и лежащим на поверхности отличием тут является то, что сила, действующая на движущуюся частицу (или на магнитный диполь) вычисляются именно через а не через . Любой другой физически корректный и осмысленный метод измерения также даст возможность измерить именно хотя для формального расчёта иногда оказывается более удобным — в чём, собственно, и состоит смысл введения этой вспомогательной величины (иначе без неё вообще обходились бы, используя только
↑ Однако надо хорошо понимать, что ряд фундаментальных свойств этой «материи» в корне отличается от свойств того обычного вида «материи», который можно было бы обозначить термином «вещество».
↑ См. параграф Преобразования Лоренца для электромагнитного поля (ф-лы 6.38) курса «Электричество и магнетизм» на сайте МИФИ, кафедра общей физики.
↑ Для однородного поля это выражение даёт нулевую силу, поскольку равны нулю все производные B по координатам.
↑ ¹ ² Сивухин Д. В. Общий курс физики. — Изд. 4-е, стереотипное. — М.: Физматлит; Изд-во МФТИ, 2004. — Т. III. Электричество. — 656 с. — ISBN 5-9221-0227-3; ISBN 5-89155-086-5..
↑ Главный редактор А. М. Прохоров. Вихревые токи // Физический энциклопедический словарь. — Советская энциклопедия. — Москва, 1983. Физическая энциклопедия.
↑ При рассмотрении задач не на микроскопическом масштабе, а на т. н. физически бесконечно малом масштабе (ФЭ,Л-М.у. Архивная копия от 3 мая 2011 на Wayback Machine)
↑ Индукция (в физике) // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
↑ Здесь и далее используется видоизмененное правило Эйнштейна суммирования по повторяющимся индексам, то есть обозначение $a_{i}T_{{ij}}b_{j}$ следует понимать как $sum _{{ij}}a_{i}T_{{ij}}b_{j}$ .
↑ «Привязанными» к кристаллу магнетика, то есть связанные с его ориентацией в пространстве.
↑ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ Whittaker, E. T.^?!. A History of the Theories of Aether and Electricity (англ.). — Dover Publications, 1951. — P. 34. — ISBN 0-486-26126-3.

Ссылки[править | править код]

Влияние слабых магнитных полей на биосистемы (видео)
Действие магнитного поля на движущиеся заряды^{[уточнить]}
Учебный фильм про магнитное поле^{[уточнить]}

Источник

Определение 1

Самоиндукция – это значимый частный случай электромагнитной индукции, когда магнитный поток, изменяясь и вызывая ЭДС индукции, создается током в самом контуре.

В случае, когда ток рассматриваемого контура по каким-либо причинам изменен, то имеет место изменение и магнитного поля этого тока, а значит и собственного магнитного потока, проходящего через контур. В контуре создается ЭДС самоиндукции, создавая препятствие для изменений тока в контуре (по правилу Ленца).

Собственный магнитный поток Φ, который проходит через контур или катушку с током, является пропорциональным силе тока I: Φ=LI.

Определение 2

Коэффициент пропорциональности L в формуле Φ=LI есть коэффициент самоиндукции или индуктивность катушки. Единица индуктивности в СИ носит название генри (Гн). Индуктивность контура или катушки равна 1 Гн, когда при силе постоянного тока 1 А собственный поток составляет 1 Вб: 1 Гн=1 Вб1 А.

Расчет индуктивности

Пример 1

Для наглядности произведем расчет индуктивности длинного соленоида, который имеет N витков, площадь сечения S и длину l. Соленоид – это цилиндрическая катушка индуктивности, у которой длина много больше диаметра. Магнитное поле соленоида задается формулой:

B=μ0nI,

где I является обозначением тока в соленоиде, n = Ne указывает число витков на единицу длины соленоида.

Магнитный поток внутри катушки соленоида, проходящий через все N витков, составляет:

Φ=B·S·N=μ0n2Sl

Таким образом, индуктивность соленоида будет выражена формулой:

L=μ0n2S·l=μ0n2V,

где V=Sl – объем соленоида, содержащий магнитное поле.

Результат, который мы получили, не берет в расчет краевых эффектов, а значит он является приближенно верным лишь для катушек достаточной длины. Когда соленоид заполнен веществом, имеющим магнитную проницаемость μ, при заданном токе I индукция магнитного поля будет возрастать по модулю в μ раз, а значит и индуктивность катушки с сердечником тоже получит увеличение в μ раз:

Lμ=μ·L=μ0·μ·n2·V.

Определение 3

ЭДС самоиндукции, которая возникает в катушке при постоянном значении индуктивности, в соответствии с законом Фарадея записывается в виде формулы:

δинд=δL=-∆Φ∆t=-L∆I∆t.

ЭДС самоиндукции является прямо пропорциональной индуктивности катушки и скорости изменения силы тока в ней.

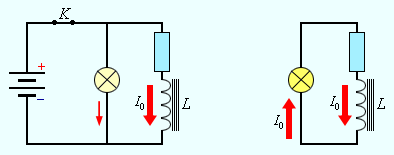
Магнитное поле выступает носителем энергии. Так же, как заряженный конденсатор обладает запасом электрической энергии, катушка, по виткам которой проходит ток, обладает запасом магнитной энергии. Включив электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, при размыкании ключа будем наблюдать короткую вспышку лампы (рис. 1.21.1). Ток в цепи появится под влиянием ЭДС самоиндукции. Источником энергии, которая будет выделяться в этом процессе электрической цепью, будет служить магнитное поле катушки.

Рисунок 1.21.1. Магнитная энергия катушки. В момент размыкания ключа K лампа ярко вспыхнет.

Закон сохранения энергии позволяет говорить, что вся энергия, составляющая запас катушки, будет выделена в виде джоулева тепла. Обозначим как R полное сопротивление цепи, тогда за время Δt будет выделено количество теплоты ΔQ=I2·R·Δt.

Ток в цепи составляет:

I=δLR=-LR∆I∆t

Выражение для ΔQ можем записать так:

∆Q=-L·I·∆I=-Φ(I)∆I

В данной записи ΔI < 0; значение тока в цепи постепенно снижается от изначального I0 до нуля. Полное количество теплоты, которое выделится в цепи, возможно получить, осуществив действие интегрирования в пределах от I0 до 0. Тогда получим:

Q=LI022

Графический вывод формулы

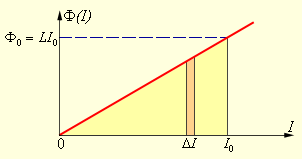
Существует возможность получить записанную формулу, используя графический метод. Для этого отобразим на графике зависимость магнитного потока Φ(I) от тока I (рис. 1.21.2). Полное количество выделившейся теплоты, которое равно изначальному запасу энергии магнитного поля, определится как площадь получившегося на рис. 1.21.2 треугольника:

Рисунок 1.21.2. Вычисление энергии магнитного поля.

В итоге формула энергии Wм магнитного поля катушки с индуктивностью L, создаваемого током I, будет записана в виде формулы:

Wм=ΦI2=LI22=Φ22L

Используем выражение, которое мы получили, для энергии катушки к длинному соленоиду с магнитным сердечником. Применяя указанные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, получим запись:

Wм=μ0·μ·n2·I22V=B22μ0·μV

В этой формуле V является объемом соленоида. Полученное выражение демонстрирует нам, что магнитная энергия имеет локализацию не в витках катушки, по которым проходит ток, а распределена по всему объему, в котором возникло магнитное поле.

Определение 4

Объёмная плотность магнитной энергии – это физическая величина, которая равна энергии магнитного поля в единице объема: Wм=B22μ·μ.

В свое время Максвелл продемонстрировал, что указанная формула (в нашем случае выведенная для длинного соленоида) верна для любых магнитных полей.

Источник

Явление самоиндукции заключается в возникновении индукционного тока (тока самоиндукции) в катушке при изменении силы тока в ней.

В опыте, демонстрирующем самоиндукцию при размыкании цепи, лампа, перед тем как погаснуть, ярко вспыхивает.

Появление мощного тока самоиндукции при размыкании цепи свидетельствует о том, что магнитное поле тока в катушке обладает энергией. Работа по созданию индукционного тока определяется уменьшением энергии магнитного поля. В свою очередь, энергия магнитного поля копится за счёт источника тока при совершении работы по преодолению тока самоиндукции, препятствующего увеличению тока в цепи.

Экспериментально выведена формула энергии магнитного поля катушки с током:

где (L) — индуктивность катушки (Гн), (I) — сила тока в катушке (А).

Энергия магнитного поля равна половине произведения индуктивности катушки на квадрат силы тока в ней.

Источник

Согласно закону сохранения энергии энергия магнитного поля, созданного током, равна той энергии, которую должен затратить источник тока (гальванический элемент, генератор на электростанции и др.) на создание тока. При размыкании цепи эта энергия переходит в другие виды энергии.

То, что для создания тока необходимо затратить энергию, т. е. необходимо совершить работу, объясняется тем, что при замыкании цепи, когда ток начинает нарастать, в проводнике появляется вихревое электрическое поле, действующее против того электрического поля, которое создается в проводнике благодаря источнику тока. Для того чтобы сила тока стала равной I, источник тока должен совершить работу против сил вихревого поля. Эта работа идет на увеличение энергии магнитного поля тока.

При размыкании цепи ток исчезает, и вихревое поле совершает положительную работу. Запасенная током энергия выделяется. Это обнаруживается, например, по мощной искре, возникающей при размыкании цепи с большой индуктивностью.

Записать выражение для энергии тока I, текущего по цепи с индуктивностью L (т.е. для энергии магнитного поля тока), можно на основании аналогии между инерцией и самоиндукцией, о которой мы говорили в прошлой теме.

Если самоиндукция аналогична инерции, то индуктивность в процессе создания тока должна играть ту же роль, что и масса при увеличении скорости тела в механике. Роль скорости тела в электродинамике играет сила тока I как величина, характеризующая движение электрических зарядов.

Если это так, то энергия магнитного поля тока WМ будет подобна кинетической энергии тела в механике. Поэтому ее можно определить формулой:

Энергия магнитного поля тока

WМ=LI22

Магнитное поле, созданное электрическим током, обладает энергией, прямо пропорциональной квадрату силы тока.

Пример №1. В катушке индуктивностью 0,15 Гн и очень малым сопротивлением r сила тока равна 4 А. Параллельно катушке присоединили резистор сопротивлением R>> r. Какое количество теплоты выделится в катушке и в резисторе после быстрого отключения силы тока?

При параллельном подключении к катушке большого сопротивления R>> r, сила тока, идущая через катушку, почти не изменяется. Энергия в катушке равна:

WМ=LI22

При отключении источника тока система катушка–сопротивление станет изолированной. Для изолированной системы справедлив закон сохранения энергии. В данном случае это означает, что вся энергия, запасенная в катушке, выделится в виде тепла в катушке и резисторе:

WМ=0,15·422=1,2 (Дж)

Задание EF17636

Катушка индуктивности подключена к источнику постоянного тока. Как изменится энергия магнитного поля катушки при увеличении силы тока через катушку в 3 раза?

Ответ:

а) уменьшится в 3 раза

б) увеличится в 9 раз

в) увеличится в 3 раза

г) уменьшится в 9 раз

Алгоритм решения

1.Записать формулу, определяющую энергию магнитного поля тока.

2.Установить, как изменится энергия магнитного поля тока при увеличении силы тока через катушку в 3 раза.

Решение

Энергия магнитного поля тока определяется формулой:

WМ=LI22

Видно, что энергия магнитного поля тока прямо пропорционально зависит от квадрата силы тока в катушке. Следовательно, если сила тока увеличится втрое, то энергия магнитного поля увеличится в 3², то есть в 9 раз.

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF22688

Энергия магнитного поля катушки с током равна 0,64 Дж. Индуктивность катушки равна 20 мГн. Какова сила тока в катушке?

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения в СИ.

2.Записать формулу, определяющую энергию магнитного поля тока.

3.Выполнить решение задачи в общем виде.

4.Подставить неизвестные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

Индуктивность катушки: L = 20 мГн.
Энергия магнитного поля катушки с током: W_M = 0,64 Дж.

20 мГн = 0,02 Гн

Формула для нахождения энергии магнитного поля тока:

WМ=LI22

Отсюда сила тока равна:

I=√2WМL=√2·0,640,02=8 ⎛⎝А⎞⎠

Ответ: 8

pазбирался: Алиса Никитина | обсудить разбор

Задание EF22800

На рисунке показана схема электрической цепи, состоящей из источника тока с ЭДС ε = 12 В и внутренним сопротивлением r = 1 Ом, двух резисторов с сопротивлениями R₁ = 7 Ом и R₂ = 4 Ом, конденсатора электроёмкостью С = 3 мкФ и катушки с индуктивностью L = 32 мкГн. Какое количество теплоты выделится на резисторе R₂ после размыкания ключа К? Сопротивлением провода катушки пренебречь. Ответ запишите в мкДж.

1.Записать исходные данные и перевести единицы измерения в СИ.

2.Записать закон электромагнитной индукции для двигающихся стержней.

3.Выполнить решение задачи в общем виде.

4.Подставить неизвестные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

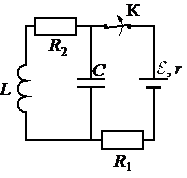
• ЭДС источника тока: ε = 12 В.

• Сопротивление источника тока: R = 1 Ом.

• Сопротивление первого резистора: R1 = 7 Ом.

• Сопротивление второго резистора: R2 = 4 Ом.

• Электроемкость конденсатора: C = 3 мкФ.

• Индуктивность катушки: L = 32 мкГн.

3 мкФ = 3∙10^–6Ф

32 мкГн = 32∙10^–6 Гн

До размыкания ключа электрический ток протекает через последовательно соединённые резисторы R1, R2 и катушку L. После размыкания ключа вся накопленная в элементах цепи энергия выделится в виде тепла на резисторе R₂:

E=Wкон+Wкат

Энергия электрического поля в конденсаторе определяется формулой:

Wкон=CU22

Напряжение U на конденсаторе можно выразит из закона Ома для участка цепи:

U=IR2

Чтобы выразить силу тока, потребуется записать закон Ома для полной цепи:

I=εR+r

Так как в цепи есть два последовательно соединенных резистора, общее сопротивление цепи будет равно сумме их сопротивлений:

R=R1+R2

Тогда закон Ома для полной цепи примет вид:

I=εR1+R2+r

Тогда напряжение на конденсаторе равно:

U=εR2R1+R2+r

Следовательно, энергия электрического поля в конденсаторе будет равна:

Wкон=C2(εR2R1+R2+r)2

Энергия электромагнитного поля в катушке определяется формулой:

Wкат=LI22=L2(εR1+R2+r)2

Следовательно, на втором резисторе выделится энергия, равная:

E=C2(εR2R1+R2+r)2+L2(εR1+R2+r)2

Ответ: 40

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 2.8k

Источник

Определение магнитной энергии

Энергия магнитного поля соленоида

Тест по теме «Энергия магнитного поля»

Источники и регистраторы поля[править | править код]

Вычисление магнитного поля[править | править код]

Единицы измерения[править | править код]

Проявление магнитного поля[править | править код]

Силовое воздействие на заряды и токи[править | править код]

Взаимодействие двух магнитов[править | править код]

Явление электромагнитной индукции[править | править код]

Математическое представление[править | править код]

Магнитные свойства веществ[править | править код]

Энергия магнитного поля[править | править код]

История развития представлений о магнитном поле[править | править код]

См. также[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Расчет индуктивности

Графический вывод формулы

Вам также может понравиться

Цзу сань ли как найти эту точку

Как найти владельца почты яндекс

Как найти название исполнителя по музыке

Добавить комментарий Отменить ответ