Содержание:
Энергия электрического поля:
Для зарядки проводника выполняется работа по преодолению силы отталкивания между зарядами. За счет этой работы проводник получает энергию. Полученная энергия заряженного тела количественно равна работе, выполненной при его зарядке, т.е. 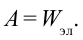

Среднее значение потенциала тела равно среднему арифметическому его начальных и конечных значений, т.е.

Поставляя значении 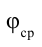 в уравнение (7.21), получим следующее выражение:
в уравнение (7.21), получим следующее выражение:

Значит, работа, выполненная при зарядке тела, равняется половине произведения его заряда на потенциал. При зарядке тела его потенциал плавно, т.е. линейно изменяется согласно формуле 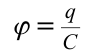 . Здесь
. Здесь 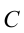 – электрическая емкость проводника. Тогда выражение (7.23) можно записать следующим образом:
– электрическая емкость проводника. Тогда выражение (7.23) можно записать следующим образом:

Согласно соотношению 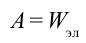 , формулу для расчета энергии электрического поля изолированного заряженного тела можно записать в виде
, формулу для расчета энергии электрического поля изолированного заряженного тела можно записать в виде
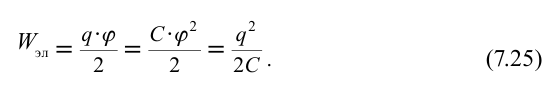
Если заряженное тело является конденсатором, то при расчете энергии (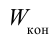 ) его электрического поля величину заряда в формуле (7.25) нужно заменить на величину зарядов на одной обкладке конденсатора, а потенциал заменить на разницу потенциалов между обкладками, т.е., можно записать:
) его электрического поля величину заряда в формуле (7.25) нужно заменить на величину зарядов на одной обкладке конденсатора, а потенциал заменить на разницу потенциалов между обкладками, т.е., можно записать:
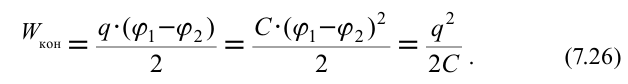
Исходя из этого, формулу определения электрической энергии конденсатора можно записать в виде:
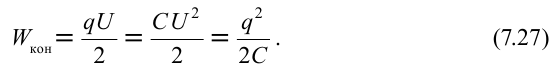
Энергия заряженного тела сосредоточена в электрическом поле, созданном вокруг него, величина энергии зависит от объема пространства, занимаемого полем и напряженности поля.
Рассмотрим частный случай плоского заряженного конденсатора.
Электрическое поле, созданное зарядами обкладок плоского конденсатора, сосредоточено в среде между его обкладками. Объем пространства можно вычислить по формуле 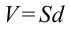 .
.
Учитывая емкость заряженного плоского конденсатора 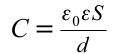 и зависимость между разницей потенциалов обкладок и напряженностью поля конденсатора, с учетом формулы (7.27), получим следующее соотношение:
и зависимость между разницей потенциалов обкладок и напряженностью поля конденсатора, с учетом формулы (7.27), получим следующее соотношение:
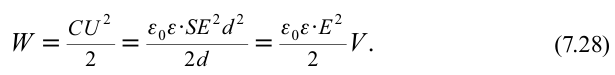
Энергия заряженного плоского конденсатора прямо пропорциональна квадрату напряженности созданного им поля и объему пространства, занимаемого этим полем. Энергия, приходящаяся на удельную единицу поля, называется объемной плотностью энергии. То есть:
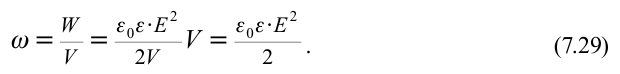
Каждый конденсатор имеет свойство накапливать в себе не только заряд, но и энергию. Энергия, полученная конденсатором, сосредоточена в среде между его обкладками. Эту энергию невозможно хранить длительное время. Конденсатор с течением времени передает полученный заряд в окружающую среду, т.е. разряжается.
При разрядке конденсатора через цепь с маленьким электрическим сопротивлением энергия передается практически мгновенно.
Образец решения задачи:
Емкость плоского воздушного конденсатора равна 0,1 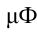 , разность потенциалов 200 В. Вычислите энергию электрического поля в конденсаторе.
, разность потенциалов 200 В. Вычислите энергию электрического поля в конденсаторе.
Дано:
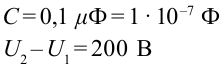
Найти:
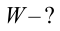
Формула:
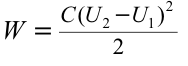
Решение:
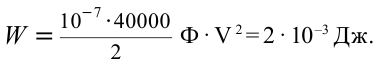
Ответ: 2 мДж.
Основные понятия, правила и законы:
| Закон сохранения зарядов | Алгебраическая сумма зарядов всех тел внутри любой закрытой системы не меняется, т.е.: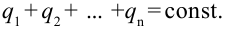 |
| Силовые линии электрического поля |
Линии, показывающие направления силы, действующие со стороны поля на положительный заряд, введенный в электрическое поле. Силовые линии электрического поля, образованного положительным зарядом, направлены от заряда, а в случае отрицательного заряда – направлены к нему. |
| Напряженность электрического поля |
Напряженность электрического поля – векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы 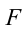 , действующей на , действующей нанеподвижный заряд, помещенный в данную точку поля, к величине этого заряда 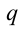 : :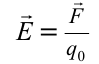 |
| Напряженность поля, создаваемого точечным зарядом 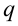 на расстоянии на расстоянии 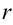 . . |
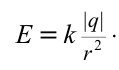 |
| Принцип суперпозиции электрического поля. |
Напряженность электростатического поля, создаваемого в данной точке системой зарядов, равна векторной сумме напряженностей полей, создаваемых в этой точке каждым зарядом в отдельности: 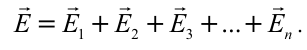 |
| Напряженность электрического поля в точках внутри заряженного шара (сферы) и за его пределами |
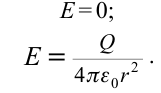 |
| Поляризация диэлектрика. |
Деформация электронной оболочки атомов (молекул) диэлектрика под воздействием электрического поля, в результате чего центры положительных и отрицательных зарядов атома не накладываются друг на друга. |
| Диэлектрическая восприимчивость. |
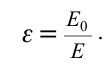 |
| Напряженность поля в точке на расстоянии 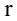 от точечного заряда, от точечного заряда,расположенного внутри диэлектрика. |
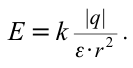 |
Потенциальная энергия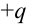 заряда, находящегося заряда, находящегосяна расстоянии 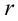 от неподвижного положительного от неподвижного положительногозаряда 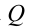 |
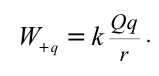 |
| Потенциал точечного заряда 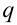 . . |
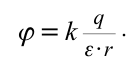 |
| Электрическое напряжение. |
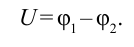 |
| Консервативная сила. | Сила, работа которой не зависит от траектории перемещения. |
| Объемная плотность энергии. |
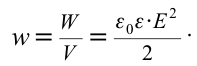 |
Энергия электрического поля
В заряженном конденсаторе обкладки имеют разноименные .заряды и взаимодействуют благодаря наличию электрического поля. О телах, которые взаимодействуют, говорят, что они имеют энергию. Таким образом можно утверждать, что заряженный конденсатор имеет энергию.
Наличие энергии в заряженном конденсаторе можно подтвердить опытами. Для этого возьмем конденсатор довольно большой емкости, источник тока, лампочку и составим цепь, показанную на рисунке 1.44. Сначала переведем переключатель в положение 1, зарядив таким образом конденсатор от источника тока.
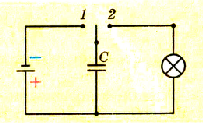
Pиc. 1.44. Схема цепь, в которой лампочка вспыхивает за счет энергии заряженного конденсатора
Если после этого перевести переключатель в положение 2, то увидим кратковременную вспышку света вследствие накала нити лампочки.
Наблюдаемое явление можно объяснить тем, что заряженный конденсатор имел энергию, благодаря которой была выполнена работа по накалу спирали лампочки.
Согласно закону сохранения энергии работа, выполненная при разрядке конденсатора, равна работе, выполненной при его зарядке. Расчет этой работы и соответственно потенциальной энергии заряженного конденсатора должен учитывать особенности процесса зарядки конденсатора. Зависимость заряда Q от времени зарядки t показана на графике (рис. 1.45).
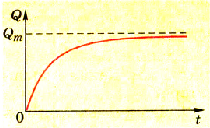
Pиc. 1.45. Изменение заряда конденсатора при его зарядке
Поскольку заряд конденсатора изменяется не пропорционально времени, вести расчет на основании формулы A = QEd нельзя, ведь напряженность поля также все время изменяется. Вместе с тем разность потенциалов между обкладками при зарядке линейно изменяется от нуля до определенного максимального значения (рис. 1.46).
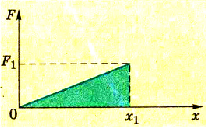
Рис. 1.46. К расчету работы электрического поля в конденсаторе
Поэтому работа, которая выполняется при зарядке конденсатора, равна:
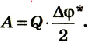
Если учесть, что 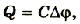 то
то
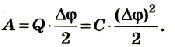
Таким образом, энергия электрического поля в конденсаторе равна:
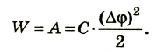
Приняв во внимание, что 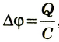 , получим:
, получим: 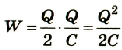 .
.
Задача:
Импульсную контактную сварку медной проволоки совершают при помощи разряда конденсатора электроемкостью 1000 мкФ при разности потенциалов между обкладками 1500 В. Какова средняя мощность импульсного разряда, если его дли тельность 2 мкс и КПД установки равен 4 %?
|
Дано: |
Решение |
| N – ? |
Средняя полезная мощность определяется с учетом времени выполнения работы:
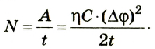
Подставив значения физических величин, получим:
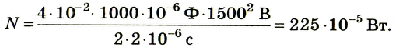
Ответ: полезная мощность, которую развивает сварочная установка, равна 225 ∙ 10-5 Вт.
Влияние электрического поля на живые организмы
Многие люди понятие электричества и электрического поля связывают только с электризацией различных тел, мощными электрическими машинами, средствами электроники и т. п. Вместе с тем электрические явления происходят и в живой природе. И это не только электризация шерсти кошки или собаки, когда их гладят рукой, но и более сложные формы, связанные с их жизнедеятельностью. В природе существуют живые организмы, способные генерировать электричество и использовать его для охоты, защиты и ориентирования в пространстве.
Одним из таких живых существ является электрический угорь (рис. 1.47). Он может генерировать разность потенциалов между отдельными частями своего тела до 360 В. Разряды, которые создает эта рыба, живые существа ощущают на расстоянии до 20 см.

Рис. 1.47 Электрический угорь
Свойства электрического угря использовали древние врачи для лечения подагры, мигрени, эпилепсии и т. п.
Аналогичные свойства и у электрического ската-торпедо (рис. 1.48). Он может на протяжении 15 с генерировать до 150 разрядов за секунду по 80 В каждый.

Pиc. 1.48 Электрический скат
Электрические явления играют существенную роль и в физиологии человека. Одним из мощных генераторов человека является сердце. На рисунке 1.49 показаны о к ни потенциальные поверхности тела человека при активной работе сердца.
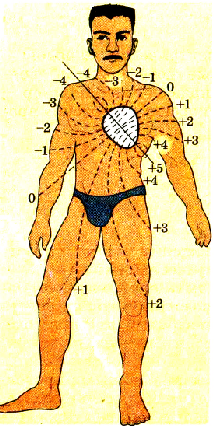
Рис. 1.49. Эквипотенциальные растений.
Хотя эти потенциалы сравнительно невелики – несколько милливольт, но их используют для диагностирования болезней сердца. Записывая эти потенциалы, специальные аппараты создают кардиограммы, по которым врач определяет состояние человека.
В физиотерапевтических кабинетах используют лечебный метод -фарадизацию, когда человека подвергают действию электрического поля и таким образом лечат некоторые болезни.
Исследования ученых показали, что под действием электрического поля улучшаются свойства семян растений. Растения, выращенные поверхности человека из таких семян, существенно улучшают спою урожайность. Даже трава растет интенсивнее под линиями электропередач, где существует сильное электрическое поле.
Если человека определенным образом изолировать от действия электрического поля «Земли, то его состояние существенно ухудшается. Некоторые люди чувствуют себя не комфортно в цельнометаллических вагонах, самолетах, автомобилях, где электрическое поле Земли экранируется металлическими корпусами транспортных средств.
- Электрическое поле заряженных неподвижных тел
- Напряженность электрического поля
- Принцип суперпозиции электрических полей
- Проводники в электрическом поле
- Электрическое поле заряженного шара
- Электрические явления в физике
- Потенциал поля точечного заряда в физике
- Работа электрического поля при перемещении заряда в физике
Энергия электрического поля
Содержание:
- Что такое энергия электрического поля
- Энергия заряженного конденсатора
- Как рассчитать энергию электрического поля через напряженность, формула
- Объемная плотность электрической энергии
Что такое энергия электрического поля
Электрическое поле — одна из двух компонент электромагнитного поля, представляющая собой векторное поле, существующее вокруг тел или частиц, обладающих электрическим зарядом, а также возникающее при изменении магнитного поля.
Энергия электрического поля — энергия проводника, обладающего зарядом, которая равна работе, затраченной, чтобы зарядить этот проводник.
Физик Майкл Фарадей сделал следующие выводы об электрическом поле:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- Каждый заряд формирует вокруг себя электрическое поле определенной мощности.
- Электрическое поле воздействует на другой заряд с определенной силой.
Электрическое поле обладает рядом свойств:
- поле материально;
- источником является заряд;
- обнаружить поле можно, исходя из действия на заряд;
- поле распределяется непрерывно в пространстве;
- при удалении от заряда поле слабеет.
Тело, обладающее зарядом, действует на другие тела, притягивая и отталкивая их. По отношению к заряженному объекту другие тела поворачиваются и перемещаются. Для любого электрического поля характерен запас энергии. В случае исчезновения электрического поля его электроэнергия трансформируется обратно в работу.
Энергия заряженного конденсатора
Конденсатор — двухполюсник с постоянным или переменным значением емкости и малой проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. Емкость конденсатора измеряется в фарадах.
Компоненты конденсаторов в виде проводников обозначают обкладками. Наиболее простым примером конденсатора является совокупность двух плоских пластин. Данные элементы способны проводить электрический ток и расположены параллельно относительно друг друга. Пластины удалены на небольшое по сравнению с их габаритами расстояние и отделены диэлектрическим материалом.
В плоском конденсаторе можно наблюдать электрическое поле:
- Основное — в области между пластин.
- Слабое или поле рассеяния — около краев пластин и во внешней среде.
Опытным путем было доказано, что конденсатор, обладая электрическим полем, вмещает определенный запас энергии. Для ее расчета необходимо найти сумму работы внешних сил, необходимых для питания конденсатора. Такой процесс является последовательным переносом минимальных порций заряда Δq > 0 с одном пластины на другую.
Один элемент при этом будет постепенно приобретать положительный заряд, а другой — заряжаться отрицательно. Транспортировка заряда осуществляется при условии, что пластины уже обладают неким зарядом q. Разность потенциалов между ними будет определена по формуле:
(U=frac{q}{C})
В процессе переноса некоторого заряда Δq вешние силы совершают работу, которая определяется следующим уравнением:
(Delta A=UDelta q=frac{qDelta q}{C})
Энергию We конденсатора, емкость которого составляет С, а заряд равен Q, можно рассчитать с помощью интегрирования предыдущей формулы в пределах от 0 до Q:
(W_{e}=A=frac{Q^{2}}{2C})
Следует учитывать следующее условие:
(Q=CU)
Тогда энергия заряженного конденсатора будет переписана в другом эквивалентном уравнении:
(W_{e}=A=frac{Q^{2}}{2C}=frac{CU^{2}}{2}=frac{QU}{2})
Электрическая энергия (We) будет рассматриваться в качестве потенциальной энергии, которая находится в запасе заряженного конденсатора. Для расчета электрической энергии справедливо применять формулу, с помощью которой определяют потенциальную энергию деформированной пружины ((Ер)):
(E_{p}=frac{kx^{2}}{2}=frac{F^{2}}{2k}=frac{Fx}{2})
Где k является жесткостью пружины, (х) — деформацией, а (F = kx) равно внешней силе.
Исходя из современных представлений, электрическую энергию можно наблюдать в области между пластинами конденсатора, то есть в пространстве с электрическим полем. Отсюда появилось название энергии электрического поля.
Как рассчитать энергию электрического поля через напряженность, формула
В качестве примера можно рассмотреть плоский конденсатор. Его однородное электрическое поле в этом случае будет обладать напряженностью. Данная величина определяется по формуле:
(E=frac{U}{d})
Емкость конденсатора будет рассчитываться таким образом:
(C=frac{varepsilon _{0}varepsilon S}{d})
Исходя из приведенных равенств, энергия электрического поля будет равна:
(W_{e}=frac{CU^{2}}{2}=frac{varepsilon _{0}varepsilon SE^{2}d^{2}}{2d}=frac{varepsilon _{0}varepsilon E^{2}}{2}V)
Где V = Sd является объемом пространства между пластинами конденсатора, который вмещает электрическое поле.
Объемная плотность электрической энергии
Расчет физической величины We выглядит следующим образом:
(W_{e}=frac{varepsilon _{0}varepsilon E^{2}}{2}V)
Таким образом, (We) представляет собой электрическую или потенциальную энергию единицы объема пространства, в котором сформировано электрическое поле. Данная величина — объемная плотность электрической энергии. Для того чтобы найти энергию поля, созданного путем распределения электрически заряженных частиц в пространстве, необходимо интегрировать объемную плотность по всему объему, для которого характерно наличие электрического поля.
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
1 Энергия системы точечных зарядов
Формулу
![]() можно рассматривать как взаимную
можно рассматривать как взаимную
потенциальную энергию зарядов![]() и
и![]() ,
,
находящихся на расстоянии![]() (рис.1).
(рис.1).

Рис.1
Если мы теперь в поле двух зарядов
![]() и
и![]() внесем
внесем
третий заряд![]() ,
,
то благодаря свойству аддитивности
энергии взаимодействий, получим:
![]() .
.
Преобразуем эту сумму следующим образом.
Представим каждое слагаемое
![]() в симметричном виде:
в симметричном виде:![]() ,
,
поскольку![]() .
.
Тогда
![]() .
.
Сгруппируем члены с одинаковыми первыми
индексами:
![]()
Каждая сумма в круглых скобках – это
энергия
![]() взаимодействия
взаимодействия![]() -го
-го
заряда с остальными зарядами.
Поэтому можно последнее выражение
переписать так:
![]()
Обобщим это выражение на систему,
состоящую из
![]() точечных зарядов
точечных зарядов![]() .
.
Итак, энергия взаимодействия системы
точечных зарядов
![]() (3.1)
(3.1)
Имея в виду, что
![]() ,
,
где![]() -i-ый заряд системы,
-i-ый заряд системы,![]() – потенциал, создаваемый всеми зарядами,
– потенциал, создаваемый всеми зарядами,
кроме![]() ,
,
в той точке, где находится заряд![]() ,
,
получим окончательное выражение:
![]() (3.2)
(3.2)
Если заряды распределены непрерывно,
то, разлагая систему зарядов на
совокупность элементарных зарядов
![]() и переходя от суммирования в (3.2) к
и переходя от суммирования в (3.2) к
интегрированию, получаем
![]() ,
,
(3.3)
где
![]() – потенциал, создаваемый всеми зарядами
– потенциал, создаваемый всеми зарядами
системы в элементе объемом![]() .
.
2 Энергия заряженных проводника и конденсатора
Энергия уединенного проводника.
Пусть проводник имеет заряд![]() и потенциал
и потенциал![]() .
.
Поскольку![]() на поверхности проводника, получим
на поверхности проводника, получим
![]()
Учитывая, что
![]()
![]() (3.4)
(3.4)
Любое из этих выражений определяет
энергию заряженного проводника.
Энергия заряженного конденсатора.
Предположим, что (+![]() )
)
и![]() – заряд и потенциал положительно
– заряд и потенциал положительно
заряженной обкладки конденсатора, (-![]() )
)
и![]() – отрицательно заряженной обкладки
– отрицательно заряженной обкладки
(рис. 2).

Рис. 2
Согласно формуле (3.3) интеграл можно
разбить на две части – для одной и другой
обкладок. Тогда
![]() .
.
Приняв во внимание, что
![]() ,
,
получим для энергии заряженного
конденсатора три выражения:
![]() (3.5)
(3.5)
3 Энергия и плотность энергии электрического поля
Выразим энергию заряженного плоского
конденсатора через напряженность
![]() электрического поля. Подставим в формулу
электрического поля. Подставим в формулу
![]() выражение
выражение![]() ,
,
получим
![]() .
.
Поскольку
![]() и
и![]() (объем между обкладками конденсатора),
(объем между обкладками конденсатора),
то
![]() .
.
Как будет показано в следующей главе,
вспомогательной характеристикой поля
в веществе является вектор электрического
смещения
![]() ,
,
который связан с вектором напряженности
электрического поля![]() соотношением
соотношением![]() .
.
С учетом этого соотношения полученную
формулу можно представить в виде:
 (3.6)
(3.6)
Эти формулы справедливы для однородного
поля, заполняющего объем
![]() .
.
Энергия распределена по объему
конденсатора равномерно. Следовательно,
в единице объема поля содержится энергия
![]() (3.7)
(3.7)
Выражения (3.7) определяют плотность
энергии электрического поля.
Формулы (3.7) справедливы для любого
электрического поля. Если поле неоднородно,
то плотность энергии в некоторой точке
определяется по формулам (3.7) подстановкой
значений
![]() (или
(или![]() )
)
и![]() в этой точке.
в этой точке.
Зная плотность энергии в каждой точке,
можно найти энергию поля, заключенную
в любом объеме
![]() .
.
Для этого нужно вычислить интеграл
![]() (3.8)
(3.8)
Примеры решения задач
Задача 1Четыре одинаковых точечных
заряда![]() находятся
находятся
в вершинах тетраэдра с ребром![]() .
.
Найти энергию взаимодействия зарядов
этой системы.
Решение:
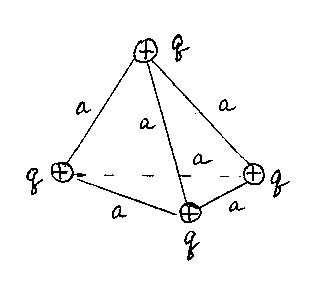
-
способ. Энергия взаимодействия каждой
пары зарядов здесь одинакова и равна
![]() .
.
Как видно из рисунка, всего таких
взаимодействующих пар шесть, поэтому
энергия взаимодействия всех точечных
зарядов данной системы
![]() .
.
2. способ.
![]() ,
,
где потенциал![]() в месте нахождения одного из зарядов,
в месте нахождения одного из зарядов,
равен![]() .
.
Поэтому
![]() .
.
Задача 2(С.3.114)Точечный заряд![]() = 1 мкКл помещается в центре шарового
= 1 мкКл помещается в центре шарового
слоя из однородного и изотропного
диэлектрика с![]() = 3. Внутренний радиус слоя
= 3. Внутренний радиус слоя![]() = 100 мм, внешний
= 100 мм, внешний![]() = 200 мм. Найти энергию
= 200 мм. Найти энергию![]() ,
,
заключенную в пределах диэлектрика.
Решение:
Напряженность поля в диэлектрике
![]() .
.
Разобьем диэлектрик на шаровые слои
радиуса
![]() и толщины
и толщины![]() .
.
Объем слоя![]() .
.
Плотность энергии в слое
![]()
Энергия, заключенная в слое
![]() :
:
![]()
Проинтегрировав это выражение по
![]() в пределах от
в пределах от![]() до
до![]() ,
,
найдем энергию, заключенную в диэлектрике:
![]() Дж.
Дж.
Задача 3Найдем работу, которую надо
совершить против электрических сил,
чтобы удалить диэлектрическую пластинку
из плоского заряженного конденсатора.
Предполагается, что заряд![]() конденсатора
конденсатора
остается постоянным. Емкость конденсатора
без диэлектрика равна![]() .
.
Решение:
Работа против электростатических сил
в этой системе пойдет на приращение ее
электрической энергии:
![]() ,
,
где
![]() – энергия поля между обкладками
– энергия поля между обкладками
конденсатора при наличии диэлектрика,![]() – при отсутствии диэлектрика. Отсюда
– при отсутствии диэлектрика. Отсюда
![]() .
.
Задача 4(С 3.111)Заряд![]() распределен равномерно по объему шара
распределен равномерно по объему шара
радиусом![]() .
.
Полагая![]() =1, найти электрическую энергию шара
=1, найти электрическую энергию шара![]() ,
,
а также отношение энергии![]() ,
,
локализованной внутри шара, к энергии![]() в окружающем пространстве.
в окружающем пространстве.
Решение:
Прежде всего найдем с помощью теоремы
Гаусса поле внутри и вне шара:
![]() (
(![]() );
);![]() (
(![]() ).
).
Теперь вычислим электрическую энергию
шара:
 .
.
Отсюда следует:
![]() ;
;![]() .
.
Тесты
1.
Емкость плоского конденсатора
пропорциональна:
1.
расстоянию между его пластинами. 2.
отношению площади его пластин к расстоянию
между ними. 3. произведению площади его
пластин на расстояние между ними. 4.
заряду пластин. 5. потенциалу пластин.
2.
Напряженность электрического поля
внутри проводника:
1.
определяется объемной плотностью заряда
в проводнике. 2. равняется нулю. 3.
определяется зарядом на поверхности
проводника. 4. определяется потенциалом
проводника. 5. зависит от напряженности
электрического поля в пространстве,
окружающем проводник.
3.
Три конденсатора одинаковой емкости
соединены параллельно. Результирующая
емкость получается
1.
равной емкости каждого из конденсаторов.
2. в три раза меньше емкости каждого из
конденсаторов. 3. в три раза больше
емкости каждого из конденсаторов.
4. Электроемкость проводника зависит
от:
1. формы и размеров, 2. площади
поверхности, 3. массы и рода вещества,
4. заряда и напряжения, 5. свойств
окружающей среды.
1.1., 2., 3. 2. 3., 4., 5. 3. 1., 2., 5.
4. 2., 3., 5.
5. Емкость батареи состоящей из пяти
одинаковых конденсаторов емкостью 1
мкФ, изображенной на рисунке равна:
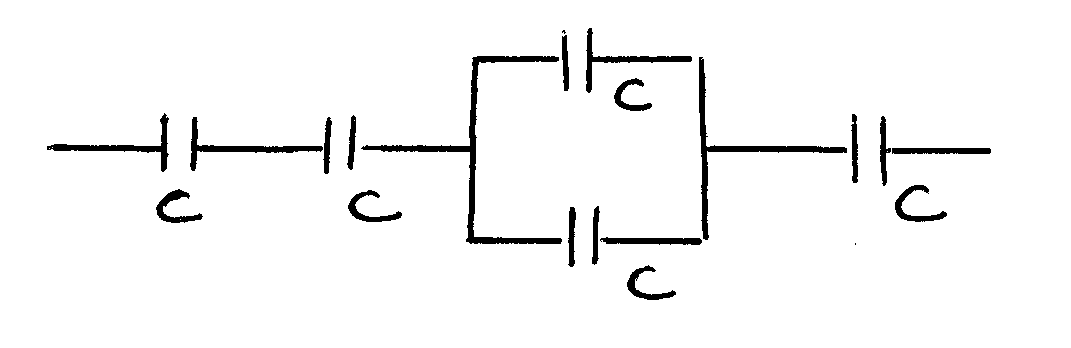
1. 3,5 мкФ 2. 0,286 мкФ 3. 5 мкФ
4. 0,2 мкФ
6. Взаимной электроемкостью тел называют:
-
 2.
2.
 3.
3.
 .
.
7. Плоский воздушный конденсатор
подключили к источнику тока, а затем не
отключая от источника, погрузили в
керосин с диэлектрической проницаемостью,
равной 2. Найти отношение заряда,
первоначально находившегося на обкладках
конденсатора, к конечному заряду.
1. 0,5 2. 1 3. 2 4. 4.
8. Разность
потенциалов между обкладками конденсаторов
емкостью![]() мкФ
мкФ
изменилась на 175 В. Определите изменение
заряда конденсатора.
1.![]() Кл
Кл
2.![]() Кл
Кл
3.![]() Кл
Кл
4.0.
9. Указать неправильнуюформулу для
электроемкости плоского конденсатора
.
1.
![]() 2.
2.![]() 3.
3.![]() 4.
4.![]() ;
;
10. Конденсатор имеет емкость
![]() пФ.
пФ.
Какой заряд находится на каждой из его
обкладок, если разность потенциалов
между ними![]() В?
В?
1.![]() Кл 2.
Кл 2.![]() Кл
Кл
3.![]() Кл
Кл
4.![]() эВ.
эВ.
11. Потенциал φ, заряд qи
емкость
![]() уединенного проводника связаны
уединенного проводника связаны
соотношением:
1.![]() 2.
2.![]() 3.
3.![]() 4.
4.![]() .
.
12. Изменится ли
заряд конденсатора, подключенного к
источнику напряжения, если раздвинуть
его пластины?
1. заряд конденсатора
увеличится 2. заряд конденсатора не
изменится 3. заряд конденсатора
уменьшится 4. заряд конденсатора
не зависит от его емкости 5. заряд
конденсатора не зависит от
расстояния между пластинами.
13. Вектор напряженности электростатического
поля:
1. ортогонален эквипотенциальной
поверхности 2. направлен по касательной
к эквипотенциальной поверхности 3.
направлен под углом π./4 к эквипотенциальной
поверхности, 4. может иметь любое
направление.
14. Внутри полой проводящей сферы помещен
электрический заряд. Электрическое
поле будет существовать:
1. и вне и внутри сферы 2. только
вне сферы 3. только внутри сферы
4. ни там, ни там.
15. Электроемкость С уединенной сферы
радиуcаRв
среде равна:
1.![]()
2.![]()
3.![]()
4.![]()
16. Между обкладками конденсатора, на
концах которого поддерживается постоянная
разность потенциалов, поместили слой
диэлектрика с диэлектрической
проницаемостью ε. Напряженность поля
в диэлектрике по отношению к напряженности
поля вне его:
1.увеличилась в ε раз 2. уменьшилась
в ε раз 3.обратилась в нуль 4. не
изменилась.
17. Для проводника,
помещенного в электростатическое поле,
характерно:
1. отсутствие поля
внутри проводника 2. усиление поля
внутри проводника 3. ослабление поля
вблизи острия проводника 4. силовые
линии поля направлены по касательной
к поверхности проводника 5. потенциал
проводника максимален на его поверхности.
18. Изменится ли энергия заряженного
воздушного конденсатора, если, при
отключенном источнике, раздвинуть его
пластины?
1. Изменится за счет энергии внешних
сил, совершающих работу по раздвижению
пластин. 2.Не изменится, так как заряд
на конденсаторе не изменяется
3.Нельзя дать однозначный ответ, так как
не известны численные значения исходных
данных 4.Энергия уменьшится.
19. Потенциальная энергия взаимодействия
пластин заряженного плоского конденсатора
(указать неверныйответ):
1.
![]() 2.
2.![]() 3.
3.![]() 4.
4.![]() ,
,
где
![]() и
и![]() – заряд и потенциал первой пластины,
– заряд и потенциал первой пластины,![]() и
и![]() – заряд и потенциал второй пластины;
– заряд и потенциал второй пластины;
5. все перечисленные варианты правильные.
20. Как изменится
энергия заряженного конденсатора, не
отключенного от источника, если уменьшить
расстояние между обкладками в два раза?
.
1. уменьшится в 2
раза 2. увеличится в 2 раза 3. не
изменится 4. увеличится в 4 раза
5. уменьшится в 4 раза.
21. Плотность энергии wэлектростатического поля с напряженностьюEв среде с диэлектрической
проницаемостью ε равна:
1.
![]() 2.
2.![]() 3.
3.![]() 4.
4.![]() .
.
22. Какую из формул нельзя использовать
для расчета энергии заряженного
конденсатора?
1.
![]() 2.
2.![]() 3.
3.![]() 4.
4.![]()
15
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Электрическое поле вызывает перемещение свободных зарядов и может выполнять работу, а это значит, что оно обладает энергией. Согласно теории близкодействия, вся энергия взаимодействия заряженных тел сконцентрирована в электрическом поле этих тел.
Электрическая энергия наэлектризованного проводника
Чтобы зарядить проводник, надо выполнить работу против кулоновских сил отталкивания между одноименно заряженными частицами. Для уточнения этого тезиса предположим, что процесс зарядки отдельного тела осуществляется последовательным переносом на него порций dqdq заряженных частиц из бесконечности, где потенциал Ф0=0Ф_0 = 0. При этом работой переноса первой порции можно пренебречь, но в дальнейшем для увеличения заряда тела на dqdq надо выполнить все большую работу dA=dqφdA = dqφ, где φφ соответствующее промежуточное значение потенциала проводника. Принимая q=Сφq = Сφ, получаем
dA=СφdφdA = Сφdφ
Общая работа при электризации проводника от потенциала 00 до φφ составляет
A=C∫0φφdφ=Cφ22A=Cintlimits_{0}^{varphi }{varphi d}varphi =frac{C{{varphi }^{2}}}{2}
По закону сохранения энергии работа электризации расходуется на увеличение энергии заряженного проводника. Итак, электрическую энергию наэлектризованного проводника определяют так:
We=Cφ22=qφ2=q22C{{W}_{e}}=frac{C{{varphi }^{2}}}{2}=frac{qvarphi }{2}=frac{{{q}^{2}}}{2C}
где q,φ,Сq, φ, С – заряд, потенциал и электроемкость проводника.
Поскольку с заряженным проводником связывается электрическое поле, точнее можно сказать, что данная формула выражает энергию электрического поля.
Энергия заряженного конденсатора
Выразим эту энергию через напряженность ЕЕ поля. Для этого применим формулу к заряженному плоскому конденсатору, поле которого однородное и локализовано, а энергия
We=CU22{{W}_{e}}=frac{C{{U}^{2}}}{2}
Подставив в уравнение значения емкости и напряжения, найдем формулу для определения энергии поля заряженного конденсатора
We=ε0εE22Sd{{W}_{e}}=frac{{{varepsilon }_{0}}varepsilon {{Epsilon }^{2}}}{2}Sd
Плотность энергии электрического поля
Поскольку Sd – объем поля между обмотками, плотность энергии электрического поля
we=WeSd=ε0εE22{{w}_{e}}=frac{{{W}_{e}}}{Sd}=frac{{{varepsilon }_{0}}varepsilon {{Epsilon }^{2}}}{2}
Учитывая, что D=ε0εED = ε_0εΕ, окончательно получим
we=ε0εE22=ED2=D22ε0ε{{w}_{e}}=frac{{{varepsilon }_{0}}varepsilon {{Epsilon }^{2}}}{2}=frac{ED}{2}=frac{{{D}^{2}}}{2{{varepsilon }_{0}}varepsilon }
Зная объемную плотность энергии we, можно определить общую энергию произвольного электрического поля. Если поле неоднородно, то его можно разделить на бесконечно малые объемы, в пределах которых оно остается однородным. Тогда полная энергия электрического поля в объеме VV составит
We=∫Vwedv=∫Vε0εE22dv{{W}_{e}}=intlimits_{V}{{{w}_{e}}dv=}intlimits_{V}{frac{{{varepsilon }_{0}}varepsilon {{Epsilon }^{2}}}{2}dv}
Согласно энергии электрического поля по теории относительности можно определить массу поля, а именно:
me=Wec2m_e = frac{W_e}{c^2}
где сс – скорость света.
Итак, электрическое поле характеризуется напряженностью ЕЕ, потенциалом φφ, энергией WeW_e (или плотностью энергии wew_e) и массой mem_e.
Тест по теме «Энергия электрического поля»
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 января 2022 года; проверки требует 1 правка.
Эне́ргия электромагни́тного по́ля — энергия, заключенная в электромагнитном поле[источник не указан 3867 дней]. Сюда же относятся частные случаи чистого электрического и чистого магнитного поля.
| Виды энергии: | ||
|---|---|---|
| Механическая | Потенциальная Кинетическая |
|
| ‹♦› | Внутренняя | |
| Электромагнитная | Электрическая Магнитная |
|
| Химическая | ||
| Ядерная | ||
 |
Гравитационная | |
 |
Вакуума | |
| Гипотетические: | ||
 |
Тёмная | |
| См. также: Закон сохранения энергии |
Работа электрического поля по перемещению заряда[править | править код]
Понятие работы 


где 
Во многих задачах рассматривается непрерывный перенос заряда в течение некоторого времени между точками с заданной разностью потенциалов 
где 
Мощность электрического тока в цепи[править | править код]
Мощность 

Это наиболее общее выражение для мощности в электрической цепи.
С учётом закона Ома
электрическую мощность, выделяемую на сопротивлении 
так и через напряжение:
Соответственно, работа (выделившаяся теплота) является интегралом мощности по времени:
Энергия электрического и магнитного поля[править | править код]
Для электрического и магнитного полей их энергия пропорциональна квадрату напряжённости поля. Строго говоря, термин «энергия электромагнитного поля» является не вполне корректным. Вместо него в физике обычно используют понятие плотности энергии электромагнитного поля (в определённой точке пространства). Общая энергия поля равняется интегралу плотности энергии по всему пространству.
Плотность энергии электромагнитного поля является суммой плотностей энергий электрического и магнитного полей.
В системе СИ:
В вакууме (а также в веществе при рассмотрении микрополей):
где E — напряжённость электрического поля, B — магнитная индукция, D — электрическая индукция, H — напряжённость магнитного поля, с — скорость света, 



В системе СГС:[1]
Энергия электромагнитного поля в колебательном контуре[править | править код]
Энергия электромагнитного поля в колебательном контуре:
где:
- U — электрическое напряжение в цепи,
- C — электроемкость конденсатора,
- I — сила тока,
- L — индуктивность катушки или витка с током.
Потоки энергии электромагнитного поля[править | править код]
Для электромагнитной волны плотность потока энергии определяется вектором Пойнтинга S (в русской научной традиции — вектор Умова — Пойнтинга).
В системе СИ вектор Пойнтинга равен 
Вместе с тем, формула для плотности потока энергии может быть обобщена для случая стационарных электрических и магнитных полей и имеет тот же вид: 
Факт существования потоков энергии в постоянных электрических и магнитных полях может выглядеть странно, но не приводит к каким-либо парадоксам; более того, такие потоки обнаруживаются в эксперименте.
См. также[править | править код]
- Электричество
- Коэффициент мощности
- Счётчик электрической энергии
Примечания[править | править код]
- ↑ С. А. Ахманов, С. Ю. Никитин. Физическая оптика. — М.: Изд-во МГУ, 1998. ISBN 5-211-04858-X, ISBN 978-5-211-04858-4, на стр. 47