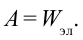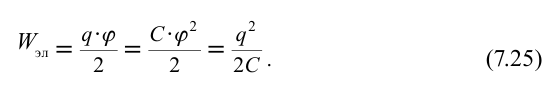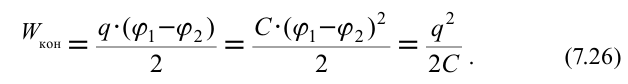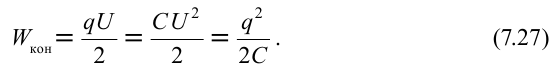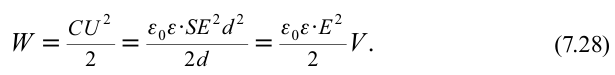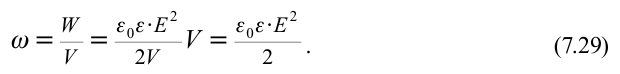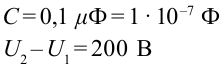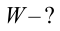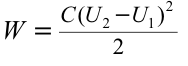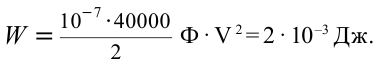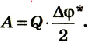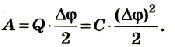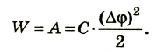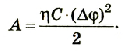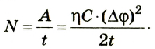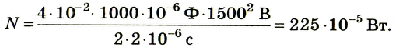Для школьников.
Если электростатическое поле создаётся двумя точечными зарядами
находящимися на расстоянии
друг от друга, то потенциальная энергия их взаимодействия выражается формулой:
Можно сказать так: Потенциальная энергия взаимодействующих зарядов равна произведению потенциала, создаваемого первым зарядом в точке нахождения второго заряда, на величину второго заряда.
Можно сказать и так: Потенциальная энергия взаимодействующих зарядов равна произведению потенциала, создаваемого вторым зарядом в точке нахождения первого заряда, на величину первого заряда.
Потенциальная энергия взаимодействия двух точечных зарядов – это и есть энергия электростатического поля, созданного ими.
Обладая энергией, электрическое поле может совершить работу. Энергия электростатического поля численно равна работе, которую могут совершить заряды при их удалении друг от друга в бесконечность.
Для получения формулы, по которой можно найти энергию электрического поля, созданного неподвижным заряженным проводником, применяют уравнение
есть потенциал, создаваемый всеми остальными зарядами в точке нахождения одного из зарядов.
Он одинаков для всех точек проводника, так как поверхность проводника является эквипотенциальной поверхностью.
Заряд всего проводника можно представить как сумму множества точечных зарядов. Тогда, пользуясь формулой (1) (см. Занятие 55), можно получить выражения для энергии поля уединённого проводника.
Что произойдёт после этого соединения?
Таким образом, получены формулы, по которым можно рассчитать энергию электростатического поля заряженного проводника.
На примере показано, что если электрическое поле создаётся несколькими проводниками, то энергия поля складывается из собственных энергий проводников и энергий их взаимодействия.
Общая энергия соединённых заряженных проводников уменьшается, так как при прохождении зарядов по проволоке выделяется энергия в виде тепла.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: Три одинаковых заряда закреплены на одной прямой. Какую работу надо совершить, чтобы удалить средний заряд?
Следующая запись: Более чётко о нахождении энергии электростатического поля. Поле конденсатора.
Ссылки на занятия до электростатики даны в Занятии 1.
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45.
Будем считать
среду, в которой находятся электрические
заряды и заряженные тела, однородной и
изотропной, не обладающей сегнетоэлектрическими
свойствами.
Заряжая некоторый
проводник, необходимо совершить
определенную работу против кулоновских
сил отталкивания между одноименными
электрическими зарядами. Эта работа
идет на увеличение электрической энергии
заряженного проводника, которая в данном
случае аналогична потенциальной энергии
в механике.
Рассмотрим
проводник, имеющий электроемкость
,
заряди потенциал
.
Работа, совершаемая против сил
электростатического поля при перенесении
зарядаиз бесконечности на проводник равна
.
Для того, чтобы
зарядить тело от нулевого потенциала
до потенциала
,
необходимо совершить работу.
Ясно, что энергия заряженного тела равна
той работе, которую нужно совершить,
чтобы зарядить это тело:.
Энергию
называют собственной энергией заряженного
тела. Ясно, что собственная энергия есть
не что иное, как энергия электростатического
поля этого тела.
1.4.3. Энергия заряженного конденсатора. Объемная плотность энергии электростатического поля
Пусть
потенциал обкладки конденсатора, на
которой находится заряд
,
равен,
а потенциал обкладки, на которой находится
заряд,
.
Энергия такой системы зарядов,
то есть равна собственной энергии
системы зарядов, где– напряжение между обкладками конденсатора,
.
Рассмотрим
плоский конденсатор. Энергия, заключенная
в единице объема электростатического
поля называется объемной плоскостью
энергии. Эта объемная плоскость должна
быть одинаковой во всех точках однородного
поля, а полная энергия поля пропорциональна
его объему. Известно, что
,
,
тогда для энергии имеем:,
но– объем электростатического поля между
обкладками конденсатора, то есть.
Тогда объемная плотность энергииоднородного электростатического поля
конденсатора равна,
и определяется его напряженностью или
смещением. В случае неоднородных
электрических полей
Найдем
энергию сферического конденсатора. На
расстоянии
от центра заряженного шара напряженность
его электростатического поля равна.
Рассмотрим бесконечно тонкий шаровой
слой, заключенный между сферами радиусови
.
Объем такого слоя:.
Энергия слояследовательно,
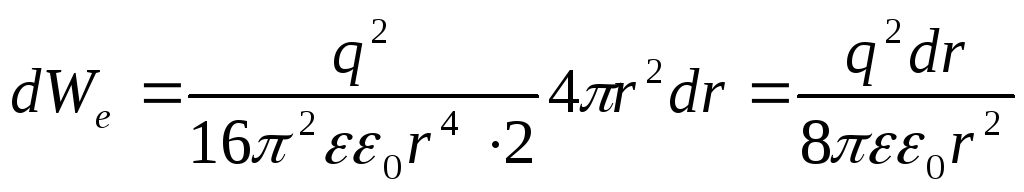
Тогда полная
энергия заряженного шара равна:
,
где
– радиус шара. Емкость шара
,
следовательно,– энергия электростатического поля
сферического конденсатора равна его
собственной энергии, так как заряженное
тело потому и обладает электрической
энергией, что при его зарядке была
совершена работа против сил создаваемого
им электростатического поля.
1.4.4.Энергия поляризованного диэлектрика. Объемная плотность энергии электрического поля в диэлектрике
Рассмотрим
однородный изотропный диэлектрик,
находящийся во внешнем электрическом
поле. Процесс поляризации связан с
работой по деформации электронных орбит
в атомах и молекулах и по повороту осей
молекул-диполей вдоль поля. Ясно, что
поляризованный диэлектрик должен
обладать запасом электрической энергии.
Если
поле напряженностью
создано в вакууме,
,
то объемная плотность энергии этого
поля в точке с напряженностьюравна:
Докажем, что
объемная плотность энергии поляризованного
диэлектрика в этой точке выражается
формулой:.
Рассмотрим
диэлектрик с неполярными молекулами.
Молекулы такого диэлектрика являются
упругими диполями. Электрический момент
упругого диполя, находящегося в поле с
напряженностью
,
равен,
где– поляризуемость диполя, или в скалярной
форме:
, (1.4.1)
где
– заряд и плечо диполя.
На
заряд
со стороны поля действует сила
,
которая при увеличении длины диполя насовершает работу
.
Из выражения (1.4.1) получаем:,
поэтому
. (1.4.2)
Чтобы
найти работу
поля при деформации одного упругого
диполя, надо проинтегрировать выражение
(1.4.2):
.
Работа
равна той потенциальной энергии, которой
обладает упругий диполь в электрическом
поле напряженностью.
Пусть– число диполей в единице объема
диэлектрика. Тогда потенциальная энергия
всех этих диполей, то есть объемная
плотность энергии поляризованного
диэлектрика равна:.
Однако– модуль вектора поляризации, тогда
.
Известно, что,
и,
тогда,
что и требовалось доказать.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
08.03.2015550.91 Кб49.doc
- #
- #
ГЛАВА IV. ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
§ 28. Энергия заряженного проводника
Заряд q, находящийся на некотором проводнике, можно рассматривать как систему точечных зарядов 

Здесь 


Поверхность проводника является эквипотенциальной. Поэтому потенциалы тех точек, в которых находятся точечные заряды 


Приняв во внимание соотношение (26.2), можно написать

Любое из этих выражений дает энергию заряженного проводника.
Электрическое поле вызывает перемещение свободных зарядов и может выполнять работу, а это значит, что оно обладает энергией. Согласно теории близкодействия, вся энергия взаимодействия заряженных тел сконцентрирована в электрическом поле этих тел.
Электрическая энергия наэлектризованного проводника
Чтобы зарядить проводник, надо выполнить работу против кулоновских сил отталкивания между одноименно заряженными частицами. Для уточнения этого тезиса предположим, что процесс зарядки отдельного тела осуществляется последовательным переносом на него порций dqdq заряженных частиц из бесконечности, где потенциал Ф0=0Ф_0 = 0. При этом работой переноса первой порции можно пренебречь, но в дальнейшем для увеличения заряда тела на dqdq надо выполнить все большую работу dA=dqφdA = dqφ, где φφ соответствующее промежуточное значение потенциала проводника. Принимая q=Сφq = Сφ, получаем
dA=СφdφdA = Сφdφ
Общая работа при электризации проводника от потенциала 00 до φφ составляет
A=C∫0φφdφ=Cφ22A=Cintlimits_{0}^{varphi }{varphi d}varphi =frac{C{{varphi }^{2}}}{2}
По закону сохранения энергии работа электризации расходуется на увеличение энергии заряженного проводника. Итак, электрическую энергию наэлектризованного проводника определяют так:
We=Cφ22=qφ2=q22C{{W}_{e}}=frac{C{{varphi }^{2}}}{2}=frac{qvarphi }{2}=frac{{{q}^{2}}}{2C}
где q,φ,Сq, φ, С – заряд, потенциал и электроемкость проводника.
Поскольку с заряженным проводником связывается электрическое поле, точнее можно сказать, что данная формула выражает энергию электрического поля.
Энергия заряженного конденсатора
Выразим эту энергию через напряженность ЕЕ поля. Для этого применим формулу к заряженному плоскому конденсатору, поле которого однородное и локализовано, а энергия
We=CU22{{W}_{e}}=frac{C{{U}^{2}}}{2}
Подставив в уравнение значения емкости и напряжения, найдем формулу для определения энергии поля заряженного конденсатора
We=ε0εE22Sd{{W}_{e}}=frac{{{varepsilon }_{0}}varepsilon {{Epsilon }^{2}}}{2}Sd
Плотность энергии электрического поля
Поскольку Sd – объем поля между обмотками, плотность энергии электрического поля
we=WeSd=ε0εE22{{w}_{e}}=frac{{{W}_{e}}}{Sd}=frac{{{varepsilon }_{0}}varepsilon {{Epsilon }^{2}}}{2}
Учитывая, что D=ε0εED = ε_0εΕ, окончательно получим
we=ε0εE22=ED2=D22ε0ε{{w}_{e}}=frac{{{varepsilon }_{0}}varepsilon {{Epsilon }^{2}}}{2}=frac{ED}{2}=frac{{{D}^{2}}}{2{{varepsilon }_{0}}varepsilon }
Зная объемную плотность энергии we, можно определить общую энергию произвольного электрического поля. Если поле неоднородно, то его можно разделить на бесконечно малые объемы, в пределах которых оно остается однородным. Тогда полная энергия электрического поля в объеме VV составит
We=∫Vwedv=∫Vε0εE22dv{{W}_{e}}=intlimits_{V}{{{w}_{e}}dv=}intlimits_{V}{frac{{{varepsilon }_{0}}varepsilon {{Epsilon }^{2}}}{2}dv}
Согласно энергии электрического поля по теории относительности можно определить массу поля, а именно:
me=Wec2m_e = frac{W_e}{c^2}
где сс – скорость света.
Итак, электрическое поле характеризуется напряженностью ЕЕ, потенциалом φφ, энергией WeW_e (или плотностью энергии wew_e) и массой mem_e.
Тест по теме «Энергия электрического поля»
Содержание:
Энергия электрического поля:
Для зарядки проводника выполняется работа по преодолению силы отталкивания между зарядами. За счет этой работы проводник получает энергию. Полученная энергия заряженного тела количественно равна работе, выполненной при его зарядке, т.е.
Среднее значение потенциала тела равно среднему арифметическому его начальных и конечных значений, т.е.
Поставляя значении 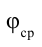
Значит, работа, выполненная при зарядке тела, равняется половине произведения его заряда на потенциал. При зарядке тела его потенциал плавно, т.е. линейно изменяется согласно формуле 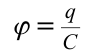
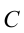
Согласно соотношению 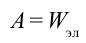
Если заряженное тело является конденсатором, то при расчете энергии (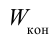
Исходя из этого, формулу определения электрической энергии конденсатора можно записать в виде:
Энергия заряженного тела сосредоточена в электрическом поле, созданном вокруг него, величина энергии зависит от объема пространства, занимаемого полем и напряженности поля.
Рассмотрим частный случай плоского заряженного конденсатора.
Электрическое поле, созданное зарядами обкладок плоского конденсатора, сосредоточено в среде между его обкладками. Объем пространства можно вычислить по формуле 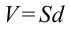
Учитывая емкость заряженного плоского конденсатора 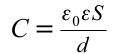
Энергия заряженного плоского конденсатора прямо пропорциональна квадрату напряженности созданного им поля и объему пространства, занимаемого этим полем. Энергия, приходящаяся на удельную единицу поля, называется объемной плотностью энергии. То есть:
Каждый конденсатор имеет свойство накапливать в себе не только заряд, но и энергию. Энергия, полученная конденсатором, сосредоточена в среде между его обкладками. Эту энергию невозможно хранить длительное время. Конденсатор с течением времени передает полученный заряд в окружающую среду, т.е. разряжается.
При разрядке конденсатора через цепь с маленьким электрическим сопротивлением энергия передается практически мгновенно.
Образец решения задачи:
Емкость плоского воздушного конденсатора равна 0,1 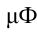
Дано:
Найти:
Формула:
Решение:
Ответ: 2 мДж.
Основные понятия, правила и законы:
| Закон сохранения зарядов | Алгебраическая сумма зарядов всех тел внутри любой закрытой системы не меняется, т.е.: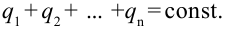 |
| Силовые линии электрического поля |
Линии, показывающие направления силы, действующие со стороны поля на положительный заряд, введенный в электрическое поле. Силовые линии электрического поля, образованного положительным зарядом, направлены от заряда, а в случае отрицательного заряда – направлены к нему. |
| Напряженность электрического поля |
Напряженность электрического поля – векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы 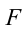 , действующей на , действующей нанеподвижный заряд, помещенный в данную точку поля, к величине этого заряда 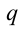 : :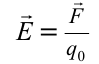 |
| Напряженность поля, создаваемого точечным зарядом 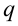 на расстоянии на расстоянии 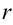 . . |
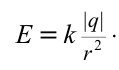 |
| Принцип суперпозиции электрического поля. |
Напряженность электростатического поля, создаваемого в данной точке системой зарядов, равна векторной сумме напряженностей полей, создаваемых в этой точке каждым зарядом в отдельности: 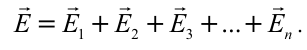 |
| Напряженность электрического поля в точках внутри заряженного шара (сферы) и за его пределами |
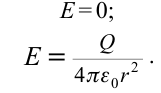 |
| Поляризация диэлектрика. |
Деформация электронной оболочки атомов (молекул) диэлектрика под воздействием электрического поля, в результате чего центры положительных и отрицательных зарядов атома не накладываются друг на друга. |
| Диэлектрическая восприимчивость. |
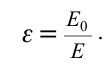 |
| Напряженность поля в точке на расстоянии 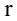 от точечного заряда, от точечного заряда,расположенного внутри диэлектрика. |
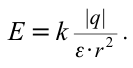 |
Потенциальная энергия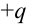 заряда, находящегося заряда, находящегосяна расстоянии 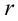 от неподвижного положительного от неподвижного положительногозаряда 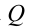 |
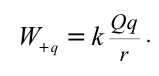 |
| Потенциал точечного заряда 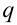 . . |
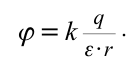 |
| Электрическое напряжение. |
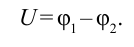 |
| Консервативная сила. | Сила, работа которой не зависит от траектории перемещения. |
| Объемная плотность энергии. |
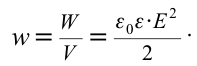 |
Энергия электрического поля
В заряженном конденсаторе обкладки имеют разноименные .заряды и взаимодействуют благодаря наличию электрического поля. О телах, которые взаимодействуют, говорят, что они имеют энергию. Таким образом можно утверждать, что заряженный конденсатор имеет энергию.
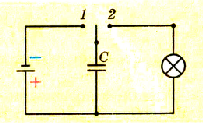
Наличие энергии в заряженном конденсаторе можно подтвердить опытами. Для этого возьмем конденсатор довольно большой емкости, источник тока, лампочку и составим цепь, показанную на рисунке 1.44. Сначала переведем переключатель в положение 1, зарядив таким образом конденсатор от источника тока.
Pиc. 1.44. Схема цепь, в которой лампочка вспыхивает за счет энергии заряженного конденсатора
Если после этого перевести переключатель в положение 2, то увидим кратковременную вспышку света вследствие накала нити лампочки.
Наблюдаемое явление можно объяснить тем, что заряженный конденсатор имел энергию, благодаря которой была выполнена работа по накалу спирали лампочки.
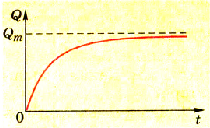
Согласно закону сохранения энергии работа, выполненная при разрядке конденсатора, равна работе, выполненной при его зарядке. Расчет этой работы и соответственно потенциальной энергии заряженного конденсатора должен учитывать особенности процесса зарядки конденсатора. Зависимость заряда Q от времени зарядки t показана на графике (рис. 1.45).
Pиc. 1.45. Изменение заряда конденсатора при его зарядке
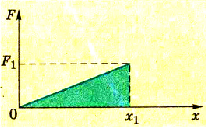
Поскольку заряд конденсатора изменяется не пропорционально времени, вести расчет на основании формулы A = QEd нельзя, ведь напряженность поля также все время изменяется. Вместе с тем разность потенциалов между обкладками при зарядке линейно изменяется от нуля до определенного максимального значения (рис. 1.46).
Рис. 1.46. К расчету работы электрического поля в конденсаторе
Поэтому работа, которая выполняется при зарядке конденсатора, равна:
Если учесть, что 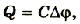
Таким образом, энергия электрического поля в конденсаторе равна:
Приняв во внимание, что 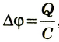
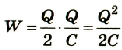
Задача:
Импульсную контактную сварку медной проволоки совершают при помощи разряда конденсатора электроемкостью 1000 мкФ при разности потенциалов между обкладками 1500 В. Какова средняя мощность импульсного разряда, если его дли тельность 2 мкс и КПД установки равен 4 %?
|
Дано: |
Решение |
| N – ? |
Средняя полезная мощность определяется с учетом времени выполнения работы:
Подставив значения физических величин, получим:
Ответ: полезная мощность, которую развивает сварочная установка, равна 225 ∙ 10-5 Вт.
Влияние электрического поля на живые организмы
Многие люди понятие электричества и электрического поля связывают только с электризацией различных тел, мощными электрическими машинами, средствами электроники и т. п. Вместе с тем электрические явления происходят и в живой природе. И это не только электризация шерсти кошки или собаки, когда их гладят рукой, но и более сложные формы, связанные с их жизнедеятельностью. В природе существуют живые организмы, способные генерировать электричество и использовать его для охоты, защиты и ориентирования в пространстве.
Одним из таких живых существ является электрический угорь (рис. 1.47). Он может генерировать разность потенциалов между отдельными частями своего тела до 360 В. Разряды, которые создает эта рыба, живые существа ощущают на расстоянии до 20 см.
Рис. 1.47 Электрический угорь
Свойства электрического угря использовали древние врачи для лечения подагры, мигрени, эпилепсии и т. п.
Аналогичные свойства и у электрического ската-торпедо (рис. 1.48). Он может на протяжении 15 с генерировать до 150 разрядов за секунду по 80 В каждый.
Pиc. 1.48 Электрический скат
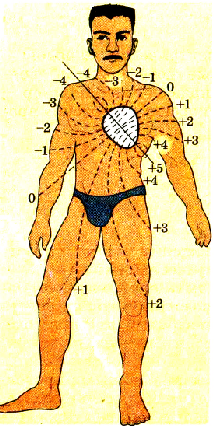
Электрические явления играют существенную роль и в физиологии человека. Одним из мощных генераторов человека является сердце. На рисунке 1.49 показаны о к ни потенциальные поверхности тела человека при активной работе сердца.
Рис. 1.49. Эквипотенциальные растений.
Хотя эти потенциалы сравнительно невелики – несколько милливольт, но их используют для диагностирования болезней сердца. Записывая эти потенциалы, специальные аппараты создают кардиограммы, по которым врач определяет состояние человека.
В физиотерапевтических кабинетах используют лечебный метод -фарадизацию, когда человека подвергают действию электрического поля и таким образом лечат некоторые болезни.
Исследования ученых показали, что под действием электрического поля улучшаются свойства семян растений. Растения, выращенные поверхности человека из таких семян, существенно улучшают спою урожайность. Даже трава растет интенсивнее под линиями электропередач, где существует сильное электрическое поле.
Если человека определенным образом изолировать от действия электрического поля «Земли, то его состояние существенно ухудшается. Некоторые люди чувствуют себя не комфортно в цельнометаллических вагонах, самолетах, автомобилях, где электрическое поле Земли экранируется металлическими корпусами транспортных средств.
- Электрическое поле заряженных неподвижных тел
- Напряженность электрического поля
- Принцип суперпозиции электрических полей
- Проводники в электрическом поле
- Электрическое поле заряженного шара
- Электрические явления в физике
- Потенциал поля точечного заряда в физике
- Работа электрического поля при перемещении заряда в физике