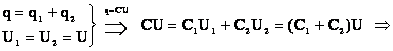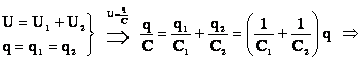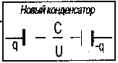Как найти энергию последовательно соединенных конденсаторов - Сайт, где вы сможете решить свои вопросы

Основные ссылки

CSS adjustments for Marinelli theme

Вы здесь

Главная » Соединения конденсаторов. Энергия…

Соединения конденсаторов. Энергия электрического поля конденсатора.

Соединения конденсаторов .
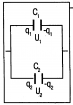
Параллельное соединение конденсаторов
Обкладки конденсаторов соединяют попарно, т.е. в системе остается два изолированных проводника, которые и представляют собой обкладки нового конденсатора

Вывод: При параллельном соединении конденсаторов заряды складываются, напряжения одинаковые, емкости складываются. Т.о., *общая емкость больше емкости любого из параллельно соединенных конденсаторов*
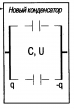
Последовательное соединение конденсаторов
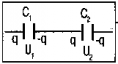
Производят только одно соединение, а две оставшиеся обкладки – одна от конденсатора С₁ другая от конденсатора С₂ – играют роль обкладок нового конденсатора.

Вывод: При последовательном соединении конденсаторов напряжения складываются, заряды одинаковы, складываются величины, обратные емкости. Т.о., *общая емкость меньше емкости любого из последовательно соединенных конденсаторов.*
Энергия электрического поля конденсатора. Под энергией электрического поля конденсатора будем понимать энергию одной его обкладки, находящейся в поле, созданном другой обкладкой. Тогда: Формулы справедливы для любого конденсатора.	Пример: С=2мкФ; U=1000В. t=10-6c.W=1 Дж – опасно для жизни!

Плотность энергии. – плотность энергии (энергия единицы объема). Формула справедлива для полей любых конденсаторов и, кроме того, для полей, меняющихся со временем (неэлектростатических).

Источник

Содержание:

Последовательное соединение конденсаторов
Параллельное соединение конденсаторов
Смешанное соединение конденсаторов
Пример расчета

В данной статье приведены различные схемы соединения конденсаторов, а так же формулы их расчета с примером.

Последовательное соединение конденсаторов

Если условно разделить выводы каждого из конденсаторов на первый и второй выводы последовательное соединение конденсаторов будет выполняется следующим образом: второй вывод первого конденсатора соединяется с первым выводом второго конденсатора, второй вывод второго конденсатора, соединяется с первым выводом третьего и так далее. Таким образом мы получим группу (блок) последовательно соединенных конденсаторов с двумя свободными выводами — первым выводом первого конденсатора в блоке и вторым выводом последнего конденсатора, через которые данный конденсаторный блок и подключается в электрическую цепь.

Схема последовательного соединения конденсаторов будет иметь следующий вид:

Фактически последовательное соединение конденсаторов имеет следующий вид:

При данной схеме соединения заряды на конденсаторах будут одинаковы:

Q_общ=Q₁=Q₂=Q₃,

где: Q₁, Q₂, Q₃ — соответственно заряд на первом, втором, третьем и т.д. конденсаторах

Напряжение на каждом конденсаторе при такой схеме зависит от его емкости:

U₁=Q/C₁; U₂=Q/C₂; U₃=Q/C₃, где:

U₁, U₂, U₃ — соответственно напряжение на первом, втором, третьем конденсаторах
C₁, C₂, C₃— соответственно емкости первого, второго, третьего конденсаторов

При этом общее напряжение составит:

U_общ=U₁+U₂+U₃+…+U_n

Рассчитать общую емкость конденсаторов при последовательном соединении можно по следующим формулам:

При последовательном соединении двух конденсаторов:

С_общ=(C₁*C₂)/(C₁+C₂)

При последовательном соединении трех и более конденсаторов:

1/С_общ=1/C₁+1/C₂+1/C₃+…+1/C_n

Параллельное соединение конденсаторов

Если условно разделить выводы каждого из конденсаторов на первый и второй выводы параллельное соединение конденсаторов будет выполняется следующим образом: первые выводы всех конденсаторов соединяются в одну общую точку (условно — точка №1) вторые выводы всех конденсаторов соединяются в другую общую точку (условно — точка №2). В результате получается группа (блок) параллельно соединенных конденсаторов подключение которой к электрической цепи производится через условные точки №1 и №2.

Схема параллельного соединения конденсаторов будет иметь следующий вид:

Таким образом параллельное соединение конденсаторов будет иметь следующий вид:

При данной схеме напряжение на всех конденсаторах будет одинаково:

U=U₁=U₂=U₃

Заряд же на каждом из конденсаторов будет зависеть от его емкости:

Q₁=U*C₁; Q₂=U*C₂; Q₃=U*C₃

При этом общий заряд цепи будет равен сумме зарядов всех параллельно подключенных конденсаторов:

Q_общ=Q₁+Q₂+Q₃…+…Q_n.

Рассчитать общую емкость конденсаторов при параллельном соединении можно по следующей формуле:

С_общ=C₁+C₂+C₃+…+C_n

Смешанное соединение конденсаторов

Схема в которой присутствует две и более группы (блока) конденсаторов с различными схемами соединения называется схемой смешанного соединения конденсаторов.

Приведем пример такой схемы:

Для расчетов такие схемы условно разделяются на группы одинаково соединенных конденсаторов, после чего расчеты ведутся для каждой группы по формулам приведенным выше.

Для наглядности приведем пример расчета общей емкости данной схемы.

Пример расчета

Условно разделив схему на группы получим следующее:

Как видно из схемы на первом этапе мы выделили 3 группы (блока) конденсаторов, при этом конденсаторы в первой и второй группе соединены последовательно, а конденсаторы в третьей группе — параллельно.

Произведем расчет каждой группы:

Группа 1 — последовательное соединение трех конденсаторов:

1/C_1,_2,₃= 1/C₁+1/C₂+1/C₃= 1/5+1/15+1/10=0,2+0,067+0,1 = 0,367 → C_1,_2,₃= 1/0,367 = 2,72 мкФ

Группа 2 — последовательное соединение двух конденсаторов:

С_4,5= (C₄*C₅)/(C₄+C₅)= (20*30)/(20+30) = 600/50 = 12 мкФ

Группа 3 — параллельное соединение трех конденсаторов:

С_6,7,8= C₆+C₇+C₈= 5+25+30 = 60 мкФ

В результате расчета схема упрощается:

Как видно в упрощенной схеме осталась еще одна группа из двух параллельно соединенных конденсаторов, произведем расчет ее емкости:

Группа 4 — параллельное соединение двух групп конденсаторов:

С_1,2,3,4,5= C_1,2,3+C_4,5= 2,72+12 = 14,72 мкФ

В конечном итоге получаем простую схему из двух последовательно соединенных групп конденсаторов:

Теперь можно определить общую емкость схемы:

С_общ= (C_1,2,3,4,5*C_6,7,8)/(C_1,2,3,4,5+C_6,7,8) = 14,72*60/14,72+60 = 883,2/74,72 = 11,8 мкФ

Была ли Вам полезна данная статья? Или может быть у Вас остались вопросы? Пишите в комментариях!

Не нашли на сайте статьи на интересующую Вас тему касающуюся электрики? Напишите нам здесь. Мы обязательно Вам ответим.

↑ Наверх

Источник

Элементы цепи могут быть подключены двумя способами:

последовательно
параллельно

Проиллюстрируем данные подключения на примере двух конденсаторов (рис. 1).

последовательное соединение конденсаторов

Рис. 1. Последовательное соединение конденсаторов

Логическая зарядка конденсаторов происходит как показано на рис.1. Приходя из цепи, электрон останавливается на левой обкладке (пластине) конденсатора. При этом, благодаря своему электрическому полю (электризация через влияние), он выбивает другой электрон с правой обкладки, уходящий дальше в цепь (рис. 1.1). Этот образовавшийся электрон приходит на левую обкладку следующего конденсатора, соединённого последовательно. И всё повторяется снова. Таким образом, в результате «прохождения» через последовательную цепь конденсаторов «одного» электрона, мы получаем заряженную систему с одинаковыми по значению зарядами на каждом из конденсаторов (рис. 1.2).

Кроме того, напряжение на последовательно соединённой батареи конденсаторов есть сумма напряжений на каждом из элементов (аналог последовательного сопротивления проводников).

Рис. 2. Последовательное соединение конденсаторов

Часть задач школьной физики касается поиска общей электроёмкости участка цепи, логика такого поиска: найти такую электроёмкость, которым можно заменить цепь, чтобы параметры напряжения и заряда остались неизменными (рис. 2). Пусть заряд на обоих конденсаторах — $displaystyle {{C}_{1}}$ (помним, что они одинаковы), электроёмкости — $displaystyle {{C}_{2}}$ , $displaystyle {{U}_{1}}$ и соответствующие напряжения — $displaystyle {{U}_{2}}$ и $displaystyle {{U}_{2}}$ .

Учитывая определение электроёмкости:

$displaystyle C=frac{q}{U}$ (1)

Тогда:

$displaystyle {{U}_{1}}=frac{q}{{{C}_{1}}}$ (2)

$displaystyle {{U}_{2}}=frac{q}{{{C}_{2}}}$ (3)

$displaystyle {{U}_{0}}=frac{q}{{{C}_{0}}}$ (4)

Памятуя о том, что конденсаторы соединены последовательно, получаем:

$displaystyle {{U}_{0}}={{U}_{1}}+{{U}_{2}}$ (5)

Тогда:

$displaystyle Rightarrow frac{1}{{{C}_{0}}}=frac{1}{{{C}_{1}}}+frac{1}{{{C}_{2}}}$ $displaystyle Rightarrow frac{1}{{{C}_{0}}}=frac{1}{{{C}_{1}}}+frac{1}{{{C}_{2}}}$ (6)

Или в общем виде:

$displaystyle frac{1}{{{C}_{0}}}=sumlimits_{i}{frac{1}{{{C}_{i}}}}$ (7)

Для цепи из двух последовательных соединений:

$displaystyle {{C}_{0}}=frac{{{C}_{1}}{{C}_{2}}}{{{C}_{1}}+{{C}_{2}}}$ (8)

параллельное соединение конденсаторов

Рис. 3. Параллельное соединение конденсаторов

Параллельное подключение конденсаторов представлено на рисунке 3. При внесении электрона в систему, у него есть выбор: пойти на верхний или нижний конденсатор. При большом количестве электронов заполнение обкладок конденсатора происходит прямо пропорционально электроёмкости конденсаторов.

Рис. 4. Параллельное соединение конденсаторов. Поиск полной электроёмкости

Опять попробуем решить задачу по поиску полной ёмкости конденсаторов (рис. 4). Помним, что при параллельном подключении напряжения на элементах одинаковы, тогда:

$displaystyle {{q}_{1}}={{C}_{1}}U$ (9)

$displaystyle {{q}_{2}}={{C}_{2}}U$ (10)

$displaystyle {{q}_{0}}={{C}_{0}}U$ (11)

С учётом того, что $displaystyle {{q}_{0}}={{q}_{1}}+{{q}_{2}}$ , получим:

$displaystyle {{C}_{0}}U={{C}_{1}}U+{{C}_{2}}U$ (12)

Сокращаем:

$displaystyle {{C}_{0}}={{C}_{1}}+{{C}_{2}}$ (13)

Или в общем виде:

$displaystyle {{C}_{0}}=sumlimits_{i}{{{C}_{i}}}$ (14)

Вывод: в задачах, в которых присутствует цепь, необходимо рассмотреть, какое конкретно соединение рассматривается, а потом использовать соответствующую логику рассуждений:

Источник

Для
получения необходимого значения
электроёмкости конденсаторы часто
соединяют в батареи. Различают два вида
соединений конденсаторов: параллельное
и последовательное^{^}.

При
параллельном соединении конденсаторов
соединяют одноимённо заряженные обкладки
(рис.2.14, а). При этом общий заряд батареи
равен:

Так как

то

Ёмкость
такой батареи равна:

.
(2.35)

При
параллельном соединении конденсаторов
общая ёмкость системы равна сумме
ёмкостей всех конденсаторов:

.
(2.36)

При
последовательном соединении конденсаторов
соединяют разноимённо заряженные
обкладки (рис.2.14, б). При этом заряд
батареи равен:

.
(2.37)

Разность
потенциалов между точками А
и В
равна:

.
(2.38)

Из
выражений (2.37) и (2.38) следует, что

.
(2.39)

При
последовательном соединении конденсаторов
общая ёмкость системы рассчитывается
по формуле:

.
(2.40)

Если
в батарею соединены
конденсаторов одинаковой ёмкости
,
то общая ёмкость соединения рассчитывается
по формулам:

при
параллельном соединении
;

(2.41)
при
последовательном соединении
.

(2.42)

2.7. Энергия электрического поля

Силы,
с которыми взаимодействуют заряженные
тела, консервативны, (их работа не зависит
от пути). Следовательно, система заряженных
тел обладает потенциальной энергией.

Получим
выражение для потенциальной энергии
системы точечных зарядов.

Рассмотрим
вначале систему из двух зарядов q₁
и q₂.
Потенциальная энергия их взаимодействия
выражается формулой:

.
(2.43)

Выражение

определяет потенциал точки поля, в
которой находится первыйзаряд;

– потенциал точки поля, в которой находится
второй заряд. Поэтому для потенциальной
энергии можно записать

.
(2.44)

или

.
(2.45)

Если
система содержит N
точечных зарядов, то для потенциальной
энергии их взаимодействия можно получить:

или

.
(2.46)

Получим выражение
для энергии заряженного проводника.

Рассмотрим
уединенный проводник. Электроемкость
проводника равна С,
на проводнике имеется заряд q,
его потенциал равен
,
и для всех точек проводника он одинаков:.
(2.47)

Заряд,
на проводнике можно рассмотреть как
систему N
точечных зарядов:

.
(2.48)

Энергия
заряженного проводника есть энергия
их взаимодействия и для неё справедлива
формула (2.46).

Преобразуем
формулу (2.46) с учетом (2.47) и (2.48), получим:

.
(2.49)

Так
как
,
то для энергии заряженного проводника
можно записать выражение:

.
(2.50)

Получим
выражение для энергии
заряженного конденсатора.
Заряженный конденсатор – система,
состоящая из отрицательных зарядов
,
сосредоточенных на одной обкладке с
потенциаломи положительных зарядов,
сосредоточенных на другой обкладке с
потенциалом.

;

Энергия
такой системы зарядов равна:

.
(2.51)

Так
как
,
то

.
(2.52)

Согласно
современным представлениям носителем
энергии являются не заряды, а само
электрическое поле.

Выразим
энергию заряженного конденсатора через
напряженность поля характеристику
самого поля: его напряженность Е.

Возьмем
плоский конденсатор. Его электроёмкость
выражается формулой:

.
(2.53)

Электрическое
поле внутри конденсатора однородно и
разность потенциалов равна:

.
(2.54)

Подставим
(2.53) и (2.54) в формулу (2.52), получим:

.
(2.55)

Обозначим
отношение
.
Эта величина называетсяобъёмной
плотностью энергии;
она численно равна энергии электрического
поля, заключённой в единице объёма.

.
(2.56)

С
учётом того, что напряжённость и
электрическое смещение связаны друг с
другом (),
для объёмной плотности энергии можно
записать:

.
(2.52)

Эта
формула получена нами для однородного
электрического поля. Она справедлива
также и для неоднородных полей.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Практически ни одно электронное устройство не обходится без конденсатора. Он может стоять на входе или выходе устройства, перед или после некоторых элементов. Применяется последовательное и параллельное соединение конденсаторов. Как и для чего их подключать тем или иным способом и будем обсуждать.

Содержание статьи

1 Что такое конденсатор и его основные характеристики
2 Что он из себя представляет и как работает
3 Где и для чего используются
4 Как подключать конденсаторы
- 4.1 Параллельное подключение конденсаторов
  - 4.1.1 Расчёт суммарной ёмкости
  - 4.1.2 Пример расчёта
- 4.2 Последовательное соединение
  - 4.2.1 Как определить ёмкость последовательно соединенных конденсаторов
  - 4.2.2 Пример расчёта
5 Почему электролитические конденсаторы выходят из строя и что делать
- 5.1 Как подобрать замену
- 5.2 Что будет, если поставить конденсатор большей ёмкости?

Что такое конденсатор и его основные характеристики

Конденсатор — это радиодеталь, которая работает как накопитель электрической энергии. Чтобы понятнее было, как он работает, его можно представить как своего рода небольшой аккумулятор. Обозначается двумя параллельными чёрточками.

Обозначения различных типов конденсаторов на схемах. Чаще всего из строя выходят электролитические конденсаторы, так что стоит запомнить их обозначение

Основная характеристика конденсатора любого типа — ёмкость. Это то количество заряда, которое он в состоянии накопить. Измеряется в Фарадах (сокращенно просто буква F или Ф), а вернее, в более «мелких» единицах:

микрофарадах — мкФ это 10^-6 фарада,
нанофарадах — нФ это 10^-9 фарада;
пикофарадах — пФ это 10^-12 фарада.

Вторая важная характеристика — номинальное напряжение. Это то напряжение, при котором гарантирована длительная безотказная работа. Например, 4700 мкФ 35 В, где 35 В — это номинальное напряжение 35 вольт.

У крупных по размеру конденсаторов, ёмкость и напряжение указаны на корпусе

Нельзя ставить конденсатор в цепь с более высоким напряжением чем то, которое на нём указано. В противном случае он быстро выйдет из строя.

Можно использовать конденсаторы на 50 вольт вместо конденсаторов на 25 вольт. Но это порой нецелесообразно, так как те, которые рассчитаны на более высокое напряжение, дороже, да и габариты у них больше.

Что он из себя представляет и как работает

В самом простейшем случае конденсатор состоит из двух токопроводящих пластин (обкладок), разделённых слоем диэлектрика.

Между обкладками находится слой диэлектрика — материала плохо проводящего электрический ток

На пластины подаётся постоянный или переменный ток. Вначале, пока энергия накапливается, потребление энергии конденсатором высокое. По мере «наполнения» ёмкости оно снижается. Когда заряд набран полностью, токопотребления вообще нет, источник питания как бы отключается. В это время конденсатор сам начинает отдавать накопленный заряд. То есть, он на время становится своеобразным источником питания. Поэтому его и сравнивают с аккумулятором.

Где и для чего используются

Как уже говорили, сложно найти схему без конденсаторов. Их применяют для решения самых разных задач:

Для сглаживания скачков сетевого напряжения. В таком случае их ставят на входе устройств, перед микросхемами, которые требовательны к параметрам питания.
Для стабилизации выходного напряжения блоков питания. В таком случае надо искать их перед выходом.

Часто можно увидеть электролитические цилиндрические конденсаторы
Датчик прикосновения (тач-пады). В таких устройствах оной из «пластин» конденсаторов является человек. Вернее, его палец. Наше тело обладает определённой проводимостью. Это и используется в датчиках прикосновения.
Для задания необходимого ритма работы. Время заряда конденсаторов разной ёмкости отличается. При этом цикл заряд/разряд конденсатора остаётся величиной постоянной. Это и используется в цепях, где надо задавать определённый ритм работы.
Ячейки памяти. Память компьютеров, телефонов и других устройств — это огромное количество маленьких конденсаторов. Если он заряжен — это единица, разряжен — ноль.
Есть стартовые конденсаторы, которые помогают «разогнать» двигатель. Они накапливают заряд, потом резко его отдают, создавая требуемый «толчок» для разгона мотора.
В фотовспышках. Принцип тот же. Сначала накапливается заряд, затем выдаётся, но преобразуется в свет.

Конденсаторы встречаются часто и область их применения широка. Но надо знать как правильно их подключить.

Как подключать конденсаторы

В электротехнике есть два основных вида соединения деталей — параллельное и последовательное. Конденсаторы также можно подключать по любому из указанных способов. Есть ещё особая — мостовая схема. Она имеет собственную область использования.

В схеме может быть последовательное и параллельное соединение конденсаторов

Параллельное подключение конденсаторов

При параллельном соединении все конденсаторы объединены двумя узлами. Чтобы параллельно подключить конденсаторы, скручиваем попарно их ножки, обжимаем пассатижами, потом пропаиваем. У некоторых конденсаторов большие корпуса (банки), а выводы маленькие. В таком случае используем провода (как на рисунке ниже).

Так физически выглядит параллельное подключение конденсаторов

Если конденсаторы электролитические, следите за полярностью. На них должны стоять «+» или «-«. При их параллельном подключении соединяем одноимённые выводы — плюс к плюсу, минус — к минусу.

Расчёт суммарной ёмкости

При параллельном подключении конденсаторов их номинальная ёмкость складывается. Просто суммируете номиналы всех подключённых элементов, сколько бы их ни было. Два, три, пять, тридцать. Просто складываем. Но следите, чтобы размерность совпадала. Например, складывать будем в микрофарадах. Значит, все значения переводим в микрофарады и только после этого суммируем.

Расчёт ёмкости при параллельном подключении конденсаторов

Когда на практике применяют параллельное соединение конденсаторов? Например, тогда, когда надо заменить «пересохший» или сгоревший, а нужного номинала нет и бежать в магазин некогда или нет возможности. В таком случае подбираем из имеющихся в наличии. В сумме они должны дать требуемое значение. Все их проверяем на работоспособность и соединяем по приведенному выше принципу.

Пример расчёта

Например, включили параллельно два конденсатора — 8 мкФ и 12 мкФ. Следуя формуле, их номиналы просто складываем. Получаем 8 мкФ + 12 мкФ = 20 мкФ. Это и будет суммарная ёмкость в данном случае.

Пример расчёта конденсаторов при параллельном подключении

Последовательное соединение

Последовательным называется соединение, когда выход одного элемента соединяется со входом другого. Сравнить можно с вагонами или цепочкой из лампочек. По такому же принципу последовательно соединяют и конденсаторы.

Вот что значит последовательно соединить конденсаторы

При подключении полярных электролитических «кондеров» надо следить за соблюдением полярности. Плюс первого конденсатора подаете на минус второго и так далее. Выстраиваете цепочку.

Существуют неполярные (биполярные) электролитические конденсаторы. При их соединении нет необходимости соблюдать полярность.

Как определить ёмкость последовательно соединенных конденсаторов

При последовательном соединении конденсаторов суммарная ёмкость элементов будет меньше самого маленького номинала в цепочке. То есть, ёмкость последовательно соединённых конденсаторов уменьшается. Это также может пригодиться при ремонте техники — замена конденсатора требуется часто.

Последовательно соединённые конденсаторы

Использовать формулу расчёта приведённую выше не очень удобно, поэтому её обычно используют в преобразованном виде:

Формула расчёта ёмкости при последовательном соединении

Это формула для двух элементов. При увеличении их количества она становится значительно сложнее. Хотя, редко можно встретить больше двух последовательных конденсаторов.

Пример расчёта

Какая суммарная ёмкость будет если конденсаторы на 12 мкФ и 8 мкФ соединить последовательно? Считаем: 12*8 / (12+8) = 96 / 20 = 4,8 мкФ. То есть, такая цепочка соответствует номиналу 4,8 мкФ.

Пример расчета ёмкости при последовательном подключении конденсаторов

Как видите, значение меньше чем самый маленький номинал в последовательности. А если подключить таким образом два одинаковых конденсатора, то результат будет вполовину меньше номинала. Например, рассчитаем для двух ёмкостей по 12 мкФ. Получим: 12*12 / (12 + 12) = 144 / 24 = 6 мкФ. Проверим для 8 мкФ. Считаем: 8*8 / (8+8) = 64 / 16 = 4 мкФ. Закономерность подтвердилась. Это правило можно использовать при подборе номинала.

Почему электролитические конденсаторы выходят из строя и что делать

Зачастую, чтобы отремонтировать вышедшую из строя электронную технику, достаточно найти и заменить вздувшиеся конденсаторы. Дело в том, что срок жизни их небольшой — 1000-2000 тысячи рабочих часов. Потом он обычно выходит из строя и требуется его замена. И это при нормальном напряжении не выше номинального. Так происходит потому, что диэлектрик в конденсаторах, чаще всего, жидкий. Жидкость понемногу испаряется, меняются параметры и, рано или поздно, конденсатор вздувается.

Электролитические конденсаторы имеют специальные насечки на верхушке корпуса, чтобы при выходе из строя избежать взрыва

Высыхает электролит не только во время работы. Даже просто «от времени». Это конструктивная особенность электролитических конденсаторов. Поэтому не стоит ставить выпаянные из старых схем конденсаторы или те, которые несколько лет (или десятков лет) хранятся в мастерской. Лучше купить «свежий», но проверьте дату производства.

Можно ли продлить срок эксплуатации конденсаторов? Можно. Надо улучшить теплоотвод. Чем меньше греется электролит, тем медленнее высыхает. Поэтому не стоит ставить аппаратуру вблизи отопительных приборов.

Для улучшения отвода тепла ставят радиаторы

Второе — надо следить за тем, чтобы хорошо работали кулера. Третье — если рядом стоят детали, которые активно греются во время работы, надо конденсаторы каким-то образом от температуры защитить.

Как подобрать замену

Если часто приходится менять один и тот же конденсатор, его лучше заменить на более «мощный» — той же ёмкости, но на большее напряжение. Например, вместо конденсатора на 25 вольт, поставить конденсатор на 35 вольт. Только надо иметь в виду, что более мощные конденсаторы имеют большие размеры. Не всякая плата позволяет сделать такую замену.

Конденсатор той же ёмкости, но рассчитанный на большее напряжение, имеет больший размер

Можно поставить параллельно несколько конденсаторов с тем же напряжением, подобрав номиналы так, чтобы получить требуемую ёмкость. Что это даст? Лучшую переносимость пульсаций тока, меньший нагрев и, как следствие, более продолжительный срок службы.

Что будет, если поставить конденсатор большей ёмкости?

Часто приходит в голову идея поставить вместо сгоревшего или вздувшегося конденсатор большей ёмкости. Ведь он должен меньше греться. Так, во всяком случае, кажется. Ёмкость практически никак не связана со степенью нагрева корпуса. И в этом выигрыша не будет.

Устройство электролитического конденсатора

По нормативным документам отклонение номинала конденсаторов допускается в пределах 20%. Вот на эту цифру можете спокойно ставить больше/меньше. Но это может привести к изменениям в работе устройства. Так что лучше найти «родной» номинал. И учтите, что не всегда можно ставить большую ёмкость. Можно если конденсатор стоит на входе и сглаживает скачки питания. Вот тут большая ёмкость уместна, если для её установки достаточно места. Это точно нельзя делать там, где конденсатор работает как фильтр, отсекающий заданные частоты.

Можно менять на ту же ёмкость, но чуть более высокое напряжение. Это имеет смысл. Но размеры такого конденсатора будут намного больше. Не в любую плату получится его установить. И учтите, что корпус его не должен соприкасаться с другими деталями.

Источник

Основные ссылки

CSS adjustments for Marinelli theme

Вы здесь

Соединения конденсаторов. Энергия электрического поля конденсатора.

Последовательное соединение конденсаторов

Параллельное соединение конденсаторов

Смешанное соединение конденсаторов

Пример расчета

2.7. Энергия электрического поля

Что такое конденсатор и его основные характеристики

Что он из себя представляет и как работает

Где и для чего используются

Как подключать конденсаторы

Параллельное подключение конденсаторов

Расчёт суммарной ёмкости

Пример расчёта

Последовательное соединение

Как определить ёмкость последовательно соединенных конденсаторов

Пример расчёта

Почему электролитические конденсаторы выходят из строя и что делать

Как подобрать замену

Что будет, если поставить конденсатор большей ёмкости?

Вам также может понравиться

Что такое работа тела как ее найти

Синий экран на компьютере виндовс 10 как исправить с помощью командной строки windows

Как исправит нос оперативно

Добавить комментарий Отменить ответ