В сегодняшней статье решаем задачи по физике. Тема – эффект Комптона.
Подпишитесь на наш телеграм, там много полезных материалов для учебы. А если хотите скидку, ищите ее на нашем втором канале для клиентов.
Нужна помощь?
Доверь свою работу кандидату наук!
Задачи на тему «эффект Комптона»
Не знаете, с чего начать решение? Вот вам общая памятка по решению физических задач и более 40 формул, держите их под рукой!
Кстати, у нас есть еще и справочник с теорией. Нужна теория по эффекту Комптона? Пожалуйста!
Задача на эффект Комптона №1
Условие
Узкий пучок монохроматического рентгеновского излучения падает на рассеивающее вещество. Найти угол комптоновского рассеяния, если длина волны излучения увеличилась на 1 пм.
Решение
Запишем формулу эффекта Комптона:
λ’-λ=2λсеsin2θ2
Отсюда найдем искомый угол θ:
θ=2acrsin∆λ2λec=2arcsin1·10-122·2,4263·10-12=53,95°
Ответ: θ=53,95°.
Задача на эффект Комптона №2
Условие
Гамма-излучение с длиной волны 0,83·10-13 м рассеялось на свободных протонах под углом 180°. Найти энергию фотона после рассеяния.
Решение
По формуле эффекта Комптона:
λ’=λ+λpc·1-cosθ
Отсюда:
λ’=0,83·10-13+1,3214·10-15·1–1≈8,56·10-14 м
Выразим энергию через длину волны:
Е’=hcλ’=6,62·10-34·3·1088,56·10-14=2,32·10-12Дж
Ответ: 2,32 пДж
Задача на эффект Комптона №3
Условие
В результате комптоновского рассеяния под углом 174° длина волны фотона стала равной 8 пм. Во сколько раз уменьшилась частота фотона?
Решение
Из формулы для эффекта Комптона найдем:
λ’-λ=λес·1-cosθλ=λ’-λec·1-cosθλ=8·10-12-2,4263·10-121–0,9945≈3,16·10-12 м
Частоту фотона после рассеяния найдем из формулы для длины волны:
λ=сϑϑ=сλ=3·1083,16·10-12=94,87·1018 Гц
Частота фотона до рассеивания:
ϑ’=сλ’=3·1088·10-12=37,47·1018 Гц
Отсюда:
ϑϑ’=94,8737,47≈2,5
Ответ: уменьшилась в 2,5 раза.
Задача на эффект Комптона №4
Условие
В результате эффекта Комптона фотон с энергией ε1=1,02 МэВ рассеян на свободных электронах на угол θ=150°. Определить энергию рассеянного фотона.
Решение
Согласно формуле Комптона изменение длины волны фотона при рассеянии на свободном электроне:
∆λ=hcE01-cosθ
Здесь E0 – энергия покоя электрона.
С учетом того, что ε=hϑ=hcλ и λ=hcε, первую формулу можно переписать в следующем виде:
hcε-hcε1=hcε01-cosθ
Отсюда можно найти энергию рассеянного фотона ε2:
1ε2-1ε1=1-cosθE0ε2=ε1E0E0+ε11-cosθ
Энергия покоя электрона равна E0=mc2
Подставим значения и рассчитаем:
Е0=9,11·10-31·9·1016=8,199·10-14 Дж=0,511·106 эВ=0,511 МэВε2=1,02·0,5110,511+1,021-сos150°=0,216 МэВ
Ответ: 0,216 МэВ.
Задача на эффект Комптона №5
Условие
При каком угле рассеивания фотонов происходит максимально возможное изменение длины волны?
Решение
Длина волны рассеянного фотона в результате эффекта Комптона возрастает тем больше, чем больше угол рассеивания фотона. Максимально возможное значение этого угла θ=180°, т.е. фотон меняет направление движения на противоположное. Тогда формула Комптона принимает вид:
λ’-λ=2λс
Ответ: 180°.
Нужно больше задач? Не проблема! Вот, например, задачи на фотоэффект.
Вопросы на тему «эффект Комптона»
Вопрос 1. В чем суть эффекта Комптона?
Ответ. Эффект Комптона – явление, сопровождающее рассеяние электромагнитного излучения на свободных (слабосвязанных) электронах атома, приводящее к изменению его частоты (длины волны).
Вопрос 2. Какие закономерности существуют для комптоновского рассеяния?
Ответ. Комптоновское рассеяние подчиняется следующим закономерностям:
- рассеянное излучение обладает высокой интенсивностью для веществ с малым атомным весом и малой интенсивностью для веществ с большим атомным весом;
- при увеличении угла рассеяния интенсивность рассеянного излучения в эффекте Комптона возрастает (интенсивность при классическом рассеянии падает с увеличением угла рассеяния);
- смещение длины волны рассеянного излучения зависит от угла рассеяния;
- при одинаковых углах рассеяния величина смещения одна и та же для всех рассеивающих веществ.
Вопрос 3. Что такое комптоновская длина волны?
Ответ. Комптоновская длина волны является постоянной величиной для частицы, на которой происходит рассеяние электромагнитного излучения.
λс=hmc
Здесь m – масса частицы, на которой происходит рассеяние.
Вопрос 4. Запишите формулу Комптона.
Ответ. Формула комптона имеет вид:
∆λ=λ’-λ=λс1-cosθ
Здесь λ – длина волны падающего излучения, λ’– длина волны рассеянного излучения, θ – угол рассеяния, λс – комптоновская длина волны.
Вопрос 5. Какую премию получил Комптон за открытие данного эффекта?
Ответ. В 1927 году Комптон (совместно с Вильсоном) получил Нобелевскую премию.
Посмотри примеры работ и убедись, что мы поможем на совесть!
Нужна помощь в решении задач? В профессиональном сервисе для учащихся вам помогут решить любую, хоть с тремя звездочками. Обращайтесь в любое время.
| Квантовая механика |
|---|
|
|
Основа
|
|
Фундаментальные понятия
|
|
Эксперименты
|
|
Формулировки
|
|
Уравнения
|
|
Интерпретации
|
|
Развитие теории
|
|
Сложные темы
|
|
Известные учёные
|
|
См. также
|
| См. также: Портал:Физика |
Эффе́кт Ко́мптона (ко́мптон-эффе́кт, ко́мптоновское рассе́яние) — упругое рассеяние фотона заряженной частицей, обычно электроном, названное в честь первооткрывателя Артура Холли Комптона. Если рассеяние приводит к уменьшению энергии, поскольку часть энергии фотона передаётся отражающемуся электрону, что соответствует увеличению длины волны фотона (который может быть рентгеновским или гамма-фотоном), то этот процесс называется эффектом Комптона. Обратное комптоновское рассеяние происходит, когда заряженная частица передаёт фотону часть своей энергии, что соответствует уменьшению длины волны кванта света.
Обнаружен американским физиком Артуром Комптоном в 1923 году в экспериментах с рентгеновским излучением[1][2]; за это открытие Комптон стал лауреатом Нобелевской премии по физике за 1927 год.
Эффект Комптона по природе подобен фотоэффекту — разница заключается в том, что при фотоэффекте фотон полностью поглощается электроном, тогда как при комптоновском рассеянии он только меняет направление движения и энергию[3].
Вступление[править | править код]
Рис. 1: Схема эксперимента Комптона. Комптоновское рассеяние происходит в графитовой мишени слева. Щель пропускает рентгеновские фотоны, рассеянные под выбранным углом. Энергия рассеянного фотона измеряется с помощью брэгговского рассеяния в кристалле справа в сочетании с ионизационной камерой; камера могла измерять только полную энергию, выделяемую с течением времени, а не энергию отдельных рассеянных фотонов
Комптоновское рассеяние является примером упругого рассеяния[4][5] света на свободной заряженной частице, где длина волны рассеянного света отличается от длины волны падающего излучения. В первоначальном эксперименте Комптона (см. Рис. 1) энергия рентгеновского фотона (≈17 кэВ) была намного больше, чем энергия связи атомного электрона, поэтому электроны можно было считать свободными после рассеяния. Величина, на которую изменяется длина волны света, называется комптоновским сдвигом. Хотя ядерное комптоновское рассеяние существует[6], комптоновское рассеяние обычно относится к взаимодействию, в котором участвуют только электроны атома.
Эффект наблюдал Артур Холли Комптон в 1923 году в Вашингтонском университете в Сент-Луисе и в последующие годы этот эффект подтвердил его аспирант Ю. Х. Ву. Комптон получил Нобелевскую премию по физике 1927 года за своё открытие.
Этот эффект демонстрирует, что свет не может быть объяснён исключительно как волновое явление[7]. Томсоновское рассеяние, следующее из классической теории рассеяния электромагнитных волн заряженными частицами, не может объяснить сдвиги в длине волны при низкой интенсивности, потому что классически свет должен быть достаточной интенсивности для того, чтобы электрическое поле ускоряло заряженную частицу до релятивистской скорости, вызывало отдачу из-за радиационного давления и связанный с ним доплеровский сдвиг рассеянного света[8], но эффект стал бы сколь угодно малым при достаточно низких интенсивностях света независимо от длины волны. Таким образом, свет ведёт себя так, как будто он состоит из частиц, что объясняет низкоинтенсивное комптоновское рассеяние. Или предположение, что электрон можно рассматривать как свободный, неверно, что приводит к фактически бесконечной массе электрона, равной массе ядра (см., например, комментарий ниже об упругом рассеянии рентгеновских лучей, вызванном этим эффектом). Эксперимент Комптона убедил физиков в том, что свет можно рассматривать как поток частицеподобных объектов (квантов, называемых фотонами), энергия которых пропорциональна частоте световой волны.
Рис.2: Фотон с длиной волны 


Как показано на рис.2, взаимодействие между электроном и фотоном приводит к тому, что электрон получает часть энергии, а фотон с оставшейся энергией излучается в направлении, отличном от исходного, так что общий импульс системы также сохраняется. Если у рассеянного фотона ещё достаточно энергии, процесс может повториться. В этом сценарии электрон рассматривается как свободный или слабосвязанный. Экспериментальная проверка сохранения импульса в отдельных процессах комптоновского рассеяния Боте и Гейгером, а также Комптоном и Саймоном была важна для опровержения теории Бора — Крамерса — Слэтера, которая основывалась на старой квантовой теории.
Комптоновское рассеяние — один из трёх конкурирующих процессов при взаимодействии фотонов с веществом. При энергиях от нескольких эВ до нескольких кэВ, соответствующих спектру от видимого света до мягкого рентгеновского излучения, фотон может быть полностью поглощён, а его энергия может оторвать электрон от основного атома, процесс, известный как фотоэффект. Фотоны высокой энергии 1,022 МэВ и выше могут бомбардировать ядро и вызывать образование электрон-позитронной пары. Этот процесс называется рождением пар. Комптоновское рассеяние является наиболее важным процессом при взаимодействии в промежуточной области энергий.
Описание явления[править | править код]
К началу 20-го века исследования взаимодействия рентгеновских лучей с веществом шли полным ходом. Было замечено, что когда рентгеновские лучи известной длины волны взаимодействуют с атомами, рентгеновские лучи рассеиваются под углом 

В 1923 году Комптон опубликовал в Physical Review статью, в которой объяснил рентгеновский сдвиг, приписывая частицеподобный импульс световым квантам. Эйнштейн предложил световые кванты в 1905 году для объяснения фотоэффекта, но Комптон не основывался на работе Эйнштейна. Энергия световых квантов зависит только от частоты света. В своей статье Комптон вывел математическую связь между сдвигом длины волны и углом рассеяния рентгеновских лучей, предположив, что каждый рассеянный рентгеновский фотон взаимодействует только с одним электроном. Его статья завершается отчётом об экспериментах, которые подтвердили полученное им соотношение:
- где:
— начальная длина волны,
— длина волны после рассеяния,
— постоянная Планка ,
— масса покоя электрона,
— скорость света
— угол рассеяния.
Величина 



Комптон обнаружил, что у некоторых рентгеновских лучей не наблюдается сдвиг длины волны, несмотря на то, что они рассеиваются на большие углы; в каждом из этих случаев фотон не мог выбить электрон[9]. Таким образом, величина этого сдвига связана не с комптоновской длиной волны электрона, а с комптоновской длиной волны всего атома, которая может быть в 10000 раз меньше. Это известно как «когерентное» рассеяние на всём атоме, поскольку атом остается неповреждённым и не получает внутреннего возбуждения.
В первоначальных экспериментах Комптона, приведённых выше, непосредственно измерялся сдвиг длины волны. В современных экспериментах принято измерять энергии, а не длины волн рассеянных фотонов. Для данной энергии падающего кванта 

Невозможность классического толкования[править | править код]
В классической электродинамике взаимодействие электрона с электромагнитной волной, при учёте только электрической составляющей, описывается следующим образом: под действием периодических возмущений, электрон начинает колебаться с той же частотой, что и набегающая волна, и излучать новые электромагнитные волны той же частоты.
Если учесть в том числе и магнитное поле, то движение электрона будет описываться сложным дифференциальным уравнением, и, в случае если поле достаточно сильное, чтобы разогнать электрон до релятивистских скоростей, электрон может начинать излучать на частотах, отличных от частоты начальной волны[10].
Однако ни в коем случае классическая теория не предполагает существование у электронов отдачи — волна распределена в пространстве и не может «сконцентрироваться» на одном электроне и выбить его из атома. Поэтому регистрация таких электронов точно указывает на неполноту классического описания, а именно, на корпускулярно-волновую природу света[11].
Квазиклассический подход позволяет получить только изменение длины волны рассеянного фотона. Для вычисления сечения рассеяния необходимо применить уравнения квантовой электродинамики. Такое распределение даёт Формула Клейна — Нишины.
При росте энергии фотона вероятность рассеяния постепенно уменьшается, причём вероятность рассеяния на большие углы уменьшается быстрее.
Угол рассеяния электрона отдачи отличается от угла рассеяния фотона, и, в случае рассеяния на свободном электроне, описывается уравнением[12]:
- где
— угол рассеяния фотона.
Вывод формулы рассеяния[править | править код]
Рис. 3: Энергии фотона при 500 кэВ и электрона после комптоновского рассеяния.
Фотон γ с длиной волны λ сталкивается с электроном e в атоме, который рассматривается как покоящийся. Столкновение заставляет электрон испытывать отдачу, и новый фотон γ‘ с длиной волны λ‘ отлетает под углом θ к первоначальному направлению движения фотона. (Далее e‘ — электрон после столкновения.) Комптон допускал возможность того, что взаимодействие иногда ускоряет электрон до скоростей, достаточно близких к скорости света, что требует применения специальной теории относительности Эйнштейна для правильного описания его энергии и импульса.
В заключение статьи Комптона 1923 года он сообщил о результатах экспериментов, подтверждающих предсказания его формулы рассеяния, тем самым подтверждая предположение, что фотоны несут импульс, а также энергию в виде квантов. В начале своего вывода он постулировал выражение для импульса фотона, приравнивая уже установленное Эйнштейном соотношение массы и энергии 







Закон сохранения энергии 
Комптон постулировал, что фотоны несут импульс[9] и таким образом, из закона сохранения импульса, импульсы частиц должны быть аналогичным образом связаны соотношением:
в котором первоначальный импульс электрона 
Энергии фотонов связаны с частотами соотношениями:
- где
— постоянная Планка.
Перед событием рассеяния электрон рассматривается как достаточно близкий к состоянию покоя, так что его полная энергия полностью состоит из его массы покоя, исходя из его энергии для 
После рассеяния существует возможность того, что электрон может быть ускорен до значительной доли от скорости света, что означает, что его полная энергия должна быть представлена с использованием релятивистского соотношения энергия-импульса в виде:
После подстановки этих величин в выражение для сохранения энергии получается:
Это выражение можно использовать, чтобы найти величину импульса рассеянного электрона:
Эта величина импульса, полученного электроном (ранее равная нулю), превышает отношение энергию/c, потерянную фотоном:
Уравнение (1) связывает различные энергии, рассмотренные при столкновении. Изменение импульса электрона включает релятивистское изменение энергии электрона, поэтому оно не связано просто с изменением энергии, происходящим в классической физике. Изменение величины импульса фотона связано не только с изменением его энергии, оно также предполагает изменение направления.
Решение уравнения для сохранения импульса относительно импульса рассеянного электрона приводит к:
Использование скалярного произведения даёт квадрат его величины:



После замены слагаемых с импульсом фотона на 
Приравнивая альтернативные выражения для этого импульса, получается выражение:
которое после раскрытия квадрата и перестановки членов преобразуется к виду:
Разделив обе стороны на 
Наконец, поскольку 
Кроме того, угол 
Сечение эффекта Комптона описывается формулой Клейна — Нишины.
Рассеяние на связанном электроне[править | править код]
Рис. 4. Схематическое изображение рассеяния фотона на электроне внешней оболочки атома
В случае, если электрон, на котором рассеивается фотон, находится в атоме, то картина рассеяния усложняется.
В случае, если энергия связи электрона больше энергии налетающего фотона, то электрон не выбивается из оболочки, и фотон рассеивается всем атомом как одним целым. В таком случае вместо массы электрона в формуле для изменения длины волны будет стоять масса атома, которая в десятки тысяч раз больше — а значит, и изменение длины волны будет в десятки тысяч раз меньше. Поэтому низкоэнергетические фотоны (например, видимого диапазона) рассеиваются почти упруго — такое рассеяние называется рэлеевским.
Другим возможным вариантом является рамановское рассеяние, при котором часть энергии фотона переходит в энергию собственных колебаний молекулы или наоборот.
В случае собственно комптоновского рассеяния, если энергия налетающего фотона значительно больше 



В случае, если 
Вероятность рассеяния близка к нулю при низких энергиях налетающего фотона, она постепенно возрастает при увеличении энергии, а затем спадает. Положение пика зависит от эффективного заряда ядра: чем он больше, тем большей энергии соответствует пик. Также, чем больше значение заряда ядра, тем меньше, в абсолютных величинах, пиковое сечение рассеяния[16].
В угловом распределении при росте заряда ядра подавляются вылеты с малым углом — то есть, наибольшую вероятность при рассеянии на K-электронах тяжёлых элементов имеет отражение на 180°, даже для высоких энергий[14].
Ещё одной особенностью рассеяния на электронах в атоме является уширение спектральной линии, соответствующей заданному углу рассеяния. То есть, если при рассеянии на свободном электроне, любому углу соответствует конкретное значение 
Поскольку обычно у атома есть много электронов с разной энергией связи, то при одной и той же энергии падающего фотона для некоторых электронов рассеяние будет происходить по комптоновскому типу, а для других (энергия связи которых больше энергии фотона) — по рэлеевскому, в зависимости от того, с электроном какой оболочки провзаимодействовал фотон. Поэтому реальные спектры рассеянных фотонов обычно содержат два пика — один из них совпадает с частотой падающего света, а второй — с менее энергетическими комптоновскими фотонами[18].
Комптоновское рассеяние на связанном электроне является основным способом потери энергии в веществе для гамма-квантов среднего диапазона энергий от 100 кэВ (1 МэВ для тяжёлых атомов) до нескольких МэВ. Для фотонов меньшей энергии важнее процессы рэлеевского рассеяния и фотоэффекта, а для более высокоэнергетических — процессы рождения электрон-позитронных пар в кулоновском поле ядра[19].
Некоторые особые случаи комптоновского рассеяния[править | править код]
Двойное рассеяние[править | править код]
Иногда в процессе рассеяния электрон может поглотить один фотон, а испустить два. Такой процесс происходит значительно реже обычного рассеяния. Наиболее вероятным является случай, когда один из образовавшихся фотонов очень низкоэнергетический, и вероятность излучения двух фотонов с близкими энергиями — минимальная[20].
Также, возможно излучение трёх и более фотонов, однако оно подавляется с множителем (постоянной тонкой структуры) (1/137)n-1, где n — количество фотонов[14].
При излучении двух и более фотонов теряется прямая зависимость между углом отклонения и изменением длины волны, поэтому правильный учёт шума от двойного комптон-эффекта необходим для точного измерения нормального эффекта Комптона.
Нелинейное рассеяние[править | править код]
В случае, если интенсивность падающего света очень велика, электрон может поглотить несколько фотонов, и испустить один — такой процесс называется нелинейным комптоновским рассеянием. Его сечение, в отличие от обычного рассеяния, зависит от плотности фотонов в пучке[21]. Рассеяние по такому каналу становится вероятным, когда напряжённость поля, создаваемого электромагнитной волной, превышает напряжённость поля в атоме (которая даже для водорода имеет величину около 4·1010 В/м[22]) более чем в 137 раз. Такие условия возникают при очень высокой интенсивности излучения и на 2020 год являются достижимыми лишь с помощью нескольких самых мощных в мире лазеров[23] (интенсивность излучения которых должна быть выше чем 1021 Вт/см[24]). В природе такие процессы могут реализовываться на поверхности нейтронных звёзд[15].
Рассеяния на тяжёлых частицах[править | править код]
Фотоны могут рассеиваться на протонах и нейтронах так же как на электронах, однако из-за того, что нуклоны почти в 2000 раз тяжелее электрона, изменение длины волны также в тысячи раз меньше, а потому заметным становится лишь для очень высокоэнергетических фотонов[15]. Кроме того, взаимодействие нуклонов в ядре значительно сложнее взаимодействия электрона с ядром, что также влияет на форму спектра рассеянных фотонов[25].
Применение[править | править код]
Измеряя интенсивность рассеянного света можно с большой точностью определить электронную плотность в теле[26].
Если объект имеет сложное внутреннее строение, то можно разделить рассеянное излучение, идущее от каждого отдельного участка вдоль луча. Таким образом работает комптоновская томография[27]. Её главным преимуществом является возможность просканировать объект, даже если отсутствует полный доступ к нему (невозможно произвести полный оборот излучателя и детектора), а недостатком — низкое разрешение.
Анализируя сечение комптоновского рассеяния при различных энергиях, можно установить распределение моментов движения электронов в различных оболочках. Зависимость сечения от энергии называется комптоновским профилем вещества[28]. Также знание комптоновского профиля нужно для высокоточной рентгенографии, поскольку комптоновское рассеяние зашумляет картину рентгеновской тени.
Использование эффекта Комптона позволяет создавать лазеры с плавной регулировкой длины волны — такая регулировка происходит вследствие вращения мишени вокруг рассеивателя[29].
Если фотон детектируется сначала одним детектором, а затем — другим, то, анализируя изменение энергии фотона, можно определить его начальную траекторию[30]. Так работают комптоновские гамма-телескопы[en], имеющие очень широкое поле зрения. Например, телескоп на орбитальной обсерватории «Комптон» имеет поле зрения в 1 стерадиан.
Обратное комптоновское рассеяния релятивистских электронов на реликтовом микроволновом излучении создаёт фотоны отдачи с энергией 50-100 кэВ[14]. Это явление известно как эффект Сюняева — Зельдовича. Детектируя такие высокоэнергетические фотоны, можно изучать крупномасштабное распределение материи во Вселенной. Самый полный обзор источников такого излучения был сделан космическим телескопом «Планк»[31].
Комптоновское рассеяние[править | править код]
Комптоновское рассеяние имеет первостепенное значение для радиобиологии, поскольку это наиболее вероятное взаимодействие гамма-лучей и рентгеновских лучей высоких энергий с атомами в живых организмах — применяется в лучевой терапии[32].
В материаловедении комптоновское рассеяние можно использовать для исследования волновой функции электронов в веществе в импульсном представлении[33].
Комптоновское рассеяние — важный эффект в гамма-спектроскопии, который приводит к возникновению комптоновского края, поскольку гамма-лучи также рассеиваются за пределы используемых детекторов. Комптоновское подавление используется для обнаружения паразитного рассеяния гамма-лучей, для учёта этого эффекта.
Магнитное комптоновское рассеяние[править | править код]
Магнитное комптоновское рассеяние — это модификация ранее упомянутой техники, которая включает намагничивание кристаллического образца, под действием высокоэнергетических циркулярно-поляризованных фотонов. Путём измерения энергии рассеянных фотонов и изменения намагниченности образца генерируются два разных комптоновских профиля (один для импульсов со спином вверх и один для импульсов со спином вниз). Разница между этими двумя профилями даёт магнитный профиль Комптона (МПК), определяемый функцией 
- где
— количество неспаренных электронов в системе;
и
представляют собой трёхмерные распределения электронов по импульсам для электронов с основным и неосновным проекциями спина, соответственно.
Поскольку этот процесс рассеяния некогерентен (нет фазового соотношения между рассеянными фотонами), МПК представляет объёмные свойства образца и измеряет основное состояние. Это означает, что МПК идеален для сравнения с теоретическими методами, такими как теория функционала плотности. Площадь под графиком МПК прямо пропорциональна спиновому моменту системы, поэтому в сочетании с методами измерения полного магнитного момента (такими как СКВИД-магнитометрия) может использоваться для выделения как спинового, так и орбитального вкладов в общий магнитный момент системы. Форма МПК также даёт представление о происхождении магнетизма в системе[34].
Обратный комптоновский эффект[править | править код]
Если фотон рассеивается на движущихся электронах, то энергия рассеянного фотона может быть больше, чем энергия падающего (соответственно, энергия электрона после столкновения уменьшается). Такой процесс называют обратным комптоновским рассеянием. Этот процесс является основным механизмом потери энергии релятивистскими электронами в межзвёздном пространстве. Если начальные скорости фотонов распределены изотропно, то средняя энергия рассеянных фотонов будет равняться[35]:
Энергия рассеянного на электроне фотона:
- где:
— угол между направлениями их движения;
— угол между направлениями движения падающего и рассеянного фотона;
[35] — безразмерная скорость электрона.
В случае «лобового» столкновения[35]:
В случае обратного эффекта Комптона изменение длины волны падающего света зависит от его начальной энергии, тогда как для неподвижных электронов такой зависимости нет.
Обратный эффект Комптона ответственен за рентгеновское излучение галактических источников, рентгеновскую составляющую реликтового фонового излучения (эффект Сюняева — Зельдовича), трансформацию плазменных волн в высокочастотные электромагнитные волны[36]. Эффект также наблюдается, когда фотоны космического микроволнового фона движутся через горячий газ, окружающий скопление галактик. Фотоны реликтового излучения рассеиваются электронами в этом газе до более высоких энергий, что приводит к эффекту Сюняева — Зельдовича. Наблюдения этого эффекта обеспечивают практически независимые от красного смещения средства обнаружения скоплений галактик.
Обратное комптоновское рассеяние играет важную роль в астрофизике. В рентгеновской астрономии предполагается, что аккреционный диск, окружающий черную дыру, создаёт тепловой спектр. Фотоны с более низкой энергией из этого спектра, рассеиваются до более высоких энергий релятивистскими электронами в окружающей короне. Предполагается, что это вызывает степенну́ю составляющую в рентгеновских спектрах (0,2-10 кэВ) аккреции черных дыр[источник не указан 758 дней].
Некоторые установки синхротронного излучения рассеивают лазерный свет от ускорительного электронного луча. Это комптоновское обратное рассеяние производит фотоны высоких энергий в диапазоне от МэВ до ГэВ[37][38] и впоследствии используются в экспериментах по ядерной физике.
Примечания[править | править код]
- ↑ Комптон А. Рассеяние рентгеновских лучей как частиц // Эйнштейновский сборник 1986—1990. — М.: Наука, 1990. — С. 398—404. — 2600 экз.
- ↑ Филонович С. Р. Артур Комптон и его открытие // Эйнштейновский сборник 1986—1990. — М.: Наука, 1990. — С. 405—422. — 2600 экз.
- ↑ Prof. Jeffrey Coderre. Interactions of Photons with Matter. ocw.mit.edu (2004).
- ↑ Юдин Г. Л. Комптона эффект // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.: «Комптон рассмотрел упругое рассеяние фотона на свободном покоящемся электроне».
- ↑ Биленький С. М. Рассеяние микрочастиц // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.: «Рассеяние микрочастиц — процесс столкновения частиц, в результате которого либо меняются их импульсы (упругое рассеяние) или наряду с изменением импульсов меняются также внутр[енние] состояния частиц, либо образуются др[угие] частицы (неупругие процессы)».
- ↑ Christillin P. (1986). “Nuclear Compton scattering”. J. Phys. G: Nucl. Phys. 12 (9): 837—851. Bibcode:1986JPhG…12..837C. DOI:10.1088/0305-4616/12/9/008.
- ↑ Griffiths, David. Introduction to Elementary Particles. — Wiley, 1987. — P. 15, 91. — ISBN 0-471-60386-4.
- ↑ C. Moore. Observation of the Transition from Thomson to Compton Scattering in Optical Multiphoton Interactions with Electrons.
- ↑ 1 2 3 Taylor, J.R. Modern Physics for Scientists and Engineers / J.R. Taylor, C.D. Zafiratos, M.A. Dubson. — 2nd. — Prentice Hall, 2004. — P. 136–9. — ISBN 0-13-805715-X.
- ↑ Сивухин, 1986, p. 31.
- ↑ Сивухин, 1986, p. 32.
- ↑ Сивухин, 1986, p. 30.
- ↑ Борн М. Атомная физика. — М.: Мир, 1965. — С. 389.
- ↑ 1 2 3 4 Прохоров, 1990, p. 431.
- ↑ 1 2 3 Прохоров, 1990, p. 432.
- ↑ Mikhailov Aleksandr, …, Nefiodov Andrei (2018). “Ionization-Excitation of Helium-Like Ions at Compton Scattering”. Journal of Experimental and Theoretical Physics. 127: 620—626. DOI:10.1134/S1063776118090170. Дата обращения 26 липня 2020.
- ↑ Kaplan Ilya, …, Yudin Gennadiy (1975). “Nonrelativistic compton effect for a bound electron” (PDF). Journal of Experimental and Theoretical Physics. 69 (1): 9—22. Дата обращения 26 липня 2020.
- ↑ R. Nave. Compton Scattering Data. HyperPhysics. Дата обращения: 26 липня 2020. Архивировано 23 лютого 2010 года.
- ↑ Ишханов,Капитонов,Кэбин, 2007, p. 535.
- ↑ Mandl Franz et. al. (1952). “The theory of the double Compton effect”. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 215 (1123): 497—507. DOI:10.1098/rspa.1952.0227.
- ↑ Ivanov Dmitry et. al. (2006). “Complete Description of Non-Linear Compton and Breit-Wheeler Processes”. Acta Physica Polonica B. 37 (4): 1073.
- ↑ Dr. Susan Lea. Electric fields in dielectrics. San Francisco State University (2006).
- ↑ Danson; et al. (2019). “Petawatt and exawatt class lasers worldwide” (PDF). High Power Laser Science and Engineering. 7: 54. DOI:10.1017/hpl.2019.36.
- ↑ Bisesto; et al. (2018). “Evolution of the electric fields induced in high intensity laser–matter interactions”. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 909: 398—401. DOI:10.1016/j.nima.2018.03.040.
- ↑ Bernardini et. al. (1960). “Proton compton effect”. Il Nuovo Cimento (1955-1965). 18: 1203—1236. DOI:10.1007/BF02733177. Дата обращения 31 липня 2020.
- ↑ Sharaf, Jamal (2001). “Practical aspects of Compton scatter densitometry”. Applied Radiation and Isotopes. 54 (5): 801—809. DOI:10.1016/S0969-8043(00)00333-X. Дата обращения 26 липня 2020.
- ↑ Redler (2018). “Compton scatter imaging: A promising modality for image guidance in lung stereotactic body radiation therapy”. Medical Physics. 45 (3): 1233—1240. DOI:10.1002/mp.12755. Дата обращения 26 липня 2020.
- ↑ Rao; et al. (2002). “Doppler Broadening and its Contribution to Compton Energy-Absorption Cross Sections: An Analysis of the Compton Component in Terms of Mass-Energy Absorption Coefficient” (PDF). Journal of Physical and Chemical Reference Data. 31 (3): 769. DOI:10.1063/1.1481880. Дата обращения 26 липня 2020.
- ↑ Источники гамма-излучения. Ядерная физика в Интернете. Дата обращения: 26 липня 2020. Архивировано 21 березня 2021 года.
- ↑ The Imaging Compton Telescope (COMPTEL). Nasa.gov (2005). Дата обращения: 27 липня 2020. Архивировано 21 березня 2021 года.
- ↑ Planck Collaboration (2014). “Planck 2013 results. XXIX. The Planck catalogue of Sunyaev-Zeldovich sources” (PDF). Astronomy & Astrophysics. 571: 41. DOI:10.1051/0004-6361/201321523. Дата обращения 7 березня 2021.
- ↑ Camphausen KA, Lawrence RC. «Principles of Radiation Therapy» in Pazdur R, Wagman LD, Camphausen KA, Hoskins WJ (Eds) Cancer Management: A Multidisciplinary Approach. 11 ed. 2008.
- ↑ I. G. Kaplan (2003). “Compton scattering beyond the impulse approximation”. Physical Review B. 68: 235104. arXiv:cond-mat/0304294. DOI:10.1103/PhysRevB.68.235104.
- ↑ Malcolm Cooper. X-Ray Compton Scattering. — OUP Oxford, 14 October 2004. — ISBN 978-0-19-850168-8.
- ↑ 1 2 3 Эффект Комптона. Ядерная физика в Интернете. Дата обращения: 25 липня 2020. Архивировано 21 березня 2021 года.
- ↑ Комптона эффект // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- ↑ GRAAL home page. Lnf.infn.it. Дата обращения: 8 ноября 2011.
- ↑ Duke University TUNL HIGS Facility. Дата обращения: 31 января 2021.
Литература[править | править код]
- Сивухин Д. В. Атомная физика // Общий курс физики. — М.: Наука, 1986. — Т. 5. — 426 с.
- Комптона эффект // Физическая энциклопедия / А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — 703 с.
- Ишханов Б. С., Капитонов И. М., Кэбин Э. И. Частицы и атомные ядра: Основные понятия. — М.: ЛКИ, 2007. — 584 с.
Полное сечение фотоэффекта σφ ≈ 54 σФ[K ] , причем
σФ[L] σФ[K ] ≈ 15 и σФ[M ] σФ[L] ≈ 14 .
Фотоэффект сопровождается испусканием характеристического рентгеновского излучения возбужденных атомов в результате перехода электронов на вакантные места в соответствующей электронной оболочке. Энергия возбуждения атома может также передаваться электронам внешней оболочки атома. В этом случае кроме фотоэлектронов с энергией Ee появляются электроны с энергией, близкой к значению энергии ионизации Ei (энергии связи электрона на i-й оболочке атома) – это электроны Оже. Оже-электроны с большей вероятностью наблюдаются при фотоэффекте на атомах с малыми и средними Z.
Энергия связи электрона на K оболочке атома, а, следовательно, и характеристического рентгеновского излучения возбужденных атомов и Оже-электронов зависит от Z вещества. Для атома алюминия 13Al EK =2,5
кэВ, для 29Cu – 10 кэВ, а для 82Pb – 88 кэВ.
Угловое распределение фотоэлектронов зависит от их энергии. При малых энергиях (десятки кэВ) фотоэлектроны испускаются преимущественно в направлении, перпендикулярном пучку фотонов. С ростом энергии угол вылета фотоэлектронов уменьшается.
Фотоэффект является главным механизмом поглощения фотонного излучения малых энергий в тяжелых веществах. Так, в Al фотоэффект преобладает при Eγ <60 кэВ, а в свинце при Eγ <600 кэВ.
Наряду с фотоэффектом, при котором вся энергия фотона передается атомному электрону, взаимодействие гаммаизлучения с электронами атомов среды может приводить к его рассеянию, т.е. отклонению от первоначального направления распространения на некоторый угол θ.
Экспериментально сначала было изучено рассеяние сравнительно мягкого электромагнитного излучения (длинноволновое рентгеновское излучение), а уже потом – жесткого (коротковолновое рентгеновское и γ- излучения). Поэтому первые экспериментальные результаты показали практическую неизменность длины волны при рассеянии. Эти результа-
100
ты были объяснены при помощи классической теории рассеяния электромагнитного излучения, развитой ранее для объяснения рассеяния света.
Согласно этой теории электрон под действием падающей на него электромагнитной волны приходит в вынужденные колебания с частотой колебаний напряженности электрического поля фотона и, следовательно, сам становится излучателем электромагнитных волн такой же частоты. Это и есть рассеянная волна.
В простейшем случае рассеяния неполяризованной первичной волны на одном электроне дифференциальное сечение рассеяния равно:
dσ= (re2 /2)(1+cos2 θ)dΩ ,
где rе=е2/mеc2 . Полное сечение рассеяния на одном электроне
|
σ= |
8π |
2 |
-24 2 |
|
|
re |
=0,66·10 |
см . |
||
|
3 |
Эти формулы впервые получил Дж. Дж. Томсон. Сечение томсоновского рассеяния не зависит от длины волны падающего излучения и симметрично относительно плоскости θ = 90º.
Классическая теория рассеяния справедлива при hν « mеc2 . Если это условие не выполняется, то наблюдается рассеяние с изменением длины волны.
Детальное изучение рассеяния электромагнитного излучения с изменением длины волны было проведено в 1923 году Комптоном.
В результате опытов Комптона обнаружено следующее.
1.Спектр рассеянного излучения, кроме первоначальной длины волны λ0, содержит также смещенную линию с длиной волны λ′ > λ0.
2.λ= λ′ – λ0 растет с увеличением угла рассеяния.
3.При данном угле рассеяния ( λ)θ не зависит от λ0.
4.( λ)θ постоянна для всех рассеивающих веществ.
Эти закономерности нельзя объяснить классической волновой теорией, согласно которой длина волны рассеянного излучения должна быть такой же, как и падающего. Объяснение наблюдаемых явлений дано Комптоном и Дебаем с помощью квантовой теории.
В том случае, когда энергия фотона значительно превышает энергию связи электрона, можно рассматривать упругое столкновение фотона со свободным электроном.
Для получения соотношения, связывающего длину волны рассеянного излучения с углом рассеяния, запишем законы сохранения энергии и им-
101
пульса в предположении, что электрон свободен. Закон сохранения энергии:
|
hν = hν′+ Ee |
= hν′+ mec2 ( |
1 |
−1) , |
(2.11) |
||
|
− β2 |
||||||
|
1 |
||||||
|
где β=v/c. |
pγ |
= pγ ‘ + pe или: |
||||
|
Закон сохранения импульса |
||||||
|
hν / c = hν ′/ c + me v / 1− β 2 |
. В скалярной форме |
|||||
|
me2 β2c4/(1-β2) = (hν)2+(hν′)2 – 2hνhν′cosθ. |
(2.12) |
|||||
|
Решая совместно уравнения (2.11) и (2.12), получаем: |
||||||
|
(c/ν′) – (c/ ν) = (h/mec)(1-cosθ) |
||||||
|
или |
||||||
|
λ′ -λ = Λ (1-cosθ) = 2 Λ sin2(θ/2), |
(2.13) |
|||||
|
где Λ= h/mec =2,42-10-10 см – комптоновская длина |
волны электрона. Из |
формулы (2.13) следует, что длина волны смещенной линии λ′ растет с
|
углом рассеяния θ таким образом, что для θ=0 |
λ=0, для θ= =π/2 λ= |
|
|
Λ, а для θ=π |
λ=2 Λ. |
|
|
При рассеянии под данным углом θ величина |
λ не зависит от λ. По- |
этому эффект Комптона несуществен для длинноволнового излучения, когда λ « λ (например, для света и даже мягкого рентгеновского излучения), и наоборот, играет большую роль для коротковолнового излучения, когда λ ~λ .
Таким образом, в результате комптоновского рассеяния изменяется энергия и направление распространения фотона, а также возникает комптоновский электрон. Преобразуя выражение (2.13) , получим связь между энергией рассеянного фотона Eγ‘, энергией падающего фотона Eγ и углом рассеяния θ (относительно первоначального направления фотона). Из законов сохранения энергии и импульса можно получить также связь между энергией комптоновского электрона Ee и углом его вылета ϕ:
|
Eγ′ = |
Eγ |
, |
(2.14) |
||||||
|
1+ |
Eγ |
(1−cosθ) |
|||||||
|
m c2 |
|||||||||
|
e |
|||||||||
|
Ee = |
2Eγ γ |
, |
(2.15) |
||||||
|
(1+ 2γ +(1+γ )2 tgϕ) |
102
|
где γ = |
Eγ |
, а связь между углами θ и φ можно найти по формуле: |
|
|
m c2 |
|||
|
e |
tg(θ 2) = ctgϕ(1+γ )
Из приведенных соотношений (2.14) и (2.15) следует, что фотоны, рассеянные на углы θ≥90º , всегда имеют энергию Eγ‘≤ 0,511 МэВ независимо от начальной энергии, а при θ=180º – в диапазоне от 0,17 до 0,25 МэВ. Максимальную кинетическую энергию имеют комптоновские электроны, вылетающие в направлении движения первичных фотонов, то есть при ϕ=0. Эту максимальную энергию можно найти из соотношения:
(Ee )max = me c2 12+γ22γ .
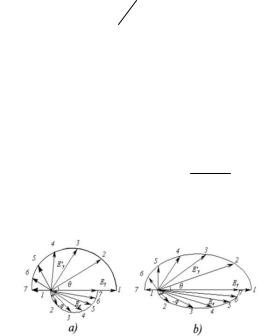
Процесс рассеяния проиллюстрирован на полярных диаграммах, представленных на рис. 2.8.
Рис. 2.8. Полярные диаграммы рассеяния фотонов на свободных электронах,
где а) Eγ=0,64 МэВ; b) Eγ=2.55 МэВ
Верхняя половина диаграммы характеризует энергию Eγ‘ фотонов, рассеянных под углом θ, нижняя – кинетическую энергию электронов отдачи (комптоновских электронов), вылетающих под углом ϕ, связанному с углом θ. Значения энергий рассеянных фотонов и электронов пропорциональны длинам соответствующих радиусов-векторов. В соответствии с законом сохранения энергии сумма векторов верхней и нижней половины, отмеченных одинаковыми цифрами, равны радиусу полуокружности, который характеризует энергию первичного фотона Eγ, летящего в направлении 1.
Дифференциальное сечение комптоновского рассеяния, может быть найдено по формуле Клейна – Нишины – Тамма:
103
|
dσ |
k |
r2 |
Eγ′ 2 |
Eγ |
Eγ′ |
|||||
|
= |
0 |
+ |
− sin2 θ Z , |
|||||||
|
dΩ |
2 |
Eγ |
Eγ |
|||||||
|
Eγ′ |
||||||||||
где r0 =e2 mc2 – классический радиус электрона, Z – порядковый номер атома.
Приведенное соотношение определяет вероятность комптоновского рассеяния в направлении угла θ в единицу телесного угла на Z электронах (то есть на атоме с порядковым номером Z).
Полное сечение комптоновского рассеяния может быть получено интегрированием приведенного выше соотношения по всему телесному углу:
|
2 |
(γ + |
1) |
1 |
4 |
1 |
2 |
|||||||||
|
Z |
|||||||||||||||
|
σk =π r0 |
1 |
−2 |
2 |
ln (2γ +1)+ |
+ |
− |
(2γ +1) |
(2.16) |
|||||||
|
γ |
γ |
2 |
γ |
2 |
|||||||||||
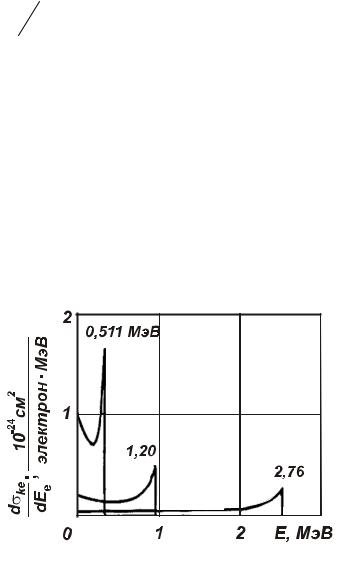
Спектр электронов отдачи приведен на рис. 2.9. Видно, что при высоких энергиях распределение комптоновских электронов почти равновероятно, за исключением области вблизи энергии фотонов, где имеется значительный подъем.
Рис. 2.9. Спектр энергии отдачи электронов
104
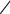
Так как каждый электрон индивидуально участвует в процессе рассеяния, то сечение рассеяния пропорционально Z. σк ~ Z/Eγ.
При hν » mc2 формула (2.16) преобразуется к виду:
|
σк ~ |
NZ |
2Eγ |
+ |
1 |
||
|
ln |
, |
|||||
|
Eγ |
mc |
2 |
2 |
|||
где N – число атомов в единице объема.
Комптоновское рассеяние преобладает в диапазоне энергий 0.6 МэВ<Eγ<5 МэВ для Pb и 0.06 МэВ<Eγ<15 МэВ для Al.
2.2.3. Образование пар электрон-позитрон
При больших энергиях фотонов наряду с фотоэффектом и эффектом Комптона может происходить еще один вид элементарного взаимодействия фотона с веществом – эффект образования пары электрон-позитрон, который был предсказан Дираком в 1928 году.
Процесс образования пар может происходить только при энергиях фотонов, превышающих суммарную энергию покоя электрона и позитрона, то есть при Eγ>2mec 2 .
В пустоте пары из одного фотона образоваться не могут. Процесс может идти в поле ядра, в поле электрона, при взаимодействии двух фотонов и при соударении двух электронов.
Процесс образования пар в кулоновском поле ядра является в 103 раз более вероятным процессом для гамма-излучения средних энергий, чем на электронах.
Сечение образования пар на электронах и ядрах атома пропорционально Z2 и довольно сложным образом зависит от энергии. Вначале сечение образования пар растет очень быстро, затем рост замедляется и
при очень большой энергии (Eγ >>137mec2Z 13 )достигает постоянного значения, зависящего от атомного номера материала. Приближенно за-
|
висимость можно записать: σ |
≈ Z 2 |
E |
. Общий вид зависимо- |
|||
|
ln |
γ |
|||||
|
п |
2m c2 |
|||||
|
сти σп(Eγ) показан на рис. 2.10. |
e |
|||||
105
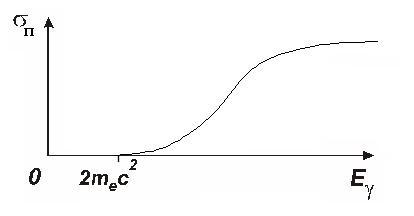
Энергия фотона распределяется почти равновероятно между электронами и позитронами. Однако с ростом энергии фотонов преобладающим становится асимметричное распределение энергии.
Образовавшиеся электроны и позитроны вылетают под некоторым углом к направлению движения фотона. В среднем этот угол θmec2/E, где E – кинетическая энергия электрона или позитрона. При больших энергиях фотонов значение E велико и угол θ стремится к нулю.
При регистрации фотонов по эффекту образования пар имеет существенное значение то, что позитроны через очень короткое время аннигилируют, испуская преимущественно два фотона с энергией 0,511 МэВ. Аннигиляция имеет наибольшую вероятность при малой энергии позитронов, поэтому угол между направлениями аннигиляционных фотонов близок к 180º.
Рис. 2.10. Зависимость сечения образования пар от энергии фотонного излучения
2.2.4. Полный коэффициент ослабления фотонного излучения в веществе
Полное микроскопическое сечение взаимодействия фотонов с веществом σ равно сумме сечений, характеризующих основные процессы взаимодействия: фотопоглощение, комптоновское рассеяние и образование электронно-позитронных пар: σ =σф+ σК+ σп. Макроскопические сечения взаимодействия излучения с веществом (см-1) получаются из микроскопических (см2/атом) умножением на число атомов в единице объема N. Поэтому можно записать:
106
|
1) для фотоэффекта μф= σф N; |
|
2) для комптоновского взаимодействия μК= σК N; |
|
3) для образования пар μп= σп N . |
|
Макроскопические сечения μф, μК и μп называются линейными коэф- |
|
фициентами фотоэффекта, комптоновского взаимодействия и образо- |
|
вания пар соответственно. Сумму этих парциальных макроскопических |
|
сечений называют линейным коэффициентом ослабления фотонного из- |
|
лучения в веществе: |
|
μ=μф+μк+μп. |
|
Три коэффициента, входящие в это соотношение, различным образом |
|
зависят от Z атомов вещества и энергии гамма-излучения, о чем свиде- |
|
тельствуют рассмотренные выше закономерности. Таким образом, мож- |
|
но записать следующие зависимости для линейных коэффициентов: |
|
μф (ρ/А)(Z5/(Eγ)7/2), μK (ρ/А)(Z/Eγ), μп (ρ/А)(Z2ln(Eγ)). |
|
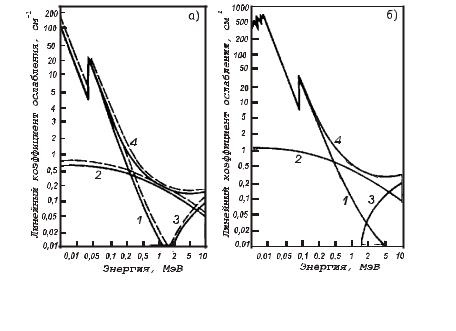
Рис. 2.11. Энергетическая зависимость линейных коэффициентов ослабления фотонов |
|
в NaI (сплошная линия), CsI (штриховая линия) (а) и BGO (б): |
|
1 — μф; 2 — μк; 3 — μп; 4 — μ |
107

Зависимость линейных коэффициентов взаимодействия фотонов с веществом сцинтилляционных детекторов от энергии приведена на рис. 2.11.
2.2.5. Закон ослабления потока фотонного излучения при прохождении через вещество
При прохождении через вещество узкого пучка моноэнергетических фотонов наблюдается экспоненциальное ослабление интенсивности излучения. Это обусловлено тем, что фотоны выбывают из пучка в результате единичного акта взаимодействия (рис. 2.12). Какая-то часть фотонов (случай а), пройдет через вещество, не испытав взаимодействия, другая часть (случай б), будет поглощена, третья часть (случай в) испытает рассеяние и выйдет за пределы регистрируемого пучка.
Рис. 2.12. Иллюстрация взаимодействия пучка фотонов с веществом. Условные обозначения: Д- детектор
Допустим, что узкий моноэнергетический пучок фотонов числом N0 падает нормально на пластину вещества, толщиной d (рис. 2.13). В бесконечно тонком слое dx. , лежащем на глубине х от поверхности пластины, уменьшение числа фотонов dN будет пропорционально только числу фотонов N(х), дошедших до этого слоя, и его толщине dx, т.е
dN= – μ N(x)dx, (2.17)
где μ – коэффициент пропорциональности, или линейный коэффициент ослабления, знак минус означает уменьшение N с увеличением x. Физический смысл линейного коэффициента ослабления: относительное ослабление потока фотонов на единице пути, размерность [μ]= см-1. Величину, обратную линейному коэффициенту ослабления, называют длиной
свободного пробега λ фотонов в веществе: λ = 1μ .
108
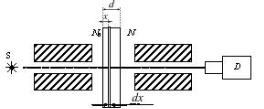
Рис. 2.13. Ослабление пучка фотонов. Условные обозначения: S-источник, D-детектор
Интегрируя (2.17), получаем экспоненциальный закон ослабления гамма-излучения веществом для узкого пучка:
N(x) =N0 e-μx . (2.18)
Толщина слоя поглощающего вещества x1/2, соответствующая уменьшению интенсивности пучка в два раза, называется слоем (толщиной) половинного ослабления. Величина x1/2 имеет важное практическое значение для оценки ослабления потока излучения и обычно приводится в справочниках. Величина x1/2 =ln2/μ = 0,693/μ. является математическим аналогом периода полураспада и может быть найдена экспериментально.
Вместо линейного коэффициента μ часто используют массовый ко-
эффициент ослабления μm (см2/г) и массовую толщину dm (г/см2):
μm = μ/ρ , dm =ρd, и тогда формула (2.18) приобретает вид
N=N0·exp(-μm dm)
2.3.Прохождение нейтронов через вещество
При рассмотрении взаимодействия нейтронов с веществом необходимо учитывать следующие особенности. Нейтроны не имеют электрического заряда, поэтому они не взаимодействуют с электрическим полем ядер и электронов. По сравнению с другими видами излучения нейтроны проходят через вещество, не испытывая столкновений с ядрами атомов, сравнительно большие расстояния, измеряемые сантиметрами. Электромагнитное взаимодействие нейтрона с электроном определяется величиной взаимодействия между их магнитными моментами. Но оно настолько мало, что его энергия достигает энергии ионизации атома (~10 эВ) лишь на расстояниях порядка 10-11 см. Таким образом, сечение ионизационного торможения нейтрона оказывается равным 10-22 см2, то есть приблизительно в 106 раз меньше, чем для заряженной частицы. Правда,
109
эта величина существенно больше, чем сечение взаимодействия быстрого нейтрона с ядрами (~10-24 см2), однако если учесть, что в процессе взаимодействия с электроном нейтрон теряет лишь ничтожную часть своей энергии (~10 эВ), тогда как при ядерном столкновении может потерять значительную ее долю (при лобовом столкновении с протоном – всю), то понятна малая роль ионизационных потерь при движении нейтрона в среде. Эффект от взаимодействия магнитных моментов нейтрона
иэлектрона становится заметным только тогда, когда магнитные моменты всех электронов ориентированы одинаковым образом (в ферромагнетиках). В этом случае взаимодействие магнитных моментов нейтрона и электронов приводит к макроскопическому эффекту дополнительного рассеяния, изучение которого позволяет оценить магнитный момент нейтрона, а также определять магнитную структуру материала.
Основным видом взаимодействия нейтронов с веществом является их взаимодействие с атомными ядрами. В зависимости от того, попадает нейтрон в ядро или нет, его взаимодействие с ядрами можно разделить на два класса:
1)упругое потенциальное рассеяние на потенциале ядерных сил без попадания нейтрона в ядро (п, п)пот;
2)ядерные реакции разных типов: (п, γ), (п, р), (п, а), реакция деления
идр.; неупругое рассеяние (п, п’); упругое рассеяние с заходом нейтрона
вядро—упругое резонансное рассеяние (п, n)рез.
Относительная роль каждого процесса определяется величиной соответствующих сечений. В некоторых веществах, для которых роль упругого рассеяния относительно высока, быстрый нейтрон теряет свою энергию в серии последовательных актов упругого соударения с ядрами вещества (замедление нейтронов). Процесс замедления продолжается до тех пор, пока кинетическая энергия нейтрона не сравняется с энергией теплового движения атомов замедляющего вещества (замедлителя). Такие нейтроны называются тепловыми. Дальнейшие столкновения тепловых нейтронов с атомами замедлителя практически не изменяют энергии нейтронов и приводят только к перемещению их в веществе (диффузия тепловых нейтронов), которое продолжается до тех пор, пока нейтрон не поглотится ядром какого-либо атома.
Поскольку характер взаимодействия нейтронов с веществом определяется их энергией, удобно ввести классификацию нейтронов различных энергетических групп. Хотя строгой общепринятой классификации нейтронов по спектральным группам нет, но существуют вполне устано-
110
вившиеся названия отдельных групп, выделяемых из общего класса медленных нейтронов.
Так, «холодными» называют нейтроны с энергией <0,005 эВ, т. е. в несколько раз меньше средней тепловой энергии. Они получаются при фильтрации тепловых нейтронов сквозь образцы поликристаллов за счет низкоэнергетической области спектра тепловых нейтронов. Среди холодных нейтронов можно выделить группу «ультрахолодных». Основой ее характеристики служит явление полного отражения от материальной стенки. Так как коэффициент преломления обычных веществ для нейтронов очень мал, то полное отражение испытывают лишь очень длинноволновые нейтроны с энергией порядка 10-7 эВ и скоростью меньше
10м/с. Их и называют ультрахолодными.
Тепловые нейтроны образуют довольно определенную и важную
группу, находящуюся в тепловом равновесии с окружающей средой. Спектр их приблизительно максвелловский, средняя энергия 3/2 kT при 20° С равна 0,038 эВ. Менее определенна группа нейтронов, известных под названием резонансных. К ней относятся замедленные, но еще не достигшие теплового равновесия нейтроны. Нижняя граница их спектра практически определяется «прозрачностью» кадмиевой фольги, поглощающей тепловые нейтроны, и равна приблизительно 0,4 эВ. Верхняя граница не очень определенна, так же как и граница спектра медленных нейтронов. Физическая сущность определения данной группы состоит в том, что в этой спектральной области взаимодействие нейтронов с ядрами характеризуется отдельными резонансными пиками, в первую очередь, с ядрами урана-238, ширина пика которых значительно меньше интервала между ними. Это условие у тяжелых ядер нарушается уже при энергии >10 кэВ, а у легких ядер соблюдается до нескольких мегаэлектронвольт.
Среди резонансных нейтронов иногда выделяют группу надтепловых (или закадмиевых), непосредственно примыкающих к тепловым.
Подавляющее большинство источников непосредственно испускает быстрые нейтроны. Для получения медленных нейтронов источник помещают внутрь какого-либо замедлителя, в котором нейтроны теряют энергию в результате многократных столкновений с ядрами. В этом случае, очевидно, спектр быстрых нейтронов, непосредственно испускаемых источником, существен лишь в том отношении, что от него слегка зависят оптимальные условия замедления. Например, чем больше энергии первичных нейтронов, тем больше должна быть толщина замедлите-
111
ля. Вообще же процесс замедления устраняет признаки спектра первичных нейтронов, поэтому для получения медленных нейтронов существен лишь выход и активность источника и допустим любой спектр первичных нейтронов.
Впервые нейтроны были получены в реакции взаимодействия α- частиц радия с ядрами бериллия:
|
49 Be (α,n)126 C , W=5,5 МэВ. |
(2.19) |
Эта реакция до сих пор используется для получения нейтронов с широким энергетическим спектром в таких радионуклидных источниках, как, например: (Pu-Be), (Po-Be), (Ra-Be) и ряд других. Исторически первым источником нейтронов был (Ra—Be)-источник. Он изготовлялся в виде герметической ампулы, внутри которой находилась смесь Ra с Be. Большой разброс в энергии нейтронов объясняется тем, что с ядрами взаимодействуют α-частицы разных энергий (4,8 — 7,7 МэВ), испускаемые не только ядрами Ra, но и находящимися с ним в радиоактивном равновесии продуктами его распада .
Кроме того, в результате реакции (2.19) ядро 126 C образуется не толь-
ко в основном, но и в возбужденных состояниях, что также приводит к расширению нейтронного спектра. (Ra—Be)-источник отличается очень высоким выходом нейтронов (около 2·107 на 1 г Ra). Существенным недостатком источника является то, что наряду с нейтронами он испускает также гамма-излучение, фон которого часто мешает проведению эксперимента.
Этого недостатка не имеет (Ро—Be) -источник, так как α-распад Ро практически не сопровождается испусканием фотонов. Спектр (Ро—Be)- источника изображен на рис. 2.14. Этот источник также характеризуется высоким выходом нейтронов (около 3*106 на 1 кюри Ро).
Общим недостатком обоих нейтронных источников является широкий энергетический спектр. Кроме того, Po как α-излучатель обладает очень малым периодом полураспада – всего 138,4 суток.
Наряду с источниками Ро-Be довольно широкое распространение получили источники Pu-Be и Am-Be. В первом из них α-излучателем служит 239Pu с периодом полураспада около 24000 лет, во втором – 241Am с периодом полураспада 470 лет. Энергии α-частиц равны соответственно 5,1 МэВ и 5,4 МэВ, т. е. близки к энергии α-частиц Ро. Поэтому спектры нейтронов также очень схожи.
112
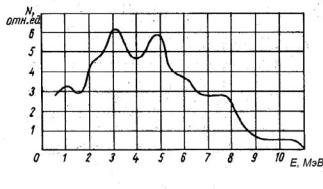
W = 3,25 МэВ;
Рис. 2.14. Спектр нейтронов (Ро – Be)-источника
Для получения моноэнергетических нейтронов широко используются различные реакции, часть из которых была уже рассмотрена нами ранее.
Например, реакции:
21H+ 21H → 23 He+n ,
21H+31H → 42 He+n ,. W = 17,6 МэВ,
нашли применение в нейтронных генераторах для получения нейтронов с энергиями соответственно 2,5 и 14 МэВ. При этом энергия падающих дейтонов может быть относительно невысокой (начиная со 150 кэВ).
Кроме этих реакций для той же цели широко применяются реакции p+ 31H →23 He +n, W= – 0,82 МэВ;
р + 73 Li →74 Be + п, W= – 1,65 МэВ,
в которых получаются нейтроны с энергией En=60 кэВ и Eп=30 кэВ соответственно, когда реакции идут при пороговых значениях энергии протонов Eр=Eмин. При Eр>Eмин с помощью этих реакций можно получить моноэнергетические нейтроны с большей энергией, если регистрировать нейтроны, вылетающие под определенным углом к падающим протонам.
Моноэнергетические нейтроны можно получить также в фото-яденых реакциях, таких, например, как реакция фоторасщепления дейтона:
γ + 21H →p+n, W= – 2,23 МэВ,
113
идущей под действием фотонов радионуклидного источника 20881Tl ,
Еγ =. 2.62 МэВ. Анализ этой реакции показывает, что она может служить источником нейтронов с энергией Еп=200 кэВ, так как фотон из-за равной нулю массы практически не передает импульса дейтрону в процессе ядерной реакции и образующиеся в ней протон и нейтрон имеют приблизительно одинаковые энергии независимо от направления их движения.
Фотонейтронные источники надо изготовлять так, чтобы образование нейтронов шло только под действием фотонного излучения. К числу таких источников относится (124Sb+Be)-источник, испускающий моноэнергетические нейтроны с энергией около 30 кэВ. Радиоактивная сурьма для этого источника приготовляется предварительным облучением в ядерном реакторе.
Для получения нейтронов используется также реакция (γ,п), идущая под действием фотонов, образующихся на электронных ускорителях.
Интенсивные пучки быстрых и медленных нейтронов можно получать с помощью ускорителей и ядерных реакторов. В ускорителях получаются быстрые нейтроны по реакциям (α, п), (р, п) или (d, п), идущих при соударении ускоренных α -частиц, протонов или дейтонов с мишенью. В наиболее распространенных типах ядерных реакторов получаются медленные (в основном тепловые) нейтроны, которые образуются в результате замедления нейтронов, испускаемых в процессе деления ядер урана или плутония. В обоих случаях пучки нейтронов имеют несравненно большую плотность потока, чем пучки нейтронов от радионуклидных источников. В особенности интенсивные пучки нейтронов [~1018 нейтрон/ (см2с)] получаются на ядерных реакторах, работающих в импульсном режиме.
Разработка методов получения трансурановых элементов открыла возможность использовать в качестве источников нейтронов изотопы, испытывающие спонтанное деление. Известно, что деление (в частности, и спонтанное) сопровождается испусканием нейтронов. Характеристики источников приведены в табл. 2.1.
Большинство из перечисленных в таблице изотопов испытывает α- распад, а спонтанное деление происходит с относительно малой вероятностью. Поэтому на каждый акт деления приходится большое число α – частиц.
114
В качестве лабораторного источника нейтронов наиболее удобен спонтанно делящийся 252Cf. Из-за малого периода деления он оказывается высоко активным источником нейтронов.
Таблица 2.1 Характеристики источников нейтронов спонтанного деления
|
Радио- |
Период по- |
Отношение числа |
Число |
ней- |
|
α-распадов к числу |
тронов на |
акт |
||
|
нуклид |
лураспада (лет) |
актов деления |
деления |
|
|
233Pu |
2,85 |
1,3·109 |
1,9 |
|
|
238Pu |
89,4 |
5,5·108 |
2,0 |
|
|
240Pu |
6,6*103 |
1,9·107 |
2,1 |
|
|
242Pu |
3,79*105 |
1,9·105 |
2,3 |
|
|
242Cm |
0,44 |
1,6·107 |
2,3 |
|
|
244Cm |
18,4 |
7,6·105 |
2,6 |
|
|
252Cf |
2,6 |
-40 |
3,7 |
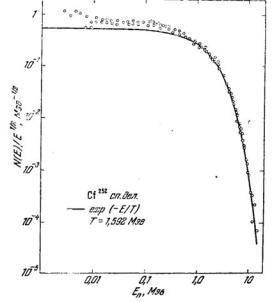
Спектр нейтронов спонтанно делящихся изотопов сплошной и подобен спектру нейтронов вынужденного деления, вызванного нейтронами. На рис. 2.15 показан спектр нейтронов спонтанного деления Cf252 .Он близок по форме к максвелловскому спектру.
Рис. 2.15. Спектр нейтронов спонтанного деления Cf252
115
N(E) ~ E1/2 e-E/T с «температурой» Т = 1,592 МэВ. При небольшой энергии (< 0,5 МэВ) виден приблизительно ~20 %-ный избыток по сравнению с максвелловским спектром, изображенным сплошной линией, который объясняется тем, что, в отличие от молекул, которые находятся в тепловом равновесии со средой без процесса замедления, тепловые нейтроны возникают только в результате притока быстрых нейтронов.
2.3.1.Виды взаимодействий нейтронов с ядрами
2.3.1.1.Радиационный захват нейтронов
Одним из самых распространенных видов ядерных реакций под действием нейтронов являются реакции вида (п,γ) или (A,Z)+n→(A+l,Z)+ γ, в результате которых образуется ядро (А+1, Z), обычно β-радиоактивное. Так как реакции вида (п, γ) сводятся к захвату нейтрона с последующим испусканием фотона, они называются реакциями радиационного за-
хвата нейтрона.
Реакции радиационного захвата с большой вероятностью идут под действием медленных нейтронов с энергией от 0 до 500 кэВ и широко используются для их детектирования.
Пример (n, γ)-реакции – процесс захвата нейтронов с энергией 1,46 эВ индием:
11549 In +n→11649 In + γ.
Образующийся в этом процессе радиоактивный изотоп 11649 In распада-
ется с периодом полураспада T1/2= 54 мин. Применение детекторов из индия очень удобно для выполнения лабораторных исследований процессов замедления и диффузии нейтронов:
2.3.1.2. Реакции с образованием протонов, или (n,p) – реакции
Под действием нейтронов с энергией Еn≈ 0,5—10 МэВ часто идет реакция вида (n, р):
(A, Z)+n → (A, Z-1)+p.
Обычно (n, р) -реакции имеют энергию W>0 (так как mп>mр), а если W<0, то |W|≈l МэВ. Однако для того чтобы образующийся протон мог преодолеть кулоновский барьер при вылете из ядра, нейтрон должен иметь достаточно большую энергию.
116
|
Примерами |
(n,р)-реакций |
являются |
пороговая |
реакция |
|
1632S+n → 3215 P+p , |
у которой W ≈ – 0,92 МэВ, и реакция 147 N+n → 146 C+p , |
имеющая W≈0,6 МэВ и идущая даже на тепловых нейтронах, так как барьер легкого ядра для образующихся протонов относительно невысок. Реакция применяется при регистрации тепловых нейтронов методом ядерных фотоэмульсий, в которых возникают треки от протонов длиной несколько микрон.
2.3.1.3. Реакции с образованием α-частиц
Очень широко используются в ядерной физике реакции вида
(n, α):
(A,Z) +n→(A-3,Z-2)+ 42 He.
Для эффективного протекания (n, α)–реакций также нужны нейтроны с энергиями от 0,5 до 10 МэВ. Однако в некоторых случаях энергия реакции оказывается настолько велика, а кулоновский барьер настолько мал, что реакция с большой вероятностью идет на тепловых нейтронах.
Примером таких реакций являются:
63 Li +n→31H + 42 He , W=4,5 МэВ, 105 B + n → 73 Li + 42 He , W= 2,8 МэВ,
которые используются для регистрации нейтронов, в том числе – тепловых. При этом сечения данных реакций настолько велики (900·10-24 и 4000·10-24 см2 соответственно), что как литий, так и бор можно использо-
вать в виде естественных смесей изотопов (в составе которых 63 Li содержится 7,5%, а 105 B – 19%).
2.3.1.4. Реакции деления
При облучении тяжелых ядер (Тh, Pa, U, трансурановые элементы) нейтронами с энергией Еn>1 МэВ (а для некоторых изотопов урана и трансурановых элементов даже тепловыми нейтронами) происходит реакция деления тяжелого ядра на два ядра-осколка со средними массами, примерно относящимися как 2/3:
(A,Z) +n→(A1,Z1)+(A2,Z2),
где A1+A2=A+1, Z1+Z2=Z, Ā1:Ā2≈2:3, а знак черты означает среднее значение.
117
2.3.1.5. Реакции с образованием двух и большего числа нуклонов
При Еn>10 МэВ становятся возможными реакции вида (п, 2п), (п, пр), (п, 3п) и другие, которые широко используются в качестве детекторов быстрых нейтронов. Большой порог реакций вида (n, 2n) и аналогичных им объясняется тем, что энергия отделения двух нуклонов, как правило, больше, чем энергия отделения одного нуклона.
2.3.1.6. Неупругое рассеяние нейтронов
Нейтрон с энергией в несколько сот килоэлектронвольт после попадания в ядро может перевести его в возбужденное состояние и снова вылететь из него, но уже с меньшей энергией, причем вылететь из ядра может необязательно тот нейтрон, который в него попал. Такой процесс называется неупругим рассеянием нейтрона. Граничная энергия Еn>0,5 МэВ (как и в других рассмотренных случаях) сугубо ориентировочна, так как ее значение для каждого конкретного ядра зависит от расположения уровней возбужденных состояний.
Сечение неупругого рассеяния σinel увеличивается от легких элементов к тяжелым. Это происходит не только вследствие увеличения геометрического сечения, но и вследствие увеличения числа возможных уровней возбуждения, так как. плотность уровней у тяжелых ядер больше, чем у легких.
Сечение неупругого рассеяния σinel увеличивается с энергией нейтрона для всех элементов. При энергии 1,5 МэВ оно вполне заметно даже на легких элементах, а при En=3 МэВ σinel для всех исследованных элементов достигают нескольких барн (10-24 см2), т.е. порядка геометрических сечений ядер. Это вполне естественно, так как по мере роста энергии рассеиваемого нейтрона увеличивается число уровней, при возбуждении которых возможно неупругое рассеяние. По этой причине вероятность образования в результате акта рассеяния ядра в возбужденном состоянии увеличивается.
Средние потери энергии при неупругом рассеянии увеличиваются от легких элементов к тяжелым. Это явление также связано с распределением уровней ядер, образующихся в результате акта рассеяния, и ростом сечения неупругого рассеяния.
118
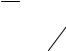
2.3.1.7. Упругое рассеяние нейтронов
Последний процесс, на котором мы остановимся, — упругое рассеяние. Как известно, в результате упругого рассеяния ядро остается в прежнем состоянии, а нейтрон сохраняет свою первоначальную кинетическую энергию в Ц – системе. (в Л-системе сохраняется суммарная кинетическая энергия нейтрона и ядра).
Упругое рассеяние нейтронов очень широко используется для регистрации быстрых нейтронов методом наблюдения следов ядер отдачи (чаще всего протонов отдачи) в различных трековых приборах (камера Вильсона, ядерная фотоэмульсия, пузырьковая камера и другие), а также для регистрации ядер отдачи ионизационными методами (ионизационные камеры, счетчики).
Упругое рассеяние нейтронов может идти через образование составного ядра с последующим испусканием нейтрона или в результате отклонения нейтрона ядром без образования составного ядра. В первом случае рассеяние называется резонансным, а во втором – потенциаль-
ным.
Потенциальное рассеяние является простейшим процессом взаимодействия нейтронов с ядрами. Формула сечения рассеяния в потенциальном поле взаимодействия (резонанса нет) для нейтронов небольших энергий, для которых сечение рассеяния характеризуется изотропией,
вычисляется по формуле: σпот = 4π R2 .
Эффективное сечение резонансного рассеяния определяется формулой Брейта Вигнера:
|
σ(n, n) =σs |
= f (I ) |
λ2 |
Γ 2 |
|||||
|
n |
, |
|||||||
|
4π |
(E |
− E )2 |
+ 1 |
|||||
|
Γ2 |
||||||||
|
n |
0 |
4 |
||||||
а полное эффективное сечение рассеяния при l=0 в области энергий вблизи резонанса
|
Γ 2 |
−4 |
R Γ |
(E |
− E) |
|||
|
σ = 4π R2 +π |
2 |
n |
n |
0 |
|||
|
0 |
|||||||
|
(E − E )2 +(Γ |
2 |
)2 |
|||||
|
0 |
|||||||
складывается из трех составляющих: потенциального рассеяния, резонансного рассеяния и интерференционного члена, происходящего от сложения амплитуд потенциального и резонансного рассеяния и меняю-
119

|
щего знак при переходе через резонанс, где |
и 0 – приведенные дли- |
ны волн нейтрона. ( =λ/2π), соответствующие энергиям Е и Е0 (Е0 – начальная энергия).
Изменение энергии при рассеянии однозначно связано с углом рассеяния. Эта связь вытекает из законов сохранения энергии и импульса.
E = E′+ EM , PM2 = p2 + p′2 − 2 pp′cosθ ,
где Е и р , Е` и р` – энергия и импульс нейтрона до и после столкновения, ЕМ и рМ –энергия и импульс ядра после столкновения, θ – угол рассеяния нейтрона. Отсюда:
|
E′ = E |
m2 |
M 2 |
2 |
2 |
||
|
cosθ + |
−sin |
θ , |
||||
|
(M + m)2 |
m2 |
|||||
где M – масса ядра , рассеивающего нейтрон, m – масса нейтрона, при M=m, то есть при рассеянии на водороде получим:
E′ = E cos2 θ и Ep =Ecos2 ϕ,
где φ – угол отдачи протона. Таким образом, при однократном соударении нейтрона с протоном энергия нейтрона (протона) может принять любое значение в пределах от нуля до E0. При этом измерения энергии протонов отдачи, сделанные с помощью ионизационной камеры, а также результаты других опытов показали, что все значения энергии протонов (а, следовательно, и нейтронов) равновероятны, так что спектр рассеянных нейтронов после первого соударения имеет вид:
f1(E)dE=dE/Eo.
Спектр нормирован на единицу. Средняя энергия нейтронов после первого соударения, очевидно, равна E0/2.
Среднее число столкновений, необходимое для достижения энергии E, равно
120

|
∞ |
||||||||||
|
= |
∑nfn (E) |
= |
1 |
ln |
E0 |
|||||
|
n |
1 |
, |
(2.20) |
|||||||
|
∞ |
E |
|||||||||
|
∑ fn (E) |
ξ |
|||||||||
|
1 |
где ξ – среднелогарифмическая потеря энергии при одном соударении:
ξ = ln(E‘ E” ) =1+α ln(1−α) , где α = ( AA +−11)2
(E’ и E” – энергия нейтрона до и после соударения).
Из формулы (2.20) следует, что величина ξ является одной из важнейших характеристик замедлителя . Чем больше ξ, тем лучше (при прочих равных условиях) замедлитель. При достаточно больших A(A>12) ξ
≈2/(A+2/3) ≈2/A.
Взаключение сделаем два замечания относительно особенностей замедления в области больших и малых энергий нейтронов.
1. В приведенных рассуждениях учитывалось замедление нейтронов только из-за упругих соударений с ядрами. В общем случае замедление нейтронов может происходить также за счет неупругих соударений, если кинетическая энергия нейтронов превышает энергию возбуждения первого возбужденного уровня рассеивающего ядра. Однако для легких ядер, которые являются наилучшими замедлителями, первый возбужденный уровень обычно отстоит от основного на несколько мегаэлектронвольт. Поэтому в большинстве практических задач, в которых рассматривается замедление нейтронов с относительно невысокой начальной энергией (средняя энергия нейтронов спектра деления 2 МэВ) на легких ядрах, эффект неупругого рассеяния можно не учитывать.
Втяжелых ядрах первый возбужденный уровень расположен ближе к основному, чем в легких (среднее расстояние составляет несколько сотен килоэлектронвольт). Поэтому замедление нейтронов на тяжелых ядрах в результате неупругого рассеяния происходит достаточно эффективно. Но
ив этом случае роль неупругого рассеяния ограничивается несколькими первыми соударениями. Из-за большой потери кинетической энергии в этих соударениях оставшаяся у нейтронов энергия оказывается недостаточной для возбуждения ядра, и дальнейший процесс замедления протекает только в результате упругих соударений.
2. Если энергия замедляющегося нейтрона становится сравнимой с энергией химической связи атомов замедлителя (E~1 эВ), то характер
121
замедления нейтронов (скорость замедления, угловое распределение) изменяется. Это происходит, главным образом, из-за возрастания эффективной массы частицы, с которой сталкивается нейтрон.
Если при энергиях En>1 эВ атомы водорода, входящие в состав молекул замедлителя (например, воды), можно было считать свободными, то при En ≈1 эВ этого делать нельзя. Нейтрон с такой энергией не выбивает протона из молекулы, а возбуждает в ней колебательные или вращательные уровни, а при En <1эВ упруго рассеивается на ней как на единой тяжелой частице. Таким образом, приведенная масса сталкивающихся нейтрона и протона возрастает вдвое. Это приводит к изменению сечения рассеяния, средней потери энергии в одном соударении и среднего косинуса угла рассеяния.
Кроме химической связи на процесс замедления нейтронов с энергией ниже ~ 1 эВ влияет тепловое движение атомов замедлителя. Процесс замедления в области энергий ниже 1 эВ (для воды в области En <0,3 эВ) называется термализацией. Главная особенность термализации – снижение скорости замедления. Заключительная стадия термализации — установление теплового равновесия нейтронов с атомами замедлителя.
Условием эффективного протекания процесса замедления является существенное превышение сечения рассеяния нейтронов ядрами замедлителя над сечением захвата. В этом случае энергия нейтронов в процессе замедления будет спадать до тех пор, пока не сравняется с энергией теплового движения атомов замедлителя: Eтепл=k Т , где k – постоянная Больцмана; Т – абсолютная температура. Нейтроны с такими энергиями называются тепловыми.
Нетрудно подсчитать, что при комнатной температуре (T≈300 K) наиболее вероятная скорость теплового движения нейтронов равна 2,2-105 см/с, а соответствующая ей энергия теплового движения kT≈ 0,025 эВ, что иллюстрируется рис. 2.16.
Последующие соударения тепловых нейтронов с ядрами вещества не приводят к дальнейшему замедлению нейтронов, так как они с равной вероятностью могут как потерять, так и приобрести энергию порядка kT (все ядра атомов вещества имеют энергию такого порядка). Поэтому при последующих соударениях тепловые нейтроны только перемещаются (диффундируют) в веществе с сохранением в среднем энергии теплового движения до тех пор, пока не поглотятся каким-либо ядром или не вылетят за пределы замедлителя.
122
−E
EekT
E-3/2
Рис. 2.16 . Спектр замедленных нейтронов
В результате в замедлителе будет происходить накопление тепловых нейтронов. Спектр нейтронов в замедлителе должен быть близок к максвелловской кривой с приподнятым «правым крылом» из-за непрерывно поступающих в замедлитель быстрых нейтронов. Расчет показывает, что спад числа нейтронов при больших энергиях должен происходить по закону Т-3/2 . Эти нейтроны, энергия которых превышает энергию нейтронов максвелловского спектра, называются надтепловыми.
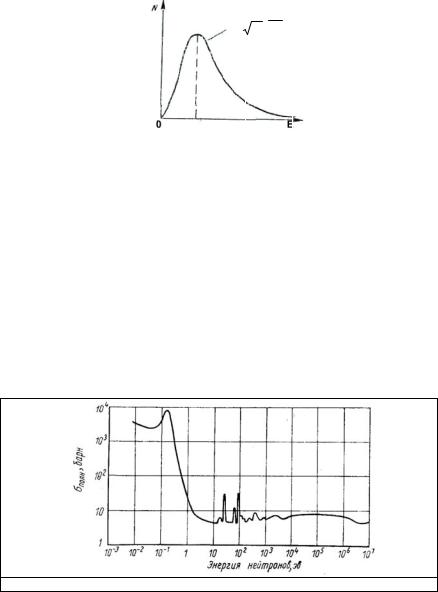
Сечение поглощения нейтронов кадмием имеет резонансный уровень при En=0,176 эВ. Совместное действие закона 1/v и резонансного поглощения приводит к тому, что кадмий весьма эффективно поглощает нейтроны с энергией меньше 0,4 эВ (рис 2.17). Лист кадмия толщиной 1 мм пропускает примерно 1/1000 долю падающих на него тепловых нейтронов. Поэтому кадмий является очень хорошим поглотителем тепловых нейтронов.
Рис. 2.17. Зависимость сечения поглощения нейтронов кадмием от их энергии
123

2.3.2.Элементы теории замедления
Впроцессе замедления нейтрон двигается по сложной траектории, перемещаясь от одного ядра замедлителя к другому. Средний путь, проходимый нейтроном между двумя последовательными соударениями,
называется средней длиной свободного пробега λs. Очевидно, что:
где п – концентрация ядер в среде; σs – эффективное сечение рассеяния. Из формулы (2.21) следует, что величина λs различна для разных сред и является функцией энергии нейтронов для данной среды. Величина λs (как и ξ) является одной из важнейших характеристик замедлителя, так как чем меньше λs , тем быстрее происходит замедление. Коэффициент
ξ/λs называется замедляющей способностью замедлителя.
При каждом акте рассеяния нейтрон отклоняется от первоначального направления, так что его путь в замедлителе – зигзагообразный. Весь путь, пройденный нейтроном за время замедления от первоначальной энергии Eо до заданной энергии E, равен
−
n
= ∑λs (Ei ) ,
1
−
где n – среднее число соударений, необходимых для замедления нейтронов от энергии E0 до энергии E определяется по соотношению (2.20).
Если пренебречь зависимостью λs от энергии, то грубо ориентировоч-
|
− − |
− |
|
ное значение можно получить: = nλs |
, где λs – длина свободного |
пробега, усредненная по энергетическому интервалу, в котором рассматривается замедление.
θ
λs θ
r=∆ r<<∆
Риса. 2.18. Траектории движения нейтронаб
Для решения некоторых задач (например, для расчета защиты) очень важно знать, на какое расстояние r смещаются нейтроны в процессе замедления от первоначальной точки. Ясно, что величина не может служить мерой этого смещения, так как из-за статистического
124

характера процесса замедления нейтрон в одном случае сместится почти на (рис. 2.18, а), в другом случае процесс замедления закончится в окрестности первоначальной точки (см. рис. 2.18, 6).
Можно показать, что средний квадрат перемещения приблизительно равен
r 2 = 2n(λs )2
(1− 2 / 3A)
Tраектории движения нейтронов в водородном замедлителе больше вытянуты вперед, чем в тяжелом. Количественно это отличие может быть охарактеризовано средним значением косинуса угла рассея-
нияcosθ , которое равно нулю для изотропного рассеяния и растет с ростом анизотропии.
Можно показать, что для замедлителя, состоящего из ядер с массовым числом А, cosθ = 2/3A . Эта величина и входит в знаменатель предыду-
щей формулы. Величину λt = λs (1−cosθ) часто называют транс-
портной длиной, или длиной переноса.
Вчастном случае водородного замедлителя λt=3λs .
2.3.3.Макроскопическое сечение взаимодействия нейтронов с веществом для многокомпонентных сред
Вслучае взаимодействия нейтрона с ядром суммарная вероятность взаимодействия определяется суммой парциальных макроскопических сечений всех процессов рассеяния и поглощения, а для делящихся ядер –
исечения деления. Σ – макроскопическое сечение –вычисляется по формуле Σ=п·σ , где п=NАρ/A, где NА –число Авогадро, ρ –плотность .
Вслучае, когда зависимостью сечения от энергии можно пренебречь, для количества нейтронов, прошедших слой вещества x, можно воспользоваться соотношением N=N0exp(-Σx).
Вотличие от фотонов энергетическую зависимость нейтронных сечений (рис.2.19) из-за их сложного характера не удается аппроксимировать какими-либо простыми формулами. Многочисленные данные по сечениям взаимодействия нейтронов с различными ядрами в форме таблиц и графиков приводятся в ряде справочников или отчетов МАГАТЭ, в базах данных, приводимых в Internet, периодически переиздаваемом по мере появления новых экспериментальных данных. Из-за обилия таких дан-
125
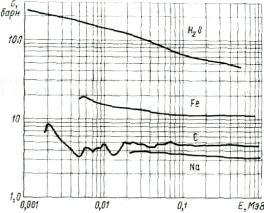
Рис. 2.19. Энергетические зависимости полных сечений взаимодействия нейтронов со средой
ных, получаемых различными авторами, и зачастую из-за их несогласованности и противоречивости получили распространение библиотеки так называемых «оцененных данных», рекомендованных для пользователя. Для удобства использования и обработки эти библиотеки приходится хранить в памяти ЭВМ.
Для тепловых нейтронов, как правило, σ имеет постоянное значение для элементов, слабо поглощающих нейтроны (кислород, углерод, кремний и т. п.), или монотонно возрастает по мере уменьшения энергии для элементов, заметно поглощающих нейтроны (литий, бор и т. п.).
Если рассматриваемое вещество состоит из нескольких типов ядер, то макроскопическое сечение
|
определяется по формуле: |
|||||||
|
Σ=n1σ1+ n2σ2 +.. + niσi+… , |
|||||||
|
где ni – число ядер i-го сорта в 1см3 вещества, σi |
– микроскопическое се- |
||||||
|
чение данного процесса для этих ядер. Для молекулы: |
|||||||
|
Σ = |
ρN Ав |
(ν σ |
+ν σ |
+…+ν |
σ |
i1 |
+…) , |
|
M |
1 1 |
1 1 |
i |
||||
где νi – число атомов сорта i в одной молекуле.
2.4. Основы радиационной физики
При прохождении ядерных излучений через вещество практический интерес представляет не только изменение параметров самого излучения, связанное с его взаимодействием в веществе, но и те изменения, которые происходят в веществе под действием прошедшего через него излучения. Эти изменения касаются как структуры вещества, так и его электронного состояния. Электронное состояние изменяется оттого, что при прохождении заряженных частиц через вещество происходит ионизация его атомов и молекул. Освободившийся электрон может быть захвачен на
126
примесный уровень запрещенной зоны и дальнейшая его судьба определяется скоростью рекомбинации его с ионами, также образовавшимися в результате акта ионизации. Если рекомбинация подавлена, то в материале может возникнуть пространственный заряд. Образование пространственного заряда приводит к изменению физико-механических свойств материала. Из сказанного ясно, что образование пространственного заряда
– свойство электроизоляционных материалов, поскольку в металлах и даже в полупроводниках рекомбинация протекает быстро. Однако в полупроводниках также возможно изменение проводимости под действием облучения, например, возможно их радиационное легирование. Общим свойством всех материалов, испытавших воздействие излучения, является образование в них структурных дефектов, происхождение которых связано с актами упругого рассеяния частиц в материале.
В равновесном состоянии твердое тело практически не содержит дефектов, если оно при этом представляет собой совершенный монокристалл. В поликристаллических материалах дефекты существуют и без воздействия излучения; происхождение их связано с термообработкой, многофазностью, существованием границ зерен и т.п. Дефекты структуры бывают нескольких видов, простейшие из которых – вакансия и межузельный атом внедрения. Оценим энергию, необходимую для образования вакансии. Будем считать, что энергия, которую необходимо затратить для удаления одного атома в 3-4 раза больше энергии диссоциации. В металлах эта величина около 25-30 эВ, в диэлектриках – около 15 эВ. Если энергия, переданная в упругом соударении атому, превышает эту величину, то в материале образуется вакансия.
Пороговую энергию частицы с массой А, необходимую для образования вакансии, можно вычислить следующим образом. Из импульсной диаграммы (импульсная диаграмма ядерных реакций, см.рис. 1.14) следует, что максимальный импульс, переданный атому вещества, равен 2A‘ p /(A‘+A) , где A’ – массовое число атомов среды, р– импульс нале-
тающей частицы. Далее, используя соотношение E = p2 / 2m , можно
оценить пороговую энергию образования дефекта. Для электронов оценка минимальной энергии, необходимой для смещения атома из положения равновесия получается из таких же соображений, но надо иметь в виду, что электроны – релятивистские частицы, поэтому вместо формулы, приведенной выше, связь между кинетической энергией и импульсом
127

частицы задается соотношением: p2c2 = Ek (Ek + 2mc2 ) . Численные
оценки дают пороговую энергию электронов, равную ~100 кэВ, тогда как для более тяжелых частиц эта энергия получается меньше.
Смещенные атомы, в свою очередь, способны вызывать смещения, если их кинетическая энергия больше минимальной энергии, необходимой для образования смещенного атома. Спектр энергий смещенных атомов зависит от того, каким образом происходит взаимодействие налетающей частицы и атома решетки. Среднюю энергию можно найти по формуле
|
Emax |
||||||
|
∫ Eσ(E0 , E)dE |
||||||
|
= |
Emin |
, |
||||
|
E |
||||||
|
E |
||||||
|
max |
||||||
|
∫ |
σ(E0 , E) |
Emin
где E0 , E – энергии налетающей частицы и смещенного атома, σ(E0 , E) −сечение рассеяния частицы с энергией E0 и энергией сме-
щенного атома E ;. Еmin, Emax – минимальное и, соответственно, максимальное значение энергии, передаваемой смещенному атому.
Например, если налетающая частица – протон, то взаимодействие ее с атомом решетки при больших энергиях протона сводится к кулоновскому взаимодействию, а сечение взаимодействия подчиняется закону Резерфорда.
Если падающая частица – быстрый нейтрон, то взаимодействие нейтрона с ядром атома решетки в основных чертах есть взаимодействие упругих шаров, следовательно, сечение рассеяния есть сечение процесса
упругого рассеяния нейтронов. Зная среднюю энергию, E образующегося атома смещения, можно оценить, сколько смещенных атомов этот
атом может произвести. Это число равно E / 2Ed , где Ed – энергия об-
разования дефекта.
Точно так же количество смещенных данной частицей атомов, N, можно оценить по формуле: N = E / 2Ed min , где Ed min − минимальная
кинетическая энергия частицы, которая требуется для образования смещения.
Образовавшиеся дефекты (смещенные атомы и вакансии) мигрируют
128
по кристаллу. Скорость миграции определяется, прежде всего, температурой, причем возможна миграция дефектов непосредственно в процессе облучения образца. Мигрируя, межузельные атомы и вакансии могут:
•рекомбинировать;
•захватывать примесь;
•стекать к границам однородной области, например, к границе кристаллита или межфазной границе;
•мигрировать далее, рекомбинируя уже в другой однородной облас-
ти.
Естественный результат всех этих процессов – полное восстановление физико-механических свойств материала, то есть отжиг его структурных дефектов. Следует ожидать, что отжиг проходит в несколько стадий. На самой начальной стадии (Т~10K) происходит рекомбинация «своих», то есть соседних вакансий и межузельных атомов. На следующей стадии уничтожаются ассоциации примесь – вакансия, поэтому она существует не во всех материалах. Характерная температура протекания этой стадии отжига 80-100 К. После протекания этой стадии отжига резко возрастает вероятность рекомбинации «чужих», то есть отдаленных первоначально друг от друга вакансий и межузельных атомов. Поскольку при этом происходит частичное восстановление свойств материала, то также происходит отжиг дефектов. Характерная температура этой стадии – ~100К – 300К. Дальнейшая миграция дефектов приводит к их стоку на границы зерен или фаз и образованию кластеров, то есть скоплений дефектов по границам однородных фаз. Отжиг этих дефектов происходит при их стоке с границ, что возможно при температурах 500 – 700К.
Образование радиационных дефектов при облучении вещества различными ядерными излучениями
Электроны и фотоны
Образование дефектов электронами и фотонами подобно друг другу, поскольку при облучении образца фотонами сначала за счет одного из трех основных процессов взаимодействия фотонов с веществом образуются электроны, которые и производят смещения атомов. Поскольку, как правило, в задачах прикладной ядерной физики энергия электронов не превосходит несколько МэВ, число производимых электроном смещений невелико, да и энергия смещенных атомов мала. Это означает, что при
129
облучении электронами, как правило, образуется малое число дефектов, которые должны отжигаться при температуре не выше 300 К. Эффектами, связанными с образованием кластеров, можно, как правило, пренебречь.
Медленные нейтроны
Медленные нейтроны сами по себе создать в образце дефекты не могут, поскольку их кинетическая энергия меньше энергии, необходимой для образования дефекта. Однако медленные нейтроны участвуют в ядерных реакциях, поэтому дефекты в образце создаются за счет продуктов ядерных реакций, наиболее распространенной из которых является радиационный захват с последующим испусканием фотона, являющегося генератором дефектов по рассмотренному выше механизму. Если в результате ядерной реакции образуются тяжелые частицы, то число смещенных атомов возрастает.
Быстрые нейтроны
Быстрые нейтроны взаимодействуют с ядрами атомов вещества в основном по закону упругих соударений. По этой причине максимальная переданная ядру атома в соударении энергия достаточно велика и, например, для водорода она в среднем составила бы половину энергии нейтрона. Следовательно, быстрые нейтроны создают наибольшее количество дефектов в веществе. Отжиг этих дефектов возможен только при температуре не менее 500 К.
Протоны и другие тяжелые заряженные частицы
Особенность взаимодействия заряженных частиц достаточно высокой энергии заключается в том, что рассеяние их подчиняется закону Резерфорда. Это означает, что преобладает рассеяние на малые углы и, значит, энергия в соударениях передается небольшими порциями. По данной причине среднее число смещенных атомов, образованных заряженными частицами, всегда меньше, чем число смещенных атомов, образованных быстрыми нейтронами. Преобладающий тип дефекта в этом случае – кластер небольшого размера. Отжиг этих дефектов происходит при температуре около 500 К.
130
Вопросы к разделу 2
1.Каковы основные процессы взаимодействия заряженных частиц с веществом?
2.Для каких частиц, электронов или протонов, радиационное торможение играет большую роль?
3.Как объяснить вид зависимости числа тяжелых заряженных частиц и электронов от толщины проходимого ими материала?
4.Какой энергетический спектр имеет тормозное излучение?
5.Какова роль многократного рассеяния для тяжелых заряженных частиц и электронов?
6.Что является источником излучения при прохождении быстрой заряженной частицы через среду при показателе преломления среды большем единицы?
7.Может ли черенковское излучение быть рентгеновским?
8.Может ли переходное излучение лежать в рентгеновском диапазоне и, если может, то при каких условиях?
9.Можно ли создать узкий пучок электромагнитного излучения в среде? Какова его природа?
10.Какие основные процессы при взаимодействии фотонов с веществом вы знаете?
11.Испускаются ли какие-либо излучения при фотоэффекте?
12.Может ли при фотоэффекте испуститься электрон в направлении по импульсу фотона? Какова природа такого электрона и его энергия?
13.Какой энергетический спектр имеет рассеянное излучение при комптон-эффекте?
14.Может ли энергия электрона при комптон-эффекте равняться энергии фотоэлектрона при заданной энергии падающего фотона?
15.Каков предельный угол вылета комптоновского электрона?
16.При каких условиях эффект образования пар наблюдается в поле ядра? В поле электрона?
17.Чему равна предельно допустимая энергия электрона пары в веществе при заданной энергии падающего фотона?
18.Может ли процесс образования пар сопровождаться электромагнитным излучением? Какова его природа?
19.Каковы основные процессы взаимодействия нейтронов с вещест-
вом?
20.Что такое макроскопическое сечение взаимодействия?
131
21.Чему равна средняя энергия нейтрона в водороде после одного акта замедления?
22.На какой стадии замедление нейтронов в воде и в водороде происходит неодинаково?
23.Почему спектр замедленных нейтронов даже в отсутствие их поглощения отличен от максвелловского?
24.Как изменится спектр замедленных нейтронов при наличии их поглощения средой?
25.От каких факторов зависит число радиационных дефектовсме- щений в материале?
132
3. МЕТОДЫ РЕГИСТРАЦИИ ЯДЕРНЫХ ИЗЛУЧЕНИЙ
Принятые обозначения в разделе 3
I – энергия ионизации атома или молекулы;
Wвозб. – энергия возбуждения молекулы; ν – линейная частота колебаний;
N – число пар ионов;
d – диаметр; толщина рабочего слоя детектирования; энергетическое разрешение; λ – средняя длина свободного пробега; длина волны;
w – скорость дрейфа частиц;
ε – напряжённость электрического поля; E – кинетическая энергия частиц;
p– давление газа; вероятность взаимодействия;
μ– подвижность частиц;
R – пробег частиц; сопротивление цепи; J – ток в цепи;
U – разность потенциалов между электродами; амплитуда импульса; q – заряд частиц;
V – импульс напряжения;
D – коэффициент диффузии частиц; C – ёмкость в цепи;
m – коэффициент газового усиления за счёт вторичной ионизации; число световых фотонов, испущенных сцинтиллятором;
M – полный коэффициент газового усиления; коэффициент усиления ФЭУ; γ – вероятность фотоэффекта и вторичной эмиссии;
N – число частиц;
n – плотность частиц; скорость счёта импульсов; ρ – удельное сопротивление;
V – объём детектора;
t – время протекания процесса;
T± – время собирания положительного или отрицательного заряда; Wp – энергия образования пары носителей;
133
me – масса электрона;
Fп – доля энергии, потерянной частицей в сцинтилляторе; Cnp – коэффициент световой конверсии;
Tp – прозрачность сцинтиллятора;
Sm – максимальная спектральная чувствительность детектора;
α– коэффициент рекомбинации ионов и электронов;
–наклон плато счётной характеристики газоразрядного детектора; η – эффективность регистрации излучения детектором; ε – полная эффективность детектора; Ω – относительный телесный угол; ω – телесный угол;
Sдет – площадь детектора;
τ – время высвечивания сцинтиллятора.
1/ 2 – ширина линии энергетического спектра, соответствующая значениям энергии, равным половине максимально вероятного
134
3.1. Физические основы методов регистрации ядерных излучений
Основным условием, позволяющим использовать ядерные излучения для решения различных научных и практических задач, является возможность их регистрации (обнаружения), измерения их потока и энергии
иидентификации.
Внастоящее время существует большое число методов детектирования излучений, причём универсального метода, одинаково пригодного для всех случаев практики, нет. Это объясняется большим разнообразием задач, с которыми приходится иметь дело при использовании ядерных излучений.
Так, например, в зависимости от конкретных условий бывает необходимо измерять либо дозу излучения, либо суммарную (интегральную) плотность потока какого-либо участка спектра излучения, либо производить спектральные измерения, то есть измерять величину плотности вероятности распределения энергии по различным участкам спектра.
Для регистрации излучения оно должно проявить себя каким-либо образом, то есть вступить во взаимодействие с веществом детектора. Обнаружение отдельных видов излучения (альфа-, бета-, гамма-, нейтронов
ит.д.) имеет свои специфические особенности, обусловленные свойствами данного вида излучений.
Можно сказать, что действие всех детекторов излучения основано на первичных или вторичных эффектах, возникающих при взаимодействии излучения с веществом, причём, в конечном счёте, эти эффекты сводятся
кионизирующему действию излучения в газах, твёрдых веществах или жидкостях. Если заряженные частицы непосредственно производят эти эффекты (ионизация, возбуждение), то для нейтральных частиц (фотоны, нейтроны) необходимо предварительное взаимодействие их с веществом детектора или радиатора (т.е. с веществом, расположенным в непосредственной близости от детектора), в результате которого образуются за-
ряженные частицы (e–, e+, p, d, α, осколки деления).
3.2. Газовые ионизационные детекторы
Если рабочей средой в детекторах является газ, то такие детекторы называются детекторами с газовым наполнением.
135
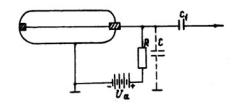
Рис. 3.1. Типичная схема включения газовых ионизационных детекторов
Действие их основано на ионизации газа под влиянием излучений радионуклидов.
К этой наиболее распространённой группе относятся: ионизационные камеры, пропорциональ-ные газовые детекторы, счётчики Гейгера – Мюллера, коронные счетчики.
Отличие между этими детекторами заключается как в видоизменениях конструк-
ций, так и в различных режимах их работы. Все газовые ионизационные детекторы представляют собой конденсаторы, в которых пространство между электродами заполнено каким-либо «рабочим» газом (рис.3.1). Ионизационные методы регистрации основаны на измерении заряда или тока, создаваемого заряженными частицами при прохождении их в газовой полости конденсатора. Незаряженные частицы (фотон, нейтрон) непосредственно ионизационный эффект не создают. Однако в результате акта их взаимодействия с веществом возникают вторичные заряженные частицы, которые также создают в газе ионизационный эффект.
В результате ионизации при прохождении заряженных частиц в газах образуются электроны и ионы. Если ионизация происходит в объёме между двумя электродами прибора (представляющего собой конденсатор), имеющими разный потенциал, то в результате движения электронов и ионов к электродам в цепи возникает ток. В зависимости от значения напряжённости электрического поля в газовом промежутке эти детекторы обладают разными свойствами. Типичная зависимость числа собираемых носителей заряда N, (тока в цепи или амплитуды импульса) от напряжения между электродами, снятая при неизменной плотности потока излучения, показана на рис.3.2. Она имеет шесть характерных участков. Данная зависимость получила название вольт-амперная характеристика газонаполненных ионизационных детекторов.
136

N
Рис. 3.2. Вольт-амперная характеристика газонаполненных детекторов при двух различных величинах ионизационного эффекта:
1 – область диффузии и рекомбинации; 2 – область работы ионизационных камер; 3 – область работы пропорциональных детекторов; 4 – область ограниченной пропорциональности; 5 – область работы детекторов с самостоятельным разрядом; 6 – область непрерывного разряда
3.2.1. Ионизация газов. Движение электронов и ионов в газах
Процесс ионизации заключается в удалении из молекул или атомов газа одного или нескольких электронов. Для их удаления необходима энергия (отбираемая у ионизирующего излучения). Величина этой энергии зависит от энергии ионизации атома I. Напомним, что энергией ионизации называется наименьшее количество энергии, необходимое для отрыва электрона от свободного, невозбуждённого нейтрального атома.
Вместо ионизации может иметь место возбуждение атома, когда энергия, переданная атому, недостаточна для отрыва электрона:E< I. Возбу-
137
ждение снимается испусканием фотонов Wвозб. = hν через t 10-8 с (время жизни атома в возбуждённом состоянии).
Некоторые газы (He, Ar, Ne) имеют метастабильные уровни возбуждения с временем жизни t 10-3 – 10-4 с. Переход электрона с метастабильных уровней на основной уровень запрещён правилами отбора. В качестве примера в табл. 3.1 приведены некоторые характеристики двух газов.
Средняя энергия образования одной пары носителей заряда Wp существенно больше I газа, так как часть энергии расходуется на диссоциацию молекул и их возбуждение; кроме того, образовавшиеся электроны и ионы приобретают определённую кинетическую энергию.
|
Таблица 3.1 |
||||||
|
Некоторые характеристики газов Ar и He |
||||||
|
Газ |
I, эВ |
Wвозб.,эВ |
Wметаст.уров., эВ |
Длина волны |
||
|
фот. изл., нм |
||||||
|
Ar |
15,7 |
11,6 |
11,5 |
104,8 |
||
|
He |
24,5 |
20,6 |
19,7 |
85,4 |
Величина Wp слабо зависит от вида и энергии частицы и от состава газа. Wp можно определить по энергии Е, потерянной частицей при её пролёте через газ, и по числу пар ионов n, образовавшихся в результате ионизации Wp = E/n.
Вприкладной ядерной физике обычно поступают наоборот, зная Wp, определяют энергию частицы, измеряя величину заряда, созданного ею в газе.
Вгазоразрядных детекторах излучений различают несколько способов ионизации газа: первичная ионизация – ионизация, возникающая под действием излучения (наличие электрического поля между электродами на первичную ионизацию не влияет); вторичная ионизация, возникающая или под действием первичных электронов, приобретающих в электрическом поле кинетическую энергию, достаточную для ионизации (ударная ионизация), или в результате фотоэффекта от фотонов, возникающих при снятии возбуждения с атомов или молекул газа.
При прохождении заряженных частиц в газе создаются свободные электроны и положительные ионы, в результате взаимодействия нейтральных атомов или молекул и электронов могут также образовываться отрицательные ионы. Поведение образовавшихся носителей заряда зави-
138
сит от условий в камере – величины электрического поля и типа наполняющего газа.
При отсутствии электрического поля свободные электроны движутся хаотически и испытывают соударения с молекулами газа. Средний пробег электрона в газе между двумя соударениями обратно пропорционален числу молекул в единице объёма:
|
λe |
= |
5 , 6 4 |
; |
λe ≈ |
1 |
, |
|
|
n 0 π d 2 |
n 0 d 2 |
||||||
|
2 |
где n0 [1/см3] – число атомов или молекул в 1 см3; d – «эффективный» диаметр атомов в см.
Для большинства используемых в детекторах газов средний пробег электрона при нормальных условиях находится в пределах 10-5 – 10-4 см.
При наложении электрического поля возникает дрейф электронов против поля.
Средняя скорость дрейфа we = μe εp ; [см/с]
μе – подвижность электронов [см2·гПа/(В·с)]; ε – напряжённость электрического поля [В/см]; p – давление газа [гПа].
Величина μе различна для разных газов и слабо зависит от отношения
ε/p: для малых ε/p (≤ 1 В/(см·гПа) μе ≈ 106 см2·гПа/(В·с); для больших ε/p
(≥10 В/(см·гПа) μе → 107 см2·гПа/(В·с).
Скорость дрейфа we определяет быстродействие газоразрядных детекторов.
Оценим we в плоскопараллельной ионизационной камере, наполнен-
ной Ar при p = 1040 гПа, U = 2 кВ, d = 4 см, μe = 106 см2·гПа/(В·с): we = μе•ε/p = 106•(2000/4)/1040 0,5•106 см/с.
В некоторых газах свободные электроны могут, как указывалось выше, после соударений с нейтральными атомами или молекулами захватываться, «прилипать» к ним, образуя отрицательные ионы. Скорость образования отрицательных ионов можно характеризовать вероятностью прилипания (или коэффициентом прилипания) h электрона к молекуле, с которой он сталкивается. Коэффициент прилипания h сильно зависит от скорости движения электрона (т.е. от его энергии и ε), а также от рода газа.
139
Движение положительных и отрицательных ионов в газе аналогично движению электронов, лишь μ+ и μ– значительно меньше μе , так, скорость дрейфа:
|
w+ = μ+· |
ε |
; μ+ = 1380 см2·гПа/(В·с); μ– = 1710 см2·гПа/(В·с) (для Ar). |
|
p |
Положительные и отрицательные ионы (или электроны) могут при встрече рекомбинировать, образуя нейтральные атомы или молекулы (нежелательный факт). Число актов рекомбинации, происходящих в единице объёма за единицу времени (скорость рекомбинации), равно:
dn+/dt = dn–/dt = –αn+n–;
где α – коэффициент рекомбинации, n+ – плотность положительных зарядов, n– – плотность отрицательных зарядов.
Коэффициент рекомбинации зависит от вида газа и средней энергии ионов и электронов. При рекомбинации ионов α≈10-6 см3/с, а при рекомбинации электронов и ионов α≈10-10 см3/с.
Пусть в момент t = 0 образованы заряды с одинаковой плотностью n0 = n+ = n––, если заряды исчезают только в результате рекомбинации, то:
n+(t) = n– (t) = n0(t) = n0/(1 + αn0t). (3.1)
При работе на участке насыщения (участок 2 на рис.3.2) изменение рабочего напряжения почти не сказывается на величине сигнала. Однако во многих случаях (регистрация альфа-частиц или регистрация в камерах с большим давлением) напряжение, соответствующее этому участку, столь велико, что приходится использовать участок 1 вольт-амперной характеристики, несмотря на связанные с этим неудобства.
Процесс рекомбинации идет тем эффективнее, чем больше концентрация ионов. Поэтому при возрастании плотности потока излучения (и увеличении концентрации ионов) насыщение будет достигаться при больших значениях напряжения.
Альфа-частицы на своём пути образуют «колонны ионов» с очень высокой плотностью ионов. При этом имеет место колонная рекомбинация ионов, которая происходит даже при очень высоких напряжениях (так, при атмосферном давлении плотность ионов в колонне 3·104 пар/см, рекомбинация в этом случае происходит даже при напряжённостях, равных 2000 – 3000 В/см). Поэтому при работе с альфа-излучением насыщение практически достигается лишь при пониженных давлениях в камере.
При очень малых давлениях камера работает в режиме насыщения, однако при этом пробег альфа-частиц большой и обычно превышает
140
размеры камеры. Поэтому лишь часть энергии частиц расходуется на ионизацию газа. При увеличении давления ток растёт сначала линейно, а затем скорость роста уменьшается, так как начинает сказываться рекомбинация ионов в колоннах. Если и дальше увеличивать давление, то рост тока прекращается и затем ток даже уменьшается из-за интенсивной рекомбинации.
Поток бета-частиц обычно равномерно ионизирует газ во всём объёме камеры. В этом случае имеет место объёмная рекомбинация ионов, которая значительно слабее сказывается из-за относительно малой средней концентрации ионов в объёме камеры. Поэтому при атмосферном давлении режим насыщения может быть достигнут даже при весьма большой плотности потока бета-излучения.
Соотношение (3.1) позволяет оценить допустимую плотность ионизации без значительных потерь на рекомбинацию, если задано время сбора зарядов. Если t ≈10-3 с и потери не должны превышать 10 %, то αn0 ≤ 102, то есть допустимая концентрация положительных ионов и электронов должна быть ≤1012 см-3, так как α ≈10-10 см3/с.
Такая средняя плотность ионов и электронов при атмосферном давлении в воздухе возникает при плотности потока электронов 1010 1/см2с и энергии Еe 1 МэВ.
Электроны и ионы, как и молекулы любого газа, движутся в среднем всегда в направлении меньшей концентрации частиц данного вида. Это среднее движение обычно характеризуют коэффициентом диффузии D – постоянным для данного вида частиц в заданных условиях. Изменение
|
числа |
частиц |
в |
единице |
объёма |
в |
единицу |
времени |
|
∂n/∂t = |
D n, где |
знак |
означает лапласиан. |
Можно считать, что |
D = λv/3, где λ – длина свободного пробега, v – скорость. Коэффициент D различен для ионов и электронов.
3.2.2. Регистрация ядерных излучений ионизационными камерами
Ионизационными камерами называются конденсаторы любой формы, применяемые для измерения ионизационных токов.
Ионизационная камера представляет собой ионизационный детектор излучения, в котором не используется эффект газового усиления (детекторы работают только в области 1 и 2 «вольт-амперной» характеристики (см. рис.3.2)). Поэтому для величины тока, текущего в цепи ионизационной камеры, справедливо неравенство: J≤N0e, где N0 – число пар ионов,
141
образуемых в рабочем пространстве камеры в единицу времени, e – заряд электрона; N0 пропорционально плотности потока излучения. При работе камеры в режиме насыщения имеет место равенство J=Jнас= N0e. Следовательно, по току насыщения можно определить число пар ионов, прямо пропорциональное интенсивности излучения. В общем случае:
Jнас = e ∫ N0 (x, y, z)dxdydz ,
Va
где Va – чувствительный объём камеры, N0 – число пар ионов, возникающих в единице объема камеры за единицу времени в точке с координатами (x,y,z). По Jнас в рассматриваемом общем случае также можно определить интенсивность источника излучения.
В зависимости от способа измерения существуют два типа ионизационных камер: токовые (или интегральные) и импульсные.
Интегральными ионизационными камерами называются камеры,
работающие в режиме измерения среднего тока (они выдают непрерывную, аналоговую информацию о средней величине тока).
Импульсные ионизационные камеры предназначены для регистра-
ции отдельных частиц, которые создают в ней импульсы напряжения. Интегральные ионизационные камеры измеряют величину заряда,
создаваемого излучением в газе q = N0e, где N0 – число пар электронов и положительных ионов. Существует нижний порог чувствительности ионизационной камеры. Этот порог определяется способом измерения заряда, или, чаще, способом измерения тока. Практически, нижний порог
равен: N0 min 100 пар/с; это соответствует току J 10–17 A. Минимальный ток, который можно измерить камерой, ограничен ес-
тественной радиоактивностью материалов и космическим излучением. Космические излучения и почва создают в 1 см3 объёма камеры ионизацию, приводящую к току 10–18 А. Многие материалы испускают и некоторое количество α-частиц. Так, 100 см2 стали испускают 3 α-частицы в час; 100 см2 припоя – 300 α/час. Одна α-частица в час создаёт ток 10–17 А. Имеются также токи утечки через изоляторы.
Ионизационные токи в камерах, используемых в практике применения радионуклидов и ядерных излучений, имеют очень малую величину ( 10-9 – 10-13 А). Поэтому измерение этих токов производится косвенно, по падению напряжения Uвых на нагрузочном сопротивлении R, включаемом последовательно в цепь ионизационной камеры. Величина R
142

обычно велика и составляет 109 ÷ 1010 Ом. Поэтому к изоляции коллекторного электрода предъявляются очень жёсткие требования (их сопротивление должно быть на 2 – 3 порядка больше R).
Токи утечки можно уменьшить, используя дополнительные электроды, позволяющие создавать небольшую, близкую к нулю, разность потенциалов между этим электродом и собирающим электродом. В таком случае дополнительный электрод называют охранным (охранным кольцом) (рис.3.3). Роль охранного электрода видна на диаграмме эквивалентных схем камеры с охранным электродом и без него (рис.3.4).
|
Рис.3.3. Устройство плоской ио- |
Рис.3.4. Схема цилиндрической камеры без ох- |
|
низационной камеры:1 — элек- |
ранного кольца (а) и с ним (б). Показаны экви- |
|
троды; 2 — изоляторы; 3 — до- |
валентные схемы включения камер: |
|
полнительный электрод; 4 — кор- |
Rи—R1+R2 — сопротивление изоляторов каме- |
|
пус камеры |
ры; R — нагрузочное сопротивление |
Применение охранных электродов позволяет уменьшить токи утечки до 10-16 А, т. е. сделать их меньше тока, обусловленного космическим излучением в камерах с объемом 100 см3. Дополнительные электроды помогают и выровнять поле в камерах. При измерениях токов, вызванных ионизирующим излучением, необходимо точно определить рабочий объем камеры и быть уверенным, что в нем поле достаточно для получения токов насыщения. Дополнительный электрод камеры, изображенной на рис.3.3, четко ограничивает область, с которой производится сбор электронов и ионов (заштрихованная область камеры). При такой конструкции поле на границах рабочего объема камеры практически не искажается.
Ионизационные камеры могут быть самых различных конфигураций: плоские, сферические, цилиндрические и объёмом от долей 1 см3 при
143
измерении тепловыделения в экранах реакторов до десятков и сотен литров при исследовании распределения рассеянного излучения в воздухе.
Если интенсивность излучения меняется, то ток в камере и, следовательно, потенциал на R тоже изменятся. Но изменения будут происходить с запозданием, время которого определяется τ = RC, где C – суммарная ёмкость камеры и измерительного прибора. R = 1012 Ом; C = 10-11 Ф. Следовательно, RC 10 с, т.е. заметить изменения интенсивности ионизирующего излучения с частотой более 0,1 Гц интегральными ионизационными камерами невозможно.
Уменьшение погрешностей измерения интенсивности излучения может быть достигнуто при использовании дифференциальной камеры. Это фактически две камеры, имеющие общий коллекторный электрод. Обе камеры работают в режиме насыщения. Высоковольтные электроды камер находятся под напряжением противоположного знака относительно коллекторного электрода.
На одну из камер падает поток измеряемого излучения nизм, на другую
– излучение от эталонного источника nэт. При равенстве ионизационных токов, создаваемых обоими излучениями, суммарный ток, текущий через нагрузочное сопротивление R, будет равен нулю. Следовательно, Uвых также равно нулю. При изменениях nизм появится выходной сигнал. В такой дифференциальной камере влияние температуры, давления и других факторов может быть незначительным. Особенно удобно использовать дифференциальную камеру в компенсационных схемах, в которых величина nэт устанавливается такой, чтобы выходной сигнал был всё время равен нулю.
Ионизационные камеры обладают наибольшей эффективностью регистрации α– и β-излучения. Эффективность камер к γ-излучению мала. Для её увеличения в камерах, предназначенных для измерения характеристик гамма-излучения, электроды изготовляются из материалов с большим Z (обычно свинец), а также внутри камер делаются перегородки, увеличивающие выход вторичных электронов.
Для регистрации больших потоков нейтронов применяются интегральные многопластинчатые борные ионизационные камеры и камеры деления. Графитовые пластинки – электроды покрывают тонким ( 0,4 мг/см2) слоем бора или делящегося вещества. Для исключения фона в борных камерах часто применяют дифференциальные камеры: одну с покрытием бора, другую – без. В камерах деления большая энергия ос-
144
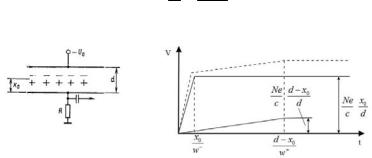
колков и небольшой их пробег позволяют уверенно дискриминировать акты деления от других реакций, в которых образуются заряженные частицы.
Чтобы регистрировать отдельные частицы, нужно чтобы камера работала в импульсном режиме. Назначение импульсных ионизационных камер состоит в регистрации отдельных частиц, определении их числа и энергии. Конструкции импульсных камер те же, что и интегральных ионизационных камер. Главное отличие – в методах регистрации ионизационного тока: требуется специальный импульсный усилитель с большим (до 106) коэффициентом усиления.
Схема включения ионизационной камеры в импульсном режиме работы (рис. 3.5) позволяет измерить заряд или ток, который обусловлен движением ионов в камере, созданных отдельной ионизирующей частицей.
Если RC больше времени движения ионов в камере, то амплитуда импульса напряжения определяется отношением заряда электронов q, образуемых в камере регистрируемой частицей, к сумме емкости камеры и паразитных емкостей C (рис.3.5, правая часть):
V = Cq = NC e ,
где N – число пар ионов.
Рис. 3.5. Включение плоской камеры в импульсном режиме (а) и форма импульса напряжения при RC » d/w+ (б)
Если число пар ионов, созданных в камере ионизирующей частицей, пропорционально ее энергии, то с помощью ионизационной камеры в импульсном режиме можно исследовать их распределение по поглощенной в камере энергии. Форма импульса и его длительность определяются постоянной времени RC и скоростью движения электронов и ионов. Длительность импульса даже при малых значениях RC не может
145

быть меньше времени движения электронов в камере. Во время движения заряженной частицы в ионизационной камере происходит зарядка и разрядка емкости C. Приращение заряда dq на этой емкости за время dt при условии, что потенциал катода равен единице, запишется в виде:
dq=e·εv(t)v(t)·dt,
где εv(t) – составляющая вектора напряженности электрического поля вдоль скорости движения заряда v(t) (в данном случае скорости дрейфа, w(t)).
Уменьшение заряда на емкости C пропорционально величине заряда q(t) и 1/RC, т.е.:
dq=-q(t)٠( 1/RC)·dt.
Таким образом, изменение заряда на емкости С описывается дифференциальным уравнением:
dqdt = −q(t) RC1 + e εv (t) w(t) .
Решение этого уравнения имеет вид:
t
q(t) =e−t / RC ∫e εv (t ‘) w(t ‘) e−t ‘/ RC dt ‘ .
0
Полученный результат справедлив при 0 ≤ t ≤ t*, где t* — время движения зарядов от места образования до собирающего электрода.
Для плоской камеры εv = const и w = const
q (t) = e εv w RC [1 — exp (—t/RC)] и V (t) = e εv w RC [ 1 — exp (— t/RC)]/C.
При t≥t *
V (t) = V* exp (— t’/RC),
где V * = eεv w RC [ 1 – exp (- t* / RC)]/ C ; t’ = t –t* ; t’ > 0.
Такое изменение напряжения, обусловлено движением как положительных, так и отрицательных ионов и суммарное изменение напряже-
ния будет иметь следующий вид:
V(t) = V+(t) + V– (t).
Для постоянной RC, большой по сравнению с временем сбора ионов d/w+, получаем (см. рис.3.5,б):
|
V |
− |
(t) = |
Ne w− |
t; |
V |
+ |
(t) = |
Ne w+ |
t , |
|
C d |
C d |
||||||||
146
причем выражения для V– (t) и V+ (t) справедливы при 0 ≤ t ≤ x0/w– и 0 ≤ t ≤ (d – x0)/w+ соответственно. В итоге, импульс напряжения
Vмакс= V+макс + V–макс =Ne/C и не зависит от места образования ионов в камере.
Ионизационные камеры широко применяются в дозиметрии, для измерения альфа-активности препарата, помещаемого во внутрь камеры, для контроля потоков нейтронов в активной зоне реактора, т.е. мощности реактора. Импульсные ионизационные камеры находят применение в спектрометрии излучений.
3.2.3.Методы регистрации ионизационными детекторами
сгазовым усилением
При достаточно высокой напряженности поля между электродами детектора дрейфующие к аноду электроны между соударениями могут приобрести энергию, достаточную для ионизации молекул газа. Такие условия приводят к росту тока или амплитуды импульсов. Это явление – увеличение числа электронов за счет вторичной ионизации – называют газовым усилением. Увеличение ионизационного эффекта в результате вторичной ионизации характеризуют коэффициентом газового усиления M, который определяют как отношение числа пар ионов, созданных в счетчике в лавинообразном процессе, к числу пар ионов, созданных ионизирующей частицей.
3.2.3.1. Пропорциональные счетчики
Рассмотрим область 3 вольт-амперной характеристики (см. рис.3.2). В этой области амплитуды импульсов возрастают в 10-100 раз за счёт газового усиления, и при этом сохраняется пропорциональность между амплитудами импульсов и начальной ионизацией. Эту область называют
областью работы пропорционального счетчика. При дальнейшем уве-
личении напряжения пропорциональность нарушается, а затем амплитуда импульса оказывается не зависящей от первичной ионизации (области
4 и 5 на рис.3.2.).
Для осуществления вторичной ионизации нужно, чтобы между столкновениями электрон приобрёл энергию, достаточную для ионизации атомов и молекул газа. Оценим необходимую для этого напряжённость электрического поля ε. Кинетическая энергия E, приобретаемая электроном на пути λ при напряжённости электрического поля ε равна E= e ε λ. Для осуществле-
147

ния ионизации эта энергия должна быть больше или равна Iион, где I – энергия ионизации. Таким образом: e ε λ ≥ I. Средний свободный пробег электрона между соударениями в водороде при давлении 100 мм.рт.ст. (133 гПа) составляет порядка 10-3 см. Для ионизации необходима энергия, большая 15 эВ. Таким образом, нужно поле напряжённостью ε > 1,5•104 В/см. Такое поле может быть получено в цилиндрических камерах вблизи тонкого центрального электрода.
|
ε = |
U0 |
(3.2) |
||
|
, |
||||
|
r ln( |
r |
) |
||
|
2 |
||||
|
r |
||||
|
1 |
где U0 – напряжение, приложенное к камере; r2,r1 – радиусы внешнего и внутреннего электродов камеры (катода и анода).
Пусть λион – путь, необходимый для приобретения энергии E = I, следовательно должно быть λион < λ0 – длины свободного пробега.
Для того, чтобы пробег электрона был не меньше λион, необходимо и достаточно, чтобы он не испытал соударений на пути λион.
Оценим, какова вероятность ионизации на единице пути. Если λ0 – длина свободного пробега электрона, то полное число соударений электрона с молекулами газа на пути 1 см, пренебрегая его участием в тепловом движении, можно считать равным 1/λ0.
Вероятность соударений, приводящих к ионизации, равна exp(-λион/λ0). Тогда:
α = 1 exp(− λион ) ,
λ0 λ0
где α – коэффициент ударной ионизации, равный числу пар ионов, образованных электроном на пути 1 см.
Длина свободного пробега электрона обратно пропорциональна давлению λ0 1/p, а λ0ион = Iион/e ε,
|
тогда |
α = ap exp(− bp) |
или |
α |
= a exp( |
b |
) , a и b – постоянные для |
|
p |
ε |
|||||
|
ε |
p |
|||||
данного газа.
Рассмотрим плоскую камеру (см. рис.3.5). Пусть на расстоянии x0 от анода образовалось N0 пар ионов. dN = α N0dr – приращение числа электронов, создаваемых N0 первичными электронами на пути dr. Полное
148
число образовавшихся пар ионов в объёме камеры, если ионизация происходит на расстоянии x0 от анода
N(x0) = N0 eαx0 .
Коэффициент газового усиления m =N(x0)/N0 = eαx0 – мера увеличения ионизационного эффекта. Он может принимать значения от 1 (ионизация возникла возле анода) до eαd, где d – расстояние между электродами.
Коэффициент газового усиления плоской камеры резко зависит от пути, пройденного электронами. Если поле постоянно, то коэффициент газового усиления является функцией места первичной ионизации. Это явление крайне нежелательно, поскольку оно исключает возможность определения энергии частицы по созданной ею ионизации. Но вероятность вторичной ионизации зависит от напряженности поля. Поэтому в полях с резким градиентом можно получить очень узкую область, в которой в основном будет происходить вторичная ионизация. Цилиндрические детекторы с анодом в виде очень тонкой нити с диаметром, много меньшим диаметра катода, имеют резко неоднородное поле [см. (3.1)]. В цилиндрическом детекторе ударная ионизация происходит только вблизи нити – остальная часть детектора работает как ионизационная камера в режиме тока насыщения. В таких детекторах коэффициент газового усиления практически не зависит от места первичной ионизации. Поэтому истинными пропорциональными счётчиками с газовым усилением, практически не зависящим от места попадания частицы, являются детекторы цилиндрической формы.
Кроме процессов ударной ионизации, существенную роль играет фотоэффект на катоде. Возбуждённые при ударной ионизации молекулы испускают фотоны электромагнитного излучения. При их поглощении на катоде возможно образование фотоэлектронов, которые ускоряются и снова образуют фотоэлектроны.
Если начальная лавина состояла из N электронов, то в результате полного газового усиления получим:
Nγ = Nm + γNm2 + γ2Nm3 + … = Nm(1 + γm + γ2m2 + …),
где γ – вероятность фотоионизации (вероятность появления одного фотоэлектрона на один вторичный электрон);
M = Nγ/N = m/(1 – γm)
– полное газовое усиление.
149
Для обычно применяемых катодов γ≈10-5 – 10-4. В пропорциональной области m~102 – 103. Поэтому M ≈ m. Разряд гасится возникающим вокруг анода пространственным зарядом.
Форма импульса
Пусть в цилиндрическом пропорциональном счетчике на расстоянии rо от его центра в результате первичной ионизации создано N пар ионов. В начальный момент времени электроны начинают двигаться к аноду в области, где напряженность ε мала.. Пока в счетчике не наступает газовое усиление, то есть пока электроны дрейфуют в области с низкой напряженностью поля, импульс можно описать соотношениями для цилиндрической ионизационной камеры. Максимальный импульс за счет движения электронов и ионов первичной ионизации будет в M раз меньше результирующего импульса, и, следовательно, им можно пренебречь при достаточно большом газовом усилении. Это время называют временем
дрейфа – tдр 0 – 10-7 с.
Затем электроны попадают в область ударной ионизации и начинается нарастание импульса за время Т– (время сбора электронов), сопоставимое с tдр. Время развития лавины, то есть время, в течение которого происходит вторичная ионизация, мало. Действительно, газовое усиление осуществляется на расстоянии от центрального электрода, равном нескольким диаметрам нити (~0,1 см). Скорость дрейфа электронов в этой области около 105 м/с, то есть время развития лавины Т– 10-7 – 10-8с.
Дальнейшее нарастание импульса напряжения V(t) на аноде счётчика обусловлено перемещением положительных ионов из области удар-
ной ионизации в направлении катода. T+ (время собирания положительных ионов) в 103 – 104 раз большее tдр.
T+=(r22-r2кр)p·ln(r2/r1)/2μ+U0 , где μ+ – подвижность положительных ионов, rкр –расстояние от анода, где поле достаточно для вторичной ионизации. T+ ~100 мкс, но при больших значениях R, когда RC T+, длительность импульса, складывающаяся из времени нарастания и времени спада, составляет несколько сот микросекунд и даже миллисекунд. Восстановление потенциала происходит по закону V = Ve-t/RC.
Форму импульса можно представить следующим соотношением:
|
V (t) = |
MNe |
exp( |
−t + B)[ln(1+ |
t |
) + |
t |
+…] , |
|
|
2C ln(r |
/ r ) |
RC |
||||||
|
RC |
B |
|||||||
|
2 |
1 |
где B=r2крp·ln(r2/r1)/2μ+U0
150

Максимальное снижение потенциала на аноде имеет место в момент
|
нейтрализации положительных ионов на катоде. |
||||
|
Длительность импульса можно |
||||
|
уменьшить благодаря своеобраз- |
||||
|
ной форме импульса (логарифми- |
||||
|
ческая зависимость |
V(t), за время |
|||
|
порядка нескольких |
микросекунд |
|||
|
импульс вырастает почти до поло- |
||||
|
вины своего максимального зна- |
||||
|
чения). |
||||
|
Для этого уменьшают R и ис- |
||||
|
пользуют только начальную, бы- |
||||
|
струю часть импульса (рис.3.6). |
||||
|
Рис. 3.6.Форма импульса в пропорцио- |
Хотя амплитуда уменьшается в |
|||
|
нальном счетчике |
несколько раз, свойство пропор- |
циональности величине первичной ионизации сохраняется, просто амплитуды всех импульсов уменьшатся в одинаковое число раз.
3.2.3.2.Счётчики Гейгера – Мюллера
Сувеличением разности потенциалов в газовом промежутке в цилиндрическом счётчике с тонкой нитью – анодом, коэффициент газового усиления М растёт, а с его ростом растёт и число фотоэлектронов. При
некотором напряжении на счётчике Uзаж произведение m·γ ≈ 1 и, следовательно, М → ∞ – это означает, что в счетчике возникает непрерывный самоподдерживающийся разряд. Но ток не будет бесконечно большим из-за возникающего объёмного заряда, уменьшающего электрическое поле вблизи нити. Это приводит к уменьшению m, а, следовательно, и M, то есть возникает саморегулирование и в результате, при сохранении постоянной разности потенциалов, течёт конечной величины ток.
Разряд в счетчике появляется при образовании в газовом промежутке хотя бы одного электрона. При сохранении на электродах необходимой разности потенциалов разряд будет самоподдерживающимся. Для регистрации отдельных частиц возникший разряд необходимо погасить. По способу гашения разряда счётчики делятся на три группы:
несамогасящиеся (медленные); самогасящиеся (быстрые);
151
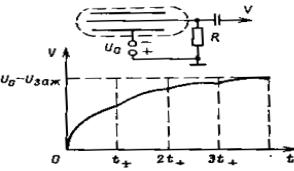
низковольтные самогасящиеся (галогенные).
Напряжение зажигания счетчика Uзаж , зависит от природы заполняющего счетчик газа и от геометрии счетчика. Uзаж иногда называют «гейгеровским» порогом.
Uзаж при r2 = 50 мм и r1 = 0,05 мм и давлении 100 гПа составляет 500 В для гелия, 800 В для водорода и 1200 В для воздуха. Внутреннее со-
противление газового промежутка 107 Ом.
Несамогасящийся счётчик
Несамогасящийся счётчик обычно заполняется инертным газом до давления приблизительно в три раза меньше нормального. После прохождения через объём заряженной частицы, электроны и ионы, возникшие в результате первичной ионизации, устремляются к соответствующим электродам, причем центральный электрод – нить – всегда заряжен положительно – анод (рис.3.7).
Вблизи нити электрическое поле имеет большую напряжённость, и возникает электронно-фотонная лавина. Фотоны практически не поглощаются в газе и попадают на катод. Вследствие внешнего фотоэффекта на катоде, в газовый объём счетчика попадают выбитые фотонами электроны и под действием поля движутся к нити – аноду, в свою очередь, образуя электронно-фотонные лавины. Процесс повторяется многократно, заряд охватывает нить счётчика целиком. Электроны достигают нити (анода) за t 10-8 – 10-7 с. Время дрейфа положительных ионов 10-5 – 10-4 с.
Рис. 3.7. Схема включения счетчика Гейгера – Мюллера и форма импульса (t+ — время движения ионов от анода до катода) и его временные характеристики
152
Таким образом, за время прохождения нескольких электроннофотонных лавин, рождённые положительные ионы остаются практически на месте. Вторичная ионизация происходит возле нити, поэтому вокруг неё образуется чехол положительных зарядов, который снижает напряжённость поля и гасит разряд. Но через время t 10-4 с положительные ионы подходят к катоду. При нейтрализации ионов образуются молекулы в возбужденном состоянии. Испускаемые при снятии возбуждения фотоны могут выбивать с поверхности катода электроны, которые под действием электрического поля устремляются к аноду. Если за это время потенциал нити восстановится и примет значение, большее Uзаж (т.е. снова возможна ударная ионизация), то процесс повторится – возникнет непрерывный разряд. В противном случае разряд в счётчике прекратится.
Для прекращения разряда используются специальные электрические схемы гашения или выбирается большое значение сопротивления на-
грузки R , так, чтобы RC >> T+, т.е. RC ≈ 10-3 – 10-2 с. При C ≈ 10 пФ R 108 Ом. Это – медленный счётчик.
Самогасящийся счётчик
Другой способ гашения разряда применяется в самогасящемся счётчике путём добавки к основному газу (например, аргону) так называемых гасящих примесей. Это пары органических жидкостей, например, метиловый, этиловый спирты. Разряд в счетчике с добавкой паров спирта (аргон 90%, пары спирта 10%, общее давление 133 гПа) прекращается самопроизвольно, независимо от сопротивления R. В таком счетчике электроны, созданные в результате первичной ионизации, возбуждают и ионизуют вблизи анода атомы аргона и молекулы спирта, причем атомов аргона значительно больше, чем молекул спирта.
Фотоны, испускаемые атомами аргона в возбужденном состоянии, эффективно поглощаются молекулами спирта. Это связано с тем, что UионAr =15,7 В, UвозбAr =11,57 В, а Uионспирт =11,3 В. Потенциал ионизации гасящего газа должен быть ниже первого потенциала возбуждения основ-
ного газа, то есть Uиондобавка <Uвозбосн. газ и Uиондобавка < Uионосн. газ . Средняя длина
свободного пробега фотонов до поглощения молекулой спирта около 1 мм при давлении паров спирта 13 гПа. За счет фотоионизации молекул спирта разряд распространяется вдоль нити: далекие от нити счетчика области не участвуют в развитии разряда, поскольку фотоны, испускае-
153
мые атомами аргона, имеют малые пробеги, а возбужденные атомы сконцентрированы вблизи нити. Время развития разряда определяется скоростью распространения его вдоль анода. Скорость эта невелика и составляет 106 – 107 см/с. Образовавшиеся вблизи анода ионы аргона и спирта экранируют электрическое поле, и на этом первая стадия разряда прекращается.
Во время дрейфа ионов к катоду происходит около 104 соударений их с атомами и молекулами. При соударении ионов аргона с молекулами спирта возможна ионизация молекул спирта и нейтрализация атомов аргона. Этот процесс имеет сравнительно большую вероятность, поскольку, несмотря на то, что вероятность ионизации равна около 10-3 в одном столкновении, число столкновений не менее нескольких сотен. Поэтому к катоду подходят только ионы молекул спирта. Это обстоятельство оказывается решающим.
Ионы добавки нейтрализуются на катоде, не вызывая эмиссии электронов в объём счётчика, так как вероятность диссоциации возбужденной молекулы спирта значительно больше вероятности испускания фотона, и независимо от потенциала нити разряд заканчивается.
Полная длительность процессов определяется временем дрейфа положительных ионов t 10-4 с.
Самогасящийся счетчик имеет ограниченный срок службы, поскольку при каждом импульсе в счетчике диссоциирует 109 – 1010 молекул спирта, а всего их 1020. Таким образом, ресурс счетчика 109 – 1010 импульсов.
Галогенные счётчики
Счетчики, наполненные инертными газами (Ar, Ne) с незначительной примесью (~0,1 %) двухатомных газов галоидов (Cl2, Br2, I2) при определенных условиях также обладают свойством гашения разряда. Такие счетчики называют галогенными. Галогенные счетчики имеют сравнительно низкое рабочее напряжение (200 – 400 В), и их срок службы практически не ограничен. Развитие и гашение разряда в галогенных счетчиках происходят следующим образом: электроны, образовавшиеся в результате попадания заряженной частицы в объем счетчика, во время дрейфа к аноду в результате соударений передают свою энергию в основном атомам инертного газа, переводя его в метастабильное состояние (энергии для ионизации не хватает).
154
Время жизни атомов в метастабильном состоянии невелико (τ 10-4 – 10-2 с), а энергия испускаемых фотонов оказывается выше энергии ионизации молекул галоидов. Кроме того, за это время атом испытывает большое количество соударений, в том числе и с молекулами галоидов, например, Br2. При соударениях может происходить ионизация молекул Br2. Для неона потенциал ионизации равен 21,5 эВ, энергия возбуждения 16,9 эВ, а потенциал ионизации для молекул брома 12,8 эВ.
Фотоны, испускаемые возбужденными атомами инертных газов, вопервых, ионизуют молекулы галоидов и, во-вторых, достигают катода (концентрация галоидов мала) и вырывают из него фотоэлектроны. Этот процесс происходит до тех пор, пока вблизи анода не образуется объемный заряд (ионы галоидов). Из-за низкого напряжения на галогенных счетчиках и из-за большой роли в развитии разряда фотоэлектронов из катода развитие разряда происходит сравнительно медленно.
После того как разряд в счетчике прекратился, вблизи анода находятся ионы галоидов, которые дрейфуют к катоду, где и нейтрализуются. Поскольку потенциал ионизации галоидов сравнительно мал, то вероятность вырвать из катода дополнительный электрон невелика. Кроме того, поверхность катода в галогенных счетчиках специально обрабатывают, чтобы повысить работу выхода электронов.
Срок службы галогенных счетчиков неограничен, так как нет диссоциации молекул галоида.
3.2.3.3. Характеристики счетчиков Гейгера – Мюллера Разрешающая способность
Счетчики с самостоятельным разрядом предназначены только для счёта частиц, поэтому можно говорить только о временной разрешающей способности.
Работа счётчиков характеризуется тремя важными временными характеристиками:
мертвым временем; разрешающим временем; временем восстановления.
После попадания в счётчик частицы и развития разряда счётчик теряет способность регистрировать излучение до тех пор, пока напряжённость поля на поверхности анода не достигнет гейгеровского порога. Этот период называется мертвым временем счётчика tм, оно определя-
155
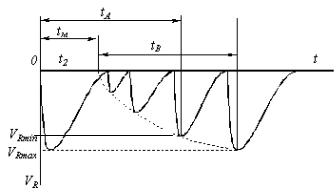
ется, в основном, скоростью движения ионов в газе (рис 3.8). По истечении мёртвого времени, начиная с некоторого момента, счётчик вновь начинает регистрировать излучения, но амплитуды импульсов вначале остаются ниже нормального значения, так как поле в счётчике не достигло максимальной величины. Момент начала счёта tA, или разрешающее время зависит также от выбранного порога дискриминации счетной аппаратуры VRmin.
Рис. 3.8. Осциллограммы импульсов на выходе газоразрядного детектора
Промежуток времени, необходимый для полного восстановления величины импульса, называется временем восстановления tВ.
Временное разрешение детектора tд равно ширине на половине высоты распределения отрезков времени t*, где t* – интервал времени от момента попадания частицы в детектор до момента появления сигнала в регистрирующем устройстве.
При большой плотности потока излучения часть частиц не регистрируется из-за наличия мёртвого времени, в данном случае tA, поэтому необходимо вносить соответствующую поправку:
|
nист = |
nизм |
, 1/с, |
||
|
1−n |
t |
|||
|
изм |
A |
где nизм – измеренная скорость счета, nист – скорость счета, которая была бы при отсутствии просчетов.
Эффективность регистрации излучений
Под эффективностью регистрации η счётчика понимают отношение числа зарегистрированных импульсов Nизм к числу попавших в чувстви-
156

тельный объём счётчика частиц или фотонов излучения Nист за одинаковые промежутки времени:
η= Nизм 100% .
Nист
Реже используют понятие чувствительности детектора: S = nизм/φ, [см2] – отношение числа импульсов в секунду (скорости счета) к плотности потока частиц φ в том месте, где расположен детектор.
Чтобы развился разряд в счетчике, достаточно образования одной пары ионов. Если частица создает в среднем N пар ионов, то вероятность не создать ни одной пары в счетчике равна (по закону Пуассона) ехр(-N), и, следовательно, эффективность регистрации заряженных частиц в самогасящемся счетчике η=1-exp(-N) . Для регистрации заряженных час-
тиц счетчики должны иметь или тонкие стенки, или специальные тонкостенные окна, чтобы заряженные частицы могли проникать внутрь счетчика. В этом случае для α– и β– излучения эффективность близка к 100 %. В случае заряженных частиц N = s p l (s – удельная ионизация; р –
давление; l – путь в счетчике).
Для регистрации фотонов обычно применяют счетчики с толстыми стеклянными стенками (примерно 1 мм). Реже используют счетчики со специальными металлическими катодами. Регистрация фотона, попавшего в счетчик, происходит в том случае, если в результате взаимодействия появляется электрон, который достигает чувствительного объема счетчика. Очевидно, подавляющее число электронов рождается в стенках счетчика. В зависимости от толщины катода счетчика и энергии фотона меняется число электронов, попадающих в чувствительный объем счетчика. Эффективность регистрации гамма-излучения газоразрядными счётчиками зависит от коэффициента поглощения излучения материалом катода и колеблется в пределах 1 – 2%.
Для гамма-излучения число пар ионов N можно оценить по следующей формуле:
N ≈ 2K1 (Rфμф + K2 Rk μk + 2Rn μn ) ,
где μф; μk; μn – коэффициенты поглощения гамма-излучения в материале катода счетчика при фотоэффекте, комптон-эффекте и образовании пар; Rф, Rk, Rn – пробеги образующихся электронов; K1 – доля электронов, по-
157
падающая из катода в газ; K2 – коэффициент, учитывающий распределение по энергиям комптоновских электронов.
Газоразрядные счетчики регистрируют и нейтроны. Регистрация нейтронов происходит в результате или упругого рассеяния нейтронов на ядрах газа, заполняющего счетчик, или образования фотонов в реакциях неупругого рассеяния и радиационного захвата на ядрах вещества, окружающего счетчик. Нейтроны низких энергий (<100 кэВ) в счетчике со смесью спирт – аргон будут упруго рассеиваться на ядрах водорода. Эффективность регистрации таких нейтронов – порядка сотых долей процента.
Для нейтронов более высокой энергии эффективность еще меньше. Если же счетчик окружить кадмием и поместить в замедлитель нейтронов (воду, парафин), то нейтроны будут регистрироваться по γ- излучению захвата в водороде и кадмии. Чувствительность такого устройства, напоминающего всеволновой счетчик, к нейтронам может быть достаточно высокой.
Счётная характеристика
Качество газоразрядного детектора определяется видом зависимости между скоростью счета n и напряжением, приложенным к детектору. Эта зависимость называется рабочей (или счетной) характеристикой де-
тектора, она изображена на рис.3.9.
n
n2
na 
|
0 |
U1 Ua |
U2 |
U |
Рис. 3.9. Рабочая характеристика газоразрядного детектора
158

При значениях разности потенциалов, лежащих ниже области самостоятельного разряда, импульсы тока имеют различную амплитуду. Регистрирующая схема обладает некоторым порогом чувствительности. С ростом напряжения растет число импульсов, амплитуда которых достаточна для регистрации. Этим фактором обусловлен рост начального участка счетной характеристики.
В области самостоятельного разряда каждая ионизирующая частица вызывает импульс с большой амплитудой, достаточной для регистрации. Поэтому в области самостоятельного разряда у идеального счетчика скорость счета не зависит от напряжения и определяется числом частиц, попавших в счетчик. В действительности с ростом напряжения наблюдается слабое увеличение числа зарегистрированных импульсов.
Этот наклон характеристики зависит от числа ложных разрядов и послеразрядов, а также краевых эффектов (например, увеличение чувствительного объема детектора), то есть от процессов, резко проявляющихся с увеличением рабочего напряжения. Область напряжения, где скорость счета остается почти постоянной, называется «плато» счетчика. Плато является рабочей областью напряжений, при которых производится измерение с детектором. У хороших детекторов ширина «плато» составляет 200 – 300 В, а наклон его не превышает нескольких процентов на
100 В.
Наклон плато определяется по формуле
= (n2 − n1 ) 10000 , % на 100 В. n1 (U 2 −U1 )
При дальнейшем увеличении напряжения в детекторе возникает непрерывный разряд и детектор быстро выходит из строя.
Обычно в качестве рабочей точки на характеристике na ,Ua выбирают середину плато. При широком плато выбирают рабочую точку ближе к гейгеровскому порогу.
Детектор имеет ограниченный срок службы. По мере распада многоатомных молекул его счетная характеристика постепенно ухудшается – укорачивается ширина плато и увеличивается его наклон, поэтому нужно периодически проверять счетную характеристику счетчика.
3.3. Кристаллические, полупроводниковые детекторы
Кристаллические детекторы представляют собой твердотельные ионизационные камеры, в которых носители заряда, образовавшиеся при
159
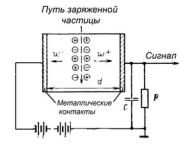
Рис. 3.10. Схема включения твердотельной камеры
поглощении излучения, собираются на электродах камеры. Возникающие импульсы тока используются для регистрации излучений. Число образовавшихся носителей заряда зависит только от энергии, потерянной излучением в материале детектора, и не зависит от вида излучения. Это обусловливает характерное для ионизационных камер линейное соотношение между амплитудой импульса и потерянной энергией для всех ви-
дов излучений. Следовательно, такими детекторами удобно определять энергию излучений, то есть осуществлять их спектрометрию.
Кристаллический детектор, показанный на рис.3.10 – это небольшой кристалл, две противоположные стороны которого покрыты электродами. К электродам подводится напряжение.
Кристаллические детекторы обладают рядом преимуществ по сравнению с газонаполненными ионизационными камерами:
гораздо лучшее энергетическое разрешение; на два – три порядка большая масса вещества, заключенная в чувст-
вительном объеме, что особенно существенно при регистрации фотонов и заряженных частиц высокой энергии.
Прохождение заряженной частицы вызывает в диэлектрике образование разноименных носителей зарядов (электронов и дырок). Внешнее напряжение U создает внутри кристалла электрическое поле. Электроны и дырки движутся под действием этого поля к электродам. По мере того как носители смещаются, они индуцируют на электродах заряд, пропорциональный пройденной ими разности потенциалов.
Благодаря большой плотности и большой тормозной способности вещества детектора в нем полностью теряют энергию частицы с высокой энергией, например электроны и протоны. Пробеги их в воздухе часто превышают 1 м, но они полностью поглощаются в кремнии толщиной 1 мм. По этой же причине велика эффективность регистрации гамма-излучения кристаллическим
детектором. При необходимости можно создать очень тонкие детекторы, тогда они поглощают лишь небольшую часть энергии частиц и применяются для измерения удельных потерь энергии dE/dx . Если затем измерить полную энергию частиц Е с помощью детектора, в котором они
160
To use your Google Account on a browser (like Chrome or Safari), turn on cookies if you haven’t already.
Important: If you get a message that cookies are turned off, you need to turn them on to use your account.
In Chrome
- On your computer, open Chrome.
- At the top right, click More
Settings.
- Under “Privacy and security,” click Site settings.
- Click Cookies and site data.
- From here, you can:
- Turn on cookies: Next to “Blocked,” turn on the switch.
- Turn off cookies: Turn off Allow all cookies.
Learn how to change more cookie settings in Chrome.
In other browsers
For instructions, check the support website for your browser.
Why cookies are helpful
Cookies are files created by sites you visit. They make your online experience easier by saving browsing information. With cookies, sites can:
- Keep you signed in
- Remember your site preferences
- Give you locally relevant content
We use cookies to improve our services. To learn more, read our Privacy Policy.
Fix problems
If you can’t use your Google Account and get a message that cookies are turned off:
- Follow the steps above to turn on cookies.
- Try signing in again.
If you still get the error message, here are some possible solutions. Try each one, then try signing in.
- Open a new browser window.
- Clear your browser’s cache and cookies. Learn how to clear cache and cookies.
- Browse in private. Learn how to browse privately in Chrome.
- Change your browser’s privacy settings. Learn how to change privacy settings.
Was this helpful?
How can we improve it?
Данная тема будет посвящена решению задач, связанных с
расчетом энергии и импульса фотонов.
Задача 1. Определите энергию, массу и импульс фотона,
если соответствующая ему длина волны равна 1,6 ∙ 10−12
м.
|
ДАНО: |
РЕШЕНИЕ Энергия фотона определяется по формуле Массу фотона можно определить из формулы Импульс фотона |
|
|
Ответ: W
= 1,2 ∙ 10−13 Дж; m = 1,4 ∙ 10−30 кг; р = 4,1
∙ 10−22 кг ∙ м/с.
Задача 2. Электрон, пройдя разность потенциалов 4,9 В,
сталкивается с атомом ртути и переводит его в первое возбужденное состояние.
Какую длину волны имеет фотон, соответствующий переходу атома ртути в
нормальное состояние?
|
ДАНО: |
РЕШЕНИЕ Определим энергию, которую приобретает электрон, пройдя в Энергия вылетевшего фотона Приравняем эти два уравнения Тогда длина волны фотона |
|
|
Ответ: длина волны фотона равна 250
нм.
Задача 3. Работа выхода электрона из металла 4,5 эВ.
Энергия падающего фотона 4,9 эВ. Если свет падает на пластинку нормально, а
электрон вылетает перпендикулярно пластинке, то чему равно изменение модуля
импульса металлической пластинки при вылете из нее одного электрона?
|
ДАНО: |
РЕШЕНИЕ Рассматриваемая система (металлическая пластинка — фотон — Импульс системы в начальном состоянии будет определяться Импульс системы в конечном состоянии будет складываться из Тогда закон сохранение импульса Изменение импульса пластинки Запишем закон сохранения импульса в проекциях на нормаль Импульс, переданный фотоном Импульс, преданный электроном Из уравнения Эйнштейна для фотоэффекта Тогда импульс переданный электроном Тогда изменение модуля импульса металлической пластины |
|
|
Ответ: изменение модуля импульса
пластинки равно 3,44 ∙ 10−25 кг ∙ м/с
Задача 4. Энергия фотона рентгеновского излучения 0,3
МэВ. Фотон был рассеян при соударении со свободным покоящимся электроном, в
результате чего его длина волны увеличилась на 0,0025 нм. Определить: энергию
рассеянного фотона; угол, под которым вылетел электрон отдачи; кинетическую
энергию электрона отдачи.
|
ДАНО: |
РЕШЕНИЕ Согласно условию задачи, при рассеянии рентгеновского Уменьшение энергии фотона означает уменьшение частоты Энергия рассеянного фотона Длина волны рассеянного излучения Длина волны падающего излучения Длина волны рассеянного излучения Тогда энергия рассеянного фотона Проверим размерности Определим угол, под которым вылетает электрон отдачи. Для Так как время взаимодействия фотона с электроном мало, то Закон сохранения импульса в проекциях на ось Ох Закон сохранения импульса в проекциях на ось Оу Тогда Импульс падающего фотона Энергия падающего фотона Аналогично для рассеянного фотона Тогда И Формула Комптона Тогда Комптоновская длина волны электрона Тогда Закон сохранения энергии Тогда кинетическая энергия электрона отдачи |
|
|
Ответ: W’
= 0,2 МэВ; φ = 31о; Wk = 0,1 МэВ.

























































































































