Основные ссылки
CSS adjustments for Marinelli theme

Вы здесь
Главная » Соединения конденсаторов. Энергия…
Соединения конденсаторов. Энергия электрического поля конденсатора.
|
Соединения конденсаторов . |
|
|
Параллельное соединение конденсаторов |
|
|
Обкладки конденсаторов соединяют попарно, т.е. в системе остается два изолированных проводника, которые и представляют собой обкладки нового конденсатора |
|
|
|
|
|
Вывод: При параллельном соединении конденсаторов
Т.о., общая емкость больше емкости любого из параллельно соединенных конденсаторов |
|
|
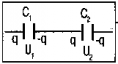
Последовательное соединение конденсаторов |
|
|
Производят только одно соединение, а две оставшиеся обкладки – одна от конденсатора С1 другая от конденсатора С2 – играют роль обкладок нового конденсатора. |
|
|
|
|
|
Вывод: При последовательном соединении конденсаторов
Т.о., общая емкость меньше емкости любого из последовательно соединенных конденсаторов. |
|
|
Энергия электрического поля конденсатора. Под энергией электрического поля конденсатора будем понимать энергию одной его обкладки, находящейся в поле, созданном другой обкладкой. Тогда: Формулы справедливы для любого конденсатора. |
Пример: С=2мкФ; U=1000В. t=10-6c.W=1 Дж |
|
|
|
|
Плотность энергии. Формула справедлива для полей любых конденсаторов и, кроме того, для полей, меняющихся со временем (неэлектростатических). |
|
Главная
→
Примеры решения задач ТОЭ
→
Расчет электрической цепи постоянного тока с конденсаторами
Расчет электрической цепи постоянного тока с конденсаторами
Расчет электрической цепи постоянного тока с конденсаторами
Основные положения и соотношения
1. Общее выражение емкости конденсатора
C= Q U .
2. Емкость плоского конденсатора
C= ε a ⋅S d = ε r ⋅ ε 0 ⋅S d ,
здесь
S — поверхность каждой пластины конденсатора;
d — расстояние между ними;
εa = εr·ε0 — абсолютная диэлектрическая проницаемость среды;
εr — диэлектрическая проницаемость среды (относительная диэлектрическая проницаемость);
ε 0 = 1 4π⋅ с 2 ⋅ 10 −7 ≈8,85418782⋅ 10 −12 Ф м – электрическая постоянная.
3. При параллельном соединении конденсаторов С1, С2, …, Сn эквивалентная емкость равна
C= C 1 + C 2 +…+ C n = ∑ k=1 n C k .
4. При последовательном соединении конденсаторов эквивалентная емкость определяется из формулы
1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .
Для двух последовательно соединенных конденсаторов эквивалентная емкость составляет:
C= C 1 ⋅ C 2 C 1 + C 2 ,
а напряжения между отдельными конденсаторами распределяются обратно пропорционально их емкостям:
U 1 =U⋅ C 2 C 1 + C 2 ; U 2 =U⋅ C 1 C 1 + C 2 .
5. Преобразование звезды емкостей в эквивалентный треугольник емкостей или обратно (рис. а и б)
Рис. 0
осуществляется по формулам:
Y→Δ { C 12 = C 1 ⋅ C 2 ΣC ; C 13 = C 1 ⋅ C 3 ΣC ; C 23 = C 2 ⋅ C 3 ΣC , где ΣC= C 1 + C 2 + C 3 , Δ→Y { C 1 = C 12 + C 13 + C 12 ⋅ C 13 C 23 ; C 2 = C 12 + C 23 + C 12 ⋅ C 23 C 13 ; C 3 = C 13 + C 23 + C 13 ⋅ C 23 C 12 .
6. Энергия электростатического поля конденсатора:
W= C⋅ U 2 2 = Q⋅U 2 = Q 2 2C .
7. Расчет распределения зарядов в сложных цепях, содержащих источники э.д.с. и конденсаторы, производится путем составления уравнений по двум законам:
1) По закону сохранения электричества (закон сохранения электрического заряда): алгебраическая сумма зарядов на обкладках конденсаторов, соединенных в узел и не подключенных к источнику энергии, равна алгебраической сумме зарядов, имевшихся на этих обкладках до их соединения:
ΣQ=Σ Q ′ .
2) По второму закону Кирхгофа: алгебраическая сумма э. д. с. в замкнутом контуре равна алгебраической сумме напряжений на участках контура, в том числе на входящих в него конденсаторах:
∑ k=1 n E k = ∑ k=1 n U C k = ∑ k=1 n Q k C k .
Приступая к решению задачи, надо задаться полярностью зарядов на обкладках конденсаторов.
Решение задач на расчет электрической цепи постоянного тока с конденсаторами
Задача. Доказать формулу эквивалентной емкости при последовательном соединении конденсаторов (рис. 1).
Рис. 1
Решение
На рис. 1 представлено последовательное соединение трех конденсаторов. Если батарею конденсаторов подключить к источнику напряжения U12, то на левую пластину конденсатора С1 перейдет заряд +q, на правую пластину конденсатора С3 заряд –q.
Вследствие электризации через влияние правая пластина конденсатора С1 будет иметь заряд –q, а так как пластины конденсаторов С1 и С2 соединены и были электронейтральны, то вследствие закона сохранения заряда заряд левой пластины конденсатора C2 будет равен +q, и т. д. На всех пластинах конденсаторов при таком соединении будет одинаковый по величине заряд.
Найти эквивалентную емкость — это значит найти конденсатор такой емкости, который при той же разности потенциалов будет накапливать тот же заряд q, что и батарея конденсаторов.
Разность потенциалов U12 = φ1 — φ2 складывается из суммы разностей потенциалов между пластинами каждого из конденсаторов
U 12 = φ 1 − φ 2 =( φ 1 − φ A )+( φ A − φ B )+( φ B − φ 2 )= U 1A + U AB + U B2 .
Воспользовавшись формулой напряжения на конденсаторе
U= q C ,
запишем
q C = q C 1 + q C 2 + q C 3 .
Откуда эквивалентная емкость батареи из трех последовательно включенных конденсаторов
1 C = 1 C 1 + 1 C 2 + 1 C 3 .
В общем случае эквивалентная емкость при последовательном соединении конденсаторов
1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .
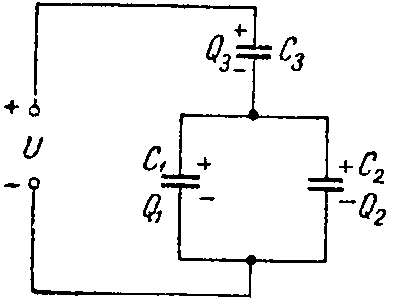
Задача 1. Определить заряд и энергию каждого конденсатора на рис. 2, если система подключена в сеть с напряжением U = 240 В.
Рис. 2
Емкости конденсаторов: C1 =50 мкФ; C2 =150 мкФ; C3 =300 мкФ.
Решение
Эквивалентная емкость конденсаторов C1 и C2, соединенных параллельно
C12 = C1 + C2 = 200 мкФ,
эквивалентная емкость всей цепи равна
C= C 12 ⋅ C 3 C 12 + C 3 = 200⋅300 500 =120 мкФ.
Заряд на эквивалентной емкости
Q = C·U = 120·10–6·240 = 288·10–4 Кл.
Той же величине равен заряд Q3 на конденсаторе C3, т.е. Q3 = Q = 288·10–4 Кл; напряжение на этом конденсаторе
U 3 = Q 3 C 3 = 288⋅ 10 −4 300⋅ 10 −6 =96 В.
Напряжение на конденсаторах C1 и C2 равно
U1 = U2 = U — U3 = 240 — 96 = 144 В.
их заряды имеют следующие значения
Q1 = C1·U1 = 50·10–6·144 = 72·10–4 Кл;
Q2 = C2·U2 = 150·10–6·144 = 216·10–4 Кл.
Энергии электростатического поля конденсаторов равны
W 1 = Q 1 ⋅ U 1 2 = 72⋅ 10 −4 ⋅144 2 ≈0,52 Дж; W 2 = Q 2 ⋅ U 2 2 = 216⋅ 10 −4 ⋅144 2 ≈1,56 Дж; W 3 = Q 3 ⋅ U 3 2 = 288⋅ 10 −4 ⋅96 2 ≈1,38 Дж.
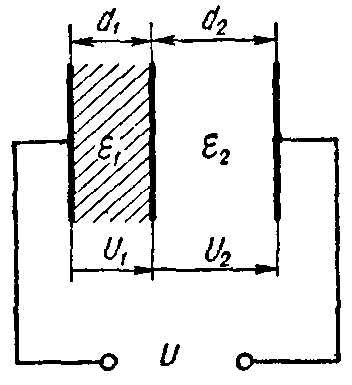
Задача 2. Плоский слоистый конденсатор (рис. 3), поверхность каждой пластины которого S = 12 см2, имеет диэлектрик, состоящий из слюды (εr1 = 6) толщиною d1 = 0,3 мм и стекла (εr2 = 7) толщиною d2 =0,4 мм.
Пробивные напряженности слюды и стекла соответственно равны E1 = 77 кВ/мм, E2 = 36 кВ/мм.
Рис. 3
Вычислить емкость конденсатора и предельное напряжение, на которое его можно включать, принимая для более слабого слоя двойной запас электрической прочности.
Решение
Эквивалентная емкость слоистого конденсатора определится как емкость двух последовательно соединенных конденсаторов
C= C 1 ⋅ C 2 C 1 + C 2 = ε a1 ⋅S d 1 ⋅ ε a2 ⋅S d 2 ε a1 ⋅S d 1 + ε a2 ⋅S d 2 = ε a1 ⋅ ε a2 ⋅S ε a1 ⋅ d 2 + ε a2 ⋅ d 1 .
Подставляя сюда числовые значения, предварительно заменив εa1 = εr1·ε0 и εa2 = εr2·ε0, получим
C= ε 0 ⋅ ε r1 ⋅ ε r2 ⋅S ε r1 ⋅ d 2 + ε r2 ⋅ d 1 =8,85⋅ 10 −12 ⋅ 6⋅7⋅12⋅ 10 −4 6⋅0,4⋅ 10 −3 +7⋅0,3⋅ 10 −3 =99⋅ 10 −12 Ф.
Обозначим общее напряжение, подключаемое к слоистому конденсатору, через Uпр, при этом заряд конденсатора будет равен
Q = C·Uпр.
Напряжения на каждом слое будут равны
U 1 = Q C 1 = C⋅ U пр ε a1 ⋅S d 1 = ε a2 ⋅ d 1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр ; U 2 = Q C 2 = C⋅ U пр ε a2 ⋅S d 2 = ε a1 ⋅ d 2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр .
Напряженности электростатического поля в каждом слое
E 1 = U 1 d 1 = ε a2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ′ пр ; E 2 = U 2 d 2 = ε a1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ″ пр .
Здесь U’np — общее напряжение, подключаемое к конденсатору, при котором пробивается первый слой, a U”np — общее напряжение, при котором происходит пробой второго слоя.
Из последнего выражения находим
U ′ пр = E 1 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a2 =49,5 кВ; U ″ пр = E 2 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a1 =27,0 кВ.
Таким образом, более слабым слоем является второй; согласно условию, принимая для него двойной запас прочности, находим, что конденсатор может быть включен на напряжение, равное
27,0 кВ / 2 = 13,5 кВ.
Задача 3. Обкладки плоского конденсатора с воздушным диэлектриком расположены на расстоянии d1 = 1 см друг от друга. Площадь обкладок S = 50 см2. Конденсатор заряжается до напряжения U = 120 В и затем отсоединяется от источника электрической энергии.
Определить, какую надо совершить работу, если увеличить расстояние между пластинами до d2 = 10 см. Краевым эффектом можно пренебречь; другими словами, емкость конденсатора можно считать обратно пропорциональной расстоянию между обкладками.
Решение
Энергия заряженного плоского конденсатора равна
W 1 = C 1 ⋅ U 2 2 = ε 0 ⋅S d 1 ⋅ U 2 2 ,
где С1 — емкость до раздвижения обкладок.
Так как конденсатор отключен от источника, то при изменении расстояния между обкладками его заряд остается постоянным. Поэтому из~ соотношения
Q = C2·U2,
где C2 — емкость конденсатора после раздвижения обкладок, следует, что, так как C2 = ε0·S/d2 стало меньше в 10 раз (d2 увеличилось в 10 раз), то напряжение на конденсаторе U2 увеличилось в 10 раз, т. е. U2 = 10U.
Таким образом, энергия конденсатора после отключения и раздвижения обкладок на расстояние d2 будет больше первоначальной
W 2 = ε 0 ⋅S d 2 ⋅ U 2 2 2 = ε 0 ⋅S 10 d 1 ⋅ ( 10U ) 2 2 =10⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =10⋅ W 1 .
Увеличение энергии произошло за счет работы внешних сил, затраченной на раздвижение обкладок.
Таким образом, надо совершить работу, равную
W 2 − W 1 =9⋅ W 1 =9⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =2,86⋅ 10 −7 Дж.
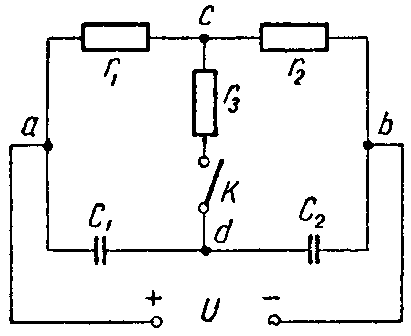
Задача 4. Для схемы (рис. 4) определить напряжение каждого конденсатора в двух случаях: при замкнутом и разомкнутом ключе К.
Даны: C1 = 30 мкФ; C2 = 20 мкФ; r1 = 100 Ом. r2 = 400 Ом. r3 = 600 Ом, U = 20 В.
Решение
Ключ К разомкнут. Конденсаторы соединены между собой последовательно; их ветвь находится под полным напряжением источника; напряжение распределяется между ними обратно пропорционально емкостям
U 1 = C 2 C 1 + C 2 ⋅U= 20⋅ 10 −6 30⋅ 10 −6 +20⋅ 10 −6 ⋅20=8 В; U 2 =U− U 1 =20−8=12 В.
Рис. 4
Ключ К замкнут. Через сопротивления r1 и r2 протекает ток
I= U r 1 + r 2 = 20 500 =0,04 А,
а через сопротивление r3 ток не протекает.
Поэтому точки c и d равнопотенциальны (φc = φd). Следовательно, напряжение между точками a и c (Uac = φa — φc) равно напряжению между точками a и d (Uad = φa — φd).
Таким образом, напряжение на первом конденсаторе равно падению напряжения на сопротивлении r1
UC1 = I·r1 = 0,04·100 = 4 В.
Аналогично напряжение на втором конденсаторе равно
UC2 = I·r2 = 0,04·400 = 16 В.
Задача 5. Определить напряжение на зажимах конденсаторов и их энергию после перевода рубильника из положения 1 в положение 2, показанное пунктиром на рис. 5, если U = 25 В; C1 = 5 мкФ; C2 = 120 мкФ. Конденсатор C2 предварительно не был заряжен.
Рис. 5
Решение
Когда рубильник находится в положении 1, то конденсатор C1 заряжен до напряжения U и его заряд равен
Q = C1·U = 5·10–6·25 = 125·10–6 Кл.
После перевода рубильника в положение 2, заряд Q распределяется между конденсаторами C1 и C2 (рис. 5). Обозначим эти заряды через Q’1 и Q’2.
На основании закона сохранения электричества имеем
Q = Q’1 + Q’2 = 125 10–6 Кл. (1)
По второму закону Кирхгофа имеем
0= U C1 − U C2 = Q ′ 1 C 1 − Q ′ 2 C 2 ,
или
Q ′ 1 5⋅ 10 −6 − Q ′ 2 120⋅ 10 −6 =0. (2)
Решая уравнения (1) и (2), найдем
Q’1 = 5 10–6 Кл; Q’2 = 120 10–6 Кл.
Доставка свежих и аппетитных японских суши в Новороссийске – ям ям..
Напряжение на зажимах конденсаторов станет равным
U C1 = Q ′ 1 C 1 = U C2 = Q ′ 2 C 2 = 5⋅ 10 −6 5⋅ 10 −6 =1 В.
Энергия обоих конденсаторов будет равна
W= C 1 ⋅ U C1 2 2 + C 2 ⋅ U C2 2 2 =62,5⋅ 10 −6 Дж.
Подсчитаем энергию, которая была запасена в конденсаторе С1, при его подключении к источнику электрической энергии
W нач = C 1 ⋅U 2 = 5⋅ 10 −6 ⋅ 25 2 2 =1562,5⋅ 10 −6 Дж.
Как видим, имеет место большая разница в запасе энергии до и после переключения. Энергия, равная 1562,5·10–6 — 62,5·10–6 = 1500·10–6 Дж, израсходовалась на искру при переключении рубильника из положения 1 в положение 2 и на нагревание соединительных проводов при перетекании зарядов из конденсатора C1 в конденсатор C2 после перевода рубильника в положение 2.
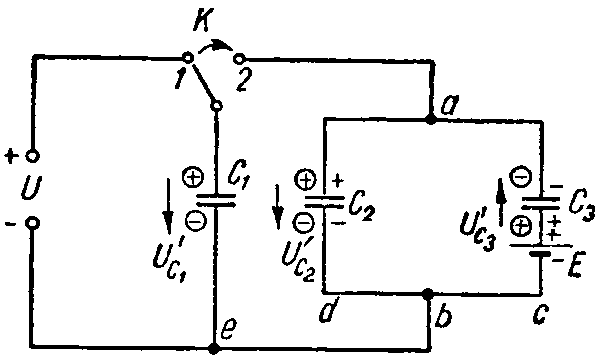
Задача 6. Вычислить напряжение, которое окажется на каждом из конденсаторов схемы (рис. 6) после перевода рубильника К из положения 1 в положение 2.
Емкости конденсаторов равны: C1 = 10 мкФ; C2 = 30 мкФ; C3 = 60 мкФ; напряжение U = 30 В, а э. д. с. E = 50 В.
Рис. 6
Решение
Рубильник находится в положении 1. Заряд конденсатора C1 равен
Q1 = C1·U = 10·10–6·30 = 0,3·10–3 Кл.
В указанном положении рубильника конденсаторы C2 и C3 соединены последовательно друг с другом, поэтому их заряды равны: Q2 = Q3. Знаки зарядов показаны на рис. 6 отметками без кружков. По второму закону Кирхгофа имеем
E= U C2 + U C3 = Q 2 C 2 + Q 3 C 3 = Q 2 ⋅ C 2 + C 3 C 2 ⋅ C 3 ,
откуда
Q 2 = Q 3 = C 2 ⋅ C 3 C 2 + C 3 ⋅E= 30⋅ 10 −6 ⋅60⋅ 10 −6 90⋅ 10 −6 ⋅50=1⋅ 10 −3 Кл.
При переводе рубильника в положение 2 произойдет перераспределение зарядов. Произвольно задаемся новой полярностью зарядов на электродах (показана в кружках; предположена совпадающей с ранее имевшей место полярностью); соответствующие положительные направления напряжений на конденсаторах обозначены стрелками. Обозначим эти заряды через Q’1, Q’2 и Q’3. Для их определения составим уравнения на основании закона сохранения электрических зарядов и второго закона Кирхгофа.
Для узла a
Q’1 + Q’2 — Q’3 = Q1 + Q2 — Q3. (1)
Для контура 2ebda2
0= U ′ C1 − U ′ C2 = Q ′ 1 C 1 − Q ′ 2 C 1 .
Для контура bcadb
E= U ′ C2 − U ′ C3 = Q ′ 2 C 2 + Q ′ 3 C 3 .
Уравнения (1) — (3), после подстановки числовых значений величин, примут вид
Q’1 + Q’2 — Q’3 = 0,3·10–3; (4)
3Q’1 — Q’2 = 0; (5)
2Q’2 + Q’3 = 3·10–3. (6)
Решая совместно уравнения (4) — (6), получим
Q’1 = 0,33·10–3 Кл; Q’2 = 0,99·10–3 Кл; Q’3 = 1,02·10–3 Кл.
Так как знаки всех зарядов оказались положительными, то фактическая полярность обкладок соответствует предварительно выбранной.
Напряжения на конденсаторах после перевода рубильника будут равны
U C1 = Q ′ 1 C 1 = 0,33⋅ 10 −3 10⋅ 10 6 =33 В; U C2 = Q ′ 2 C 2 = 0,99⋅ 10 −3 30⋅ 10 6 =33 В; U C3 = Q ′ 3 C 3 = 1,02⋅ 10 −3 60⋅ 10 6 =17 В.
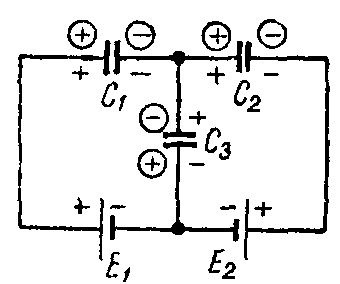
Задача 7. Определить заряд и напряжение конденсаторов, соединенных по схеме рис. 7, если C1 = 5 мкФ; C2 = 4 мкФ; C3 = 3 мкФ; э. д. с. источников E1 = 20 В и E2 = 5 В.
Рис. 7
Решение
Составим систему уравнений на основании закона сохранения электричества и второго закона Кирхгофа, предварительно задавшись полярностью обкладок конденсаторов, показанной в кружках
− Q 1 + Q 2 − Q 3 =0; E 1 = U C1 − U C3 = Q 1 C 1 − Q 3 C 3 ; E 2 =− U C2 − U C3 =− Q 2 C 2 − Q 3 C 3 .
Подставляя сюда числовые значения и решая эту систему уравнений, получим, что Q1 = 50 мкКл; Q2 = 20 мкКл; Q3 = –30 мкКл.
Таким образом, истинная полярность зарядов на обкладках конденсаторов C1 и C2 соответствует выбранной, а у конденсатора C3 — противоположна выбранной.
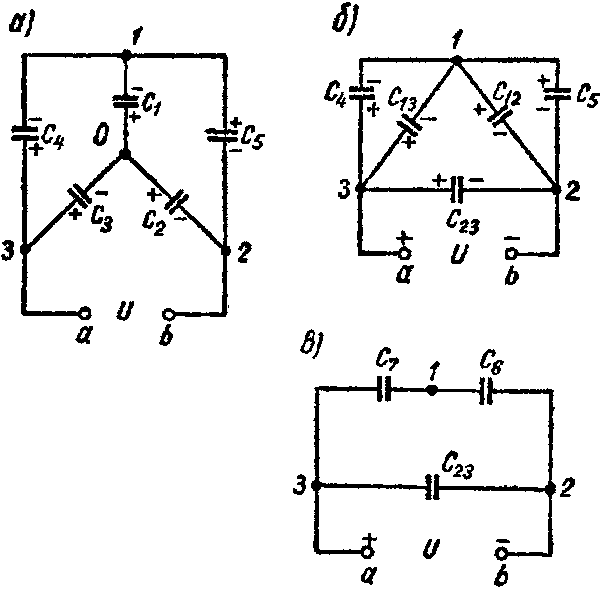
Задача 8. Пять конденсаторов соединены по схеме рис. 3-22, а, емкости которых C1 = 2 мкФ; C2 = 3 мкФ; C3 = 5 мкФ; C4 = 1 мкФ; C5 = 2,4 мкФ.
Рис. 8
Индивидуалка Дана (34 лет) т.8 926 650-82-63 Москва, метро Сокол.
Определить эквивалентную емкость системы и напряжение на каждом из конденсаторов, если приложенное напряжение U = 10 В.
Решение
1-й способ. Звезду емкостей C1, C2 и C3 (рис. 8, а) преобразуем в эквивалентный треугольник емкостей (рис. 8, б)
C 12 = C 1 ⋅ C 2 C 1 + C 2 + C 3 =0,6 мкФ; C 13 = C 1 ⋅ C 3 C 1 + C 2 + C 3 =1,0 мкФ; C 23 = C 2 ⋅ C 3 C 1 + C 2 + C 3 =1,5 мкФ.
Емкости C12 и C5 оказываются соединенными параллельно друг другу и подключенными к точкам 1 и 2; их эквивалентная емкость
C6 = C12 + C5 = 3 мкФ.
Аналогично
C7 = C13 + C4 = 2 мкФ.
Схема принимает вид изображенный на рис. 8, в. Емкость схемы между точками а и b равняется
C ab = C 23 + C 6 ⋅ C 7 C 6 + C 7 =2,7 мкФ.
Вычислим напряжение на каждом из конденсаторов.
На конденсаторе C7 напряжение равно
U 7 = C 6 C 6 + C 7 ⋅U=6 В.
Таково же напряжение и на конденсаторах C4 и C13
U4 = U31 = 6 В.
Напряжение на конденсаторе C6 равно
U6 = U — U7 = 4 В;
U5 = U12 = 4 В.
Вычислим заряды
Q4 = C4·U4 = 6·10–6 Кл;
Q5 = C5·U5 = 9,6·10–6 Кл;
Q12 = C12·U12 = 6·10–6 Кл;
Q13 = C13·U31 = 2,4·10–6 Кл.
По закону сохранения электричества для узла 1 схем 8, а и б имеем
–Q4 — Q1 + Q5 = –Q4 — Q13 + Q12 + Q5,
отсюда
Q1 = Q13 — Q12 = 3,6·10–6 Кл,
а напряжение на конденсаторе, емкостью C1 составляет
U 1 = Q 1 C 1 =1,8 В.
Далее находим напряжения и заряды на остальных конденсаторах
U31 = U1 + U3,
отсюда
U3 = U31 — U1 = 4,2 В;
Q3 = C3·U3 = 21·10–6 Кл,
также
U12 = U2 — U1 = 4,2 В,
откуда
U2 = U12 + U1 = 5,8 В;
Q2 = C2·U2 = 17,4·10–6 Кл.
Так как знаки всех зарядов оказались положительными, то фактическая полярность зарядов на обкладках совпадает с предварительно выбранной.
2-й способ. Выбрав положительные направления напряжений на конденсаторах (а тем самым и знаки зарядов на каждом из них) по формуле закона сохранения электричества (закона сохранения заряда) составляем два уравнения и по второму закону Кирхгофа три уравнения (рис. 8, а)
для узла 1
Q5 — Q1 — Q4 = 0; (1)
для узла О
Q1 + Q2 — Q3 = 0; (2)
для контура О13О
Q 1 C 1 − Q 4 C 4 + Q 3 C 3 =0; (3)
для контура О12О
Q 1 C 1 + Q 5 C 5 − Q 2 C 2 =0; (4)
для контура a3О2b
Q 3 C 3 + Q 2 C 2 =U. (5)
Система уравнений (1) — (5) — содержит пять неизвестных: Q1, Q2, Q3, Q4 и Q5. Решив уравнения, найдем искомые заряды, а затем и напряжения на конденсаторах. При втором способе решения эквивалентную емкость схемы Сab можно найти из отношения
C ab = Q U ,
где Q = Q3 + Q4, или Q = Q2 + Q5.
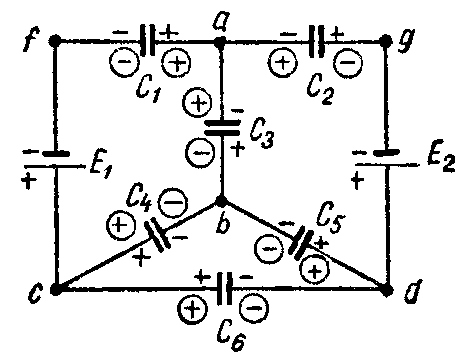
Задача 9. В схеме рис. 9 найти распределение зарядов, если E1 = 20 В; E2 = 7 В; C1 = 7 мкФ; C2 = 1 мкФ; C3 = 3 мкФ; C4 = 4 мкФ; C5 = C6 = 5 мкФ.
Рис. 9
Решение
При выбранном распределении зарядов (в кружках), как показано на схеме, система уравнений будет иметь вид:
для узла а
Q1 + Q2 + Q3 = 0;
для узла b
–Q3 — Q4 — Q5 = 0;
для узла c
–Q1 + Q4 + Q6 = 0;
для контура afcba
E 1 = U C1 + U C4 − U C3 = Q 1 C 1 + Q 4 C 4 − Q 3 C 3 ;
ля контура gdbag
E 2 = U C5 − U C3 + U C2 = Q 5 C 5 − Q 3 C 3 + Q 2 C 2 ;
для контура cbdc
0= U C4 − U C5 − U C6 = Q 4 C 4 − Q 5 C 5 − Q 6 C 6 .
Подставляя сюда числовые значения и решая полученную систему шести уравнений, найдем искомые заряды
Q1 = 35 мкКл; Q2 = –5 мкКл; Q3 = –30 мкКл;
Q4 = 20 мкКл; Q5 = 10 мкКл; Q6 = 15 мкКл.
Таким образом, истинные знаки зарядов Q1, Q4, Q5 и Q6 соответствуют выбранным, а знаки Q2 и Q3 противоположны выбранным.
Фактическое расположение знаков зарядов на конденсаторах дано не в кружках.
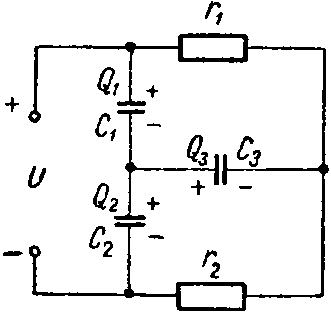
Задача 10. Определить заряд и энергию каждого конденсатора в схеме (рис. 10). Данные схемы: C1 = 6 мкФ; C2 = 2 мкФ; C3 = 3 мкФ; r1 = 500 Ом; r2 = 400 Ом; U = 45 В.
Рис. 10
Решение
Через сопротивления протекает ток
I= U r 1 + r 2 =0,05 А.
Задавшись полярностью зарядов на обкладках конденсаторов, составим систему уравнений:
− Q 1 + Q 2 + Q 3 =0; U= U C1 + U C2 = Q 1 C 1 + Q 2 C 2 ; I⋅ r 1 = U C1 + U C3 = Q 1 C 1 + Q 3 C 3 ,
или
Q 1 = Q 2 + Q 3 ; 45= Q 1 6⋅ 10 −6 + Q 2 2⋅ 10 −6 ; 25= Q 1 6⋅ 10 −6 + Q 3 3⋅ 10 −6 .
Решив эту систему уравнений, найдем, что
Q1 = 90 мкКл; Q2 = 60 мкКл; Q3 = 30 мкКл.

параллельное соединение конденсаторов,
Расчет цепи конденсаторов,
Конденсатор в цепи постоянного тока,
Цепи с конденсаторами
Комментарии
1 Энергия системы точечных зарядов
Формулу
можно рассматривать как взаимную
потенциальную энергию зарядови
,
находящихся на расстоянии(рис.1).
Рис.1
Если мы теперь в поле двух зарядов
и
внесем
третий заряд,
то благодаря свойству аддитивности
энергии взаимодействий, получим:
.
Преобразуем эту сумму следующим образом.
Представим каждое слагаемое
в симметричном виде:
,
поскольку.
Тогда
.
Сгруппируем члены с одинаковыми первыми
индексами:
Каждая сумма в круглых скобках – это
энергия
взаимодействия
-го
заряда с остальными зарядами.
Поэтому можно последнее выражение
переписать так:
Обобщим это выражение на систему,
состоящую из
точечных зарядов
.
Итак, энергия взаимодействия системы
точечных зарядов
(3.1)
Имея в виду, что
,
где-i-ый заряд системы,
– потенциал, создаваемый всеми зарядами,
кроме,
в той точке, где находится заряд,
получим окончательное выражение:
(3.2)
Если заряды распределены непрерывно,
то, разлагая систему зарядов на
совокупность элементарных зарядов
и переходя от суммирования в (3.2) к
интегрированию, получаем
,
(3.3)
где
– потенциал, создаваемый всеми зарядами
системы в элементе объемом.
2 Энергия заряженных проводника и конденсатора
Энергия уединенного проводника.
Пусть проводник имеет заряди потенциал
.
Посколькуна поверхности проводника, получим
Учитывая, что
(3.4)
Любое из этих выражений определяет
энергию заряженного проводника.
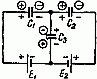
Энергия заряженного конденсатора.
Предположим, что (+)
и– заряд и потенциал положительно
заряженной обкладки конденсатора, (-)
и– отрицательно заряженной обкладки
(рис. 2).
Рис. 2
Согласно формуле (3.3) интеграл можно
разбить на две части – для одной и другой
обкладок. Тогда
.
Приняв во внимание, что
,
получим для энергии заряженного
конденсатора три выражения:
(3.5)
3 Энергия и плотность энергии электрического поля
Выразим энергию заряженного плоского
конденсатора через напряженность
электрического поля. Подставим в формулу
выражение
,
получим
.
Поскольку
и
(объем между обкладками конденсатора),
то
.
Как будет показано в следующей главе,
вспомогательной характеристикой поля
в веществе является вектор электрического
смещения
,
который связан с вектором напряженности
электрического полясоотношением
.
С учетом этого соотношения полученную
формулу можно представить в виде:

Эти формулы справедливы для однородного
поля, заполняющего объем
.
Энергия распределена по объему
конденсатора равномерно. Следовательно,
в единице объема поля содержится энергия
(3.7)
Выражения (3.7) определяют плотность
энергии электрического поля.
Формулы (3.7) справедливы для любого
электрического поля. Если поле неоднородно,
то плотность энергии в некоторой точке
определяется по формулам (3.7) подстановкой
значений
(или
)
ив этой точке.
Зная плотность энергии в каждой точке,
можно найти энергию поля, заключенную
в любом объеме
.
Для этого нужно вычислить интеграл
(3.8)
Примеры решения задач
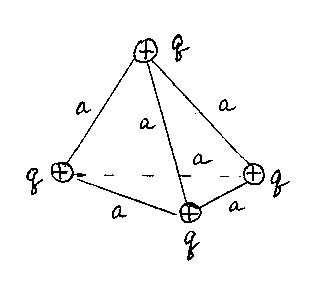
Задача 1Четыре одинаковых точечных
заряданаходятся
в вершинах тетраэдра с ребром.
Найти энергию взаимодействия зарядов
этой системы.
Решение:
-
способ. Энергия взаимодействия каждой
пары зарядов здесь одинакова и равна
.
Как видно из рисунка, всего таких
взаимодействующих пар шесть, поэтому
энергия взаимодействия всех точечных
зарядов данной системы
.
2. способ.
,
где потенциалв месте нахождения одного из зарядов,
равен.
Поэтому
.
Задача 2(С.3.114)Точечный заряд= 1 мкКл помещается в центре шарового
слоя из однородного и изотропного
диэлектрика с= 3. Внутренний радиус слоя
= 100 мм, внешний
= 200 мм. Найти энергию
,
заключенную в пределах диэлектрика.
Решение:
Напряженность поля в диэлектрике
.
Разобьем диэлектрик на шаровые слои
радиуса
и толщины
.
Объем слоя.
Плотность энергии в слое
Энергия, заключенная в слое
:
Проинтегрировав это выражение по
в пределах от
до
,
найдем энергию, заключенную в диэлектрике:
Дж.
Задача 3Найдем работу, которую надо
совершить против электрических сил,
чтобы удалить диэлектрическую пластинку
из плоского заряженного конденсатора.
Предполагается, что зарядконденсатора
остается постоянным. Емкость конденсатора
без диэлектрика равна.
Решение:
Работа против электростатических сил
в этой системе пойдет на приращение ее
электрической энергии:
,
где
– энергия поля между обкладками
конденсатора при наличии диэлектрика,– при отсутствии диэлектрика. Отсюда
.
Задача 4(С 3.111)Зарядраспределен равномерно по объему шара
радиусом.
Полагая=1, найти электрическую энергию шара
,
а также отношение энергии,
локализованной внутри шара, к энергиив окружающем пространстве.
Решение:
Прежде всего найдем с помощью теоремы
Гаусса поле внутри и вне шара:
(
);
(
).
Теперь вычислим электрическую энергию
шара:

Отсюда следует:
;
.
Тесты
1.
Емкость плоского конденсатора
пропорциональна:
1.
расстоянию между его пластинами. 2.
отношению площади его пластин к расстоянию
между ними. 3. произведению площади его
пластин на расстояние между ними. 4.
заряду пластин. 5. потенциалу пластин.
2.
Напряженность электрического поля
внутри проводника:
1.
определяется объемной плотностью заряда
в проводнике. 2. равняется нулю. 3.
определяется зарядом на поверхности
проводника. 4. определяется потенциалом
проводника. 5. зависит от напряженности
электрического поля в пространстве,
окружающем проводник.
3.
Три конденсатора одинаковой емкости
соединены параллельно. Результирующая
емкость получается
1.
равной емкости каждого из конденсаторов.
2. в три раза меньше емкости каждого из
конденсаторов. 3. в три раза больше
емкости каждого из конденсаторов.
4. Электроемкость проводника зависит
от:
1. формы и размеров, 2. площади
поверхности, 3. массы и рода вещества,
4. заряда и напряжения, 5. свойств
окружающей среды.
1.1., 2., 3. 2. 3., 4., 5. 3. 1., 2., 5.
4. 2., 3., 5.
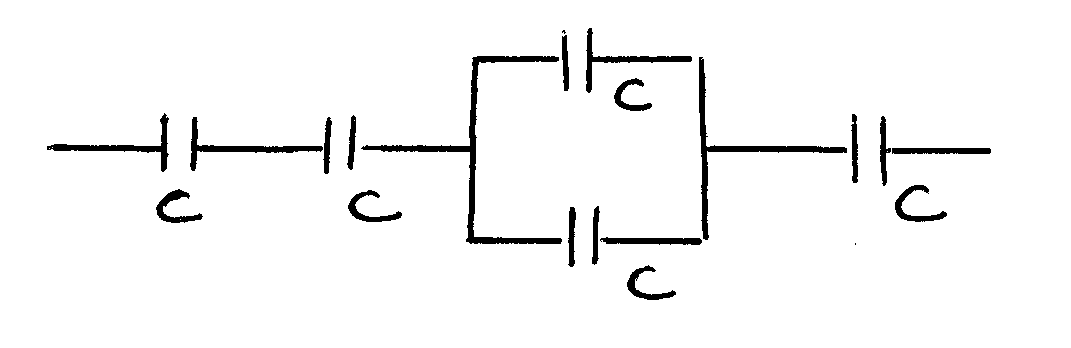
5. Емкость батареи состоящей из пяти
одинаковых конденсаторов емкостью 1
мкФ, изображенной на рисунке равна:
1. 3,5 мкФ 2. 0,286 мкФ 3. 5 мкФ
4. 0,2 мкФ
6. Взаимной электроемкостью тел называют:
-
2.
3.
.
7. Плоский воздушный конденсатор
подключили к источнику тока, а затем не
отключая от источника, погрузили в
керосин с диэлектрической проницаемостью,
равной 2. Найти отношение заряда,
первоначально находившегося на обкладках
конденсатора, к конечному заряду.
1. 0,5 2. 1 3. 2 4. 4.
8. Разность
потенциалов между обкладками конденсаторов
емкостьюмкФ
изменилась на 175 В. Определите изменение
заряда конденсатора.
1. Кл
2.Кл
3. Кл
4.0.
9. Указать неправильнуюформулу для
электроемкости плоского конденсатора
.
1.
2.
3.
4.
;
10. Конденсатор имеет емкость
пФ.
Какой заряд находится на каждой из его
обкладок, если разность потенциалов
между нимиВ?
1. Кл 2.
Кл
3. Кл
4.эВ.
11. Потенциал φ, заряд qи
емкость
уединенного проводника связаны
соотношением:
1.2.
3.
4.
.
12. Изменится ли
заряд конденсатора, подключенного к
источнику напряжения, если раздвинуть
его пластины?
1. заряд конденсатора
увеличится 2. заряд конденсатора не
изменится 3. заряд конденсатора
уменьшится 4. заряд конденсатора
не зависит от его емкости 5. заряд
конденсатора не зависит от
расстояния между пластинами.
13. Вектор напряженности электростатического
поля:
1. ортогонален эквипотенциальной
поверхности 2. направлен по касательной
к эквипотенциальной поверхности 3.
направлен под углом π./4 к эквипотенциальной
поверхности, 4. может иметь любое
направление.
14. Внутри полой проводящей сферы помещен
электрический заряд. Электрическое
поле будет существовать:
1. и вне и внутри сферы 2. только
вне сферы 3. только внутри сферы
4. ни там, ни там.
15. Электроемкость С уединенной сферы
радиуcаRв
среде равна:
1.
2.
3.
4.
16. Между обкладками конденсатора, на
концах которого поддерживается постоянная
разность потенциалов, поместили слой
диэлектрика с диэлектрической
проницаемостью ε. Напряженность поля
в диэлектрике по отношению к напряженности
поля вне его:
1.увеличилась в ε раз 2. уменьшилась
в ε раз 3.обратилась в нуль 4. не
изменилась.
17. Для проводника,
помещенного в электростатическое поле,
характерно:
1. отсутствие поля
внутри проводника 2. усиление поля
внутри проводника 3. ослабление поля
вблизи острия проводника 4. силовые
линии поля направлены по касательной
к поверхности проводника 5. потенциал
проводника максимален на его поверхности.
18. Изменится ли энергия заряженного
воздушного конденсатора, если, при
отключенном источнике, раздвинуть его
пластины?
1. Изменится за счет энергии внешних
сил, совершающих работу по раздвижению
пластин. 2.Не изменится, так как заряд
на конденсаторе не изменяется
3.Нельзя дать однозначный ответ, так как
не известны численные значения исходных
данных 4.Энергия уменьшится.
19. Потенциальная энергия взаимодействия
пластин заряженного плоского конденсатора
(указать неверныйответ):
1.
2.
3.
4.
,
где
и
– заряд и потенциал первой пластины,
и
– заряд и потенциал второй пластины;
5. все перечисленные варианты правильные.
20. Как изменится
энергия заряженного конденсатора, не
отключенного от источника, если уменьшить
расстояние между обкладками в два раза?
.
1. уменьшится в 2
раза 2. увеличится в 2 раза 3. не
изменится 4. увеличится в 4 раза
5. уменьшится в 4 раза.
21. Плотность энергии wэлектростатического поля с напряженностьюEв среде с диэлектрической
проницаемостью ε равна:
1.
2.
3.
4.
.
22. Какую из формул нельзя использовать
для расчета энергии заряженного
конденсатора?
1.
2.
3.
4.
15
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
По какой формуле вычисляется изменение энергии при параллельном соединении конденсаторов?
DanilaDNL
Знаток
(412),
закрыт
6 лет назад
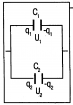
Задача. Заряды двух конденсаторов ёмкостью C1 и C2 соответственно равны q1 и q2. Найти изменение энергии при параллельном соединении этих конденсаторов.
Дополнен 6 лет назад
Так, формулу вычисления энергии нашел E = q^2/(2C). Но что значит “Найти изменение энергии”?
Лучший ответ
marat aminov
Просветленный
(32951)
6 лет назад
энергия до соединения в батарею равна E1=q1^2/2C1+q2^2/2C2, после соединения она равна E2=(q1+q2)^2/2(C1+C2). изменение энергии равно dE=E1-E2. ответ dE=(q1C2-q2C1)^2/2C1C2(C1+C2).
Остальные ответы
Владимир Замятин
Оракул
(64975)
6 лет назад
С использованием формулы энергии конденсатора E = q^2/(2C).
Krab Bark
Искусственный Интеллект
(263227)
6 лет назад
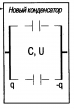
Найти разницу между энергией в конденсаторах до соединения и после соединения, когда заряд объединенного конденсатора стал q=q1+q2, а емкость C=C1+C2.
|
Можно ли так рассчитать энергию системы из двух конденсаторов?ilootuma 7 лет назад
По формуле W=q^2/2C,где q-заряд на пластинах,а C-общая электроёмкость. Грустный Роджер 7 лет назад Можно. Собственно, именно так и НУЖНО. Только надо отчётливо понимать, что q – это заряд на ёмкости С. Если расчёт ведётся для общей ёмкости системы, то и заряд надо брать для неё же.
в избранное
ссылка
отблагодарить ilootuma Понятно.К сожалению,я для системы брала заряд 1-ого конденсатора,что видимо не правильно.Тогда уж я не знаю как решать эту задачу.Если интересно,то эта задача из ДВИ в МГУ 2015.
Грустный Роджер Схема соединения какая?
ilootuma Два конденсатора соединяются.Потом к ним присоединяется,как я поняла,последовательно проводник с большим сопротивлением.И надо посчитать,какая энергия выделится на проводнике.
ЛенивыйЖирныйКот 7 лет назад Вся фишка в том, что этот заряд Q сложно посчитать в реальности. Применяют видоизменённую формулу Eк = CU^2/2.
в избранное
ссылка
отблагодарить ilootuma А если до присоединения,на одном конденсаторе был заряд Q ,а на втором не было заряда,и когда их соединят,то можно считать что заряд системы равен этому Q,и тогда уже рассчитать энергию с этим Q.
Грустный Роджер Это та же самая формула, если учесть, что q = CU.
Знаете ответ? |
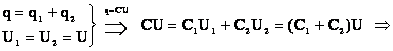
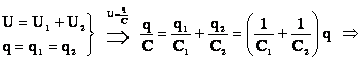
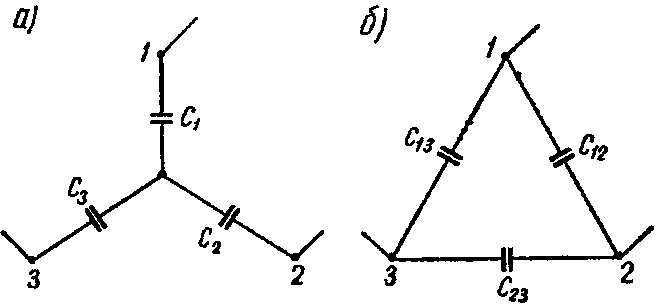
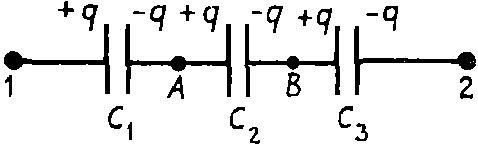
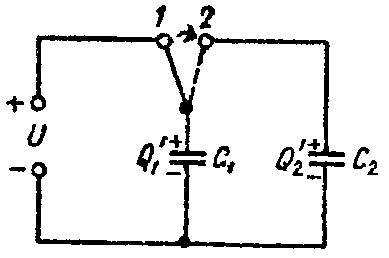


 .
.