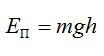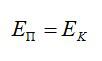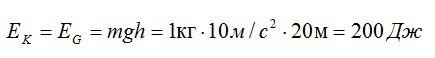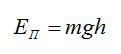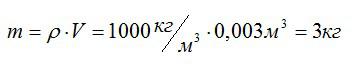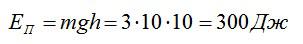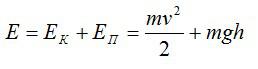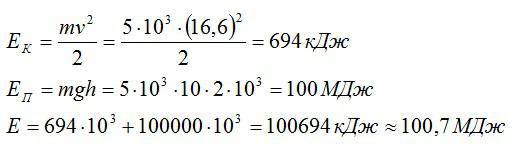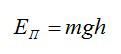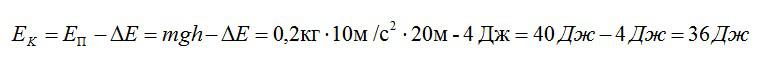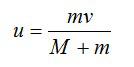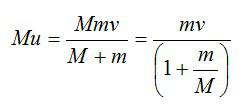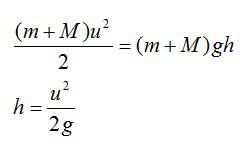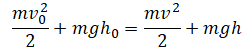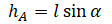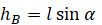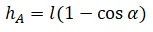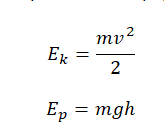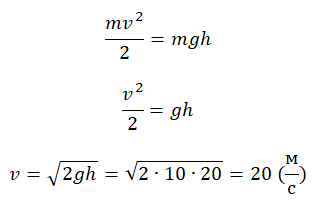А почему-бы и нет? У нас уже были задачи на свободное падение, законы Ньютона, силу трения и проч. и проч. Сегодня решаем задачи на кинетическую и потенциальную энергию.
А вообще, помните, что мы занимаемся далеко не только решением задач. Наш телеграм – это полезная информация для студентов всех специальностей, новости, лайфхаки, акции и скидки.
Задачи на кинетическую и потенциальную энергию
Приведем примеры задач на нахождение кинетической и потенциальной энергии с решением. Прежде чем приступать к практике, почитайте теорию по теме, повторите общую памятку по решению задач по физике и на всякий случай держите под рукой полезные формулы.
Задача №1 на кинетическую энергию
Условие
Максимальная высота, на которую поднимается тело массой 1 кг, подброшенное вертикально вверх, составляет 20 м. Найдите, чему была равна кинетическая энергия сразу же после броска.
Решение
Потенциальная энергия тела над поверхностью Земли составляет:
Здесь m – масса тела, g – ускорение свободного падения, h – высота. Согласно закону сохранения энергии, потенциальная энергия тела в наивысшей точке должна равняться кинетической энергии тела в начальный момент, то есть:
Принимая ускорение свободного падения равным 10 м/с2, находим кинетическую энергию тела сразу же после броска:
Ответ: 200 Дж.
Задача №2 на потенциальную энергию
Условие
Чему равна потенциальная энергия трех кубических дециметров воды на высоте 10 м?
Решение
По определению, потенциальная энергия равна в поле силы тяжести равна:
Масса трех кубических дециметров воды (трех литров) легко находится из формулы для плотности воды:
Осталось вычислить потенциальную энергию:
Ответ: 300 Дж.
При решении задач не забывайте переводить все размерности величин в систему СИ.
Задача №3 на полную механическую энергию
Условие
Какова полная механическая энергия дирижабля массой 5 тонн, если он летит на высоте 2 км со скоростью 60 км/ч?
Решение
Полная механическая энергия состоит из кинетической и потенциальной энергий:
Вычислим:
Ответ: 100,7 МДж.
Задача №4 на кинетическую и потенциальную энергию
Условие
Шарик массой 200 г падает с высоты 20 м с начальной скоростью, равной нулю. Какова его кинетическая энергия в момент перед ударом о землю, если потеря энергии за счет сопротивления воздуха составила 4 Дж? (Ответ дайте в джоулях.) Ускорение свободного падения принять равным 10 м/с2.
Решение
Перед началом падения потенциальная энергия шарика составляет:
По закону сохранения энергии, эта энергия должна перейти в кинетическую энергию Ек за вычетом потери за счет сопротивления воздуха дельта Е. Таким образом, можем найти кинетическую энергию:
Ответ: 36 Дж.
Задача №5 кинетическую и потенциальную энергию
Условие
Шарик висит на нити. В нем застревает пуля, летящая горизонтально, в результате чего нить отклоняется на некоторый угол. Как изменятся при увеличении массы шарика следующие величины: импульс, полученный шариком в результате попадания в него пули; скорость, которая будет у шарика тотчас после удара; угол отклонения нити?
Решение
Согласно закону сохранения импульса, скорость шарика с застрявшей в нем пулей равна
Здесь M и m – массы шарика и пули соответственно, v – скорость пули перед ударом. Таким образом, при увеличении массы шарика его скорость после удара уменьшится.
Найдем импульс, переданный шарику при попадании пули:
Следовательно, с увеличением массы шарика переданный ему импульс увеличивается.
Согласно закону сохранения энергии, кинетическая энергия пули перейдет в потенциальную энергию шарика с пулей:
Таким образом, при увеличении массы шарика угол отклонения нити уменьшится, поскольку уменьшится скорость u.
Ответ: см решение выше.
Вопросы на потенциальную и кинетическую энергию
Вопрос 1. Что такое энергия? Что такое механическая энергия?
Ответ. Для энергии существует множество определений. В наиболее общем смысле:
Энергия – мера способности тела совершать работу.
Механическая энергия – это энергия, связанная с движением тела или его положением в пространстве. Механическая энергия в механике описывается суммой кинетической и потенциальной энергии.
Вопрос 2. Сформулируйте закон сохранения энергии
Ответ. Закон сохранения энергии является фундаментальным физическим принципом. Для каждого вида энергии он имеет свою формулировку. Для механической энергии:
Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остается неизменной.
Вопрос 3. Какие силы называются консервативными?
Ответ. Консервативные, или потенциальные силы – это силы, работа которых не зависит от формы траектории. В качестве примера такой силы можно привести силу тяжести.
Вопрос 4. Какую энергию называют кинетической?
Ответ. Кинетическая энергия является энергией движения. Ею обладают только движущиеся тела, она зависит от массы тела и его скорости.
Вопрос 5. Какую энергию называют потенциальной?
Ответ. Потенциальная энергия является энергией взаимодействия в поле консервативных сил. Она зависит от положения тела и выбора системы отсчета. Например, потенциальная энергия тела в поле силы тяжести зависит от массы тела, ускорения свободного падения и высоты над нулевым уровнем.
Не знаете, как решать задачи на кинетическую или потенциальную энергию? Проблемы с выполнением любых других студенческих работ? Обращайтесь в профессиональный сервис для учащихся за помощью и консультациями.
- Онлайн Калькуляторы
- Примеры решений
- Найти репетитора
- Рефераты
- Заказать решение
- Справочник
- ГДЗ онлайн
- Все о ЕГЭ
- О проекте

- Главная
- Онлайн калькуляторы
- Калькулятор расчета потенциальной энергии, массы или высоты
Посчитайте потенциальную энергию, высоту или массу тела
Потенциальная энергия тела – это скалярная физическая величина, равная работе, совершаемой потенциальной силой при перемещении тела из одной точки в другую, потенциальная энергия которой принята за ноль.
Формула потенциальной энергии
$$E_{p}=m g h$$
где m – масса тела, g – ускорение свободного падения, равное 9.8 м/с2, h – высота тела над произвольно выбранным нулевым уровнем.
Решили сегодня: раз, всего раз
Другие онлайн калькуляторы
- Узнать площадь боковой поверхности конуса
- Калькулятор для вычисления кинетической энергии тела
- Рассчитать закон Ома для участка цепи
- Рассчитать силу притяжения
Вы поняли, как решать? Нет?
- Правила
- Комментарии
- Ответы на вопросы
Рассчитайте цену решения ваших задач


Калькулятор
стоимости
Решение контрольной
от 300 рублей
*
* Точная стоимость будет определена после загрузки задания для исполнителя
+Загрузить файл
Файлы doc, pdf, xls, jpg, png не более 5 МБ.

Привет.
Я Настя из ИвГУ (это город Иваново).
«Сегодня от своего лица хочу поблагодарить этот сайт за помощь мне с учебой. Здесь я пользовалась не только материалами, но и нашла преподавателей которые решали мне задачи.
Если тебе нужно что-то сделать в универе, я сама рекомендую. А также пользуйся моей ссылкой и получай 300 руб. на счёт при регистрации.»
Пунктуация и орфография автора сохранены
Получить 300 руб. от Насти
Webmath — преподаватель со стажем более 5 лет выполнит учебную работу за вас
Договор
Строго соблюдаем условия договора от заказа до защиты
Наши авторы
10 000+ преподавателей и научных сотрудников
Гарантии
Точное соответствие ТЗ с бесплатными доработками
АкцияСкидка 25% на вашу работу + речь в подарок. Дарим вам 100₽ на первый заказ!
Дано:
Решение:
На высоте h потенциальная энергия тела равна mgh, а кинетическая энергия равна нулю. Полная энергия равна
На высоте h1 потенциальная энергия
равна mgh1, а кинетическая энергия равна Еполн –
Отсюда
В момент падения на землю кинетическая энергия
В механике все силы делятся на две группы: консервативные и неконсервативные.
Консервативные силы
Консервативными, или потенциальными, называются такие силы, работа которых не зависит от траектории, а определяется только начальным и конечным положениями тела. Работа таких сил по перемещению тела по замкнутой траектории всегда равна нулю. Примеры потенциальных (консервативных) сил:
- сила тяжести
- сила упругости
- гравитационная сила
Неконсервативные силы
Неконсервативными называются такие силы, работа которых зависит от траектории. Сама сила в этом случае зависит от модуля и направления вектора скорости. Работа таких сил может приводить к выделению тепла — часть механической энергии при этом превращается в тепловую. Примеры неконсервативных сил:
- сила упругости
- сила сопротивления среды
Полная механическая энергия — это сумма потенциальной и кинетической энергии тела в определенный момент времени:
E = Ek + Ep
Закон сохранения механической энергии
В замкнутой системе, в которой действуют консервативные силы, механическая энергия сохраняется.
E = const
Определение
Замкнутая система — это система, в которой тела, входящие в нее, взаимодействуют только друг с другом, а влиянием внешних сил можно пренебречь.
Согласно закону сохранения энергии, сумма потенциальной и кинетической энергии системы до взаимодействия тел равна сумме потенциальной и кинетической энергий системы после их взаимодействия:
Ek0 + Ep0 = Ek + Ep
Закон сохранения механической энергии для движения в поле тяжести Земли
Примеры определения полной механической энергии в начальном и конечном положении
| Пример | Полная механическая энергия в начальной точке (А) | Полная механическая энергия в конечной точке (В) |
|
Спуск по наклонной плоскости из состояния покоя |
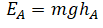
Высоту, на которой изначально находилось тело, можно рассчитать по формуле: |
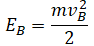 |
|
Подъем по наклонной плоскости |
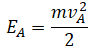 |
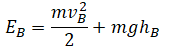
Высоту, на которую поднялось тело, можно рассчитать по формуле: |
|
Груз на нити |
Высоту, на которой изначально находилось тело, можно рассчитать по формуле: |
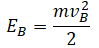 |
|
Вертикальный выстрел из пружинного пистолета |
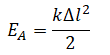 |
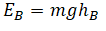 |
Пример №1. Камень брошен вертикально вверх. В момент броска он имел кинетическую энергию, равную 30 Дж. Какую потенциальную энергию относительно поверхности земли будет иметь камень в верхней точке траектории полета? Сопротивлением воздуха пренебречь.
Так как это условно замкнутая система (сопротивлением воздуха мы пренебрегаем), мы можем применить закон сохранения энергии:
Ek0 + Ep0 = Ek + Ep
Учтем, что в момент броска камень находился на поверхности земли. Поэтому он обладал максимальной кинетической энергией и нулевой потенциальной. Но в верхней точке траектории его скорость стала равна нулю. Поэтому его кинетическая энергия тоже стала равна нулю. Зато потенциальная энергия в этой точке возросла до максимума. Поэтому:
Ek0 + 0 = 0 + Ep
Ek0 = Ep
Следовательно, потенциальная энергия в верхней точки траектории полета равна 30 Дж.
Задание EF19083
Шарик массой 100 г падает с высоты 100 м с начальной скоростью, равной нулю. Чему равна его кинетическая энергия в момент перед падением на землю, если потеря энергии за счёт сопротивления воздуха составила 20 Дж?
Алгоритм решения
- Записать исходные данные и перевести единицы измерения величин в СИ.
- Записать закон сохранения механической энергии.
- Записать закон сохранения применительно к задаче.
- Выполнить общее решение.
- Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
- Масса шарика: m = 100 г.
- Высота, с которой начал падать шарик: h = 100 м.
- Энергия, потерянная за счет сопротивления воздуха: Q = 20 Дж.
100 г = 0,1 кг
Закон сохранения механической энергии для замкнутой системы:
Ek0 + Ep0 = Ek + Ep = const
Согласно условию задачи, система не является замкнутой, так как на шарик действует сила сопротивления воздуха. Поэтому закон сохранения энергии примет вид:
Ek0 + Ep0 = Ek + Ep + Q
Шарик начал падать из состояния покоя, поэтому начальная кинетическая энергия равна нулю. В момент приземления кинетическая энергия максимальная, а потенциальная равна нулю. Поэтому:
Ep0 = Ek + Q
Потенциальная энергия определяется формулой:
Ep0 = mgh
Следовательно:
mgh = Ek + Q
Отсюда кинетическая энергия шарика в момент перед падением на землю равна:
Ek = mgh – Q = 0,1∙10∙100 – 20 = 80 (Дж)
Ответ: 80
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17731
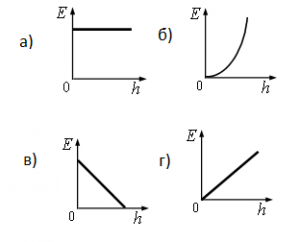
Алгоритм решения
- Записать закон сохранения энергии.
- Установить зависимость полной механической энергии от высоты.
- Найти тип графику, соответствующий выявленной зависимости.
Решение
Запишем закон сохранения механической энергии:
E = const
Полная механическая энергия тела равна:
E = Ek + Ep
Исходя из закона, сумма потенциальной и кинетической энергии в начальный момент движения тела равно сумме потенциальной и кинетической энергии в конечный момент времени:
Ek0 + Ep0 = Ek + Ep
Так как полная механическая энергия не меняется с течением времени, ее графиком должна быть прямая, параллельная оси времени. Поэтому верный ответ — а.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22589
Тело, брошенное вертикально вверх от поверхности Земли, достигло максимальной высоты 20 м. С какой начальной скоростью тело было брошено вверх? Сопротивлением воздуха пренебречь.
Ответ:
а) 4,5 м/с
б) 10 м/с
в) 20 м/с
г) 40 м/с
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать закон сохранения механической энергии.
3.Записать закон сохранения применительно к задаче.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Из условия задачи известна только высота h = 20 м.
Закон сохранения механической энергии для замкнутой системы:
Ek0 + Ep0 = Ek + Ep = const
Тело изначально находилось на поверхности Земли, поэтому его начальная потенциальная энергия равна нулю. Но кинетическая энергия в момент броска была максимальной. В верхней точке траектории скорость тела нулевая, поэтому кинетическая тоже равна нулю. Но потенциальная энергия в этот момент времени максимальна.
Поэтому:
Ek0 = Ep
Кинетическая и потенциальная энергии определяются формулами:
Приравняем их:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17696
Если многократно сжимать пружину, то она нагревается. Это можно объяснить тем, что
Ответ:
а) потенциальная энергия пружины переходит в кинетическую
б) кинетическая энергия пружины переходит в потенциальную
в) часть работы внешних сил переходит во внутреннюю энергию пружины
г) пружина нагревается в процессе ударов молекул воздуха о частицы вещества пружины
Алгоритм решения
- Сформулировать закон сохранения механической энергии.
- Установить причины нагревания пружины.
Решение
Закон сохранения механической энергии формулируется так: «Полная механическая энергия замкнутой системы постоянна».
Замкнутая система — эта система, составные элементы которой действуют только друг с другом, и внешние силы на систему не действуют. Но если пружину сжимать и разжимать много раз, то пружина не будет являться замкнутой системой. Поэтому закон сохранения энергии в ней не сохраняется. Но ни потенциальная, ни кинетическая энергии, ни их превращение друг в друга не вызывает нагревания. К этому может привести только воздействие внешней силы, часть которой переходит во внутреннюю.
Верный ответ – в.
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18127
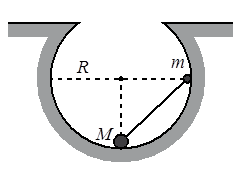
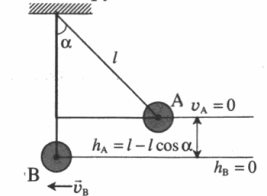
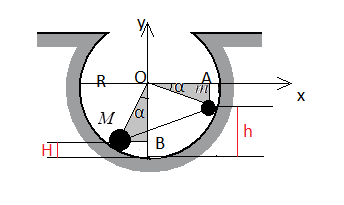
В начальный момент шарики удерживаются в положении, изображённом на рисунке. Когда их отпустили без толчка, шарики стали скользить по поверхности выемки. Максимальная высота подъёма шарика массой М относительно нижней точки выемки оказалась равной 12 см. Каков радиус выемки R?
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж конечного положения шариков. Обозначить их высоты, выбрать нулевой уровень отсчета потенциальной энергии. Выбрать систему координат.
3.Записать закон сохранения энергии.
4.Выполнить общее решение задачи.
5.Подставить известные данные и выполнить вычисление искомой величины.
Решение
Запишем исходные величины:
• Масса первого шарика: m = 30 г.
• Масса второго шарика: M = 60 г.
• Максимальная высота подъема шарика М: H = 12 см.
Переведем единицы измерения величин в СИ:
30 г = 0,03 кг
60 г = 0,06 кг
12 см = 0,12 м
Выполним чертеж:
Нулевой уровень — нижняя точка выемки.
Запишем закон сохранения энергии:
Ek0 + Ep0 = Ek + Ep = const
В начальном положении кинетическая энергия обоих шариков равна 0. Потенциальная энергия шарика М тоже равна нулю, так как он находится на нулевом уровне. Потенциальная энергия шарика m равна:
Ep0m = mgR
Кинетическая энергия шариков после установления равновесия тоже будет равна нулю. Но b[ потенциальная энергия будет отличной от нуля:
Epm = mgh
EpM = MgH
Поэтому закон сохранения энергии применительно к задаче примет вид:
mgR = mgh + MgH
Преобразуем выражение и получим:
mgR−mgh=MgH
R−h=MgHmg=MHm
При движении гантели по поверхности выемки высоты подъема большого и малого шаров связаны. Рассмотрим прямоугольные треугольники OmA и OMB. Для них справедливы следующие равенства:
MB = mA = R – h
OA = OB = R – H
OM = Om = R
Это дает нам право воспользоваться теоремой Пифагора:
(R−h)2=R2−OA2=R2−(R−H)2
Следовательно:
(R−h)2=R2−(R2−2RH+H2)=2RH−H2
Подставим в это выражение правую часть ранее полученного выражения:
R−h=MHm
(MHm)2=2RH−H2
Теперь можем выразить и вычислить радиус:
2RH=(MHm)2+H2
R=(MHm)2+H22H
R=(Mm)2H2+H2=(0,060,03)20,122+0,122=0,3 (м)
Ответ: 0,3
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18087
Шайба массой m, скользящая по гладкой горизонтальной поверхности, налетает на лежащую неподвижно на той же поверхности шайбу массой 3m такого же размера. После частично неупругого удара первая шайба остановилась. Какова была кинетическая энергия первой шайбы до удара, если при ударе выделилось количество теплоты Q?
Ответ:
а) 3Q/2
б) 2Q
в) 9Q/2
г) 8Q
Алгоритм решения
1.Записать исходные данные.
2.Записать закон сохранения импульса.
3.Записать закон сохранения энергии с учетом выделения тепла при ударе.
4.Выполнить решение в общем виде.
5.Выразить искомую величину.
Решение
Запишем исходные данные:
• Масса второй шайбы: 3m.
• Количество выделенной теплоты при ударе: Q.
До удара двигалась только первая шайба, вторая покоилась, поэтому импульс второй шайбы равен нулю. После удара первая шайба остановилась, поэтому ее импульс стал равен нулю. Но начала двигаться вторая шайба. Поэтому закон сохранения импульса при ударе примет вид:
mv=3mV
Отсюда скорость второй шайбы равна v/3.
Запишем закон сохранения энергии с учетом того, что при ударе выделилось тепло:
Ek1=Ek2+Q
Кинетическую энергию второй шайбы можно выразить как доля от кинетической энергии первой шайбы, а также как произведение половинной массы на половинный квадрат:
Ek2=Ek1x=3mV22=3mv22·9
x — доля кинетической энергии второй шайбы от кинетической энергии первой шайбы.
Кинетическая энергия первой шайбы равна:
Ek1=mv22
Теперь можем выразить x:
3mv22·9=mv22x
x=13
Следовательно, на кинетическую энергию второй шайбы ушла 1/3 часть кинетической энергии первой шайбы, а в виде тепла выделилось 2/3 этой энергии. Отсюда:
Q=23Ek1
Ek1=32Q
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18122
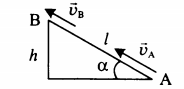
Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?
Ответ:
а) 27 г
б) 64 г
в) 81 г
г) 100 г
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.
3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса пластилиновой пули: m = 9 г.
• Скорость пластилиновой пули: v = 20 м/с.
• Максимальный угол отклонения нити: α = 60°.
Переведем единицы измерения величин в СИ:
Сделаем чертеж:
Нулевой уровень — точка А.
После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:
mv=(m+M)V
После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.
Закон сохранения энергии для точки В:
(m+M)V22=(m+M)gh
V22=gh
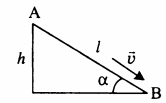
Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:
V=√2glcosα
Подставим это выражение в закон сохранения импульса для точки А и получим:
Выразим массу груза:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 6.5k
2010-03-24 22:30
Рассмотрим, как изменяется кинетическая и потенциальная энергия тела, брошенного вверх.
При подъеме тела скорость его убывает по закону
, где
— начальная скорость,
— время. Кинетическая энергия при этом также убывает, изменяясь по закону
.
Так как начальная кинетическая энергия тела равна
, то к моменту
убыль кинетической энергии
. (101.1)
С другой стороны, высота тела в момент
есть
.
Следовательно, приращение потенциальной энергии за время
равно
. (101.2)
Сравнивая это выражение с (101.1), видим, что приращение потенциальной энергии за время
равно убыли кинетической энергии за то же время. Таким образом, при движении тела вверх его кинетическая энергия постепенно превращается в потенциальную. Когда движение вверх прекратилось (наивысшая точка подъема), вся кинетическая энергия полностью превратилась в потенциальную. При движении тела вниз происходит обратный процесс: потенциальная энергия тела превращается в кинетическую.
При этих превращениях полная механическая энергия (т. е. сумма кинетической и потенциальной энергий) остается неизменной, так как при подъеме убыль кинетической энергии полностью покрывается приращением потенциальной (а при падении — наоборот). Если потенциальную энергию тела у поверхности земли считать равной нулю (§ 97), то сумма кинетической и потенциальной энергий тела на любой высоте во время подъема или падения будет равна
, (101.3)
т. е. остается равной начальной кинетической энергии тела. Этот вывод представляет собой частный случай одного из важнейших законов природы — закона сохранения энергии.
101.1.
С башни высоты 20 м брошен камень со скоростью 15 м/с. Найдите скорость камня при падении его на землю и сравните ее со скоростью падения с той же высоты, но без начальной скорости. Сопротивлением воздуха пренебречь.
101.2.
Считая известными формулу (101.2) и зависимость потенциальной энергии от высоты, выведите закон движения тела, брошенного по вертикали.